Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
- Мы отвечаем на сообщения в течение 2-3 дней. К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
Подробнее о том, как задавать вопросы по уроку
Операции над множествами: объединение, пересечение, дополнение и различие
17 авг. 2022 г.
читать 2 мин
Набор — это набор предметов.
Мы обозначаем набор с помощью заглавной буквы, а элементы в наборе определяем с помощью фигурных скобок. Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:
А = {1, 2, 3}
В этом руководстве объясняются наиболее распространенные операции с множествами, используемые в теории вероятностей и статистике.
Союз
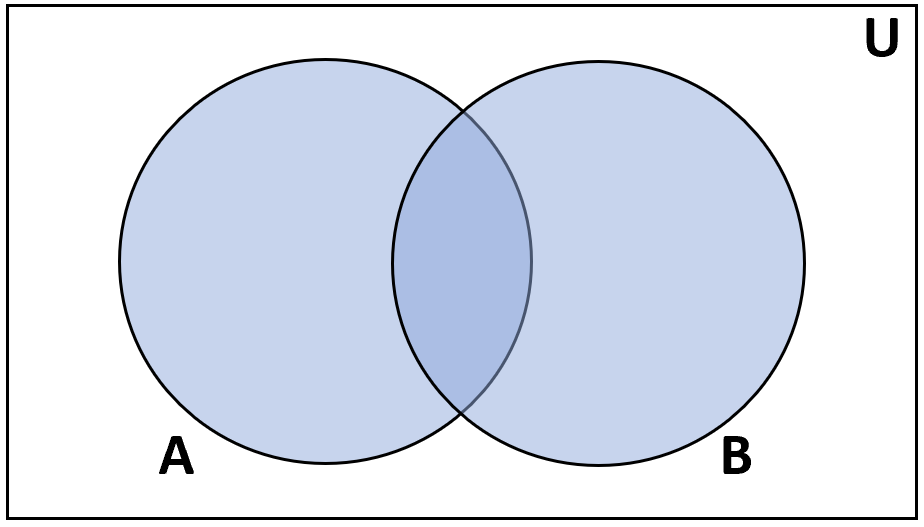
Определение: Объединение множеств A и B — это множество элементов, которые находятся либо в A, либо в B.
Обозначение: А ∪ В
Примеры:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
Перекресток
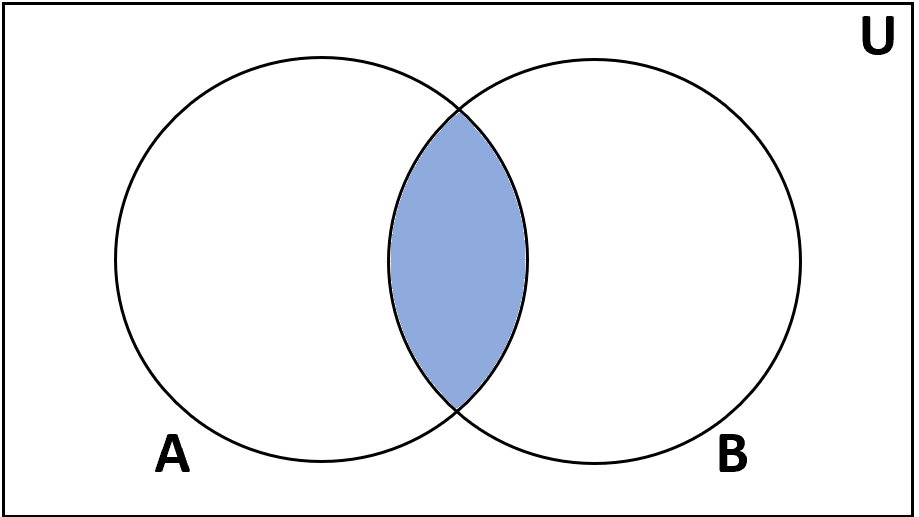
Определение: Пересечение множеств A и B — это множество элементов, которые находятся как в A, так и в B.
Обозначение: А ∩ В
Примеры:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
Дополнение
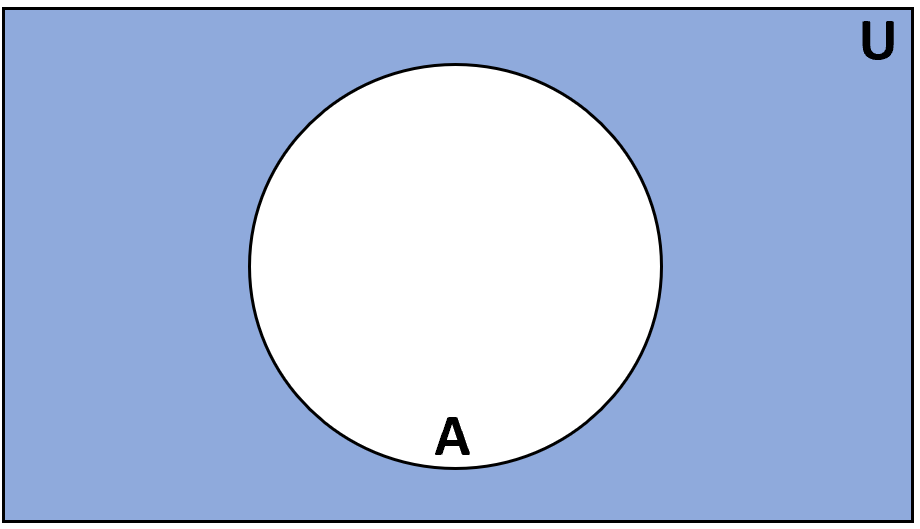
Определение: Дополнением множества A называется множество элементов, которые входят в универсальное множество U, но не входят в A.
Обозначение: A’ или A c
Примеры:
- Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
- Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}
Разница
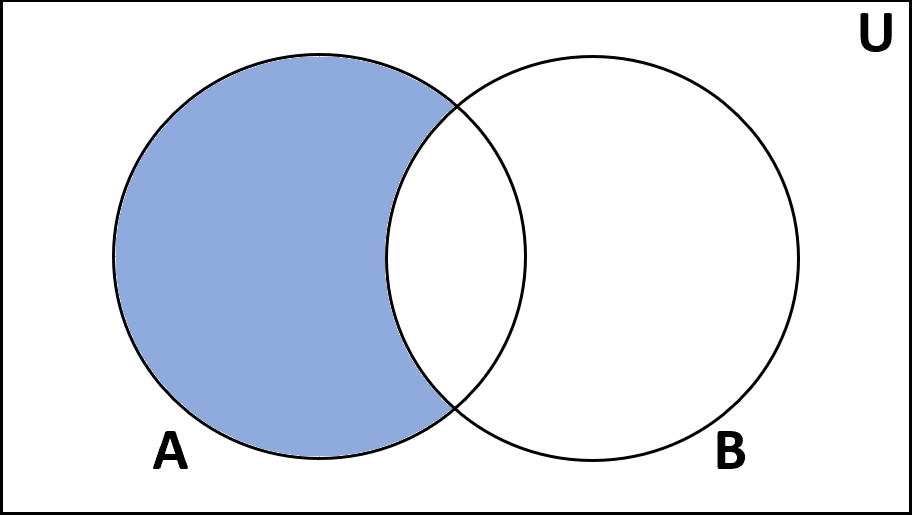
Определение: Разность множеств А и В — это множество элементов, которые есть в А, но отсутствуют в В.
Обозначение: А – Б
Примеры:
- {1, 2, 3} – {2, 3, 4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
Симметричная разница
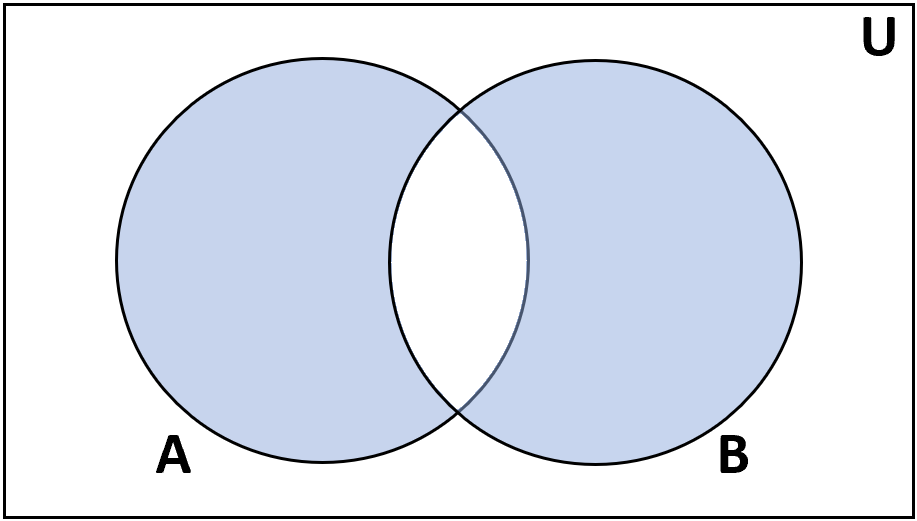
Определение: Симметричная разность множеств A и B — это множество элементов, которые находятся либо в A, либо в B, но не в обоих.
Обозначение: А Δ В
Примеры:
- {1, 2, 3} ∆ {2, 3, 4} = {1, 4}
- {1, 2} ∆ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
Декартово произведение
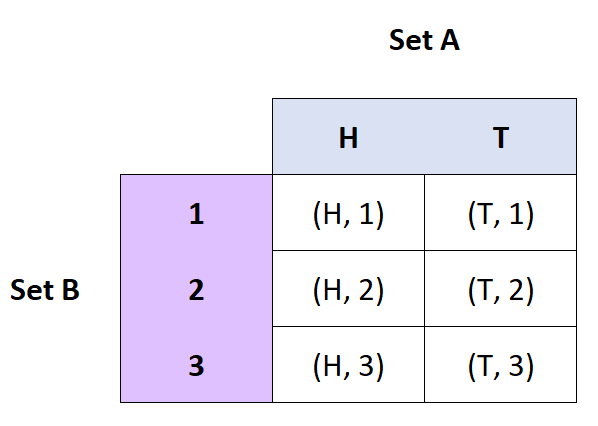
Определение: Декартово произведение множеств A и B — это множество упорядоченных пар из A и B.
Обозначение: А х В
Примеры:
- Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
- Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Н, 2), (Н, 3)}
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.

Пусть U — столь обширное множество, что все рассматриваемые множества окажутся его подмножествами.
U — универсальное множество (иначе оно называется основное множество). Универсальным множеством для элементарной арифметики является, например, множество Z — множество всех целых чисел; для аналитической геометрии универсальное множество есть R — множество всех действительных чисел (числовая прямая), а также R² — множество упорядоченных пар (числовая плоскость).
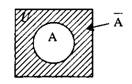 Дополнением множества А (обозначение Ā или сА) называется множество элементов универсального множества U, не принадлежащих множеству А.
Дополнением множества А (обозначение Ā или сА) называется множество элементов универсального множества U, не принадлежащих множеству А.
Ā={x|xͼU, xɇA}. (1)
Если U изобразить в виде прямоугольника, то множество заштриховано на рис.
Основные свойства операции дополнения

Свойства 6) и 7) называют правилами де Моргана.
Операция симметрической разности
Симметрической разностью (обозначение АΔВ) множеств А и В называется множество элементов, которые принадлежат только множеству А или только множеству В.
АΔВ={x| xͼA и xɇB} или АΔВ={x| xͼB и xɇA} (2)
Иначе можно записать:
АΔВ=(A/B)U(b/A) (2а)
На рис. 2 симметрическая разность АΔВ заштрихована.
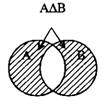
Рис. 2
Во многих приложениях
теории множеств рассматриваются только
такие множества, которые содержатся в
некотором фиксированном множестве.
(Например, киты в классе млекопитающих,
множество прямоугольных треугольников
в классе треугольников, в геометрии —
только множество точек данного
пространства, в арифметике — множество
чисел).
В настоящем
параграфе буквами А,
В,
С… будем
обозначать множества, содержащиеся в
некотором фиксированном множестве,
которое будем называть пространством
или универсумом
и обозначать символом 1.
Так как
![]() для каждогоА,
для каждогоА,
то
![]() (1)
(1)
Множество 1–А
называется
дополнением
множества А
и обозначается символом
![]() или –А.
или –А.
![]() .
.
Очевидно, что ![]() (2)
(2)
Так как ( ),
),
то используя формулу (10) §4, получаем
закон двойного дополнения:
![]() (3)
(3)
Полагая в законах
де Моргана (§4, (8)) А=1
и заменяя В
и С
соответственно на А
и В,
получаем
 (4)
(4)
То есть дополнение
произведения двух множеств равно сумме
их дополнений, а дополнение суммы двух
множеств равно произведению их дополнений.
Следует отметить,
что формулы, которые мы получаем, введя
понятие дополнения, аналогичны законам
алгебры высказываний, приведенным в
§1. Действительно, достаточно в
высказываниях (1) — (4) настоящего параграфа
заменить знак равенства (=) знаком
эквивалентности (![]() )
)
и интерпретировать буквы как переменные
высказывания, а символы![]() как дизъюнкцию, конъюнкцию, ложное
как дизъюнкцию, конъюнкцию, ложное
высказывание и истинное высказывание
(![]() ),
),
и мы получим законы алгебры высказываний.
И обратно, при соответствующей замене
символов в законах алгебры высказываний
получаются теоремы алгебры множеств.
Учитывая этот факт, отметим, что вычисления
для множеств, являющихся подмножествами
данного фиксированного множества 1,
легчи всего проводить, если при этих
вычислениях применяются только операции![]() .
.
Вычитание (), можно
определить при помощи операции дополнения
(–) и одной из операций
![]() или
или![]() .
.
В самом деле,

Отношение включения
можно свести к отношению равенства:
![]() (5)
(5)
В самом деле,
умножая обе части выражения
![]() на –В,
на –В,
получаем
![]() ,
,
откуда следует, что![]() ,
,
поскольку![]() .
.
Обратно, пусть
![]() .
.
Тогда:
![]() .
.
Так как
![]() ,
,
то из (5) следует![]() ,
,
а поскольку изX=0
и Y=0
следует, что
![]() ,
,
получаем:
![]() (6)
(6)
Из (5) легко вывести,
что
![]() (7)
(7)
Совокупность всех
множеств, содержащихся в 1, образует
кольцо, если в качестве сложения
рассматривать операцию «![]() »,
»,
а в качестве умножения — операцию «![]() ».
».
Это кольцо отличается от кольца множеств,
рассмотренного в §5, тем, что оно имеет
единицу — множество 1.
В самом деле,
равенства (1) показывают, что множество
1 обладает характерным для единицы
кольца свойством VIII
§5.
Отсюда следует,
что вычисления в алгебре множеств можно
формально уподобить вычислениям в
алгебре чисел.
§6. Конституенты.
В этом параграфе
нас будут интересовать множества,
получающиеся из производных n
множеств при помощи операций сложения
(![]() ),
),
умножения (![]() )
)
и вычитания ().
Мы покажем, что
таких множеств конечное число и что все
они могут быть представлены в некотором
специальном виде, называемом нормальным.
Пусть
![]() …
…![]() – произвольные подмножества пространства
– произвольные подмножества пространства
1, которое на протяжении всего этого
параграфа будет оставаться фиксированным.
Обозначим
 для i
для i
=1,2,3…n.
Очевидно, что
![]()
Каждое множество
вида
![]() ⇋
⇋![]() ,
,
(![]() )
)
назовем конституентой
(К).
Так как каждый из
индексов
![]() может принимать только два значения, 0
может принимать только два значения, 0
и 1, то общее число конституент не
превосходит![]() .
.
Например, пусть
n=2
и
![]()
 ,
,
где
![]() —
—
зависимые множества.
Итак,
![]()
![]()
![]()
![]() .
.
Тогда существуют
только три конституенты:
![]() ,
,
![]() ,
,![]() .
.
Рассмотрим свойства
конституент.
-
Различные
конституенты не пересекаются.
Действительно,
если конституенты
![]() и
и![]() ,
,
где
![]()
![]() ,
,
не совпадают, то
![]() ,
,
по крайней мере, для одного![]() .
.
Но тогда![]() и тем более
и тем более![]() .
.
-
Сумма всех
конституент равна 1.
Для доказательства
этого утверждения сначала заметим, что
 ,
,
а затем раскроем скобки, используя закон
дистрибутивного умножения (![]() )
)
относительно сложения (![]() )
)
(§4, (3)):
![]()
![]()

![]() конституент,
конституент,
![]()
-
Множество
 равно сумме конституент, содержащих
равно сумме конституент, содержащих
сомножитель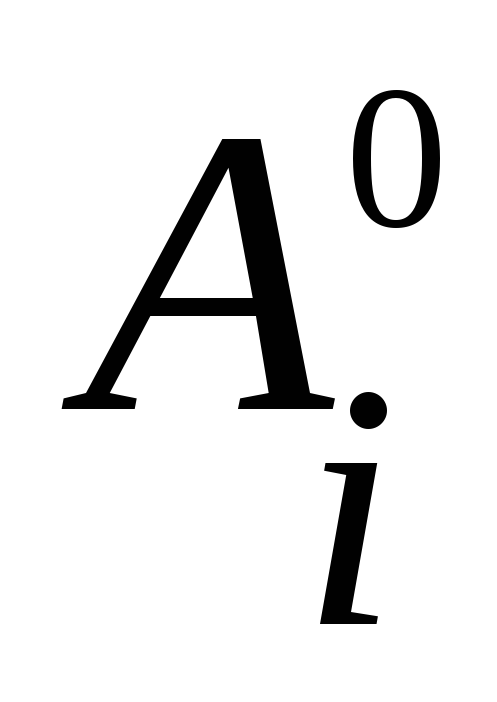 .
.
Действительно,
![]() (*),
(*),
( h
=![]() )
)
где
![]() – все конституенты. Тогда в силу п.1 §6
– все конституенты. Тогда в силу п.1 §6
равенство (*) можем умножить на![]() :
:
![]()
Если
![]() (
(![]() )
)
содержит сомножитель, то![]() ,
,
так как
![]()
Если же
![]() содержит
содержит![]() ,
,
то![]() .
.
Отсюда и следует, что![]() является суммой тех конституент, которые
является суммой тех конституент, которые
содержат сомножитель![]() .
.
Теорема 1. Каждое
непустое множество, образованное из
множеств
![]() при помощи операций сложения (
при помощи операций сложения (![]() ),
),
умножения (![]() ),
),
и вычитания (), является суммой некоторого
числа конституент.
Д о к а з а т е
л ь с т в о.
Теорема верна для множеств
![]() .
.
Поэтому достаточно показать, что если
множества X
и Y
являются суммами некоторого числа
конституент, то и множества
![]()
![]() ,
,![]() ,XY
,XY
(если они непустые) можно представить
в виде суммы конституент.
Пусть X
и Y
представимы в виде суммы конституент
![]()
Тогда
-
 и, значит,
и, значит,
 является суммой конституент.
является суммой конституент.
Из закона
дистрибутивности умножения относительно
сложения
![]() получим:
получим:
![]()
Если
![]() ,
,
то![]() ;
;
в противном случае![]() .
.
Отсюда и следует,
что произведение
![]() либо пусто, либо представлено в виде
либо пусто, либо представлено в виде
суммы некоторого числа конституент
![]()
Если среди
конституент
![]() встречаются все конституенты
встречаются все конституенты![]() ,
,
то
-
 .
.
В противном случае
пусть
![]() —
—
конституенты из ряда (множества)![]() ,
,
которые не встречаются среди![]() .
.
Тогда

поскольку
![]() (
( ).
).
Теорема доказана.
Теорема 2. Из n
множеств при помощи операций
![]() ,
,![]() и можно образовать не более, чем
и можно образовать не более, чем![]() множеств.
множеств.
Действительно,
каждое такое множество (за исключением
пустого), образованное из множеств
![]() при помощи операций
при помощи операций![]() ,
,![]() и , в силу теоремы 1 является суммой
и , в силу теоремы 1 является суммой
конституент, число которых не более![]() .
.
Тогда число различных сумм будет
![]() .
.
Важную роль играет частный случай, когда
все конституенты отличны от нуля. В этом
случае множества
![]() называютсянезависимыми.
называютсянезависимыми.
Теорема 3. Если
множества
![]()
независимы, то число различных конституент
равно
![]() .
.
Д о к а з а т е
л ь с т в о.
Если
![]() ,
,
 (1)
(1)
и не все равенства
![]()
![]()
. . . . . .
![]() верны, то
верны, то![]() .
.
Действительно,
если, например,
![]() ,
,![]() ,
,
то, умножая обе части последнего равенства
в (1) на![]() ,
,
получаем![]() .
.
Следовательно, если множества![]() независимы, то (1) верно только в том
независимы, то (1) верно только в том
случае, когда![]() ,
,
что и доказывает теорему.
Пример.
Пусть множество
![]() составлено из всех таких последовательностей
составлено из всех таких последовательностей![]() ,
,
что каждое![]() равно либо 0, либо 1, но
равно либо 0, либо 1, но![]() .
.
Множества![]() независимы. Действительно,
независимы. Действительно,![]() состоит из всех последовательностей
состоит из всех последовательностей
(![]() ),
),
для которых![]() ,
,
поэтому
![]() .
.
Применим теперь
конституенты для решения следующей
проблемы элиминации
(лат. eliminatio
– исключение, удаление). Введем
обозначения:
![]() {А
{А
содержит по крайней мере n
элементов}
![]() {А
{А
содержит точно n
элементов}
Пусть
![]() – последовательности чисел 0 и 1;
– последовательности чисел 0 и 1;
![]() – последовательности
– последовательности
неотрицательных целых чисел.
Нас интересует
необходимое и достаточное условие
существование такого множества X,
что утверждения
 (I)
(I)
справедливы.
Рассуждения:
-
Пусть сначала n
= 1. Если
вместо
 запишемi,
запишемi,
j,
p,
q,
A,
то получим решение:
![]() (II)
(II)
Действительно,
если существует множество X,
удовлетворяющее условиям (I),
и i=j=1,
то A
является суммой двух непересекающихся
множеств, имеющих соответственно p
и q
элементов, а значит, A
состоит точно из (p+q)
элементов.
Если же
![]() ,
,
тоА
– сумма двух непересекающихся множеств,
каждое из которых имеет по крайней мере
p
(а второе — q)
элементов. Тогда А
имеет (p+q)
элементов. Обратно, если выполнено
условие (II),
то достаточно в качестве X
взять произвольное подмножество
множества А,
содержащее p
элементов.
-
Теперь пусть
 ,
,
и множества попарно не пересекаются (то есть
попарно не пересекаются (то есть ,
,
( ).
).
Сначала потребуем меньшего, а именно,
чтобы для каждогоS
(S
= 1,2,…,n)
существовало такое
 ,
,
что
![]() (III)
(III)
Как мы уже знаем
(см. (II)),
для этого необходимо и достаточно, чтобы
![]() для S
для S
= 1,2,…,n
(IV)
Очевидно, что это
необходимое
условие того, что существует множество
X,
удовлетворяющее (I),
потому что если такое X
существует, то мы можем взять
![]() .
.
Покажем, что это
условие является и достаточным.
Возьмем в качестве X
множество
![]()
Тогда (по закону
де Моргана)
![]()
Так как множества
![]() (i
(i
=1,2,…,n)
не пересекаются, то
![]() ,
,
![]() ,
,
то есть, принимая
во внимание (III),
убеждаемся, что X
удовлетворяет условиям (I).
Предположим теперь,
что для каждой пары r,
s
(1≤r,
s≤n)
либо![]() ,
,
либо![]() .
.
Обозначим условия
(I):

Покажем, что если
![]() ,
,
то
![]() ,
,
либо
![]() ,
,
либо
![]() .
.
Действительно,
если
![]() ,
,
то
-
 ,
,
когда

и
-
 ,
,
когда

Если
![]() и
и![]() ,
,
то
-
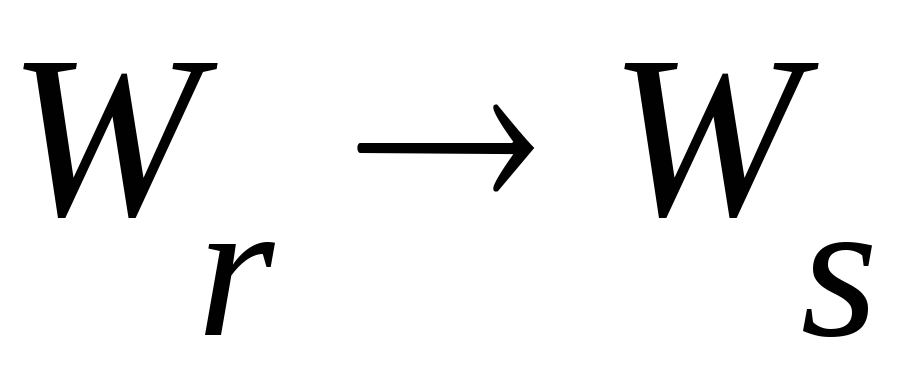 ,
,
когда

и
-
 ,
,
когда
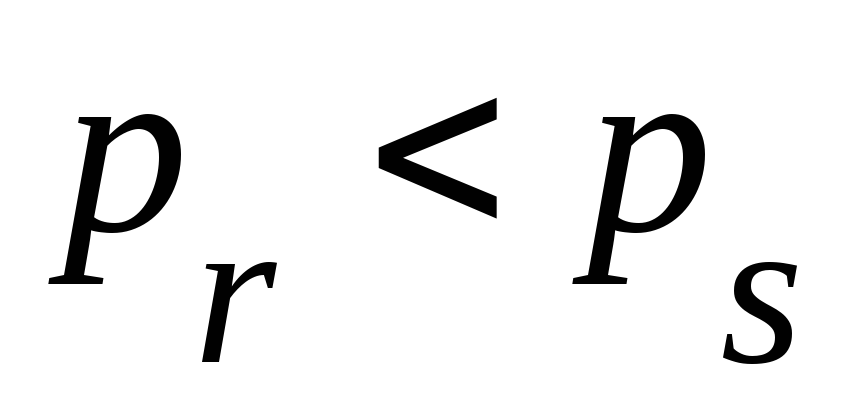 .
.
Если же
![]() ,
,
то
-
 ,
,
когда

и
-
 в
в
противном случае ( ).
).
Аналогично
доказывается, что либо
![]() ,
,
либо
![]() ,
,
либо
![]() .
.
Итак, или конъюнкция
условий (I)
ложна, или в ней можно опустить некоторые
сомножители так, чтобы в полученной
эквивалентной конъюнкции никакие два
из множеств
![]() не повторялись. Таким образом, рассмотренный
не повторялись. Таким образом, рассмотренный
случай сводится к предыдущему.
Сведем теперь
общий случай к случаю, когда множества
![]() либо не пересекаются, либо совпадают.
либо не пересекаются, либо совпадают.
В связи с этим заметим, что если![]() ,
,
то


Отсюда по индукции
получаем, что если множества
![]() попарно не пересекаются, то условие
попарно не пересекаются, то условие
вида![]() можно представить в виде дизъюнкции
можно представить в виде дизъюнкции
конъюнкций:
 .
.
Представим теперь
каждое из множеств
![]() в виде суммы конституент. Согласно
в виде суммы конституент. Согласно
сделанному выше замечанию, каждое из
условий (I)
можно представить в виде дизъюнкции
некоторых конъюнкций вида
![]()
или
![]() .
.
Используя
дистрибутивность конъюнкции относительно
дизъюнкции, представим конъюнкцию
условий (I)
в виде дизъюнкции условий, каждое из
которых в свою очередь является
конъюнкцией некоторого числа сомножителей
вида
![]() или
или
![]() .
.
При этом отдельные
конституенты, входящие в каждую такую
конъюнкцию, или совпадают, или не
пересекаются, что и сводит этот случай
к предыдущему.
Пример.
Найти необходимое и достаточное
условие существования множества X,
для которого
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Эти условия
эквивалентны конъюнкции условий
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
откуда искомое
необходимое и достаточное условие есть
 .
.
Другими словами,
конституенты
![]() и
и![]() должны быть непустыми, а конституента
должны быть непустыми, а конституента![]() должна содержать по крайней мере два
должна содержать по крайней мере два
элемента.
From Wikipedia, the free encyclopedia

If A is the area colored red in this image…

… then the complement of A is everything else.
In set theory, the complement of a set A, often denoted by A∁ (or A′),[1] is the set of elements not in A.[2]
When all sets in the universe, i.e. all sets under consideration, are considered to be members of a given set U, the absolute complement of A is the set of elements in U that are not in A.
The relative complement of A with respect to a set B, also termed the set difference of B and A, written 
Absolute complement[edit]

The absolute complement of the white disc is the red region
Definition[edit]
If A is a set, then the absolute complement of A (or simply the complement of A) is the set of elements not in A (within a larger set that is implicitly defined). In other words, let U be a set that contains all the elements under study; if there is no need to mention U, either because it has been previously specified, or it is obvious and unique, then the absolute complement of A is the relative complement of A in U:[3]
Or formally:
The absolute complement of A is usually denoted by A∁. Other notations include 

Examples[edit]
- Assume that the universe is the set of integers. If A is the set of odd numbers, then the complement of A is the set of even numbers. If B is the set of multiples of 3, then the complement of B is the set of numbers congruent to 1 or 2 modulo 3 (or, in simpler terms, the integers that are not multiples of 3).
- Assume that the universe is the standard 52-card deck. If the set A is the suit of spades, then the complement of A is the union of the suits of clubs, diamonds, and hearts. If the set B is the union of the suits of clubs and diamonds, then the complement of B is the union of the suits of hearts and spades.
- When the universe is the universe of sets described in formalized set theory, the absolute complement of a set is generally not itself a set, but rather a proper class. For more info, see universal set.
Properties[edit]
Let A and B be two sets in a universe U. The following identities capture important properties of absolute complements:
De Morgan’s laws:[5]
Complement laws:[5]
Involution or double complement law:
Relationships between relative and absolute complements:
Relationship with a set difference:
The first two complement laws above show that if A is a non-empty, proper subset of U, then {A, A∁} is a partition of U.
Relative complement[edit]
Definition[edit]
If A and B are sets, then the relative complement of A in B,[5] also termed the set difference of B and A,[6] is the set of elements in B but not in A.

The relative complement of A in B:
The relative complement of A in B is denoted 


Formally:
Examples[edit]
Properties[edit]
Let A, B, and C be three sets. The following identities capture notable properties of relative complements:
Complementary relation[edit]
A binary relation 





Here, 






Together with composition of relations and converse relations, complementary relations and the algebra of sets are the elementary operations of the calculus of relations.
LaTeX notation[edit]
In the LaTeX typesetting language, the command setminus[7] is usually used for rendering a set difference symbol, which is similar to a backslash symbol. When rendered, the setminus command looks identical to backslash, except that it has a little more space in front and behind the slash, akin to the LaTeX sequence mathbin{backslash}. A variant smallsetminus is available in the amssymb package. The symbol 

complement. (It corresponds to the Unicode symbol ∁.)
In programming languages[edit]
Some programming languages have sets among their built in data structures. Such a data structure behaves as a finite set, that is, it consists of a finite number of data that are not specifically ordered, and may thus be considered as the elements of a set. In some cases, the elements are not necessary distinct, and the data structure codes multisets rather than sets. These programming languages have operators or functions for computing the complement and the set differences.
These operators may generally be applied also to data structures that are not really mathematical sets, such as ordered lists or arrays. It follows that some programming languages may have a function called set_difference, even if they do not have any data structure for sets.
See also[edit]
- Algebra of sets – Identities and relationships involving sets
- Intersection (set theory) – Set of elements common to all of some sets
- List of set identities and relations – Equalities for combinations of sets
- Naive set theory – Informal set theories
- Symmetric difference – Elements in exactly one of two sets
- Union (set theory) – Set of elements in any of some sets
Notes[edit]
- ^ “Complement and Set Difference”. web.mnstate.edu. Retrieved 2020-09-04.
- ^ a b “Complement (set) Definition (Illustrated Mathematics Dictionary)”. www.mathsisfun.com. Retrieved 2020-09-04.
- ^ The set in which the complement is considered is thus implicitly mentioned in an absolute complement, and explicitly mentioned in a relative complement.
- ^ Bourbaki 1970, p. E II.6.
- ^ a b c Halmos 1960, p. 17.
- ^ Devlin 1979, p. 6.
- ^ [1] The Comprehensive LaTeX Symbol List
References[edit]
- Bourbaki, N. (1970). Théorie des ensembles (in French). Paris: Hermann. ISBN 978-3-540-34034-8.
- Devlin, Keith J. (1979). Fundamentals of contemporary set theory. Universitext. Springer. ISBN 0-387-90441-7. Zbl 0407.04003.
- Halmos, Paul R. (1960). Naive set theory. The University Series in Undergraduate Mathematics. van Nostrand Company. ISBN 9780442030643. Zbl 0087.04403.
External links[edit]
- Weisstein, Eric W. “Complement”. MathWorld.
- Weisstein, Eric W. “Complement Set”. MathWorld.











