Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 января 2021 года; проверки требуют 29 правок.
Дополнительный код (англ. “two’s complement”, иногда “twos-complement”) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. В англоязычной литературе «обратный код» называют «дополнением единиц» (англ. “ones’ complement”), а «дополнительный код» называют «дополнением двойки» (англ. “two’s complement”).
Дополнительный код для отрицательного числа можно получить инвертированием его двоичного модуля и прибавлением к инверсии единицы, либо вычитанием числа из нуля.
Дополнительный код двоичного числа определяется как величина, полученная вычитанием числа из наибольшей степени двух (из 2N для N-битного второго дополнения).
Представление отрицательного числа в дополнительном коде[править | править код]
При записи числа в дополнительном коде старший разряд является знаковым. Если значение старшего разряда равно 0, то это значит, что в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом.
Двоичное 8-разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах, равно 
Примеры:
| Десятичное представление |
Двоичное представление (8 бит), код: | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 0111 1111
|
0111 1111
|
0111 1111
|
| 1 | 0000 0001
|
0000 0001
|
0000 0001
|
| 0 | 0000 0000
|
0000 0000
|
0000 0000
|
| −0 | 1000 0000
|
1111 1111
|
— |
| −1 | 1000 0001
|
1111 1110
|
1111 1111
|
| −2 | 1000 0010
|
1111 1101
|
1111 1110
|
| −3 | 1000 0011
|
1111 1100
|
1111 1101
|
| −4 | 1000 0100
|
1111 1011
|
1111 1100
|
| −5 | 1000 0101
|
1111 1010
|
1111 1011
|
| −6 | 1000 0110
|
1111 1001
|
1111 1010
|
| −7 | 1000 0111
|
1111 1000
|
1111 1001
|
| −8 | 1000 1000
|
1111 0111
|
1111 1000
|
| −9 | 1000 1001
|
1111 0110
|
1111 0111
|
| −10 | 1000 1010
|
1111 0101
|
1111 0110
|
| −11 | 1000 1011
|
1111 0100
|
1111 0101
|
| −127 | 1111 1111
|
1000 0000
|
1000 0001
|
| −128 | — | — | 1000 0000
|
Дополнительный код в иной системе счисления[править | править код]
Тот же принцип можно использовать и в компьютерном представлении любой системы счисления, например, для десятичных чисел.
Преобразования на примере десятичной системы счисления[1][править | править код]
Положительное число[править | править код]
Изменение значений текущих разрядов числа не производится, но дописывается знаковый старший разряд, значение которого равно 0. Например число [+12’345] будет иметь следующее представление – [012’345]
Отрицательное число[править | править код]
Дописываем знаковый старший разряд, равный большей цифре данной системы счисления, в нашем случае – это 9, а также изменяем остальные разряды по определённому правилу; пусть значение цифры каждого разряда будет представлено переменной x , кроме знакового, тогда представим следующий алгоритм действий:
- Присвоим переменной x новое значение, равное выражению 9 – x (процесс получения обратного кода) – например отрицательное число [-12345] в прямом коде от старшего к младшему разряду будет иметь вид [9′12345], где 9 – знаковая цифра, а в обратном представлении кода будет иметь следующий вид – [9’87654].
- К результирующему числу прибавим 1, так число [9’87654] (первое дополнение) будет иметь вид [987’655] (доп. код).
- Если возникла ситуация переноса разряда, в результате которого образовался новый разряд, то его (старший разряд) опускаем, а результирующее число считаем положительным. Результирующее положительное число будет одинаково представлено, как в прямом, так и в дополнительном коде. Например, имея возможность представить в таком виде отрицательный и положительный нуль, разберём их перевод в дополнительный код (1 знаковый и 4 дополнительных разряда):
- [+0] в прямом коде [0’0000]. Первое и второе дополнения равны [0’0000].
- [-0] в прямом коде [9’0000]. Первое дополнение – [9’9999]. При получении второго дополнения старший разряд числа [(1)0’0000] опускаем и получаем результирующее значение [0’0000], как у числа [+0].
Идея представления десятичного (как и любого другого) числа в дополнительном коде, идентична правилам для двоичной системы счисления и может использоваться в гипотетическом процессоре:
| Привычное
представление |
Прямой
код |
Первое
дополнение |
Второе
дополнение |
|---|---|---|---|
| … | … | … | … |
| +13 | 0’0013 | 0’0013 | 0’0013 |
| +12 | 0’0012 | 0’0012 | 0’0012 |
| +11 | 0’0011 | 0’0011 | 0’0011 |
| +10 | 0’0010 | 0’0010 | 0’0010 |
| +9 | 0’0009 | 0’0009 | 0’0009 |
| +8 | 0’0008 | 0’0008 | 0’0008 |
| … | … | … | … |
| +2 | 0’0002 | 0’0002 | 0’0002 |
| +1 | 0’0001 | 0’0001 | 0’0001 |
| +0 | 0’0000 | 0’0000 | 0’0000 |
| -0 | 9’0000 | 9’9999 | 0’0000 |
| -1 | 9’0001 | 9’9998 | 9’9999 |
| -2 | 9’0002 | 9’9997 | 9’9998 |
| -3 | 9’0003 | 9’9996 | 9’9997 |
| -4 | 9’0004 | 9’9995 | 9’9996 |
| … | … | … | … |
| -9 | 9’0009 | 9’9990 | 9’9991 |
| -10 | 9’0010 | 9’9989 | 9’9990 |
| -11 | 9’0011 | 9’9988 | 9’9989 |
| -12 | 9’0012 | 9’9987 | 9’9988 |
| -13 | 9’0013 | 9’9986 | 9’9987 |
Арифметика в дополнительном коде[править | править код]
Сложение и вычитание[править | править код]
Оба числа представляются в дополнительном коде. Дополнительный код обоих чисел имеет одинаковое количество разрядов. В данном представлении числа складываются.
Знаки разные: Если в процессе сложения образуется выходящий за пределы первоначальных чисел разряд, то он опускается. Результирующее значение считается положительным, где прямой и дополнительный коды являются идентичными. Иначе — отрицательным в виде дополнительного кода.
Например:
- [1234] + [-78] → [0’1234] + [9’9922] = [(1)0’1156] = [1156].
- [-1234] + [78] → [9’8766] + [0’0078] = [9’8844] = [-1156].
Знаки одинаковые:
- Положительные числа. Разряд не опускается, результат положительный.
- Отрицательные числа. Разряд опускается, результат отрицательный в дополнительном коде.
Например:
- [1234] + [78] → [0’1234] + [0’0078] = [0’1312] = [1312].
- [-1234] + [-78] → [9’8766] + [9’9922] = [(1)9’8688] → (первое дополнение) [0’1311] → (второе дополнение или обычное представление) [0’1312]. При переводе из дополнительного кода в обычное представление результирующее значение является абсолютным.
Преобразование в дополнительный код[править | править код]
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
- Если старший (знаковый) разряд числа, записанного в прямом коде, равен 0, то число положительное и никаких преобразований не делается;
- Если старший (знаковый) разряд числа, записанного в прямом коде, равен 1, то число отрицательное, все разряды числа, кроме знакового, инвертируются, а к результату прибавляется 1.
Пример.
Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный код.
Прямой код отрицательного числа -5:
1000 0101
Инвертируем все разряды числа, кроме знакового, получая таким образом обратный код (первое дополнение) отрицательного числа -5:
1111 1010
Добавим к результату 1, получая таким образом дополнительный код (второе дополнение) отрицательного числа -5:
1111 1011
Для преобразования отрицательного числа -5, записанного в дополнительном коде, в положительное число 5, записанное в прямом коде, используется похожий алгоритм. А именно:
1111 1011
Инвертируем все разряды отрицательного числа -5, получая таким образом положительное число 4 в прямом коде:
0000 0100
Добавив к результату 1 получим положительное число 5 в прямом коде:
0101
И проверим, сложив с дополнительным кодом
0000 0101 + 1111 1011 = 0000 0000, пятый и старше разряды выбрасываются.
p-адические числа[править | править код]
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ичная система счисления, то число, противоположное 00015 (110), равно 44445 (−110).
Реализация алгоритма преобразования в дополнительный код (для 8-битных чисел)[править | править код]
Pascal[править | править код]
if (a < 0) then a := ((not a) or 128) + 1;
C/C++[править | править код]
int convert(int a) { if (a<0) a = ~(-a) + 1; return a; }
Преимущества и недостатки[править | править код]
Преимущества[править | править код]
- Общие инструкции (процессора) для сложения, вычитания и левого сдвига для знаковых и беззнаковых чисел (различия только в арифметических флагах, которые нужно проверять для контроля переполнения в результате).
- Отсутствие числа «минус ноль».
Недостатки[править | править код]
- Представление отрицательного числа визуально не читается по обычным правилам, для его восприятия нужен особый навык или дополнительные вычисления для приведения в обычный вид.
- В некоторых представлениях (например, двоично-десятичный код) или их составных частях (например, мантисса числа с плавающей запятой) дополнительное кодирование неудобно.
- Модуль наибольшего числа не равен модулю наименьшего числа. Например, для восьмибитного целого со знаком, максимальное число: 12710 = 011111112, минимальное число: -12810 = 100000002. Соответственно, не для любого числа существует противоположное. Операция изменения знака может потребовать дополнительной проверки.
Пример программного преобразования[править | править код]
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными.
C# .NET / C style[править | править код]
byte b1 = 254; //11111110 (бинарное) byte b2 = 121; //01111001 (бинарное) byte c = 1<<(sizeof(byte)*8-1); //2 возводится в степень 7. Результат: 10000000 (бинарное) byte b1Conversion=(c ^ b1) - c; //Результат: -2. А фактически, двоичный дополнительный код. byte b2Conversion=(c ^ b2) - c; //Результат остаётся 121, потому что знаковый разряд - ноль.
Расширение знака[править | править код]
Расширение знака (англ. Sign extension) — операция над двоичным числом, которая позволяет увеличить разрядность числа с сохранением знака и значения. Выполняется добавлением цифр со стороны старшего значащего разряда. Если число положительное (старший разряд равен 0), то добавляются нули, если отрицательное (старший разряд равен 1) — единицы.
Пример[править | править код]
| Десятичное число | Двоичное число
(8 разрядов) |
Двоичное число
(16 разрядов) |
|---|---|---|
| 10 | 0000 1010
|
0000 0000 0000 1010
|
| −15 | 1111 0001
|
1111 1111 1111 0001
|
См. также[править | править код]
- Обратный код
- Прямой код
- Целый тип
- Алгоритм Бута — специализированный алгоритм умножения для чисел в дополнительном коде
Литература[править | править код]
- Behrooz Parhami. 2.3. Complement Representation, 2.4. Two’s- and 1’s-complement numbers // Computer Arithmetic: Algorithms and Hardware Designs. — New York: Oxford University Press, 2000. — P. 22-27. — 510 p. — ISBN 0-19-512583-5.
- Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К.: Вища школа, 1987. — 375 с.
Ссылки[править | править код]
- ↑ Florida Tech. Дата обращения: 28 ноября 2020. Архивировано 8 октября 2016 года.
Двоичное число: прямой, обратный и дополнительный коды
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Прямой, обратный и дополнительный коды двоичного числа – способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Прямой код – способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) – для записи только неотрицательных чисел:
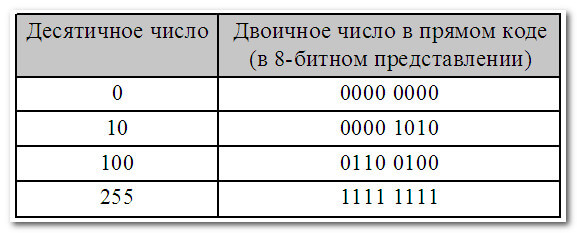 В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 – от 0 до 255)
В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 – от 0 до 255)
Второй вариант – для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае – восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
– знаковый разряд равен 0, то число положительное
– знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от – 127 до +127:
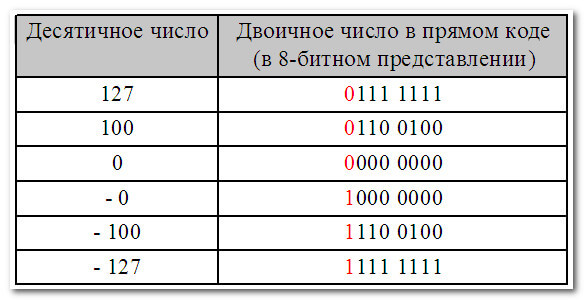 Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным – очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля – положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код – метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе – знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
(Арифметические операции с двоичными числами)
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = – 0001 1001
Необходимо их сложить:
100 + (-25) = 100 – 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд – переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = – 0000 1010
Необходимо их сложить:
5 + (-10) = 5 – 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = – 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
– арифметические операции проводятся в два этапа
– как и в прямом коде два представления нуля – положительный и отрицательный
Дополнительный код
Дополнительный код – наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
– инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
– к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 – десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 – 0000 1010 = 1111 0110 – десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере – дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
Предыдущие статьи:
1. Микроконтроллеры – первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции




 (39 голосов, оценка: 4,69 из 5)
(39 голосов, оценка: 4,69 из 5)
![]() Загрузка…
Загрузка…
Как найти прямой, обратный и дополнительный код????Примеры пожалуйста:)
Гуру
(4793),
закрыт
12 лет назад
Миоко Таканава
Гений
(51590)
12 лет назад
Для положительных чисел прямой, обратный и дополнительный коды совпадают.
Для отрицательных:
В прямом коде просто старший разряд устанавливается в единицу. Пример для 8 разрядов:
+98(10) -> 01100010(2)
-98(10) -> 11100010(2)
В обратном коде все разряды инвертируются. 0 заменяются 1, а единицы нулями. Пример:
+98(10) -> 01100010(2)
-98(10) -> 10011101(2)
В дополнителный код отрицательные числа преобразуются сначала в обратный. Затем к получившемуся коду прибавляется единица:
-98(10) -> 10011101(2)+1=10011110(2)
Сали-Мали
Просветленный
(29246)
12 лет назад
Двоичное 8-ми разрядное число с отрицательным знаком: x= – 01011101
Получаем прямой код: минус – знак числа записывается ввиде 1, коды числа записываются без изменения:
X пр. = 1.01011101.
Для преобразования прямого кода двоичного отрицательного числа в обратный код знаковый разряд оставить без изменения, а в остальных разрядах нули заменить на единицы, а единицы на нули:
Xобр. = 1.10100010 .
Для получения дополнительного кода необходимо к младшему разряду числа в обратном коде добавить единицу:
Хдоп. = 1.10100011.
Для положительных двоичных чисел (в знаковом разряде записывается 0): X пр. = Xобр. = Хдоп.
Читай внимательно: http://solidbase.karelia.ru/edu/zonna/3_ychebnik_5.htm
-
Модуль числа представить прямым кодом
в
k
двоичных разрядах. -
Значения всех разрядов
инвертировать (все
нули заменить на единицы, а единицы —
на нули), получив, таким образом,
k-разрядный
обратный код исходного
числа. -
К полученному обратному коду, трактуемому
как k-разрядное неотрицательное двоичное
число, прибавить единицу.
Обратный код является дополнением
исходного числа до числа
2k–
1, состоящего из
k
двоичных единиц. Поэтому прибавление
единицы к инвертированному коду позволяет
получить его искомый дополнительный
код.
Пример . Получим дополнительный
код числа -52 для восьми- и
шестнадцатиразрядной ячеек.
Для восьмиразрядной ячейки: 00110100 —
прямой код числа |-52| = 52;
1100 1011 — обратный код числа -52;
1100
1100 — дополнительный
код числа
-52
Для
шестнадцатиразрядной ячейки:
0000 0000 0011 0100 — прямой код числа
–|52|;
1111
1111 1100 1011 — обратный код числа -52;
1111 1111 1100 1100 — дополнительный код
числа-52.
Вопрос.
Какое минимальное отрицательное число
можно записать в k
разрядах?
Ответ.
Описанный выше алгоритм получения
дополнительного кода для отрицательного
числа знаковую единицу в левом разряде
образует автоматически при
|m|<=2k-1.
Если же 2k-1<|m|<2k,
то попытка реализации данного алгоритма
приведет к тому, что в левом разряде
будет находиться цифра 0, соответствующая
компьютерному представлению положительных
чисел, что неверно. Представим
значение
2k-|m|
в следующем виде: 2k-|m|
= 2k-1
+(2k-1
– |m|).
Здесь первое слагаемое
2k-1
соответствует единице в левом знаковом
разряде. То есть при представлении
отрицательного числа m
дополнительным кодом в самом левом
(знаковом) разряде записывается знак
отрицательного числа (единица), а в
остальных разрядах — число 2k-1
– |m|.
Следовательно, минимальное отрицательное
(максимальное по модулю) число
т,
которое можно представить в
k
разрядах, равно
-2k-1
(это ограничение и было приведено в
определении 2).
Дополнительный
восьмиразрядный код для чисел -128, -127 и
-0
приведены
в таблице:
|
Число |
-128 |
-127 |
-0 |
|
Прямой код |
1000 0000 |
01111111 |
0000 0000 |
|
Обратный код |
0111 1111 |
1000 0000 |
11111111 |
|
Дополнительный |
1000 0000 |
1000 0001 |
0000 0000 |
Отметим, что для числа -128 прямой
код совпадает с дополнительным, а
дополнительный код числа -0
совпадает с обычным нулем. При
преобразовании обратного кода для числа
-0 в его дополнительный код
правила обычной двоичной арифметики
нарушаются, а именно:
1111 11112+ 1 = 1 0000 00002 = 2k =
0.
Восстановить модуль исходного десятичного
отрицательного числа по его дополнительному
коду можно двумя способами.
Способ
1 (обратная цепочка
преобразований): вычесть единицу из
дополнительного кода, инвертировать
полученный код и перевести полученное
двоичное представление числа в десятичное.
Способ
2:
по приведенному выше алгоритму построить
дополнительный код для имеющегося
дополнительного кода искомого числа и
представить результат в десятичной
системе счисления.
Пример.
Получим десятичное значение числа по
его дополнительному коду 100101112.
Способ
1:
-
из дополнительного кода вычтем 1:
10010111 – 1 = 10010110 (получили обратный код); -
инвертируем полученный код: 01101001
(получили модуль отрицательного числа); -
переведем полученное двоичное значение
в десятичную систему счисления: 011010012
= 26 + 25 + 23 + 1 = 64 + 32 + 8 +
1 = 105.
Ответ:
-105.
Способ
2:
-
инвертируем имеющийся дополнительный
код: 01101000; -
прибавим к результату 1: 01101000 + 1 = 01101001
(получили модуль отрицательного числа); -
переведем полученное двоичное значение
в десятичную систему счисления: 011010012
= 26 + 25 + 23 + 1 = 64 + 32 + 8 +
1 = 105.
Ответ-.
-105.
Целые числа со знаком, представимые в
k
разрядах, принадлежат диапазону
[-2k-1,
2k-1
-1], который не
является симметричным относительно 0.
Это следует учитывать при программировании.
Если, например, изменить знак у наибольшего
по модулю отрицательного числа, то
полученный результат окажется уже не
представимым в том же числе разрядов.
Ниже
приведены значения границ диапазонов
для знаковых представлений в ячейках
с различной разрядностью:
|
Разрядность |
Минимальное |
Максимальное |
|
8 |
-128 |
127 |
|
16 |
-32768 |
32767 |
|
32 |
-2147483648 |
2147483647 |
|
64 |
-9223372036854775808 |
9223372036854775807 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Дополнительный код (англ. two’s complement, иногда twos-complement) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ.
Дополнительный код отрицательного числа можно получить инвертированием модуля двоичного числа (первое дополнение) и прибавлением к инверсии единицы (второе дополнение), либо вычитанием числа из нуля.
Дополнительный код (дополнение до 2) двоичного числа получается добавлением 1 к младшему значащему разряду его дополнения до 1. [1]
Дополнение до 2 двоичного числа определяется как величина, полученная вычитанием числа из наибольшей степени двух (из 2N для N-битного дополнения до 2).
Содержание
- 1 Представление отрицательного числа в дополнительном коде
- 2 Дополнительный код для десятичных чисел
- 3 Преобразование в дополнительный код
- 4 p-адические числа
- 5 Реализация алгоритма преобразования в дополнительный код (для 8-битных чисел)
- 5.1 Pascal
- 5.2 C/C++
- 6 Преимущества и недостатки
- 6.1 Преимущества
- 6.2 Недостатки
- 7 Пример программного преобразования
- 7.1 C# .NET / C style
- 8 См. также
- 9 Литература
- 10 Ссылки
Представление отрицательного числа в дополнительном коде[править | править вики-текст]
При записи числа в дополнительном коде старший разряд является знаковым. Если его значение равно 0, то в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом.
Двоичное 8-разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах равно  , что равно 127.
, что равно 127.
Примеры:
| Десятичное представление |
Двоичное представление (8 бит) | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 01111111 | 01111111 | 01111111 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | — |
| -1 | 10000001 | 11111110 | 11111111 |
| -2 | 10000010 | 11111101 | 11111110 |
| -3 | 10000011 | 11111100 | 11111101 |
| -4 | 10000100 | 11111011 | 11111100 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -7 | 10000111 | 11111000 | 11111001 |
| -8 | 10001000 | 11110111 | 11111000 |
| -9 | 10001001 | 11110110 | 11110111 |
| -10 | 10001010 | 11110101 | 11110110 |
| -11 | 10001011 | 11110100 | 11110101 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | — | — | 10000000 |
Дополнительный код для десятичных чисел[править | править вики-текст]
Тот же принцип можно использовать и в компьютерном представлении десятичных чисел: для каждого разряда цифра X заменяется на 9−X, и к получившемуся числу добавляется 1. Например, при использовании четырёхзначных чисел −0081 заменяется на 9919 (9919+0081=0000, пятый разряд выбрасывается).
При применении той же идеи к привычной 10-тичной системе счисления получится (например, для гипотетического процессора использующего 10-тичную систему счисления):
| 10-тичная система счисления (“обычная” запись) |
10-тичная система счисления, дополнительный код |
|---|---|
| … | … |
| 13 | 0013 |
| 12 | 0012 |
| 11 | 0011 |
| 10 | 0010 |
| 9 | 0009 |
| 8 | 0008 |
| … | … |
| 2 | 0002 |
| 1 | 0001 |
| 0 | 0000 |
| -1 | 9999 |
| -2 | 9998 |
| -3 | 9997 |
| -4 | 9996 |
| … | … |
| -9 | 9991 |
| -10 | 9990 |
| -11 | 9989 |
| -12 | 9988 |
| … | … |
Преобразование в дополнительный код[править | править вики-текст]
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
- Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;
- Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.
Пример. Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный. Прямой код числа −5, взятого по модулю:
101
Инвертируем все разряды числа, получая таким образом обратный код:
010
Добавим к результату 1
011
Допишем слева знаковый единичный разряд
1011
Для обратного преобразования используется тот же алгоритм. А именно:
1011
Инвертируем все разряды числа, получая таким образом обратный код:
0100
Добавим к результату 1
0101
И проверим, сложив с дополнительным кодом
0101 + 1011 = 10000, пятый разряд выбрасывается.
p-адические числа[править | править вики-текст]
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ричная система счисления, то число, противоположное 1000… (1) равно 4444…. (−1).
Реализация алгоритма преобразования в дополнительный код (для 8-битных чисел)[править | править вики-текст]
Pascal[править | править вики-текст]
if a<0 then a:=((not a) or 128) + 1;
C/C++[править | править вики-текст]
int convert(int a) { if (a < 0) a = ( ~-a|128 ) + 1; return a; }
Преимущества и недостатки[править | править вики-текст]
Преимущества[править | править вики-текст]
- Общие инструкции (процессора) для сложения, вычитания и левого сдвига для знаковых и беззнаковых чисел (различия только в арифметических флагах которые нужно проверять для контроля переполнения в результате).
- Отсутствие числа «минус ноль».
Недостатки[править | править вики-текст]
- Представление отрицательного числа не читается по обычным правилам, для его восприятия нужен особый навык или вычисления
- В некоторых представлениях (например, двоично-десятичный код) или их составных частях (например, мантисса числа с плавающей запятой) дополнительное кодирование неудобно
- Модуль наибольшего числа не равен модулю наименьшего числа. Например, для восьмибитного целого со знаком, максимальное число: 12710 = 011111112, минимальное число: -12810 = 100000002. Соответственно, не для любого числа существует противоположное. Операция изменения знака может потребовать дополнительной проверки.
Пример программного преобразования[править | править вики-текст]
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными.
C# .NET / C style[править | править вики-текст]
byte b1 = 254; //11111110 (бинарное) byte b2 = 121; //01111001 (бинарное) byte c = 1<<(sizeof(byte)*8-1); //2 возводится в степень 7. Результат: 10000000 (бинарное) byte b1Conversion=(c ^ b1) - c; //Результат: -2. А фактически, двоичный дополнительный код. byte b2Conversion=(c ^ b2) - c; //Результат остаётся 121, потому что знаковый разряд - ноль.
См. также[править | править вики-текст]
- Обратный код
- Прямой код
- Целый тип
- Алгоритм Бута – специализированный алгоритм умножения для чисел в дополнительном коде
Литература[править | править вики-текст]
- Behrooz Parhami. 2.3. Complement Representation, 2.4. Two’s- and 1’s-complement numbers // Computer Arithmetic: Algorithms and Hardware Designs. — New York: Oxford University Press, 2000. — P. 22-27. — 510 p. — ISBN 0-19-512583-5.
- Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К.: Вища школа, 1987. — 375 с.
Ссылки[править | править вики-текст]
- ↑ К.Г.Жуков “Справочное руководство пользователя Fixed-Point Blockset” 1.2. Понятие прямого, обратного и дополнительного кодов, Определение 3. Архивировано из первоисточника 23 июня 2012.
