Как найти дополнительный множитель математика

В данном материале мы разберем, как правильно приводить дроби к новому знаменателю, что такое дополнительный множитель и как его найти. После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.

Понятие приведения дроби к другому знаменателю

Вспомним основное свойство дроби. Согласно ему, обыкновенная дробь ab (где a и b – любые числа) имеет бесконечное количество дробей, которые равны ей. Такие дроби можно получить, умножив числитель и знаменатель на одинаковое число m (натуральное). Иными словами, все обыкновенные дроби могут быть заменены другими вида a·mb·m. Это и есть приведение исходного значения к дроби с нужным знаменателем.

Привести дробь к другому знаменателю можно, умножив ее числитель и знаменатель на любое натуральное число. Главное условие – множитель должен быть одинаков для обоих частей дроби. В итоге получится дробь, равная исходной.

Проиллюстрируем это примером.

Пример 1

Привести дробь 1125 к новому знаменателю.

Решение

Возьмем произвольное натуральное число 4 и умножим обе части исходной дроби на него. Считаем: 11·4=44 и 25·4=100. В итоге получилась дробь 44100.

Все подсчеты можно записать в таком виде: 1125=11·425·4=44100

Выходит, любую дробь можно привести к огромному количеству разных знаменателей. Вместо четверки мы могли бы взять другое натуральное число и получить еще одну дробь, эквивалентную исходной.

Но не любое число может стать знаменателем новой дроби. Так, для ab в знаменателе могут стоять только числа b·m, кратные числу b. Вспомните основные понятия деления – кратные числа и делители. Если число не кратно b, но делителем новой дроби оно быть не может. Поясним нашу мысль примером решения задачи.

Пример 2

Вычислить, возможно ли приведение дроби 59 к знаменателям 54 и 21.

Решение

54 кратно девятке, которая стоит в знаменателе новой дроби (т.е. 54 можно разделить на 9). Значит, такое приведение возможно. А 21 мы разделить на 9 не можем, поэтому такое действие для данной дроби выполнить нельзя.

Понятие дополнительного множителя

Сформулируем, что такое дополнительный множитель.

Определение 1

Дополнительный множитель представляет собой такое натуральное число, на которое умножают обе части дроби для приведения ее к новому знаменателю.

Т.е. когда мы выполняем это действие с дробью, мы берем для нее дополнительный множитель. Например, для приведения дроби 710 к виду 2130 нам потребуется дополнительный множитель 3. А получить дробь 1540 из 38 можно с помощью множителя 5.

Соответственно, если мы знаем знаменатель, к которому необходимо привести дробь, то мы можем вычислить для нее и дополнительный множитель. Разберем, как это сделать.

У нас есть дробь ab, которую можно привести к некоторому знаменателю c; вычислим дополнительный множитель m. Нам надо произвести умножение знаменателя исходной дроби на m. У нас получится b·m, а по условию задачи b·m= c. Вспомним, как связаны между собой умножение и деление. Эта связь подскажет нам следующий вывод: дополнительный множитель есть не что иное, как частное от деления c на b, иначе говоря, m=c:b.

Таким образом, для нахождения дополнительного множителя нам нужно разделить требуемый знаменатель на исходный.

Пример 3

Найдите дополнительный множитель, с помощью которого дробь 174 была приведена к знаменателю 124.

Решение

Используя правило выше, мы просто разделим 124 на знаменатель первоначальной дроби – четверку.

Считаем: 124:4=31.

Выполнять расчеты такого типа часто требуется при приведении дробей к общему знаменателю.

Правило приведения дробей к указанному знаменателю

Перейдем к определению основного правила, с помощью которого можно привести дроби к указанному знаменателю. Итак,

Определение 2

Для приведения дроби к указанному знаменателю нужно:

определить дополнительный множитель;
умножить на него и числитель, и знаменатель исходной дроби.

Как применить это правило на практике? Приведем пример решения задачи.

Пример 4

Выполните приведение дроби 716 к знаменателю 336.

Решение

Начнем с вычисления дополнительного множителя. Разделим: 336:16=21.

Полученный ответ умножаем на обе части исходной дроби: 716=7·2116·21=147336. Так мы привели исходную дробь к нужному знаменателю 336.

Ответ: 716=147336.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Главная
Справочники
Справочник по математике 5-9 класс
Обыкновенные дроби
Приведение дробей к общему знаменателю

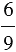
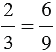
Если мы умножим числитель и знаменатель дроби на одно и то же число 3, то получим дробь , равную данной, то есть , в данном случае принято говорить, что мы дробь привели к новому знаменателю 9.

Дополнительный множитель – это число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель. При этом при приведении дроби к новому знаменателю используем основное свойство дроби и умножаем её числитель и знаменатель на дополнительный множитель. Чтобы найти дополнительный множитель необходимо новый знаменатель разделить на данный.

Например: Приведем дробь 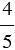к знаменателю 40. Для этого найдем дополнительный множитель, поделив 40 на 5, получим, что дополнительный множитель равен 40 : 5 = 8.

Далее воспользуемся основным свойством дроби, найдем:

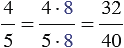
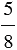
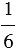
Рассмотрим дроби и . Мы видим что данные дроби имеют разные знаменатели, но с помощью основного свойства дроби мы можем их привести к одному знаменателю, другими словами к общему знаменателю.

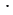
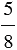
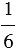
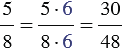
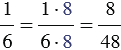
Например, общим знаменателем для данных дробей будет знаменатель, равный произведению данных знаменателей, то есть 86 = 48. Чтобы привести дробь к знаменателю 48, необходимо умножить ее числитель и знаменатель на дополнительный множитель 6, а знаменатель и числитель дроби – на дополнительный множитель 8. Имеем:

и .

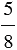
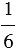
Мы привели дроби и к общему знаменателю 48. Заметим, что общий знаменатель дробей всегда должен быть кратным, каждому из данных знаменателей.

Обычно принято приводить дроби к наименьшему общему знаменателю, который равен наименьшему общему кратному знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю используем правило:

Найти наименьшее общее кратное знаменателей данных дробей, которое будет являться наименьшим общим знаменателем.
Найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей.
Умножить числитель и знаменатель каждой дроби на её дополнительный множитель.

В нашем примере НОК (6; 8) = 24, то есть наименьшим общим знаменателем наших дробей является 24.
Находим дополнительные множители: для дроби – это число 24 : 8 = 3, а для дроби – число 24 : 6 = 4.
Умножаем числитель и знаменатель каждой дроби на её дополнительный множитель:

и .

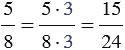
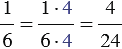
Обычно принято, дополнительный множитель писать над числителем справа, то есть наша запись будет иметь вид:

и .

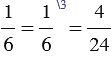
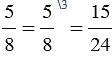
Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Сравнение, сложение и вычитание дробей с разными знаменателями

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

6 класс

Номер 241,
Мерзляк, Полонский, Якир, Учебник

Номер 248,
Мерзляк, Полонский, Якир, Учебник

Номер 282,
Мерзляк, Полонский, Якир, Учебник

Номер 297,
Мерзляк, Полонский, Якир, Учебник

Номер 1028,
Мерзляк, Полонский, Якир, Учебник

Задание 276,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 297,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 359,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 990,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 7,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1

7 класс

Номер 35,
Мерзляк, Полонский, Якир, Учебник

Номер 40,
Мерзляк, Полонский, Якир, Учебник

Номер 45,
Мерзляк, Полонский, Якир, Учебник

Номер 74,
Мерзляк, Полонский, Якир, Учебник

Номер 429,
Мерзляк, Полонский, Якир, Учебник

Номер 430,
Мерзляк, Полонский, Якир, Учебник

Номер 494,
Мерзляк, Полонский, Якир, Учебник

Номер 1028,
Мерзляк, Полонский, Якир, Учебник

Номер 1070,
Мерзляк, Полонский, Якир, Учебник

Номер 1156,
Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 15,
Мерзляк, Полонский, Якир, Учебник

Номер 18,
Мерзляк, Полонский, Якир, Учебник

Номер 133,
Мерзляк, Полонский, Якир, Учебник

Номер 135,
Мерзляк, Полонский, Якир, Учебник

Номер 201,
Мерзляк, Полонский, Якир, Учебник

Номер 242,
Мерзляк, Полонский, Якир, Учебник

Номер 243,
Мерзляк, Полонский, Якир, Учебник

Номер 251,
Мерзляк, Полонский, Якир, Учебник

Номер 254,
Мерзляк, Полонский, Якир, Учебник

Номер 255,
Мерзляк, Полонский, Якир, Учебник

Источник

Содержание материала

Сложение дробей с одинаковыми знаменателями
Видео
НОЗ и НОК
Как устроена десятичная дробь
Как привести десятичную дробь к новому знаменателю
Чтобы найти общий знаменатель, перемножим знаменатели:
Вычитание дробей с разными знаменателями

Сложение дробей с одинаковыми знаменателями

Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.

Пример.

C помощью букв это правило сложения можно записать так:

Запомните!

Записывая ответ, проверьте нельзя ли п Запомните!

Записывая ответ, проверьте нельзя ли полученную дробь сократить.

Видео

НОЗ и НОК

При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.

Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.

Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:

16=8*2; 6= 3*2

НОК (16, 6) =8*2*3= 48.

Число 48 и есть искомый НОЗ.

Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:

Найти НОК.
Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
Умножить обе части каждой дроби на их дополнительные множители.

Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:

Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

0,3
4,23
9,939

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Как привести десятичную дробь к новому знаменателю

Для приведения десятичной дроби к новому знаменателю, необходимо десятичную дробь преобразовать в обыкновенную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.

Разберём пример. Приведём десятичную дробь 2.5 к знаменателю 4.Преобразуем десятичную дробь в обыкновенную дробь. 2.5 =5/2 Найдём дополнительный множитель — для этого разделим 4 на 2 получится 4 / 2 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 10/4

2.5

2.5 × 101 × 10

2510

5 × 5 2 × 5

5 × 22 × 2

104

Чтобы найти общий знаменатель, перемножим знаменатели:

Дополнительный множитель к первой дроби:

Дробь примет вид:

Дополнительный множитель ко второй дроби:

Дробь примет вид:

Дополнительный множитель к третьей дроби:

Дробь примет вид:

Итак, были дроби:

Запишем полученные дроби с общим знаменателем:

Вычитание дробей с разными знаменателями

Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.

Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.

Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.

Пример 1. Найти значение выражения:

У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.

Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12

НОК (3 и 4) = 12

Теперь возвращаемся к дробям и

Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:

Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Получили ответ

Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы

Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:

Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):

Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.

Пример 2. Найти значение выражения

У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.

Найдём НОК знаменателей этих дробей.

Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30

НОК (10, 3, 5) = 30

Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.

Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:

Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:

Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:

Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.

Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:

В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.

Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.

Итак, находим НОД чисел 20 и 30:

Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10

Получили ответ

Опыт по приведению к общему знаменателю

Несложно сравнивать между собой, а также складывать и вычитать дроби с одинаковыми знаменателями. Но что делать, если знаменатели разные?

На рисунке 1 два сосуда с водой. В одной из них $large frac{1}{8}$ литра воды, в другой — $large frac{1}{4}$ литра. Как нам узнать, сколько воды вместе?

Рисунок 1

Можно перелить всю воду в один сосуд, то есть выполнить сложение:

$$large frac{1}{8}+frac{1}{4}$$

Тогда вся вода будет вместе, но сколько её получится? Мы же не можем записать это как $large frac{1}{8}frac{1}{4}$. Нет, нужно пробовать по-другому.

Возьмём фломастер и отметим на стенке первого сосуда уровень воды. Это будет наша мерка для $large frac{1}{8}$ литра. Теперь переливаем воду из второго сосуда и, пользуясь нашей отметкой, понимаем, на сколько повысился уровень воды.

Рисунок 2

Он повысился на $large frac{2}{8}$ литра. Получается, что

$$large frac{1}{8}+frac{1}{4}=frac{1}{8}+frac{2}{8}$$

$$large frac{1+2}{8}=frac{3}{8}$$

То, что мы сделали, называется приведение к общему знаменателю.

Замена дробей равными им дробями с одинаковыми знаменателями называется приведение к общему знаменателю.

Дополнительные множители

Каким образом мы представили $large frac{1}{4}$ как $large frac{2}{8}$? Согласно основному свойству дроби, при умножении числителя и знаменателя на одно и то же число у нас не меняется значение дроби, значит, мы можем сделать так, чтобы и у $large frac{1}{4}$ и у $large frac{1}{8}$ были одинаковые знаменатели, умножив $large frac{1}{4}$ на $large frac{2}{2}$:

$$large frac{1}{4} cdot frac{2}{2}=frac{1 cdot 2}{4 cdot 2}=frac{2}{8}$$

Числа, на которые мы умножаем числитель и знаменатель, называются дополнительными множителями.

Дополнительный множитель – это натуральное число, на которое нужно умножить числитель и знаменатель дроби, чтобы привести ее к другому знаменателю.

Часто они пишутся над дробями, вот так:

Рисунок 3

Эта тема может показаться сложной. На самом деле часто общий знаменатель и дополнительные множители подбираются как будто сам собой, интуитивно. Это получается потому, что мы знаем таблицу умножения, и, глядя на некоторые числа, легко видим, на что можно их умножить, чтобы превратить одно в другое.

Тренировка в нахождении дополнительных множителей

Попробуем. Посмотрите на эту последовательность чисел и скажите, на что нужно умножить предыдущее число, чтобы получить последующее.

$$1, 2, 4, 8, 16, 32$$

Показать ответ

Скрыть

Ещё одна последовательность:

$$3, 6, 9, 27$$

А здесь какой множитель использовали?

Показать ответ

Скрыть

Попробуем подобрать дополнительные множители для дробей. Какой множитель нужен, чтобы привести дробь $large frac{1}{2}$ и $large frac{2}{3}$ к общему знаменателю?

Общим знаменателем для этих двух дробей будет число, которое делится и на $2$ , и на $3$ . Это будет $6$ . Чтобы вычислить дополнительные множители для дроби, нужно найти число, которое при умножении на знаменатель дроби даст общий знаменатель. Следовательно, чтобы его вычислить, нужно разделить общий знаменатель на знаменатель дроби.

Значит, для дроби $frac{1}{2}$ дополнительный множитель будет $6:2=3$, а для дроби $frac{2}{3}$ дополнительный множитель $6:3=2$

Рисунок 4

Попробуйте сами. Найдите дополнительные множители для приведения дробей $frac{1}{8}$ и $frac{1}{7}$ к общему знаменателю $56$ . Приведите эти числа к общему знаменателю.

Показать решение

Скрыть

Рисунок 5

Источник