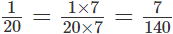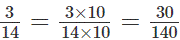Привести дробь к новому знаменателю
Для приведения обыкновенной дроби вида a/b к новому знаменателю, необходимо числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём дробь 3/4 к знаменателю 12. Найдём дополнительный множитель – для этого разделим 12 на 4 получится 12 / 4 = 3. Домножим числитель и знаменатель дроби на 3 получится дробь 9/12
Перед преобразованием дроби к новому знаменателю дробь необходимо сократить.
Разберём пример. Приведём дробь 6/8 к знаменателю 12. Знаменатель 8 не делит нацело новый знаменатель, из этого можно предположить что дробь 6/8 невозможно привести к знаменателю 12. Но если мы сократим дробь 6/8 = 3/4 то дробь без проблем можно привести к знаменателю 12. Домножив числитель и знаменатель на 3 3/4 = 9/12.
Как привести смешанное число к новому знаменателю
Для приведения смешанного числа к новому знаменателю, необходимо смешанное число преобразовать в неправильную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём дробь 5 целых 3/4 к знаменателю 12.Преобразуем смешанное число в неправильную дробь. 5 целых 3/4 = 23/4 Найдём дополнительный множитель – для этого разделим 12 на 4 получится 12 / 4 = 3. Домножим числитель и знаменатель дроби на 3 получится дробь 69/12
Как привести десятичную дробь к новому знаменателю
Для приведения десятичной дроби к новому знаменателю, необходимо десятичную дробь преобразовать в обыкновенную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём десятичную дробь 2.5 к знаменателю 4.Преобразуем десятичную дробь в обыкновенную дробь. 2.5 =5/2 Найдём дополнительный множитель – для этого разделим 4 на 2 получится 4 / 2 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 10/4
Как привести обыкновенную дробь к новому знаменателю
Для приведения обыкновенной дроби к новому знаменателю, необходимо числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём обыкновенную дробь 2/7 к знаменателю 14. Найдём дополнительный множитель – для этого разделим 14 на 7 получится 14 / 7 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 4/14
Похожие калькуляторы
Рассмотрим на примере как привести дроби к наименьшему общему знаменателю.
Пример Приведите дроби  и
и  к наименьшему общему знаменателю
к наименьшему общему знаменателю

Рассмотрим пример приведения нескольких дробей к наименьшего общего знаменателя нескольких. Для нахождения НОК нескольких чисел воспользуемся свойством: НОК(a, НОК(b, с)) = НОК(НОК(a, b), c)
Пример Приведите несколько дробей  ,
,  и
и  к наименьшему общему знаменателю
к наименьшему общему знаменателю
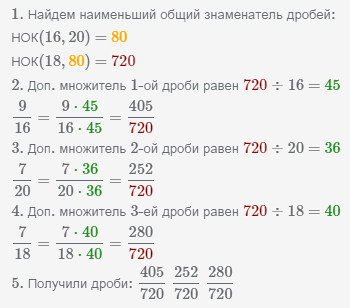
Общее кратное знаменателей НОК(16, 20, 18)=720.
Содержание материала
- Сложение дробей с одинаковыми знаменателями
- Видео
- НОЗ и НОК
- Как устроена десятичная дробь
- Как привести десятичную дробь к новому знаменателю
- Чтобы найти общий знаменатель, перемножим знаменатели:
- Вычитание дробей с разными знаменателями
Сложение дробей с одинаковыми знаменателями
Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.
Пример.
C помощью букв это правило сложения можно записать так:

Записывая ответ, проверьте нельзя ли полученную дробь сократить.
Видео
НОЗ и НОК
При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.
Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.
Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:
16=8*2; 6= 3*2
НОК (16, 6) =8*2*3= 48.
Число 48 и есть искомый НОЗ.
Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:
- Найти НОК.
- Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
- Умножить обе части каждой дроби на их дополнительные множители.
Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:
- Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
- Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
- Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Как привести десятичную дробь к новому знаменателю
Для приведения десятичной дроби к новому знаменателю, необходимо десятичную дробь преобразовать в обыкновенную дробь. Затем числитель и знаменатель дроби домножить на дополнительный множитель.
Разберём пример. Приведём десятичную дробь 2.5 к знаменателю 4.Преобразуем десятичную дробь в обыкновенную дробь. 2.5 =5/2 Найдём дополнительный множитель — для этого разделим 4 на 2 получится 4 / 2 = 2. Домножим числитель и знаменатель дроби на 2 получится дробь 10/4
2.5
=
2.5 × 101 × 10
=
2510
=
5 × 5 2 × 5
=
52
=
5 × 22 × 2
=
104
Чтобы найти общий знаменатель, перемножим знаменатели:
Дополнительный множитель к первой дроби:
Дробь примет вид:
Дополнительный множитель ко второй дроби:
Дробь примет вид:
Дополнительный множитель к третьей дроби:
Дробь примет вид:
Итак, были дроби:
Запишем полученные дроби с общим знаменателем:
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби 



Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям 
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от 


Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей 



Первый рисунок изображает дробь 


Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь 
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби 
Получили ответ
Теги
Приведение дробей к общему знаменателю
- Общий знаменатель обыкновенных дробей
- Приведение дробей к общему знаменателю
- Калькулятор приведения к общему знаменателю
Общий знаменатель обыкновенных дробей
Если обыкновенные дроби имеют одинаковые знаменатели, то про эти дроби говорят, что они имеют общий знаменатель. Например, дроби

имеют общий знаменатель 7.
Общий знаменатель — это число, которое является знаменателем для двух и более обыкновенных дробей.
Дроби, имеющие разные знаменатели, можно привести к общему знаменателю.
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это замена данных дробей, имеющих разные знаменатели, на равные им дроби, у которых одинаковые знаменатели.
Дроби можно привести либо просто к общему знаменателю, либо к наименьшему общему знаменателю.
Наименьший общий знаменатель — это наименьшее общее кратное знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю нужно:
- Выполнить сокращение дробей, если это возможно.
- Найти наименьшее общее кратное знаменателей данных дробей. Именно НОК и станет их наименьшим общим знаменателем.
- Разделить НОК на знаменатели данных дробей. Этим действием мы находим дополнительный множитель для каждой из данных дробей. Дополнительный множитель — это число, на которое надо умножить члены дроби, чтобы привести её к общему знаменателю.
- Умножить числитель и знаменатель каждой дроби на дополнительный множитель.
Пример. Привести к общему знаменателю дроби 

Решение:
- Находим НОК знаменателей данных дробей:
НОК (8, 12) = 24.
- Находим дополнительные множители:
24 : 8 = 3 (для
)
и
24 : 12 = 2 (для
).
- Умножаем члены каждой дроби на свой дополнительный множитель:
Приведение к общему знаменателю можно записывать в более краткой форме, указывая дополнительный множитель рядом с числителем каждой дроби (сверху справа или сверху слева) и не записывая промежуточные вычисления:
К общему знаменателю можно привести и более простым способом, умножив члены первой дроби на знаменатель второй дроби, а члены второй дроби — на знаменатель первой.
Пример. Привести к общему знаменателю дроби 

В качестве общего знаменателя дробей можно взять произведение их знаменателей.
Приведение дробей к общему знаменателю используется при сложении, вычитании и сравнении дробей, у которых разные знаменатели.
Калькулятор приведения к общему знаменателю
Данный калькулятор поможет вам привести обыкновенные дроби к наименьшему общему знаменателю. Просто введите две дроби и нажмите кнопку Привести
.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое дроби?
Дробь – это число, которое состоит из нескольких одинаковых частей – долей единицы, а также из одной ее части.
Обыкновенная дробь выглядит так:
В математической записи дроби число, которое находится выше черты – называется числителем, а число, которое расположено ниже – называется знаменателем. Оно показывает то, на сколько долей разделили единицу.
Первое число является делимым, а второе число служит делителем. Обыкновенные дроби могут образовывать поле рациональных чисел, если они будут с целыми числителями и ненулевыми знаменателями. Они показывают количество долей, на которые делится единица.
Математические дроби начинают изучать в школе. В основном в 5 или в 6 классах. Но также дроби очень часто используются в дальнейшей школьной и затем в вузовской программах.
История дробей
Русское слово «дробь», как и его аналоги в других языках, происходит от латинского слова «fractura» с арабским происхождением и означает в переводе: ломать или дробить. Основы теории обыкновенных дробей заложили греческие и индийские математики. Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.
Позже дроби появляются в Европейской математике, например, у Фибоначчи в 1202 году. Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).
В России, начиная с древней Руси, дроби именовали долями. А в первых отечественных учебниках по математике дроби назывались ломаными числами. Термин «дробь», как аналог латинского «fractura», впервые используется в «Арифметике» Магницкого в 1703 году как для обыкновенных, так и для десятичных дробей.
Виды дробей
Дроби бывают нескольких видов:
- обыкновенные;
- смешанные и простые;
- правильные и неправильные;
- десятичные;
- в виде процентов.
Обыкновенная дробь
Обыкновенная дробь имеет вид a/b. Число a – здесь будет являться числителем дроби, а число b – будет знаменателем.
Примеры:
- 1/2
- 6/5
- 3/1
- 7/15
Правильные и неправильные
Правильной называется дробь, у которой числитель (модуль числителя) меньше модуля знаменателя.
Пример, правильной дроби: 3/4, так как 3<4.
Неправильная дробь, наоборот, имеет числитель, который по модулю больше чем знаменатель.
Пример, неправильной дроби: 4/3, так как 4>3.
Простые и смешанные
Простая дробь содержит только числитель и знаменатель. Например, 4/3.
Смешанная дробь содержит целое число и дробь, и понимается как сумма этого числа и дроби. Например, 1 и 1/3.
Неправильную дробь всегда можно сделать смешанной, то есть выделить в ней целые части.
Десятичная дробь
Десятичная дробь — это запись дроби, в которой знаменатель не дан в явном виде, но понимается как целое число, степень десяти (напр. 10, 100, 1000 и др).
Десятичная дробь записывается через запятую в строку таким образом, чтобы отделить дробную часть от целой части. Вот так:
- 0,7 – ноль целых и 7 десятых (7/10).
- 5,42 – пять целых и 42 сотых (42/100).
- 9,245 – девять целых и 245 тысячных (245/1000).
В виде процентов
Дробь в виде процентов — это когда при переводе десятичной дроби в проценты, ее необходимо умножить на 100. Запись производится с запятыми.
Например, 0,023 = 0,023 * 100% = 2,3%
Для того чтобы перевести проценты в десятичные дроби, следует разделить число процентов на 100.
Что нужно знать, чтобы работать с дробями?
Что переводить дроби из одного вида в другой и выполнять различные операции над дробями, надо знать несколько терминов.
Наименьшее общее кратное (НОК) для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.
Наименьший общий знаменатель – это НОК, которое рассчитывается для знаменателей двух и более дробей.
Как найти наименьший общий знаменатель?
Чтобы это понять, необходимо рассмотреть следующий пример двух дробей:
1/20 и 3/14
Если нужно привести дроби с разными знаменателями к общему наименьшему знаменателю, следует найти наименьшее общее кратное (НОК) знаменателей этих дробей.
Знаменатель первой дроби равен 20.
Его нужно разложить его на простые множители: 20=2⋅5⋅2.
Далее также разложить 2 знаменатель дроби 14 на простые множители: 14 = 7*2.
Убираем повторяющиеся множители у знаменателя второй дроби и получаем:
НОК (14,20) = 2*5*2*7 = 140.
В итоге общий наименьший знаменатель равняется 140.
Как привести дробь к общему знаменателю?
Берем первую дробь 1/20 и умножаем ее на 7, чтобы прийти к 140. Для этого умножаем числитель и знаменательно на 7 и получаем:
А вторую дробь теперь следует умножить на 10 таким же образом:
Общим наибольшим делителем (НОД) нескольких чисел является самое большее целое натуральное число, на которое эти самые числа делятся без остатка.
Общий наибольший делитель обозначается в виде такой записи: НОД (18; 48) = 6.
Как следует переводить дробь?
Из смешанной дроби в обыкновенную:
- Необходимо умножить знаменатель дробной части на единицу целой части;
- К произведению, которое получилось, следует прибавить числитель дробной части;
- Сам знаменатель при этом оставить без изменений.
Из обыкновенной дроби в смешанную:
- Разделить числитель дроби на знаменатель;
- Полученный результат будет являться целой частью;
- То, что останется в результате деления (остаток) будет числителем.
Из десятичной дроби в обыкновенную или смешанную^
- Для этого действия необходимо целую часть умножать на знаменатель дробной части.
- После этого полученный результат сложить с числителем дробной части. То, что получилось в итоге, и будет числителем новой дроби, а сам знаменатель при этом останется без изменений.
Операции над дробями
С дробями можно совершать различные арифметические операции.
➕ Сложение
Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.
Далее – выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.
В конце, если возможно, сократить полученную дробь.
Например:
➖ Вычитание
Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.
Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.
Например:
✖ Умножение
Для этого умножаются числители и записывается результат, как числитель дроби.
Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.
Например:
➗ Деление
Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.
Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.
Например:
📏 Сокращение
Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.
В итоге получается равную дробь, имеющая меньший знаменатель и числитель.
Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.
Значительно упростит сокращение раскладывание знаменателя и числителя на множители.
Например:
❓ Вопросы и ответы
А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них.
Какие дроби называются простыми?
Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.
Какие дроби называются десятичными?
Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название – десятичные.
Какие дроби называются правильными?
Правильные дроби те, у которых модуль знаменателя больше модуля числителя.
Какие дроби называются неправильными?
Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.
Как разделить дробь на дробь?
Нельзя делить на 0.
Если делить на 1 – будет такое же число.
Если делить 0 на любое число, получится 0.
Какая дробь называется положительной?
Когда она больше 0.
Какая дробь называется отрицательной?
Когда перед положительной дробью ставится знак «–».
Что такое степени с дробями?
Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.
При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.
Как пользоваться калькулятором дробей?
Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.
Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор логарифмов. Вычислите онлайн натуральные, десятичные логарифмы (или с другим основанием) с решением.
- Возведение дроби в степень. Возведите онлайн любую дробь (десятичную и обыкноенную) в любую степень.
- Калькулятор процентов от числа. Рассчитайте онлайн значение процента от любого числа с помощью данного калькулятора.
- Калькулятор процентов. Рассчитайте онлайн процент от числа, на сколько процентов одно число больше или меньше другого, или сколько процентов составляет одно число от другого числа, а также прибавьте или вычтете процент к числу.
- Добавить процент к числу. Прибавьте онлайн любой процент к любому числу с помощью специального калькулятора.
- Вычесть процент из числа. Вычтете онлайн любой процент от любого числа с помощью специального калькулятора.
- На сколько процентов больше. Рассчитайте онлайн, на сколько процентов одно число больше другого.
- На сколько процентов меньше. Рассчитайте онлайн, на сколько процентов одно число меньше другого.
- Тренажер таблицы умножения. Тренируйтесь и запоминайте таблицу умножения онлайн. Выберите нужный диапазон множителей, и система сгенерирует задания.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
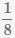 и
и 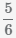 к наименьшему общему знаменателю
к наименьшему общему знаменателю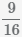 ,
, 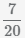 и
и 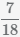 к наименьшему общему знаменателю
к наименьшему общему знаменателю