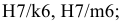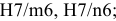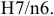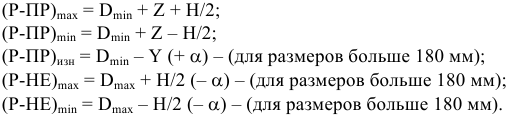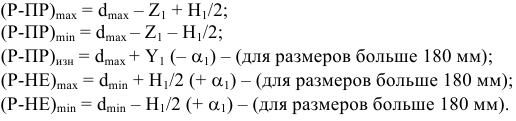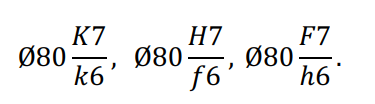Для данного размера
отверстия: Ø16+0,035+0,070определить
значение допуска: TD
= ES
– EI
= 0,070 – 0,030 = 0,040(мм) = 40мкм;
для полученного
расчетного
значения допуска по таблице допусков
(табл.1) подобрать ближайшее стандартное
значение и соответствующий номер
квалитета:
для размера Ø16
(интервал cв.10
до18) ближайший к 40мкм стандартный допуск
– 43мкм,
что соответствует 9-му
квалитету:
IT9
= 43мкм;
2.Определить стандартное значение основного отклонения.
Из двух расчетных
предельных отклонений основным
является ближайшее
к нулевой линии
(в данном случае нижнее)
EI
= +0,03 = 30мкм;
По таблицам основных
отклонений для отверстий
(нижних)
(прилож.3) ближайшее стандартное
значение к 30мкм для размера Ø16 (интервал
cв.14
до18) соответствует 32мкм
(условное обозначение – буква Е)
3.Определить второе предельное отклонение – es .
Зная стандартное
основное отклонение – EI
= 0,032мм (Е)
и стандартный допуск – TD
= 0,043мм (IT9),
определить второе предельное отклонение:
так как TD
= ES
–EI,
тогда
ES
= TD
+EI
= 0,043 + 0,032 = 0,075(мкм).
Следовательно,
буквенное (условное) обозначение поля
допуска и стандартные числовые предельные
отклонения заданного отверстия:
+0,075
+0,032
Ø16Е9(
):
4. Определить систему посадок для отверстия ø16е9:
Определить систему
посадок позволяет выявление основной
детали. Полученное поле допуска (Е9) не
является
полем допуска основного отверстия,
следовательно, основной
деталью в
этом соединении будет вал
(h),
что и определит систему
посадок.
Таким образом,
отверстие с полем допуска Е9
образует с
валом номинального размера Ø16
посадку в системе
вала (вал
– основная деталь(h);
5. Определить предельные отклонения вала:
Чтобы определить
допуск и квалитет вала, необходимо
учесть заданное условие: Т(S)
= 0,070мм, а так
как T(S)
= TD
+ Td,
то, зная величину допуска отверстия
TD
= 0,043мм
(IT6),
можно определить допуск вала:
Td
= T(S)
– TD
= 0,070 – 0,043 = 0,027(мм),
По таблице допусков
ближайшее стандартное значение допуска
вала для размера 16
совпадает с расчетным значением допуска
и соответствует 8-му квалитету IT8
= 0,027мм ;
Так как для основного
вала es
= 0, ei=
– Td,
следовательно
ei
= – 0,027мм
а поле допуска
вала принимает вид: Ø16h8(
– 0,027)
В результате: обозначение на рабочих
чертежах стандартных полей допусков
и предельных отклонений вала и отверстия,
а так же обозначение посадки на сборочном
чертеже:
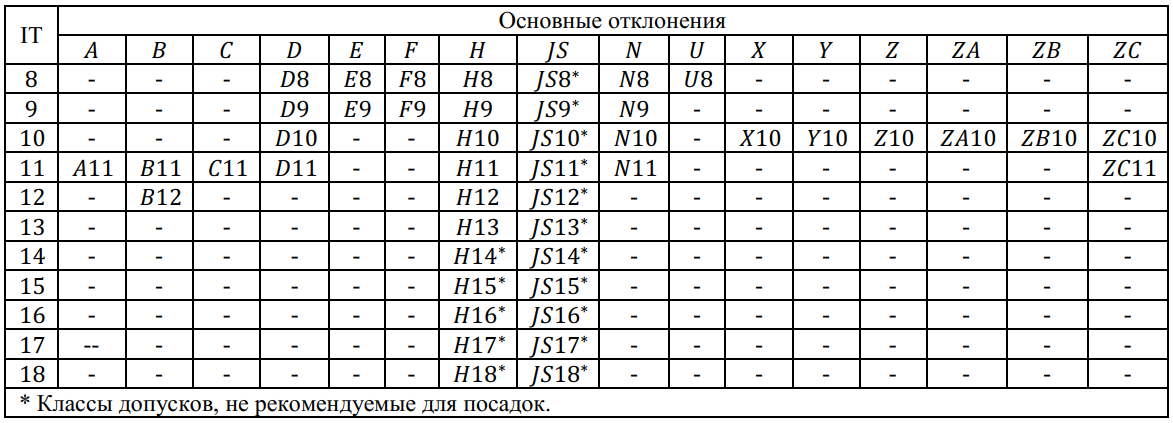
Приложение 3
ЧИСЛОВЫЕ ЗНАЧЕНИЯ
ОСНОВНЫХ (ВЕРХНИХ es)
ОТКЛОНЕНИЙ ВАЛОВ.
|
Интервал |
Основные |
||||||||||||
|
a1 |
b1 |
c |
cd |
d |
e |
ef |
f |
fg |
g |
h |
js2 |
||
|
Свыше |
До |
Для |
|||||||||||
|
3 |
–270 |
–140 |
–60 |
–34 |
–20 |
–14 |
–10 |
–6 |
–4 |
–2 |
0 |
Предельные |
|
|
3 |
6 |
–270 |
‑140 |
–70 |
–46 |
–30 |
–20 |
–14 |
–10 |
–6 |
–4 |
0 |
|
|
6 |
10 |
–280 |
–150 |
–80 |
–56 |
–40 |
–25 |
–18 |
–13 |
–8 |
–5 |
0 |
|
|
10 |
14 |
–290 |
‑150 |
–95 |
– |
–50 |
–32 |
– |
–16 |
– |
–6 |
0 |
|
|
14 |
18 |
||||||||||||
|
18 |
24 |
–300 |
‑160 |
–110 |
‑ |
–65 |
–40 |
– |
–20 |
– |
–7 |
0 |
|
|
24 |
30 |
||||||||||||
|
30 |
40 |
–310 |
–170 |
–120 |
‑ |
–80 |
–50 |
– |
-25 |
– |
–9 |
0 |
|
|
40 |
50 |
–320 |
–180 |
–130 |
|||||||||
|
50 |
65 |
–340 |
–190 |
–140 |
‑ |
–100 |
–60 |
– |
–30 |
– |
–10 |
0 |
|
|
65 |
80 |
–360 |
–200 |
–150 |
|||||||||
|
80 |
100 |
–380 |
–220 |
–170 |
‑ |
–120 |
–72 |
– |
–36 |
– |
–12 |
0 |
|
|
100 |
120 |
–410 |
–240 |
–180 |
|||||||||
|
120 |
140 |
–460 |
–260 |
–200 |
– |
–145 |
–85 |
– |
–43 |
– |
–14 |
0 |
|
|
140 |
160 |
–520 |
–280 |
–210 |
|||||||||
|
160 |
180 |
–580 |
–310 |
–230 |
|||||||||
|
180 |
200 |
–660 |
‑340 |
–240 |
– |
–170 |
–100 |
– |
–50 |
– |
‑15 |
0 |
|
|
200 |
225 |
–740 |
–380 |
–260 |
|||||||||
|
225 |
250 |
–820 |
–420 |
–280 |
|||||||||
|
250 |
280 |
–920 |
–480 |
–300 |
– |
–190 |
–110 |
– |
–56 |
– |
–17 |
0 |
|
|
280 |
315 |
–1050 |
–540 |
–330 |
|||||||||
|
315 |
355 |
–1200 |
–600 |
–360 |
– |
–210 |
–125 |
– |
–62 |
– |
–18 |
0 |
|
|
355 |
400 |
–1350 |
–680 |
–400 |
|||||||||
|
400 |
450 |
–1500 |
–760 |
–440 |
– |
–230 |
–135 |
– |
–68 |
– |
–20 |
0 |
|
|
450 |
500 |
–1650 |
–840 |
–480 |
1
Основные отклонения а и b
не предусмотрены для размеров менее 1
мм.
2
Для полей допусков от js7
до js11
нечетные числовые значения IT
могут быть округлены до ближайшего
меньшего четного числа, чтобы предельные
отклонения
были выражены целым числом микрометров.
3
Специальный случай: поле допуска m7
предусмотрено лишь для размеров свыше
3 мм.
ЧИСЛОВЫЕ ЗНАЧЕНИЯ
ОСНОВНЫХ (НИЖНИХ ei)
ОТКЛОНЕНИЙ ВАЛОВ.
|
Интервал |
Основные |
|||||||||||||||||||
|
j (для |
k (для |
m3 |
n |
p |
r |
s |
t |
u |
v |
x |
y |
z |
za |
zb |
zc |
|||||
|
Свыше |
До |
5 |
7 |
8 |
От |
До |
Для |
|||||||||||||
|
3 |
–2 |
–4 |
–6 |
0 |
0 |
+2 |
+4 |
+6 |
+10 |
+14 |
— |
+18 |
— |
+20 |
— |
+26 |
+32 |
+40 |
+60 |
|
|
3 |
6 |
–2 |
–4 |
– |
+1 |
0 |
+4 |
+8 |
+12 |
+15 |
+19 |
— |
+23 |
— |
+28 |
— |
+35 |
+42 |
+50 |
+80 |
|
6 |
10 |
–2 |
–5 |
– |
+1 |
0 |
+6 |
+10 |
+15 |
+19 |
+23 |
— |
+28 |
— |
+34 |
— |
+42 |
+52 |
+67 |
+97 |
|
10 |
14 |
–3 |
–6 |
– |
+1 |
0 |
+7 |
+12 |
+18 |
+23 |
+28 |
— |
+33 |
— |
+40 |
— |
+50 |
+64 |
+90 |
+130 |
|
14 |
18 |
+39 |
+45 |
— |
+60 |
+77 |
+108 |
+150 |
||||||||||||
|
18 |
24 |
–4 |
–8 |
– |
+2 |
0 |
+8 |
+15 |
+22 |
+28 |
+35 |
— |
+41 |
+47 |
+54 |
+63 |
+73 |
+98 |
+136 |
+188 |
|
24 |
30 |
+41 |
+48 |
+55 |
+64 |
+75 |
+88 |
+118 |
+160 |
+218 |
||||||||||
|
30 |
40 |
–5 |
–10 |
– |
+2 |
0 |
+9 |
+17 |
+26 |
+34 |
+43 |
+48 |
+60 |
+68 |
+80 |
+94 |
+112 |
+148 |
+200 |
+274 |
|
40 |
50 |
+54 |
+70 |
+81 |
+97 |
+114 |
+136 |
+180 |
+242 |
+325 |
||||||||||
|
50 |
65 |
–7 |
–12 |
– |
+2 |
0 |
+11 |
+20 |
+32 |
+41 |
+53 |
+66 |
+87 |
+102 |
+122 |
+144 |
+172 |
+226 |
+300 |
+405 |
|
65 |
80 |
+43 |
+59 |
+75 |
+102 |
+120 |
+146 |
+174 |
+210 |
+274 |
+360 |
+480 |
||||||||
|
80 |
100 |
–9 |
–15 |
– |
+3 |
0 |
+13 |
+23 |
+37 |
+51 |
+71 |
+91 |
+124 |
+146 |
+178 |
+214 |
+258 |
+335 |
+445 |
+585 |
|
100 |
120 |
+54 |
+79 |
+104 |
+144 |
+172 |
+210 |
+254 |
+310 |
+400 |
+525 |
+690 |
||||||||
|
120 |
140 |
–11 |
–18 |
– |
+3 |
0 |
+15 |
+27 |
+43 |
+63 |
+92 |
+122 |
+170 |
+202 |
+248 |
+300 |
+365 |
+470 |
+620 |
+800 |
|
140 |
160 |
+65 |
+100 |
+134 |
+190 |
+228 |
+280 |
+340 |
+415 |
+535 |
+700 |
+900 |
||||||||
|
160 |
180 |
+68 |
+108 |
+146 |
+210 |
+252 |
+310 |
+380 |
+465 |
+600 |
+780 |
+1000 |
||||||||
|
180 |
200 |
–13 |
–21 |
– |
+4 |
0 |
+17 |
+31 |
+50 |
+77 |
+122 |
+166 |
+236 |
+284 |
+350 |
+425 |
+520 |
+670 |
+880 |
+1150 |
|
200 |
225 |
+80 |
+130 |
+180 |
+258 |
+310 |
+385 |
+470 |
+575 |
+740 |
+960 |
+1250 |
||||||||
|
225 |
250 |
+84 |
+140 |
+196 |
+284 |
+340 |
+425 |
+520 |
+640 |
+820 |
+1050 |
+1350 |
||||||||
|
250 |
280 |
–16 |
–26 |
‑ |
+4 |
0 |
+20 |
+34 |
+56 |
+94 |
+158 |
+218 |
+315 |
+385 |
+475 |
+580 |
+710 |
+920 |
+1200 |
+1550 |
|
280 |
315 |
+98 |
+170 |
+240 |
+350 |
+425 |
+525 |
+650 |
+790 |
+1000 |
+1300 |
+1700 |
||||||||
|
315 |
355 |
–18 |
–28 |
‑ |
+4 |
0 |
+21 |
+37 |
+62 |
+108 |
+190 |
+268 |
+390 |
+475 |
+590 |
+730 |
+900 |
+1150 |
+1500 |
+1900 |
|
355 |
400 |
+114 |
+208 |
+294 |
+435 |
+530 |
+660 |
+820 |
+1000 |
+1300 |
+1650 |
+2100 |
||||||||
|
400 |
450 |
–20 |
–32 |
‑ |
+5 |
0 |
+23 |
+40 |
+68 |
+126 |
+232 |
+330 |
+490 |
+595 |
+740 |
+920 |
+1100 |
+1450 |
+1850 |
+2400 |
|
450 |
500 |
+132 |
+252 |
+360 |
+540 |
+660 |
+820 |
+1000 |
+1250 |
+1600 |
+2100 |
+2600 |
1
Основные отклонения а и b
не предусмотрены для размеров менее 1
мм.
2
Для полей допусков от js7
до js11
нечетные числовые значения IT
могут быть округлены до ближайшего
меньшего четного числа, чтобы предельные
отклонения
были выражены целым числом микрометров.
3
Специальный случай: поле допуска m
7 предусмотрено лишь для размеров свыше
3 мм.
ЧИСЛОВЫЕ ЗНАЧЕНИЯ
ОСНОВНЫХ (НИЖНИХ EI)
ОТКЛОНЕНИЙ ОТВЕРСТИЙ.
|
Интервал |
Основные |
||||||||||||
|
A1 |
B1 |
C |
CD |
D |
E |
EF |
F |
FG |
G |
H |
Js2 |
||
|
Свыше |
До |
Для |
|||||||||||
|
3 |
+270 |
+140 |
+60 |
+34 |
+20 |
+14 |
+10 |
+6 |
+4 |
+2 |
0 |
Предельные |
|
|
3 |
6 |
+270 |
+140 |
+70 |
+46 |
+30 |
+20 |
+14 |
+10 |
+6 |
+4 |
0 |
|
|
6 |
10 |
+280 |
+150 |
+80 |
+56 |
+40 |
+25 |
+18 |
+13 |
+8 |
+5 |
0 |
|
|
10 |
14 |
+290 |
+150 |
+95 |
– |
+50 |
+32 |
– |
+16 |
– |
+6 |
0 |
|
|
14 |
18 |
||||||||||||
|
18 |
24 |
+300 |
+160 |
+110 |
‑ |
+65 |
+40 |
– |
+20 |
– |
+7 |
0 |
|
|
24 |
30 |
||||||||||||
|
30 |
40 |
+310 |
+170 |
+120 |
– |
+80 |
+50 |
– |
+25 |
– |
+9 |
0 |
|
|
40 |
50 |
+320 |
+180 |
+130 |
|||||||||
|
50 |
65 |
+340 |
+190 |
+140 |
‑ |
+100 |
+60 |
– |
+30 |
– |
+10 |
0 |
|
|
65 |
80 |
+360 |
+200 |
+150 |
|||||||||
|
80 |
100 |
+380 |
+220 |
+170 |
‑ |
+120 |
+72 |
– |
+36 |
– |
+12 |
0 |
|
|
100 |
120 |
+410 |
+240 |
+180 |
|||||||||
|
120 |
140 |
+460 |
+260 |
+200 |
– |
+145 |
+85 |
– |
+43 |
– |
+14 |
0 |
|
|
140 |
160 |
+520 |
+280 |
+210 |
|||||||||
|
160 |
180 |
+580 |
+310 |
+230 |
|||||||||
|
180 |
200 |
+660 |
+340 |
+240 |
– |
+170 |
+100 |
– |
+50 |
– |
+15 |
0 |
|
|
200 |
225 |
+740 |
+380 |
+260 |
|||||||||
|
225 |
250 |
+820 |
+420 |
+280 |
|||||||||
|
250 |
280 |
+920 |
+480 |
+300 |
– |
+190 |
+110 |
– |
+56 |
– |
+17 |
0 |
|
|
280 |
315 |
+1050 |
+540 |
+330 |
|||||||||
|
315 |
355 |
+1200 |
+600 |
+360 |
– |
+210 |
+125 |
– |
+62 |
– |
+18 |
0 |
|
|
355 |
400 |
+1350 |
+680 |
+400 |
|||||||||
|
400 |
450 |
+1500 |
+760 |
+440 |
– |
+230 |
+135 |
– |
+68 |
– |
+20 |
0 |
|
|
450 |
500 |
+1650 |
+840 |
+480 |
ЧИСЛОВЫЕ ЗНАЧЕНИЯ
ОСНОВНЫХ (ВЕРХНИХ ES)
ОТКЛОНЕНИЙ ОТВЕРСТИЙ.
|
Интервал |
Основные |
Δ, мкм |
||||||||||||||
|
J |
K3 |
M3 |
N3 |
|||||||||||||
|
Для |
Для |
|||||||||||||||
|
Свыше |
До |
6 |
7 |
8 |
До |
Св. 8 |
До |
Св. 8 |
До 8 |
Св. 8 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
+2 |
+4 |
+6 |
0 |
0 |
–2 |
–2 |
–4 |
–4 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
6 |
+5 |
+6 |
+10 |
–1+ |
– |
–4+ |
–4 |
–8+ |
0 |
1 |
1,5 |
1 |
3 |
4 |
6 |
|
6 |
10 |
+5 |
+8 |
+12 |
–1+ |
– |
–6+ |
–6 |
–10+ |
0 |
1 |
1,5 |
2 |
3 |
6 |
7 |
|
10 |
14 |
+6 |
+10 |
+15 |
–1+ |
‑ |
–7+ |
–7 |
–12+ |
0 |
1 |
2 |
3 |
3 |
7 |
9 |
|
14 |
18 |
|||||||||||||||
|
18 |
24 |
+8 |
+12 |
+20 |
–2+ |
‑ |
–8+ |
–8 |
–15+ |
0 |
1,5 |
2 |
3 |
4 |
8 |
12 |
|
24 |
30 |
|||||||||||||||
|
30 |
40 |
+10 |
+14 |
+24 |
–2+ |
‑ |
–9+ |
–9 |
–17+ |
0 |
1,5 |
3 |
4 |
5 |
9 |
14 |
|
40 |
50 |
|||||||||||||||
|
50 |
65 |
+13 |
+18 |
+28 |
–2+ |
‑ |
–11+ |
–11 |
–20+ |
0 |
2 |
3 |
5 |
6 |
11 |
16 |
|
65 |
80 |
|||||||||||||||
|
80 |
100 |
+16 |
+22 |
+34 |
–3+ |
‑ |
–13+ |
–13 |
–23+ |
0 |
2 |
4 |
5 |
7 |
13 |
19 |
|
100 |
120 |
|||||||||||||||
|
120 |
140 |
+18 |
+26 |
+41 |
–3+ |
– |
–15+ |
–15 |
–27+ |
0 |
3 |
4 |
6 |
7 |
15 |
23 |
|
140 |
160 |
|||||||||||||||
|
160 |
180 |
|||||||||||||||
|
180 |
200 |
+22 |
+30 |
+47 |
–4+ |
‑ |
–17+ |
–17 |
–31+ |
0 |
3 |
4 |
6 |
9 |
17 |
26 |
|
200 |
225 |
|||||||||||||||
|
225 |
250 |
|||||||||||||||
|
250 |
280 |
+25 |
+36 |
+55 |
–4+ |
– |
–20+ |
–20 |
–34+ |
0 |
4 |
4 |
7 |
9 |
20 |
29 |
|
280 |
315 |
|||||||||||||||
|
315 |
355 |
+29 |
+39 |
+60 |
–4+ |
‑ |
–21+ |
–21 |
–37+ |
0 |
4 |
5 |
7 |
11 |
21 |
32 |
|
355 |
400 |
|||||||||||||||
|
400 |
450 |
+33 |
+43 |
+66 |
–5+ |
‑ |
–23+ |
–23 |
–40+ |
0 |
5 |
5 |
7 |
13 |
23 |
34 |
|
450 |
500 |
ЧИСЛОВЫЕ ЗНАЧЕНИЯ
ОСНОВНЫХ (ВЕРХНИХ ES)
ОТКЛОНЕНИЙ ОТВЕРСТИЙ.
|
Интервал |
Основные |
1
2
3
4
5 |
||||||||||||
|
от |
P |
R |
S |
T |
U |
V |
X |
Y |
Z |
ZA |
ZB |
ZC |
||
|
Свыше |
До |
До 7 квалитета |
Для |
|||||||||||
|
3 |
Отклонения как |
-6 |
-10 |
-14 |
— |
-18 |
— |
-20 |
— |
-26 |
-32 |
-40 |
-60 |
|
|
3 |
6 |
-12 |
-15 |
–19 |
— |
-23 |
— |
-28 |
— |
-35 |
-42 |
-50 |
-80 |
|
|
6 |
10 |
-15 |
-19 |
-23 |
— |
-28 |
— |
-34 |
— |
-42 |
-52 |
-67 |
-97 |
|
|
10 |
14 |
-18 |
-23 |
-28 |
— |
-33 |
— |
-40 |
— |
-50 |
-64 |
-90 |
-130 |
|
|
14 |
18 |
-39 |
-45 |
— |
-60 |
-77 |
-108 |
-150 |
||||||
|
18 |
24 |
-22 |
-28 |
-35 |
— |
-41 |
-47 |
-54 |
-63 |
-73 |
-98 |
-136 |
-188 |
|
|
24 |
30 |
+41 |
-48 |
-55 |
-64 |
-75 |
-88 |
-118 |
-160 |
-218 |
||||
|
30 |
40 |
-26 |
-34 |
-43 |
+48 |
-60 |
-68 |
-80 |
-94 |
-112 |
-148 |
-200 |
-274 |
|
|
40 |
50 |
+54 |
-70 |
-81 |
-97 |
-114 |
-136 |
-180 |
-242 |
-325 |
||||
|
50 |
65 |
-32 |
-41 |
-53 |
-66 |
-87 |
-102 |
-122 |
-144 |
-172 |
-226 |
-300 |
-405 |
|
|
65 |
80 |
-43 |
-59 |
-75 |
-102 |
-120 |
-146 |
-174 |
-210 |
-274 |
-360 |
-480 |
||
|
80 |
100 |
-37 |
-51 |
-71 |
-91 |
-124 |
-146 |
-178 |
-214 |
-258 |
-335 |
-445 |
-585 |
|
|
100 |
120 |
-54 |
-79 |
-104 |
-144 |
-172 |
-210 |
-254 |
-310 |
-400 |
-525 |
-690 |
||
|
120 |
140 |
-43 |
-63 |
-92 |
-122 |
-170 |
-202 |
-248 |
-300 |
-365 |
-470 |
-620 |
-800 |
|
|
140 |
160 |
-65 |
-100 |
-134 |
-190 |
-228 |
-280 |
-340 |
-415 |
-535 |
-700 |
-900 |
||
|
160 |
180 |
-68 |
-108 |
-146 |
-210 |
-252 |
-310 |
-380 |
-465 |
-600 |
-780 |
-1000 |
||
|
180 |
200 |
-50 |
-77 |
-122 |
-166 |
-236 |
-284 |
-350 |
-425 |
-520 |
-670 |
-880 |
-1150 |
|
|
200 |
225 |
-80 |
-130 |
-180 |
-258 |
-310 |
-385 |
-470 |
-575 |
-740 |
-960 |
-1250 |
||
|
225 |
250 |
-84 |
-140 |
-196 |
-284 |
-340 |
-425 |
-520 |
-640 |
-820 |
-1050 |
-1350 |
||
|
250 |
280 |
-56 |
-94 |
-158 |
-218 |
-315 |
-385 |
-475 |
-580 |
-710 |
-920 |
-1200 |
-1550 |
|
|
280 |
315 |
-98 |
-170 |
-240 |
-350 |
-425 |
-525 |
-650 |
-790 |
-1000 |
-1300 |
-1700 |
||
|
315 |
355 |
-62 |
-108 |
-190 |
-268 |
-390 |
-475 |
-590 |
-730 |
-900 |
-1150 |
-1500 |
-1900 |
|
|
355 |
400 |
-114 |
-208 |
-294 |
-435 |
-530 |
-660 |
-820 |
-1000 |
-1300 |
-1650 |
-2100 |
||
|
400 |
450 |
-68 |
-126 |
-232 |
-330 |
-490 |
-595 |
-740 |
-920 |
-1100 |
-1450 |
-1850 |
-2400 |
|
|
450 |
500 |
-132 |
-252 |
-360 |
-540 |
-660 |
-820 |
-1000 |
-1250 |
-1600 |
-2100 |
-2600 |
Соседние файлы в папке Раздаточный материал
- #
- #
- #
- #
- #
- #
- #
Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по разделу: допуски и посадки, с решением по каждой теме, чтобы вы смогли подготовиться к экзамену или освежить память перед контрольной работой!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Допуски и посадки в метрологии
Посадка — это характер соединения двух деталей, определяемый разностью их размеров до сборки.
Зазор — это разность между размерами отверстия и вала до сборки, если отверстие больше размера вала.
Натяг — это разность между размерами вала и отверстия до сборки, если размер вала больше размера отверстия.
Допуск посадки — это сумма допусков отверстия и вала, составляющих соединение.
Посадка с зазором — это посадка, при которой всегда образуется зазор в соединении, т.е. наименьший предельный размер отверстия больше наибольшего предельного размера вала или равен ему.
Посадка с натягом — это посадка, при которой всегда образуется зазор в соединении, т.е. наименьший предельный размер отверстия больше наибольшего предельного размера вала или равен ему.
Переходная посадка — это посадка, при которой возможно получение как зазора так и натяга в соединении, в зависимости от действительных размеров отверстия и вала.
Вал — это термин, условно применяемый для обозначения наружных элементов деталей, включая и нецилиндрические элементы.
Отверстие — это термин, условно применяемый для обозначения внутренних элементов деталей, включая и нецилиндрические элементы.
Размер — это числовое значение линейной величины (диаметра, длины и т.п.) в выбранных единицах измерения.
Квалитет — это совокупность допусков, рассматриваемых как соответствующие одному уровню точности для всех номинальных размеров.
Нормирование точности размеров деталей гладких цилиндрических соединений
Взаимозаменяемость. Основные понятия
Представьте себе, что во время работы какой-то машины износилась или сломалась деталь. Что делать? Изготовить её своими силами? Это потребует много времени, да и не всегда возможно в силу целого ряда причин. Проще взять со склада запасную деталь и заменить ею вышедшую из строя.
Возможно эта страница вам будет полезна:
Конечно, новая деталь должна по своим размерам и форме точно соответствовать заменяемой. Иначе пришлось бы потратить много времени на её подгонку. Такая несложная замена стала возможной в современном производстве машин благодаря применению принципа взаимозаменяемости.
Взаимозаменяемость — это принцип конструирования, производства и эксплуатации машин и других изделий, обеспечивающий их бесподгоночную сборку (или замену при ремонте) из независимо изготовленных сопрягаемых деталей и элементов при соблюдении предъявляемых к машинам и изделиям технических требований.
Взаимозаменяемыми могут быть детали, узлы, изделия в целом. При сборке используются стандартные крепежные детали, подшипники качения, электротехнические, резиновые, пластмассовые изделия и агрегаты, получаемые по кооперации. Есть и другое определение взаимозаменяемости, но суть понятия не изменилась.
Взаимозаменяемость — это свойство независимо изготовленных с заданной точностью деталей и составных частей машин, приборов и других изделий обеспечивать возможность беспригоночной сборки (или замены при ремонте) сопрягаемых деталей в составные части, а составных частей — в изделия при соблюдении предъявляемых к составным частям и изделиям технических требований.
Виды взаимозаменяемости:
- полная — обеспечивает возможность беспригоночной сборки (или замены при ремонте) любых независимо изготовленных с заданной точностью однотипных деталей в сборочные единицы или изделия при соблюдении предъявляемых к ним (сборочным единицам или изделиям) технических требований по всем параметрам качества. При полной взаимозаменяемости упрощается сборка, которая сводится к простому соединению деталей рабочими невысокой квалификации, сборочный процесс точно нормируется во времени, согласуется с темпом работы конвейера, и создаются возможности организации производства поточным методом, появляются возможности для автоматизации процессов изготовления и сборки изделий, упрощается ремонт изделий, т.к. любая износившаяся или поломанная деталь могут быть заменены запасными. Например, замена электрической лампочки или сломанной иглы в швейной машинке не вызывает удивления, хотя патрон для лампочки и лампочка, швейная машинка и игла были изготовлены в разное время, на разных предприятиях и даже, может быть, в разных странах;
- неполная (ограниченная) — когда для получения требуемой точности сборки применяют групповой подбор деталей (селективную сборку), компенсаторы, регулирование положения некоторых частей машин и приборов, пригонку и другие дополнительные технологические мероприятия при обязательном выполнении требований к качеству сборочных единиц и изделий. Если в телевизоре сгорел кинескоп, то новый устанавливают в старый корпус, на то же место (полная взаимозаменяемость по размерам), но, как правило, требуется регулировать некоторые характеристики, подстраивать их до требуемого уровня, т.е. по таким элементам телевизор обладает ограниченной взаимозаменяемостью;
- внешняя — это взаимозаменяемость покупных и кооперируемых изделий и сборочных единиц по эксплуатационным показателям, а также по размерам и форме присоединительных поверхностей. Внешняя взаимозаменяемость присуща только готовым изделиям или узлам. Например, электрические двигатели (по частоте вращения вала и мощности, а также по точности размера между присоединительными крепёжными отверстиями); подшипники качения (по точности самого подшипника, а также по точности размеров посадочных поверхностей — отверстию внутреннего кольца и наружной поверхности наружного кольца);
- внутренняя — это взаимозаменяемость деталей, входящих в узел, или узлов, входящих в изделие. Например, в подшипниках качения — взаимозаменяемость тел качения и колец;
- функциональная — это взаимозаменяемость по основным эксплуатационным показателям работы изделия, определяющим его служебные функции. Одно из главных условий обеспечения функциональной взаимозаменяемости — это установление связей эксплуатационных показателей с функциональными параметрами и независимое изготовление деталей и составных частей по этим параметрам с точностью, определяемой исходя из допускаемых отклонений эксплуатационных показателей в конце срока их службы.
Уровень взаимозаменяемости на производстве определяется коэффициентом взаимозаменяемости:
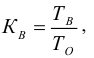
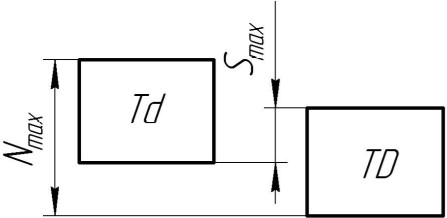
где 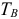
Две или несколько деталей, подвижно или неподвижно соединенные друг с другом, называются соединением (рис. 1.1).
В соединении двух деталей, входящих одна в другую, различают охватывающую и охватываемую поверхности. Для гладких цилиндрических соединений охватывающая поверхность называется отверстием, а охватываемая — валом. Соответствующие им размеры — диаметр отверстия и диаметр вала (рис. 1.2).
Понятие точности, линейные размеры и отклонения
Точностью изготовления называют степень приближения действительных значений геометрических и других параметров деталей и изделий к их заданным значениям, указанным в чертежах или технических требованиях. Достичь заданной точности — значит изготовить детали и собрать механизм так, чтобы погрешности геометрических, электрических и других параметров находились в установленных пределах.
Точность размеров — это степень приближения действительных значений размеров деталей машин к размерам, заданным на чертеже.
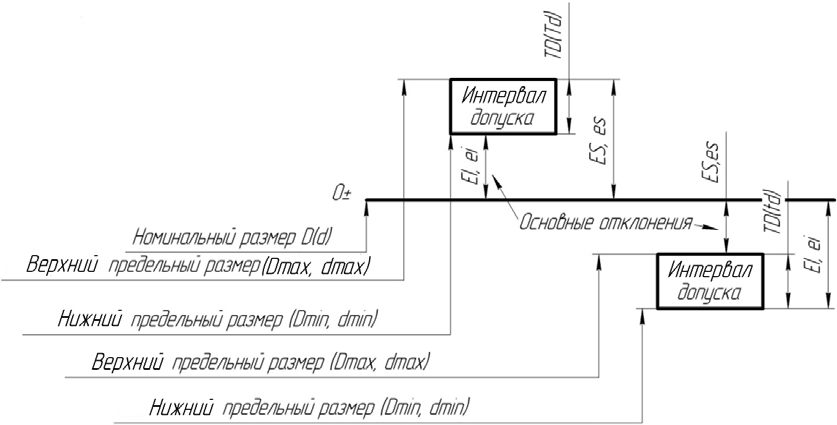
На рабочих чертежах деталей проставляют в первую очередь номинальные размеры.
Номинальный размер — это основной размер, определенный исходя из функционального назначения детали и служащий началом отсчета отклонений. Общий для отверстия и вала, составляющих соединение, номинальный размер называется номинальным размером соединения (см. рис. 1.2).
Есть и другое определение номинального размера. Номинальный размер — это размер, относительно которого определяют предельные размеры и который служит также началом отсчета отклонений. 
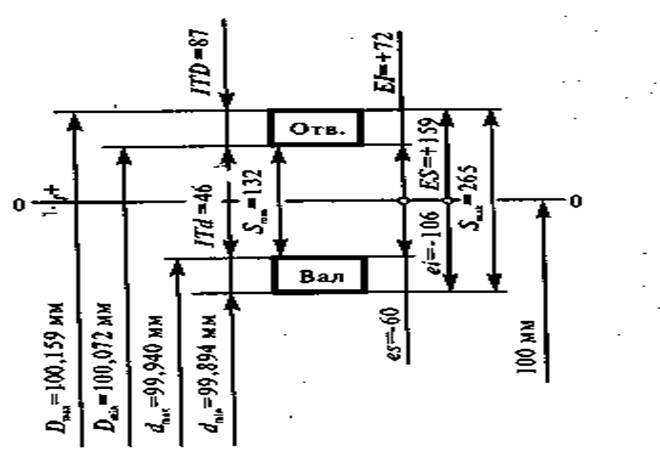
Обработать деталь точно по номинальному размеру практически невозможно из-за многочисленных погрешностей, влияющих на процесс обработки. Размеры обработанной детали отличаются от заданного номинального размера, поэтому их ограничивают двумя предельно допустимыми размерами, один из которых (больший) называется наибольшим предельным размером, а другой (меньший) — наименьшим предельным размером. В расчетах используются следующие обозначения: 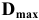
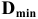
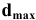
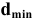
Действительный размер — размер, полученный в результате измерения с допустимой погрешностью. Например: 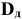
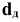
Деталь является годной, если ее действительный размер больше наименьшего предельного размера, но не превосходит наибольшего предельного размера, т.е.
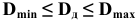
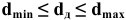
Верхнее отклонение размера — это алгебраическая разность между наибольшим предельным и номинальным размерами.
Например:
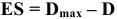
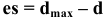
Нижнее отклонение размера — это алгебраическая разность между наименьшим предельным и номинальным размерами.
Например:
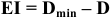
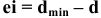
Отклонения бывают положительными, отрицательными и равными нулю. Отклонения, равные нулю, в обозначении не указываются. На чертежах номинальные и предельные линейные размеры и их отклонения проставляют в миллиметрах без указания единицы физической величины.
Пример:
Зная предельные отклонения и используя формулы их расчета, можно рассчитать значения предельных размеров:

Допуски размеров, посадки и допуск посадки
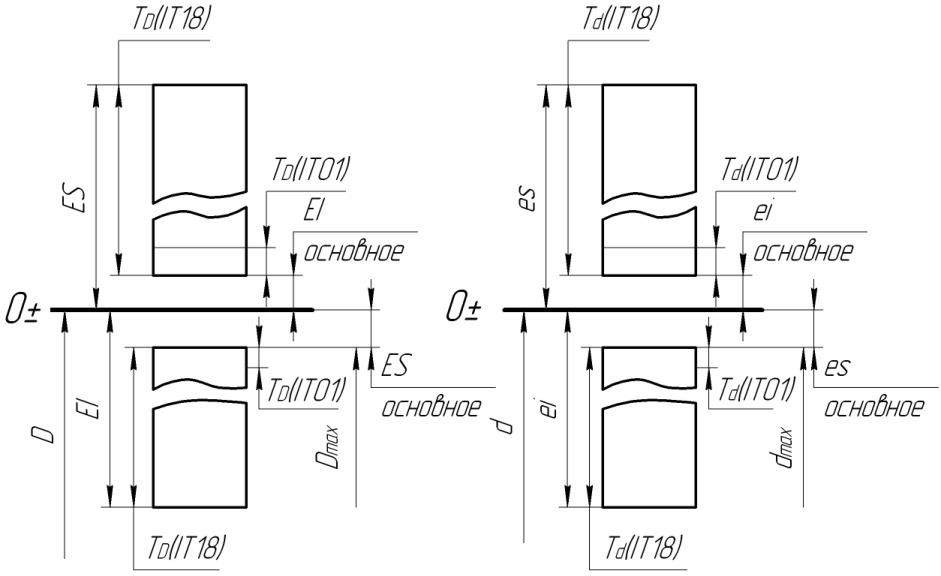
Допуском размера называется разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями.
Допуск обозначают буквой «Т» (от латинского Tolerance — допуск):
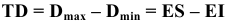
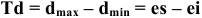
Для рассмотренных ранее примеров 1 — 6 (раздел 1.2) допуски размеров определятся следующим образом:
Допуск — величина всегда положительная. Допуск характеризует точность изготовления детали. Чем меньше допуск, тем труднее обрабатывать деталь, так как повышаются требования к точности станка, инструмента, приспособлений, квалификации рабочего. Неоправданно большие допуски снижают надежность и качество работы изделия.
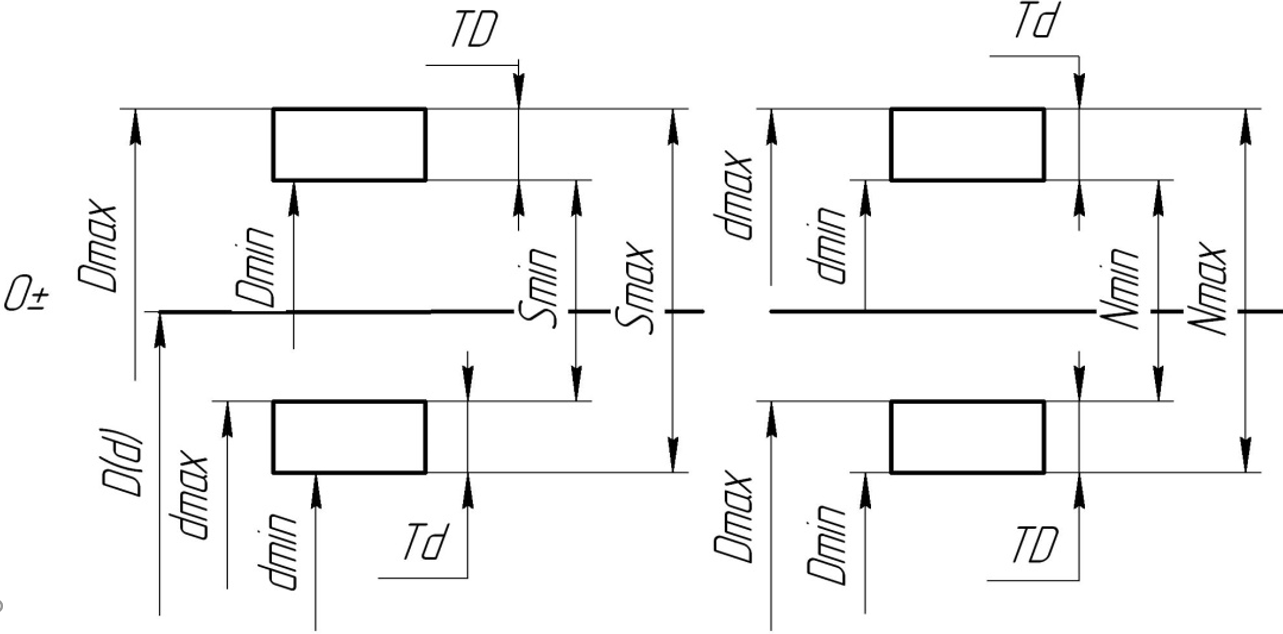
В некоторых соединениях при различных сочетаниях предельных размеров отверстия и вала могут возникать зазоры или натяги. Характер соединения деталей, определяемый значениями получающихся в нем зазоров или натягов, называется посадкой. Посадка характеризует большую или меньшую свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению.
Различают три группы посадок:
1) с гарантированным зазором;
2) переходные;
3) с гарантированным натягом.
Если размеры отверстия больше размеров вала, то в соединении возникает зазор (рис. 1.3).
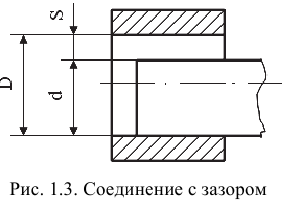
Зазор — это положительная разность между размерами отверстия и вала:
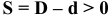
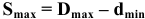
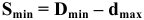
Если до сборки размеры вала больше размеров отверстия, то в соединении возникает натяг.
Натяг — это положительная разность между размерами вала и отверстия:
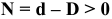
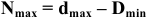
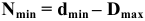
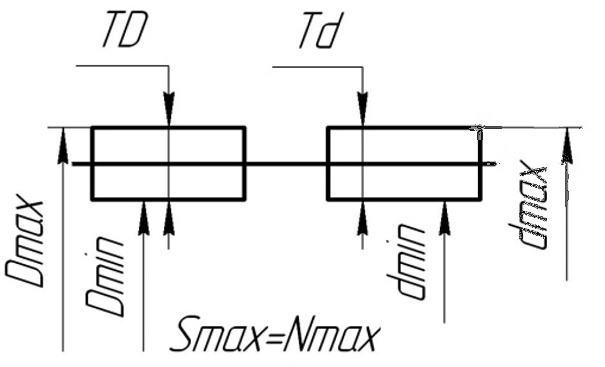
А теперь рассмотрим конкретное соединение:
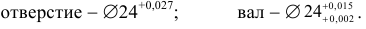
Сразу сказать, что получится в соединении (зазор или натяг) довольно нелегко. Предположим, что это соединение с зазором. Рассчитаем предельные значения зазоров для данного конкретного соединения:
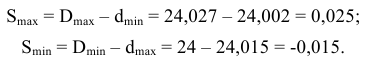
Как видим, минимальный зазор получился отрицательным. Это значит, что максимальный размер вала 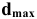
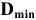
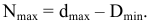
Таким образом, отрицательный минимальный зазор — это положительный максимальный натяг, т.е.
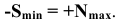
Таким образом, в рассматриваемом соединении при одном сочетании предельных размеров отверстия и вала может получиться зазор, который меняется от 0,025 мм до нуля 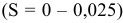
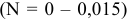
Такие посадки называются переходными.
Допуск посадки — это допуск зазора для посадок с гарантированным зазором (определяется как разность между наибольшим и наименьшим зазорами) или допуск натяга для посадок с гарантированным натягом (определяется как разность между наибольшим и наименьшим натягами). В переходных посадках допуск посадки — это сумма максимального зазора и максимального натяга.
Обозначение допуска посадки:
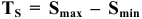
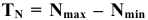
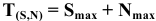
Для любой группы посадок допуск посадки можно определить по формуле

Возможно эта страница вам будет полезна:
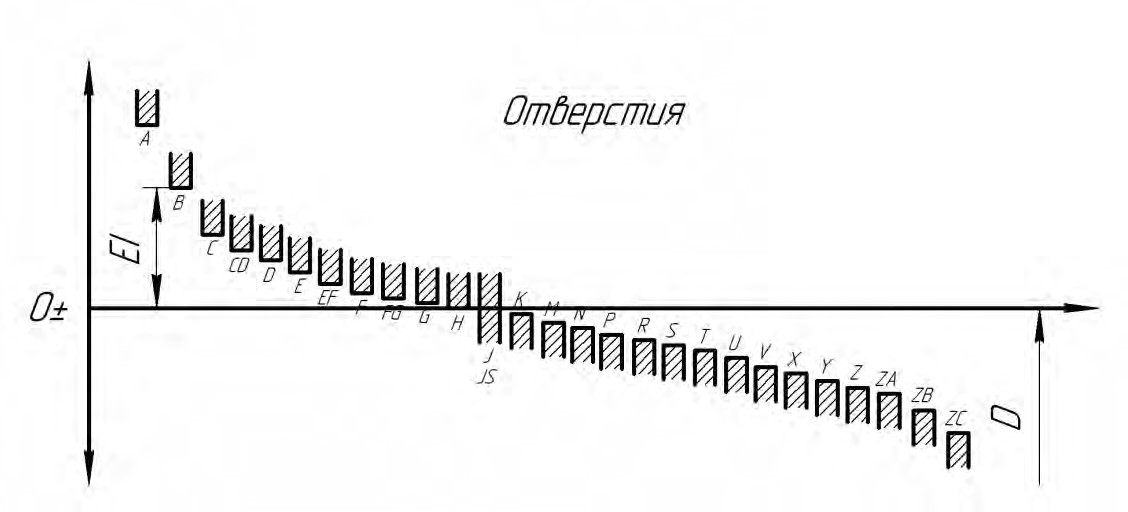
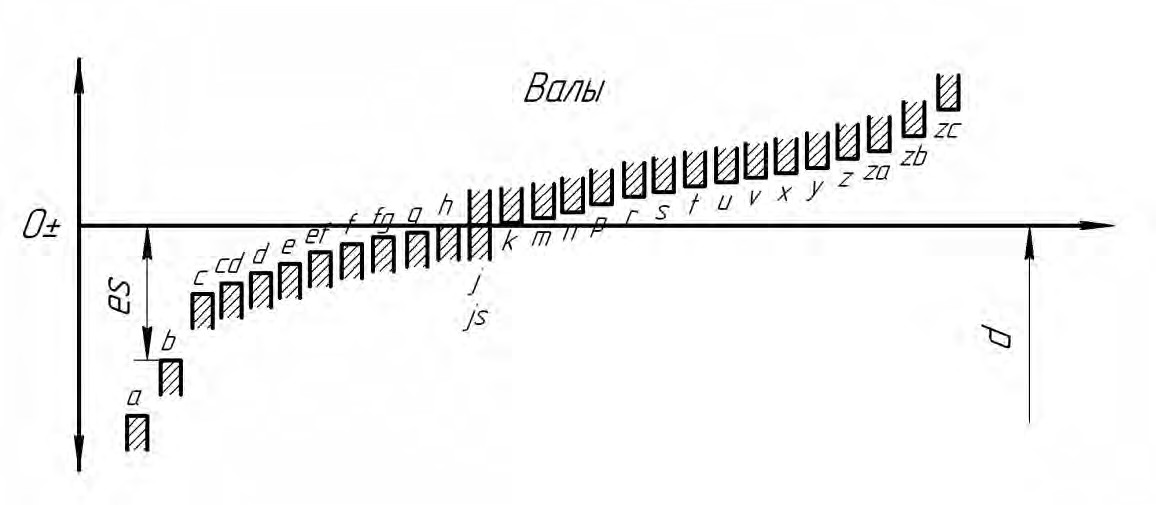
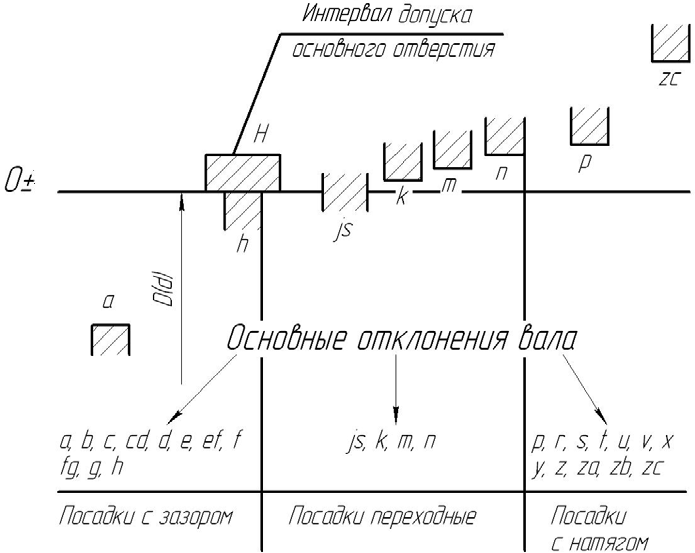
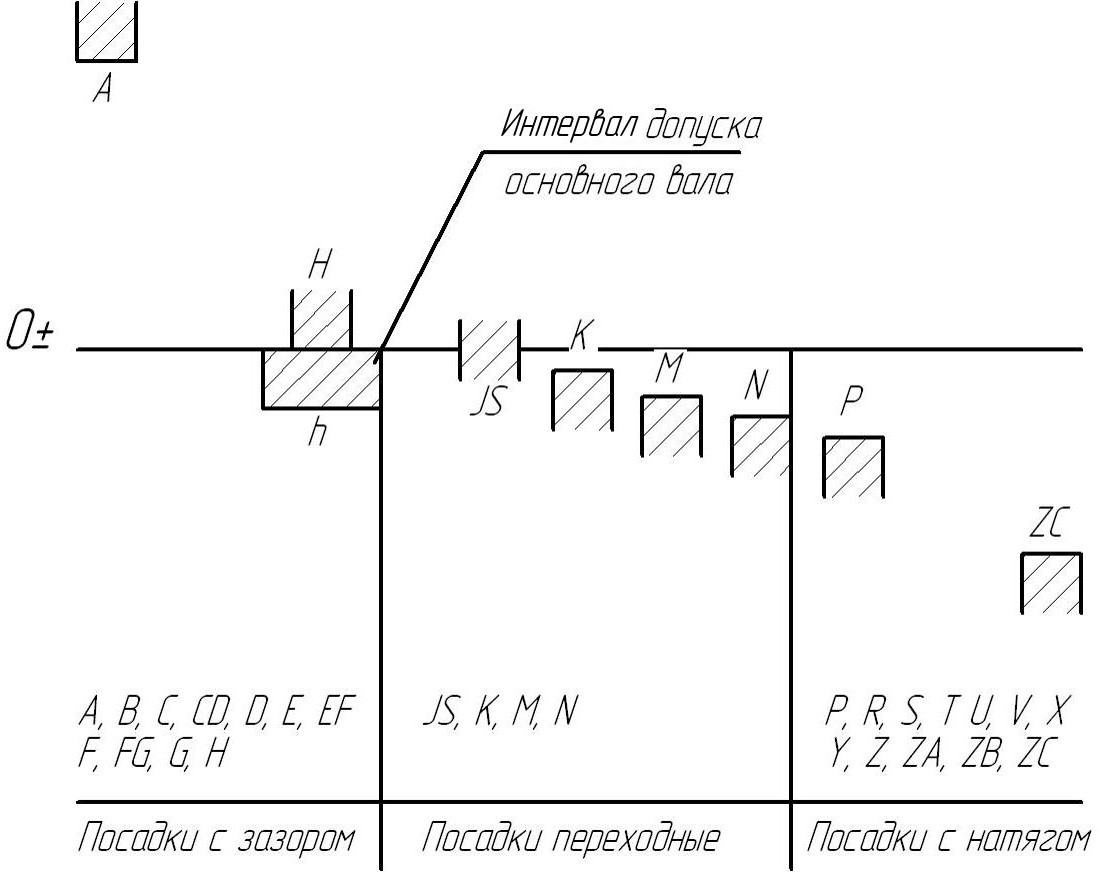
Основные отклонения
Из двух предельных отклонений стандарт выделяет одно, которое называют основным. Основное отклонение — это одно из двух отклонении (верхнее или нижнее), ближайшее к номинальному размеру.
Для ранее приведенных шести примеров простановки отклонений (см. раздел 1.2) определим числовые значения основных отклонений:
1) +0,002; 2)-0,025; 3)+0,007; 4)0; 5)0; 6) не определено.
В шестом примере определить основное отклонение невозможно, оба отклонения равно удалены от номинального размера.
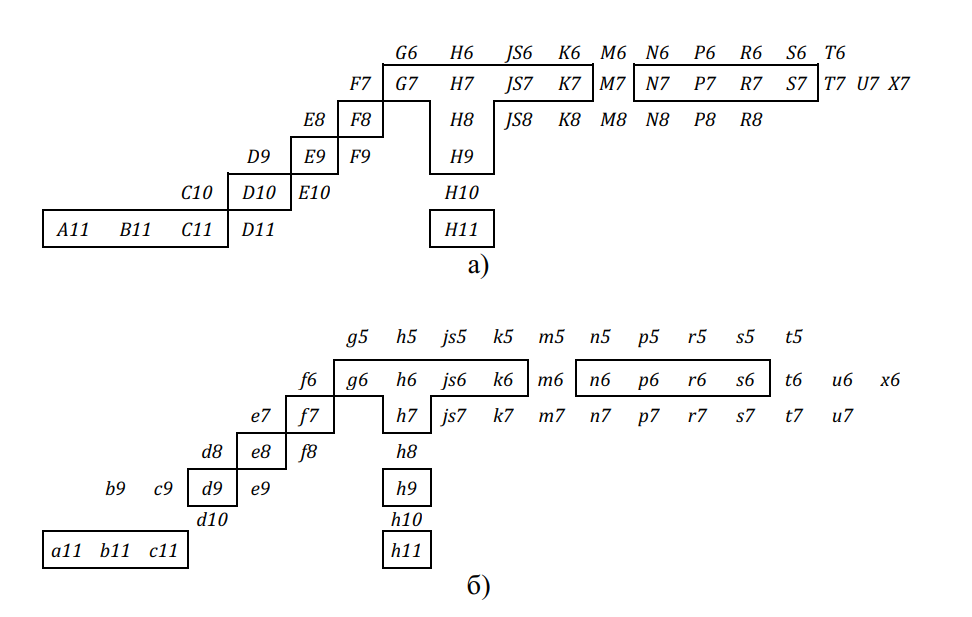
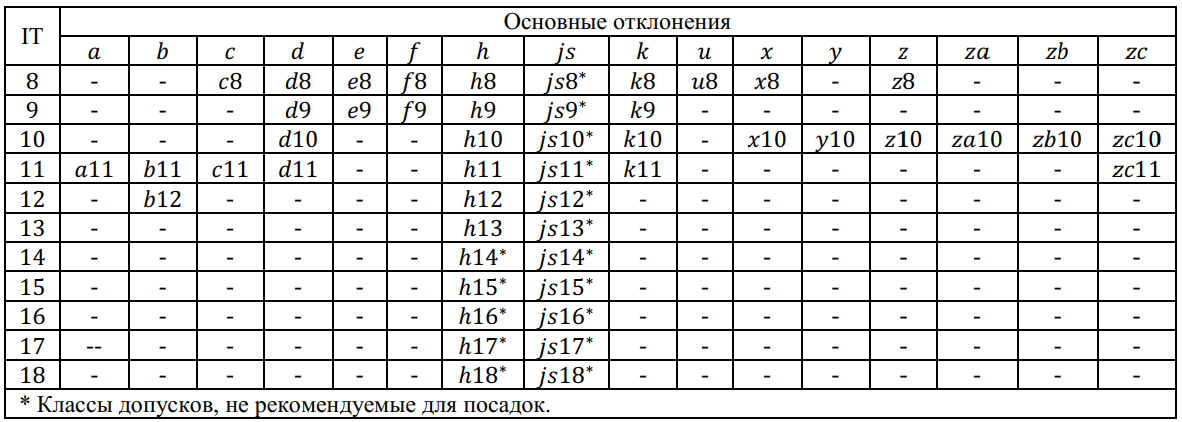
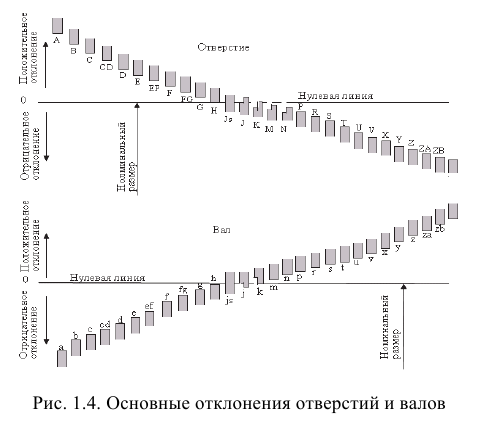
Основные отклонения обозначают буквами латинского алфавита (рис. 1.4):
- прописными буквами — основные отклонения отверстий
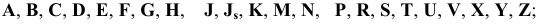
- строчными буквами — основные отклонения валов
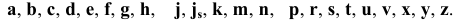
Основные отклонения от 
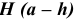
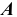
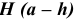
Основные отклонения 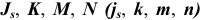
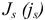
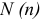
Основные отклонения 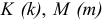
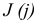
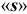
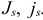
Основные отклонения от 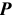
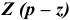
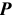
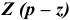
Основные отклонения вала и отверстия, обозначенные одноименной буквой (для данного интервала размеров), равны по величине, но противоположны по знаку, например:
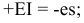
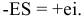
Квалитеты
В каждом изделии детали разного назначения изготавливают с различной точностью. Для нормирования требуемых уровней точности установлены квалитеты (степени точности) изготовления размеров деталей. Под квалитетом понимают совокупность допусков, характеризуемых постоянной относительной точностью для всех номинальных размеров данного диапазона (например, от 1 до 500 мм).
Точность в пределах одного квалитета зависит только от номинального размера. Стандартом установлено 20 квалитетов: 01, 0, 1, 2, 3… 18. Квалитет определяет допуск на изготовление, а следовательно, и соответствующие методы и средства обработки и контроля деталей машин. Наивысшей точности соответствует квалитет 01, а низшей — 18 квалитет. Значит, чем больше номер квалитета, тем больше допуск размера.
Квалитеты 01, 0, 1 предназначены для нормирования точности размеров плоскопараллельных концевых мер длины.
Квалитеты 2, 3, 4 — для нормирования точности размеров гладких калибров-пробок и калибров-скоб, деталей измерительных приборов и инструментов.
Квалитеты 5 и 6 предназначены для нормирования точности размеров деталей высокоточных ответственных соединений (шпинделей прецизионных станков, шеек коленчатых валов и др.).
К валите ты 7, 8 являются наиболее распространенными. Они предусмотрены для размеров точных ответственных соединений в машиностроении, например: деталей двигателей внутреннего сгорания, автомобилей, самолетов, металлорежущих станков.
По квалитету 9 преимущественно выполняют размеры деталей тепловозов, паровых машин, подъемно-транспортных механизмов, полиграфических, сельскохозяйственных машин.
Квалитет 10 предназначен для размеров неответственных соединений, например для деталей тракторов, вагонов.
Квалитеты 11, 12 предназначены для нормирования точности размеров деталей, образующих неответственные соединения, в которых допустимы большие зазоры и их колебания, например размеров крышек, фланцев.
Квалитеты 13 — 18 предназначены для неответственных размеров деталей, не входящих в соединения с другими деталями, т.е. для свободных размеров, а также для межоперационных размеров.
Допуск квалитета условно обозначают прописными латинскими буквами 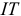
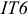
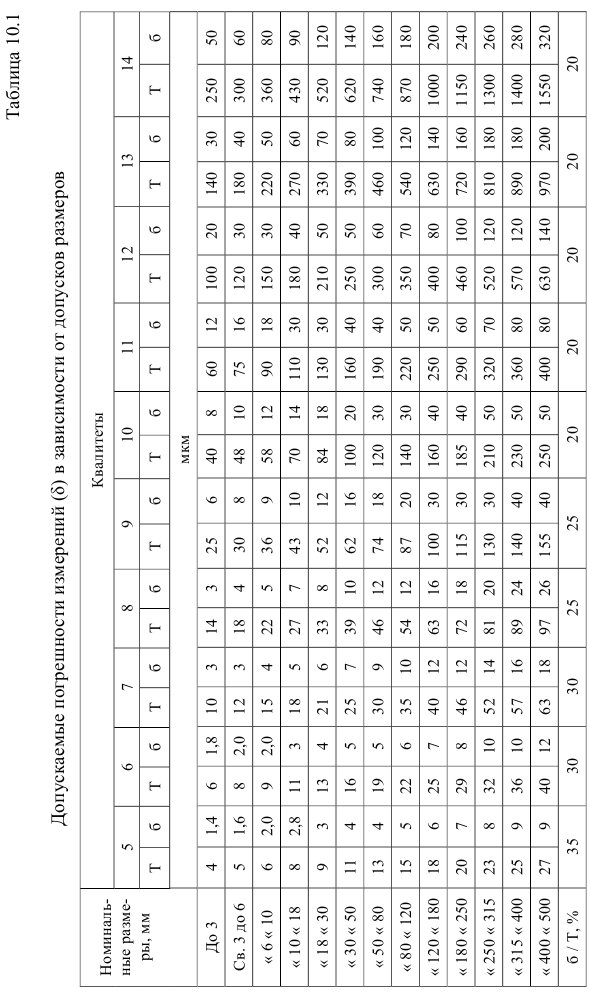
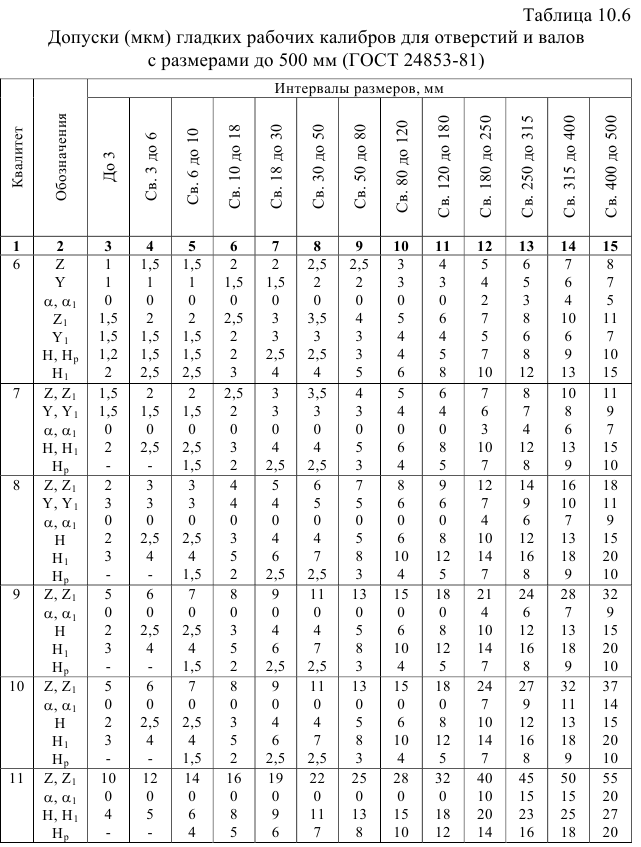
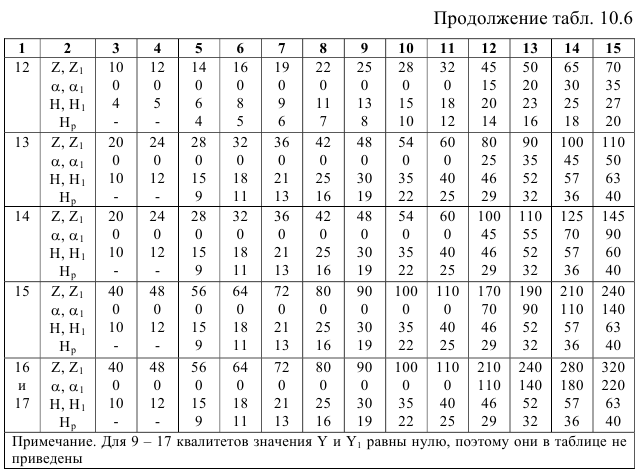
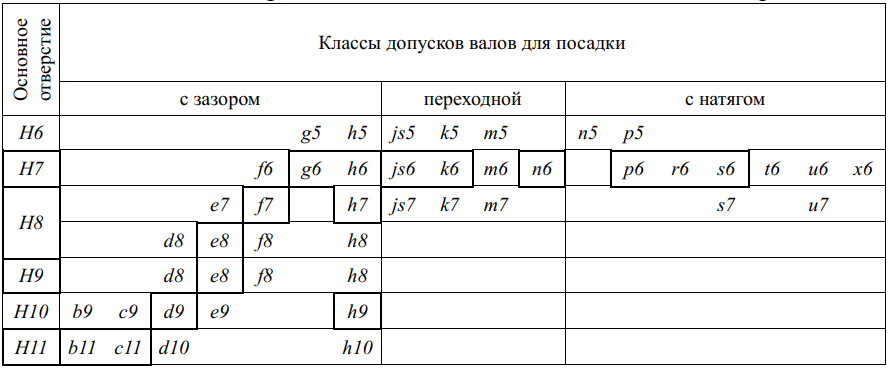
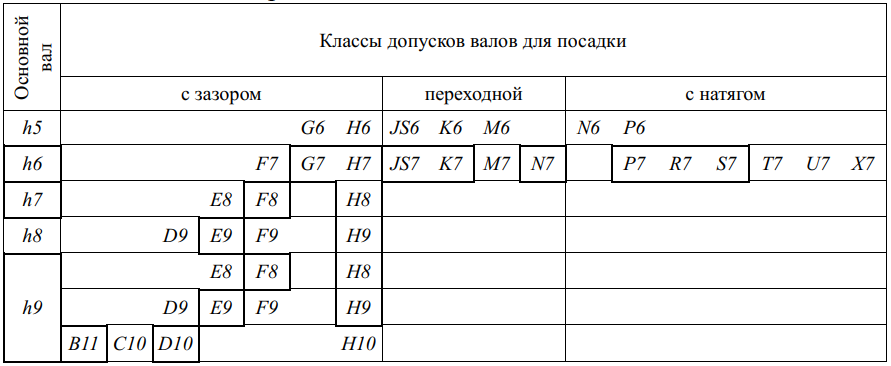
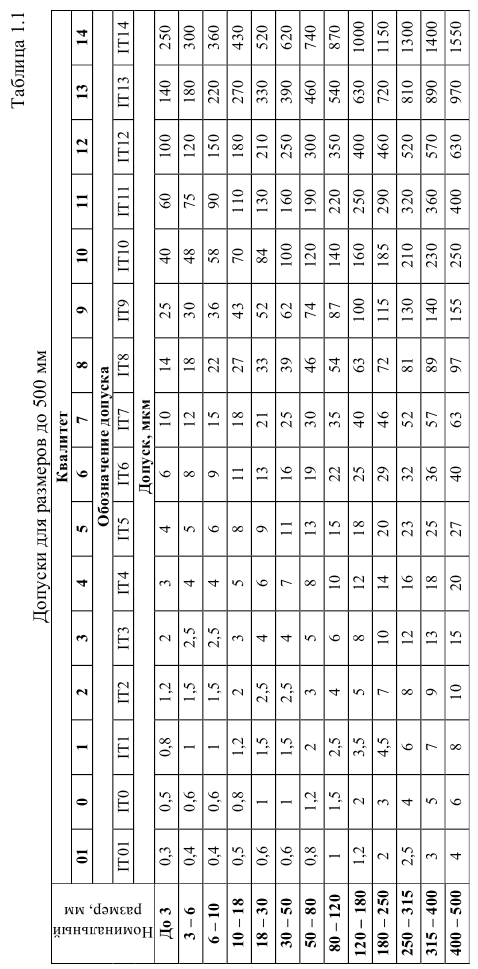
Значения допусков для размеров до 500 мм приведены в табл. 1.1.
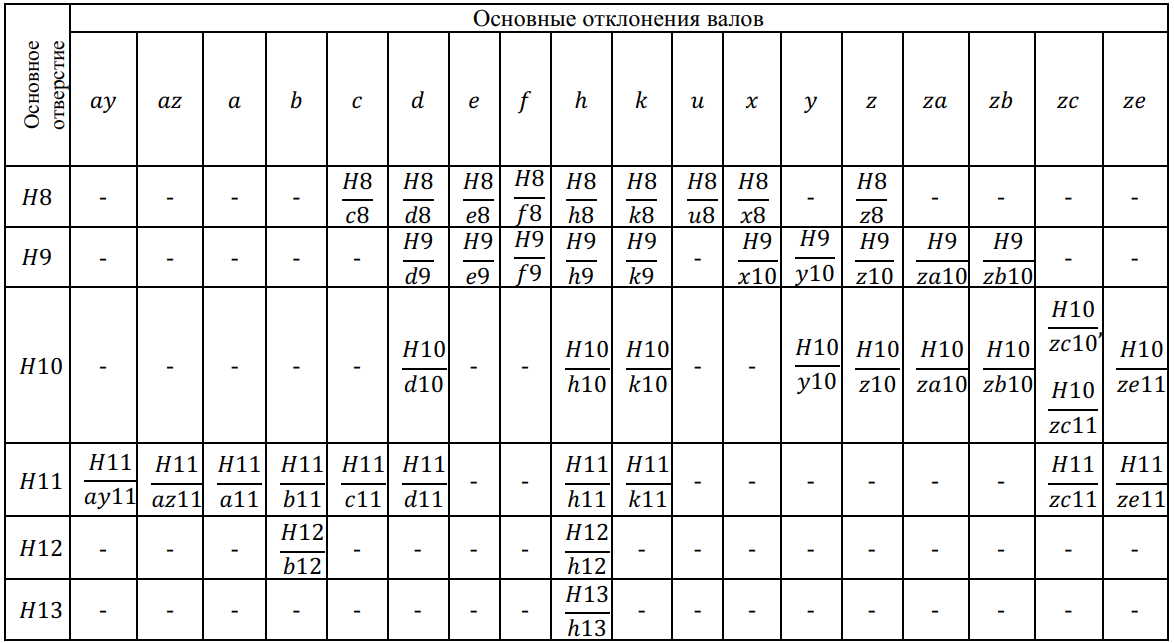
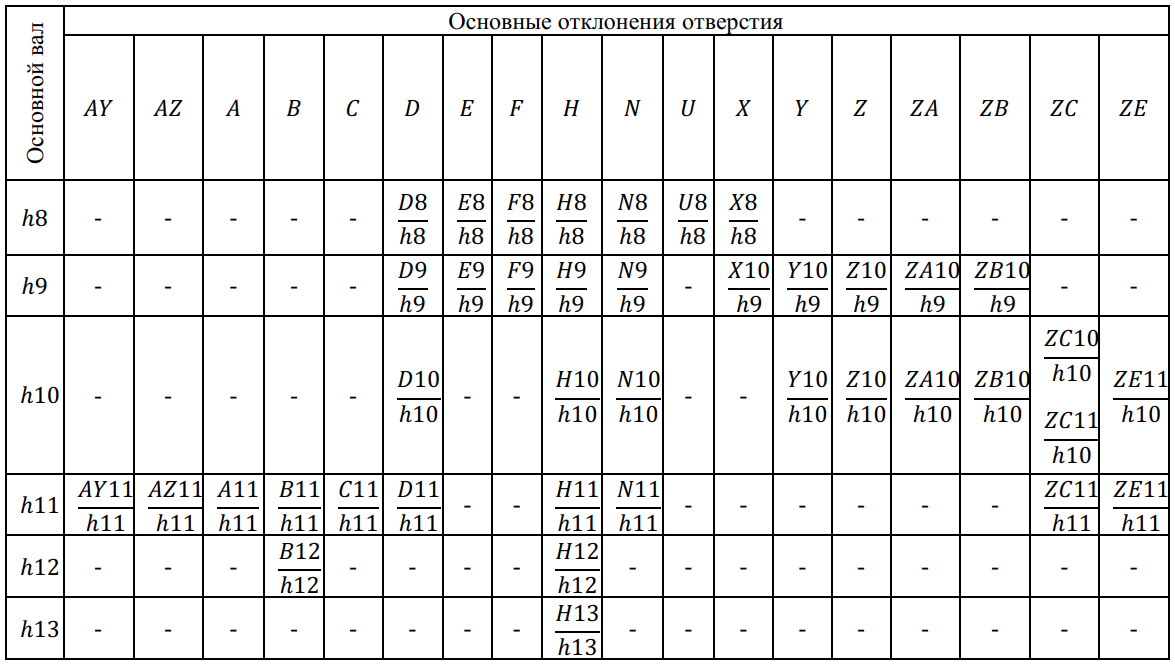
Система отверстия и система вала
Обозначение посадок
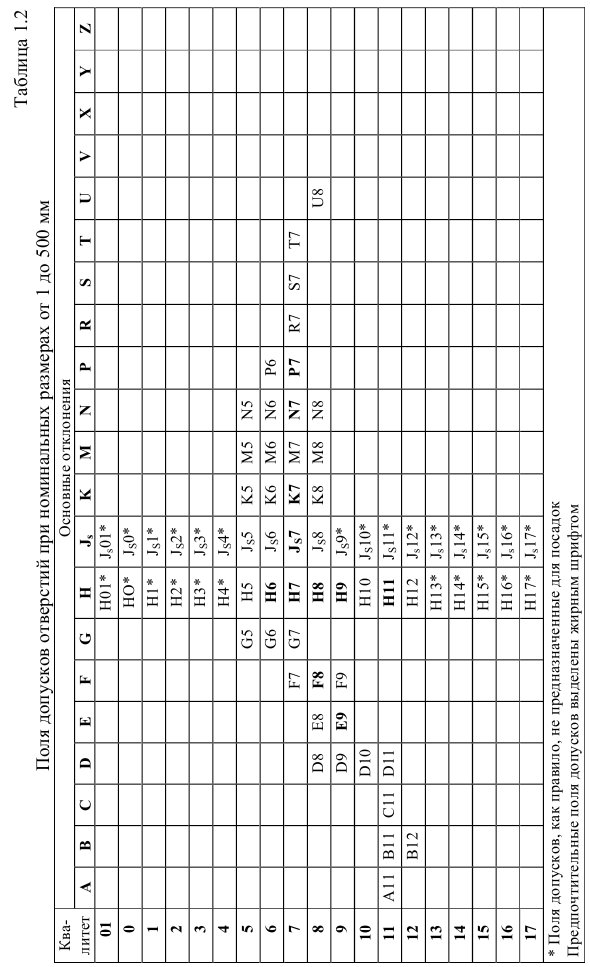
Сочетание основного отклонения и квалитета образует ноле допуска размера детали.
Например:
Посадки на чертежах обозначают дробью: в числителе пишут поле допуска отверстия, а в знаменателе — поле допуска вала.
Посадки предусмотрены в двух системах: системе посадок основного отверстия и системе посадок основного вала.
Система посадок основного отверстия или просто система отверстия — это совокупность посадок, в которых предельные отклонения отверстии одинаковы (при одном номинальном размере и квалитете), а различные посадки достигаются изменением предельных отклонении валов.
Основное отверстие — это отверстие, которое обозначается буквой 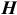
Например:
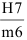
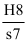
Система посадок основного вала или просто система вала — это совокупность посадок, в которых предельные отклонения валов одинаковы (при одном номинальном размере и одном квалитете), а различные посадки достигаются путем изменения предельных отклонении отверстии.
Основной вал — это вал, который обозначается буквой 
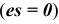
При обозначении посадок в системе вала в знаменателе (где пишется всегда поле допуска вала) будет стоять основной вал 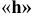
Например:
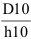
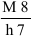
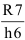
Стандарт разрешает любое сочетание полей допусков отверстий и валов, например: 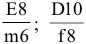
И в то же время для всех диапазонов размеров установлены рекомендуемые посадки и для размеров 1 — 500 мм из них выделены предпочтительные, например: 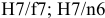
Унификация посадок позволяет обеспечить однородность конструктивных требований к соединениям и облегчить работу конструкторов по назначению посадок. Комбинируя различные варианты предпочтительных полей допусков валов и отверстий, можно значительно расширить возможности системы по созданию различных посадок без увеличения набора инструментов, калибров и другой технологической оснастки. В каждой отрасли можно сократить число полей допусков и посадок, введя ограничительный стандарт (отраслевой или стандарт предприятия).
По экономическим соображениям носадки следует назначать, главным образом, в системе отверстия и реже в системе вала. Это сокращает номенклатуру режущих и измерительных инструментов, предназначенных для обработки и контроля отверстий. Точные отверстия обрабатывают дорогостоящим режущим инструментом (зенкерами, развертками, протяжками). Каждый из них применяют для обработки только одного размера с определенным полем допуска. Валы независимо от их размеров обрабатывают одним и тем же резцом или шлифовальным кругом. В системе отверстия различных по предельным размерам отверстий меньше, чем в системе вала, а следовательно, меньше номенклатура режущего инструмента, необходимого для обработки отверстий.
Однако в некоторых случаях по конструктивным соображениям приходится применять систему вала, например, когда требуется чередовать соединения нескольких отверстий одинакового номинального размера, но с различными посадками на одном валу, или гнездо в корпусе для установки подшипника выполняется по системе вала.
В рекомендуемых и предпочтительных посадках точных квалитетов для размеров от 1 до 3150 мм допуск отверстия, как правило, на один-два квалитета больше допуска вала, поскольку точное отверстие технологически получить труднее, чем точный вал, вследствие худших условий отвода теплоты, недостаточной жесткости, повышенной изнашиваемости и сложности направления режущего инструмента для обработки отверстий.
Увеличение допуска отверстия при сохранении допуска посадки повышает срок службы разверток и протяжек, так как при этом допускается больший их износ по диаметру и большее число заточек.
Стандарт в технически обоснованных случаях допускает применение посадок, отличающихся от рекомендуемых, но образованных из числа полей допусков валов и отверстий, предусмотренных этим стандартом. Однако в этих случаях посадка должна в первую очередь относиться к системе отверстия или к системе вала.
К 1980 г. ЕСДП должна была полностью заменить действующую ранее в СССР систему допусков и посадок ОСТ, но в старых документах (до 1977 — 1980 гг.) — конструкторской документации, справочниках, учебной литературе даны обозначения по ОСТ, поэтому в табл. 1.4 и 1.5 представлены сопоставления полей допусков по ОСТ и ЕСДП.
Возможно эта страница вам будет полезна:
Схематичное изображение полей допусков
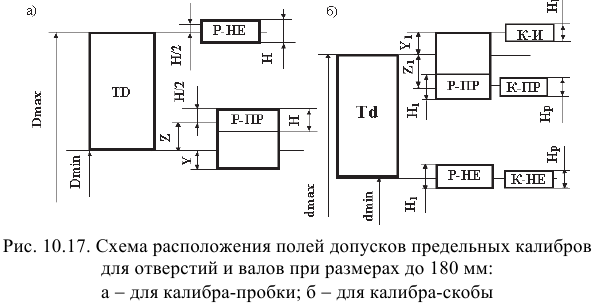
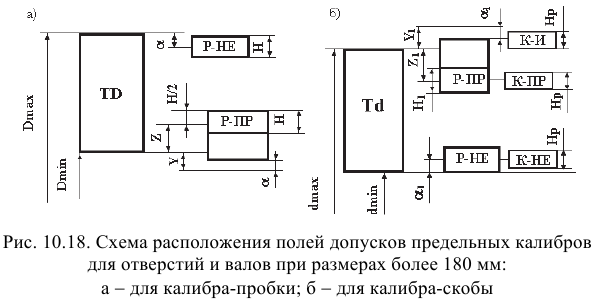
Для упрощения допуски можно изображать графически в виде полей допусков. Поле допуска — пространство, ограниченное двумя линиями, соответствующими наибольшему и наименьшему размерам. Оно определяется величиной допуска и его положением относительно нулевой линии. Нулевая линия — это линия, соответствующая номинальному размеру соединения. Вверх от этой линии откладывают положительные отклонения, а вниз — отрицательные (рис. 1.5, 1.6).
Условное обозначение предельных отклонений и посадок
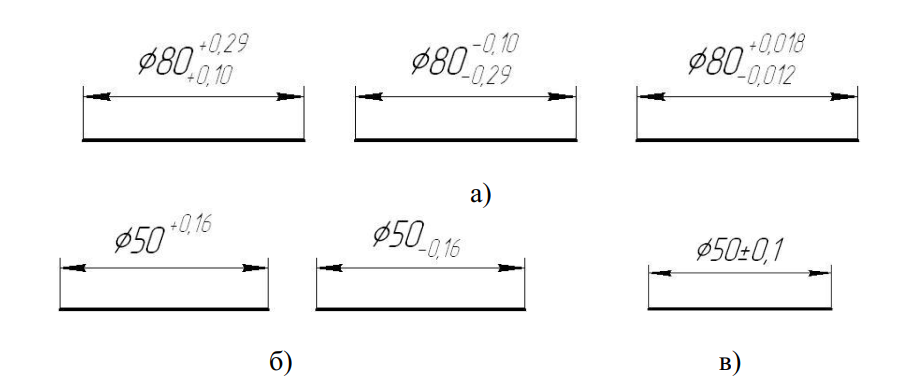
Предельные отклонения линейных размеров указывают на чертежах условными (буквенными) обозначениями полей допусков или числовыми значениями предельных отклонений, а также буквенными обозначениями полей допусков с одновременным указанием справа в скобках числовых значений предельных отклонений (рис. 1.7, а — в).
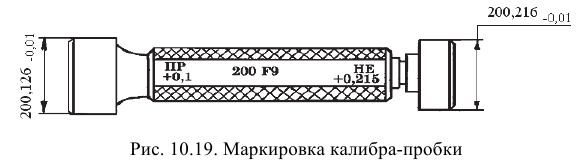
Посадки и предельные отклонения размеров деталей, изображенных на чертеже в собранном виде, указывают дробью: в числителе — буквенное обозначение поля допуска или числовые значения предельных отклонений отверстия либо буквенное обозначение поля допуска с указанием справа в скобках числовых значений предельных отклонений отверстия, в знаменателе — аналогичное обозначение поля допуска вала (рис. 1.7, г, г)). Иногда для обозначения посадки указывают предельные отклонения только одной из сопрягаемых деталей (рис. 1.7, е).
В условных обозначениях полей допусков нужно обязательно указывать числовые значения предельных отклонений в следующих случаях:
- для размеров, не включенных в ряд нормальных линейных размеров, например 41,5 Н7(‘°’02>);
- при назначении предельных отклонений, условные обозначения которых не предусмотрены ГОСТ 25347-82, например для пластмассовой детали (см. рис. 1.7, д).
Предельные отклонения следует назначать для всех размеров, проставленных на рабочих чертежах, включая несопрягаемые и неответственные размеры. Если предельные отклонения для размера не назначены, возможны лишние затраты (когда стремятся получить этот размер более точным, чем нужно) или увеличение массы детали.
Для линейных размеров от 1 до 10 ООО мм неуказанные предельные отклонения назначают по ГОСТ 30893.1-2002 ОНВ. Общие допуски. Предельные отклонения линейных и угловых размеров с неуказанными допусками.
Предельные отклонения линейных размеров (табл. 1.6), кроме размеров притуплённых кромок (наружных радиусов скругления и высот фасок), нормируют по классам точности общих допусков:
точный — 

На чертежах неуказанные предельные отклонения размеров задаются текстом в виде технических условий, например для среднего класса точности: «Общие допуски по ГОСТ 30893.1 — ш» или «ГОСТ 30893.1 — ш». ГОСТ 30893.1 устанавливает дополнительные варианты назначения предельных отклонений линейных размеров с неуказанными допусками (табл. 1.7). Назначение дополнительных вариантов предельных отклонений линейных размеров с неуказанными допусками при новом проектировании рекомендуется ограничить.
Обозначение 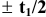
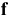
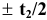

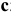
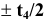
Обозначение неуказанных допусков по дополнительным вариантам (для класса точности — средний):
Вариант 1 — «Общие допуски по ГОСТ 30893.1: 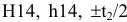
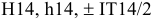
Вариант 2 — «Общие допуски по ГОСТ 30893.1: 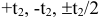
Кроме того, используется ГОСТ 30893.2-2002 ОНВ. Общие допуски. Допуски формы и расположения поверхностей, не указанные индивидуально. Введён 01.01.2004.
Общие допуски цилиндричности, точности формы продольного сечения, наклона, перекоса осей, позиционного отклонения, полного радиального и торцевого биения, формы заданного профиля и формы заданной поверхности не устанавливаются. Отклонения этих видов косвенно ограничиваются допусками на линейные и угловые размеры или другими видами допусков формы и расположения, в том числе и общими.
Общий допуск круглости для элементов с неуказанными на чертеже предельными отклонениями размеров равен допуску на диаметр, но не должен превышать общий допуск на радиальное биение.
Классы точности для неуказанных предельных отклонений формы и расположения поверхностей: 
Указание на чертежах:
«Общие допуски формы и расположения — ГОСТ 30893.2 — 
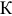
«Общие допуски ГОСТ 30893.2 — 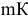
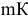

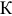
Методы выбора посадок и области их применения
Выбор посадок производится в зависимости от назначения деталей и их поверхностей, условий работы соединения одним из трех методов.
- Метод прецедентов или аналогов. Посадка выбирается по аналогии с посадкой в надежно работающем узле. Сложность метода заключается в оценке и сопоставлении условий работы посадки в проектируемом узле и аналоге.
- Метод подобия — развитие метода прецедентов. Посадки выбираются на основании рекомендаций отраслевых технических документов и литературных источников. Недостатком метода является, как правило, отсутствие точных количественных оценок условий работы сопряжений.
- Расчетный метод является наиболее обоснованным методом выбора посадок. Посадки рассчитываются на основании полуэмпирических зависимостей. Однако формулы не всегда учитывают сложный характер физических явлений, происходящих в соединении.
В любом случае новые опытные образцы изделий перед запуском в серийное производство проходят целый ряд испытаний, по результатам которых отдельные посадки могут быть подкорректированы. Квалификация конструктора, в частности, определяется и тем, потребовалась ли корректировка посадок в разработанном им узле.
Применение посадок с зазором. Посадки 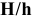
Посадка 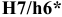
- — предпочтительная посадка.
Посадки 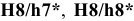
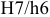
Посадки 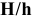
Посадки 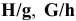
Посадки 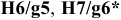
Посадки 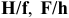
Посадки 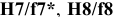
Посадки 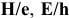
Посадки 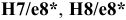
Посадки 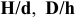
Посадки 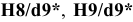
Посадка 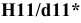
Применение переходных посадок. Переходные посадки применяются только в точных квалитетах — с 4-го по 8-й, используются как центрирующие и предназначены для неподвижных, но разъемных соединений, так как обеспечивают легкую сборку и разборку, требуют, как правило, дополнительного крепления соединяемых деталей шпонками, штифтами, болтами и т.п.
Посадки 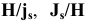
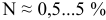
Посадка 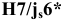
Посадки 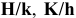
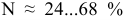
Посадка 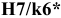
Посадки 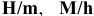
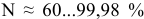
Посадка 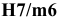
Посадки 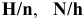
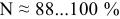
Посадка 
Применение посадок с натягом. Они используются для передачи крутящих моментов и осевых сил без дополнительного крепления, а иногда для создания предварительно напряженного состояния у сопрягаемых деталей.
Посадки предназначены для неподвижных и неразъемных соединений. Относительная неподвижность деталей обеспечивается силами трения, возникающими на контактирующих поверхностях вследствие их упругой деформации, создаваемой натягом при сборке соединения.
Преимущество посадок — отсутствие дополнительного крепления, что упрощает конфигурацию деталей и их сборку. Посадки обеспечивают высокую нагрузочную способность сопряжения, которая резко возрастает с увеличением диаметра сопряжения. В то же время прочность и качество сопряжения зависят от материала сопрягаемых деталей, шероховатостей их поверхностей, формы, способа сборки (сборка под прессом или способ термических деформаций) и т.п.
Посадки 
Посадка 
Посадки 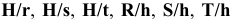
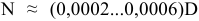
Посадки 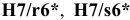
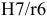
Посадки 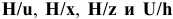
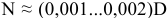
Посадки 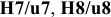
Возможно эта страница вам будет полезна:
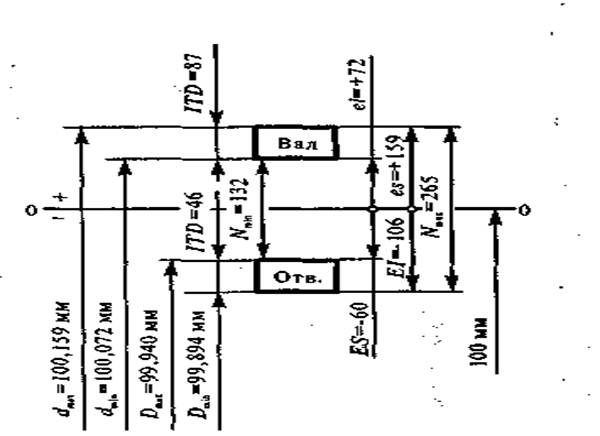
Пример 1
Дано:
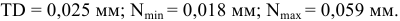
Определить:
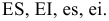
Решение:
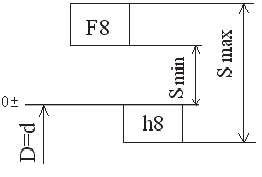
Построим для заданной посадки схему полей допусков и обозначим на схеме данные по условию задачи:
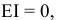
по условию, так как отверстие основное; тогда
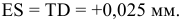
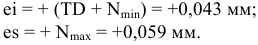
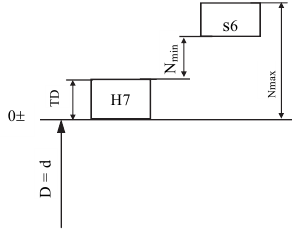
Ответ:
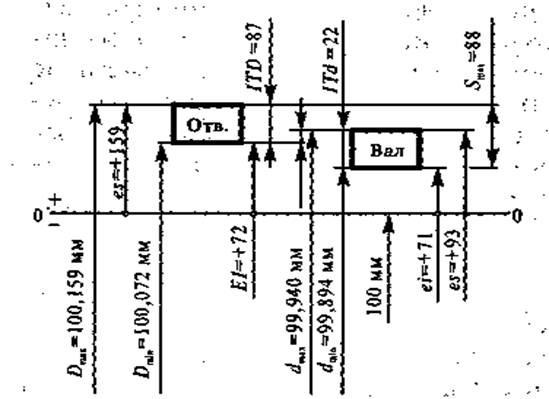
Пример 2
Дано:
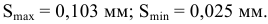
Определить:
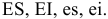
Решение:
Построим для заданной посадки схему полей допусков и обозначим на схеме данные по условию задачи:
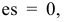
по условию, так как вал основной;
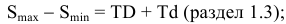
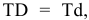
по условию, так как квалитеты одинаковые, тогда
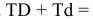

Ответ:
Нормирование точности подшипниковых соединений
Классы точности и поля допусков подшипников
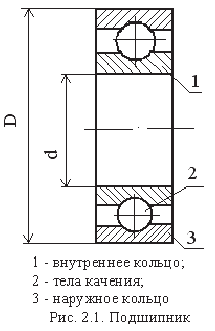
Подшипник качения представляет собой сложный узел (рис. 2.1), состоящий из внутреннего 1 и наружного 3 колец, тел качения 2, которыми являются шарики, ролики или иглы. Посадочные размеры, по которым подшипник качения соединяется с валом и корпусом, следующие: внутренний диаметр 
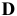
Подшипники качения являются стандартными изделиями, которые изготавливают на специализированных подшипниковых заводах. Они обладают полной внешней взаимозаменяемостью по присоединительным поверхностям колец и ограниченной внутренней взаимозаменяемостью между телами качения и кольцами. Комплекты шариков, роликов и кольца подшипников подбирают селективным методом.
Основные присоединительные размеры подшипников качения, по которым они монтируются на валах (осях) и в корпусах машин и приборов, установлены ГОСТ 520-2002.
По ГОСТ 520-2002 на подшипники установлены классы точности, которые характеризуются значениями предельных отклонений размеров, формы, взаимного положения поверхностей. Для шариковых и роликовых радиальных и шариковых радиально-упорных подшипников установлены следующие классы в порядке повышения точности:
8, 7, нормальный, 6, 5, 4, Т, 2.
Допуски подшипников 8 и 7-го классов точности устанавливают в нормативных документах.
Для роликовых конических подшипников установлены классы точности:
8, 7, 0, нормальный, 6Х, 6, 5, 4, 2.
Для упорных и упорно-радиальных подшипников установлены классы: 8, 7, нормальный, 6, 5, 4, 2.
В большинстве узлов машин применяют подшипники качения «нормального» класса точности.
Класс точности «нормальный» соответствует классу точности 0 (нуль).
Класс точности проставляется перед обозначением подшипника (класс «О» не указывается), например: 5-208 или 208.
В общем машиностроении в основном используются подшипники О и 6 классов точности. В подшипниках качения оба кольца принимают в качестве основных деталей системы допусков, т.е. соединение «внутреннее кольцо — вал» выполняется в системе основного отверстия; соединение «наружное кольцо — корпус» выполняется в системе основного вала.
Предельные отклонения для подшипников качения назначают на средние диаметры посадочных поверхностей, которые обозначают: 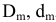
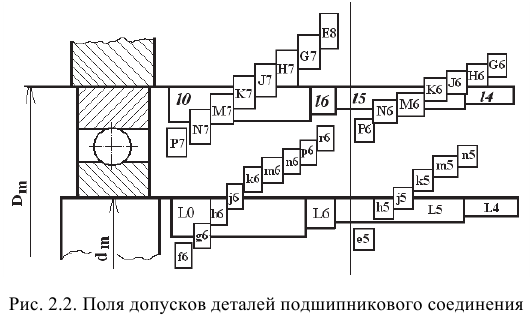
Основное отклонение для среднего диаметра отверстия подшипника обозначают 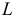
Поля допусков (
Поле допуска на наружный диаметр кольца подшипника (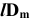
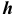
Поле допуска на внутренний диаметр (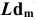
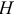
Посадки с большими натягами не применяют из-за тонкостенной конструкции колец подшипников.
Предельные отклонения диаметров даны отдельно для наружных и внутренних колец для средних диаметров (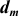
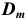
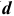
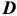
Виды нагружения колец подшипника. Выбор посадок
При назначении посадок колец подшипника на вал и в отверстие корпуса следует учитывать условия работы механизма: какая деталь вращается (вал или корпус), число оборотов вращающейся детали, характер нагрузки (величину, направление и характер действующих на подшипник нагрузок), режим работы (легкий, средний, тяжелый), а также класс точности, тип и размеры подшипника, условия его установки и эксплуатации, требования к точности вращения и т.п.
С вращающейся деталью кольцо подшипника должно соединяться по посадке с натягом (для исключения обкатки и проскальзывания), а с неподвижной деталью — по посадке с небольшим зазором (для обеспечения регулировки подшипника и компенсации температурных расширений валов или корпусов).
В зависимости от условий работы различают три вида нагружения колец: местное, циркуляционное и колебательное (рис. 2.3).
При местном нагружении (рис. 2.3, а) кольцо воспринимает результирующую радиальную нагрузку 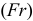
При циркуляционном погружении (рис. 2.3, 6) кольцо воспринимает действующую на подшипник результирующую радиальную нагрузку 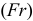
При колебательном погружении (рис. 2.3, в) неподвижное кольцо воспринимает ограниченным участком дорожки качения равнодействующую 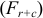
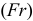
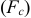
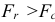
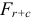
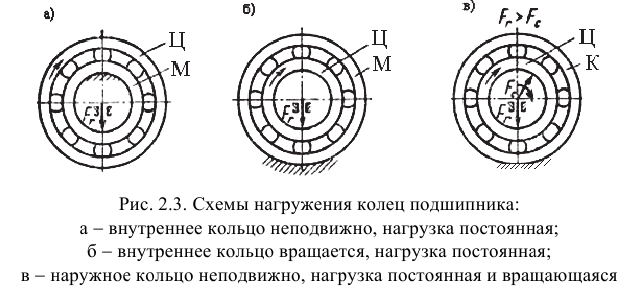
В зависимости от вида нагружения колец шариковых и роликовых подшипников в табл. 2.1 приведены рекомендуемые поля допусков посадочных мест валов и отверстий корпусов.
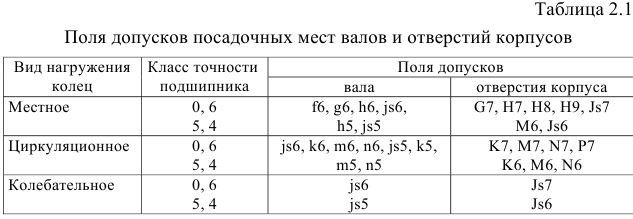
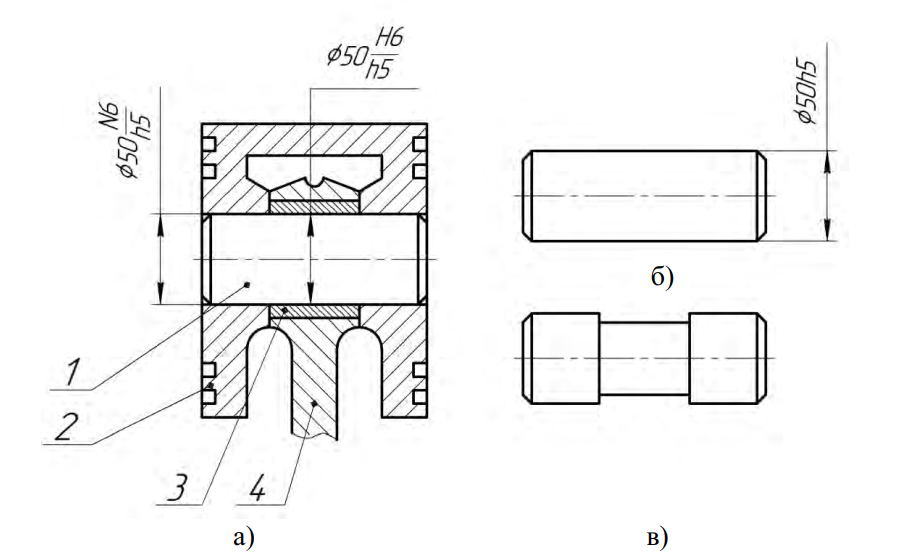
Примеры обозначения посадок подшипников качения на чертежах: — подшипник класса точности 0 на вал с номинальным диаметром 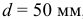
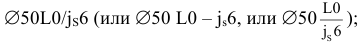
- то же в отверстие корпуса с номинальным диаметром 90 мм, с полем допуска
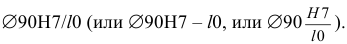
Допускается на сборочных чертежах подшипниковых узлов указывать размер, поле допуска или предельные отклонения на диаметр, сопряженный с подшипником, например для вала 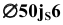
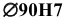
Пример решения задачи
Выбрать и рассчитать посадки на соединения подшипника с корпусом и валом в узле редуктора. Назначить отклонения формы и шероховатость посадочных поверхностей. Построить схемы полей допусков соединений. Начертить эскиз узла и деталей соединения подшипника с простановкой посадок, отклонений формы, шероховатости поверхностей.
Пример 3
Условие: подшипник шариковый, радиальный,
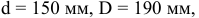
вращается вал, режим работы — нормальный, класс точности 0.
Решение:
1) Определяем предельные отклонения поля допуска внутреннего кольца подшипника 
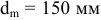
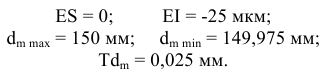
2) Определяем предельные отклонения поля допуска наружного кольца подшипника 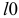
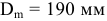
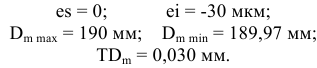
3) Определяем вид нагружения колец. Так как вращается вал, а корпус неподвижен (т.е. внутреннее кольцо вращается, а наружное неподвижно), то внутреннее кольцо нагружено циркуляционно, наружное — местно.
4) Определяем поля допусков посадочных поверхностей (приложения 3, 4):
вал — 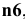

соединение:
внутреннее кольцо — вал 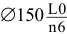
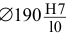
5) Определяем предельные отклонения посадочных поверхностей вала и отверстия корпуса и их предельные размеры (приложения 5 — 8):
вал
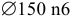
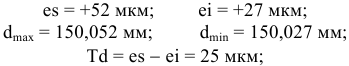
отверстие
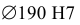
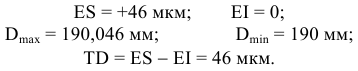
6) Определяем предельные зазоры и натяги соединений.
Внутреннее кольцо — вал 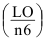
Наружное кольцо — корпус 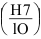
7) Определяем шероховатость посадочных поверхностей (приложение 9):
вала — 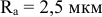
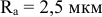
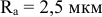
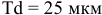
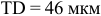
8) Построим схемы полей допусков деталей подшипникового соединения, обозначим зазоры и натяги (рис. 2.4).
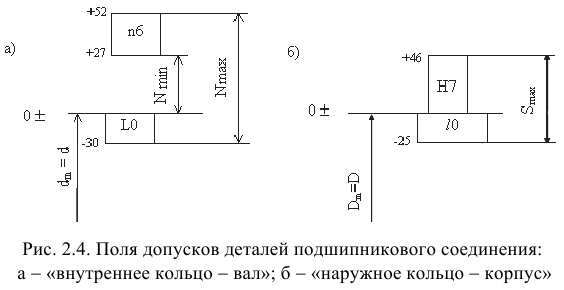
9) Выполним чертежи деталей подшипникового соединения и сборочный чертеж (рис. 2.5).
Нормирование точности шпоночных соединений
Допуски и посадки шпоночных соединений
Шпоночное соединение — это соединение с валом различных деталей (зубчатых колес, муфт, роликов, маховиков, втулок и др.) с помощью шпонки, которая входит в пазы вала и втулки.
Шпонки служат для передачи крутящего момента, предотвращения проворачивания втулки на валу, обеспечения фиксации взаимного положения деталей в узле; с их помощью достигается сравнительно легкая разборка и сборка узла при небольших требованиях к точности центрирования соединяемых деталей.
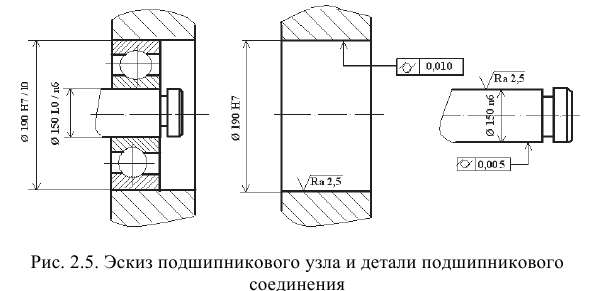
В машиностроении наиболее распространены шпоночные соединения с призматическими (рис. 3.1) и сегментными шпонками.
Основной посадочный размер шпоночного соединения — ширина шпонки и пазов вала и втулки, т.е. размер 
Поля допусков для обоих типов шпонок одинаковы, посадки выполняют по системе основного вала, т.е. по ширине 
Стандарт устанавливает соединение призматических шпонок с пазами валов и втулок трех видов (рис. 3.2): свободное (для направляющих шпонок), нормальное (для массового и серийного производства), плотное (для единичного производства).
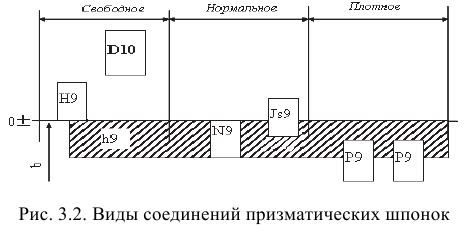
Для свободных соединений установлены поля допусков: для пазов на валу 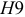
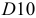
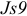
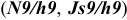
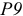
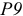
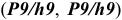
Для сегментных шпонок применяют только нормальные и плотные соединения.
Все остальные размеры шпоночного соединения (см. рис. 3.1) являются непосадочными, на них установлены следующие поля допусков:
Предельные отклонения на глубину паза вала 
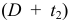
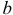
Предельные отклонения полей допусков 
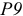
Пример 4
Для соединения зубчатого колеса с валом 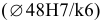
Решение:
1) По таблицам ГОСТ 23360-78 находим размеры (приложение 10):
2) По таблице для призматических шпонок при нормальном соединении поля допусков по размеру 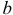
для шпонки — 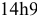
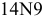
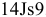
3) По таблицам находим предельные отклонения (см. приложения 5 — 8):
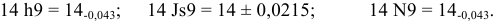
Размеры вала 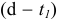
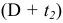
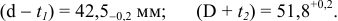
4) Определяем натяги и зазоры между пазом втулки и шпонкой 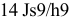
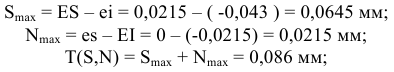
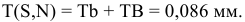
5) Определяем натяги и зазоры между пазом вала и шпонкой 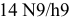
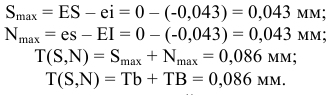
6) Строим схему расположения полей допусков деталей шпоночного соединения (рис. 3.3).
Нормирование точности шлицевых соединений
Допуски и посадки шлицевых соединений
Шлицевые соединения предназначены для передачи крутящих моментов с одновременной возможностью осевого перемещения втулки вдоль вала. Шлицевые соединения, по сравнению со шпоночными, имеют следующие преимущества: лучшее центрирование и направление посаженных на вал деталей, более равномерное распределение нагрузки по высоте зуба (шлица), меньшую концентрацию напряжений.
В зависимости от профиля зубьев различают шлицевые соединения трех видов: прямобочные, эвольвентные и треугольные (рис. 4.1).
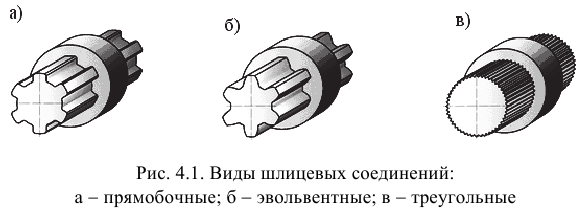
Наибольшее распространение получили шлицевые соединения с прямобочным профилем и четным числом зубьев (ГОСТ 1139-80′).
Шлицевые соединения с эвольвентным профилем зубьев по сравнению с прямобочными обладают существенными преимуществами: они имеют большую нагрузочную способность и циклическую прочность, обеспечивают лучшее центрирование и направление деталей, проще в изготовлении, так как их можно фрезеровать методом обкатки и т.п.
Шлицевые соединения с треугольным профилем нестандартизованы, их чаще применяют вместо посадок с натягом, а также при тонкостенных втулках для передачи небольших крутящих моментов.
Шлицевые соединения называют подвижными, когда детали, насаживаемые на вал, имеют возможность осевого перемещения (например, зубчатые колеса коробок передач, муфты сцепления и другие узлы), и неподвижными, если втулка не может перемещаться относительно вала.
Посадки шлицевых соединений назначают в зависимости от способа центрирования. Существует три способа центрирования: по наружному 
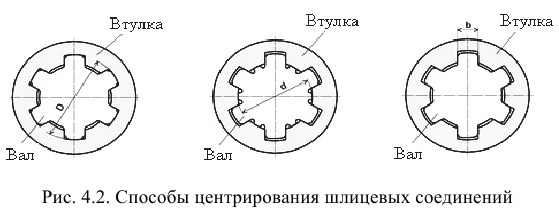
Центрирование но наружному диаметру 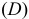
Центрирование по внутреннему диаметру 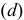
Центрирование но боковым сторонам зубьев 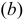
Посадки шлицевых прямобочных соединении (ГОСТ 1139-80*) назначают в системе отверстия по центрирующей цилиндрической поверхности и боковым поверхностям впадин втулки и зубьев вала (т.е. по 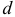
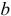
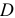
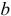
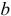
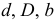
Посадки назначают в зависимости от способа центрирования по ГОСТ 1139-80*. Поля допусков на нецентрирующие диаметры прямобоч-ного шлицевого соединения:
Допуски и посадки шлицевых эвольвент пых соединении установлены ГОСТ 6033-80*. Центрирование осуществляется по боковым поверхностям зубьев (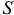
Шлицевые соединения с треугольным профилем зубьев центрируют только по боковым сторонам зубьев (см. рис. 4.2).
Примеры обозначения посадок шлицевых соединений
Соединения с прямобочным профилем
Центрирование по 
это означает: число зубьев 
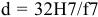
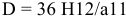
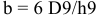
Условное обозначение деталей этого соединения:
- втулки:
- вала:
Центрирование по 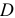
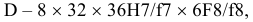
это означает: число зубьев 
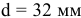
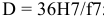
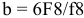
Условное обозначение деталей этого соединения:
- втулки:
;
- вала:
.
Центрирование по 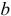
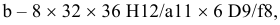
это означает: число зубев 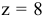
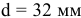
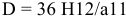
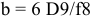
Условное обозначение деталей этого соединения:
- втулки:
- вала:
Соединения с эвольвентным профилем
Центрирование но 
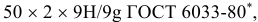
это означает: номинальный диаметр соединения 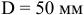
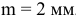
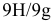
Условное обозначение деталей соединения:
- втулки:
;
- вала:
.
Центрирование но 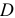
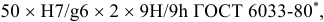
это означает: номинальный диаметр соединения 
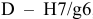
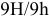
Условное обозначение деталей соединения:
- втулки:
;
- вала:
.
Центрирование но внутреннему диаметру 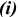
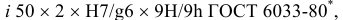
это означает: номинальный диаметр соединения 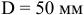
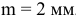
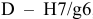
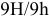
Условное обозначение деталей соединения:
- втулки:
;
- вала:
.
Нормирование шероховатости поверхности, точности формы и расположения поверхностей
Шероховатость поверхности
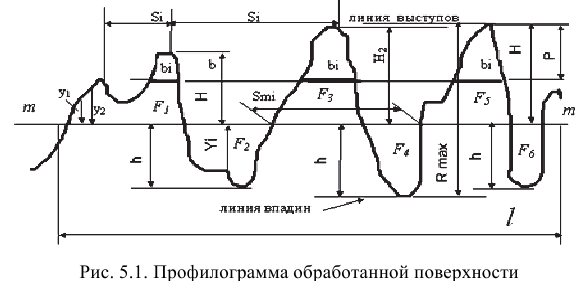
Шероховатость поверхности — это совокупность неровностей поверхности с относительно малыми шагами, выделенная с помощью базовой длины (ГОСТ 2789-73).
Условно границу между отклонениями формы поверхности различных порядков можно установить по значению отношения шага 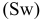
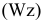
при 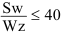
при 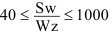
при 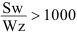
Базовая длина 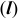
В качестве параметров (критериев) для оценки шероховатости в России и в большинстве стран мира принято шесть параметров:
- высотные параметры:
1) 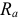
2) 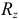
3) 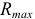
- шаговые параметры:
4) 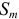
5) 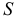
- опорный параметр:
6) 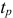
При обозначении шероховатости на чертежах все высотные параметры задаются числовыми значениями в микрометрах (мкм) без указания единицы величины, все шаговые параметры задаются числовыми значениями в миллиметрах (мм) без указания единицы, опорный параметр задается числовыми значениями в процентах (%) и тоже без указания единицы величины. Рассмотрим каждый из этих параметров.
Среднее арифметическое отклонение профиля определяется следующим образом:
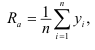
где 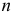
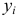
Средняя линия профиля — базовая линия, имеющая форму геометрического профиля и параллельная основному направлению профиля по всей базовой длине, так что в пределах базовой длины суммы площадей, заключенных между этой линией и профилем, по обе ее стороны одинаковы, т.е.
(если 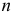
Средняя линия профиля обозначается буквой 
Высота неровностей профиля по десяти точкам определяется по формуле
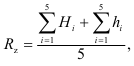
где 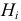
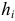
Максимальная высота неровностей профиля (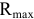
Линия выступов — линия, параллельная средней линии и проходящая через наивысшую точку профиля в пределах базовой длины.
Линия впадин профиля — линия, параллельная средней линии и проходящая через низшую точку профиля в пределах базовой длины.
Средний шаг неровностей определяется по формуле
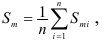
где 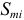
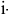
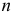
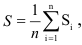
где 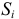
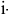
Относительная опорная длина профиля определяется по формуле
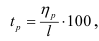
где 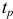
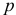
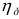
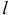
Опорная длина профиля 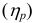
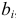
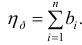
Значение уровня сечения (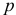
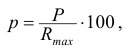
где 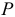
Обозначение шероховатости на чертежах
Стандарт устанавливает три знака для обозначения шероховатости поверхности (рис. 5.2):
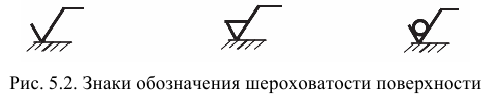
Первый знак применяют, когда способ обеспечения шероховатости конструктором не определен.
Второй знак применяют, когда шероховатость поверхности должна быть обеспечена удалением слоя металла.
Третий знак применяют для обозначения шероховатости поверхности, полученной литьем, ковкой, штамповкой, прокаткой и т.п., т.е. без удаления слоя металла. Последний знак применяют также в обозначении шероховатости поверхности, к обработке которой требования не установлены.
Обозначения шероховатости поверхностей на изображении изделия располагают на линиях контура, выносных линиях (по возможности ближе к размерной линии) или на полках линий-выносок. Допускается при недостатке места располагать обозначения шероховатости на размерных линиях или на их продолжениях, на рамке допуска формы, а также разрывать выносную линию (рис. 5.3).
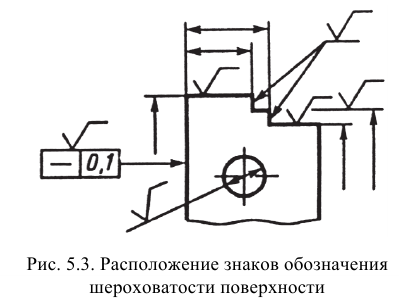
Шероховатость обозначают на чертеже для всех выполняемых по данному чертежу поверхностей изделия, независимо от методов их образования, кроме поверхностей, шероховатость которых не обусловлена требованиями конструкции.
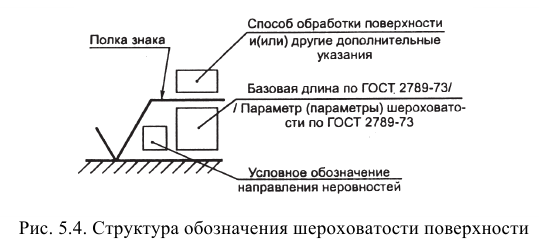
Структура обозначения шероховатости поверхности приведена на рис. 5.4.
Значение параметра шероховатости указывают в обозначении шероховатости после соответствующего символа, например:
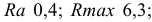
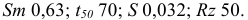
Примечание. В примере 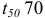
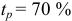
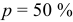
При указании наибольшего значения параметра шероховатости в обозначении приводят параметр шероховатости без предельных отклонений, например:
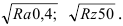
При указании наименьшего значения параметра шероховатости после обозначения параметра следует указывать «min», например: 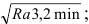
При указании диапазона значений параметра шероховатости поверхности в обозначении шероховатости приводят пределы значений параметра, размещая их в две строки, например:

В верхней строке приводят значение параметра, соответствующее более грубой шероховатости.
При указании номинального значения параметра шероховатости поверхности в обозначении приводят это значение с предельными отклонениями, например:
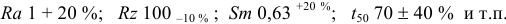
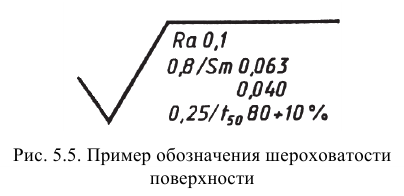
При указании двух и более параметров шероховатости поверхности в обозначении шероховатости значения параметров записывают сверху вниз в следующем порядке (рис. 5.5): параметры высоты неровностей профиля, параметры шага неровностей профиля, относительная опорная длина профиля.
Из параметров шероховатости 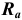
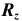
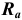
Над полкой знака шероховатости записывают вид обработки поверхности только в том случае, когда он является единственным для получения требуемого качества поверхности (рис. 5.6).
Под полкой знака указывают базовую длину только тогда, когда высотные параметры 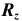
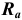
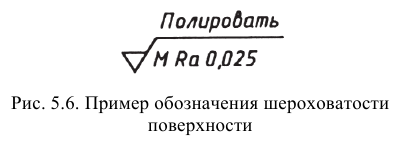
Допускается применять упрощенное обозначение шероховатости поверхностей с разъяснением его в технических требованиях чертежа по примеру, указанному на рис. 5.7. В упрощенном обозначении используют знак 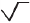
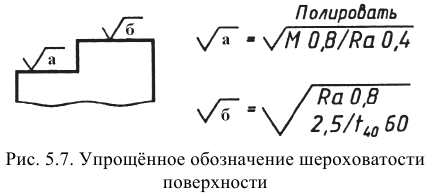
Условные обозначения направления неровностей должны соответствовать приведенным в табл. 5.1. Условные обозначения направления неровностей приводят на чертеже при необходимости (см. рис. 5.6).
При обозначении изделия с разрывом обозначение шероховатости наносят только на одной части изображения, по возможности ближе к месту указания размеров (рис. 5.8). При указании одинаковой шероховатости для всех поверхностей изделия обозначение шероховатости помещают в правом верхнем углу чертежа и на изображение не наносят (рис. 5.9).
Если шероховатость поверхности детали должна быть разной, то в правом верхнем углу чертежа наносят обозначение преобладающей по числу поверхностей шероховатости и знак 
Если шероховатость одной и той же поверхности различна на отдельных участках, то эти участки разграничивают сплошной тонкой линией с нанесением соответствующих размеров и обозначения шероховатости (рис. 5.12). Через заштрихованную зону линию границы между участками не проводят (рис. 5.13).
Обозначение шероховатости рабочих поверхностей зубьев зубчатых колес и эвольвентных шлиц условно наносят на линии делительной поверхности (рис. 5.14).
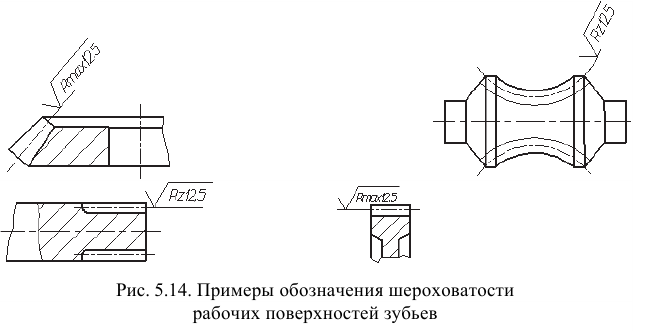
Обозначение шероховатости поверхности профиля резьбы наносят по общим правилам при изображении профиля или условно на выносной линии для указания размера резьбы (рис. 5.15), на размерной линии или на ее продолжении (рис. 5.16).

Если шероховатость контура должна быть одинаковой, то обозначение наносится один раз со знаком окружности о (рис. 5.17). Диаметр знака равен 4…5 мм. В обозначении одинаковой шероховатости поверхностей, плавно переходящих одна в другую, знак о не приводят (рис. 5.18).
Обозначение шероховатости поверхностей повторяющихся элементов изделия (отверстий, пазов, зубьев и т.п.), количество которых указано на чертеже, а также обозначение шероховатости одной и той же поверхности наносят один раз, независимо от числа изображений.
Обозначение шероховатости симметрично расположенных элементов симметричных изделий наносят один раз.
Допускаемые значения 
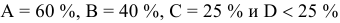
Существуют три основных метода измерения шероховатости поверхности:
1) определение параметров шероховатости сравнением с образцами;
2) бесконтактный метод при использовании приборов светового сечения, двойного микроскопа, микроинтерферометра и др.;
3) контактный метод с использованием щуповых приборов различных моделей, например профилографа-профилометра и др.
В конструкторской документации, справочниках, учебной литературе, выпущенной до 1980 г. и разработанной до введения ГОСТ 2789-73 и ГОСТ 2.309-73, требования к шероховатости указывались по классам и разрядам шероховатости. В табл. 5.3 приведены ранее применявшиеся условные обозначения классов и разрядов шероховатости и соответствующие им числовые значения параметров 
Отклонения и допуски формы поверхностей
Под отклонением формы поверхности понимают отклонение формы реальной поверхности от формы номинальной поверхности.
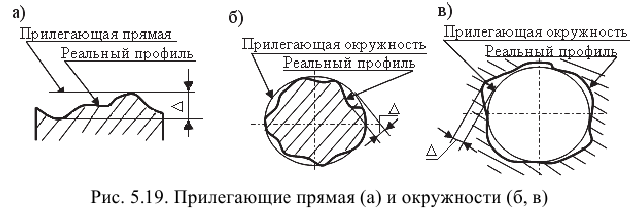
Номинальная поверхность — идеальная поверхность, номинальная форма которой задана чертежом или другой технической документацией. Реальные поверхности у детали получаются после изготовления. В основу нормирования и количественной оценки отклонений формы и расположения положен принцип прилегающих прямых, поверхностей и профилей.
Прилегающая прямая — прямая, соприкасающаяся с реальным профилем и расположенная вне материала детали так, чтобы отклонения от нее до наиболее удаленной точки реального профиля было минимальным (рис. 5.19, а).
Прилегающая окружность — это окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения или максимального диаметра, вписанного в реальный профиль внутренней поверхности вращения (рис. 5.19, б, в). Различают также прилегающую плоскость, прилегающий цилиндр и т.п.
Приняты следующие буквенные обозначения:

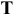
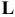
Отклонения формы плоских поверхностей
Комплексный показатель, характеризующий точность формы плоских поверхностей, — это отклонение от плоскостности 
Частными видами отклонений от плоскостности являются выпуклость и вогнутость. Условных обозначений эти показатели не имеют, поэтому на чертеже обозначают поверхность (русскими прописными буквами), а в технических требованиях делают соответствующую запись (рис. 5.21).
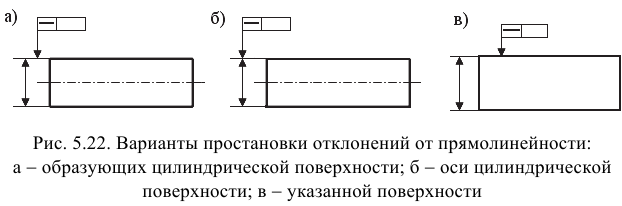
Показателем, характеризующим также точность формы плоских поверхностей, является отклонение от прямолинейности (-). Отклонение от прямолинейности плоскости определяют как наибольшее расстояние (
Отклонения формы цилиндрических поверхностей
Комплексным показателем точности формы цилиндрической поверхности является отклонение от цилиндричности (

Рассмотрим показатели точности формы цилиндрической поверхности в продольном сечении:
- комплексный показатель — отклонение профиля продольного сечения (
);
- частные виды отклонений, характеризующих точность формы в продольном сечении — конусообразность, бочкообразность, седлообразность.
Отклонение профиля продольного сечения — наибольшее расстояние (
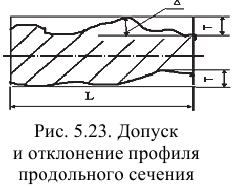
Поле допуска (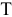
Конусообразность — отклонение продольного сечения, при котором образующие прямолинейны, но не параллельны (рис. 5.24, а).
Бочкообразность — отклонение профиля продольного сечения, при котором образующие непрямолинейны, и диаметры увеличиваются от краев к середине сечения (рис. 5.24, 6).
Седлообразностъ — отклонение профиля продольного сечения, при котором образующие непрямолинейны, и диаметры уменьшаются от краев к середине сечения (рис. 5.24, в).
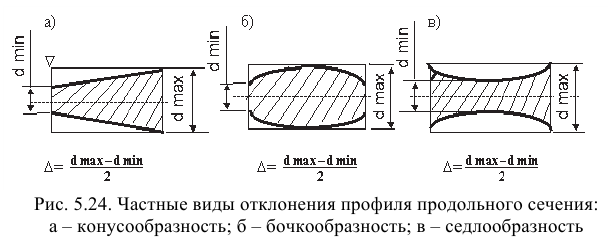
Бочкообразность чаще всего возникает при обтачивании тонких длинных валов в центрах без люнетов (в средней части под влиянием сил резания возникают большие упругие прогибы, чем по краям). Толстые короткие валы чаще получаются седлообразными из-за большого смещения вала по краям (составляющие силы резания распределяются между обоими центрами более равномерно). Бочкообразность и седлообразность могут возникнуть также вследствие погрешности направляющих станин станков и других причин. Причиной конусообразности являются износ резца, несовпадение геометрических осей шпинделя и пиноли задней бабки станка (смещение центров), отклонение от параллельности оси центров направляющим станины.
Рассмотрим показатели точности формы цилиндрической поверхности в поперечном сечении. Комплексный показатель — отклонение от круглости (

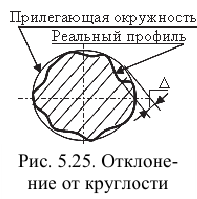
Допуск круглости (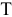
Частными видами отклонений от круглости являются овальность и огранка.
Овальность — отклонение от круглости, при котором реальный профиль представляет собой овалообразную фигуру, наибольший и наименьший диаметры которой находятся во взаимно перпендикулярных направлениях (рис. 5.26, а).
Огранка — отклонение от круглости, при котором реальный профиль представляет собой многогранную фигуру. Огранка может быть с четным и нечетным числом граней и характеризуется равенством размера 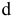
Овальность детали возникает, например, вследствие биения шпинделя токарного или шлифовального станка, дисбаланса детали и других причин. Появление огранки вызвано изменением положения мгновенного центра вращения детали, например при бесцентровом шлифовании.
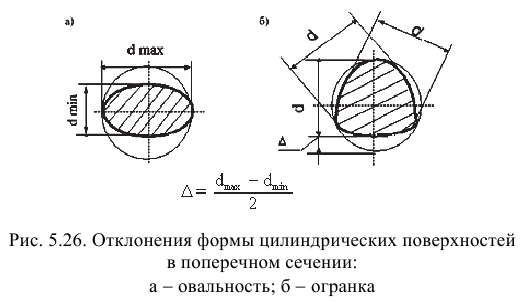
Примеры обозначений отклонений формы цилиндрических поверхностей представлены на рис. 5.27 и 5.28.
Отклонения расположения поверхностей
Отклонением расположения поверхности или профиля называют отклонение реального расположения поверхности (профиля) от его номинального расположения.
Рассмотрим примеры отклонений расположения поверхностей.
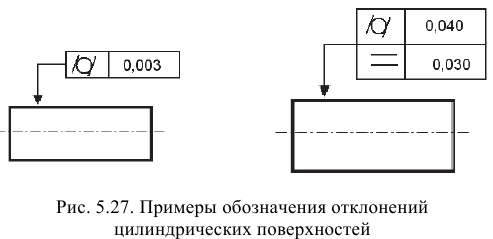
Отклонение от параллельности плоскостей (осей, оси и плоскости) — разность (
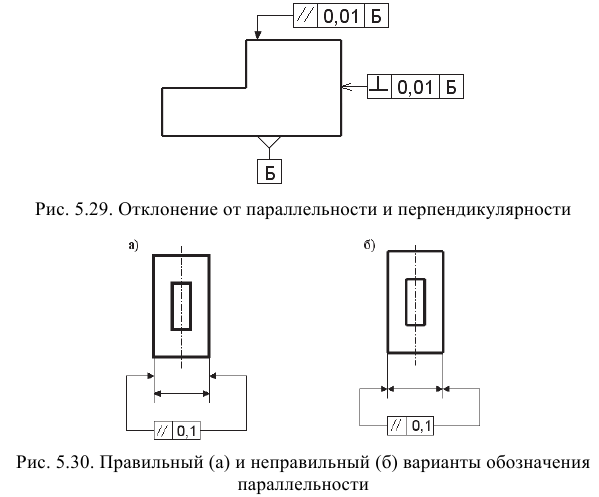
Отклонение от перпендикулярности плоскостей (осей, оси и плоскости) — отклонение угла между плоскостями от прямого угла (90°), выраженное в линейных единицах на длине нормируемого участка (см. рис. 5.29).
Отклонение от соосности относительно общей оси — это наибольшее расстояние (
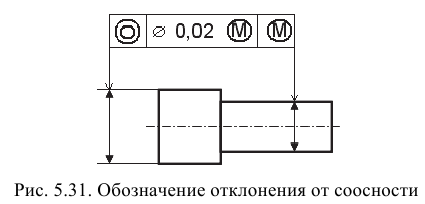
Допуск соосности в диаметральном выражении равен удвоенному наибольшему допускаемому значению отклонения от соосности, а в радиусном выражении — наибольшему допускаемому значению этого отклонения. Поле допуска соосности — область в пространстве, ограниченная цилиндром, диаметр которого равен допуску соосности в диаметральном выражении 
Ранее эти отклонения определяли только в радиусной мере.
Отклонение от симметричности относительно базовой плоскости -наибольшее расстояние (
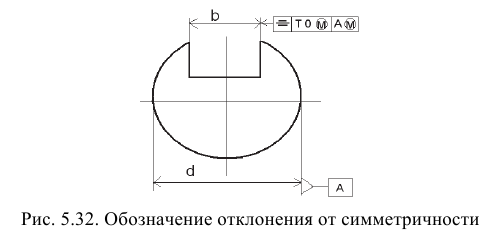
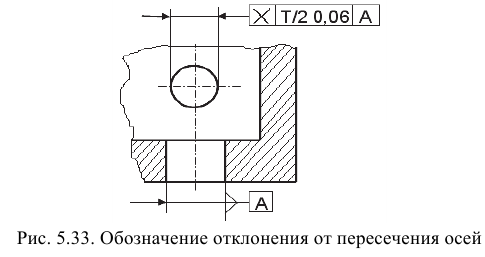
Отклонение от пересечения осей, которые номинально должны пересекаться, определяют как наименьшее расстояние между рассматриваемой и базовой осями (рис. 5.33).
Позиционное отклонение — наибольшее расстояние (
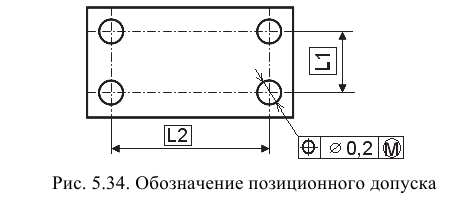
Отклонение наклона плоскости (оси, прямой) относительно плоскости (оси, прямой) — отклонение угла между плоскостью и базовой плоскостью от номинального угла, выраженное в линейных единицах на длине нормируемого участка (рис. 5.35).
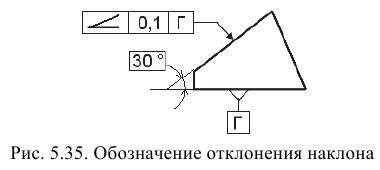
Суммарные отклонения и допуски формы и расположения поверхностей
Радиальное биение поверхности вращения относительно базовой оси является результатом совместного проявления отклонения от круглости профиля рассматриваемого сечения и отклонения его центра относительно базовой оси.
Если определяют разность наибольшего и наименьшего расстояний от всех точек реальной поверхности в пределах нормированного участка 
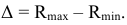
Оно является результатом совместного проявления отклонения от цилиндричности поверхности и отклонения от ее соосности относительно базовой оси (рис. 5.36).
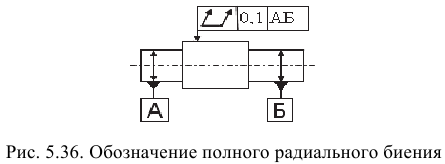
Торцовое биение (полное) — разность (
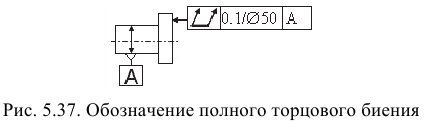
Отклонение формы заданного профиля — наибольшее отклонение 
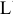
Отклонение формы заданной поверхности — наибольшее отклонение 
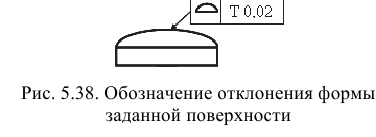
Зависимый и независимый допуски расположения (формы)
Допуски расположения или формы, устанавливаемые для валов или отверстий, могут быть зависимыми и независимыми.
Зависимым называют переменный допуск расположения или формы, минимальное значение которого указывается в чертеже или в технических требованиях и которое допускается превышать на величину, соответствующую отклонению действительного размера поверхности детали от проходного предела (наибольшего предельного размера вала или наименьшего предельного размера отверстия) (рис. 5.39).
Допуск расположения или формы может быть зависимым как от точности размеров рассматриваемых поверхностей, так и от точности размеров базовой поверхности.
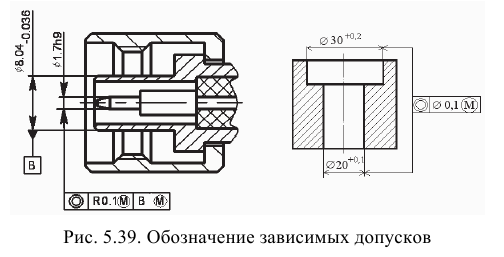
Независимым называют допуск расположения или формы поверхностей, числовое значение которого постоянно и не зависит от действительных размеров рассматриваемых поверхностей.
Нормирование точности формы и расположения поверхностей
Согласно ГОСТ 24643-81, для каждого вида допуска формы и расположения поверхностей установлено 16 степеней точности. Числовые значения допусков увеличиваются от одной степени к другой. Существует связь между точностью размеров деталей (квалнтетом) и точностью формы или расположения поверхностей (степенью точности).
Допуск формы поверхности не может быть больше допуска па размер этой поверхности. Таким образом, для нормирования точности формы используется часть от допуска на размер. Стандарт устанавливает следующие уровни относительной геометрической точности формы:
Допуски формы цилиндрических поверхностей, соответствующие уровням 
Допуски формы и расположения можно ограничивать полем допуска размера (см. раздел 1.8).
На чертежах допуски формы и расположения поверхностей указывают только, когда они должны быть меньше допусков размера или неуказанных допусков по ГОСТ 25670-83.
Назначение степени точности формы в зависимости от квалитета размера можно осуществлять, пользуясь табл. 5.4.
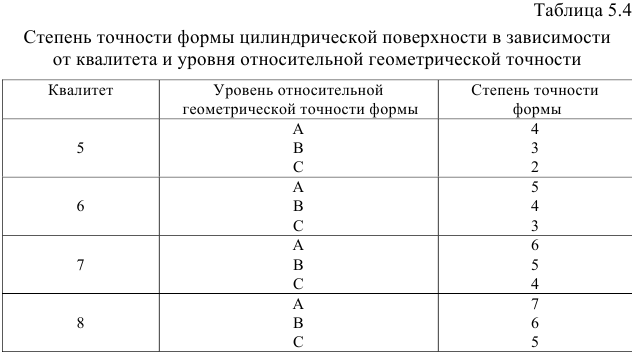
Степень точности формы и расположения для уровня 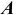
Рассмотрим пример нормирования отклонения от цилиндричности (рис. 5.40). Вал обрабатывается под подшипник качения, поэтому диаметр и поле допуска вала выбраны верно. Как получено отклонение от цилиндричности?
По правилам нормирования для поверхности под подшипник необходимо выбрать повышенные требования к точности формы. То есть от допуска на размер нужно взять 20 % для определения допуска формы
В соответствии с табл. 5.4 определим степень точности формы вала. Для 6 квалитета и повышенного уровня точности формы получаем 4 степень точности формы. По таблицам отклонений цилиндричности для диаметра 30 и степени точности формы 4 допуск цилиндричности равен 3 мкм или 0,003 мм, что подтверждает полученное расчётом значение.
Таким образом, на чертеже вала должно стоять отклонение от цилиндричности, равное 0,003 мм.
Обозначение на чертежах допусков формы и расположения поверхностей деталей
Вид допуска формы и расположения принято обозначать на чертеже знаками (графическими символами), приведенными в табл. 5.5. Знак и числовое значение допуска вписывают в рамку (размеры рамки произвольные), указывая на первом месте знак, на втором — числовое значение допуска в миллиметрах (без указания единицы) и на третьем (при необходимости) — буквенное обозначение базы или поверхности, с которой связан допуск расположения (см. примеры обозначения). Рамку соединяют с элементом, к которому относится допуск, сплошной линией, заканчивающейся стрелкой. Если допуск относится к оси или плоскости симметрии, соединительная линия должна быть продолжением размерной; если допуск относится к общей оси (плоскости симметрии), соединительную линию проводят к общей оси.
Перед числовым значением допуска следует указывать:
1) символ 
2) символ 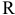
3) символ 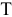
4) символ 
5) слово «сфера» и символы 
Если допуск относится к участку поверхности заданной длины (площади), то ее значение указывают рядом с допуском, отделяя от него наклонной линией (задача 7 из раздела 5.8). Если необходимо назначить допуск на всей длине поверхности и на заданной длине, то допуск на заданной длине указывают под допуском на всей длине (задача 8 из раздела 5.8).
Суммарные допуски формы и расположения поверхности, для которых не установлены отдельные графические знаки, обозначают знаками составных допусков: сначала знак допуска расположения, затем знак допуска формы (задача 9 из раздела 5.8).
Базу обозначают зачерненным треугольником, который соединяют соединительной линией с рамкой допуска. Чаще базу обозначают буквой и соединяют ее с треугольником.
Если базой является ось или плоскость симметрии, треугольник располагают в конце размерной линии соответствующего размера поверхности. В случае недостатка места стрелку размерной линии допускается заменять треугольником.
Обозначение зависимых допусков:
Если допуск расположения или формы не указан как зависимый, то его считают независимым.
Зависимые допуски расположения и формы обозначают условным знаком (буквой 
1) после числового значения допуска, если зависимый допуск связан с действительными размерами рассматриваемых поверхностей (задача 6 из раздела 5.8);
2) после буквенного обозначения базы или без буквенного обозначения базы в третьей части рамки, если этот допуск связан с действительными размерами базовой поверхности (см. рис. 5.34);
3) после числового значения допуска и буквенного обозначения базы или без буквенного обозначения базы, если зависимый допуск связан с действительными размерами рассматриваемого и базового элемента (см. рис. 5.39).
Возможно эта страница вам будет полезна:
Нормирование точности резьбовых соединений
Виды и основные параметры резьб
В зависимости от эксплуатационного назначения резьбы делятся на общие и специальные.
К резьбам общего назначения относятся: крепежные (метрическая, дюймовая), кинематические (трапецеидальная, прямоугольная, упорная), трубные (цилиндрическая, коническая), арматурные.
Резьбы специального назначения (круглая, окулярная и т.д.) применяются только в определенных изделиях.
Резьбы подразделяются:
- по профилю витков на треугольные, трапецеидальные, упорные (пилообразные), прямоугольные, круглые;
- по числу заходов на однозаходные, многозаходные;
- в зависимости от направления вращения контура осевого сечения на правые и левые;
- по принятой единице измерения линейных размеров на метрические и дюймовые.
Из всего многообразия резьб нами будет рассмотрена крепежная цилиндрическая метрическая резьба. Номинальные размеры параметров резьбы общие как для наружной (болта), так и для внутренней (гайки) резьб. Основные параметры цилиндрической резьбы (ГОСТ 11708-82) следующие (рис. 6.1):
- наружный диаметр
;
- средний диаметр
;
- внутренний диаметр
;
- шаг резьбы
;
- угол профиля резьбы
;
- высота исходного треугольника
;
- угол подъема
;
- длина свинчивания
.
Допуски и посадки метрических резьб
В зависимости от эксплуатационных требований к степени подвижности резьбовых соединений стандартами установлены поля допусков, образующие посадки трех групп: с зазором (ГОСТ 16093-81), переходные (ГОСТ 24834-81) и с натягом (ГОСТ 4608-81).
Наружная резьба (болт) нормируется по среднему и наружному диаметрам (
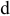
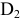

Допуски диаметров 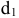
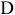
Положение поля допуска диаметра резьбы определяется основным отклонением (верхним 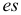
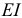
Длины свинчивания резьбы подразделяются на три группы: короткие 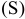
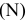
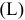
Поле допуска диаметра резьбы образуется сочетанием степени точности и основного отклонения. Поле допуска резьбы образуется сочетанием поля допуска среднего диаметра (d2, D2) с полем допуска диаметра выступов (диаметров d и D|).
Обозначение поля допуска диаметра резьбы состоит из цифры, обозначающей степень точности, и буквы, обозначающей основное отклонение. Например:
Обозначение поля допуска резьбы состоит из обозначения поля допуска среднего диаметра, помещенного на первом месте, и обозначения поля допуска диаметра выступов. Например:
где 
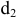
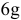
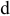
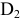
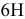

Если обозначение поля допуска диаметра выступов совпадает с обозначением поля допуска среднего диаметра, то оно в обозначении поля допуска резьбы не повторяется. Например:
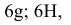
где 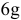
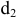
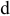
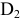

В условном обозначении резьбы обозначение поля допуска должно следовать за обозначением размера резьбы. Примеры обозначения резьбы
С крупным шагом:
С мелким шагом:
Левой резьбы:
В соответствии со сложившейся во многих странах практикой поля допусков сгруппированы в три класса точности: точный, средний и грубый. Понятие о классах точности условное (на чертежах и калибрах указывают не классы, а поля допусков), его используют для сравнительной оценки точности резьбы.
Длина свинчивания (
1) если она относится к группе 
2) если она относится к группе 
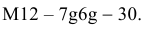
Посадка в резьбовом соединении обозначается дробью, в числителе которой указывают обозначение поля допуска внутренней резьбы, а в знаменателе — обозначение поля допуска наружной резьбы. Например:

Переходные посадки в резьбовых соединениях применяются, если необходимо обеспечить их неподвижность в процессе работы без создания большого натяга и предназначаются для наружных резьб (резьба на ввинчиваемом конце шпильки).
Для переходных посадок предусмотрены поля допусков:
Посадки с натягом в резьбовых соединениях применяются, когда необходимо устранить возможность самоотвинчивания без применения дополнительных элементов заклинивания (только за счет натяга), предназначены эти посадки для нагруженных резьб.
Для посадки с натягом предусмотрены поля допусков:
Незначительное увеличение натяга в резьбовом соединении может вызвать быстрый рост напряжений и появление пластических деформаций, поэтому возникает необходимость проведения селективной сборки с сортировкой резьбовых деталей на две или три размерные группы (рис. 6.2).
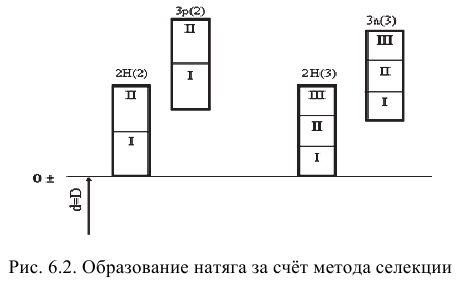
При обозначении посадок с натягом резьбовых соединений в скобках указывается число сортировочных групп по среднему диаметру. Например:
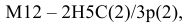
где в скобках указано число сортировочных групп по среднему диаметру.
Пример 5
Расшифровать обозначение посадки резьбового соединения.
Условие: Дано резьбовое соединение 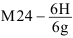
Решение:
Резьба метрическая, наружный диаметр резьбы — 24 мм. Поле допуска резьбы гайки 
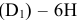
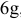
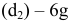
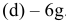
Возможно эта страница вам будет полезна:
Нормирование точности цилиндрических зубчатых передач
Погрешности изготовления и сборки зубчатых передач вызывают динамические нагрузки, шум, вибрации, нагрев, концентрацию напряжений на отдельных участках зубьев. При назначении допусков на зубчатые колеса и точность монтажа для достижения качественной работы передачи преследуются следующие цели:
- обеспечить кинематическую точность, т.е. согласованность углов поворота ведущего и ведомого колес передачи;
- обеспечить плавность работы, т.е. ограничить циклические погрешности, многократно повторяющиеся за один оборот колеса;
- обеспечить полноту контакта зубьев, т.е. такое прилегание зубьев по длине и высоте, при котором нагрузка от одного зуба к другому передается по контактным линиям, максимально использующим всю активную поверхность зуба;
- обеспечить боковой зазор для устранения заклинивания зубьев при работе и ограничения мертвых ходов в передаче.
В связи с этим для зубчатых колес и передач по ГОСТ 1643-81 установлены нормы: кинематической точности, плавности работы, контакта зубьев и бокового зазора.
Этот стандарт распространяется на эвольвентные цилиндрические зубчатые передачи внешнего и внутреннего зацепления с диаметром делительной окружности до 6300 мм, модулем от 1 до 55 мм, шириной венца до 1250 мм.
ГОСТ 1643-81 устанавливает 12 степеней точности зубчатых колес и передач, которые обозначаются в порядке убывания точности цифрами 1, 2, 3… 12. Для каждой степени точности (кроме 1 и 2) установлены независимые нормы допустимых отклонений параметров, определяющих кинематическую точность (табл. 7.1), плавность работы (табл. 7.2) и контакт зубьев передачи (табл. 7.3).
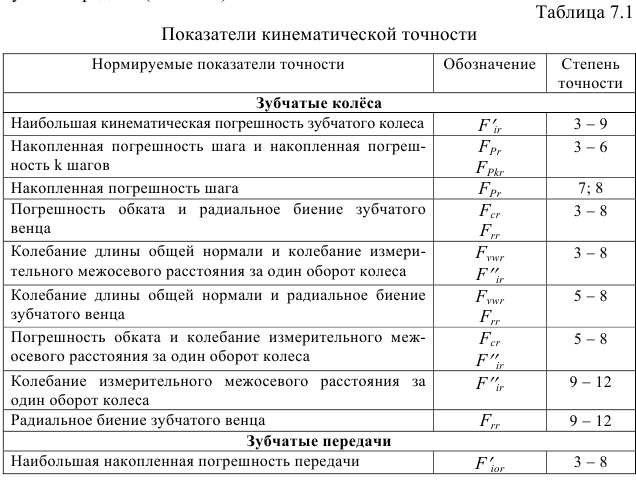
Допуски зубчатых передач
Системой допусков на зубчатые передачи устанавливают гарантированный боковой зазор (
Для зубчатых передач с модулем свыше 1 мм установлено шесть видов сопряжений:
которые определяют величину гарантированного наименьшего бокового зазора 
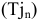
Вместо предусмотренных допусков для каждого вида сопряжений при необходимости могут быть использованы увеличенные допуски 
Для нерегулируемых передач с модулем свыше 1 мм установлено шесть классов отклонений межосевого расстояния, обозначаемых в порядке убывания точности римскими цифрами:
Гарантированный боковой зазор в каждом сопряжении обеспечивается при соблюдении предусмотренных классов отклонений межосевого расстояния (табл. 7.4):
В обоснованных случаях это соответствие между видом сопряжения и классом отклонений межосевого расстояния может изменяться.
Условные обозначения точности зубчатых колес и передач
При обозначении точности зубчатых колес и передач указывают степени точности по трем основным погрешностям зубчатых колес (кинематической, плавности, боковому контакту), вид сопряжения зубьев колес в передаче и вид допуска на боковой зазор. Вид допуска на боковой зазор в обозначении не указывается, если соблюдено соответствие с видом сопряжения (см. табл. 7.4).
Если все погрешности назначены по одной степени точности, то обозначение производится одной цифрой и буквой. Например:
где 7 — степень точности по всем нормам точности (кинематической, плавности работы и контакта зубьев); С — вид сопряжения; с — допуск на боковой зазор (в обозначении не указан).
При комбинировании норм из разных степеней точности обозначение примет следующий вид:
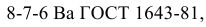
где 8 — степень точности по нормам кинематической точности; 7 — степень точности по нормам плавности; 6 — степень точности по нормам контакта зубьев; В — вид сопряжения; а — вид допуска на боковой зазор.
При изменении соответствия между видом сопряжения и классом отклонения межосевого расстояния в обозначении после вида сопряжения и вида допуска через косую черту указывается класс отклонения межосевого расстояния и через тире — рассчитанный гарантированный боковой зазор (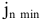
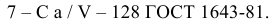
Если в цилиндрических зубчатых передачах на какую-либо из норм точности степень точности не задастся, то вместо номера этой степени точности ставится буква 
Контроль элементов зубчатых колес
Контроль колес по всем показателям не является необходимым. Устанавливаются взаимно равноправные комплексы нормируемых показателей, подлежащих контролю. Один из комплексов приведен в табл. 7.5.
Размерные цепи
Качество машин и приборов обеспечивается, в числе других мер, точностью расположения деталей, узлов и механизмов, образующих конечное изделие. При этом число операций, связанных с подгонкой деталей и регулированием их положения в процессе сборки, должно сводиться к минимуму. Зазоры, предельные размеры и другие параметры, координирующие взаимное положение собираемых объектов, как правило, зависят от режимов работы, конструктивных, технологических и эксплуатационных особенностей деталей, узлов и конечных изделий, поэтому часто взаимосвязь между предельными размерами и допусками собираемых деталей и узлов устанавливают с помощью расчетов, основанных на теории размерных цепей.
Размерная цепь — совокупность размеров, образующих замкнутый контур и непосредственно участвующих в решении поставленной задачи.
С помощью размерных цепей можно решать конструкторские, технологические, измерительные и прочие задачи. Расчет размерных цепей позволяет обоснованно назначать допуски на взаимосвязанные размеры деталей и сборочных единиц; облегчает правильную простановку размеров на чертежах, согласованную с порядком обработки деталей и сборки механизмов. Размерные цепи применяют для определения операционных допусков, пересчета конструкторских баз на технологические, для выбора измерительных баз и т.д.
Звено размерной цепи — один из размеров, образующих размерную цепь. Один и тот же механизм, даже одна деталь, могут иметь несколько размерных цепей.
Размерные цепи обозначают прописными буквами русского алфавита 
Замыкающее звено — звено размерной цепи, которое получается последним в процессе изготовления или сборки.
Составляющие звенья могут быть увеличивающими или уменьшающими:
-увеличивающее звено — звено, с увеличением которого увеличивается и замыкающее звено;
-уменьшающее звено — звено, с увеличением которого замыкающее звено уменьшается.
Увеличивающие звенья обозначают буквой со стрелкой вправо, например:
уменьшающие — со стрелкой влево, например:
В качестве замыкающих звеньев используют детали (например, комплект прокладок), зазоры, натяги и т.п. Поэтому числовые значения указанных звеньев могут быть положительными, отрицательными и равными нулю.
При решении размерных цепей встречаются два вида задач:
Первая задача:
По заданным номинальным размерам и предельным отклонениям составляющих звеньев цепи определить номинальный размер и предельные отклонения замыкающего звена. Например:
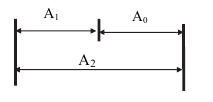
Дано:
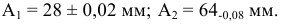
Определить:
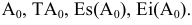
Вторая задача:
По заданным номинальным размерам всех звеньев цепи и заданным предельным отклонениям замыкающего звена определить допуски и предельные отклонения составляющих звеньев цепи. Например:
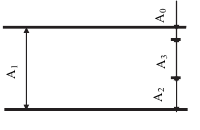
Дано:
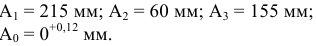
Определить:
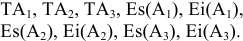
Методы решения размерных цепей
Существуют следующие методы решения размерных цепей:
1) метод, обеспечивающий полную взаимозаменяемость, или метод «максимума-минимума»;
2) методы, обеспечивающие неполную взаимозаменяемость:
- теоретико-вероятностный;
- групповой подборки деталей (селективная сборка);
- регулирования;
- пригонки.
Основные расчетные формулы метода «максимум-минимум»
Метод «максимума-минимума» основан на предположении, что при сборке механизма возможно сочетание увеличивающих звеньев, изготовленных по наибольшим предельным размерам, с уменьшающими звеньями, изготовленными по наименьшим предельным размерам, или наоборот.
Этот метод расчета обеспечивает полную взаимозаменяемость в процессе сборки и эксплуатации изделий. Однако допуски составляющих размеров, вычисленные по этому методу, особенно для размерных цепей, содержащих много звеньев, могут получиться в техническом и экономическом отношениях неоправданно малыми. Поэтому данный метод применяют для проектирования размерных цепей, имеющих малое число составляющих звеньев невысокой точности.
Первая задача
Номинальный размер замыкающего звена можно определить по формуле (см. пример первой задачи):
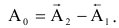
Если принять общее количество звеньев цепи 
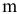
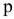
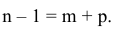
В общем виде формула для расчета номинального размера замыкающего звена будет такой:
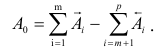
Для примера (раздел 8.1)
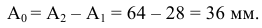
На основании равенства (8.1) получим
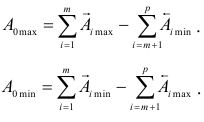
Вычтем почленно из равенства (8.2) равенство (8.3), получим
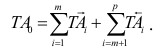
Так как сумма увеличивающих и уменьшающих звеньев есть все составляющие звенья цепи, то полученное равенство можно упростить
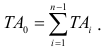
Таким образом, допуск замыкающего звена равен сумме допусков всех составляющих звеньев в цепи.
Чтобы вывести формулы для расчета предельных отклонений замыкающего звена, вычтем почленно из равенства (8.2) равенство (8.1) и из равенства (8.3) равенство (8.1), получим
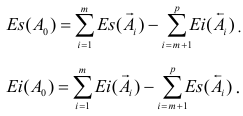
Таким образом, верхнее отклонение замыкающего размера равно разности сумм верхних отклонений увеличивающих и нижних отклонений уменьшающих размеров; нижнее отклонение замыкающего размера равно разности сумм нижних отклонений увеличивающих и верхних отклонений уменьшающих размеров.
Для примера первой задачи (см. раздел 8.1) получим
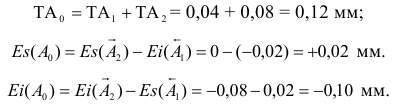
Таким образом,
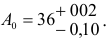
Определим допуск замыкающего звена через полученные предельные отклонения
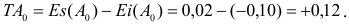
Это значение совпадает с ранее найденным значением допуска, что подтверждает правильность решения задачи.
Вторая задача
При решении второй задачи допуски составляющих размеров определяют по заданному допуску замыкающего размера 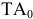
1) При решении способом равных допусков — на составляющие размеры назначают примерно равные допуски, руководствуясь средним допуском.
Итак, предполагаем, что
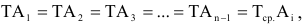
тогда сумма допусков всех составляющих размеров равна произведению числа составляющих звеньев на средний допуск, т.е.
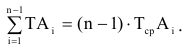
Подставим это выражение в равенство (8.4):
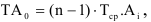
отсюда
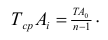
По найденному значению 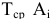
При этом должны быть выполнены следующие условия: принятые допуски должны соответствовать стандартным допускам, сумма допусков составляющих размеров должна равняться допуску замыкающего размера, т.е. должно выполняться равенство (8.4). Если при стандартных допусках равенство (8.4) не может быть обеспечено, то на один составляющий размер устанавливают нестандартный допуск, определяя его значение по формуле
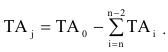
Способ равных допусков прост и дает хорошие результаты, если номинальные размеры составляющих звеньев размерной цепи находятся в одном интервале.
Решим пример второй задачи (см. раздел 8.1) способом равных допусков по формуле (8.7)
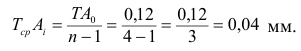
Получим
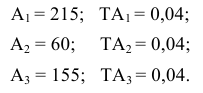
В этом примере равенство (8.4) соблюдается, и корректировать допуск одного из составляющих размеров нет необходимости.
Распишем равенство (8.5) для данного примера
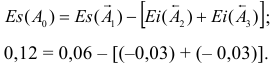
Числовые значения предельных отклонений составляющих размеров выбраны условно.
Получим

Проверим соблюдение равенства (8.6)
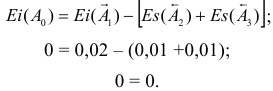
Таким образом, получим ответ
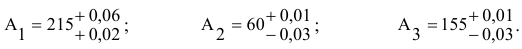
2) Более универсальным и упрощающим подбор допусков при любом разнообразии размеров составляющих звеньев является способ допусков одного квалитета.
При этом способе на размеры всех составляющих звеньев (кроме корректирующего 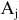
Рекомендуется на охватывающие размеры назначать допуски с основным отклонением 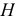
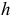
Для вывода формулы исходной зависимостью служит равенство (8.4)
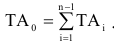
Однако допуск любого размера можно вычислить по формуле
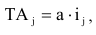
где 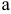
Подставим в формулу (8.4) вместо допусков составляющих размеров произведение:
Так как

то
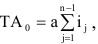
отсюда
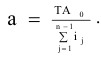
По найденному числу единиц допуска (а) подбирают ближайший квалитет, по которому назначают допуски составляющих размеров. Для удовлетворения условия (8.4) на один из составляющих размеров, как и в предыдущем способе, допуск назначают по формуле (8.8).
Решим пример второй задачи способом назначения допусков одного квалитета по формуле (8.9)
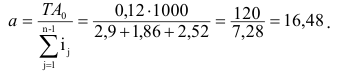
Принимаем: 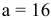
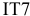
По таблицам справочников назначаем допуски составляющих звеньев цепи по седьмому квалитету:
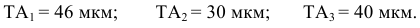
Равенство (8.4) не соблюдается, так как
В качестве корректирующего используем звено 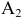
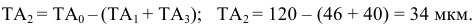
Итак, получим
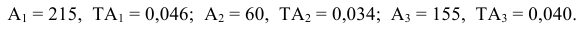
Верхнее отклонение замыкающего звена определяется по формуле
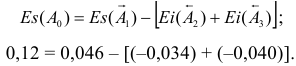
Получим

Нижнее отклонение замыкающего звена
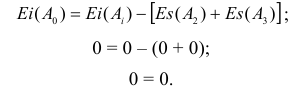
Таким образом, получим ответ
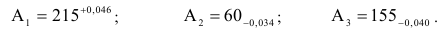
Выводы
Так как допуск замыкающего звена зависит от числа составляющих размеров, то основное правило проектирования размерных цепей можно сформулировать так: при конструировании деталей, узлов сборочных единиц и механизмов необходимо стремиться к тому, чтобы число размеров, образующих размерную цепь, было минимальным. Это принцип кратчайшей размерной цепи.
На чертежах указывают только составляющие размеры с предписанными отклонениями. Замыкающие размеры обычно получаются автоматически в результате обработки деталей или сборки, поэтому их не контролируют и на чертежах не обозначают.
Проставлять на чертежах размеры замкнутыми цепочками не рекомендуется. Особенно недопустимо проставлять замыкающие размеры с отклонениями, так как при изготовлении детали это вызывает брак.
В качестве замыкающих размеров следует принимать наименее ответственные размеры, которые могут иметь большие отклонения.
Возможно эта страница вам будет полезна:
Рекомендации по выбору посадок
В курсе «Детали машин» изучают конструкции деталей и сборочных единиц машин и методы их расчета. При выполнении самостоятельных работ по дисциплине «Нормирование точности и технические измерения» на чертежах общих видов и рабочих чертежах задаются посадки цилиндрических сопряжений, а также допуски размеров, допуски формы и расположения поверхностей.
При выборе посадок, допусков размеров деталей, а также допусков формы и расположения следует учитывать: назначение детали в сборочной единице, роль отдельных ее поверхностей (цилиндрических, конических, торцовых), влияние отклонений размеров, формы и расположения осей или поверхностей детали на смежные с ней детали, влияние суммы отклонений точностных параметров всех деталей на качественные показатели изделия (точность и плавность вращения, бесшумность, долговечность).
Детали подшипниковых узлов
Кольца, втулки
Между подшипниками и базовыми торцами валов или корпусов часто расположены дистанционные кольца и втулки. Условимся называть втулками детали, у которых отношение длины 
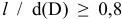
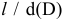
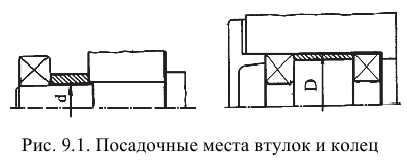
С уверенностью можно лишь сказать, что при 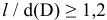
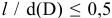
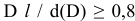
Если выбор полей допусков отверстия и вала ничем не обусловлен, рекомендуется принимать посадки колец па вал: 
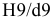
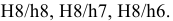
Если поля допусков валов заданы в связи с установкой соседних деталей, следует применять для гарантии зазора поля допусков отверстий колец: 
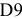
Поле допуска наружного диаметра колец, установленных в отверстиях корпусов, во всех случаях следует принимать 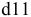
При длине кольца 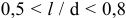
Стаканы
В стаканах обычно размещают подшипники фиксирующей опоры вала червяка и опоры вала конической шестерни. Иногда стаканы применяют для удобства сборки. Для легкости установки стаканов в корпусные детали желательно применение посадок с зазором. Но иногда возможно их смещение в пределах зазоров, что вызовет изменение положения оси вращения вала и, как следствие, увеличение концентрации нагрузки, поэтому в соединении стаканов с корпусом зазоры нежелательны. В связи с этим рекомендуется применять следующие переходные посадки для стаканов:
- нерегулируемые в осевом направлении —
- регулируемые в осевом направлении —
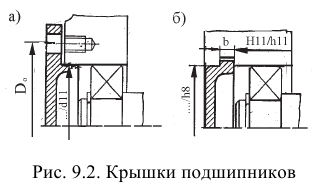
Крышки подшипников
На рис. 9.2 показаны накладная и закладная крышки без отверстия для прохода вала. Торцовые поверхности крышек свободны и не используются в качестве базовых для установки подшипников качения. Единственное назначение таких крышек -закрыть отверстие корпусной детали.
Точное центрирование таких крышек по отверстию корпуса не требуется, поэтому поле допуска центрирующей поверхности накладной крышки принимают по 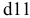
Поле допуска центрирующей поверхности закладных крышек любой конструкции в целях уплотнения против вытекания смазки принимают 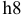
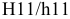
Зубчатые и червячные передачи
Передача нагрузки с колеса на вал соединением с натягом
Соединение обеспечивает точную установку колеса на вал и высокую нагрузочную способность, поэтому соединения с натягом получают все большее распространение, особенно в редукторостроении, несмотря на высокую концентрацию напряжений, вызываемую соединением.
Основным способом сборки для осуществления соединения с натягом колес с валами является нагрев колеса.
Рекомендуемые посадки:
Передача момента шпоночным соединением
При передаче через шпоночное соединение вращающего момента возникают значительные местные деформации вала и ступицы около шпоночного паза, а также деформации самой шпонки. Наличие шпоночного паза приводит к асимметричной деформации вала и ступицы, в результате чего давление по рабочим граням шпонки и шпоночным пазам вала и ступицы распределяется неравномерно.
Рекомендуемые посадки:
- для цилиндрических прямозубых колес —
6;
- для цилиндрических косозубых и червячных колес —
;
- для конических колес —
;
- для неподвижных колес коробок передач (при необходимости сборки внутри корпуса) —
.
Передача момента шлицевым соединением
При одинаковых габаритах шлицевые соединения имеют большую нагрузочную способность и обеспечивают большее сопротивление усталости вала, чем шпоночное соединение. Они обеспечивают хорошее центрирование и направляют детали по валу, поэтому они являются основными для соединения с валом подвижных вдоль вала зубчатых колес коробок передач. Рекомендуемые посадки представлены в табл. 9.1.
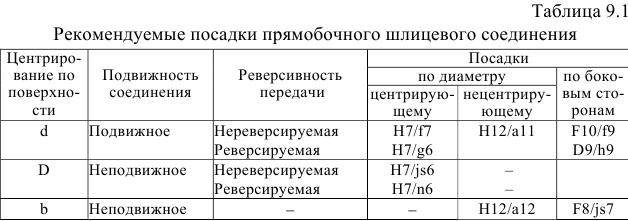
Муфты, шкивы, звездочки
Муфты, шкивы, звездочки — эти детали, как правило, надевают на консольные концы валов. В большинстве случаев их монтаж осуществляется после того, как собран основной узел, поэтому одним из основных требований, предъявляемых к соединениям муфт, шкивов, звездочек с валами, является легкость сборки.
Рекомендуемые посадки при применении шпоночных соединений:
- для муфт —
- для звездочек —
- для шкивов —
Кстати тут дополнительная теория из учебников.
Всё о технических измерениях
«Измеряй все доступное измерению и делай доступным все недоступное ему»
Галилео Галилей
Нет ни одной области практической деятельности человека, где можно было бы обойтись без количественных оценок, получаемых в результате измерений. Роль измерений непрерывно возрастает во всех областях науки и техники. И это естественно: каждому продвижению вперед в области естественных и технических наук, каждому открытию, созданию новых машин, изделий и материалов предшествует большое число многообразных измерений. Как следствие, растут требования к качеству измерений. Большое значение приобретает также достоверность и надежность измерений. Все больше возрастает и роль метрологии — науки об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Измерения являются одним из путей познания природы человеком. Измерения количественно характеризуют окружающий материальный мир, раскрывая действующие в природе закономерности. Об этом очень образно сказал основоположник отечественной метрологии Д. И. Менделеев: «Наука начинается с тех пор, как начинают измерять». Известно аналогичное высказывание и основоположника английской метрологии Томсона: «Каждая вещь известна лишь в той степени, в какой её можно измерить».
Без измерений невозможно существование современной науки, промышленности, сельского хозяйства, медицины, торговли. Измерения необходимы в военном деле, в быту, в спорте и во многих других видах деятельности человека. Они выполняются не только в разных земных условиях, но и в атмосфере, в космосе, на других планетах. Измерения позволяют управлять технологическими процессами, предприятиями, народным хозяйством в целом. Огромное значение имеют измерения в повышении качества продукции. Много измерительных приборов применяются в быту. Измерительная информация стала неотъемлемой спутницей человека. Можно с уверенностью сказать, что измерения сопровождают нас в течение всей жизни.
Принимая во внимание, что в машиностроении ежегодно выполняются десятки миллиардов измерений, что требования к качеству продукции непрерывно повышаются, следует рассматривать метрологическое обеспечение как один из крупных резервов повышения эффективности машиностроительного производства. Массовость и значимость измерений обусловили превращение метрологии в активный инструмент повышения качества работ и эффективности производства.
Основные термины и определения
Основные термины и определения даны в соответствии с РМГ 29-99. Постановлением Государственного комитета Российской Федерации по стандартизации и метрологии от 17 мая 2000 г. № 139-ст межгосударственные Рекомендации РМГ 29-99 введены в действие непосредственно в качестве Рекомендаций по метрологии Российской Федерации с 1 января 2001 г. (взамен ГОСТ 16263-70).
Измерение — это совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.
В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути, сравнивают ее размер с единицей, хранимой линейкой, и, произведя отсчет, получают значение величины (длины, высоты, толщины и других параметров детали).
С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчет.
Приведенное определение понятия «измерение» удовлетворяет общему уравнению измерений, что имеет существенное значение в деле упорядочения системы понятий в метрологии. В нем учтена техническая сторона (совокупность операций), раскрыта метрологическая суть измерений (сравнение с единицей) и показан гносеологический аспект (получение значения величины).
От термина «измерение» происходит термин «измерять», которым широко пользуются на практике. Все же нередко применяются такие термины, как «мерить», «обмерять», «замерять», «промерять», не вписывающиеся в систему метрологических терминов. Их применять не следует. Не следует также применять такие выражения, как «измерение значения» (например, мгновенного значения напряжения или среднего квадратического значения), так как значение величины — это уже результат измерений.
В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая и не определена единица измерений этой величины), практикуется оценивание таких величин по условным шкалам.
Измерения, отнесенные к линейным, радиусным и угловым величинам, называют техническими измерениями.
Физическая величина — это одно из свойств физического объекта (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но в количественном отношении индивидуальное для каждого из них.
Размер физической величины — это количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу.
Значение физической величины — это выражение размера физической величины в виде некоторого числа принятых для нее единиц.
Числовое значение физической величины — это отвлеченное число, входящее в значение величины.
Истинное значение физической величины — это значение физической величины, которое идеальным образом характеризует в качественном и количественном отношении соответствующую физическую величину. Истинное значение физической величины может быть соотнесено с понятием абсолютной истины. Оно может быть получено только в результате бесконечного процесса измерений с бесконечным совершенствованием методов и средств измерений.
Возможно эта страница вам будет полезна:
Действительное значение физической величины — это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Система физических величин — это совокупность физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимают за независимые, а другие определяют как функции независимых величин.
В названии системы величин применяют символы величин, принятых за основные. Так, система величин механики, в которой в качестве основных приняты длина 
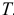
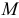
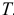
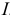

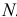
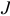
Основная физическая величина — это физическая величина, входящая в систему величин и условно принятая в качестве независимой от других величин этой системы.
Производная физическая величина — это физическая величина, входящая в систему величин и определяемая через основные величины этой системы. Примеры производных величин механики системы 
Размерность физической величины — это выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе величин за основные с коэффициентом пропорциональности, равным 1.
Степени символов основных величин, входящих в одночлен, в зависимости от связи рассматриваемой физической величины с основными, могут быть целыми, дробными, положительными, отрицательными. Понятие размерность распространяется и на основные величины. Размерность основной величины в отношении самой себя равна единице, т.е. формула размерности основной величины совпадает с ее символом. В соответствии с международным стандартом ИСО 31/0, размерность величин следует обозначать знаком dim. В системе величин 
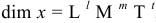
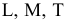
Показатель размерности физической величины — это показатель степени, в которую возведена размерность основной физической величины, входящая в размерность производной физической величины. Показатели степени 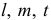

Размерная физическая величина — это физическая величина, в размерности которой хотя бы одна из основных физических величин возведена в степень, не равную нулю. Например, сила 
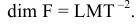
Безразмерная физическая величина — это физическая величина, в размерность которой основные физические величины входят в степени, равной нулю.
Аддитивная физическая величина — это физическая величина, разные значения которой могут быть суммированы, умножены на числовой коэффициент, разделены друг на друга. К аддитивным величинам относятся длина, масса, сила, давление, скорость, время и др.
Нсаддитивная физическая величина — это физическая величина, для которой суммирование, умножение на числовой коэффициент или деление друг на друга ее значений не имеет физического смысла. Например, термодинамическая температура.
Единица физической величины — это физическая величина фиксированного размера, которой условно присвоено числовое значение, равное единице, и применяемая для количественного выражения однородных с ней физических величин.
Система единиц физических величин — это совокупность основных и производных единиц физических величин, образованная в соответствии с принципами для заданной системы физических величин, например международная система единиц (СИ), принятая в 1960 г.
В зависимости от метрологического назначения измерения делятся на технические и метрологические. Данный классификационный признак не предусмотрен РМГ 29-99 и дается для общего обозрения.
Технические измерения проводятся рабочими СИ. Они являются наиболее массовым видом измерений. Например, измерение давления пара в котле при помощи манометра.
Метрологические измерения выполняются при помощи эталонов с целью воспроизведения единиц физических величин для передачи их размера рабочим СИ.
Выбор измерительных средств
При выборе измерительных средств для контроля изделий учитывают совокупность метрологических (цена деления, погрешность измерения и др.), эксплуатационных и экономических показателей. К эксплуатационным и экономическим показателям относятся: повторяемость измеряемых размеров (массовость) и доступность их для контроля; стоимость и надежность измерительных средств; продолжительность работы (до ремонта); время, затрачиваемое на настройку и процесс измерения; масса, габариты и рабочая нагрузка.
Выбор измерительных средств в зависимости от точности измерении
При выборе средств измерения точность средств измерений должна быть достаточно высокой по сравнению с заданной точностью выполнения измеряемого размера, а трудоемкость измерений и их стоимость должны быть, возможно, более низкими, обеспечивающими наиболее высокие производительность труда и экономичность.
Правильный выбор измерительных средств с учетом допускаемых погрешностей измерений размеров до 500 мм регламентирует ГОСТ 8.051-81. Стандарт предусматривает значения допускаемых погрешностей измерений в зависимости от допусков на обработку. Значения допускаемых погрешностей измерений приведены в табл. 10.1.
Пределы допускаемых погрешностей измерений установлены из расчета (в среднем) от 20 до 35 % значения допуска (с учетом квалитетов).
Погрешность измерительного средства должна быть меньше допускаемой погрешности измерения. Предельные погрешности различных СИ приведены в табл. 10.2 и 10.3.

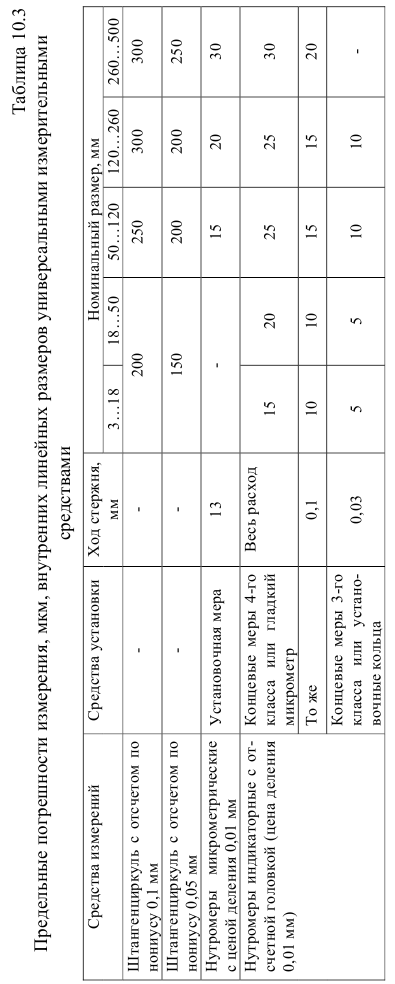
Пример. Выбрать средство для измерения в условиях серийного производства диаметра элемента вала 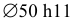
По табл. 10.1 находим допуск размера вала 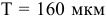
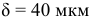
По табл. 10.2 подбираем средство измерений наружных размеров. Здесь указаны предельные погрешности измерения различными средствами. Подбираем по этой таблице средство, имеющее диапазон измерения, включающий в себя номинальный диаметр 50 мм, и имеющее предельную погрешность измерения, близкую к 40 мкм, т.е. к допускаемой погрешности измерения рассматриваемой ступени вала. Лучше всех этим требованиям удовлетворяет скоба индикаторная с диапазоном измерения 0…50 мм, ценой деления 0,01 мм и предельной погрешностью измерения 15 мкм. Эта скоба подходит и по производительности измерения для условий серийного производства.
Выбор измерительных средств в зависимости от организационно-технических форм контроля
Детали в процессе их изготовления могут подвергаться сплошному 100%-му контролю и выборочному контролю.
Сплошному контролю подлежат детали и узлы по так называемым аварийным параметрам и таким, которые определяют эксплуатационные показатели машин или приборов в целом.
При стабильном технологическом процессе изготовления деталей и сборки узлов и изделий, когда появление брака маловероятно, целесообразно применять выборочный контроль деталей, узлов и изделий. Наиболее часто применяют статистический метод выборочного контроля. Этот метод применяется для приемки готовых изделий (приемочный контроль) и для управления точностью в процессе производства (управляющий контроль).
Сплошной и выборочный приемочный контроль относятся к пассивным формам контроля, при которых только регистрируются результаты измерения, а на ход технологического процесса эти измерения не влияют. При пассивных формах контроля используют универсальные измерительные приборы и инструменты.
Для повышения качества машин, сокращения потерь от брака и повышения производительности труда необходимо применять активные формы контроля, при которых результаты измерения используются для регулирования точности технологических процессов.
Рассмотрим систему централизованного статистического контроля (СЦСК — 1). Эта система предназначена для автоматического регулирования точности технологических процессов с целью недопущения появления брака и сокращения количества подналадок технологического процесса.
Эта система контроля позволяет также анализировать точность работы станков и технологической оснастки.
СЦСК — 1 состоит из ряда измерительных позиций, установленных на соответствующих станках, и управляющей счетной машины УСМ — 5, установленной на центральном контрольном пункте (рис. 10.1).
На измерительных позициях определяют отклонения действительных размеров от заданных. Эти отклонения затем первично преобразуются в соответствующие им числа электрических импульсов.
Счетная машина имеет два счетчика: счетчик-повторитель (СП), который производит вторичное преобразование отклонений в число импульсов, и счетчик-накопитель, суммирующий все импульсы при измерении всех деталей.
Накопленное число импульсов автоматически сравнивается с пределом, заданным для данной измерительной позиции и хранящимся в памяти счетной машины. Если число, накопленное на счетчике-накопителе, превысит это предельное число, то срабатывают специальная схема совпадения и реле исполнительного органа (ИО), контакты которого включают сигнализацию о браке; подается команда на прекращение обработки или на подналадку станка.
Связь счетной машины с соответствующими измерительными позициями осуществляется с помощью программного счетчика ПС — 1 по определенной программе.
Система централизованного статистического контроля является универсальной системой, так как к ней могут быть подключены измерительные позиции, стоящие на любых станках. К счетной машине могут быть подключены построитель гистограммы, карты статистического контроля, а также суммирующая десятиклавишная машина с дистанционным управлением типа СД — 107 — Д.
Выбор измерительных средств в зависимости от масштабов производства
При индивидуальном и мелкосерийном производстве объекты производства часто меняются, высокое качество изделий не гарантируется ходом технологического процесса, а зависит от индивидуальных навыков и квалификации рабочего. Поэтому при индивидуальном и мелкосерийном производстве необходимы тщательный пооперационный контроль деталей, соответствующие универсальные измерительные средства и контролеры высокой квалификации.
При серийном производстве изготавливаются взаимозаменяемые детали, узлы и изделия, номенклатура которых не изменяется в течение длительного времени. Однородность деталей по качеству достигается применением специализированного оборудования, инструмента, оснастки. Работа ведется по отработанной пооперационной технологии. Поэтому пооперационный контроль не обязателен. Контроль осуществляется после ряда операций или после окончательного изготовления деталей универсальными измерительными средствами, специализированными контрольными приспособлениями, жесткими предельными калибрами и шаблонами.
При массовом производстве номенклатура изделий постоянна. Качество изделий обеспечивается отработанной технологией, широким применением специализированного оборудования, приспособлений и инструмента, а также контрольными операциями, которые являются составной частью единого технологического процесса. При массовом производстве широко применяются высокопроизводительные механизированные и автоматические контрольно-измерительные средства.
Выбор измерительных средств в зависимости от конструктивных особенностей контролируемой детали
Конструктивная форма, число контролируемых параметров, габариты и масса детали также влияют на выбор типа измерительного средства.
Детали больших габаритов и большой массы контролируются переносными измерительными средствами.
При большом количестве контролируемых параметров рекомендуется применять многомерные контрольно-измерительные устройства.
Автоматы особо эффективны при контроле деталей простой геометрической формы, небольшого веса, с небольшим числом контролируемых параметров.
При выборе средства измерения необходимо учитывать также материал контролируемой детали, жесткость ее конструкции и шероховатость поверхности.
Размеры тонкостенных деталей предпочтительно контролировать бесконтактным методом или на приборах с небольшим измерительным усилием.
ЗАДАНИЯ К РАЗДЕЛУ 10.2: Выбрать средство для измерения в условиях серийного производства следующего размера по своему варианту (номер варианта соответствует последней цифре номера зачетной книжки).
Средства измерений линейных размеров
Меры длины концевые плоскопараллельные
Концевые меры длины — это однозначные меры, размер которых образован противоположными измерительными поверхностями. Наиболее распространены в машиностроении плоскопараллельные концевые меры длины (КМД). Особенность КМД заключается в том, что их измерительные поверхности имеют высокую плоскостность, параллельны между собой и обладают весьма малой шероховатостью. Эти свойства обеспечивают одинаковое для данной меры расстояние между измерительными поверхностями в любом месте. Конструкция всех КМД практически одинакова — это пластины с двумя противоположными плоскопараллельными измерительными поверхностями.
Материалом для изготовления КМД служат, в подавляющем большинстве, хромистые закаленные стали, применяют также и твердый сплав ВК6М.
Концевые меры длины делятся на рабочие и образцовые.
Рабочие концевые меры длины предназначены для регулировки и настройки на размер показывающих измерительных приборов (рис. 10.2), для непосредственных измерений, а также для выполнения особо точных разметочных работ и наладки станков.
Рабочие КМД разделяются по классам точности. Класс точности меры показывает, какое отклонение имеет действительный размер данной меры от ее номинального размера. Классы точности концевых мер — это ряды допусков на изготовление их действительных размеров в зависимости от значений их номинальных размеров. Концевые меры длины выпускают по следующим классам точности: 0, 1,2, 3.
Кроме того, установлены дополнительные классы точности: 00, 01. Эти классы применяют по согласованию между потребителем и изготовителем.
Для мер, находящихся в эксплуатации, установлены также классы точности 4 и 5. Они присваиваются концевым мерам, значительно изношенным и изменившим размер.
Образцовые меры применяют для передачи размера единицы длины от первичного эталона концевым мерам меньшей точности и для поверки и градуировки измерительных приборов длины. Образцовые КМД делят по разрядам: 1, 2, 3, 4.
Разряд концевых мер длины показывает, с какой погрешностью измерения производится аттестация действительного размера длины концевой меры. Разряды — это ряды значений погрешностей измерения, допускаемых при аттестации КМД.
Притираемость измерительных поверхностей концевой меры — это способность измерительных поверхностей КМД сцепляться друг с другом при смещении в плотно прижатом состоянии. Такое сцепление (притирание) КМД происходит благодаря высокой плоскостности и малой шероховатости их измерительных поверхностей и позволяет собирать из отдельных мер блоки КМД. Суммарный размер такого блока равен сумме размеров мер, вошедших в него. Блоки из КМД можно получить практически любого требуемого размера.
Инструментальные заводы выпускают КМД, скомплектованные в наборы и уложенные в отдельные футляры для того, чтобы из них можно было собирать блоки необходимых размеров. Особенность комплектовки всех наборов заключается в том, что в набор должны быть вложены меры одного класса точности. При поверке мер во время эксплуатации набору присваивается единый класс точности, равный низшему классу точности меры из числа вложенных в данный набор.
Примеры условного обозначения КМД:
- Набор № 2 концевых мер длины из стали, класса точности 1: Концевые меры 1 — Н2 ГОСТ 9038-90;
- Набор № 3 концевых мер из твердого сплава, класса точности 2: Концевые меры 2 — НЗ — Т ГОСТ 9038-90;
- Концевая мера длиной 1,49 мм из стали, класса точности 3: Концевая мера 3-1,49 ГОСТ 9038-90;
- Комплект образцовых концевых мер длины 1-го разряда: Концевые меры образцовые 1 — КО ГОСТ 9038-90;
- Набор № 3 образцовых концевых мер 2-го разряда: Концевые меры образцовые 2 — НОЗ ГОСТ 9038-90.
Штангенинструменты
Штангенинструментами называют средства измерений линейных размеров, основными частями которых являются штанга со шкалой и нониус — вспомогательная шкала для уточнения отсчета показаний.
Штангенциркули
Штангенциркули предназначены для измерения наружных и внутренних размеров изделий, некоторыми из них можно еще измерять глубину выемок и высоту уступов. Основные типы штангенциркулей предусмотрены ГОСТ 166-89 «Штангенциркули. Технические условия» и приведены в табл. 10.4. Конструкция основных типов штангенциркулей приведена на рис. 10.3.
Штангенциркули с отсчетом по нониусу 0,1 мм делятся на классы точности: 1 и 2.
Примеры условного обозначения штангенциркулей:
- 1) штангенциркуль ШЦ — II — 250 — 0,05 ГОСТ 166-89;
- 2) штангенциркуль ШЦ — II — 250 — 630 — 0,1 — 1 ГОСТ 166-89;
- Тип II с диапазоном измерения 250 — 630 мм, значением отсчета по нониусу 0,1 мм, класс точности 1;
- 3) штангенциркуль ШЦК — 1 — 150 — 0,02 ГОСТ 166-89;
- 4) штангенциркуль ШЦЦ -1 — 125 — 0,01 ГОСТ 166-89.
Штангенглубиномеры
Штангенглубиномеры (рис. 10.4) применяются для прямого измерения глубины выемок и высоты уступов. Штангенглубиномеры бывают нормальные (ШГ), с острием (2ШГ), с уступом (ЗШГ). Отсчет по нониусу для всех штангенглубиномеров составляет 0,05 мм.
Примеры условного обозначения штангенглубиномеров:
- 1) ШГ — 200 ГОСТ 162-90;
- 2) 2ШГ- 160 ГОСТ 162-90;
- 3) ЗШГ-160-400 ГОСТ 162-90.
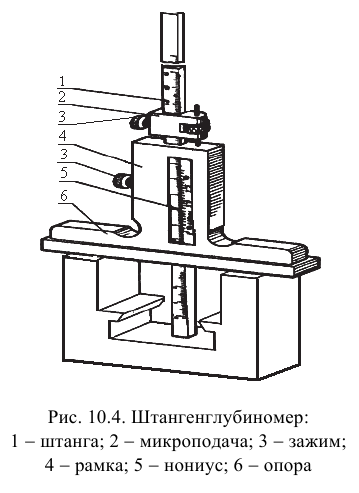
Штангенрейсмасы
Штангенрейсмасы (рис. 10.5) применяются для пространственной разметки и прямых измерений на точной плите расстояний от базовых поверхностей до выемок, выступов и осей отверстий. Типы штангенрейсмасов: ШР — с отсчетом по нониусу;
ШРК — с отсчетным устройством с круговой шкалой; ШРЦ — с электронным цифровым отсчетным устройством. Примеры условного обозначения штангенрейсмасов:
- 1) ШР-250-0,05 ГОСТ 164-90;
- 2) ШРК-250-0,02 ГОСТ 164-90;
- 3) ШРЦ-250-0,01 ГОСТ 164-90.
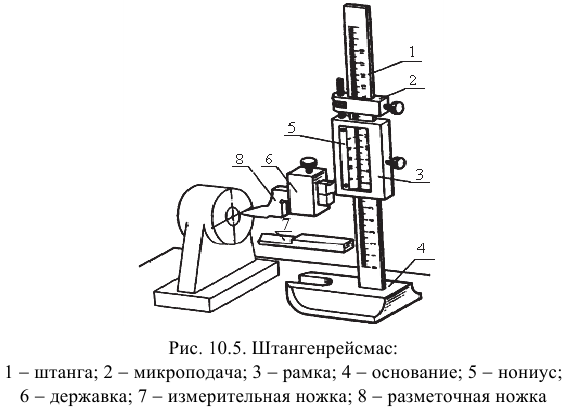
Микрометрические инструменты
Микрометрическими инструментами называют средства измерений линейных размеров, основанные на использовании винтовой пары, называемой микропарой.
Микрометры
Основные типы микрометров представлены в ГОСТ 6507-90 «Микрометры. Технические условия» и приведены в табл. 10.5. Конструкция микрометров приведена на рис. 10.6.
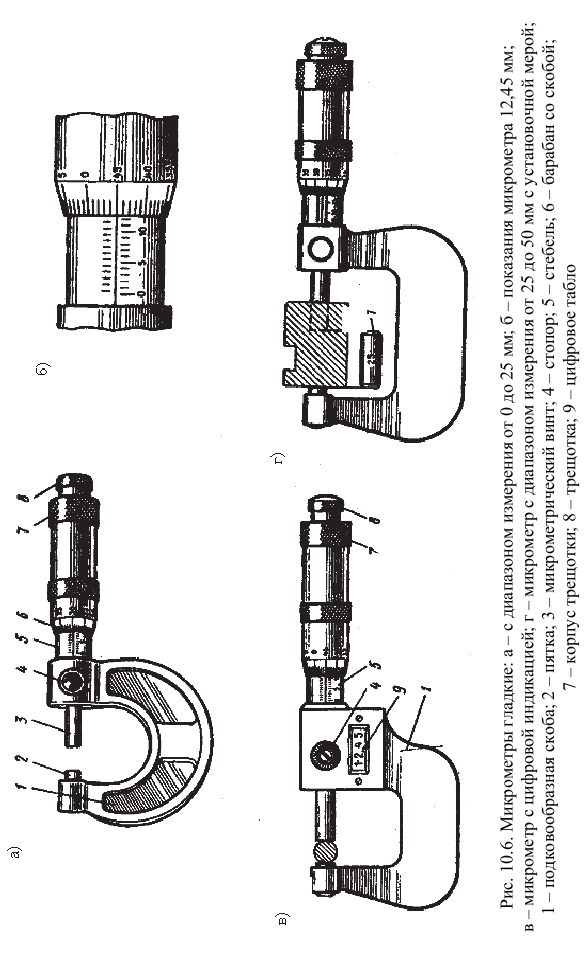
Для удобства и ускорения отсчета показаний промышленность выпускает гладкий микрометр с цифровой индикацией (рис. 10.6, в). Цена деления шкалы барабана — 0,01 мм. Микрометры выпускают классов точности 1 и 2.
Примеры условного обозначения микрометров:
- 1) МК 50 — 1 ГОСТ 6507-90. Микрометр гладкий с диапазоном измерений 25 — 50, 1 класса точности;
- 2) МК Ц 75 ГОСТ 6507-90. Микрометр гладкий с электронным цифровым отсчетным устройством, диапазон измерений 50 — 75 мм;
- 3) МЛ-10 ГОСТ 6507-90.
Микрометрические глубиномеры
Микрометрические глубиномеры (рис. 10.7) применяются для измерения глубины выемок и высоты уступов в деталях машин.
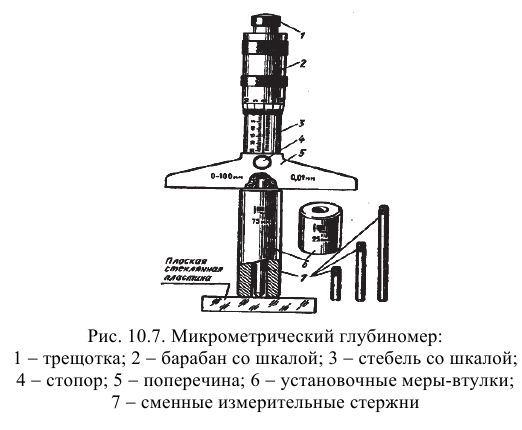
Пример условного обозначения микрометрического глубиномера:
ГМ — 100 ГОСТ 7470-92. Глубиномер микрометрический, диапазон измерений 0-100 мм.
Микрометрические нутромеры
Микрометрическими нутромерами (рис. 10.8) измеряют размеры отверстий, ширину пазов и другие внутренние линейные размеры и отклонения формы деталей машин. Максимальный размер, измеряемый микрометрической головкой с индикатором и удлинителем, — 10 000 мм.
Примеры условного обозначения микрометрических нутромеров:
- 1) НМ 75 ГОСТ 10-88;
- 2) ИМИ 2500-4000 ГОСТ 10-88.
Микрометры рычажные
Типы рычажных микрометров установлены ГОСТ 4381-87: MP и МРИ. Рычажный микрометр (рис. 10.9) в отличие от гладкого не имеет трещотки для ограничения усилия измерения. Измерительное усилие ограничивает пружина, которая прижимает подвижную пятку к поверхности детали, а деталь к торцу микровинта.

Условное обозначение рычажных микрометров:
MP 50 ГОСТ 4381-87;
МРИ 400-0,01 ГОСТ 4381-87.
Индикаторные инструменты
Индикаторные или рычажно-механические приборы предназначены для контроля линейных размеров и отклонений формы и расположения поверхностей. Используют эти приборы главным образом для относительных измерений.
Индикаторы часового типа
Из рычажно-механических приборов наиболее широко применяются индикаторы часового типа (ГОСТ 577-67) от 0 до 10 мм и малогабаритные от 0 до 2 мм.
Индикаторами часового типа (рис. 10.10) оснащают ряд измерительных приборов общего и специального назначения. Интервалы измерений: от 0 до 5 мм.

Скобы с отсчетным устройством Типы, основные параметры и технические требования к скобам установлены ГОСТ 11098-75: CP и СИ (скобы рычажные и скобы индикаторные). Рычажная скоба не имеет собственного размерного устройства, и измерение ею производится методом сравнения с мерой (рис. 10.11).

Индикаторные скобы (рис. 10.12) служат для измерения линейных размеров деталей цилиндрической формы в серийном производстве машин. Они удобны в применении, производительны, но обладают относительно невысокой точностью. Чаще всего ими измеряют гладкие валы после токарной обработки резцами или после круглой шлифовки, но при допусках на размер не менее 0,05 мм. Условное обозначение скоб: CP 50 ГОСТ 11098-75; СИ 50 ГОСТ 11098-75.

Нутромеры индикаторные
Технические условия на индикаторные нутромеры предусмотрены ГОСТ 868-82. Индикаторные нутромеры имеют цену деления 0,01 мм и делятся на два класса точности: 1 и 2.
Второй класс точности предусмотрен для диапазона измерения свыше 250 мм.
Условное обозначение индикаторного нутромера:
НИ 10 — 18 — 1 ГОСТ 868-82 (диапазон измерения 10-18 мм; 1 класс точности).
Глубиномеры индикаторные
Технические условия и условное обозначение глубиномеров индикаторных (рис. 10.13) предусмотрены ГОСТ 7661-67.
Пример условного обозначения глубиномера индикаторного:
ГИ- 100 ГОСТ 7661-67.

Индикаторы многооборотные
Технические условия на многооборотные индикаторные головки (МИГ) предусмотрены ГОСТ 9696-82. Стандартом предусмотрено два типа
головок: 1 и 2. Первый тип (рис. 10.14) имеет цену деления 0,001 мм, второй тип — 0,002 мм. МИГ делятся на классы точности: 0 и 1. Кроме того, предусмотрены индикаторы повышенной точности.
Примеры условного обозначения многооборотных индикаторных головок:
1 МИГ — 1 ГОСТ 9696-82 (тип 1, класс точности 1);
1 МИГ П ГОСТ 9696-82 (тип 1, повышенной точности).
Нутромеры с ценой деления 0,001 и 0,002 мм
Технические условия на нутромеры предусмотрены ГОСТ 9244-75. Цена деления шкалы 0,001 мм предусмотрена для нутромеров с диапазоном измерения от 2 до 10 мм, а цена деления 0,002 мм для нутромеров с диапазоном от 10 до 260 мм.
Примеры условного обозначения нутромеров:
Нутромер 6-10 ГОСТ 9244-75;
Нутромер 10-18 ГОСТ 9244-75.
Специальные измерительные средства (калибры гладкие)
Классификация калибров
Калибром по ГОСТ 27284-87 называется техническое средство контроля, воспроизводящее геометрические параметры элементов изделия, определяемые заданными предельными линейными или угловыми размерами, и контактирующее с элементом изделия по поверхностям, линиям или точкам.
Калибры бывают нормальные и предельные.
Нормальный калибр — это калибр, воспроизводящий заданный линейный или угловой размер и форму сопрягаемой с ним поверхности контролируемого элемента изделия. О годности деталей судят по равномерности зазора между проверяемым профилем и рабочим профилем нормального калибра.
Предельный калибр — это калибр, воспроизводящий проходной и (или) непроходной пределы геометрических параметров элементов изделия. Предельные калибры предназначены для контроля деталей с точностью от IT6 по ITM и позволяют установить, находится ли проверяемый размер в пределах допуска.
Предельные калибры для отверстий и валов подразделяют на проходной калибр (ПР), контролирующий предел максимума материала, и непроходной (НЕ), контролирующий предел минимума материала.
По назначению калибры подразделяются следующим образом:
- рабочие калибры (Р-ПР, Р-НЕ) пробки и скобы, применяемые для контроля деталей при их изготовлении;
- контрольные калибры (контркалибры), предназначенные для контроля размеров рабочих калибров-скоб проходных (К-ПР) и непроходных (К-НЕ) в процессе их изготовления, а также для контроля износа (К-И) проходных рабочих калибров-скоб при их эксплуатации (они являются непроходными).
Для контроля гладких цилиндрических отверстий предназначены ка-либры-пробки (рис. 10.15), для валов — калибры-скобы (рис. 10.16), состоящие из проходной (ПР) и непроходной (НЕ) сторон.
Деталь считают годной, если проходной калибр под действием собственной массы проходит, а непроходной калибр не проходит по контролируемой поверхности детали.
Для контроля отверстий номинальных размеров свыше 100 мм изготовляют неполные калибры-пробки (рис. 10.15, б). Чаще всего полные пробки делают двусторонними (рис. 10.15, а), а неполные — односторонними (см. рис. 10.15, б).
Если проходной калибр не проходит, брак детали является исправимым, если непроходной калибр проходит — брак неисправим.
Калибры-скобы бывают жесткие листовые и регулируемые. На инструментальных заводах чаще всего изготовляют регулируемые скобы с литым или штампованным корпусом, со вставками, переставляемыми на разные номинальные размеры по блокам КМД.
Допуски гладких предельных калибров
Номинальным размером проходной пробки является минимальный предельный размер контролируемого отверстия 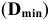
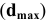
Номинальным размером непроходной пробки является максимальный размер контролируемого отверстия 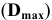
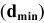
Предельные отклонения калибров отсчитываются от соответствующих номинальных размеров, т.е. от предельных размеров контролируемых деталей. Для проходных калибров, износ которых вызывает искажение характера посадки, устанавливается также граница допустимого износа.
При назначении предельных отклонений калибров для отверстий и валов с размерами свыше 180 мм учитывается компенсация погрешностей контроля, вызываемых упругими деформациями калибров и деталей.
На схемах полей допусков (рис. 10.17 и 10.18) и в формулах для определения размеров калибров приняты следующие обозначения:
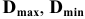
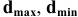
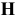

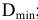
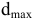
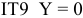
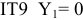
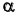
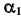
Формулы для расчета предельных размеров рабочих и контрольных калибров приведены ниже.
Рабочие калибры-пробки:
Рабочие калибры-скобы:
Контрольные калибры:
В приведённых формулах значения 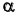
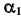
При размерах до 180 мм (см. рис. 10.17) для проходных калибров, контролирующих отверстия и валы 6, 7 и 8 квалитетов, допускается выход размера изношенного калибра за поле допуска изделия на величину соответственно 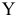
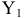
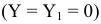
При размерах свыше 180 мм (см. рис. 10.18) поле допуска непроходного калибра и граница износа проходного калибра смещаются внутрь поля допуска изделия на величину, учитывающую погрешность контроля калибрами (
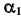
Маркировка калибров
При маркировке на калибр наносятся номинальный размер с буквенным обозначением поля допуска контролируемой детали, цифровые значения предельных отклонений детали в миллиметрах, тип калибра (например: ПР, НЕ, К И) и товарный знак завода изготовителя (рис. 10.19).
Размер калибра, проставленный на его чертеже, называется исполнительным. В качестве исполнительного размера калибра-пробки принимается её наибольший предельный размер с отрицательным нижним отклонением, равным допуску на изготовление, а скобы — её наименьший предельный размер с положительным верхним отклонением, равным допуску на изготовление.
Числовые значения допусков и отклонений калибров выбираются по табл. 10.6 в зависимости от квалитета и номинального размера контролируемого изделия.
Координатные измерительные машины
Координатными измерительными машинами (КИМ) называют автоматические средства для определения линейных и угловых размеров, а также отклонений формы и расположения поверхностей и осей сложных корпусных деталей.
КИМ позволяет осуществлять перечисленные виды измерений в двух, трех и четырех координатах: 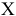
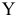
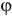
Работают машины в двух режимах: либо осуществляется перемещение измерительного наконечника до контакта с измеряемой поверхностью, и с помощью отсчетных устройств определяется ее положение в системе координат, либо измерительный наконечник по заданной программе перемещается в точки, соответствующие номинальным значениям определяемых размеров, а отсчетные устройства позволяют оценить отклонения положения действительных поверхностей от номинального значения. Чаще КИМ работают в первом режиме.
Основными узлами машин являются направляющие, по которым перемещается измерительная каретка с наконечником, отсчетные и счетно-решающие системы. Для уменьшения погрешности измерения КИМ снабжены либо направляющими качения, либо аэростатическими (на воздушной подушке) направляющими. Аэростатические направляющие высокоточных машин иногда изготовляют из твердых каменных пород, не подверженных (в отличие от металлических) температурным деформациям.
В качестве отсчетных устройств в КИМ используют специальные устройства — индуктосины. Они представляют собой электрическую машину со статором, развернутым в виде линейки, на поверхность которой печатным способом нанесены обмотки. Для этих же целей могут применяться и растровые фотоэлектрические преобразователи.
Современные КИМ оснащены ЭВМ, осуществляющими обработку результатов измерений, пересчет полученных значений размеров в зависимости от положения произвольно расположенной на столе машины контролируемой детали, печатание результатов измерений с указанием действительных значений измеренных параметров или их отклонений от заданных и их цифровую индикацию на специальных табло. Кроме того, ЭВМ руководит перемещениями каретки с измерительным наконечником, обеспечивая его последовательное автоматическое касание всех поверхностей, подлежащих контролю.
Раньше эта операция осуществлялась в соответствии с предварительно составленной программой (для каждого типоразмера деталей), введенной в ЭВМ. Существенным недостатком такого метода является необходимость затрачивать время на написание программы, ее запись на программоноситель и отладку, что требует привлечения к процессам измерения программистов.
Современные конструкции машин позволяют оператору без программы быстро «обучить» машину выполнять измерения интересующих параметров конкретной детали. Для этого надо вручную переместить каретку с измерительным наконечником, касаясь этим наконечником поверхностей, подлежащих контролю. Машина запоминает эти движения и сама записывает их в виде управляющей программы, которую потом использует для измерения аналогичных деталей. При необходимости эта программа заносится в память машины и может быть использована в любое время. КИМ находят также широкое применение при разметке корпусных деталей.
Координатная измерительная машина ВЕ-111 (рис. 10.20, в) позволяет проводить измерения и разметку по четырем координатам. Измеряемую деталь 4 устанавливают на самоустанавливающихся домкратах 5 стола 6, осуществляющего поворот детали вокруг вертикальной оси. Устройство 3 измерительным наконечником или разметочной головкой перемещается по осям 
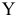
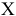
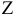
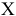
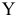
Результаты измерений по четырем координатам считывают с цифрового отсчетного устройства 9 ЭВМ или печатаются на бумажной ленте принтера 8. Данная машина обеспечивает возможность измерения и разметки деталей размером до 750 х 460 х 630 мм.
Существующие модели координатных измерительных машин позволяют измерять и размечать детали размерами от 400…500 мм до 10… 16 м. Наибольшее распространение получили машины для измерения деталей размером не более 500… 1000 мм.
Содержание страницы
- 1. Основные термины и определения
- 2. Основные отклонения
- 3. Классы допусков
- 3.1. Нанесение предельных отклонений размеров и обозначение классов допусков на чертежах
- 3.2. Выбор классов допусков
- 4. Посадки
- 4.1. Образование посадок
- 4.2. Посадки в системе отверстия и вала
- 4.3. Обозначения посадок
- 4.4. Применение внесистемных и системных посадок
- 4.5. Назначение посадок и квалитетов
- 4.6. Примеры использования посадок
- 4.7. Области ориентировочного применения квалитетов
- 5. Классы допусков и посадки соединений деталей из пластмасс
1. Основные термины и определения
Основные термины и определения, относящиеся к системе допусков на линейные размеры, установлены в стандарте ГОСТ 25346-2013 (ISO 286-1: 2010).
Размерный элемент – геометрическая форма, определяемая линейным или угловым размером. Размерными элементами могут быть цилиндр, сфера, две параллельные плоскости, конус, призма.
Номинальный размер (D, d) – это размер геометрического элемента идеальной формы, определенной чертежом. Номинальный размер используют для расчета предельных размеров.
Реальная поверхность детали – совокупность физически существующих геометрических элементов, которые отделяют всю деталь от окружающей среды.
Действительный размер – размер, установленный измерением с допустимой погрешностью.
Предельные размеры – два предельно допустимых размера, между которыми должен находиться или которым может быть равен действительный размер. Эти размеры имеют название – верхний предельный размер (Dmax, dmax) и нижний предельный размер (Dmin, dmin). Предельные размеры могут быть больше или меньше номинального размера, один из предельных размеров может быть равен номинальному.
Предельное отклонение – алгебраическая разность между одним из предельных размеров и номинальным.
Верхнее предельное отклонение:
для отверстия: ES = Dmax − D, (1)
для вала: es = dmax − d. (2)
Нижнее предельное отклонение:
для отверстия: EI = Dmin − D, (3)
для вала: ei = dmin − d. (4)
Допуск – это разность между верхним и нижним предельными размерами или между верхним и нижним предельными отклонениями:
допуск отверстия:
TD = Dmax– Dmin = ES − EI, (5)
допуск вала:
Td = dmax – dmin = es – ei. (6)
Интервал допуска – совокупность значений размера между пределами допуска, включая эти пределы. Он определяется значением допуска и его расположением относительно номинального размера. Пределы допуска могут располагаться по одну или по обе стороны относительно номинального размера. На графическом изображении интервалов допусков (рис. 1) номинальному размеру соответствует нулевая линия, которая обычно располагается горизонтально.
Рисунок 1 – Графическое изображение интервалов допусков
Основное отклонение – предельное отклонение, определяющее расположение интервала допуска относительно номинального размера. Основным является то из предельных отклонений, которое соответствует предельному размеру, ближайшему к номинальному (рис. 1).
2. Основные отклонения
Основные отклонения стандартизованы (ГОСТ 25346-2013). Предусмотрено по 27 вариантов основных отклонений для валов и отверстий. Каждому из основных отклонений соответствует определенный уровень относительно номинального размера (на схемах – относительно нулевой линии), от которого должен начинаться интервал допуска (рис. 2).
Значения основных отклонений, как правило, независимы от допусков. Каждое расположение основного отклонения обозначается латинской буквой – малой для валов и большой для отверстий. Для дополнительных отклонений, введенных в систему ISO, обозначение состоит из двух букв. Это либо отклонения, занимающие промежуточное положение между двумя соседними отклонениями (cd, ef, fg), либо отклонения, располагающиеся за отклонением z (za, zb, zc).
Ряды основных отклонений для отверстий и валов построены на основе правил – общего и специального. Согласно общему правилу, основные отклонения отверстий равны по значению и противоположны по знаку основным отклонениям валов. Например, основные отклонения EI для отверстий от A до H и основные отклонения es для валов от a до h равны по модулю. Для построения некоторых основных отклонений отверстий применяется специальное правило.
а)
б)
Рисунок 2 – Схемы расположения основных отклонений отверстий (а) и валов (б)
Буквой h обозначается верхнее отклонение вала, равное нулю; буквой H – нижнее отклонение отверстия, равное нулю. Буквами js, JS обозначаются симметричные расположения интервалов допусков вала и отверстия относительно нулевой линии.
3. Классы допусков
Квалитетом называют группу допусков на линейные размеры, характеризующуюся общим обозначением. Квалитеты являются критериями относительной точности. Установлено 20 квалитетов, которые обозначаются: IT01, IT0, IT1, …, IT18. Самые точные квалитеты IT01 и IT0 введены дополнительно к основным системным квалитетам IT1…IT18.
Классом допуска называют сочетание основного отклонения и квалитета.
Запись, включающая номинальный размер и класс допуска, содержит информацию о значении допуска и положении интервала допуска относительно номинального размера. Значение допуска зависит от номера квалитета и номинального размера.
Единица допуска – это мера точности, устанавливающая соотношение между величиной допуска и номинальным размером, а также учитывающая влияние технологических, метрологических, конструктивных параметров. Зависимость между единицей допуска и линейным размером установлена экспериментально и для размеров до 500 мм имеет вид:
(7)
где D – среднее геометрическое из крайних значений интервалов номинальных размеров, мм.
Величина допуска вычисляется по формуле:
T = a ∙ i, (8)
где a – количество единиц допуска, строго постоянное для каждого квалитета (табл. 1).
Для квалитетов IT6 и грубее количество единиц допуска возрастает в геометрической последовательности со знаменателем 1,6. Через каждые 5 квалитетов количество единиц допуска увеличивается в 10 раз.
Таблица 1 – Соответствия между квалитетами и количеством единиц допуска
| IT | 01 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| a | 1 | 1,4 | 2 | 2,7 | 3,7 | 5,1 | 7 | 10 | 16 | 25 |
| IT | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| a | 40 | 64 | 100 | 160 | 250 | 400 | 640 | 1000 | 1600 | 2500 |
При известных численных значениях номинального диаметра, основного отклонения и допуска можно определить второе отклонение, ограничивающее интервал допуска (рис. 3)
а) б)
Рисунок 3 – Схемы образования интервалов допусков для отверстия (а) и вала (б)
Для тех классов допусков, у которых основным является нижнее отклонение, верхнее отклонение вычисляется по формулам:
для отверстия ES = EI + TD, (9)
для вала es = ei + Td. (10)
Если основное отклонение верхнее, то нижнее отклонение:
для отверстия EI = ES − TD, (11)
для вала ei = es − Td.(12)
На базе одного номинального размера и основного отклонения возможно рассчитать по 20 классов допусков для отверстия и вала (по количеству квалитетов).
3.1. Нанесение предельных отклонений размеров и обозначение классов допусков на чертежах
При нанесении предельных отклонений размеров на чертежах необходимо руководствоваться следующими указаниями.
Для всех размеров, нанесенных на чертежах, должны быть указаны предельные отклонения. Линейные размеры и предельные отклонения на чертежах указывают в миллиметрах без обозначения единиц измерения. Предельные отклонения размеров указывают непосредственно после номинальных размеров. Предельные отклонения размеров относительно низкой точности допускается не указывать непосредственно после номинальных размеров, а указывать в виде общей записи в технических требованиях чертежа.
Предельные отклонения указывают шрифтом с уменьшенной высотой цифр, верхнее отклонение указывают над нижним (рис. 4 а).
Отклонение, равное нулю, не указывают (рис. 4 б).
Для симметричных интервалов допусков отклонение указывают один раз (рис. 4, в), при этом высота цифр, определяющих отклонения, должна быть равна высоте шрифта номинального размера.
Такой способ указания отклонений рекомендуется для размеров, проверка которых может быть осуществлена показывающими приборами.
Класс допуска обозначают сочетанием буквы (букв) основного отклонения и порядкового номера квалитета, при этом указывают значение номинального размера элемента, например: ∅40g6, ∅40Н7.
Такой способ обозначения рекомендуется для размеров, контроль которых может быть осуществлен предельными калибрами.
Смешанный способ обозначения классов допусков предполагает указание условными обозначениями и числовыми значениями предельных отклонений (рис. 5).
Применение смешанного способа рекомендуется тогда, когда неизвестно, какими средствами будет контролироваться размер – предельными калибрами или приборами.
Рисунок 4 – Указание предельных отклонений размеров: а – верхнего и нижнего; б – нулевого; в – симметричных
Рисунок 5 – Обозначения классов допусков смешанным способом
Общие допуски на размеры элементов, которые не указаны непосредственно у размера, нормируются в соответствии с ГОСТ 30893.1- 2002.
Общие допуски установлены по четырем классам точности:
- точный f,
- средний m,
- грубый c,
- очень грубый v.
Между классами точности общих допусков и квалитетами существуют примерные соотношения:
- точный f соответствует IT12,
- средний m – IT14,
- грубый c – IT15…IT16,
- очень грубый v – IT17.
Указание общих допусков должно содержать номер стандарта и буквенное обозначение класса точности. Например, для класса точности средний: «Общие допуски по ГОСТ 30893.1 – m» или «ГОСТ 30893.1 – m».
Обозначение указывают на чертеже в составе технических требований в правом нижнем углу листа, над основной надписью.
3.2. Выбор классов допусков
В стандарте ГОСТ 25347-2013 приведены перечни сформированных в соответствии с рассмотренной системой классов допусков. Для номинальных размеров из диапазона до 500 мм эти перечни содержат 203 класса допусков для отверстий и 204 класса допусков для валов. Для этих классов допусков приведены таблицы с указанными в них стандартными значениями предельных отклонений. Данные классы допусков называют специальными или классами допусков широкого выбора.
В стандарте ГОСТ 25346-2013 из перечней специальных классов допусков отобраны классы допусков общего применения. Выделено 45 классов допусков общего применения для отверстий и 50 классов допусков общего применения для валов (рис. 6).
Рисунок 6 – Классы допусков общего применения и предпочтительные классы допусков: а – отверстий, б – валов
В свою очередь, из классов допусков общего применения отобраны предпочтительные классы допусков, которые необходимо применять в первую очередь. Отобрано по 17 предпочтительных классов допусков для отверстий и валов. На рис. 6 предпочтительные классы допусков обведены в рамку.
Практика показывает, что на основе предпочтительных классов допусков можно до 90-95% обеспечить потребность в посадках, максимально унифицировать изделия и сократить номенклатуру размерных инструментов и калибров.
4. Посадки
4.1. Образование посадок
Посадка – характер соединения двух деталей, определяемый разностью их размеров до сборки.
Номинальный размер посадки – размер, общий для отверстия и вала, составляющих соединение.
Зазор (S) – разность между размерами отверстия и вала до сборки, когда размер отверстия больше размера вала.
Натяг (N) – разность между размерами вала и отверстия до сборки, когда размер вала больше размера отверстия.
Посадка с зазором – посадка, при которой в соединении всегда образуется зазор, т.е. нижний предельный размер отверстия Dmin больше верхнего предельного размера вала dmax. При графическом изображении (рис. 7 а) интервал допуска отверстия расположен над интервалом допуска вала.
Наибольший Smax (наименьший Smin) зазор равен разности предельных размеров отверстия и вала:
Smax = Dmax − dmin = ES − ei, (13)
Smin = Dmin − dmax = EI − es. (14)
Посадка с натягом – посадка, при которой в соединении всегда образуется натяг, т.е. нижний предельный размер вала dmin больше верхнего предельного размера отверстия Dmax. При графическом изображении интервал допуска вала располагается над интервалом допуска отверстия (рис. 7 б).
Наибольший Nmax (наименьший Nmin) натяг равен разности предельных размеров вала и отверстия:
Nmax = dmax − Dmin = es − EI, (15)
Nmin = dmin − Dmax = ei − ES. (16)
Переходная посадка – посадка, при которой в соединении возможно образование зазора или натяга в зависимости от действительных размеров сопрягаемых деталей. При графическом изображении интервалы допусков могут перекрываться полностью (рис. 7 в) или частично (рис. 7 г, д). При частичном перекрытии интервалов допусков в сопряжении могут преобладать посадки с зазором (рис. 7, г) или с натягом (рис. 7, д).
а) б)
в)
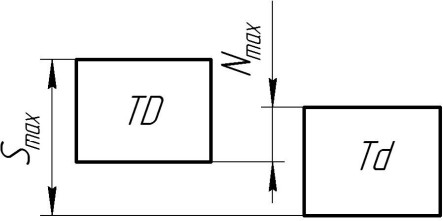
г) д)
Рисунок 7 – Схемы образования внесистемных посадок: а – с зазором; б – с натягом; в, г, д – переходных
Диапазон посадки – это арифметическая сумма допусков отверстия и вала, образующих соединение. Диапазон посадки характеризует ее точность.
Для посадки c зазором и посадки с натягом диапазон равен разности предельных значений зазора или натяга:
TS = Smax − Smin = TD + Td, (17)
TN = Nmax − Nmin = TD + Td.(18)
Диапазон переходной посадки равен сумме наибольшего предельного натяга и наибольшего предельного зазора:
TS(N) = Nmax + Smax = TD + Td. (19)
4.2. Посадки в системе отверстия и вала
Для унификации деталей и инструментов наиболее рациональным является такой способ образования посадок, когда одна деталь (отверстие или вал) в различных посадках имеет постоянное расположение интервала допуска, а требуемый характер посадки обеспечивается подбором расположения интервала допуска другой сопрягаемой детали.
Деталь, имеющая постоянное расположение интервала допуска, является базовой в системе образования посадок. В качестве базовых элементов принимают основные отверстия и основные валы, у которых основные отклонения равны нулю, т.е. нижний предельный размер отверстия и верхний предельный размер вала равны номинальному.
Посадки в системе отверстия – посадки, у которых требуемый зазор или натяг получают сочетанием различных классов допусков валов с классом допуска основного отверстия (рис. 8 а).
Интервалы допусков валов, образованные на базе основных отклонений от a до h (a, b, c, cd, d, e, ef, f, fg, g, h), будут расположены ниже интервала допуска основного отверстия, т.е. размеры валов меньше минимального размера отверстия, а значит, в сопряжении будет только зазор.
Интервалы допусков валов, образованные на базе основных отклонений от js до n (js, k, m, n), будут частично перекрываться с интервалом допуска отверстия, а значит, в сопряжении возможен и зазор, и натяг в зависимости от действительных размеров сопрягаемых деталей.
Интервалы допусков валов, образованные на базе основных отклонений от p до zc (p, r, s, t, u, v, x, y, z, za, zb, zc), будут расположены выше интервала допуска основного отверстия, т.е. размеры валов будут превышать размеры верхнего предельного размера основного отверстия, а значит, в сопряжении будет только натяг.
Посадки в системе вала – посадки, у которых требуемый зазор или натяг получают сочетанием различных классов допусков отверстий с классом допуска основного вала (рис. 8 б).
а)
б)
Рисунок 8 – Схемы образования посадок: а – в системе отверстия, б – в системе вала
Характер относительного положения интервалов допусков в системах отверстия и вала одинаков, значит, наличие зазора или натяга в сопряжении определяется только основными отклонениями и не зависят от системы. При этом, одноименные основные отклонения вала и отверстия образуют в обеих системах одинаковые посадки, т.е. отклонения A– H (a– h) образуют посадки с зазором, JS– N (js– n) – переходные и – ZC (p– zc) – посадки с натягом.
4.3. Обозначения посадок
Обозначение посадки на сборочном чертеже оформляется в виде дроби. Перед дробью указывают номинальный размер сопряжения. В числителе дроби указывают класс допуска отверстия, в знаменателе – класс допуска вала, например:
В текстовой части удобно обозначения посадок указывать в следующем виде: Ø80 K7/k6, Ø80 H7/f6, Ø80 7/h6.
Классы допусков отверстия и вала в посадке могут быть выполнены с одинаковой точностью (H8/e8, 9/h9) или с различной точностью. Как правило, более точно выполняется класс допуска вала. Посадки при точности размеров вала и отверстия с 4-го по 7-й квалитет рекомендуется образовывать путем сопряжения отверстия на квалитет грубее, чем вал (H7/g6, H7/js6, N7/h6).
4.4. Применение внесистемных и системных посадок
Внесистемные посадки, у которых ни одна из деталей не является основной, применяются крайне редко. Например, внесистемные посадки
8/js7, D9/f7, 10/js7, 10/d9, D9/f8, D9/e8, 10/f8
применяются в шлицевых прямобочных соединениях.
Системные посадки – в системе вала и в системе отверстия – находят применение, но в разной степени. Наиболее широко применяется система отверстия, поскольку вал является более технологичным элементом по сравнению с отверстием. Требуемый зазор или натяг проще обеспечить в соединении путем обработки наружных поверхностей валов, чем внутренних поверхностей отверстия.
Система вала применяется в конструкции машин и механизмов, когда деталь может быть изготовлена из прутковых калиброванных заготовок, без обработки сопрягаемых поверхностей. Например, в системе вала образованы посадки по ширине призматических шпонок в пазы на валах и во втулках.
На участках валов одного номинального размера, но сопрягаемых по разным посадкам (рис. 9 а), сопряжение поршня двигателя с поршневым пальцем требует весьма высокой точности, отличается резко переменными нагрузками, разборке подвергается крайне редко. Для таких условий назначается посадка N6/h5 в системе вала. Сопряжение поршневого пальца с втулкой шатуна требует подвижного соединения высокой точности. Это условие соблюдается при назначении посадки H6/h5, в которой минимальный зазор равен нулю.
В этом случае применение системы вала оправдано конструктивными соображениями. Одна и та же деталь — поршневой палец, сопрягается по двум посадкам. При образовании посадок в системе вала поршневой палец представляет гладкий цилиндр (рис. 9 б). При назначении посадок в системе отверстия поршневой палец представлял бы собой ступенчатый стержень (рис. 9 в).
Система вала также применяется в случае использования стандартных деталей, например, в соединениях подшипников качения по наружному кольцу с отверстием в корпусе.
Рисунок 9 – Конструктивная схема применения системы вала: а – эскиз сборочной единицы; б – поршневой палец в системе вала; в – вид поршневого пальца при назначении посадок в системе отверстия; 1 – поршневой палец; 2 – поршень; 3 – втулка; 4 – шатун
4.5. Назначение посадок и квалитетов
Существует три способа назначения посадок и квалитетов: способ аналогов, способ подобия и расчётный.
Способ аналогов – заключается в том, что конструктор отыскивает в однотипных машинах, находящихся в эксплуатации, узел аналогичный проектируемому и назначает посадку. Сложность способа заключается в оценке и сопоставлении условий работы проектируемого узла и аналога.
Способ подобия – основан на классификации деталей и узлов машин по конструктивному и эксплуатационному признакам. Посадки назначаются на основании рекомендаций отраслевых технических документов и литературных источников. Недостатком способа является отсутствие точных количественных оценок условий работы сопряжений.
Расчётный способ выполняется для посадок с зазором наиболее ответственных деталей вращения: подшипников скольжения двигателей, станков, турбин, компрессоров, а также для возвратно-поступательного движения поршней, пружинных пар и т.д. Расчеты основаны на использовании теории гидродинамической смазки и сводятся к расчёту минимального и максимального зазора.
При расчёте посадок с натягом определяют минимально необходимый натяг, обеспечивающий прочность соединения в условиях максимально возможного нагружения и максимально возможный натяг, определяемый прочностью деталей.
Расчёт переходных посадок сводится к определению средневероятного значения натяга или зазора и ожидаемого процента получения соединений с натягом или зазором при заданных условиях производства.
Для предпочтительного применения в ГОСТ 25346-2013 выделено небольшое количество посадок (табл. 2, 3). По экономическим соображениям, в первую очередь следует выбирать те из посадок, которые заключены в рамки.
Таблица 2 – Предпочтительные посадки в системе отверстия
Таблица 3 – Предпочтительные посадки в системе вала
4.6. Примеры использования посадок
Посадки с зазором
Посадки H7/g6, H7/g5 имеют малый гарантированный зазор, что обеспечивает хорошее центрирование деталей и отсутствие ударов при перемене нагрузки. При хорошей смазке посадки применяют для сопряжения шейки коленчатого вала с шатуном в поршневом двигателе, вала ротора турбины и шпинделей станков, клапанов.
Посадки H7/f7, H7/f6 применяют для соединения деталей, которые работают в основном при умеренных и постоянных скоростях и при безударной нагрузке (например, вращающиеся в подшипниках валы и шпиндели).
Посадки H8/e8, H8/e7, H7/e8 имеют относительно большие зазоры и применяются для подвижных соединений при большой длине втулки и частоте вращения 1000 мин-1 (например, цапф валов с втулками, подшипников в центробежных насосах, в приводах шлифовальных станков и турбогенераторах, валов холостых шкивов и свободно вращающихся колес).
Посадки H8/d9, H9/d9 характеризуются относительно большими зазорами и применяются для соединения деталей, работающих с большими скоростями, когда по условиям работы деталей допускается неточное центрирование (например, в сельскохозяйственных, дорожных и других машинах).
Посадка H7/c8 применяется для деталей, работающих при высокой температуре (например, в тепловых двигателях).
Переходные посадки
Посадки H/js, JS/h образуют преимущественно зазор. Вероятность получения натяга 0,5… 5%.
Посадки H/k, K/h характеризуются увеличением количества сопряжений с натягом. Вероятность получения натяга составляет 24…68%. Посадки обеспечивают хорошее центрирование. Сборка и разборка проводится при незначительных усилиях, например, при помощи молотков. Посадки H/n, N/h обеспечивают преимущественно в сопряжении натяг, вероятность которого составляет 88…100%. Сборка и разборка осуществляется при значительных усилиях с применением прессов.
Посадки с натягом
Посадки H7/p6, 7/h6 характеризуются минимальным гарантированным натягом. Применяются в тех случаях, когда крутящие моменты или осевые силы малы; для соединения тонкостенных деталей.
Посадки H7/r6, H7/s6 характеризуются умеренными гарантированными натягами, обеспечивающими передачу нагрузок средней величины. Сборка соединений возможна под прессом в холодном состоянии, а также способом термических деформаций.
4.7. Области ориентировочного применения квалитетов
Квалитеты 4-й и 5-й применяются сравнительно редко. В особо точных соединениях, требующих высокой однородности зазора или натяга (приборные подшипники в корпусах и на валах, высокоточные зубчатые колеса на валах и оправках в измерительных приборах).
Квалитеты 6-й и 7-й применяются для ответственных соединений в механизмах, где к посадкам предъявляются высокие требования в отношении определенности зазоров и натягов для обеспечения точности перемещений, плавности хода, герметичности соединения, механической прочности сопрягаемых деталей, а также для обеспечения точной сборки деталей (подшипники качения нормальной точности в корпусах и на валах, зубчатые колеса высокой и средней точности на валах, подшипники скольжения и т.п.).
Квалитеты 8-й и 9-й применяются для посадок при относительно меньших требованиях к однородности зазоров или натягов и для посадок, обеспечивающих среднюю точность сборки посадки с зазором, для компенсации погрешностей формы и расположения сопрягаемых деталей, опоры скольжения средней точности, посадки с большими натягами).
Квалитет 10-й применяют в посадках с зазором и в тех случаях, что и 9-й, если условия эксплуатации допускают некоторое увеличение колебаний зазоров в соединениях.
Квалитеты 11-й и 12-й применяются в соединениях, где необходимы большие зазоры и допустимы их значительные колебания (грубая сборка). Эти квалитеты распространены в неответственных соединениях машин (крышки, фланцы, дистанционные кольца и т.п.).
5. Классы допусков и посадки соединений деталей из пластмасс
Пластмассы используются для получения изделий исключительно широкого диапазона от чрезвычайно малых по массе до крупногабаритных конструкций: емкости, корпуса, водопроводные колодцы и т.д.
В машиностроении и приборостроении осваивается изготовление деталей точностью до IT3 без последующей механической обработки. В мировой практике освоено производство высокоточных деталей для часовых механизмов, дисков памяти, линз, оптических волокон, миниатюрных шариков, роликовых подшипников.
Наиболее распространены детали с размерами до 500 мм; расширяется применение деталей свыше 500 мм.
Допуски и посадки деталей из пластмасс регламентируются стандартом ГОСТ 25349-88 «Основные нормы взаимозаменяемости. Единая система допусков и посадок. Поля допусков деталей из пластмасс».
Допуски и предельные отклонения относятся к размерам деталей при температуре 20°С и относительной влажности окружающего воздуха 50%.
Основные отклонения, классы допусков деталей из пластмасс приведены в табл. 4 и 5.
Таблица 4 – Классы допусков валов для номинальных размеров до 500 мм
Таблица 5 – Классы допусков отверстий для номинальных размеров до 500 мм
Посадки в соединениях пластмассовых деталей с пластмассовыми или металлическими рекомендуется назначать в соответствии с табл. 6 (в системе отверстия) и табл. 7 (в системе вала).
Таблица 6 – Рекомендуемые посадки в системе отверстия для номинальных размеров до 500 мм
Для металлических деталей в соединении с деталями из пластмасс рекомендуется назначать следующие классы допусков:
- классы допусков валов: h7, h8, h9, h10, h11, h12;
- классы допусков отверстий: H7, H8, H9, H10, H11, H12.
Контроль деталей из пластмасс должен производиться после выдержки, необходимой для релаксации внутренних напряжений материала и стабилизации размеров. Время выдержки деталей после изготовления до контроля, если оно не оговорено особо, должно быть не менее 16 ч.
Таблица 7 – Рекомендуемые посадки в системе вала для номинальных размеров до 500 мм
ООО «КВАДРО» вот уже почти четверть века является, кроме всего прочего, производителем втулок, шкивов, валов и другой продукции, получаемой токарной обработкой. Кроме изготовления втулок мы производим весьма широкий спектр работ по металлообработке, изготавливая детали на заказ по чертежам Заказчика, эскизам и образцам.
Просто поднимите трубку и позвоните нам! Или пришлите чертеж на электронную почту либо заполнив форму обратной связи в разделе Контакты.
Рассмотрим, что такое допуски на примере производства втулок (их внутренних отверстий) или валов.
Производитель втулок не идеален
Очевидно, что производитель втулок не может абсолютно точно выполнить, указанный на чертеже размер. Поэтому конструктор, исходя из требований к работе механизма, устанавливает границы, в которых должны быть выполнены размеры. На чертеже для производителя втулок конструктор указывает номинальный размер и 2 предельных отклонения: верхнее и нижнее.
Размер тогда имеет вид, например:

Выбор точности изготовления детали во многом предопределяет устанавливаемые требования к шероховатости поверхностей детали. Так же стоит упомянуть, что кроме допуска на размер существуют допуски на форму и расположение.
Изготовление втулок на различном оборудовании
Величина (для первого примера) 0,370-0,160=0,210 называется допуском. Графически допуск изображают в виде прямоугольной заштрихованной области, расположенной нужным образом относительно линии номинального размера, и называют полем допуска.
Очевидно, что при изготовлении втулки добиться того же размера допуска (например, 0,210мм) при номинальном размере, например, в 100 раз больше (2500мм) намного сложнее. Поэтому вводится понятие квалитета (степени точности): совокупности допусков, рассматриваемых как соответствующие одному уровню точности для различных номинальных размеров.
Все относительно просто: к одному квалитету относят размеры достижимые на одном и том же оборудовании, при одних и тех же условиях (например, режимах резания). К примеру, при изготовлении на токарном станке, обычно, добиваются 7-8-го квалитета точности, а на шлифовальном – 5-6-го.
Существуют формулы расчета допусков при различных квалитетах, однако на практике конструкторы и технологи при проектировании и изготовлении втулок, валов и прочих деталей пользуются таблицами.
Всего установлено 20 квалитетов. Самые точные (с очень узкими полями допусков) 01, 0, 1, 2, 3, 4, обычно, назначают при изготовлении средств измерения, квалитеты 5-11 – для сопрягаемых размеров (по которым детали собираются друг с другом), квалитеты 12-18 (с самыми широкими полями допусков) – для несопрягаемых размеров.
Отклонения от номинального размера при производстве втулок и валов
Квалитет при данном номинальном размере однозначно определяет ширину поля допуска. А вот положение этого поля допуска (его отклонение) относительно номинального размера при изготовлении втулки (ее отверстия) или вала определяется одним из 27 стандартизированных отклонений, обозначаемых буквами латинского алфавита.
Отклонения отверстий обозначаются заглавными буквами. При отклонениях размеров отверстий от A до H поля допусков находятся выше линии номинального размера (втулка будет болтаться на валу, точно соответствующем номинальному диаметру), от K до ZC – ниже линии, Js – симметрично этой линии.
Отклонения же валов обозначаются строчными буквами. При отклонениях размеров отверстий от a до h поля допусков находятся ниже линии номинального размера (вал будет болтаться во втулке, изготовленной с отверстием, точно соответствующим номинальному диаметру), от k до zc – выше линии номинального диаметра, js – симметрично этой линии.
Выбор отклонений при изготовлении втулок и валов обуславливается достижением необходимой посадки в паре вал-отверстие.
Необходимо отметить, что в системе допусков и посадок термин вал условно применяют для обозначений любых наружных (охватываемых) элементов деталей, которые могут быть и нецилиндрическими (например, длина детали). Отверстием же называют внутренние, охватывающие элементы деталей, в т.ч. нецилиндрические (например, ширина паза).
Как расшифровать размер изготавливаемой втулки?
Что мы можем сказать о размере, видя на чертеже «25H7»? Эту запись можно расшифровать следующим образом: этот размер охватывающий («отверстие») поскольку буква заглавная, номинальный размер – 25, квалитет – 7, отклонение поля допуска относительно номинального размера – H. Заглянув в таблицу, мы найдем область разрешенных размеров для этого элемента на пересечении строки «Св.24 до 30» и столбца «H7»: 25,000-25,021.
А размер 49s7 можно расшифровать так: этот размер охватываемый («вал»), номинальный размер – 49, квалитет – 7, отклонение поля допуска относительно номинального размера – s. По таблице находим, на пересечении строки «Св.40 до 50» и столбца «s7», область разрешенных размеров для этого элемента: 49,043-49,068.
Производство втулок у нас
Наше предприятие осуществляет не только изготовление втулок, валов, осей, производя токарные работы на заказ, но и производит широкий спектр иных работ по металлообработке, с которым вы можете познакомиться здесь. Просто, пришлите свои чертежи на электронную почту для изготовления деталей по чертежу!
- посадки;
- допуски на форму и расположение;
- шероховатость.
Примеры определения предельных размеров, допусков, зазоров и натягов в соединениях при различных видах посадок
Страницы работы
Содержание работы
ПРИМЕРЫОПРЕДЕЛЕНИЯПРЕДЕЛЬНЫХРАЗМЕРОВ,
ДОПУСКОВ,
ЗАЗОРОВИНАТЯГОВ
ВСОЕДИНЕНИЯХПРИРАЗЛИЧНЫХВИДАХПОСАДОК
Посадка
с зазором
Пример.
Номинальный размер вала 100 мм, нижнее отклонение вала ei =106 мкм (-0,106 мм),
верхнее
отклонение вала es =
—60 мкм (—0,06 мм).
Номинальный
размер отверстия 100 мм,
нижнее отклонение
отверстия EI = +72
мкм (+0,072 мм),
верхнее
отклонение отверстия ES = +159 мкм (+0,159 мм).
Решение.
- Наибольший предельный размер вала dmax
dmax = d + es =
100 + (-0,060) = 99,940 мм.
- Наименьший предельный размер вала dmin
dmin = d+ ei= 100 + (-0,106) = 99,894 мм.
- Поле допуска вала
ITd = dmax– dmin =
99,940 – 99,894 = 0,046 мм или ITd = es – ei =
-0,060 – (-0,106) = 0,046 мм.
- Наибольший предельный размер отверстия
Dmax= D + ES = 100 + 0,159 = 100,159 мм.
- Наименьший предельный размер
отверстия
Dmin = D + Е1 = 100
+ 0,072 = 100,072 мм.
- Поле допуска отверстия
ITD = Dmax – Dmin =
100,059 – 100,072 = 0,087 мм или ITD = ES – Е1 = 0,159 – 0,072 = 0,087 мм.
- Максимальный зазор в соединении
Smax = Dmax– dmia =
100,059 – 99,894 = 0,265 мм или Smax = ES– ei = 0,159 – (-0,106) = 0,265 мм.
- Минимальный зазор в соединении
Smia = Dmia – dmax = 100,072 – 99,940 = 0,132 мм или Smin = EI–es = 0,072 – (-0,060) = 0,132 мм.
- Допуск
посадки (зазора)
ITS = Smax – Smin =
0,265 – 0,132 = 0,133 мм или ITS = ITd
+ ITD = 0,046 + 0,087 = 0,133 мм.
пример расположения полей допуска
вала и отверстия в посадке с зазором
Посадка с натягом
Пример.
Номинальный размер вала 100 мм,
нижнее
отклонение вала ei = 72
мкм (0,072 мм),
верхнее отклонение вала es = 159 мкм (0,159 мм).
Номинальный размер
отверстия 100 мм,
нижнее отклонение
отверстия Е1~ —106 мкм (—0,106 мм),
верхнее отклонение отверстия ES = —60 мкм (—0,060 мм).
Решение.
- Наибольший предельный размер вала dmax
dmax =
d + es = 100 + (0,159) = 100,159 мм.
- Наименьший предельный размер вала dmin
dmin = d + ei= 100 + (0,072) = 100,072 мм.
- Поле допуска вала
ITD = dmax – dmin = 100,159 – 100,072 = 0,087 мм или ITd =es– ei = 0,159 –
0,072 = 0,087 мм.
- Наибольший предельный размер
отверстия
Dmax = D + ES = 100 + (-0,060) = 99,940 мм.
- Наименьший предельный размер
отверстия
Dmln= D+
EI =100 + (-0,106)
= 99,894 мм.
- Определим
поле допуска отверстия
ITD = Dmax –
Dmin = 99,940 –
99,894 = 0,046 мм или ITD = ES– Е1= -0,060 – (-0,106) = 0,046 мм.
- Максимальный натяг в соединении
Nmax= dmax– Dmin = 100,59 – 99,894 = 0,265 мм или Nmax = es– EI =0,159 – (-0,106) = 0,265 мм.
- Минимальный натяг в соединении
Nmin = dmin – Dmax = 100,072 – 99,940 = 0,132 мм или Nmin= ei – ES= 0,072 –
(-0,060) = 0,132 мм.
- Допуск посадки (натяга)
ITN = Nmax– Nmin= 0,265 – 0,132 =0,133 мм или ITN = ITd +
ITD =
0,087 + 0,046 = 0,133 мм.
пример расположения полей допуска вала и отверстия в
посадке с натягом
Переходная
посадка
Пример.
Номинальный размер вала 100 мм,
нижнее отклонение вала ei — +71 мкм (+0,071 мм),
верхнее
отклонение вала es =
+93 мкм (+0,093 мм).
Номинальный
размер отверстия 100 мм,
нижнее
отклонение отверстия ЕI= +72 мкм (+0,072 мм),
верхнее отклонение отверстия ES= +159 мкм (+0,159 мм).
Решение.
- Наибольший предельный размер вала dmax
dmax = d +
es =
100 + 0,093 = 100,093 мм.
- Наименьший предельный размер вала dmjn
dmln = d+ei= 100 + 0,071 = 100,071 мм.
- Поле допуска вала
ITd = dmax – dmin= 100,093 – 100,071 = 0,022 мм или ITd =es– ei = 0,093 –
0,071 = 0,022 мм.
- Наибольший предельный размер
отверстия
Dmax=D + ES= 100 + 0,159 = 100,159 мм.
- Наименьший
предельный размер отверстия
Dmin= D + Е1= 100 + 0,072 = 100,072 мм.
- Поле допуска
отверстия
ITD= .Dmax– Dmin
= 100,159 – 100,072 = 0,087 мм или ITD = ES– EI= 0,159 –
0,072 = 0,087 мм.
- Максимальный зазор в соединении
Smax=
Dmax– – dmin = 0,088 мм или Smax = ES– ei = 0,159 –
0,071 = 0,088 мм.
- Максимальный натяг в соединении
Nmax= dmax– Dmin= Ю0,093 – 100,072 = 0,021 мм или Nmax= es– EI= 0,093 – 0,072 = 0,021 мм.
- Допуск посадки (зазора-натяга)
ITNS = Smax + Nmax = 0,088 + 0,021 = 0,109 мм или ITN = ITd + ITD =
0,022 + 0,087 = 0,109 мм.
пример расположения полей допусков вала
и отверстия в переходной поосадке
Похожие материалы
- Способы определения коэффициентов трения и сопоставление расчетных коэффициентов с экспериментальными данными, определенными на действующей установке
- Характеристика систем передачи К-60П, К-120, К-300
- Характеристика дистанции сигнализации и связи станции Иркутск-Сортировочный (Раздел дипломной работы)
Информация о работе
Тип:
Дополнительные материалы




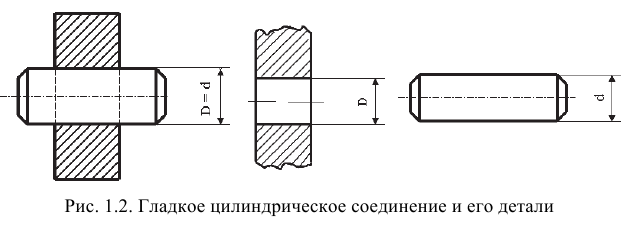
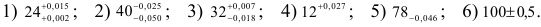
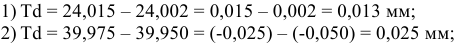

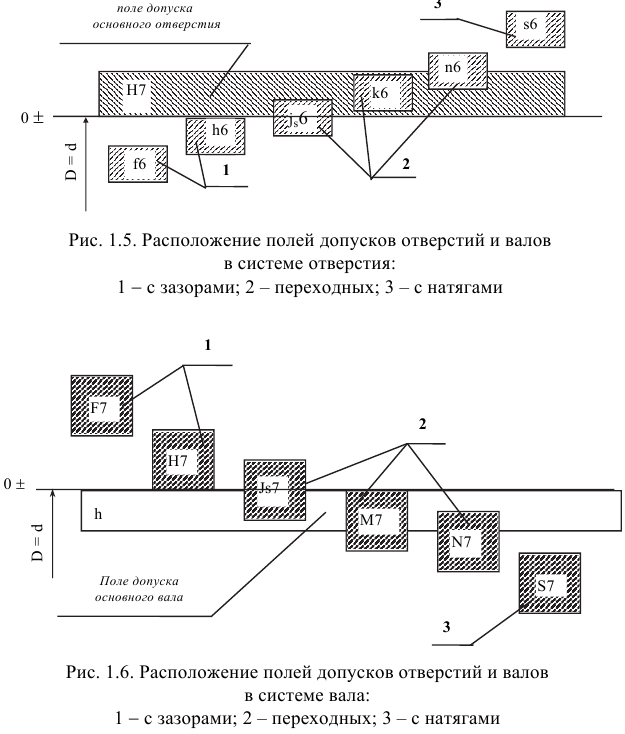
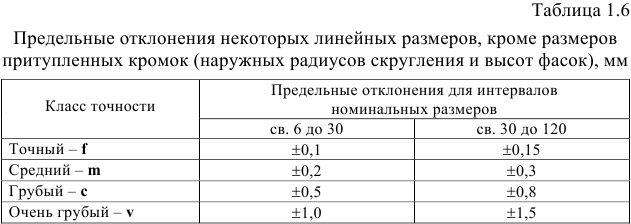
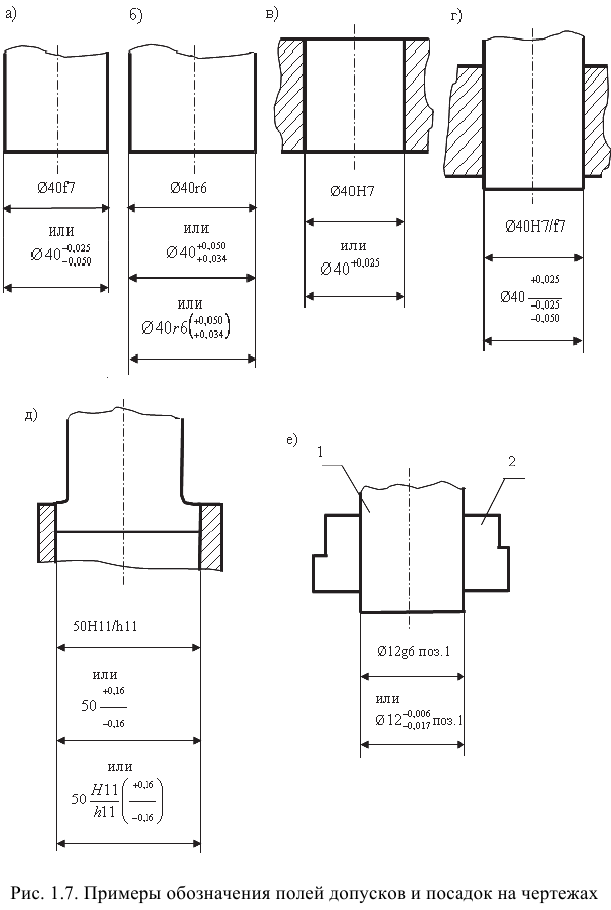
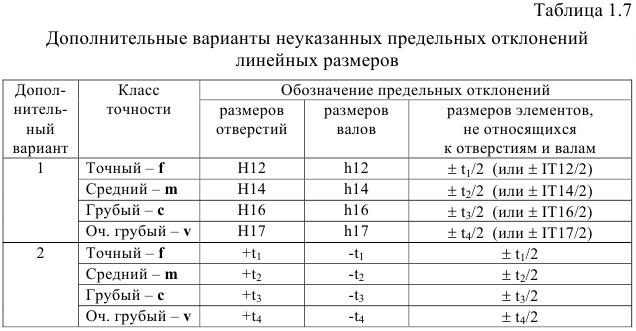
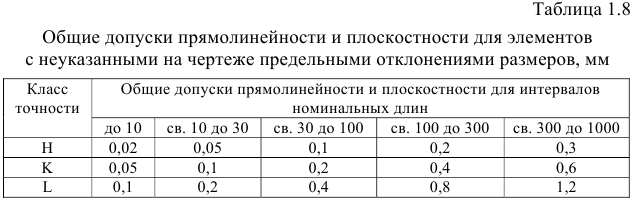
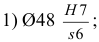
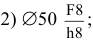
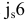
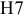
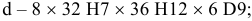
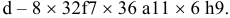
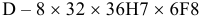 ;
;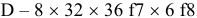 .
.
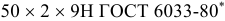 ;
;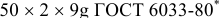 .
.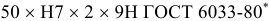 ;
;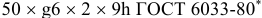 .
.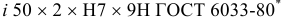 ;
;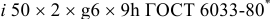 .
.
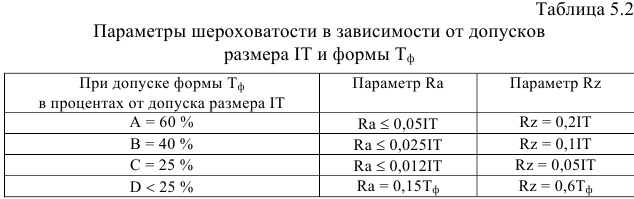
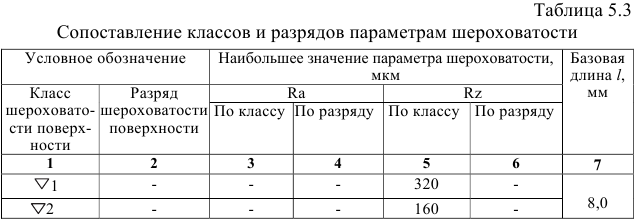
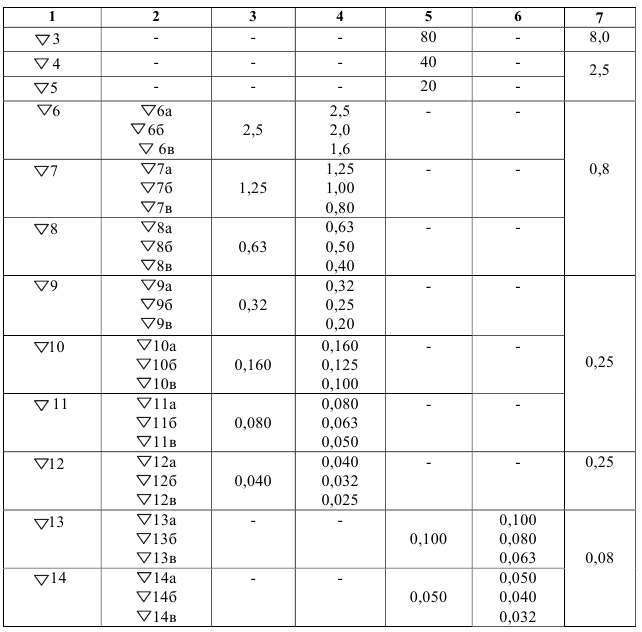
 );
);
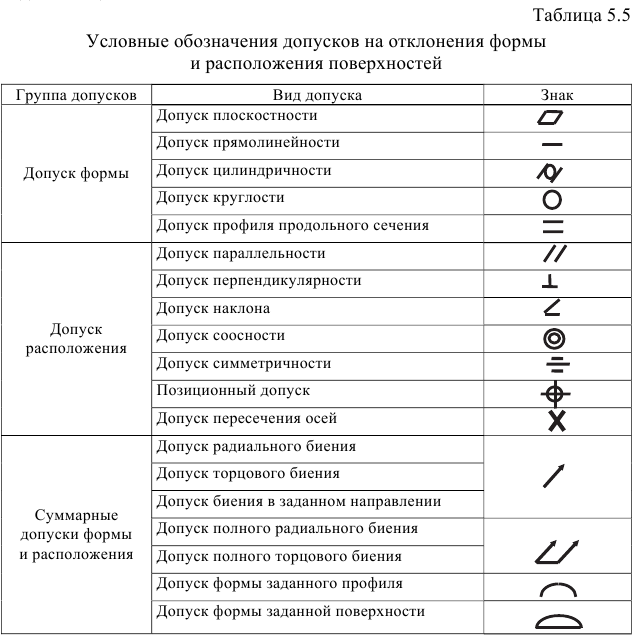
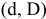 ;
;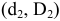 ;
;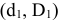 ;
; ;
;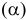 ;
;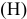 ;
;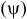 ;
;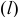 .
.
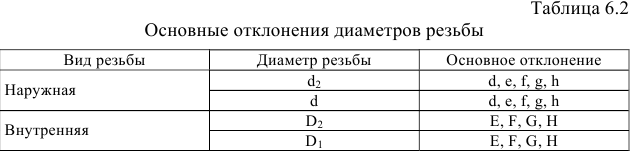
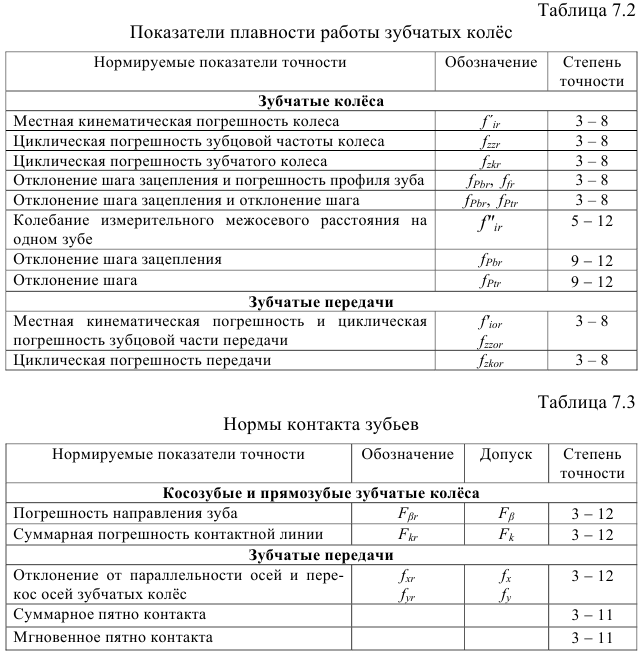


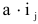
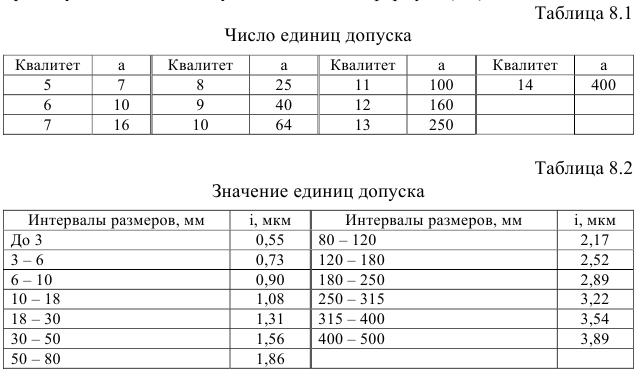
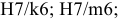
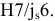
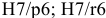 6;
6;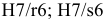 ;
;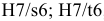 ;
;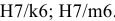 .
.