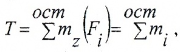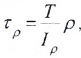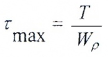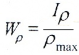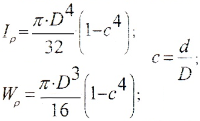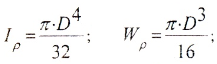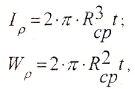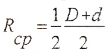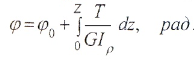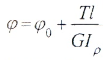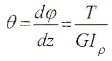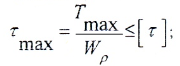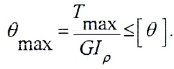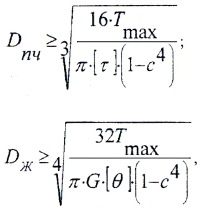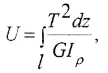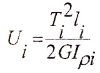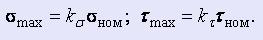Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
65
Добавлен:
30.05.2015
Размер:
1.18 Mб
Скачать
Проектный
расчет валов выполняется по напряжениям
кручения (как при чистом кручении), т.е.
при этом не учитывают напряжения изгиба,
концентрации напряжений и переменность
напряжений во времени (циклы напряжений).
Поэтому для компенсации приближенности
этого метода расчета допускаемых
напряжений на кручение принимают
заниженные, [8, с. 107]
Для
быстроходного вала
Для
тихоходного вала
9.3 Определение
геометрических параметров ступеней
вала
Определить
геометрические параметры быстроходного
и тихоходного валов
[8,
с. 109, табл. 7.1]
|
Ступень ее |
Вал-шестерня (быстроходный) |
Вал (тихоходный) |
|
|
1-я или |
d1 |
где |
где |
|
l1 |
l1=(1 |
l1=(1 |
|
|
2-я |
d2 |
d2=d1+2t=20 где |
d2=d1+2t=20+2 где |
|
l2 |
l2=1,5 |
l2=1,25 |
|
|
3-я |
d3 |
d3=d4+3,2r=18+3,2 |
d3=d4+3,2r=24+3,2 где |
|
l3 |
l3 |
||
|
4-я |
d4 |
d4= |
d4= |
|
l4 |
l4 |
||
|
5-я |
d5 |
— |
d5= |
|
l5 |
— |
l5 |
9.4 Предварительный
выбор подшипников качения
Выбор
наиболее рационального типа подшипника
для данных условий работы редуктора
весьма сложен и зависит от целого ряда
факторов: передаваемой мощности
редуктора, типа передачи, соотношения
сил зацепления, частоты вращения
внутреннего кольца подшипника, требуемого
срока службы, приемлемой стоимости,
схемы установки.
Предварительный
выбор подшипников для каждого из валов
редуктора проводится в следующем
порядке:
-
В
соответствии с таблицей определяем
тип, серию и схему установки подшипников. -
Выбираем
типоразмер подшипников по величине
диаметра d
внутреннего кольца, равного диаметру
второй d2
и четвертой d4
ступеней вала под подшипники. -
Выписываем
основные параметры подшипников:
геометрические размеры – d,
D,
B(T,c);
динамическую Сr
и статическую
Сro
грузоподъемности.
9.4.1 Быстроходный вал
В
соответствии с табл. 96 [2, с. 116] определить
тип, серию, схему установки и основные
характеристики подшипников.
Шариковые
радиальные однорядные подшипники типа
204, легкой серии. Подшипники устанавливаю
враспор.
Характеристика
подшипника
для быстроходного вала:
ГОСТ
8338-75, легкая серия, 204.
|
Вал |
Обозначение |
Размеры, |
Грузоподъемность, |
||||
|
d |
D |
B |
r |
Cr |
Cor |
||
|
л е г к а я с |
|||||||
|
быстроходный |
204 |
20 |
47 |
14 |
1,5 |
12,7 |
6,2 |
9.4.2 Тихоходный вал
В
соответствии с табл. 96 [2, с. 116] определить
тип, серию, схему установки и основные
характеристики подшипников.
Принять
Шариковые
радиальные однорядные подшипники типа
205, легкой серии.
Подшипники установить враспор.
Характеристика
подшипника:
ГОСТ
8338-75, легкая серия, 205.
|
Вал |
Обозначение |
Размеры, |
Грузоподъемность, |
||||
|
d |
D |
B |
r |
Cr |
Cor |
||
|
л е г к а я |
|||||||
|
Тихоходный |
205 |
25 |
52 |
15 |
1,5 |
14,0 |
6,95 |
Соседние файлы в папке Быкова
- #
30.05.201588.03 Кб39А2 ГОРИЗОНТАЛЬНЫЙ ВИД.с щупом.dwg
- #
30.05.201588.96 Кб39Вал.dwg
- #
- #
30.05.201580.7 Кб44Зубчатое колесо.dwg
- #
30.05.201568.54 Кб37крышка.dwg
- #
30.05.201568.93 Кб37сбоку А2.dwg
- #
30.05.2015188.61 Кб37сверху ш-вниз с манжетой с посадками.dwg
- #
30.05.201572.48 Кб36СПЕЦИФИКАЦИЯ 1.dwg
Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений:
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
- поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
- радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.
Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле:
где Iρ — полярный момент инерции.
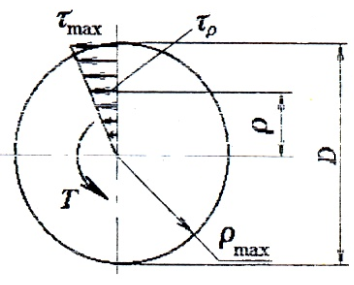
Эпюра касательных напряжений при кручении имеет следующий вид:
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax:
Здесь:
— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала:
б) для вала сплошного сечения (c=0)
в) для тонкостенной трубы (t<0,9)
где
— радиус срединной поверхности трубы.
Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле:
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем:
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:
Расчет валов сводится к одновременному выполнению двух условий:
- условию прочности:
- условию жесткости:
Для стальных валов принимается:
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
- проверочный расчет, заключающийся в проверке выполнения условий прочности и жесткости при известных значениях крутящего момента, размеров и материала вала.
- Проектировочный расчет, при котором вычисляются диаметры:
при этом берется большее из найденных значений, а затем принимается стандартное значение по ГОСТ. - Определение грузоподъемности вала:
Из двух найденных значений крутящего момента необходимо принять меньшее.
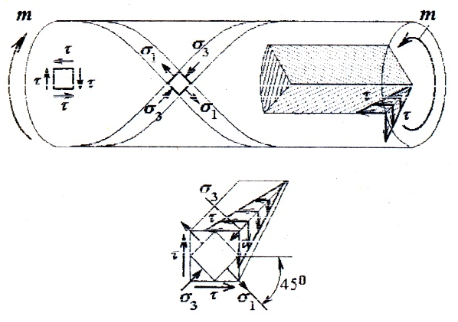
При кручении, наряду с касательными напряжениями в поперечных сечениях, в соответствии с законом парности, касательные напряжения возникают и в продольных сечениях. Таким образом, во всех точках вала имеет место чистый сдвиг.
Главные напряжения σ1 = τ, σ3 = -τ наклонены под углом α=±45о к образующей.
Потенциальная энергия упругой деформации определяется по формуле
или для участка вала при постоянном T и GIρ
Лекции по сопромату >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
5.3. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ КРУЧЕНИИ
Принимая отношение условие прочности при кручении можно представить как где Wp – полярный момент сопротивления поперечного сечения. Для круглого сечения . Для кольцевого сечения 4 ( 4) 3 (1 4) c = – коэффициент пустотелости. Если сечение некруглое (прямоугольное, треугольное, эллиптическое…), используют Iк, Wк, которые вычисляют по специальным формулам. Допускаемое напряжение при кручении [τ] = (0,5–0,6)[σ]. Виды расчетов на прочность: а) поверочный – вычисляют τmax и сравнивают его с [τ], определяя недогрузку или перегрузку в процентах, либо находят коэффициент запаса прочности и сравнивают его с нормативными значениями; б) проектный – вычисляют диаметр вала D при известных значениях T и [τ]; в) определяют допускаемый крутящий момент при известных диаметре вала D и допускаемом касательном напряжении [τ].
Допускаемые напряжения
и механические свойства материалов
Для определения допускаемых напряжений в машиностроении применяют следующие основные методы.
1. Дифференцированный запас прочности находят как произведение ряда частных коэффициентов, учитывающих надежность материала, степень ответственности детали, точность расчетных формул и действующие силы и другие факторы, определяющие условия работы деталей.
2. Табличный — допускаемые напряжения принимают по нормам, систематизированным в виде таблиц
(табл. 1 — 7). Этот метод менее точен, но наиболее прост и удобен для практического пользования при проектировочных и проверочных прочностных расчетах.
В работе конструкторских бюро и при расчетах деталей машин применяются как дифференцированный, так и. табличный методы, а также их комбинация. В табл. 4 — 6 приведены допускаемые напряжения для нетиповых литых деталей, на которые не разработаны специальные методы расчета и соответствующие им допускаемые напряжения. Типовые детали (например, зубчатые и червячные колеса, шкивы) следует рассчитывать по методикам, приводимым в соответствующем разделе справочника или специальной литературе.
Приведенные допускаемые напряжения предназначены для приближенных расчетов только на основные нагрузки. Для более точных расчетов с учетом дополнительных нагрузок (например, динамических) табличные значения следует увеличивать на 20 — 30 %.
Допускаемые напряжения даны без учета концентрации напряжений и размеров детали, вычислены для стальных гладких полированных образцов диаметром 6-12 мм и для необработанных круглых чугунных отливок диаметром 30 мм. При определении наибольших напряжений в рассчитываемой детали нужно номинальные напряжения σном и τном умножать на коэффициент концентрации kσ или kτ:
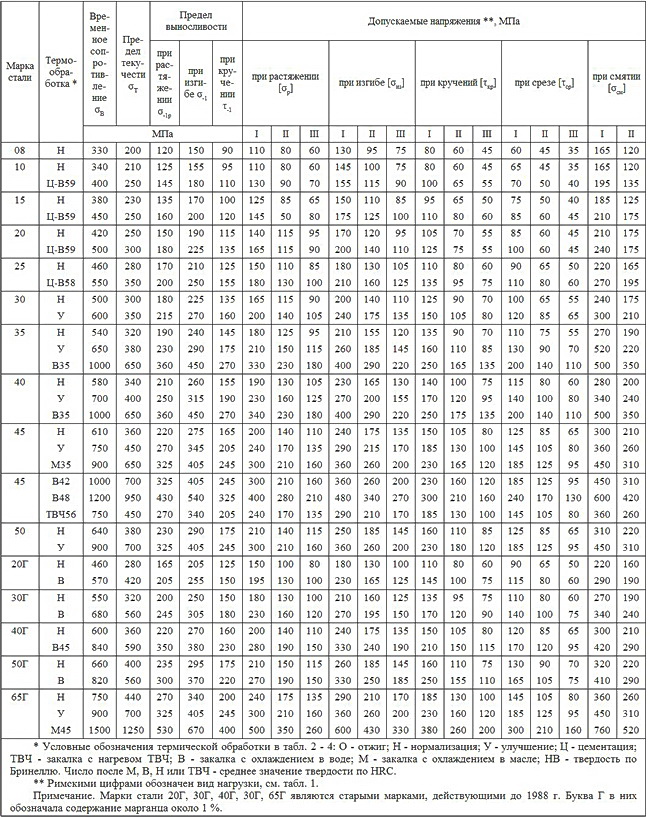
1. Допускаемые напряжения*
для углеродистых сталей обыкновенного качества в горячекатаном состоянии
| Марка стали |
Допускаемые напряжения **, МПа | |||||||||||||
| при растяжении [σp] | при изгибе [σиз] | при кручении [τкр] | при срезе [τср] | при смятии [σсм] | ||||||||||
| I | II | III | I | II | III | I | II | III | I | II | III | I | II | |
| Ст2 Ст3 Ст4 Ст5 Ст6 |
115 125 140 165 195 |
80 90 95 115 140 |
60 70 75 90 110 |
140 150 170 200 230 |
100 110 120 140 170 |
80 85 95 110 135 |
85 95 105 125 145 |
65 65 75 80 105 |
50 50 60 70 80 |
70 75 85 100 115 |
50 50 65 65 85 |
40 40 50 55 65 |
175 190 210 250 290 |
120 135 145 175 210 |
* Горский А.И.. Иванов-Емин Е. Б.. Кареновский А. И. Определение допускаемых напряжений при расчетах на прочность. НИИмаш, М., 1974.
** Римскими цифрами обозначен вид нагрузки: I — статическая; II — переменная, действующая от нуля до максимума, от максимума до нуля (пульсирующая); III — знакопеременная (симметричная).
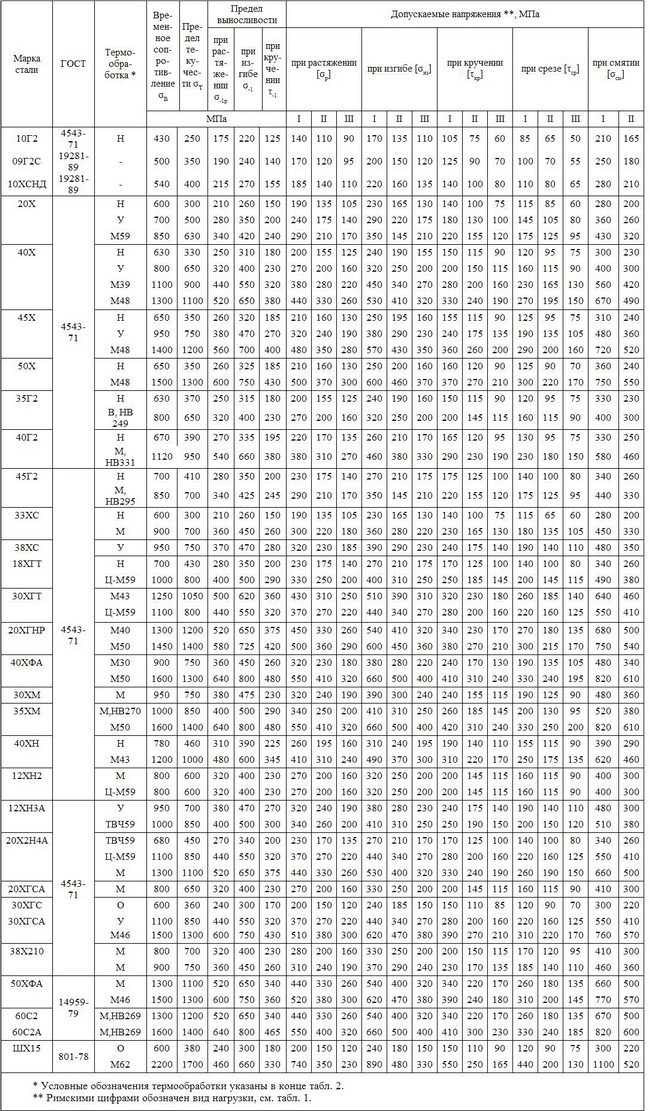
2. Механические свойства и допускаемые напряжения
углеродистых качественных конструкционных сталей
3. Механические свойства и допускаемые напряжения
легированных конструкционных сталей
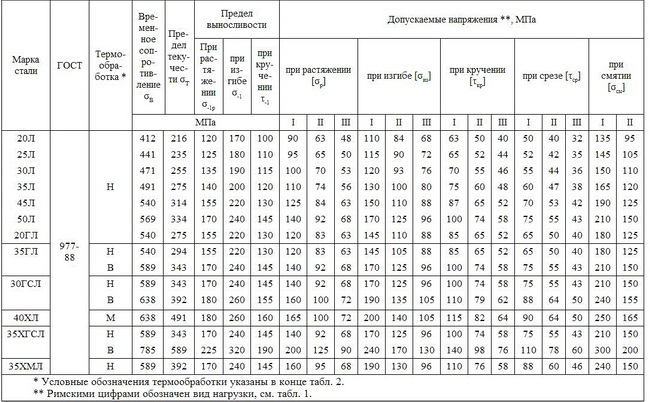
4. Механические свойства и допускаемые напряжения
для отливок из углеродистых и легированных сталей
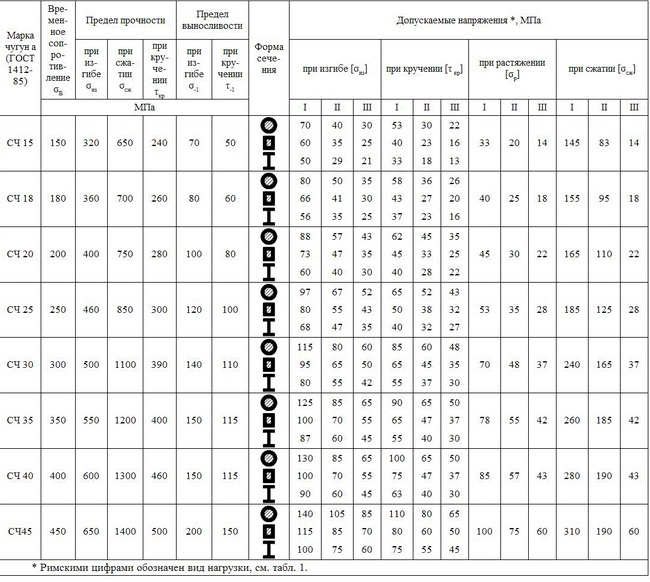
5. Механические свойства и допускаемые напряжения
для отливок из серого чугуна
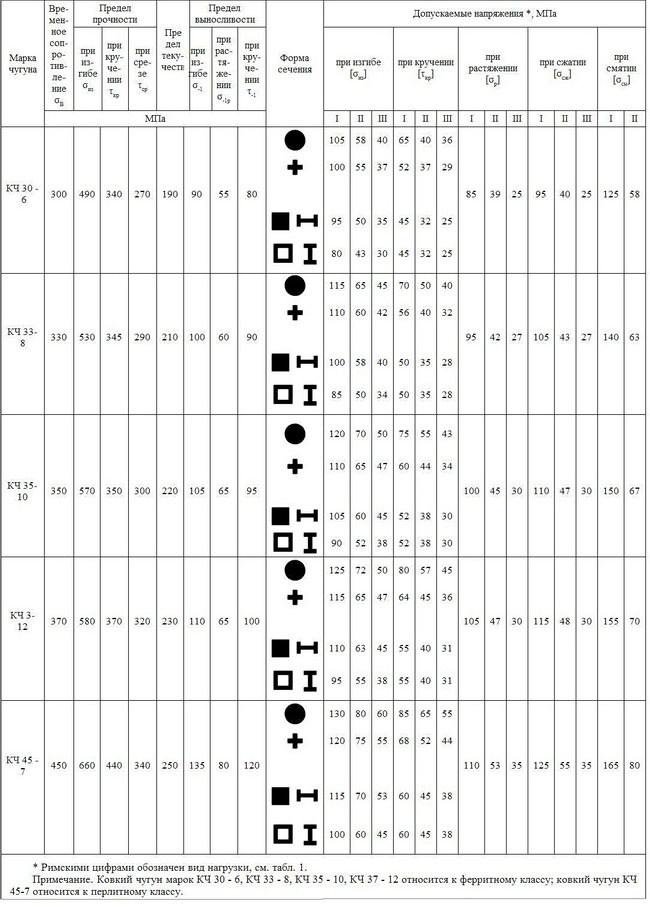
6. Механические свойства и допускаемые напряжения
для отливок из ковкого чугуна
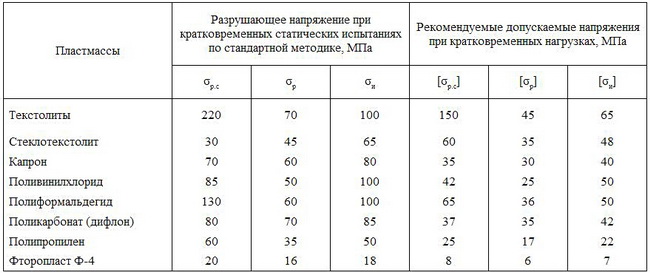
7. Допускаемые напряжения для пластмассовых деталей
Для пластичных (незакаленных) сталей при статических напряжениях (I вид нагрузки) коэффициент концентрации не учитывают. Для однородных сталей (σв > 1300 МПа, а также в случае работы их при низких температурах) коэффициент концентрации, при наличии концентрации напряжения, вводят в расчет и при нагрузках I вида (k > 1). Для пластичных сталей при действии переменных нагрузок и при наличии концентрации напряжений эти напряжения необходимо учитывать.
Для чугунов в большинстве случаев коэффициент концентрации напряжений приближенно принимают равным единице при всех видах нагрузок (I — III). При расчетах на прочность для учета размеров детали приведенные табличные допускаемые напряжения для литых деталей следует умножать на коэффициент масштабного фактора, равный 1,4 . 5.
Приближенные эмпирические зависимости пределов выносливости для случаев нагружения с симметричным циклом:
Механические свойства и допускаемые напряжения антифрикционного чугуна:
— предел прочности при изгибе 250 ÷ 300 МПа,
— допускаемые напряжения при изгибе: 95 МПа для I; 70 МПа — II: 45 МПа — III, где I. II, III — обозначения видов нагрузки, см. табл. 1.
Ориентировочные допускаемые напряжения для цветных металлов на растяжение и сжатие. МПа:
— 30. 110 — для меди;
— 60. 130 — латуни;
— 50. 110 — бронзы;
— 25. 70 — алюминия;
— 70. 140 — дюралюминия.
Источник
Выбор допускаемых напряжений на кручение
Проектный расчёт валов редуктора выполняют только по напряжениям кручения (как при чистом кручении), то есть при этом не учитывают напряжений изгиба, концентрации напряжений и переменность напряжений во времени (циклы напряжений). Для компенсации этого значения допускаемых напряжений на кручение выбирают заниженными в пределах [τ]кр = 10. 30 МПа. Меньшие значения [τ]кр для быстроходных валов, большие значения [τ]кр для тихоходных валов.
Для редукторных валов рекомендуется принимать: [τ]кр = 10-15 МПа – для быстроходных валов; [τ]кр = 15-25 МПа – для тихоходных валов.
Определение размеров ступеней валов
Редукторный вал представляет собой ступенчатое цилиндрическое тело, количество и размеры ступеней которого зависят от количества и размеров установленных на вал деталей. На рис. 1 приведены типовые конструкции валов одноступенчатых редукторов: а – быстроходный – цилиндрического; б – быстроходный – конического; в – тихоходный (l3 * — в коническом редукторе).
Проектный расчёт ставит целью определить ориентировочно геометрические размеры каждой ступени вала: её диаметр d и длину l.
Расчет ведется по формуле:

где T – вращающий момент, н·мм.
Рассчитанное значение d должно соответствовать диаметру самого тонкого участка вала (на рис.1 это размер d1). Полученное значение d необходимо увеличить на 5-7% в случае размещения на этом участке вала шпоночного или прессового соединения. Следует помнить, что диаметр вала d должен быть округлен в большую сторону до стандартного значения.
После этого разрабатывается конструкция вала, обеспечивающая технологичность изготовления и сборки.
Размеры концевого участка вала d1 и l1 определяют по ГОСТ 12080-66 или ГОСТ 12081-72 (цилиндрический или конический конец вала соответственно). Рекомендуется принимать исполнение 1 (длинный конец вала).
Диаметры последующих участков определяют с учетом высоты заплечика t на каждом участке вала. Величина t должна быть достаточной для создания надежного упора, но не чрезмерной, так как это ведет к неоправданному увеличению массы вала. Длины участков вала определяются по прорисовке, в зависимости от размеров размещенных на валу деталей.
Значения высоты t заплечика (буртика) и f величины фаски ступицы колеса и координаты фаски rmax подшипника можно определить в зависимости от диаметра ступени d по следующей таблице:
| d | 17. 24 | 25. 30 | 32. 40 | 42. 50 | 52. 60 | 62. 70 | 71. 85 |
| t | 3,5 | 3,5 | 4,0 | 4,5 | 4,6 | 5,6 | |
| rmax | 1,5 | 2,0 | 2,5 | 3,0 | 3,0 | 3,5 | 3,5 |
| f | 1.2 | 1.6 | 2,5 |
Диаметры d2 и d4 под подшипник округлить до ближайшего стандартного диаметра внутреннего кольца подшипника dп.
Диаметры ступеней (кроме d2 и d4) округлить до ближайшего стандартного значения из ряда Ra40 (ГОСТ 6636-39).
 |
| Рис. 1 Типовые конструкции валов одноступенчатых редукторов: а – быстроходный – цилиндрического; б – быстроходный – конического; в – тихоходный |
Предварительный выбор подшипников качения
В редукторах, как правило, опоры валов выполняются в виде подшипников качения. В курсовых проектах рекомендуется принимать подшипники качения серийно выпускаемые отечественной промышленностью.
Выбор наиболее рационального типа подшипника для данных условий работы редуктора весьма сложен и зависит от целого ряда факторов: передаваемой мощности редуктора, типа передачи, соотношения сил в зацеплении, частоты вращения внутреннего кольца подшипника, требуемого срока службы, приемлемой стоимости, схемы установки.
Предварительный выбор подшипников для каждого из валов редуктора проводят в следующем порядке:
1. В соответствии с рекомендациями табл. 2 определяют тип, серию и схему установки подшипников.
На первом этапе рекомендуется после определения диаметра вала под подшипники назначить по данному диаметру шарикоподшипники лёгкой или средней серии. В большинстве заданий на курсовое проектирование они проходят в дальнейших расчётах. Исключение составляют опоры вала червяка червячного редуктора, где лучше сразу назначить роликовые конические подшипники лёгкой серии в связи со значительными осевыми нагрузками.
2. По справочнику-каталогу выбирают типоразмер подшипников по величине диаметра внутреннего кольца подшипника, равного диаметру d2 и d4 ступеней вала под подшипники.
3. По выбранному из каталога типоразмеру определяют основные параметры подшипников: геометрические размеры d, D, B(T,С); динамическую Сr и статическую Сr0 грузоподъёмности. Здесь D диаметр наружного кольца подшипника, В ширина шарикоподшипника; T и С осевые размеры конического роликоподшипника.
Таблица 4.2. Предварительный выбор подшипников
| Пере-дача | Вид | Тип подшипника | Серия | Угол контакта | Схема установки |
| цилиндрическая косозубая | Б | радиальные шариковые однорядные при aw ≥ 200 мм | средняя (лёгкая) | 0° | с одной фиксир. опорой |
| Т | при Fa / FR 0,25 –роликовые конические типа 7000 | лёгкая | α = 12. 16° | ||
| коническая | Б | роликовые конические типа 7000 при n1 ≤ 1500 об/мин | лёгкая (средняя) | 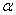 = 12. 16° = 12. 16° |
врастяжку |
| радиально-упорные шариковые типа 46000 при n1 ≥ 1500 об/мин | α = 25. 29° | ||||
| Т | роликовые конические типа 7000 или 1027000 | лёгкая | α= 29° для типа 1027000 | враспор |
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Источник
Допускаемое условное напряжение при кручении
Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор крутящий момент Мz. Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz. Нормальные силы, параллельные оси Oz, вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил касательные напряжения 

Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Ог.
Рис.1. Связь крутящего момента с касательными напряжениями
Рис.2. Иллюстрация положительного и отрицательного крутящего момента
Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 3) позволяет сформулировать следующие предпосылки теории кручения этого стержня:
поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);
расстояния между поперечными сечениями не изменяются, следовательно 
контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Ог. Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и 
материал стержня подчиняется закону Гука. Учитывая, что 


Рис.3. Иллюстрация кручения: а) исходное и б) деформированное состояния
Выведем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения. Как видно, поворот правого торцевого сечения относительно неподвижного левого на угол 


Двумя смежными сечениями вырежем элемент стержня длиной dz и, поскольку нас интересуют деформации элемента, левое сечение его будем считать неподвижным (рис. 5). При повороте правого сечения на угол 

Обратим внимание на то, что в соответствии с рис. 5 и рис. 6, а сдвиг 



Рис.5. Расчетная модель определения касательных напряжений
а) ортогональность 

Рис.6. Распределение касательных напряжений при кручении:
Здесь 
Подставляя (1) в (2) и учитывая, что
где Jp— полярный момент инерции поперечного сечения (для круга с диаметром d 
Рис.7. Распределение напряжений для кольцевого сечения
а) разрушение дерева, б) разрушение чугуна
Рис.8. Распределение исходных касательных и главных напряжений:
Подставляя выражение (3) в (1), получаем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения
Как видно из (4), сдвиги и касательные напряжения пропорциональны расстояний от оси стержня. Обратим внимание на структурные аналогии формул для нормальных напряжений чистого изгиба и касательных напряжений кручения.
Мерой деформации стержня при кручении является погонный угол закручивания стержня, определяемый по (3). Поскольку величина DJp стоит в знаменателе формулы и при заданной нагрузке (Mz через нее выражается) 
Пользуясь (3) для определения угла закручивания элемента длиной dz
найдем полный угол закручивания стержня длиной l
В случае, если по длине стержня Мz и DJp постоянны, получаем
когда эти величины кусочно-постоянны, то:
Отметим, что полученные формулы по структуре аналогичны формулам для деформаций при растяжении стержня.
Наибольшие касательные напряжения возникают у внешней поверхности стержня, т. е. при
где Wр момент сопротивления при кручении или полярный момент сопротивления

Полярный момент сопротивления, стоящий в знаменателе для максимальных касательных напряжений, очевидно, является геометрической характеристикой сечения, а условие прочности стержня при кручении принимает вид
где 
Как показали эксперименты и точное решение этой задачи в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения (рис. 7). Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d
где 
Учитывая линейный характер изменения касательных напряжений по радиусу (рис. 7) и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.
Как отмечено ранее, напряженное состояние при кручении стержня чистый сдвиг, являющийся частным случаем плоского напряженного состояния. На площадках, совпадающих с плоскостью поперечного сечения и на парных им площадках продольных сечений возникают экстремальные касательные напряжения max-min 



Особенности напряженного состояния при кручении нашли отражение в характере разрушения стержней. Так, разрушение стержня из дерева, плохо работающего на скалывание вдоль волокон, происходит от продольных трещин (рис. 8, a). Разрушение стержня из хрупкого металла (например, чугуна) происходит по винтовой линии, наклоненной к образующим под углом 45 o , т. е. по траектории главного напряжения 
РАСЧЕТ ВАЛОВ
Рассмотрим расчет вала на прочность и жесткость. Пусть известна мощность W (кВт), передаваемая вращающимся с заданным числом оборотов в минуту (n) валом от источника мощности (например, двигателя) к ее потребителю (например, станку), а момент т, передаваемый валом, требуется найти, так как численно равный этому моменту крутящий момент необходим для расчета вала.
Если число оборотов вала в минуту п и соответствующая угловая скорость 

где учтено, что 
Если мощность подается на вал через ведущий шкив, а раздается потребителям через несколько ведомых шкивов, то соответственно определяются моменты на шкивах, а затем строится эпюра крутящих моментов. Расчет вала на прочность и жесткость ведется, очевидно, по max Mz.
Определение диаметра вала из условия прочности. Условие прочности при кручении вала имеет вид (7), где допускаемые напряжения 
Требуемое значение Wp=d з /16 получаем из условия (7), принимая в нем знак равенства

откуда получаем формулу для диаметра вала кругового сечения
Определение диаметра вала из условия жесткости. Условие жесткости состоит в наложении ограничения на погонный угол закручивания вала 
Тогда, учитывая, что 
Аналогично проводятся расчеты и для вала кольцевого поперечного сечения.
Источник

 =14
=14 ,
,