Как найти допускаемое напряжение на срез

Предельные и допустимые напряжения

Предельным
напряжением считают напряжение, при
котором

в материале
возникает опасное состояние (разрушение
или опасная дефомация).

Для пластичных
материалов предельным напряжением
считают предел текучести, т. к. возникающие
пластические деформации не исчезают
после снятия нагрузки: σ_пред
=σ_т

Для хрупких
материалов, где пластические деформации
отсутствуют, а разрушение возникает по
хрупкому типу (шейки не образуется), за
предельное напряжение принимают предел
прочности: σ_пред
=σ_т

Для пластично-хрупких
материалов предельным напряжением
считают напряжение, соответствующее
максимальной деформации 0,2% (σ_0,2):

σ_пред
=σ_0,2

Допускаемое
напряжение — максимальное напряжение,
при котором материал должен нормально
работать.

Допускаемые
напряжения получают по предельным с
учетом запаса прочности: [σ]= σ_пред
/[s]

где [σ] — допускаемое
напряжение; в — коэффициент запаса
прочности; [s]
— допускаемый коэффициент запаса
прочности.

Примечание.
В квадратных скобках принято обозначать
допускаемое значение величины.

Допускаемый
коэффициент запаса прочности зависит
от качества материала, условий работы
детали, назначения детали, точности
обработки и расчета и т. д.

Он может колебаться
от 1,25 для простых деталей до 12,5 для
сложных деталей, работающих при переменных
нагрузках в условиях ударов и вибраций.

Расчеты
на прочность при растяжении и сжатии

Расчеты
на прочность ведутся по условиям
прочности — нера­венствам,
выполнение которых гарантирует прочность
детали при данных
условиях.

Для
обеспечения прочности расчетное
напряжение не должно превышать
допускаемого напряжения:
Расчетное
напряжение σ
зависит
от
нагрузки и размеров попе­речного
сечения, допускаемое только от
материала детали и
усло­вий
работы.

Существуют
три вида расчета на прочность.

Проектировочный
расчет
—
задана расчетная схема и нагрузки;
материал
или размеры детали подбираются:

определение
размеров поперечного сечения:
подбор
материала
по
величине σ_пред
можно
подобрать марку материала.

Проверочный
расчет
—
известны нагрузки, материал, размеры
детали; необходимо проверить,
обеспечена ли прочность.

Проверяется
неравенство

Определение
нагрузочной способности
(максимальной
нагрузки):

Тема 2.3 практические расчеты на срез и смятие

Понятие
о срезе и смятии. Условия прочности

Срезом
или сдвигом
называется деформация, возникающая под
действием двух близко расположенных
противоположно напра­вленных равных
сил. При этом возникают касательные
напря­жения.

Примером
элемента металлических конструкций,
работающего на срез, может служить
заклепка . При некоторой величине
действующих сил F
стержень заклепки может быть сре­зан
по сечению аа.
Силы
F
передаются путем давления стенок
отверстия на стержень заклепки.

Деформация
среза возникает также в шпоночном
соединении, схематично изображенном
на рис.
Вращающий
момент М
от
шкива передается на вал радиуса г с
помощью сил F
=М/r.
Эти
силы вызывают срез или сдвиг шпонки по
ее среднему сече­нию. Частный случай
среза — скалывание волокнистых
матери­алов, в частности древесины,
по плоскостям, параллельным волокнам.
При большом давлении может произойти
значительное смятие стенок отверстия
или стержня заклепки по поверхности их
соприкосновения. В шпоночном соединении
смятие может про­изойти по площади
контакта вала или шкива со шпонкой.

Смятием
называется
местная деформация сжатия по площад­кам
передачи давления. Возникающие нормальные
напряжения смятия
являются местными; величина их быстро
убывает при уда­лении
от площадки соприкосновения элементов.

Чтобы
найти напряжения, возникающие в сечении
аа
стержня
заклепки
под действием сил
F
,
применим
метод сечений. Рассечем мысленно стержень
заклепки на две части и рассмотрим
условия равновесия
одной из частей стержня (рис. б).

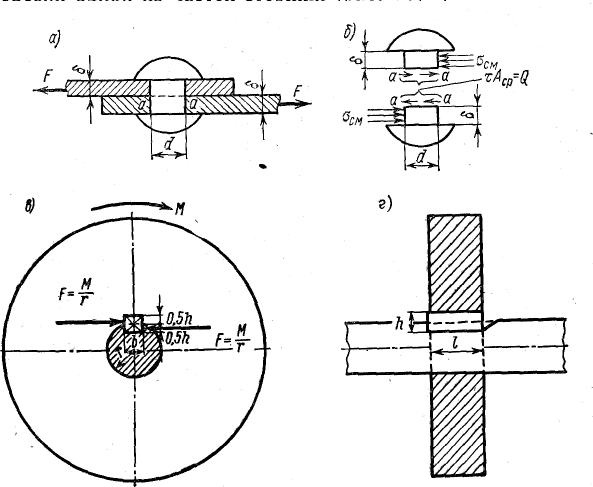
Со
стороны листа на нее передается внешняя
сила F,
а
по сечению
аа
действуют
внутренние силы. Поперечная сила Q,
возникающая
в сечении аа,
уравновешивает
внешнюю силу F
и
численно равна ей
Q
= F.

Приближенно
можно принять, что касательные напряжения
распределяются
по сечению равномерно

τ=
Q
/A_СР.

Условие
прочности элементов, работающих на
срез, имеет вид
τ
= Q
/A_ср≤[
τ
_СР],

где
A_гр
—площадь среза; [τ
_ср]
—допускаемое касательное на­пряжение.

Величину
допускаемого напряжения назначают па
основании испытаний
на срез. Обычно принимают [τ
_ср]
=(0,70…
0,80) [σ]

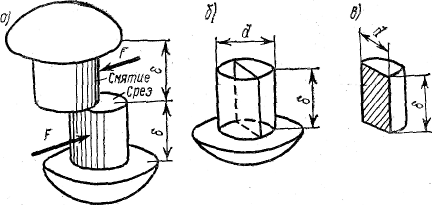
На
стержень заклепки давление со стороны
отверстия в листе передается по боковой
поверхности полуцилиндра высотой,
рав­ной
толщине листа б.

Напряжения
смятия распределены по поверхности
неравно­мерно.
Так как закон их распределения точно
неизвестен, расчет ведут упрощенно,
считая их постоянными по расчетной
площади смятия.

Проверку
элементов конструкции на смятие
производят по формуле
σ_см
= Q/А_см
≤
[σ_см]

где
А_см
— площадь смятия; [σ_см]
— допускаемое напряжение на
смятие. Обычно принимают [σ_см]
=
(1,74…2,2) [σ].
Расчет­ные
площади среза и смятия, входящие в
формулы, вычисляются
в каждом конкретном случае в зависимости
от вида соединения и характера передачи
усилий. Так, для заклепочного соединения,
изображенного на рис,
площадь
среза одной
заклепки
соответствует ее поперечному
сечению А_ор=πd²/4
.

За
площадь смятия заклепки условно принимают
ее диаметраль­ное
сечение под одним листом, т. е. прямоугольник
A_см⁼dδ.

Для
шпоночного соединения, площади
среза и смятия также нетрудно опре­делить

A_ср
= lb,

A_cм
= l0,5h.

Расчет
сварных соединений

Сварка
является наиболее механизированным и
совершенным способом соединения
элементов стальных конструкций.
Соедине­ние
сваркой элементов конструкций
осуществляется внахлестку и
встык. Соединение внахлестку производится
при помощи валиковых
(угловых) швов.

Валиковые
швы называются фланговыми, если они
расположены
параллельно
направлению силы (рис.а),
лобовыми,
если они
расположены
перпендикулярно направлению силы
(рис.б),
и
косыми, если они идут под углом к
направлению действующей
силы
(рис. в). ^!

Валиковые
швы рассчитывают на срез. Расчетное
сечение среза
— площадь А
=
lh,
где
l
—длина валикового шва; h
—
расчетная
высота шва, связанная с толщиной
свариваемых листов соотношением
(рис. б)

Н
=
δ соs45°
≈ 0,76.

Когда
сваривают листы различной толщины, то
при вычисле­нии
высоты шва в расчет вводится минимальная
толщина. Условие прочности сварного
шва имеет вид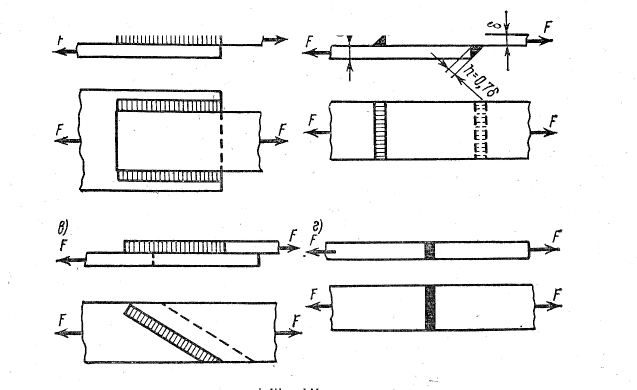

τ=
F/
lh
= F/
l
δ ≤
[τ_ср
]

где
[τ_ср
] —допускаемое напряжение на срез для
сварного шва.

Чаще
всего применяют сварное соединение
листов встык (рис.,
г), когда зазор между соединяемыми
листами заполняется расплавленным
металлом. При сравнительно большой
толщине соединяемых
элементов их кромки перед сваркой
специально обра­батывают.
Высоту шва обычно принимают равной
толщине листов.

Прочность
стыкового сварного шва, как правило, не
уступает прочности
свариваемого металла. Сварной шов в
соединении

встык
работает на тот же вид деформации, что
и соединяемые элементы,
наиболее часто — на растяжение или на
сжатие. Условие
прочности шва в этом случае имеет вид

σ=
F/
lh
= F/
l
δ ≤[σ’]

где
[σ’]
—допускаемое напряжение на растяжение
или сжатие сварного
шва.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  08.03.201514.37 Mб15Конспект лекций по ИУРЭ ДВОРСОН.doc

• #
• #
• #
• #
• #
• #
• #
• #

Сопротивление материалов

Сдвиг (срез)



Напряжения при сдвиге

Сдвигом называют такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила.

Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков, при пробивании отверстия в заготовках на штампе (рис. 1).

Рассмотрим брус площадью поперечного сечения А, перпендикулярно оси которого приложены две равные и противоположно направленные силы F; линии действия этих сил параллельны и находятся на относительно небольшом расстоянии друг от друга.
Для определения поперечной силы Q применим метод сечений (рис. 2).
Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:

Σ Y = 0  »  F – Q = 0,

откуда поперечная сила Q может быть определена, как:

Q = F.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении бруса при сдвиге.
Очевидно, что при сдвиге в поперечном сечении возникают только касательные напряжения τ.

Предполагаем, что эти касательные напряжения равномерно распределены по сечению, и, следовательно, могут быть вычислены по формуле:

τ = Q / А.

На основании полученной формулы можно сделать вывод, что форма сечения на величину напряжения при деформации сдвига не влияет.

***

Расчеты на прочность при сдвиге

Условие прочности детали конструкции заключается в том, что наибольшее напряжение, возникающее в ней (рабочее напряжение), не должно превышать допускаемое.
Расчетная формула при сдвиге:

τ = Q / А ≤ [τ]

читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое. (при обозначении предельно допустимых напряжений применяют квадратные скобки: [τ] или [σ] )
По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку.

Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлам) или скалыванием (применительно к неметаллам).
Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести.
В машиностроении для штифтов, болтов, шпонок и других деталей, работающих на срез принимают [τ_ср] = (0,25….0,35) σ_т, где σ_т – предел текучести материала изделия.

При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково.
Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.

***



Деформация Гука при сдвиге

Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abcd, на грани которого действуют только касательные напряжения τ, а противоположную грань параллелепипеда представим жестко защемленной (рис. 3).

Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bc по отношению к сечению, принятому за неподвижное.
Деформация сдвига характеризуется углом γ (гамма) и называется углом сдвига, или относительным сдвигом. Величина bb₁, на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом.
Относительный сдвиг γ выражается в радианах.

Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется закон Гука при сдвиге.
Закон Гука при сдвиге справедлив лишь в определенных пределах нагрузок и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу.

Математически закон Гука для деформации сдвига можно записать в виде равенства:

τ = G γ.

Коэффициент пропорциональности G характеризует жесткость материала, т. е. способность сопротивляться упругим деформациям при сдвиге, и называется модулем сдвига или модулем упругости второго рода.

Модуль упругости выражается в паскалях; для различных материалов его величина определена экспериментально и ее можно найти в специальных справочниках.
При проведении ответственных расчетов на срез величина модуля упругости для каждого соединения определяется опытным путем, непосредственно перед расчетом, либо берется из справочника с применением увеличенного запаса прочности.

Следует отметить, что между тремя упругими постоянными (модулями упругости) E, G и ν существует следующая зависимость:

G = E / [2(1 + ν)].

Принимая для сталей ν ≈ 0,25, получаем: G_ст ≈ 0,4 Е_ст .

***

Материалы раздела “Сопротивление материалов”:

• Основные понятия и определения
• Растяжение и сжатие
• Смятие. Контактные напряжения
• Деформация сдвига (среза)
• Деформация кручения
• Деформация изгиба



Правильные ответы на вопросы Теста № 9

№ вопроса	1	2	3	4	5	6	7	8	9	10
Правильный вариант ответа	2	3	2	1	1	3	3	1	1	2

Инструкционно-технологическая
карта

к
практическому занятию №2

Дисциплина:
Техническая
механика

Тема: Расчет на
срез и смятие.

Цель
занятия: Закрепить
теоретический материал по последовательности расчетов на срез и смятие.

Отводимое время: 2ч.

Обеспечение рабочего места:

1. рабочая тетрадь.

2. инструкционно-технологическая карта.

3. чертежные принадлежности.

Содержание
работы:

1. Ознакомиться с заданиями и методическими указаниями по их
выполнению.

2. Выполнить расчеты.

3. Выполнить задание по определить, исходя из
условий прочности на срез и смятие, необходимый диаметр болта в соединении.

ЗАДАНИЯ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ИХ
ВЫПОЛНЕНИЮ

1. общие сведения.

Срезом называется
деформация, возникающая под действием двух близко расположенных противоположно
направленных сил. При этом возникают касательные напряжения.

Примером  элемента
металлических конструкций,  работающего на срез,  служит заклёпка (рис.а).  При
некоторой величине действующих сил F
стержень заклёпки может быть срезан по сечению аа. Силы  F  (рис.
б) передаются путём давления стенок отверстия на стержень заклепки.

Чтобы найти напряжения,  возникающие
в сечении  аа  стержня заклёпки под действием сил F ,
применяется метод сечений. Рассечем мысленно стержень заклёпки на две части и
рассмотрим условие равновесия одной из частей стержня (рис. б).

Со стороны листа на неё
передаётся внешняя сила F,
а по сечению аа действуют внутренние силы.
Поперечная сила Q,
возникающая в сечении аа уравновешивает внешнюю силу F
и численно равна ей Q=
F.

Приблизительно можно
принять, что касательные напряжения распределяются по сечению равномерно

                                                 t = Q/ А_ср.

Условие прочности
элементов работающих на срез, имеет вид

                                    
t = Q/ А_ср = £ [t_ср],                           где

А_ср –
площадь среза,

Q
– поперечная сила возникающая в сечении,

[t_ср]
– допускаемое касательное напряжение.

Величину допускаемого
напряжения  назначают на основании испытаний на срез. Обычно принимают    [t_ср] = (0,7 – 0,8) [d].     

На стержень заклепки
давление со стороны отверстия в листе передается по боковой поверхности
полуцилиндра высотой, равной толщине листа d  
(рис.1а и 1б).

Напряжения смятия
распределены по поверхности неравномерно. Так как закон их распределения точно
неизвестен, расчет ведут упрощенно, считая их постоянными по расчетной площади
смятия.

Проверку элементов
конструкции на смятие проводят по формуле

                                            d_см
= Q/ А_см £ [d_см
],                     
 где

А_см
– площадь смятия,

[d_см
] – допускаемое напряжение на смятие.  Обычно
принимают  [d_см ]
= (1,7-2,2)  [d_см ]
. Расчетные площади среза и смятия (  А_ср и А_см) вычисляются
в каждом конкретном случае в зависимости от вида соединения и характера
передаваемого усилия. Так, для заклепочного соединения  на рис.1а   и 
1б площадь среза одной заклепки соответствует её поперечному сечению   А_ср
= pd²/4.
За площадь смятия заклепки условно принимается её диаметральное сечение под
одним листом, то есть прямоугольник  (рис. 1б и1в)  Асм
= dd.

Пример.

Определить, исходя из условий прочности на срез и смятие,
необходимый диаметр болта в соединении, показанном на рис. 2, если d = 20 мм; d₁ = 12 мм; допускаемые
напряжения: [t_ср] = 100 Н/мм²; [d_см] = 240 Н/мм²;
растягивающая сила F =
120кН. Болт установлен в отверстие без зазора.

Р е ш е н и е.

Так как болт работает на
срез одновременно по двум сечениям – аа  и  bb,
то общая площадь среза составит

А_ср
= 2pd²/4
= pd²/2.

Поперечная сила в болте
равна силе, растягивающей стык Q
= F.

По условию прочности на
срез имеем

А_ср
= pd²/2
³  F[t_ср],

Откуда получаем

d ³
 F/p[t_ср]
= 2120 10³/3,14 100 = 27,6 мм.

Согласно данным задачи  2d₁,   поэтому
опасной в отношении смятия является площадь смятия внутренней детали  Асм = d.

Из условия прочности на
смятие

Асм
=F/
[d_см ],             
или

d ³
F/
[d_см ], 
           отсюда

d  ³
F/
d[d_см
]  =  120   10³ / 20
 240 = 25 мм.

Из двух значений
диаметра  d,
найденных по условиям прочности на срез и смятие, следует принять большее, то
есть  d 
³

З а д а н и е.

Определить, исходя из
условий прочности на срез и смятие, необходимый диаметр болта в соединении,
показанном на  рис. а,  если d = 35 мм;
допускаемые напряжения: [t_ср]
= 120 Н/мм²; [d_см]
= 280 Н/мм²; растягивающая сила F
= 220кН. Болт установлен в отверстие без зазора.