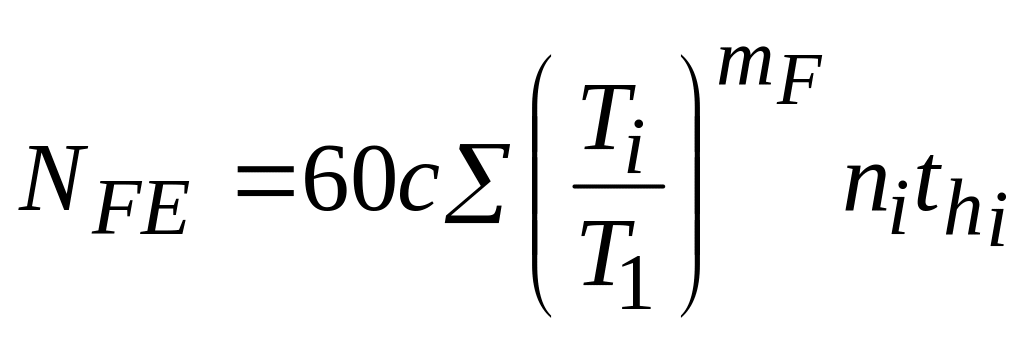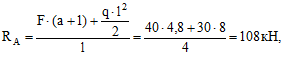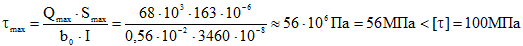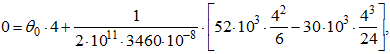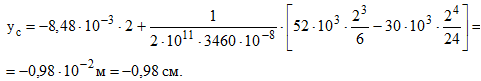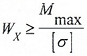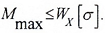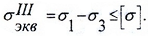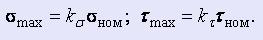Как найти допускаемое напряжение при изгибе

Допускаемые напряжения изгиба

Уравнение кривой
усталости по изгибным напряжениям имеет
вид

,

Рис. 4.8
Рис. 4.9

где m_F
=6 –
для незакалённых колёс; m_F
=9 – для
закалённых колёс.

Для
любой точки кривой усталости по изгибным
напряжениям (рис.4.8) можно записать

или

.

Обозначим

– коэффициент долговечности при расчётах
на изгибную прочность, и получим
выражение для допускаемых напряжений
изгиба

,

где
S_F
– коэффициент безопасности при
расчётах на изгибную прочность,

S_F

= 1,7…2,2
(большее значение для литых заготовок);

К_Fс
– коэффициент, учитывающий
условия работы зубьев.

При
работе зубьев одной стороной (односторонняя
нагрузка) К_Fс=
1 (рис. 4.9). При
работе зубьев двумя сторонами (двусторонняя
нагрузка – реверсивные передачи,
сателлиты) К_Fс
=0,7…0,8
(большее значение для НВ>350).

Для
всех сталей
базовое число
циклов переменных напряжений N_Fo
= 4·10⁶.

Расчётное
число циклов переменных напряжений при
постоянном режиме работы N_FE
=
60nct_h
.

При
переменном режиме нагрузки выражение
для расчётного числа циклов будет

.

При
малом числе циклов вводится ограничение
,
а также

1
К_FL

2,08 при НВ

350;

1
К_FL

1,63 при НВ
> 350.

Так
как

,
то при расчётах используют

и

.

Лекция №5

Передачи цилиндрическими колесами

С прямыми зубьями

Элементы геометрического расчета

Рис.
5.1

Рассмотрим прямой зуб
высотой h
(рис. 5.1). Делительная окружность
d
делит зуб на две части:

h_a
=
m
– головка зуба;

h_f
=
1,25m
– ножка зуба.

d_a
=
d+2h_a
= d+2m
– диаметр окружности выступов;

d_f
=d–2h_f
=
d–2,5m
– диаметр окружности впадин;

d_b
=
d_w
cos_w
– диаметр основной окружности.

Участок
поверхности зуба ниже d_b
очерчен не по эвольвенте.

Рис. 5.2

Рассмотрим влияние числа
зубьев на их форму при постоянном модуле
(рис. 5.2). При z
зубчатое колесо превращается в рейку
и зуб приобретает прямолинейные
очертания. С уменьшением z
уменьшается толщина зуба у основания
и вершины, а также увеличивается кривизна
эвольвентного профиля. Такие изменения
приводят к снижению прочности зуба. При
дальнейшем уменьшении z
появляется подрезание ножки
зуба.

При
нарезании инструментом реечного типа
по границе подрезания устанавливается
минимально допустимое число зубьев
z_min=17.

Нарезание зубьев со смещением (корригирование).

К

Рис.
5.3

орригирование зубчатых зацеплений
представляет собой улучшение свойств
зацеплений путем очерчивания рабочего
профиля зубьев различными участками
эвольвенты той же окружности (рис. 5.3).
Это достигается смещением инструмента
при нарезании зубьев. Начальная и
делительная плоскости могут совпадать
(1) и не совпадать (2). Если эти плоскости
совпадают, то расстояние от оси зубчатого
колеса до делительной плоскости рейки

E₁
=
0,5d
= 0,5mz.

Расстояние
между начальной и делительной плоскостями
инструментальной рейки называется
смещением исходного контура

X
= E₂
–E₁
=
E₂
–
0,5d.

Отношение

называется коэффициентом
смещения исходного контура.

К

Рис.
5.4

орригированием можно поднять несущую
способность передач вследствие утолщения
зуба у основания, возможности уменьшения
числа зубьев и соответственно увеличения
модуля, увеличения радиусов кривизны
эвольвентного профиля. Корригирование
устраняет подрезание зубьев при их
изготовлении и позволяет вписывать
передачу в заданное межосевое
расстояние. Коррекция зацепления может
быть высотной и угловой. При высотной
коррекции колесо нарезают с отрицательным
смещением производящей рейки равным
по абсолютной величине положительному
смещению производящей рейки шестерни.

Таким образом, x₂
=
–x₁
и

x_
=
x₁+x₂
=
0.

При
этом толщина зуба шестерни по делительной
окружности увеличивается, а толщина
зуба колеса уменьшается, но суммарная
их толщина остается постоянной. При
угловой коррекции x_=x₁+x₂>0
и сумма толщин зубьев по делительной
окружности обычно больше, чем у
некорригированных колес, поэтому оси
колес приходится раздвигать, начальные
окружности не совпадают с делительными
и угол зацепления увеличен (рис. 5.4).
Межосевое расстояние

a_w=0,5
(d_w2d_w1).

Делительное
межосевое расстояние

a=0,5(d₂d₁).

При
отсутствии коррекции, если a=a_w,
то =_w,
где
–
угол профиля производящей рейки.

В
соответствии с ГОСТ 13755-81 =20.
Увеличение  приводит
к увеличению толщины зуба у основания,
а следовательно, и к увеличению его
прочности. Поэтому в авиации применяют
=22;
25;28;
30.

d_b=d_wcos_w
и d_b=dcos,
отсюда cos_w=
cos=
cos.

Рис.
5.5

Изменение межосевого
расстояния при эвольвентных профилях
не равно сумме смещений колес и оценивается
коэффициентом воспринимаемого смещения

.
В этом случае разность суммарного
коэффициента смещения x_
и коэффициента воспринимаемого смещения
определяют значение коэффициента
уравнительного смещения y=x_
–
y.
Изменением на величину у
диаметров вершин колес удается сохранить
неизменным стандартный радиальный
зазор в зацеплении, который равен
с=0,25m.
В этом случае

d_a=d+2
(1+x–y)m;
d_f=d-2(1,25-x)m;

a_w=0,5
(d_w2d_w1)=
.

Соседние файлы в папке резьбовое_сварные_соединения

• #
• #
• #

  22.02.2023231.49 Кб0Алгоритм расчета сварных тавровых соединений.mcd

• #
• #
• #
• #

  22.02.2023243.93 Кб0ргр.xmcd

• #

  22.02.2023215.18 Кб0ргр2.xmcd

• #

  22.02.202374.37 Кб0Решетов Дмитрий Николаевич.chm

• #
• #

  22.02.2023187.9 Кб0Схема нагружения болтовых соединений..cdw

Сопротивление материалов

Напряжения при изгибе



Нормальные напряжения при чистом изгибе

Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.

Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1). Радиус кривизны нейтрального слоя балки обозначим ρ.

Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN. Это волокно в результате деформации изгиба удлинилось на величину nn₁. Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n₁F || mE):

Δ OEF ~ Δ Fnn₁.

Из подобия треугольников запишем равенство:

nn₁ / ds = y / ρ.

Так как левая часть этого равенства есть относительное удлинение, т. е. nn₁ / ds = ε, то y / ρ = ε.

Применив закон Гука при растяжении и сжатии σ = Еε, получим:

σ = Еy / ρ.

Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2.

Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3.
В плоскости поперечного сечения выделим бесконечно малую площадку dA, в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN, действующая на площадку dA, будет равна:

dN = σdA.

Составим уравнения равновесия:

1.    Σ Z = 0;    ∫dN = 0,     или:     ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0.

(ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0.
Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;

2.    Σ М_и = 0; – m + ∫y dN = 0.

Так как при чистом изгибе изгибающий момент равен внешнему моменту М_и = m, то

М_и = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y² dA,

откуда:

М_и = Е I / ρ,

где: I = ∫y² dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.

Так как при чистом изгибе балки постоянного сечения М_и = const, то:

ρ = EI / М_и = const.

Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:

σ = Еy / ρ = Ey / EI / М_и = М_и y / I.

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

σ_max = М_и y_max / I = М_и / I / y_max = М_и / W,

где W = I / y_max – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м³.

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле

σ_max = М_и / W.

Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.

***



Касательные напряжения при изгибе

Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский, который в 1855 году предложил следующую формулу:

τ = QS / (I d).

Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:

τ_max = 4Q / (3A) = 4τ_сред / 3,

***

Расчеты на прочность при изгибе

Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:

σ_max = Ми_max / W ≤ [σ]

и читается так: нормальное напряжение в опасном сечении, определенное по формуле σ_max = Ми_max / W ≤ [σ] не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W, тем меньшие напряжения возникают в сечении бруса.

Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:

1. Прямоугольное сечение размером b x h:    W_пр = bh² / 6.

2. Круглое сечение диаметром d:    W_круг = π d³ / 32 ≈ 0,1d³

3. Кольцо размером D x d:    W_кольца = ≈ 0,1 (D⁴ – d⁴) / D; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов).

***

Материалы раздела “Изгиб”:

• Понятие деформации изгиба.
• Дифференциальные зависимости при изгибе. Теорема Журавского.

Деформации растяжения и сжатия



Строительные калькуляторы — ProstoBuild.ru

Расчет балки на изгиб

Рассчитывать балку на изгиб можно несколькими вариантами:
1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)[/i]

Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.

Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент. Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.

Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.

Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала , а для хрупких (чугун) – пределу прочности . Предел текучести и предел прочности мы можем найти по таблицам ниже.

Давайте рассмотрим пару примеров:

1. [i]Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.[/i]
Для начала нам необходимо выбрать расчетную схему.

На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине , то и максимальное напряжение будет в заделке. Давайте найдем его:

По таблице сортамента двутавров находим момент сопротивления двутавра №10.

Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.

Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.

После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.

45.34 МПа Надеюсь, что данная статья была вам полезна, и рассчитываю на вашу благодарность 🙂

Источник

iSopromat.ru

Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки для заданной системы изгибающих нагрузок.

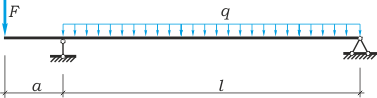
Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [ σ ]=160 МПа и [ τ ]=100 МПа, допустимый прогиб балки [f]= l/400

Определение опорных реакций

Подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

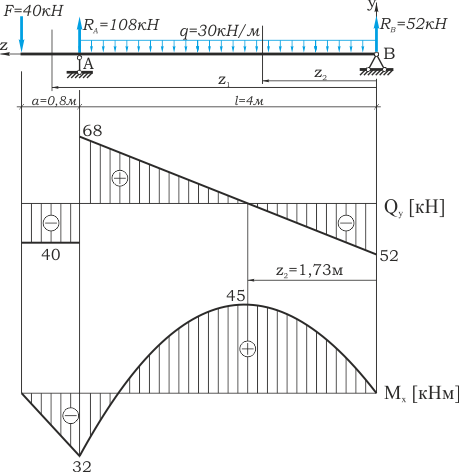
Построение эпюр Q и М

Внутренние силовые факторы Q_y и M_x в пролете балки 0 ≤ z₂ ≤ l

По этим данным построены эпюры Q и М.

Подбор сечения двутавровой балки

По сортаменту выбираем двутавр № 24, для которого W_x = 289 см 3 , I_x= 3460 см 4 , S_max = 163 см 3 , h = 24 см, b_п = 11,5 см, t = 0,95 см, d = b_c = 0,56 см, h₀ = h-2t = 22,1 см.

Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.

σ_max = M_max / W_x = 45∙10 3 / 289∙10 -6 = 156∙10 6 Па = 156 МПа

Проверка сечения балки по касательным напряжениям

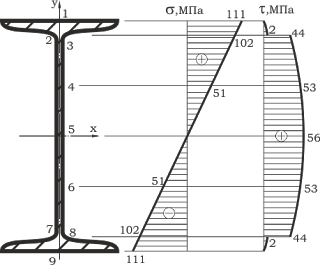
Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:

В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:

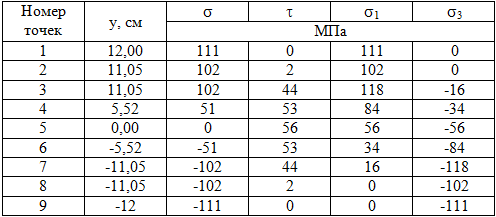
Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1

Проверка прочности балки по главным напряжениям

Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ ₁=118 МПа и σ ₃= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ ₁ — σ ₃≤ [ σ ].

Так как 118 — ( -16) = 134 θ ₀

откуда θ ₀= -8,48∙10 -3 радиан.

Прогиб в пролете при z=l/2=4/2=2 м.

Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.

Проверка жесткости балки

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x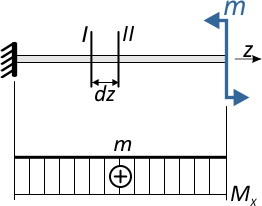

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.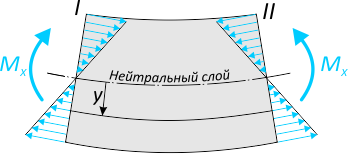

Закон распределения нормальных напряжений по высоте сечения выражается формулой: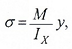

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: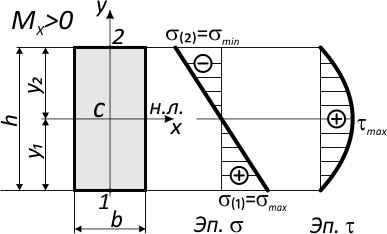

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.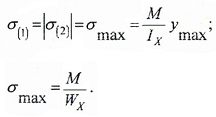

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: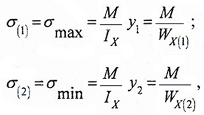

где: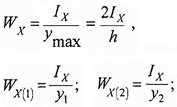

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.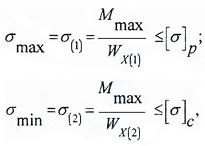

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского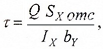

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max: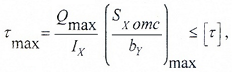

где [ τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: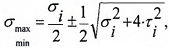

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Расчёт балок на прочность при изгибе

В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.

а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,

б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.

а) Для определения σ_(К), τ_(К) и _maxσ,_maxτ потребуется знать величины осевого момента инерции всего сечения I_Н.О., осевого момента сопротивления W_Н.О., статического момента отсечённой части и статического момента половины сечения S_max:

б) Проверка прочности:

— по условию прочности нормальных напряжений:

— по условию прочности касательных напряжений:

В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.

Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.

Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:

– уравнение прямой.

— уравнение параболы.

z₂=3м: М = 30 · 3 – 5 · 3 2 = 90 — 45 = 45кНм,

z₂=6м: М = 30 · 6 – 5 · 6 2 = 180 — 180 = 0.

Определение аналитического максимума изгибающего момента второго участка:

Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.

Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.

В данном случае максимальный момент по модулю М = 60кНм

а) сечение круглой формы d=?

б) сечение прямоугольной формы при h/b = 2:

Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:

Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:

— для круглого сечения

— для прямоугольного сечения

Воспользуемся этими формулами. Тогда

— для балки круглого сечения при :

— для балки прямоугольного сечения

Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:

А_{прямоугольного} = 865,3см 2 2 , следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.

Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.

Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:

∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.

z₂=2м: М = 40+ 104 · 2 – 10 · 2 2 = 208 кНм.

III участок

z₃=2м: М = 24 + 136·2 — 10 (2+2) 2 = 24 + 272 – 160 = 136кНм,

z₃=4м: М = 24 + 136·4 – 10 (2+4) 2 = 24 + 544 – 360 = 208 кНм.

z₃ = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.

Проверяем скачки в эпюрах:

а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М₂=24, приложенному в этом месте.

первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,

второй – под силой F=80кН и равен ей (64+16=80кН),

третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)

Наконец, проектируем двутавровое сечение.

Подбор его размеров производится из условия прочности по нормальным напряжениям :

В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления W_х нет. Есть № 40 а с W_х=1190 см 3 и № 45 а с W_х=1430 см 3

Попробуем меньший из них. Если принять двутавр № 40 а , у которого W_х=1190 см 3 , то наибольшее напряжение в опасном сечении будет:

и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.

Поэтому приходится принимать ближайший больший размер двутавра, а именно №45 а , у которого W_х=1430 см 3 . В этом случае балка будет работать с недонапряжением:

Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :

Это условие прочности выполняется, даже с избыточным запасом.

Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).

1.Определение опорных реакций

∑М(А) = F · 2 + М₁ — М₂— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М₁— М₂ – А · 8 + q·6·1 =0,Проверка:

∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.

2.Построение эпюр изгибающих моментов и поперечных сил.

z₂=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.

III участок

z₃=2м: М = 210·2 — 20·(2+2) 2 = 420 – 320 = 100кНм,

z₃=4м: М = 210·4 – 20 · (2+4) 2 = 840 – 720 = 120кНм.

3. Подбор сечений (опасное сечение по σ: |_maxМ|=131,25кНм,

опасное сечение по τ: |_maxQ|=130кН).

Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)

Принимаем: В=0,24м,

Вариант 2. Деревянное круглое

Принимаем d=0,45м,

Вариант 3. Чугун : ([σ_Р]=30МПа, [σ_с]=120МПа, [τ]=15МПа)

Принимаем b=0,19м, тогда h=0,38м, d=0,076м.

Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).

Вариант 5. Сталь, круглая труба

Принимаем D=0,22м → d = 0,6·D =0,132м.

Вариант 6. Сталь, прямоугольная труба

Принимаем b=0,13м, h=0,26м.

Кстати: какое из сечений стальной балки выгодней по расходу материала?

Двутавр — А = 72,6см 2 = 72,6·10 -4 = 0,00726м 2 ,

круглая труба –

прямоугольная труба —

Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.

Источник

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.

Закон распределения нормальных напряжений по высоте сечения выражается формулой:

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2:

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2:

где:

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[σ], [σ]_р, [σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]_с>[σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Другие видео

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

где [τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Другие видео

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >

Для определения допускаемых напряжений в машиностроении применяют следующие основные методы.
1. Дифференцированный запас прочности находят как произведение ряда частных коэффициентов, учитывающих надежность материала, степень ответственности детали, точность расчетных формул и действующие силы и другие факторы, определяющие условия работы деталей.
2. Табличный — допускаемые напряжения принимают по нормам, систематизированным в виде таблиц
(табл. 1 — 7). Этот метод менее точен, но наиболее прост и удобен для практического пользования при проектировочных и проверочных прочностных расчетах.

В работе конструкторских бюро и при расчетах деталей машин применяются как дифференцированный, так и. табличный методы, а также их комбинация. В табл. 4 — 6 приведены допускаемые напряжения для нетиповых литых деталей, на которые не разработаны специальные методы расчета и соответствующие им допускаемые напряжения. Типовые детали (например, зубчатые и червячные колеса, шкивы) следует рассчитывать по методикам, приводимым в соответствующем разделе справочника или специальной литературе.

Приведенные допускаемые напряжения предназначены для приближенных расчетов только на основные нагрузки. Для более точных расчетов с учетом дополнительных нагрузок (например, динамических) табличные значения следует увеличивать на 20 — 30 %.

Допускаемые напряжения даны без учета концентрации напряжений и размеров детали, вычислены для стальных гладких полированных образцов диаметром 6-12 мм и для необработанных круглых чугунных отливок диаметром 30 мм. При определении наибольших напряжений в рассчитываемой детали нужно номинальные напряжения σ_ном и τ_ном умножать на коэффициент концентрации k_σ или k_τ:

1. Допускаемые напряжения*
для углеродистых сталей обыкновенного качества в горячекатаном состоянии

Марка стали

Допускаемые напряжения **, МПа

при растяжении [σp]

при изгибе [σиз]

при кручении [τкр]

при срезе [τср]

при смятии [σсм]

I

II

III

I

II

III

I

II

III

I

II

III

I

II

Ст2 Ст3 Ст4 Ст5 Ст6

115 125 140 165 195

80 90 95 115 140

60 70 75 90 110

140 150 170 200 230

100 110 120 140 170

80 85 95 110 135

85 95 105 125 145

65 65 75 80 105

50 50 60 70 80

70 75 85 100 115

50 50 65 65 85

40 40 50 55 65

175 190 210 250 290

120 135 145 175 210

* Горский А.И.. Иванов-Емин Е. Б.. Кареновский А. И. Определение допускаемых напряжений при расчетах на прочность. НИИмаш, М., 1974.
** Римскими цифрами обозначен вид нагрузки: I — статическая; II — переменная, действующая от нуля до максимума, от максимума до нуля (пульсирующая); III — знакопеременная (симметричная).

2. Механические свойства и допускаемые напряжения
углеродистых качественных конструкционных сталей

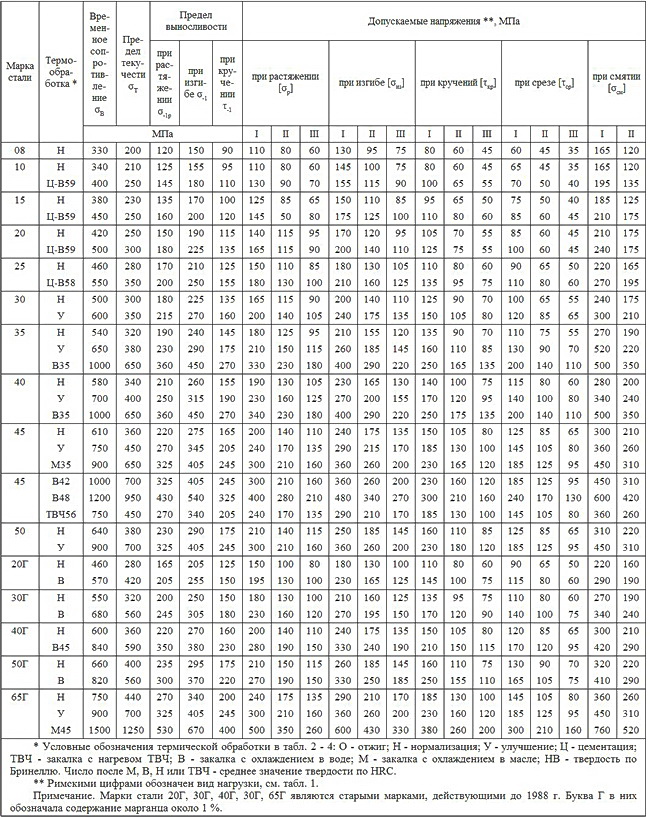
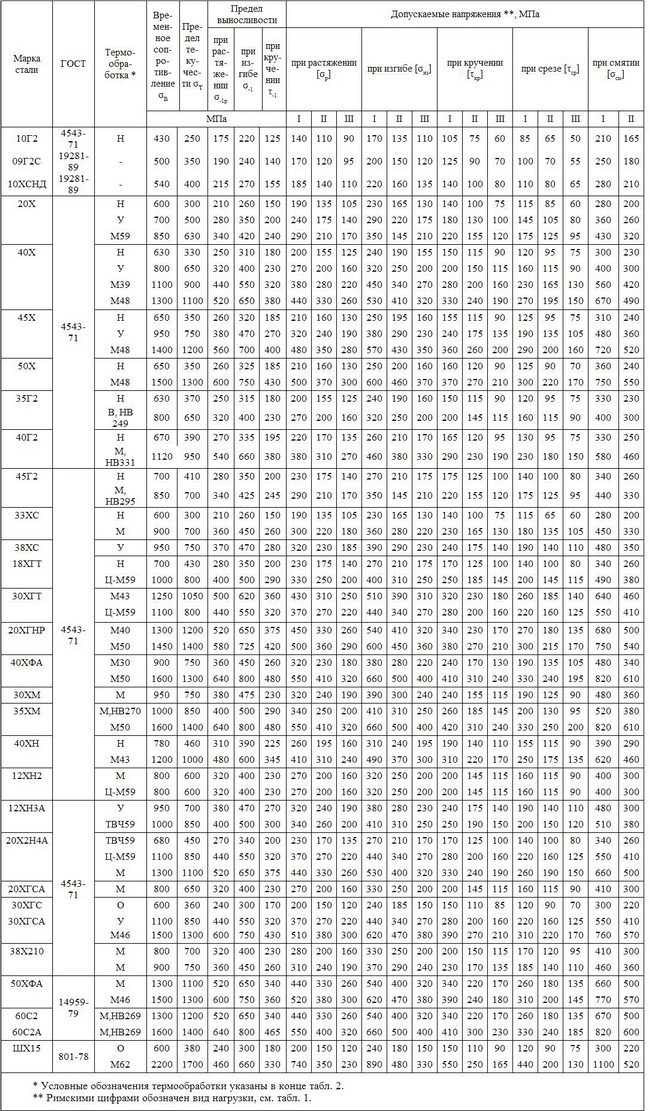
3. Механические свойства и допускаемые напряжения
легированных конструкционных сталей

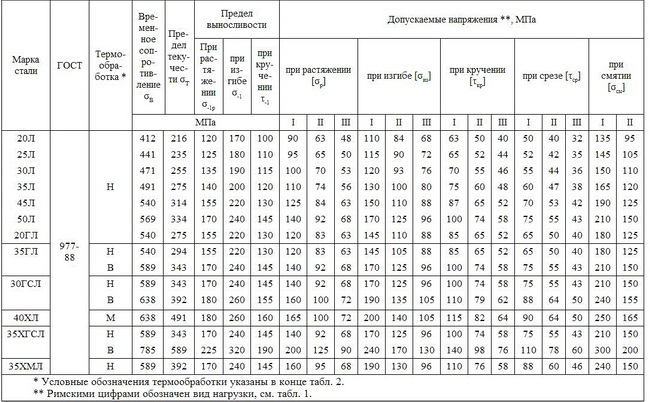
4. Механические свойства и допускаемые напряжения
для отливок из углеродистых и легированных сталей

5. Механические свойства и допускаемые напряжения
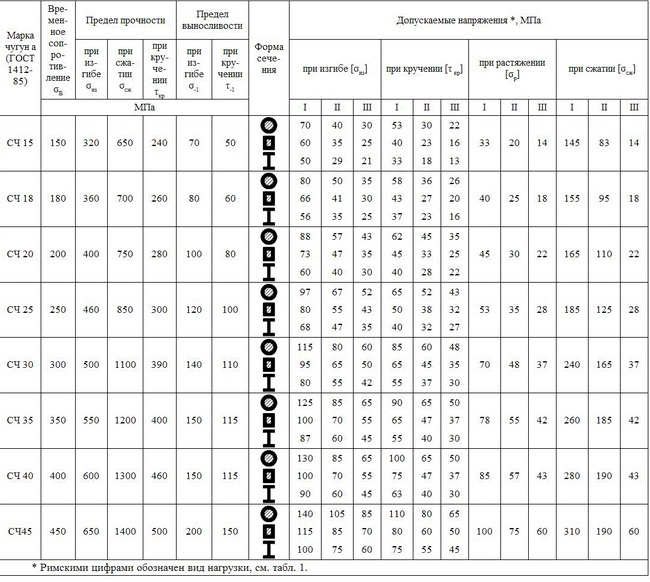
для отливок из серого чугуна

6. Механические свойства и допускаемые напряжения
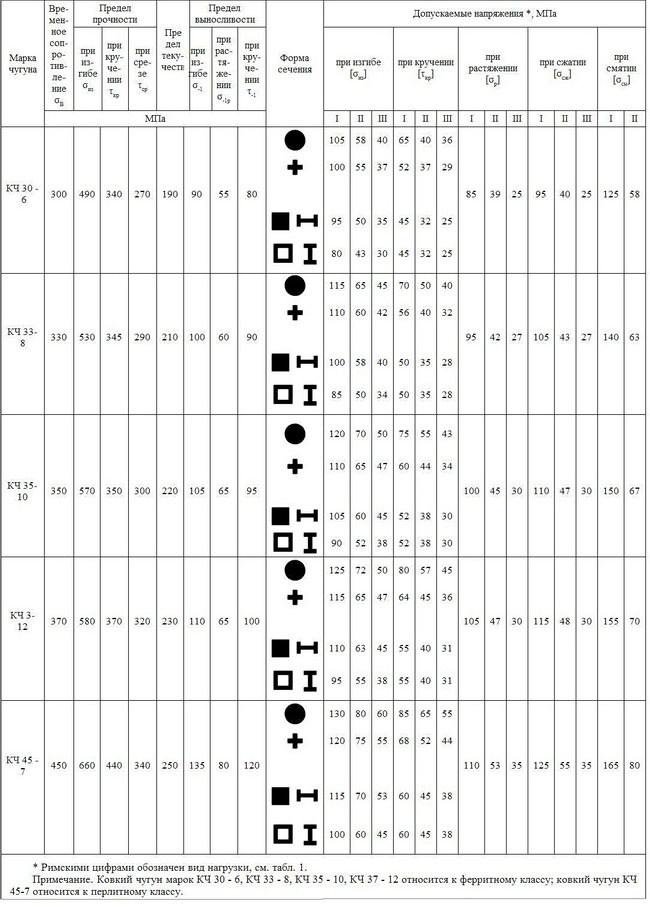
для отливок из ковкого чугуна

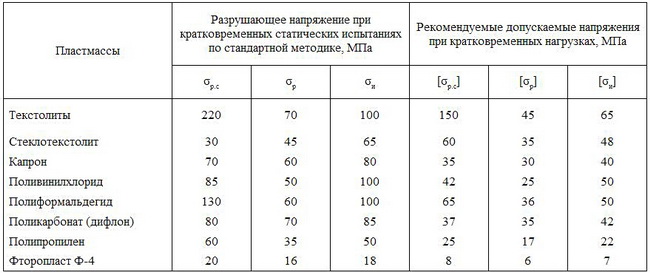
7. Допускаемые напряжения для пластмассовых деталей

Для пластичных (незакаленных) сталей при статических напряжениях (I вид нагрузки) коэффициент концентрации не учитывают. Для однородных сталей (σ_в > 1300 МПа, а также в случае работы их при низких температурах) коэффициент концентрации, при наличии концентрации напряжения, вводят в расчет и при нагрузках I вида (k > 1). Для пластичных сталей при действии переменных нагрузок и при наличии концентрации напряжений эти напряжения необходимо учитывать.

Для чугунов в большинстве случаев коэффициент концентрации напряжений приближенно принимают равным единице при всех видах нагрузок (I — III). При расчетах на прочность для учета размеров детали приведенные табличные допускаемые напряжения для литых деталей следует умножать на коэффициент масштабного фактора, равный 1,4 . 5.

Приближенные эмпирические зависимости пределов выносливости для случаев нагружения с симметричным циклом:

Механические свойства и допускаемые напряжения антифрикционного чугуна:
— предел прочности при изгибе 250 ÷ 300 МПа,
— допускаемые напряжения при изгибе: 95 МПа для I; 70 МПа — II: 45 МПа — III, где I. II, III — обозначения видов нагрузки, см. табл. 1.

Ориентировочные допускаемые напряжения для цветных металлов на растяжение и сжатие. МПа:
— 30. 110 — для меди;
— 60. 130 — латуни;
— 50. 110 — бронзы;
— 25. 70 — алюминия;
— 70. 140 — дюралюминия.

Источник

Техническая механика

Сопротивление материалов

Напряжения при изгибе

Нормальные напряжения при чистом изгибе

Как было установлено ранее, в поперечных сечениях балки при чистом изгибе возникают только нормальные напряжения растяжения и сжатия. Вопрос о распределении этих напряжений по поперечному сечению решается путем рассмотрения деформаций волокон балки.

Рассмотрим участок балки, подверженный деформации чистого изгиба. Двумя поперечными сечениями АВ и СD выделим элемент балки бесконечно малой длины ds (рис 1) . Радиус кривизны нейтрального слоя балки обозначим ρ .

Рассмотрим слой волокон mn, находящийся на расстоянии y от нейтрального слоя NN . Это волокно в результате деформации изгиба удлинилось на величину nn₁ . Ввиду малости расстояния ds заштрихованные треугольники будем считать прямолинейными; эти треугольники подобны (n₁F || mE) :

Из подобия треугольников запишем равенство:

Так как левая часть этого равенства есть относительное удлинение, т. е. nn₁ / ds = ε , то y / ρ = ε .

Применив закон Гука при растяжении и сжатии σ = Еε , получим:

Из этой формулы видно, что нормальные напряжения при изгибе распределены по высоте сечения неравномерно: максимальные напряжения возникают в волокнах, наиболее удаленных от нейтральной оси. По ширине сечения нормальные напряжения не меняются.
Распределение нормальных напряжений изображено на рис. 2 .

Полученная формула для определения нормальных напряжений неудобна, так как в нее входит радиус кривизны нейтрального слоя.
Для вывода формулы, связывающей нормальные напряжения с изгибающим моментом, применим метод сечений и рассмотрим равновесие части балки, изображенной на рис. 3 .
В плоскости поперечного сечения выделим бесконечно малую площадку dA , в пределах которой будем считать нормальные напряжения σ постоянными; тогда нормальная сила dN , действующая на площадку dA , будет равна:

Составим уравнения равновесия:

1. Σ Z = 0; ∫dN = 0, или: ∫σ dA = ∫Еy / ρ dA = Е / ρ ∫y dA = 0 .

( ρ для данного сечения, а также модуль упругости Е – величины постоянные, поэтому вынесены за знак интеграла). Поскольку ρ и Е не равны нулю, значит, ∫y dA = 0 . Этот интеграл представляет собой статический момент площади сечения относительно оси x, т. е. нейтральной оси бруса (балки). Равенство нулю статического момента инерции означает, что при изгибе нейтральная ось проходит через центр тяжести площади поперечного сечения;

2. Σ М_и = 0; — m + ∫y dN = 0 .

Так как при чистом изгибе изгибающий момент равен внешнему моменту М_и = m , то

М_и = ∫y dN = ∫y dA = ∫y Еy / ρ dA = Е / ρ ∫y 2 dA ,

где: I = ∫y 2 dA – момент инерции поперечного сечения относительно нейтральной оси; ЕI – жесткость сечения при изгибе.

Так как при чистом изгибе балки постоянного сечения М_и = const, то:

ρ = EI / М_и = const .

Следовательно, изогнутая ось такой балки представляет собой дугу окружности. Выражение радиуса кривизны подставим в формулу для определения нормальных напряжений; тогда:

σ = Еy / ρ = Ey / EI / М_и = М_и y / I .

Максимальное значение нормальные напряжения будут иметь у волокон, наиболее удаленных от нейтральной оси:

где W = I / y_max – момент сопротивления изгибу (или осевой момент сопротивления).
Момент сопротивления изгибу есть отношение осевого момента инерции поперечного сечения относительно нейтральной оси к расстоянию от этой оси до наиболее удаленного волокна.
Единица момента сопротивления сечения изгибу [W] = м 3 .

Итак, наибольшие нормальные напряжения при чистом изгибе вычисляются по формуле

Нетрудно заметить, что эта формула по своей структуре аналогична формулам для определения напряжений при растяжении, сжатии, сдвиге и кручении.

Касательные напряжения при изгибе

Очевидно, что при поперечном изгибе, вызванном приложением к балке поперечной силы, в сечениях балки должны возникнуть касательные напряжения.
Определением зависимости между внешними нагрузками, геометрическими и физическими параметрами балок и касательными напряжениями, возникающими в них, занимался русский мостостроитель Д. И. Журавский , который в 1855 году предложил следующую формулу:

Эта формула называется формулой Журавского и читается так:
касательные напряжения в поперечном сечении балки равны произведению поперечной силы Q на статический момент S относительно центральной оси части сечения, лежащей выше рассматриваемого слоя волокон, деленному на момент инерции I всего сечения относительно нейтральной оси и на ширину b рассматриваемого слоя волокон.

По формуле Журавского можно вывести зависимости для определения касательных напряжений в балках, имеющих разную форму поперечного сечения (прямоугольную, круглую и т. п.).
Например, для балки круглого сечения формула Журавского в результате преобразований выглядит так:

где Q – поперечная сила, вызывающая изгиб, А – площадь сечения балки.

Большинство балок в конструкциях рассчитывается только по нормальным напряжениям, и только три вида балок проверяют по касательным напряжениям:

— деревянные балки, т. к. древесина плохо работает на скалывание;
— узкие балки (например, двутавровые), поскольку максимальные касательные напряжения обратно пропорциональны ширине нейтрального слоя;
— короткие балки, так как при относительно небольшом изгибающем моменте и нормальных напряжениях у таких балок могут возникать значительные поперечные силы и касательные напряжения.
Максимальное касательное напряжение в двутавровой балке определяется по формуле Журавского, при этом геометрические характеристики таких балок берутся из справочных таблиц .

Расчеты на прочность при изгибе

Условие на прочность при изгибе заключается в том, что максимальное нормальное напряжение в опасном сечении не должно превышать допускаемое.
Полагая, что гипотеза о не надавливании волокон справедлива не только при чистом, но и при поперечном изгибе, мы можем нормальные напряжения при поперечном изгибе определять по такой же формуле, что и при чистом изгибе, при этом расчетная формула выглядит так:

и читается так: нормальное напряжение в опасном сечении, определенное по формуле σ_max = Ми_max / W ≤ [σ] не должно превышать допускаемое.
Допускаемое нормальное напряжение при изгибе выбирают таким же, как при растяжении и сжатии.
Максимальный изгибающий момент определяют по эпюре изгибающих моментов или расчетом.
Так как момент сопротивления изгибу W в расчетной формуле стоит в знаменателе, то чем больше W , тем меньшие напряжения возникают в сечении бруса.

Ниже приведены моменты сопротивления изгибу для наиболее часто встречающихся сечений:

1. Прямоугольное сечение размером b x h: W_пр = bh 2 / 6 .

2. Круглое сечение диаметром d: W_круг = π d 3 / 32 ≈ 0,1d 3

3. Кольцо размером D x d: W_кольца = ≈ 0,1 (D 4 – d 4 ) / D ; (момент сопротивления кольцевого сечения нельзя определять, как разность моментов сопротивления большого и малого кругов) .

Источник

Онлайн калькулятор по определению допускаемых напряжений материалов: сталей и сплавов алюминия, меди и титана.

Калькулятор онлайн определяет расчетные допускаемые напряжения σ в зависимости от расчетной температуры для различных марок материалов следующих типов: углеродистая сталь, хромистая сталь, сталь аустенитного класса, сталь аустенито-ферритного класса, алюминий и его сплавы, медь и ее сплавы, титан и его сплавы согласно ГОСТ-52857.1-2007 [1].

Исходные данные:
Расчетная температура среды Т, °С
Тип материала	углеродистая сталь хромистая сталь сталь аустенитного класса сталь аустенито-ферритного класса алюминий и его сплав медь и ее сплавы титан и его сплавы
Марка материала
Решение:
Допускаемое напряжение материала [σ], МПа	определение допускаемого напряжения

Помощь на развитие проекта premierdevelopment.ru

Send mail и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Методика расчета:

Допускаемые напряжения были определены согласно ГОСТ-52857.1-2007 [1].

для углеродистых и низколегированных сталей

для жаропрочных, жаростойких и коррозионно-стойких сталей аустенитного класса

Для расчетного срока эксплуатации до 2*10 5 ч допускаемое напряжение, расположенное ниже горизонтальной черты, умножают на коэффициент 0,9 при температуре R_e/20 — минимальное значение предела текучести при температуре 20 °C, МПа; R_р0,2/20 — минимальное значение условного предела текучести при остаточном удлинении 0,2% при температуре 20 °С, МПа. допускаемое
напряжение — наибольшие напряжения, которые можно допустить в конструкции при условии его безопасной, надежной и долговечной работы. Значение допускаемого напряжения устанавливается путем деления предела прочности, предела текучести и пр. на величину, большую единицы, называемую коэффициентом запаса. расчетная
температура — температура стенки оборудования или трубопровода, равная максимальному среднеарифметическому значению температур на его наружной и внутренней поверхностях в одном сечении при нормальных условиях эксплуатации (для частей корпусов ядерных реакторов расчетная температура определяется с учетом внутренних тепловыделений как среднеинтегральное значение распределения температур по толщине стенки корпуса (ПНАЭ Г-7-002-86, п.2.2; ПНАЭ Г-7-008-89, прил.1).

• [1],п.5.1. Расчетную температуру используют для определения физико-механических характеристик материала и допускаемых напряжений, а также при расчете на прочность с учетом температурных воздействий.
• [1],п.5.2. Расчетную температуру определяют на основании теплотехнических расчетов или результатов испытаний, или опыта эксплуатации аналогичных сосудов.
• За расчетную температуру стенки сосуда или аппарата принимают наибольшую температуру стенки. При температуре ниже 20 °С за расчетную температуру при определении допускаемых напряжений принимают температуру 20 °С.
• [1],п.5.3. Если невозможно провести тепловые расчеты или измерения и если во время эксплуатации температура стенки повышается до температуры среды, соприкасающейся со стенкой, то за расчетную температуру следует принимать наибольшую температуру среды, но не ниже 20 °С.
• При обогреве открытым пламенем, отработанными газами или электронагревателями расчетную температуру принимают равной температуре среды, увеличенной на 20 °С при закрытом обогреве и на 50 °С при прямом обогреве, если нет более точных данных.
• [1],п.5.4. Если сосуд или аппарат эксплуатируются при нескольких различных режимах нагружения или разные элементы аппарата работают в разных условиях, для каждого режима можно определить свою расчетную температуру (ГОСТ-52857.1-2007, п.5).

Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .

Источник

Adblock
detector