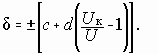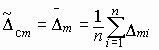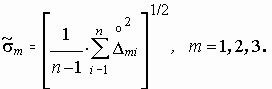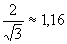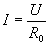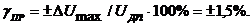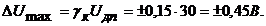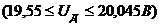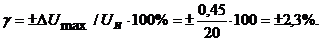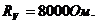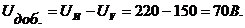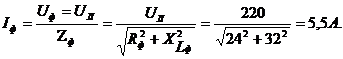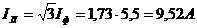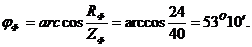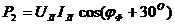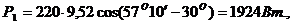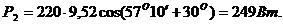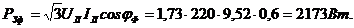Лабораторная работа № 1
ИССЛЕДОВАНИЕ ПОГРЕШНОСТЕЙ АНАЛОГОВОГО
ИЗМЕРИТЕЛЬНОГО ПРИБОРА
Цель работы
Изучить методику определения
основной погрешности измерительных
приборов на примере аналогового
вольтметра постоянного тока.
Получить навыки проведения
многократных измерений и обработки
полученных данных.
Используемые приборы
Комбинированный прибор
(тестер) типа Ц4360 или Ц4317 (исследуемый
вольтметр).
Вольтметр универсальный цифровой типа
В7-27А/1 или В7-16А (эталонный вольтметр).
Источник регулируемого постоянного
напряжения от 0 до 5В.
Лабораторное задание
1. Оценить систематическую
и случайную составляющие основной
погрешности и суммарную погрешность
аналогового вольтметра.
2. Сравнить суммарную
погрешность, полученную экспериментально,
с нормируемым значением основной
погрешности вольтметра данного типа.
3. Оценить вариацию показаний аналогового
вольтметра.
Подготовка к работе
(домашнее задание)
-
Изучить теоретический
материал, относящийся к данной работе,
по литературе [1, 2] и конспект лекций. -
Изучить описание данной
работы и заготовить в рабочей тетради
формы таблиц в соответствии с требованиями
к содержанию отчета, приведенному в
конце данного описания. -
Подготовить ответы на вопросы, которые
могут быть заданы при допуске к работе
и ее защите.
3.1. Дать определения:
-
абсолютной, относительной
и приведенной погрешностей, -
систематической и случайной
составляющих погрешности, -
доверительной вероятности
и доверительного интервала случайной
погрешности, -
основной и дополнительной погрешностей,
-
аддитивной и мультипликативной
погрешностей.
3.2. Как оценить систематическую
составляющую погрешности прибора?
3.3. Как оценить доверительный
интервал случайной погрешности
однократного измерения при заданной
доверительной вероятности и нормальном
законе распределения?
3.4. В каких случаях при
определении доверительного интервала
для случайной погрешности с нормальным
законом распределения следует использовать
распределение Стьюдента?
3.5. Как правильно представить результат
измерения?
3.6. Перечислить основные
нормируемые метрологические характеристики
средств измерений.
3.7. Каким образом нормируют
погрешности средств измерений?
3.8. Что такое класс точности
средств измерений? Какие существуют
способы задания класса точности?
3.9. Каким образом можно
оценить абсолютную погрешность результата
измерений, если известен класс точности
используемого прибора?
3.10. Что такое вариация
показаний аналогового прибора и как
можно ее оценить?
Используя техническое описание
исследуемых приборов [3], заполнить
табл.1.1.
Таблица 1.1
Основные метрологические
характеристики используемых вольтметров
(при измерении постоянного напряжения)
|
Характеристика |
Аналоговый вольтметр тип |
Цифровой вольтметр тип |
|
Верхние пределы измерения, используемые |
2,5 |
1; 10 |
|
Цена деления шкалы, В |
– |
|
|
Цена единицы младшего разряда используемых |
__ |
|
|
Нормируемая погрешность (указать, |
||
|
Класс точности |
||
|
Входное сопротивление, МОм |
Порядок выполнения работы и методические указания
1. Расчет областей значений основной погрешности вольтметров
1.1. Построить области
допускаемых основных абсолютных
погрешностей аналогового и цифрового
вольтметров (табл. 1.1) в диапазоне от 0
до 2,5 В. Пример построения показан на
рис. 1.1. Предел измерения исследуемого
вольтметра выбрать равным 2,5 В. Тогда
пределы измерения эталонного вольтметра
следует выбрать равными 1 или 10 В.
Указание.
Для простых
электроизмерительных приборов основную
погрешность обычно нормируют в форме
предельно допустимой
приведенной
погрешности – числом
, выраженным в %. Число
, записанное без указания %, определяет
класс точности такого вольтметра.
Область значений допускаемой основной
абсолютной погрешности
такого прибора можно определить с
помощью простой одночленной формулы:
,
(1.1)
здесь Uк
– значение установленного
предела измерения.
Видно, что эта погрешность не зависит
от значения измеряемого напряжения –
носит чисто аддитивный характер.
Основную погрешность более
сложных и точных цифровых вольтметров
обычно нормируют в форме предельно
допустимой относительной
погрешности, %, по
двучленной формуле вида:
(1.2)
Значения коэффициентов
c (%)
и d
(%), записанные через косую черту
(c/d),
определяют класс
точности цифрового вольтметра.
Область допускаемой основной
абсолютной
погрешности такого
вольтметра можно
вычислить по формуле:
,
U=[0,
Uк].
(1.3)
Эта погрешность растет с
увеличением измеряемого напряжения,
т.е. имеет, кроме аддитивной, еще и
мультипликативную составляющую.
Специфической особенностью
используемого в данной работе цифрового
вольтметра В7-27 является возможность
измерения напряжения до 1,999 В при
установке предела Uк
= 1 В и напряжение до 19,9 В при установке
предела Uк
=10 В. Изготовитель
гарантирует, что при измерении напряжений
U >Uк
относительная
погрешность будет находиться в
соответствии с (1.2) в пределах ±с
(%).
Поскольку абсолютная
погрешность эталонного прибора должна
быть, по крайней мере, в 3 раза меньше
погрешности исследуемого прибора, не
следует без необходимости использовать
в цифровом вольтметре В7-27 предел 10 В.
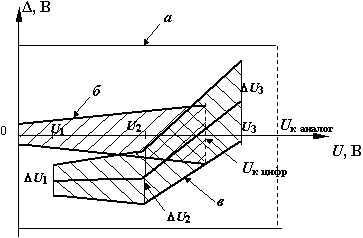
Рис.1.1. Области значений абсолютной
погрешности:
а –
нормируемая для аналогового прибора,
б –
нормируемая для цифрового прибора,
в –
полученная экспериментально для
аналогового прибора по п.3
D Um
, m
= 1, 2, 3
(1.9)
Примечание.
Фирмы-изготовители вольтметров могут
использовать и другие формулы для
нормирования предельных погрешностей
выпускаемых приборов.
1.2. Сравнить значения
абсолютных погрешностей аналогового
и цифрового вольтметров в диапазоне от
0 до 2,5 В, сделать вывод о возможности
использования цифрового вольтметра в
качестве эталонного на пределах 1 и 10
В.
2. Оценка систематической и случайной составляющих основной погрешности исследуемого вольтметра
Исследование провести для
трех точек установленного на исследуемом
вольтметре диапазона измерения 2,5В –
для трех значений напряжения: U1=(0,3-0,7)В
– в начале шкалы, U2
= (0,8-1,5)В – в середине
и U3=(1,5-1,9)
В – в конце.
2.1. Ознакомиться с кратким
описанием и органами управления
вольтметров и источника постоянного
напряжения. Включить питание источника
постоянного напряжения и цифрового
вольтметра. Проверить установку нуля
аналогового и цифрового вольтметров.
2.2. Собрать схему измерения согласно
рис. 1.2.
2.3.Установить требуемые
пределы измерения Uк
на обоих вольтметрах.
Рис. 1.2. Схема для исследования
погрешностей вольтметра
2.4. Выбрать отметку на шкале
исследуемого вольтметра, соответствующую
выбранному значению напряжения U1
. Регулируя напряжение
источника, установить показание, равное
U1,
измерить действительное значение
напряжения источника по показаниям
эталонного вольтметра U1i
и записать в табл. 1.2
(столбец 2). Всего выполнить n
измерений действительных значений
напряжения U1i
, i=1,…,n
(8
n
16), каждый раз заново
устанавливая показания исследуемого
вольтметра на выбранную отметку шкалы.
2.5. Повторить измерения п.
2.4 для выбранных значений U2
и U3
. Измеренные
действительные значения U2i
и U3i
, i =1,…,n
записать в 6 и 10-й столбцы табл. 1.2
соответственно.
2.6. Вычислить для каждого
значения напряжения U1,
U2,
U3
следующие величины.
2.6.1. Абсолютную погрешность
каждого однократного измерения
mi
= Um
–
Umi,
m =
1, 2, 3, i =
1, …, n
(1.4)
и записать их значения в 3,
7 и 11-й столбцы, внизу каждого столбца
поместить алгебраическую сумму
.
2.6.2. Оценку систематической
составляющей погрешности
,
вычислив ее значение как среднее значение
погрешности
m:
.
(1.5)
2.6.3. Случайные составляющие погрешности
каждого измерения:
(1.6)
и записать их значения в 4, 8 и 12-й столбцы.
2.6.4. Оценки среднего
квадратического отклонения случайной
составляющей погрешности (среднюю
квадратическую погрешность) однократного
измерения для трех выбранных точек
шкалы исследуемого вольтметра:
(1.7)
Для этого найти квадраты
случайных составляющих
,
i=1,…,n
и полученные числа занести в 5, 9 и 13-й
столбцы, а внизу каждого из них поместить
суммы этих квадратов
,
m=1,
2, 3. Найденные значения оценок
,
и
также
поместить в табл. 1.2.
Таблица 1.2
Результаты измерений и
расчета составляющих основной погрешности
исследуемого вольтметра
|
i |
U1 |
U2 |
U3 |
|||||||||
|
Ui |
i |
|
|
Ui |
i |
Ui |
i |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
||||||||||||
|
2 |
||||||||||||
|
· |
||||||||||||
|
· |
||||||||||||
|
· |
||||||||||||
|
i |
||||||||||||
|
· |
||||||||||||
|
· |
||||||||||||
|
n |
||||||||||||
|
= |
= |
= |
= |
= |
= |
|||||||
|
|
|
|
||||||||||
|
|
= |
|
||||||||||
|
Рдов= |
||||||||||||
|
дов1= |
дов2= |
дов3= |
2.6.5. Доверительные интервалы
случайной погрешности однократного
измерения в предположении, что закон
распределения этой случайной погрешности
– нормальный:
(1.8)
где t
– коэффициент Стьюдента, значение
которого зависит от заданного значения
доверительной вероятности Рдов
и числа проведенных измерений n.
Значения t
взять из таблицы распределения Стьюдента
(прил. 1). При обработке результатов
простых технических измерений
доверительную вероятность обычно
выбирают в пределах от 0,8 до 0,9.
Указание.
Английский исследователь Госсет
(опубликовавший свою знаменитую работу
под псевдонимом Стьюдент) в 1908 г. показал,
что если оценка среднеквадратического
отклонения получена по небольшому числу
измерений (n
17), то доверительный интервал для
случайной величины с нормальным законом
распределения следует рассчитывать с
использованием распределения, которое
впоследствии получило его имя –
распределение Стьюдента. При увеличении
числа измерений, распределение Стьюдента
сходится к нормальному распределению.
Поэтому, если число измерений велико,
при оценке доверительного интервала
можно использовать таблицы интеграла
вероятности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
6
-
ЗАДАНИЕ
Выбрать цифровой вольтметр для измерения напряжения постоянного тока (рис. 1) с учётом Rнг и условий измерения.
-
ИСХОДНЫЕ ДАННЫЕ
Вариант 87
Показания вольтметра 0,92 В
Вариация напряжения в сети питания +10%
Допускаемая погрешность измерения 2,5 %
Сила тока в цепи 2,87 мА
Температура окружающей среды +35 С.
-
РАСЧЁТ РЕЗУЛЬТИРУЮЩЕЙ ПОГРЕШНОСТИ
Прежде всего определим Rнг
Rнг = Ux /I = 0,92/2,87 = 320,5 ОМ
Так как это значение на несколько порядков меньше входных сопротивлений цифровых вольтметров, то осуществляем предварительный выбор прибора по значению осн .
П
ри измерении 0,92 В на вольтметре В7-16, предел измерения устанавливается 1 В. Для времени преобразования 20 мс, предел допускаемой основной погрешности будет равен
А
для времени преобразования 2 мс получим, что
Эти значения гораздо меньше доп = 2,5 %, поэтому не будем затруднять себя рассчитывать остальные погрешности измерения для этого прибора.
Практически такое же несущественное число получится при анализе характеристик вольтметра Ф203.
осн = 0, 208 %
В случае использования прибора В7-22 предел измерений установим равным 2 В.
Вольтметр Щ4313. Установив диапазон измерений 0,5 – 5В, получим, что
Полученное значение основной погрешности очень близко к допустимому значению (2,5 2,72), но в результате дальнейшего расчёта не выполняется условие (Р) доп. Поэтому этот вольтметр тоже не подходит.
Тогда попробуем другой наиболее близкий вольтметр – В7-22.
Определим дополнительную погрешность прибора, вызванную вариацией напряжения питания. Анализируя технические характеристики прибора приходим к выводу, что заданная вариация напряжения питания +10В является допускаемым верхним пределом (+22В) нормального значения напряжения в сети питания вольтметра. Таким образом
пит = 0
Следующим шагом будет определение дополнительной погрешности прибора, вызванной повышенной (+35С) рабочей температурой. Обратившись к техническим характеристикам данного вольтметра узнаём, что дополнительная погрешность прибора, вызванная отклонением температуры от нормальной (202С) до крайних значений рабочих температур (от -10 до +40С), не превышает половины предела допускаемой основной погрешности на каждые 10С изменения температуры.
Исходя из вышесказанного получим:
т = 0,5 осн + 0,25*осн = 0,75осн
т = 0, 435 %
Определим погрешность из-за несоответствия свойств обьекта и прибора по формуле
У
читывая, что при данном диапазоне входное сопротивление составляет 100 МОм получим, что
Поправка для этой ситематической погрешности
= 0,0000029
Исправленное значение показаний вольтметра
Uv = 0,92 + 0,0000029 = 0,9200029
Приближённо погрешность определения поправки равна погрешности определения Rнг . Так как значения I, Rнг, являются маленькими, то погрешность определения поправки является величиной второго порядка малости и ею можно пренебречь.
И
только теперь, выбрав доверительную вероятность Р = 0,95; к = 1,1 и учитывая
Получим, что
Условие (Р) доп выполняется ( 0,79 < 2,5).
Абсолютная форма представления погрешности
(Р) = 0,79*0,9200029*10-2 = 0,0072 = 0, 007 В, Р = 0,95
Результат измерения напряжения с помощью выбранного вольтметра В7-22 может быть представлен так:
U = 0,92 0,007 В; Р = 0,95; ТРЕУГ.
Для рассматриваемого диапазона измерения (0-2 В) выбранного вольтметра на рис. 2.1 и рис. 2.2 представлены графики изменения пределов основной погрешности прибора и результирующей погрешности измерения (для заданных условий) соответственно при относительной (рис. 2.1) и абсолютной форме (рис. 2.2) представления погрешностей
Из анализа графиков следует, что измеряемое значение Ux попадает в первую половину диапазона с заниженной точностью. Поэтому данный случай использования вольтметра В7-22 следует отнести к нерекомендуемым.
Исходя из экономических соображений можно предположить использовать вольтметр более грубого класса точности, чем В7-22, но удовлетворяющий заданным условиям измерения за счёт благоприятного сочетания Ux и Uпр . В этом случае измерение 0,92 В должно осуществлятся в пределе от 0 до 1,5 В. При расчёте предела допускаемой основной погрешности этого прибора предполагаем для него такое же значение осн в рабочей точке диапазона, какое было получено у нас выше (0,58 %).
Э
то значение определяем по следующей формуле:
Д
ля верхнего предела диапазона предположим
Из совместного решения вышеприведенных выражений получим d = 0,1 и c = 0,4.
Значит, для предлагаемого вольтметра получим:
При использовании этого вольтметра для Ux = 0,92 В при Uпр = 1,5 В получим осн = 0,57, что практически не отличается от значения, рассчитанного нами выше. Следовательно, дальнейшие расчёты можно не проводить.
Проведенный расчет предела основной допускаемой погрешности предлагаемого вольтметра иллюстрируется графиками, представленными на рис. 2.3, где а – пределы осн для В7-22, а b – пределы осн для предлагаемого вольтметра.
В
соответствии с требованием стандартов формула основной погрешности, получившаяся выше, должна быть преобразована следующим образом:
В итоге для предполагаемого вольтметра получим класс точности
0,5/0,1.
Проведя аналогичные преобразования формулы осн вольтметра В7-22, для него получим класс точности 0,35/0,2. Исходя из экономической целесообразности (при прочих равных условиях) на производстве предпочтительнее использовать менее точный прибор класса 0,5/0,1.
Погрешности измерений
Общие сведения об измерениях. Погрешности измерений и средств измерений
Общие сведения об измерениях
Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.
Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.
Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.
Погрешности измерений
Погрешность является одной из основных характеристик средств измерений.
Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.
Абсолютная погрешность Δa прибора есть разность между показанием прибора ах и истинным значением а измеряемой величины, т.е.
Абсолютная погрешность, взятая с обратным знаком, называется поправкой.
Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна
Приведенная погрешность γП есть выраженное в процентах отношение абсолютной погрешности Δa к нормирующему значению апр
Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).
Погрешности средств измерений
Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.
Класс точности прибора (например, амперметра) дается выражением
При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.
По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:
В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:
(α = 1) 10; 15; 20; 25; 40; 50; 60.
Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.
Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.
Примеры решения задач
Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.
- Класс точности указывают просто числом предпочтительного рода, например, 0,5. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.
Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)
постоянна и равна классу точности прибора.
Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)
уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.
Абсолютная погрешность однократного измерения
постоянна на всех отметках рабочей части шкалы прибора.
По условию задачи: Uизм = Ui = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; Uпр = 30 В – предел шкалы вольтметра.
Наибольшая абсолютная погрешность вольтметра
Источник
Как определить абсолютную погрешность измерения напряжения вольтметром
Метод и средства для измерения напряжения и тока.
При измерении напряжения и тока используют прямые и косвенные способы. Прямые измерения основаны на сравнении измеряемой величина с мерой этой величины или на непосредственной оценке измеряемой величины по отчетному устройству измерительного прибора. Косвенные измерения основаны на прямых измерениях другой величины, функционально связанной с измеряемой величиной. Например, косвенное измерение тока выполняют при помощи вольтметра, измеряющего напряжение на известном сопротивлении R0, и расчете тока по формуле
Погрешность косвенного метода измерения зависит от погрешности прямого измерения и погрешности расчета по функциональной зависимости (23). Сопротивление, используемое при косвенном измерении тока, называют шунтом. Дополнительная погрешность при косвенных измерениях обусловлена перераспределением тока между шунтом и вольтметром при изменении температуры окружающей среды. Для снижения температурной погрешности применяют специальные схемы компенсации,
В зависимости от рода тока приборы делят на четыре группы;
1) вольтметры постоянного напряжения (группа В2),
2) вольтметры переменного напряжения (группа ВЗ),
3) вольтметры импульсного напряжения (группа В4),
4) вольтметры селективные (группа В6).
Универсальные приборы, предназначенные для измерения постоянного и импульсного напряжения и тока, выделены в группу В7.
Программа работы
1. Определение основной погрешности, вариация показаний и поправку вольтметра.
2. Определение чувствительности и цены деления вольтметра.
3. Определение входного сопротивления вольтметра.
4. Определение частотного диапазона вольтметра.
5. Исследование влияния формы напряжения на показание вольтметра.
6. Определение погрешности при прямых и косвенных измерениях тока.
Порядок выполнения работы.
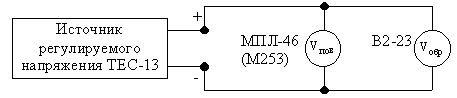
1. Определение основной погрешности, вариация показаний и поправки вольтметра выполняют по схеме, изображенной на рис. 1. В качестве поверяемого прибора используют вольтметр типа МПЛ-46, а образцовый служит цифровой вольтметр типа В2-23. Перед проведением измерений прибор В2-23 включить в сеть и выждать 10…15 мин. Затем произвести установку нуля и калибровку вольтметра И2-23 в соответствии с инструкцией по пользованию прибором. Кроме того, необходимо выполнить установку нуля вольтметра МПЛ-46, пользуясь корректором.
Для выполнения п.1 программы поверяемый вольтметр МПЛ-46 устанавливают на диапазон 15 В и измеряют напряжение на всех оцифрованных делениях шкалы, изменяя входное напряжение регулируемого источника ТЕС-13. Измерение напряжения на каждом оцифрованном делении шкалы МПЛ-46 производят дважды: один раз при возрастании напряжения (показание образцового вольтметра U’обр), а второй раз при убывание напряжения (показание образцового вольтметра U’’обр). При этом на образцовом вольтметре В2-23 необходимо выбрать поддиапазон, обеспечивающий не менее трех значащих цифр. Результаты измерений занести в ф.1.
Действительные значения на оцифрованных делениях шкалы поверяемого вольтметра определяют как среднее значение двух измерений Uср=(U’обр+U’’обр)/2.
Расчет погрешности измерений выполняют по формулам:
Абсолютная погрешность 
Относительная погрешность 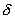

Приведенная погрешность 

где Uном=15 В – номинальное значение напряжения поверяемого.
Вариацию показаний вольтметра определяют по формулам:
Абсолютное значение вариации 
Приведенное значение вариации 

Поправку вольтметра вычисляют по формуле П=-
Из полученных значений 



Источник
Оценка абсолютной погрешности прямых измерений
Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность.
Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок.
Все остальные погрешности являются случайными.
Промахи — грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.
Приборные погрешности определяются двумя факторами:
1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия.
Абсолютная погрешность через класс точности оценивается следующим образом:
(Dx) к.т.= (g/100)A,
где g — класс точности в %, указанный на панели прибора,
А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;
2. ценой делений шкалы прибора:
(Dx) ц.д.= 
где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения.
Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда , который предписывает следующий образ действий, если физическая величина х измерена n раз:
1) имея х1 , …,хn – значений измеряемой величины х, выбираем из 
.gif)
2) находим абсолютную погрешность Dxр = 
3) Записываем результат в виде: 


Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.)
Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:
1) Вы измерили и получили несколько i = 1. m значений случайной
величины 
результаты.
2) По оставшимся n значениям определяем среднее значение величины 
.gif)
3) Определяем среднеквадратичную погрешность среднего значения 

i
4) Задаемся доверительной вероятностью a. По таблице коэффициентов
Стьюдента (Приложение 1) определяем по известному значению
числа измерений n и доверительной вероятности a коэффициент
Стьюдента tan.
5) Определяем погрешность среднего значения величины 

D
6) Записываем результат 


В научных статьях обычно приводят доверительный интервал
D 
соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора.
Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым.
В теории ошибок показывается, что результирующая погрешность 
Источник
Систематические погрешности (ошибки) обычно остаются постоянными на протяжении всей серии измерений. Например, при переключении шкалы вольтметра с одного предела на другой меняется его внутреннее сопротивление, что может внести в последующие измерения систематическую погрешность.
Систематические погрешности надо стараться отслеживать и учитывать, корректируя полученные результаты, т.е. исправляя их на необходимую величину. Однако обнаружение систематических погрешностей требует, как правило, дополнительных более точных или альтернативных экспериментов, проведение которых невозможно в рамках лабораторных работ. В этих случаях достаточно указать возможный источник ошибок.
Все остальные погрешности являются случайными.
Промахи – грубые ошибки, обычно они связаны с неправильным отсчетом по шкале прибора, нарушением условий эксперимента и т.д. Их надо отбросить. В сомнительных случаях вопрос о том, является ли данный результат промахом, решают с помощью повторного, если возможно, более точного эксперимента или привлекая математические методы обработки полученных результатов, изучение которых лежит за рамками излагаемого элементарного анализа оценки погрешностей.
Приборные погрешности определяются двумя факторами:
1. классом точности прибора, связанным с его устройством – элементной базой и принципом действия.
Абсолютная погрешность через класс точности оценивается следующим образом:
(Dx) к.т.= (g/100)A,
где g – класс точности в %, указанный на панели прибора,
А= Аmax – предел измерения для стрелочных приборов, либо А есть текущее значение для магазинов сопротивления, индуктивности, емкости;
2. ценой делений шкалы прибора:
(Dx) ц.д.= h,
где h – цена деления шкалы прибора, т.е. расстояние между ближайшими штрихами шкалы, выраженное в соответствующих единицах измерения.
Погрешности разброса возникают вследствие различия экспериментальных значений при многократном повторении измерений одной и той же величины. Простейший способ определения (Dх)р дает метод Корнфельда, который предписывает следующий образ действий, если физическая величина х измерена n раз:
1) имея х1 , …,хn – значений измеряемой величины х, выбираем из хmax и хmin и находим среднее значение х:
;
2) находим абсолютную погрешность Dxр =
3) Записываем результат в виде: с
, где a – доверительная вероятность того, что истинное значение измеренной величины находится на отрезке
.
Доверительная вероятность определяет собой долю средних значений х, полученных в аналогичных сериях измерений, попадающих в доверительный интервал. (Эта формула доказывается в теории ошибок.)
Недостатком метода Корнфельда является то обстоятельство, что вероятность приводимого результата определяется исключительно количеством n проведенных измерений и не может быть изменена посредством увеличения или уменьшения доверительного интервала ± Dх. Такую возможность предусматривает несколько более сложный метод расчета погрешностей Стьюдента [2,3,7]. Последовательность расчета погрешностей этим методом такова:
1) Вы измерили и получили несколько i = 1,…,m значений случайной
величины i. Сначала исключаем промахи, то есть заведомо неверные
результаты.
2) По оставшимся n значениям определяем среднее значение величины :
.gif)
3) Определяем среднеквадратичную погрешность среднего значения :

i
4) Задаемся доверительной вероятностью a. По таблице коэффициентов
Стьюдента (Приложение 1) определяем по известному значению
числа измерений n и доверительной вероятности a коэффициент
Стьюдента tan.
5) Определяем погрешность среднего значения величины (доверительный интервал)
D= tan s<X>
6) Записываем результат
= (
± D
) с указанием доверительной вероятности a.
В научных статьях обычно приводят доверительный интервал
D = s<X>,
соответствующий доверительной вероятности α =0,7. Такой интервал называется стандартным, при его использовании часто значение доверительной погрешности не приводят. Использование метода Стьюдента является необходимым, когда требуется знать значение физических параметров с заданной доверительной вероятностью (как в ряде лабораторных работ). На практике доверительная вероятность погрешности разброса выбирается в соответствии с доверительной вероятностью, соответствующей классу точности измерительного прибора.
Для большинства исследований, в которых не выдвигается жестких требований к вероятности полученных результатов, метод Корнфельда является вполне приемлемым.
В теории ошибок показывается, что результирующая погрешность , если все эти погрешности рассчитаны для одной и той же доверительной вероятности. На практике, т.к. суммарная погрешность округляется до одной значащей цифры, достаточно выбрать максимальную из трех вычисленных погрешностей, и если она в 3 или более раз превосходит остальные, принять ее за погрешность измеренной величины, при этом фактор, с которым связана эта погрешность и будет в данном случае определять собой точность (а вернее – погрешность) эксперимента (подробнее см. в работе [1]).
Электроизмерительные приборы подразделяются на восемь классов точности:0,05; 0,1; 0,2; 0,5; 1,5; 2,5; 4,0, указываемых на шкалах. Классы точности приборов определяют по приведенной погрешности.
Задача 1. Определить абсолютную и относительную погрешность измерения, а также поправку к показанию вольтметра типа Э-378 с диапазоном измерения 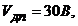
если он показал 20В.
Решение. Наибольшая абсолютная погрешность вольтметра в соответствии с классом точности
Откуда
Действительное значение измеряемой величины
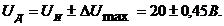
Относительная погрешность измерения
В общем виде относительная погрешность измерения имеет вид
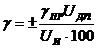
.
Задача 2. Определить добавочное сопротивление вольтметра (рис. 32) с пределом измерения 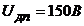
если сопротивление вольтметра
Решение.
Рис. 32
Падение напряжения на добавочном сопротивлении
Добавочное сопротивление
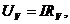
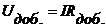
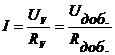
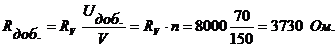
где — коэффициент добавочного сопротивления.
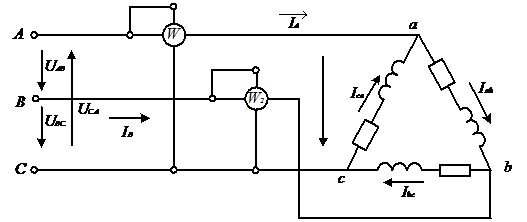
Задача 3. В сеть 3-х фазного тока с линейным напряжением 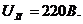
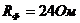
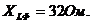
и
и трехфазную активную мощность.
Решение.
Рис.33
Из схемы включения ваттметров, представляющих собой приборы электродинамической системы, имеем
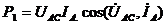
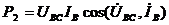
При симметричной нагрузке и сети 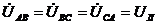
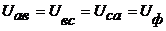
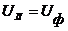
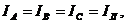
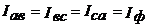
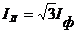
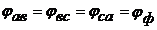
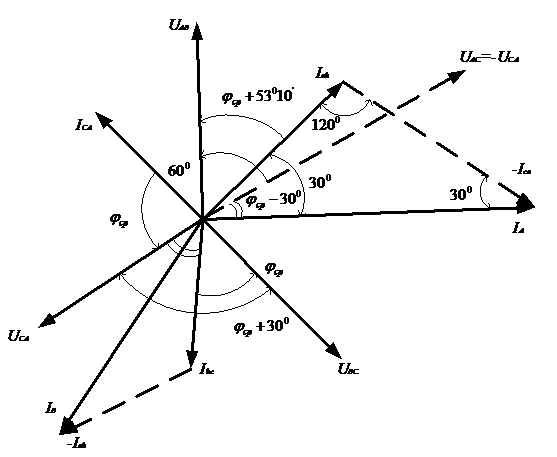
Строим векторную диаграмму (рис. 34), учитывая что
Рис. 34
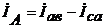
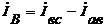
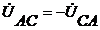
и
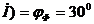
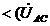
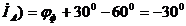
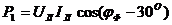
Трехфазная активная мощность
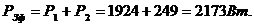
Задача 4. Для определения параметров катушки использован метод амперметра, вольтметра и ваттметра (Рис. 35). Приборы показали: амперметр