Пример расчета допустимой растягивающей силы по условию прочности при продольном нагружении.
Задача
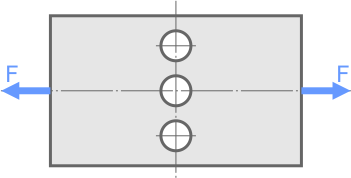
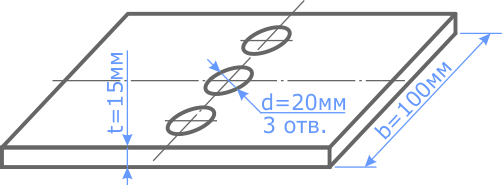
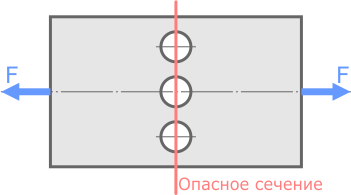
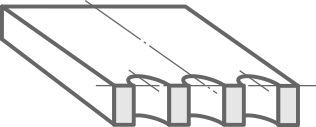
Рассчитать величину допустимой растягивающей внешней силы [F] приложенной к симметричной стальной пластине ослабленной тремя отверстиями.
Другие примеры решений >
Помощь с решением задач >
Размеры пластины: ширина b=100мм, толщина t=15мм. Диаметр отверстий d=20мм.
Принять допустимые напряжения для стали [σ]=120МПа.
Пример решения
Допустимой считается величина растягивающей силы, превышение которой приводит к нарушению прочности элемента.
Поэтому для решения задачи воспользуемся условием прочности при растяжении-сжатии:
где σ — напряжения в элементе которые не должны превышать допустимых значений [σ],
N – внутренняя продольная сила,
А – площадь поперечного сечения элемента,
Запишем данное условие прочности относительно силового фактора
Заданная пластина имеет всего один силовой участок, поэтому внутренняя сила во всех ее сечениях будет одинакова и равна внешней силе F (N=F).
Следовательно, можно записать
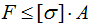
или
Прежде чем подставлять значения проанализируем заданную пластину.
По условию пластина ослаблена тремя отверстиями, поэтому очевидно, что наименее прочным будет поперечное сечение, проходящее через центры отверстий, где площадь минимальна.
Рассчитаем минимальную площадь поперечного сечения пластины
Теперь есть все данные для расчета допустимой силы:
Для того чтобы пластина оставалась прочной растягивающая сила должна быть не больше 72кН.
Превышение этого значения приведет к тому, что нормальные напряжения в опасном сечении превысят допустимые значения.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Учитывая, что
,
а
,
условие устойчивости,
получим в виде:
.
(14.26)
Если
стержень сжат одной силой
,
то в этом случае продольная силаи выражение (14.26) приобретает вид:
.
(14.27)
Местные
ослабления практически не изменяют
величину критической силы. Поэтому в
формулах (14.26), (14.27) вводится полная
площадь поперечного сечения.
Условие устойчивости
(14.27) решает три задачи:
-
Проверочный расчет
сжатых стержней. -
Подбор величины
сжимающей нагрузки. -
Проектировочный
расчет.
Рассмотрим порядок решения каждой из
этих задач.
Задача 1:
1. Так как условия закрепления концов
стержня, длина стержня, форма поперечного
сечения и его размеры известны, находим
минимальный осевой момент инерции
,
площадь,
вычисляем минимальный радиус инерции
сеченияи гибкость стержня
.
2. По таблице 14.2 определяем коэффициент
продольного изгиба
и вычисляем напряжение в стержне по
формуле:
.
3. Сравниваем полученное напряжение с
допускаемым напряжением:
.
Задача 2:
1. Выполняем пункт 1, изложенный в
предыдущей задаче.
2. По таблице 14.2 находим коэффициент
продольного изгиба
и определяем допускаемое значение силы
по
формуле:
.
Задача 3:
1. При решении этой задачи используем
метод последовательных приближений
(метод итераций) путем варьирования
величиной коэффициента продольного
изгиба
.
Так как в расчетной формуле на устойчивостьимеются две неизвестные величиныкоэффициент
и искомая площадь поперечного сечения
,
принимаем в первой попытке значение
для коэффициента продольного изгиба.
2. Определяем площадь поперечного сечения
,
находим размеры поперечного сечения,
минимальный осевой момент инерции и
минимальный радиус инерции.
3. Определяем гибкость стержня
,
и по таблице 14.2 находим коэффициент
продольного изгиба.
Еслизначительно
отличается от,
то и напряжение в стержне будет существенно
отличаться от допускаемого. В этом
случае повторяем расчет: вычисляем
среднее значениеи обращаемся к пункту 2. Если требуется
третья попытка, то определяеми т.д. Обычно при подборе сечений требуется
не более двух-трех попыток.
Рассмотрим несколько примеров определения
величины критической силы для сжатого
стержня и расчета сжатых стержней на
устойчивость.
Пример 14.1. Определить наименьшую
гибкость стержня, при которой для
вычисления критического усилия еще
применима формула Эйлера, если стержень
выполнен из стали с пределом
пропорциональностиМПа
и модулем упругостиМПа.
Решение:
1. Формула Эйлера применима,
если критические напряжения, действующие
в стержне, не превышают предела
пропорциональности:
.
Отсюда предельная величина гибкости,
при которой применима формула Эйлера,
равна:
.
Пример 14.2.Какой из двух стержней
одинаковой длины, условия закрепления
и нагружения которых также одинаковы,
является более гибким – стержень
квадратного или круглого сечения с
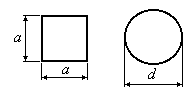
равной площадью (Рис.14.6)?
Решение:
1. По условию задачи площади поперечных
сечений стержня, приведенные на рис.14.6,
одинаковы:
или
.
Откуда.
Рис.14.6
2. Отношение гибкостей двух стержней с
одинаковыми условиями закрепления
концов и одинаковой длины обратно
пропорционально отношению минимальных
радиусов инерции их поперечных сечений
или при одинаковой площади поперечных
сечений обратно пропорционально корню
квадратному из отношения минимальных
моментов инерции сечений:
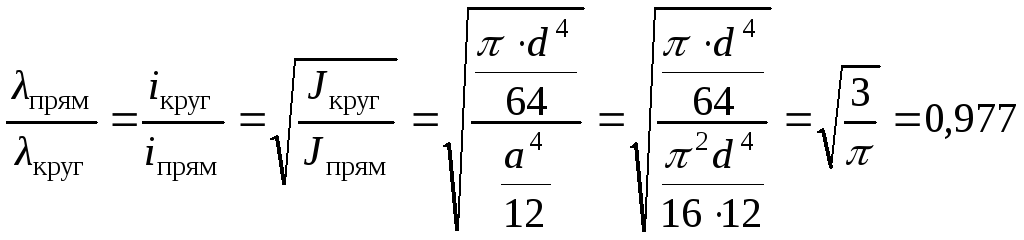
3. Таким образом, гибкость стержня с
прямоугольным сечением составляет:
или
гибкость стержня с прямоугольным
сечением составляет 97,7% от гибкости
стержня с круглым сечением. Иными
словами, гибкость стержня с круглым
сечением оказалась на 2,3% больше.
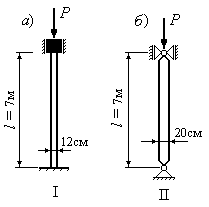
Пример.14.3.
Определить величину критического
усилия и критическое напряжение для
стойки прямоугольного поперечного
сечения 1220см2длиной 7м из дерева с модулем упругости
МПа.
В плоскости наименьшей жесткости оба
конца стойки защемлены (положение 1), а
в перпендикулярном положении (положение
2) – оба конца стойки шарнирно оперты
(Рис.14.7).
Решение
1. Определим величину критической силы
для первого положения стержня (Рис.14.7,а):
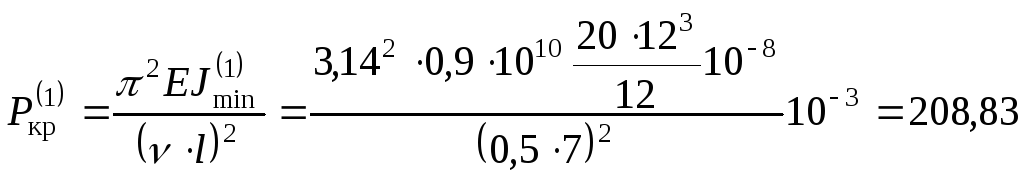
Рис.14.7
2. Определим величину критической силы
для второго положения стержня (Рис.14.7,б):
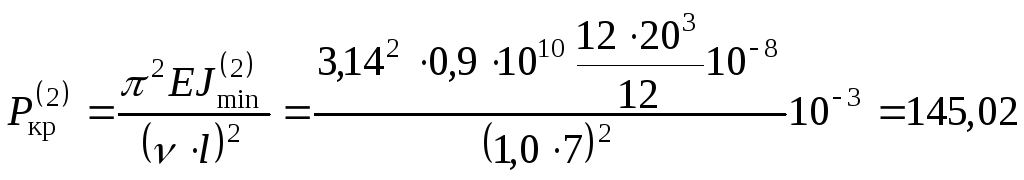
3. Из двух значений критической силы
принимаем меньшее:
кН.
Определяем критическое напряжение:
МПа.
4. Определим правомерность применения
формулы Эйлера для решения этой задачи.
Для этого определим предельное значения
гибкости для дерева, если предел
пропорциональности для дерева
МПа.
.
Гибкость стержня для первого положения
стержня равна:
.
Гибкость стержня для второго положения
стержня равна:
.
Здесь:

Таким образом, гибкость стержня для
обоих его положений оказалась выше
предельной для дерева и, следовательно,
применение формулы Эйлера для определения
критической силы было оправданным.
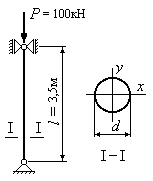
Пример 14.4.Произвести проверку
устойчивости сжатой деревянной колонны
(Рис.14.8) круглого поперечного сечения
диаметромсм
длинойм,
если основное допускаемое напряжениеМПа,
а сжимающая силакН.
Рис.14.8
Решение:
1. Определяем площадь поперечного
сечения:
см2.
2. Определяем радиус инерции сечения:
см.
-
Определяем
гибкость стержня:
.
-
По
таблице 14.2 находим с помощью линейной
интерполяции:
.
-
Определяем
величину допускаемого напряжения
устойчивости:
МПа.
-
Вычисляем
нормальные ноапряжения в сечении от
сжатия:
МПа.
8. Сравнивая
с
,
получаем:МПа
<
МПа.
Значит, устойчивость колонны обеспечена.
Пример 14.5.Для предыдущей задачи
найти величину критической силы,
доускаемое значение нагрузки и величину
коэффициента запаса устойчивости, если
для дерева модуль упругостиМПа,
предел пропорциональностиМПа.
Решение:
-
Определяем
предельную гибкость для дерева:
.
2. Определяем величину критической силы.
Гибкость стержня в предыдущем примере
составила
.
Следовательно, для определения критической
силы можно применять формулу Эйлера:
кН.
3. Находим допускаемое значение для
сжимающей силы. Значение для коэффициента
продольного изгиба берем из предыдущего
примера
:
кН.
4. Определяем коэффициент запаса
устойчивости:
.
Пример 14.6.Как изменятся величины
критической и допускаемой силы и
коэффициент запаса устойчивости, если
длину стержня уменьшить вдвое. Для
решения задачи взять данные из примера
14.5.
Решение:
1. Если длину стержня уменьшить вдвое
до
м,
сохранив при этом условия закрепления
концов стержня, гибкость стержня также
уменьшится в два раза:
.
Это значение гибкости меньше предельного,
равного
.
Следовательно, формулу Эйлера для
определения критической силы использовать
нельзя, а следует использовать для этой
цели формулу Ясинского.
-
Определяем
величину коэффициента продольного
изгиба:
.
3. Из таблицы 14.1 берем значения эмпирических
коэффициентов для дерева
МПа,
МПа
и вычисляем величину критической силы:
кН.
-
Определяем
допускаемое значение сжимающей силы:
кН.
-
Находим
коэффициент запаса устойчивости:
.
Таким образом, с уменьшением длины
стержня вдое значения для критической
и допускаемой силы увеличились,
коэффициент запаса устойчивости стал
меньше.
Пример 14.7. Подобрать из сортамента
прокатной стали двутавр для стержня
длиной 4м, сжатого центрально приложенной
силойкН.
Оба конца стержня защемлены. Материал
– Ст.3. Основное допускаемое напряжениеМПа.
Решение:
-
Принимаем
и находим площадь поперечного сечения:
см2.
Из сортамента прокатной стали выбираем
двутавр №22а с площадью
см2и минимальным радиусом инерции
см.
Находим гибкость стержня:
.
Из таблицы 14.2 определяем коэффициент
продольного изгиба:
.
Так как междуи
имеется значительная разница, переходим
ко второ й попытке.
2. Принимаем
и находим площадь поперечного сеченния
двутавра:
см2.
Из сортамента прокатной стали выбираем
двутавр №18а с площадью
см2и минимальным радиусом инерции
см.
Находим гибкость стержня:
.
Определяем коэффициент продольного
изгиба, используя данные таблицы 14.2:
.
Поскольку разница между
и
не очень большая, найдем напряжения,
возникающие в стержне:
МПа.
Стержень недогружен. Определяем
относительную величину недогруза:
.
Обычно относительная величина недогруза
или перегруза должна составлять порядка
3% по абсолютной величине. Поэтому
переходим к третьей попытке.
3. Принимаем
и находим площадь поперечного сеченния
двутавра:
см2.
В сортаменте прокатной стали имеется
двутавр №18 с площадью
см2и минимальным радиусом инерции
см.
Площадь этого двутавра меньше требуемой.
Проверим его. Находим гибкость стержня:
.
Определяем коэффициент продольного
изгиба:
.
Находим напряжение в стержне:
МПа.
Стержень оказался перегруженным.
Относительная величина перенапряжения
составляет:
.
Такое перенапряжение недопустимо.
Поэтому окончательно принимаем для
сечения стержня двутавр №18а.
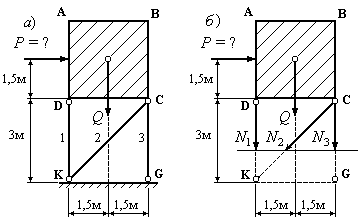
Пример 14.8. Водонапорный бак АВСD
весом
кН
поддерживается стержнями DK, CK, CGи
испытывает действие ветровой нагрузки(Рис.14.9,а).
В узлахC, D, K, Gкрепления
стержней шарнирные. Поперечные сечения
всех стержней одинаковы. При каком
наименьшем значении ветровой нагрузкистержень №1 не следует проверять на
устойчивость?
Рис.14.9
Решение:
1. Будем исходить из того, что
проверять стержень №1 на устойчивость
не следует, если этот стержень будет
либо растянут, либо не нагружен вообще.
Наименьшее значение силы
,
при котором стержень №1 не следует
проверять на устойчивость, будет таким,
при котором усилие в стержне №1 будет
равно нулю. Во всех остальных случаях
при большем значении силыстержень №1 будет растянут.
2. Рассечем стержни №1, №2, №3 горизонтальным
сечением (Рис.14.9,б) и рассмотрим равновесие
верхней части конструкции. Для нахождения
усилий в стержнях применим метод
моментных точек. Выберем в качестве
моментной точки для стержня №1 точку С
и составим относительно нее сумму
моментов сил, действующих на верхнюю
часть конструкции. Получим:
.
Принимая
,
из уравнения равновесия находимкН.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для стержневой системы, показанной на рис. 1, из условий прочности и жесткости определить допускаемое значение силы P. Расчетное сопротивление материала стержней R=200Мпа, модуль упругости E=210000Мпа, допускаемое удлинение каждого из стержней [Δ]=2мм, площадь сечения стержня AB  , стержня АС
, стержня АС  .
.
Решение.
Рассмотрим равновесие узла А. На него действует плоская сходящаяся система сил, для которой можно записать два уравнения равновесия
Из первого уравнения выразим и подставим во второе уравнение
и подставим во второе уравнение
Отсюда выразим усилия в стержнях системы через силу P
Оба стержня растянуты. Запишем условия прочности и жесткости для стержня АВ
Длины стержней найдем по теореме синусов
Подставим (3) в (4)
Из этих соотношений найдем два значения для силы P
Аналогично, записывая условия прочности и жесткости для стержня АС,
найдем еще два значения для силы P
Из полученных четырех значений в качестве допускаемой нагрузки следует принять наименьшее значение 
Проверим выполнения условий прочности и жесткости. Для стержня АВ:
Для стержня АС:
Все условия выполняются.
Ответ: 
Решение этой задачи в среде Mathcad можно посмотреть ЗДЕСЬ
Продольный изгиб
При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.
Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение.
Рассмотрим известные виды равновесия.
Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы, стремящиеся удалить её от начального положения.
Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.
При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.
При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.
Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.
Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.
Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.
Критическая сила. Критическое напряжение
Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.
При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаны Эйлером.
В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:
где Imin – минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ – геометрическая длина стержня, μ – коэффициент приведенной длины или коэффициент приведения (зависит от способов закрепления концов стержня), Значения μ приведены под соответствующей схемой закрепления стержней
Критическое напряжение вычисляется следующим образом
, где
гибкость стержня ,
а 
Введем понятие предельной гибкости.
Величина λпред зависит только от вида материала:
Если у стали 3 Е=2∙1011Па, а σпц=200МПа, то предельная гибкость
Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80
Таким образом, для стержней большой гибкости λ≥λпред критическая сила определяется по формуле Эйлера.
В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ0≤λ≤λпр, (стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.
σк=а-bλ, или Fкр= A(a— bλ)
где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа, b=1,14МПа.
При значениях гибкости стержня 0≤λ≤λ0 (стержни малой гибкости) потеря устойчивости не наблюдается.
Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.
Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба
Условием устойчивости сжатого стержня является неравенство:
Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:
1) от длины стержня, от размеров и даже от формы поперечных сечений,
2) от способа закрепления концов стержня,
3) от материала стержня.
Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.
Поэтому
Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.
Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:
В этом случае 
где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).
Коэффициент φ<1 и потому называется коэффициентом снижения основного допускаемого напряжения, то есть [σ] по прочности, или иначе коэффициентом продольного изгиба.
С учетом сказанного условие устойчивости сжатого стержня принимает вид:
Численные значения коэффициента φ выбираются из таблиц в зависимости от материала и величины гибкости стержня , где:
μ – коэффициент приведенной длины (зависит от способов закрепления концов стержня), ℓ – геометрическая длина стержня,
i – радиус инерции поперечного сечения 
Коэффициент φ изменяется в диапазоне 0≤φ≤1, зависит ,как уже говорилось, как от физико-механических свойств материала, так и от гибкости λ. Зависимости между φ и λ для различных материалов представляются обычно в табличной форме с шагом ∆λ=10.
При вычислении значений φ для стержней, имеющих значения гибкости не кратные числу 10, применяется правило линейной интерполяции.
Значения коэффициента φ в зависимости от гибкости λ для материалов
На основании условия устойчивости решаются три вида задач:
- Проверка устойчивости.
- Подбор сечения.
- Определение допускаемой нагрузки (или безопасной нагрузки, или грузоподъемности стержня: [F]=φ[σ]А.
Наиболее сложным оказывается решение задачи о подборе сечения, поскольку необходимая величина площади сечения входит и в левую, и в правую часть условия устойчивости:
Только в правой части этого неравенства площадь сечения находится в неявном виде: она входит в формулу радиуса инерции 
, от которой зависит значение коэффициента продольного изгиба φ. Поэтому здесь приходится использовать метод проб и ошибок, облеченный в форму способа последовательных приближений:
1 попытка: задаемся φ1 из средней зоны таблицы, находим 

, по таблице определяем
и сравниваем со значением φ1 . Если
, то:
2 попытка: принимаем 


, по таблице определяем
, и если
, то:
3 попытка: принимаем 


, по таблице определяем
, и т.д.
Процесс приближений продолжается до тех пор, пока разница не окажется менее 5%.

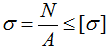
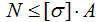
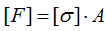
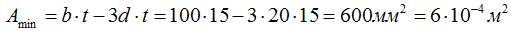
![Расчет величины допустимой силы [F]](https://isopromat.ru/wp-content/uploads/is-838.png)