Решающее значение
при проектировании контрольных
приспособлений имеет не абсолютная
погрешность измерения, а относительная
погрешность.
Относительная
погрешность измерения есть значение
предельной погрешности показания,
выраженное в долях или процентах от
значения величины, измеряемой на
контрольном приспособлении [4].
![]() (2.1)
(2.1)
где
δlim
– предельная
погрешность метода измерения деталей
на контрольных приспособлениях;
К
– коэффициент, зависящий от вида
распределения ;
δ
– допуск на
размер или же значения, заданные
техническими условиями;
β
– допускаемое соотношение между
предельной погрешностью измерения и
полем допуска на измеряемый размер
детали.
Значение
β в зависимости от поля допуска (класса
точности по ГОСТу) приведено в табл.
2.1.
[4].
Рекомендуемые
соотношения предельной погрешности
измерения и поля допуска детали
Таблица
2.1.
|
Квалитет ИСО |
% |
Квалитет ИСО |
% |
|
1 – 4 |
35 |
8 |
25 |
|
5 |
32,5 |
9 |
20 |
|
6 |
30 |
10 |
15 |
|
7 |
27,5 |
11 |
10 |
Исследования
показывают, что независимо случайные
погрешности процесса измерения, в том
числе и измерений на контрольных
приспособлениях, следует закону
нормального распределения, т.е. К=1.
Тогда допустимая
погрешность измерения выразится:
![]() (2.2)
(2.2)
Табличные значения
допустимой погрешности измерения
приведены в работе [8].
3.Определение суммарной погрешности измерения на контрольном приспособлении
Суммарная придельная
погрешность метода измерения на
контрольном приспособлении рассчитывается
по формулу:
![]() (3.1)
(3.1)
где
Δо
– погрешность
установочного узла контрольного
приспособления по линейным размерам
или по техническим условиям;
Δр
– систематические погрешности
передаточных устройств;
Δз
–погрешность
отклонения установочных размеров от
номинального;
Δδ
– погрешность
базирования деталей на установочные
узлы контрольных приспособлений;
Δус
–
погрешность совмещения измерительной
базы контролируемой детали с рабочими
поверхностями установочного узла;
Δn
– случайные
погрешности передаточных устройств;
Δэс
– погрешность
форм и взаимного расположения поверхностей
эталона;
Δм
– погрешность,
свойственная данному методу измерений;
Δ3
–
погрешность закрепления контролируемой
детали.
Рассмотрим все
составляющие поверхности измерения.
3.1.Погрешность установочного узла по линейным размерам или по техническим условиям.
Рабочие поверхности
установочных узлов часто изготовляют
с допусками 0,005 – 0,001 мм [4].
При
аттестации контрольных приспособлений
погрешность Δо
определяется
непосредственным измерением и является
систематической ошибкой.
3.2.Погрешность базирования деталей на установочные узлы контрольных приспособлений.
Погрешность
базирования деталей на установочные
узлы контрольных приспособлений Δб
называется
допусками на линейные или диаметральные
размеры измерительных базовых поверхностей
проверяемых деталей, может также
называться неправильной формой
измерительных баз проверяемых деталей
(овальность, конусность, бочкообразность
и т.д.).
Предельное
значение Δδ
с учетом допуска δ
на измерительную базу проверяемых
деталей ( допуск на диаметр базового
отверстия, пояска и т.д.) обычно может
быть определено расчетным путем. При
таких расчетах следует учесть не только
допуск δ
, но так же и величину гарантированного
зазора между измерительной базой и
рабочей поверхностью установочного
узла. Без такого зазора невозможна
легкая и быстрая установка проверяемых
деталей на установочные узлы контрольных
приспособлений.
Погрешность
базированная Δδ
является величиной случайной.
Рассмотрим
погрешность базирования деталей на
типовые установочные сборочные единицы
контрольных приспособлений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В.Д. Гвоздев. Допустимая погрешность измерений: выбор значения
(«Законодательная и прикладная метрология», 2013, №2)
Аннотация
Объектом анализа являются рекомендации по выбору допустимой погрешности измерений, содержащиеся в нормативных документах и публикациях по метрологии. Основное внимание уделено допусковому контролю качества. Подчеркивается, что концепция контроля точности линейных размеров, принятая в ГОСТ 24356, может быть причиной брака.
Ключевые слова: измерения, контроль, допустимая погрешность измерений, допускаемая погрешность измерений, допуск, оценка соответствия
Для обеспечения единства измерений необходимо, чтобы характеристики погрешности/неопределенности (далее погрешность – Δ) результата измерений не выходили за заданные (допустимые) границы. Методы определения характеристик точности результатов измерений – основная тема метрологии. Выбору значений допустимой погрешности уделяется немного внимания. Часто авторы книг ограничиваются указанием, что выбор допустимой (допускаемой) погрешности производится исходя из задач измерений. Связано это с тем, что в рамках метрологии обосновать выбор значения допустимой погрешности невозможно.
Однако оставить тему выбора допустимой погрешности без рассмотрения также нельзя, хотя бы потому, что при метрологической экспертизе проектов нормативных документов, конструкторской и технологической документации обязательно проверяют оптимальность требований к точности измерений.
Задача измерений – определение значения величины. Цели могут быть разные. Разделим их условно на две группы: 1 – получение информации о величине и 2 – контроль качества объектов.
В первом случае значения допустимой погрешности измерений обусловлены влиянием неопределенности результата измерений на последствия от принятия решения на его основе.
Например:
-если ставится задача повышения точности оценки какой-либо количественной характеристики по отношению к уже достигнутому уровню, допустимая погрешность измерения будет определяться разрядом последней цифры, надежность которой должна быть обеспечена;
-для научных и практических исследований, во многих случаях, допустимую погрешность измерений устанавливают из условия сопоставимости их результатов;
-в медицине точность измерений обусловливается взаимосвязью между изменением параметра и самочувствием пациента;
-в спорте выбор разрешающей способности средств измерений и погрешности измерений связаны с плотностью результатов спортсменов;
-при осуществлении торговых операций с продуктами, характеризуемыми массой или объемом, поставке электроэнергии, тепла, горючих и смазочных материалов и др. от значения допустимой погрешности измерений напрямую зависят экономические показатели поставщика и потребителя;
-при оценке характеристик точности технологических процессов, применении статистических методов контроля технологических процессов, статистическом приемочном контроле и входном контроле качества продукции исходят из критерия ничтожной погрешности измерения по отношению к технологическому допуску. Характеристики точности измерений принимают такими, чтобы среднеквадратическое отклонение (СКО) результата измерений было в 5…6 раз меньше СКО контролируемого параметра [1]. Если СКО контролируемого параметра неизвестно, руководствуются правилом: цена деления не должна превышать 1/6 значения допуска контролируемого параметра [2]. Погрешность измерения в этом случае рассматривают как составную часть погрешности изготовления.
При установлении требований к качеству объектов для значений показателей качества задают односторонние ограничения или двухсторонние ограничения (допуски), которые учитывают при выборе допустимой погрешности измерения. Определим место погрешности измерения при контроле показателя качества с двусторонним ограничением, то есть, когда задан допуск. Обратимся к положению, записанному в стандарте ГОСТ Р ИСО 10576-1-2006 [3]: «решение о соответствии требованиям может быть принято в том случае, если интервал неопределенности результатов измерений находится внутри области допустимых значений». Реализуя принципы оценки соответствия, установленные стандартом, изобразим области соответствия (контролируемый параметр А однозначно находится в заданных пределах) и несоответствия (контролируемый параметр А однозначно находится вне заданных пределов) на числовой оси (рис.).
Рис. Схема измерительного контроля качества отдельного объекта.
Область соответствия 1 определена условием Аmin + Δ ≤ А ≤ Аmax – Δ, области несоответствия 2 (области недопустимых значений) характеризуются неравенствами А ≤ Аmin – Δ и A ≥ Аmax + Δ. Интервалы Аmin ± Δ и Аmax ± Δ назовем областями неокончательного результата оценки соответствия 3. Если истинное значение измеряемой величины находится в области неокончательного результата оценки соответствия, то существует вероятность, что вследствие влияния погрешности измерений годное изделие может быть отнесено к бракованным (неправильно забракованное изделие), а бракованное изделие к годным (неправильно принятое изделие).
При известной функции распределения 4 погрешности измерений можно установить вероятности правильного и неверного решений о соответствии конкретного изделия. Применительно к ситуации, показанной на рисунке, если А* истинное значение величины, то Рг – вероятность признания изделия годным, а Рб = 1- Рг – вероятность забракования изделия. Если А* измеренное значение, то Рг – вероятность того, что изделие годное, а Рб – вероятность, что оно бракованное. Достоверность такой информации не высока: сведения о законе распределения случайной погрешности измерений приблизительны или отсутствуют; неисключенные систематические погрешности, рассматриваемые при вычислении суммарной погрешности как случайные величины, в практических измерениях проявляют себя как систематические составляющие, значения и знаки которых неизвестны.
В стандарте [3] не приведены правила для ситуации, когда получен неокончательный результат оценки соответствия. В тоже время отмечается, что «применение двухэтапной процедуры вместо одноэтапной процедуры в общем случае приводит к уменьшению риска» принятия ошибочных решений. Двухэтапная процедура подразумевает повторное выполнение измерений, когда границы интервала неопределенности, рассчитанные после первого этапа, выходят за пределы поля допуска (т.е. результат измерений находится в области неокончательного результата оценки соответствия). Значение измеряемой величины и её неопределенность устанавливают как комбинацию результатов измерений двух этапов.
Для сближения границ области неокончательного результата оценки соответствия применимы меры по уменьшению погрешности измерений, рассмотренные в документе [4].
Границы области соответствия сужаются до нуля при допустимой погрешности измерения равной 0,5 допуска на изготовление и расширяются до границ поля допуска при отсутствии погрешности измерений. Отсюда следует вывод, что значение погрешности измерений при двухстороннем ограничении показателя качества должно быть менее половины значения допуска и чем оно меньше, тем лучше. Вывод согласуется с мнением авторов работ [5, 6] и это единственная общая рекомендация, которую целесообразно давать в рамках метрологии.
В нормативных документах и печатных изданиях по метрологии приводятся другие указания по выбору допустимой погрешности измерений, которые якобы позволяют «достичь необходимой точности изделий с наименьшими затратами труда и материальных средств» [7].
Наиболее известное соотношение [Δ] ≈ (0,2…0,35) ТА было предложено в работе [6] и закреплено в стандарте ГОСТ 8.051 «Погрешности, допускаемые при измерении линейных размеров до 500 мм». Авторы работы [6] честно указали, что «установление допустимых погрешностей измерения носит волевой характер».
Сходные между собой указания приведены в РМГ 63 [8] и ПМГ 92-2009 [9]: «если недостаточная точность измерений не может вызвать заметных потерь или других неблагоприятных последствий, пределы допускаемых значений, например, погрешности измерений могут составлять 0,2 – 0,3 границы симметричного допуска (для несимметричного допуска – размера поля допуска) на измеряемый параметр, а для параметров, не относящихся к наиболее важным, это соотношение может быть увеличено до 0,5» [9].
Те же документы содержат и иные рекомендации: «соотношения между погрешностью измерения и половиной допуска, удовлетворяющие «требованиям обеспечения эффективности измерений»: «для наиболее важных параметров» 0,2 … 0,7; «для параметров, не относящихся к наиболее важным» 0,3 … 1.
В книге [10] оптимальное соотношение между допустимой погрешностью измерения и допуском на изготовление, обосновано критерием ничтожной погрешности и равно [Δ]=0,15TA.
Интересная по замыслу книга [5] содержит такие выводы: «при выборе СИ и МВИ для контроля и измерения вспомогательных, некритичных для качества продукции параметров следует принимать К = Δ/(ТА/2) = 0,2…0,33, не прибегая к расчетам вероятностей ошибок контроля. При проведении научно-исследовательских работ выбирают К <0,2. При фактическом К< 0,1 расчеты вероятностей ошибок поверки не производят». В другом месте книги [5] , «наиболее простой способ установления допустимой погрешности измерения – принять ее значение в долях от допуска на изделие: [Δ]= С ∙ ТА. Если принять С = 0,1…0,35, то можно не определять ошибки контроля, так как в таком случае они являются априори малыми».
Особенностью перечисленных рекомендаций является то, что они не позволяют связать выбор значений допустимой погрешности измерений с конкретными последствиями от их использования. Обоснования по выбору коэффициентов опираются на абстрактные понятия «важный» и «неважный» параметры, «эффективность измерений», «заметные» потери и «малые» ошибки контроля, «неблагоприятные последствия», «симметричный», «несимметричный» и «односторонний» допуски (допуск это разность заданных предельных значений показателей качества, а разность не может быть симметричной или односторонней). Обращает на себя внимание противоречивость и существенное различие рекомендаций, приводимых не только в разных документах, но и в некоторых случаях в одном документе, а также широких разброс границ диапазонов коэффициентов, определяющих соотношение между допустимой погрешностью измерения и половиной допуска/допуском на изготовление.
Недостаточно внимательное и критичное отношение к таким рекомендациям, может привести к неправильным выводам, что их соблюдение является гарантией корректного решения конкретных измерительных задач. С другой стороны несоблюдение требований РМГ 63-2003 и ПМГ 92-2009 при выполнении метрологической экспертизы проектов нормативных документов или конструкторской и технологической документации может рассматриваться как нарушение метрологических норм и правил.
Рассмотрим конкретный пример контроля линейных размеров деталей. Принципы оценки соответствия для линейных размеров, прописанные в ГОСТ 25346-89 [11], отличаются от описанных в ГОСТ Р ИСО 10576-1-2006: деталь признается годной, если действительный (измеренный) размер находится между предельными размерами или равен одному из них. То есть границы области соответствия совпадают с границами допуска. Вследствие этого при использовании допустимых погрешностей, устанавливаемых по ГОСТ 8.051 (0,2…0,35 ТА), к числу годных, могут быть отнесены детали с истинными размерами, выходящими за заданные границы.
Поскольку вопрос точности актуален в первую очередь для размеров сопрягаемых поверхностей, была выполнена оценка влияния погрешности измерения на значение допуска посадки. Обычно при выборе посадок используют принцип полной взаимозаменяемости, согласно которому допуск посадки ТП равен сумме допусков отверстия TD и вала Td: ТП = TD + Td.
Получаемые при сборке значения зазоров и/или натягов в сопряжении можно оценить вероятностными границами. Предположим, что систематическая составляющая погрешности измерения отсутствует. С учетом погрешности/неопределенности измерений размахи рассеяния истинных значений размеров отверстий и валов, поступающих на сборку, составят ТD* = TD + 2 ∙ ΔD и Тd* = Td +2 ∙ Δd . Представим взаимосвязь между погрешностью измерения и допуском в виде Δ = К ∙ Т. Запишем ТD* = (1+2∙К)∙TD и Тd* = (1+2∙К) ∙ Td. Найдем вероятностные значения допуска посадки: ТПв = √( TD*2 + Td*2) = (1+2К) √( TD2 + Td2)
Для стандартных рекомендуемых и предпочтительных посадок допуск отверстия равен допуску вала (тогда ТП = 2∙Td) или на один квалитет грубее (TD=1,6∙Td и ТП = 2,6∙Td). Для первого случая получим ТПв1=(1+2∙К)∙1,41∙ Td, для второго – ТПв2 = (1+2∙К) ∙ 1,89∙ Td.
Подставим значения К, принятые в ГОСТ 8.051 для сопрягаемых размеров, и вычислим вероятностные допуски посадки. Запишем, при К=0,2 – ТПв1 = 1,97∙ Td, ТПв2 =2,65 ∙ Td; при К=0,3 – ТПв1 = 2,26 ∙ Td, ТПв2 =3,03 ∙ Td.
Сравнивая ТП и ТПв, отметим, что при К = 0,2, если центры группирования размеров отверстий и валов совпадают с серединами полей допусков, влияние погрешности измерения практически не отразится на качестве сборочной единицы (1,97<2 и 2,65≈2,6). При К=0,3 существует вероятность получения брака (2,26>2 и 3,03>2,6), что требует контроля качества соединения или сортировки деталей, поступающих на сборку. Эти же меры потребуются, если настроенность технологического процесса не совпадает с серединой поля допуска (что в той или иной мере всегда присутствует).
Отметим, что значение К=0,2 в ГОСТ 8.051 принято для квалитетов более десятого, для меньших квалитетов К>0,2.
Результаты анализа показывают, что значения допустимой погрешности измерений, рекомендуемые ГОСТ 8.051, завышены. Возникает вопрос: почему это обстоятельство не стало темой для обсуждения? Причин несколько. Укажем некоторые из них. 1. При выборе метода и средств измерений создают запас метрологической надежности. 2. Для универсальных средств измерений линейных размеров реальные погрешности их применения меньше значений, приведенных в РД 50-98 [7]. Вследствие 1 и 2 практическое соотношение между погрешностью измерения и допуском оказывается меньше установленного стандартом. 3. Дополнительный запас создается при выборе стандартной посадки, допуск которой, как правило, меньше функционального допуска посадки. 4. Технологию обработки детали выбирают так, чтобы технологический допуск был меньше конструкторского. 5. Вводят производственный допуск. 6. Вместо измерительного контроля используют контроль калибрами и т.д.
Все упомянутые выше рекомендации по установлению допустимой погрешности измерений укладываются в интервал (0…0,5) ТА. Это значит, что они справедливы. Но они и не безусловны и требуют проверки обоснованности и эффективности в каждом конкретном случае.
Возможные проблемы, связанные с применением ГОСТ 8.051, обусловлены не реализованными в нем соотношениями между допустимой погрешностью и допуском размера, а концепцией оценки соответствия, прописанной в ГОСТ 25346: «предельные размеры – два предельно допустимых размера элемента, между которыми должен находиться (или которым может быть равен) действительный размер». (Действительный размер – размер элемента, установленный измерением с допускаемой погрешностью). Это означает, что границы области соответствия совпадают с границами поля допуска и что детали, истинные значения размеров которых выходят за границы поля допуска, могут быть признаны годными «на законных основаниях». Для предупреждения этих событий в качестве одного из вариантов действий ГОСТ 8.051 предлагает конструкторам назначать предельные размеры детали смещенными относительно расчетных границ внутрь поля допуска на значение погрешности измерений. Внедрение указанного предложения может вызвать следующие неудобства. 1. Использование допустимых погрешностей, установленных ГОСТ 8.051, приведет к уменьшению конструкторского допуска по сравнению с расчетным допуском примерно в 2 раза и повышению требований к технологическому оборудованию. 2. Сведения о допустимой погрешности измерений, если она отличается от стандартной погрешности, необходимо будет указывать в конструкторской документации для каждого поля допуска. 3. При использовании для контроля деталей калибров придется задавать приемочные границы, исключающие погрешности измерений.
Общие требования к нормированию предельных значений, приведенные в ГОСТ Р ИСО 10576-1-2006, включают следующее положение: «устанавливаемые предельные значения не должны включать в себя (в явном или неявном виде) неопределенность/погрешность измерений». В свете сказанного в предыдущем абзаце, весьма разумное соображение.
Концепция оценки соответствия ГОСТ Р ИСО 10576-1-2006 более гибкая и позволяет производителю продукции самому принимать решения, связанные с обеспечением и контролем качества.
Для примера рассмотрим ситуацию, когда необходимо оценить годность вала, размер которого задан 40±0,195 мм (допуск размера Td = 390 мкм). В наличии (под рукой) имеется штангенциркуль с отсчетом 0,05 мм.
Из таблиц стандарта ГОСТ 8.051 найдем допустимую погрешность измерения [Δ]=80 мкм. Для штангенциркуля в РД 50-98 [7] для диапазона измерений свыше 30 мм до 50 мм указан предел погрешности измерений 100 мкм. Погрешность измерений штангенциркулем больше допустимой погрешности: штангенциркуль использовать нельзя. Концепция ГОСТ Р ИСО 10576-1-2006 позволяет нам это сделать. Ограничив область соответствия пределами 40±0,095 мм, оценку годности вала можно выполнить без риска отнесения к годным бракованных деталей.
В книгах по метрологии большое внимание уделяют возможности установления допустимой погрешности измерения исходя из заданной вероятности отнесения изделий к неправильно забракованным m и неправильно принятым n. На основе аппарата теории вероятностей авторы работ [6, 12] получили формулы и построили графики, устанавливающие зависимость значений m и n от соотношений между погрешностью измерений, параметрами технологического процесса и допуском на изготовление. Задав значения m и n при известной характеристике погрешности технологического процесса можно оценить требуемое значение допустимой погрешности измерения. Пример решения такой задачи приведен в книге [10].
Не ставя под сомнение корректность анализа и обоснованность полученных результатов и выводов, следует обратить внимание на применимость теоретических положений для практических целей.
Предложенные в книгах [6, 10, 12] графики относятся к ситуации, когда технологический допуск превышает допуск на изготовление. Такое на практике возможно, однако не соответствует принципам выбора способа изготовления, согласно которому технологический допуск должен быть меньше допуска на изготовление. В рекомендациях [14] в зависимости от значений коэффициента точности технологический процесс оценивают как точный, при Kт =6σтех/ТА≤0,75; удовлетворительный, при Kт = 0,76÷0,98 и неудовлетворительный, при Kт > 0,98 (σтех – СКО технологического процесса).
Задача измерений/контроля в первую очередь состоит в том, чтобы количество неправильно принятых изделий свести к нулю. При Kт < 0,98 и применении методов статистического контроля и регулирования технологических процессов она решается. При серийном и массовом производстве для контроля качества продукции в основном используют альтернативные методы контроля, а не средства измерений.
Средства измерений применяют при мелкосерийном, единичном производстве и ремонте, для оценки годности небольших партий или отдельных образцов продукции. Уменьшение количества неправильно принятых и неправильно забракованных изделий будет зависеть от значения погрешности измерений и от правильной организации контроля, например на принципах изложенных выше [3]. Целесообразность организации измерительного контроля на подобных принципах отмечена в работе [14]: «при разработке методик контроля должны использоваться только «индивидуальные» характеристики достоверности контроля отдельного параметра отдельного экземпляра изделия (или пробы продукции)».
Ограничения на значения показателей качества могут быть односторонними: только сверху или только снизу. Это не значит, что второе ограничение в принципе отсутствует. Например, для отгрузки сырой нефти требования к массовой доле серы могут быть заданы в виде: массовая доля серы должна быть не более 2 %. Вторая – нижняя граница реальна и объективна – 0%. В этом случае разность граничных значений можно рассматривать как допуск. Поскольку область соответствия при оценке качества будет начинаться с нуля, значение допустимой погрешности измерения выбираем из условия [Δ] < ТА. Другой пример, требование к продукту сформулировано в виде: массовая доля компонента А (предположим, жирность молока) должна быть не менее 3,2 %. Задана нижняя граница. Объективно существует и верхняя граница 100%. Однако связывать значение допустимой погрешности измерения с диапазоном 3,2…100% опрометчиво. Для удовлетворения заданных требований здесь уместен экономический подход к выбору метода и средств измерений в сочетании с введением приемочной границы (границы соответствия), смещенной на значение Δ в сторону увеличения.
Экономический подход к выбору метода и средств измерений описан в нескольких нормативных документах (например, [8, 9]). Идея заключается в следующем: «оптимальной (в экономическом отношении и для задач, не связанных с негативными социальными последствиями, например, такими, как причинение ущерба здоровью работников) считают точность измерений, при которой сумма потерь (добавим, или дополнительных затрат) от недостаточной точности результатов измерений и расходов на измерения будет минимальной».
Экономические расчеты – основной способ обоснования выбора допустимой погрешности измерений или метода и средств измерений при контроле качества объектов. Однако они могут быть применены только для конкретных, подробно описанных ситуаций.
Использование понятия «допустимая погрешность измерений» и её нормирование при контроле качества уместно только тогда, когда ограничительные границы на значение показателя качества установлены с учетом этой погрешности. Во всех остальных случаях (не только при контроле качества) предпочтительно применение термина «заданная погрешность», в предположении, что требуемые характеристики погрешности измерений устанавливаются вне сферы метрологии (например, в квалиметрии).
Список литературы
1. Управление качеством продукции» Справочник. – М.: Изд-во стандартов, 1985. – 464 с.
2. РД 50-605-86 Методические указания по применению стандартов на статистический приемочный контроль. – М.: Изд-во стандартов, 1986. 38 с.
3. ГОСТ Р ИСО 10576-1-2006 Статистические методы. Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы. – М.: Стандартинформ, 2006. – 16 с.
4. РМГ 64-2003 ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Методы и способы повышения точности измерений. – М.: Изд-во стандартов, 2004.- 35 с.
5. Установление показателей качества продукции и технологических параметров и норм точности их измерения. / Под общ. ред. проф. А.А. Бегунова. – СПб.: ГОУВПО СПбГТУРП, 2008. – 85 с.
6. Марков Н.Н., Крайнер Г.Б., Сацердотов П.А. Погрешность и выбор средств при линейных измерениях. – М.: Машиностроение, 1967. – 392 с.
7. РД 50-98-86 Методические указания. Выбор универсальных средств измерений линейных размеров до 500 мм (По применению ГОСТ 8.051-81). – М.: Изд-во стандартов, 1987. – 105 с.
8. РМГ 63-2003 ГСИ. Обеспечение эффективности измерений при управлении технологическими процессами. Метрологическая экспертиза технической документации. – М.: Изд-во стандартов, 2004. – 27 с.
9. ПМГ 92 – 2009 ГСИ. Метрологическая экспертиза проектов нормативных документов. – М.: Стандартинформ, 2011. – 9 с.
10. Артемьев Б.Г., Голубев С.М. Справочное пособие для работников метрологических служб. – М.: Изд-во стандартов, 1990. – 428 с.
11. ГОСТ 25346-89 Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений. – М.: Изд-во стандартов, 1992. – 23 с.
12. Фрумкин В.Д., Рубичев Н.А. Теория вероятностей и статистика в метрологии и измерительной технике. – М.: Машиностроение, 1987. – 168 с.
13. Р 50-601-19-91 Применение статистических методов регулирования технологических процессов. – М.: ВНИИС, 1997. 32 с.
14. Земельман М.А. Метрологические основы технических измерений. – М.: Изд-во стандартов, 1991. – 228 с.
ПОГРЕШНОСТИ И КЛАССЫ ТОЧНОСТИ
ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Измеренная прибором величина всегда отличается от истинного значения на некоторое число, называемое погрешностью прибора. Погрешности измерительных приборов определяют поверкой, т. е. сравнением показаний поверяемого прибора с показаниями более точного, образцового прибора при измерении ими одной и той же величины. Значение измеряемой величины, определенное по образцовому прибору, принято считать действительным. Однако действительное значение отличается от истинного на погрешность, присущую данному образцовому прибору. Различают абсолютную, относительную и приведенную погрешности измерения.
Абсолютной погрешностью
измерительного прибора называют разность между его показанием и действительным значением измеряемой величины.
Относительной погрешностью
называют отношение абсолютной погрешности к действительному значению измеряемой величины, выраженное в относительных единицах или в процентах.
Приведенная погрешность
– это отношение наибольшей абсолютной погрешности к верхнему пределу измерений прибора.
По значению приведенной погрешности измерительные приборы делят на группы по классу точности. Класс точности
–
обобщенная характеристика измерительного прибора, определяющая пределы допустимых погрешностей. Для электроизмерительных приборов класс точности указывается в вида числа, равного максимальной допустимой приведенной погрешности (в %). Согласно ГОСТ 1845-59, электроизмерительные приборы делят на 8 классов по точности: 0,05; 0,1; 0,2 – образцовые приборы; 0,5; 1,0 – лабораторные; 1,5; 2,5; 4,0 – технические приборы. Образцовые приборы считаются более высокого класса точности по отношению к лабораторным и техническим приборам, а лабораторные – по отношению к техническим.
Определим по классу точности прибора его погрешности. Если прибор (например, вольтметр с верхним пределом измерений 150 В) имеет класс точности 1,0, то основная приведенная погрешность не превышает 1 %
. Максимальная абсолютную погрешность, которую может иметь прибор в любой точке шкалы не будет превышать Относительная же погрешность при этом зависит от измеряемого напряжения.
Если этим вольтметром можно измерять напряжение 10 В, то относительная погрешность может составить . Если же измерять напряжение 100 В, то относительная погрешность может составить
Из этого примера видно, что для повышения точности измерения прибор надо выбирать так, чтобы, во-первых, он имел более высокий класс точности, и чтобы, во-вторых, предел измерения был близок к значению измеряемой величины. Это означает, что для получения возможно меньших относительных ошибок, надо добиваться достаточно большого отклонения стрелки (желательно, чтобы использовалась последняя треть шкалы).
С другой стороны, для того чтобы добиться большой точности при измерении прибором более низкого класса, необходимо выбрать прибор с наименьшим возможным диапазоном измерений.
Следует правильно формулировать предложение, в котором дана количественная оценка погрешности. Например: «Измерение тока с абсолютной погрешностью до 1 мА», «Измерение тока с относительной погрешностью до 1 %.
(Выражение «Измерение тока с точностью до 1 мА» неправильно).
Источник: kursak.net
Классы точности приборов
По приведенной погрешности (по классу точности) приборы делятся на восемь классов: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.
Приборы класса точности 0,05; 0,1; 0,2; 0,5 применяются для точных лабораторных измерений и называются прецизионными
(от англ. precision – точность). В технике применяются приборы классов 1,0; 1,5: 2,5 и 4,0 (технические).
Класс точности прибора указывается на шкале прибора. Если на шкале такого обозначения нет, то данный прибор внеклассный, то есть его приведенная погрешность превышает 4%.Производитель, выпускающий прибор, гарантирует относительную погрешность измерения данным прибором, равную классу точности (приведенной погрешности) прибора при измерении величины, дающей отброс указателя на всю шкалу. Определив по шкале прибора класс точности и предельное значение, легко рассчитать его абсолютную погрешность ΔX = ± гXпр / 100%, которую принимают одинаковой на всей шкале прибора. Знаки «+» и «–» означают, что по-грешность может быть допущена как в сторону увеличения, так и в сторону уменьшения от действительного значения измеряемой величины.
При использовании приборов для конкретных измерений редко бывает так, чтобы измеряемая величина давала отброс стрелки прибора на всю его шкалу. Как правило, измеряемая величина меньше. Это увеличивает относительную погрешность измерения. Для оптимального использования приборов их подбирают так, чтобы значения измеряемой величины приходились на конец шкалы прибора, это уменьшит относительную погрешность измерения и приблизит ее к классу точности прибора. В тех случаях, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления.
Источник: fevt.ru
Виды маркирования
Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.
Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.
Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.
Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.
Определение класса точности прибора
Класс точности измерительного прибора — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых установлены в стандартах на отдельные виды средств измерений. Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.
Для того чтобы заранее оценить погрешность, которую внесет данное средство измерений в результат, пользуются нормированными значениями погрешности. Под ними понимают предельные для данного типа средства измерений погрешности.
Погрешности отдельных измерительных приборов данного типа могут быть различными, иметь отличающиеся друг от друга систематические и случайные составляющие, но в целом погрешность данного измерительного прибора не должна превосходить нормированного значения. Границы основной погрешности и коэффициентов влияния заносят в паспорт каждого измерительного прибора.
Основные способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.
На шкале измерительного прибора маркируют значение класса точности измерительного прибора в виде числа, указывающего нормированное значение погрешности. Выраженное в процентах, оно может иметь значения 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 и т. д.
Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности δs = 1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, измерительных шунтов, измерительных трансформаторов тока и напряжения и т. п.).
Это означает, что для данного измерительного прибора погрешность чувствительности δs = dx/x — постоянная величина при любом значении х. Граница относительной погрешности δ(х) постоянна и при любом значении х просто равна значению δs, а абсолютная погрешность результата измерений определяется как dx = δsx
Для таких измерительных приборов всегда указывают границы рабочего диапазона, в которых такая оценка справедлива.
Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля δо = 0,5 %. У таких приборов для любых значений х граница абсолютной погрешности нуля dx = dо = const, а δо = dо/хн.
При равномерной или степенной шкале измерительного прибора и нулевой отметке на краю шкалы или вне ее за хн принимают верхний предел диапазона измерений. Если нулевая отметка находится посредине шкалы, то хн равно протяженности диапазона измерений, например для миллиамперметра со шкалой от -3 до +3 мА, хн= 3 — (-3)=6 А.
Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %. Значение погрешности δо увеличивается обратно пропорционально х, то есть относительная погрешность δ(х) равна классу точности измерительного прибора лишь на последней отметке шкалы (при х = хк). При х = 0,1хк она в 10 раз больше класса точности. При приближении х к нулю δ(х) стремится к бесконечности, то есть такими приборами делать измерения в начальной части шкалы недопустимо.
На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».
Нормирование
Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й
Нормирование осуществляется по:
- абсолютной;
- относительной;
- приведенной.

Формулы расчета абсолютной погрешности по ГОСТ 8.401
Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.
Скачать ГОСТ 8.401-80
Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.
Как определить класс точности манометра
Манометр — измерительный прибор, который позволяет установить значение избыточного давления, действующего в трубопроводе или в рабочих частях различных видов оборудования.
Такие приборы широко применяются в системах отопления, водоснабжения, газоснабжения, других инженерных сетях коммунального и промышленного назначения. В зависимости от условий эксплуатации измерителя существуют определенные ограничения по допустимому пределу его погрешности. Поэтому важно знать, как определить класс точности манометра.
Электростатические КИП
Эти приборы работают на принципе взаимодействия заряженных электродов, которые разделены диэлектриком. Конструктивно они выглядят практически как плоский конденсатор. При этом, при перемещении подвижной части емкость системы также изменяется.
Наиболее известные из них – это устройства с линейным и поверхностным механизмом. У них немного разный принцип действия. У приборов с поверхностным механизмом емкость изменяется за счет колебаний активной площади электродов
В другом случае важно расстояние между ними
К достоинствам таких устройств относятся небольшая мощность потребления, класс точности ГОСТ, достаточно широкий частотный диапазон и т.д.
Недостатками являются небольшая чувствительность прибора, необходимость экранирования и пробой между электродами.
Что такое класс точности манометра, и как его определить
Класс точности манометра является одной из основных величин, характеризующих прибор. Это процентное выражение максимально допустимая погрешность измерителя, приведенная к его диапазону измерений.
Абсолютная погрешность представляет собой величину, которая характеризует отклонение показаний измерительного прибора от действительного значения давления. Также выделяют основную допустимую погрешность, которая представляет собой процентное выражение абсолютного допустимого значения отклонения от номинального значения. Именно с этой величиной связан класс точности.

Существует два типа измерителей давления — рабочие и образцовые.
Рабочие применяются для практического измерения давления в трубопроводах и оборудовании. Образцовые — специальные измерители, которые служат для поверки показаний рабочих приборов и позволяют оценить степень их отклонения. Соответственно, образцовые манометры имеют минимальный класс точности.
Классы точности современных манометров регламентируются в соответствии с ГОСТ 2405-88 Они могут принимать следующие значения:
Таким образом, этот показатель имеет прямую зависимость с погрешностью. Чем он ниже, тем ниже максимальное отклонение, которое может давать измеритель давления, и наоборот. Соответственно, от этого параметра зависит, насколько точными являются показания измерителя. Высокое значение указывает на меньшую точность измерений, а низкое соответствует повышенной точности. Чем ниже значение класса точности, тем более высокой является цена устройства.
Узнать этот параметр достаточно просто. Он указан на шкале в виде числового значения, перед которым размещаются литеры KL или CL. Значение указывается ниже последнего деления шкалы.
Указанная на приборе величина является номинальной. Чтобы определить фактический класс точности, нужно выполнить поверку и рассчитать его. Для этого проводят несколько измерений давления образцовым и рабочим манометром. После этого необходимо сравнить показания обоих измерителей, выявить максимальное фактическое отклонение. Затем остается только посчитать процент отклонения от диапазона измерений прибора.
Советы по выбору счетчиков
Выбор приборов учета в магазинах — достаточно большой.
Анализируя, какой счетчик электроэнергии лучше, рекомендуется обратить внимание на следующие аспекты:
- стоимость счетчика (но нельзя кидаться на слишком дешевую продукцию, так как при ее изготовлении могли применяться низкокачественные комплектующие, снижающие срок службы оборудования);
- производителя устройства, сделав выбор в пользу проверенных компаний;
- гарантийный срок прибора;
- потребление электроэнергии самими счетчиками;
- уровень шума прибора;
- возможность осуществлять сервисное обслуживание.
Не нужно сразу отказываться от покупки немного морально устаревших индукционных моделей. Они, как и электронные приборы, имеют свои преимущества. Нет необходимости также приобретать устройства, имеющие множество функций, которые не будут использоваться. К тому же большое количество микросхем в счетчиках повышает риск его выхода из строя.
Также при покупке следует убедиться в наличии хорошо читаемых пломб, начальных показаний и заводских штампов в паспорте, гарантийного талона. Приобретение регистраторов рекомендуется осуществлять в специализированных магазинах.

Важно тщательно проверить дату проведенной поверки счетчика.
Согласно ПУЭ вновь устанавливаемые приборы должны иметь пломбы госповерки с давностью:
- для трехфазных моделей: до одного года;
- для однофазных: до двух лет.
Таким образом, если дата поверки истекла, прибор не поставят на учет без проведения новой.
Важно! Рекомендации, какой счетчик электроэнергии выбрать, есть на сайте поставщика электроэнергии. В различных регионах могут быть рекомендованы к установке счетчики разных марок.
Помимо известных зарубежных производителей, продукция которых давно пользуется популярностью (ABB, GE) на рынке представлены и модели отечественных компаний (Энергомера — производитель одноименных приборов, Инкотекс, выпускающий счетчики Меркурий, Тайпит, предлагающий регистраторы Нева). Причем, их качество порой не уступает импортным, а цена — гораздо ниже.
Определение погрешности
Владельцев измерительных приборов интересует, прежде всего, величина максимальной погрешности, характерной для манометра. Она зависит не только от класса точности, но и от диапазона измерений. Таким образом, чтобы получить значение погрешности, нужно произвести некоторые вычисления. Например, для манометра с диапазоном измерений, равным 6 МПа, и классом точности 1,5 погрешность будет рассчитываться по формуле 6*1,5/100=0,09 МПа.

Необходимо отметить, что таким способом можно посчитать только основную погрешность.
Ее величина определяется идеальными условиями эксплуатации. На нее оказывают влияние только конструктивные характеристики, а также особенности сборки прибора, например, точность градуировки делений на шкале, сила трения в измерительном механизме. Однако эта величина может отличаться от фактической, поскольку существует также дополнительная погрешность, определяемая условиями, в которых эксплуатируется манометр. На нее может влиять вибрация трубопровода или оборудования, температура, уровень влажности и другие параметры.
Также точность измерения давления зависит от еще одной характеристики манометра — величины его вариации, которую определяют в ходе поверки. Это максимальная разница показаний измерителя, выявленная по результатам нескольких измерений.
Величина вариации в значительной мере зависит от конструкции манометра, а именно от способа уравновешивания, которое может быть жидкостным (давлением столба жидкости) или механическим (пружиной). Механические манометры имеют более выраженную вариацию, что часто обусловлено дополнительным трением при плохой смазке или износе деталей, потере упругости пружины и другими факторами.
Источник: grom.ru
Пределы
Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Базовый способ определения погрешности
При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.
Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.
Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5
Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.
Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.
Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.
Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

Пример расчета погрешности
Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.
Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.
Технические характеристики
Согласно документации, на схемах сети вольтметры принято обозначение окружностью с вписанной латинской буквой «V». На русских смехах он может заменяться на русскую букву «В». Более того, первая цифра после буквы в маркировке отображает тип устройства и специфику его использования. Например, В2 — вольтметр для постоянного тока, В3 — для переменного, В4 — для импульсного и т.д.
Вам это будет интересно Разновидности бытовых и промышленных электрических выключателей

Оценка характеристик прибора включает в себя следующие компоненты:
- Диапазон измерений. Он ограничивается наименьшим и наибольшим показателем, который способен изменить аппарат. Современные устройства обладают диапазоном от милливольт до киловольт. Промышленные аналоги же способны измерять как меньшие, так и большие напряжения;
- Точность измерений. Далеко не каждый домашний тестер отличается повышенной точностью измерений. Как уже было сказано, это зависит от его внутреннего сопротивления. Новые вольтметры при сравнительно небольших размерах обладают маленькими погрешностями измерений;
- Диапазон частот. Показывает чувствительность прибора к тем или иным сигналам с разными частотами, регистрируемых в сети;
- Температура и другие факторы. Эти параметры определяют показатели, при которых аппарат обладает минимальной погрешностью измерений, доступной для него;
- Собственно само внутреннее сопротивление (импеданс). Чем выше этот параметр, тем вольтметр более точен.

Важно! Технические характеристики аналоговых приборов сильно зависят от чувствительности магнитоэлектрического прибора. Чем меньше его ток полного отклонения, тем более высокосопротивительные резисторы можно использовать
Для чего используются
Разнообразные виды измерительных трансформаторов встречаются как в небольших приборах размером со спичечный коробок, так и в крупных энергетических установках. Их основное назначение – понижать первичные токи и напряжения до значений, необходимых для измерительных устройств, защитных реле и автоматики. Применение понижающих катушек обеспечивает защиту цепи низшего и высшего ранга, поскольку они разделены между собой.
Понижающие средства разделяют по признакам эксплуатации и предназначены для:
- измерений. Они передают вторичный ток на приборы;
- защиты токовых цепей;
- применения в лабораториях. Такие понижающие средства имеют высокую классность точности;
- повторного конвертирования, они относятся к промежуточным инструментам.

Измерение
Измерительный трансформатор необходим для понижения высокого тока основного напряжения и передачу его на измерительные устройства. Для подключения стандартных приборов к высоковольтной сети потребовались бы громоздкие установки. Реализовывать инструменты таких размеров экономически не выгодно и не целесообразно.
Использование понижающих трансформаторов позволяет применять обычные устройства измерения в обычном режиме, что расширяет спектр их применения. Благодаря снижению напряжения, они не требуют дополнительных модификаций. Трансформатор отделяет высоковольтное напряжение сети от питающего напряжения приборов, обеспечивая безопасность из использования. От их классности зависит точность учета электрической энергии.
Защита
Кроме питания измерительных приборов понижающие трансформаторы подают напряжение на системы защиты и автоматической блокировки. Поскольку в сетевой электросети происходят перепады и скачки напряжения, которое губительно для высокоточного оборудования цепи.

В энергетических установках оборудование делится на силовое и вторичное, которое контролирует процессы первичной схемы подключения устройств. Высоковольтная аппаратура располагается на открытых площадках или устройствах. Вторичное оборудование находится на релейных планках внутри распределительных шкафов.
Промежуточным элементом передачи информации между силовыми агрегатами и средствами измерения, управления, контроля и защиты являются понижающие или измерительные трансформаторы. Они разделяют первичную и вторичную цепь от пагубного воздействия силовых агрегатов на чувствительные измерительные приборы, а также защищают обслуживающий персонал от повреждений.
Аннотация: Рассмотрим подробный порядок операций, выполняемых при обработке результатов измерений. Содержание всех описываемых действий рассмотрено в предыдущих разделах. Проводимые расчеты основываются на предположении о нормальном распределении погрешностей, когда систематические погрешности уже учтены на предыдущих этапах работы с экспериментальными данными.
Нормирование погрешностей средств измерений
Нормирование метрологических характеристик средств измерений и заключается в установлении границ для отклонений реальных значений параметров средств измерений от их номинальных значений.
Каждому средству измерений приписываются некоторые номинальные характеристики. Действительные же характеристики средств измерений не совпадают с номинальными, что и определяет их погрешности.
Обычно нормирующее значение принимают равным:
- большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
- сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
- длине шкалы или её части, соответствующей диапазону измерения, если шкала существенно неравномерна (например, у омметра);
- номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
- модулю разности пределов измерений, если принята шкала с условным нулём (например, для температуры), и т.д.
Чаще всего за нормирующее значение принимают верхний предел измерений данного средства измерений.
Отклонения параметров средств измерений от их номинальных значений, вызывающие погрешность измерений, не могут быть указаны однозначно, поэтому для них должны быть установлены предельно допускаемые значения.
Указанное нормирование является гарантией взаимозаменяемости средств измерений.
Нормирование погрешностей средств измерений заключается в установлении предела допускаемой погрешности.
Под этим пределом понимается наибольшая (без учёта знака) погрешность средства измерения, при которой оно может быть признано годным и допущено к применению.
Подход к нормированию погрешностей средств измерений заключается в следующем:
- в качестве норм указывают пределы допускаемых погрешностей, включающие в себя и систематические, и случайные составляющие;
- порознь нормируют все свойства средств измерений, влияющие на их точность.
Стандарт устанавливает ряды пределов допускаемых погрешностей. Этой же цели служит установление классов точности средств измерений.
Классы точности средств измерений
Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности не является непосредственной оценкой точности измерений, выполняемых этим СИ, поскольку погрешность зависит еще от ряда факторов: метода измерений, условий измерений и т.д. Класс точности лишь позволяет судить о том, в каких пределах находится погрешность СИ данного типа. Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401–80.
Пределы допускаемой основной погрешности, определяемые классом точности, – это интервал, в котором находится значение основной погрешности СИ.
Классы точности СИ устанавливаются в стандартах или технических условиях. Средство измерения может иметь два и более класса точности. Например, при наличии у него двух или более диапазонов измерений одной и той же физической величины ему можно присваивать два или более класса точности. Приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины.
Пределы допускаемых основной и дополнительной погрешностей выражают в форме приведенных, относительных или абсолютных погрешностей. Выбор формы представления зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения СИ.
Пределы допускаемой абсолютной основной погрешности устанавливаются по одной из формул: 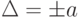 или
или 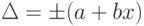 , где x – значение измеряемой величины или число делений, отсчитанное по шкале;
, где x – значение измеряемой величины или число делений, отсчитанное по шкале;
a, b – положительные числа, не зависящие от х. Первая формула описывает чисто аддитивную погрешность, а вторая – сумму аддитивной и мультипликативной погрешностей.
В технической документации классы точности, установленные в виде абсолютных погрешностей, обозначают, например, “Класс точности М”, а на приборе – буквой “М”. Для обозначения используются прописные буквы латинского алфавита или римские цифры, причём меньшие пределы погрешностей должны соответствовать буквам, находящимся ближе к началу алфавита, или меньшим цифрам. Пределы допускаемой приведенной основной погрешности определяются по формуле  , где xN – нормирующее значение, выраженное в тех же единицах, что и
, где xN – нормирующее значение, выраженное в тех же единицах, что и  ; p – отвлеченное положительное число, выбираемое из ряда значений:
; p – отвлеченное положительное число, выбираемое из ряда значений:
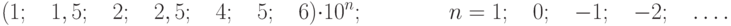
Нормирующее значение xN устанавливается равным большему из пределов измерений (или модулей) для СИ с равномерной, практически равномерной или степенной шкалой и для измерительных преобразователей, для которых нулевое значение выходного сигнала находится на краю или вне диапазона измерений. Для СИ, шкала которых имеет условный нуль, равно модулю разности пределов измерений.
Для приборов с существенно неравномерной шкалой xN принимают равным всей длине шкалы или ее части, соответствующей диапазону измерении. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на средстве измерений класс точности условно обозначают, например, в виде значка 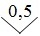 , где 0,5 – значение числа р (рис. 3.1).
, где 0,5 – значение числа р (рис. 3.1).
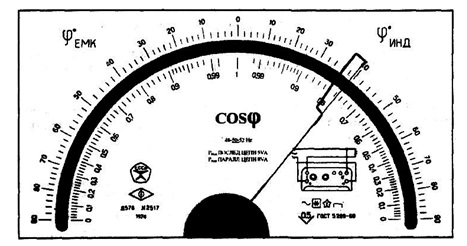
Рис.
3.1.
Лицевая панель фазометра класса точности 0,5 с существенно неравномерной нижней шкалой
В остальных рассмотренных случаях класс точности обозначают конкретным числом р, например 1,5. Обозначение наносится на циферблат, щиток или корпус прибора (рис. 3.2).
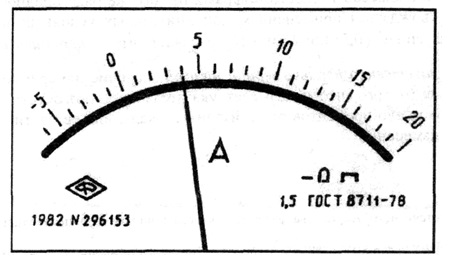
Рис.
3.2.
Лицевая панель амперметра класса точности 1,5 с равномерной шкалой
В том случае если абсолютная погрешность задается формулой 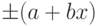 , пределы допускаемой относительной основной погрешности
, пределы допускаемой относительной основной погрешности
![delta=Delta/x=pm[c+d(|x_{k}/x|-1)]](https://intuit.ru/sites/default/files/tex_cache/3898a996678dab895193a1773d11ffc8.png) |
( 3.1) |
где с, d – отвлеченные положительные числа, выбираемые из ряда: 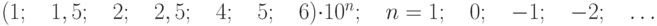 ; – больший (по модулю) из пределов измерений. При использовании формулы 3.1 класс точности обозначается в виде “0,02/0,01”, где числитель – конкретное значение числа с, знаменатель – числа d (рис. 3.3).
; – больший (по модулю) из пределов измерений. При использовании формулы 3.1 класс точности обозначается в виде “0,02/0,01”, где числитель – конкретное значение числа с, знаменатель – числа d (рис. 3.3).
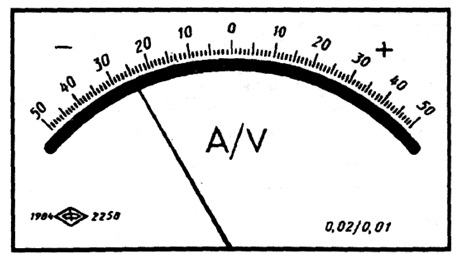
Рис.
3.3.
Лицевая панель ампервольтметра класса точности 0,02/0,01с равномерной шкалой
Пределы допускаемой относительной основной погрешности определяются по формуле 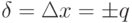 , если
, если 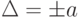 . Значение постоянного числа q устанавливается так же, как и значение числа p. Класс точности на прибор обозначается в виде
. Значение постоянного числа q устанавливается так же, как и значение числа p. Класс точности на прибор обозначается в виде 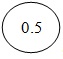 , где 0,5 – конкретное значение q (рис. 3.4).
, где 0,5 – конкретное значение q (рис. 3.4).
Рис.
3.4.
Лицевая панель мегаомметра класса точности 2,5 с неравномерной шкалой
В стандартах и технических условиях на СИ указывается минимальное значение x0, начиная с которого применим принятый способ выражения пределов допускаемой относительной погрешности. Отношение xk/x0 называется динамическим диапазоном измерения.
Правила построения и примеры обозначения классов точности в документации и на средствах измерений приведены в таблице 3.1.
Контрольные вопросы
- Поясните, что такое класс точности СИ.
- Является ли класс точности СИ непосредственной оценкой точности измерений, выполняемых этим СИ?
- Перечислите основные принципы, лежащие в основе выбора нормируемых метрологических характеристик средств измерений.
- Как нормируются приборы по классам точности?
- Какие метрологические характеристики описывают погрешность средств измерений?
- Как осуществляется нормирование метрологических характеристик средств измерений?
