Определение алгебраической дроби
Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).
Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).
Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.
Алгебраические (рациональные) дроби
Иррациональные дроби
$ frac{25+x^2}{x-4}$
$ frac{a^3-2sqrt3}{b^2-sqrt[3]13}$
$ frac{5+sqrt x}{4-x} $
$ frac{16a^frac{5}{3}+1}{4sqrt[3]a-1} $
Внимание!
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
Например: Дробь $frac{x+5}{x-4}$ существует при условии x≠4. Допустимые значения переменной ${x| x in Bbb R, x neq 4 } $.
Дробь $frac{y}{y^2-9}$ существует при условии y≠±3. Допустимые значения переменной $ { y| y in Bbb R, y neq pm 3 }$.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
$$ frac{a}{b} = frac{ma}{mb}, b neq 0, m neq 0 $$
Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:
$$ frac{2x+3y}{4x^2-9y^2} = frac{2x+3y}{(2x+3y)(2x-3y)} = frac{1}{2x-3y} $$
$$ frac{a^3-8}{a-2} = frac{(a-2)(a^2+2a+4)}{a-2} = a^2+2a+4 $$
Приведение алгебраических дробей к общему знаменателю
Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:
$$ frac{1^{(x+1)}}{x-1} – frac{1}{x^2-1} – frac{1^{(x-1)}}{x+1} = frac{x+1-1-(x-1)}{(x-1)(x+1)} = frac{1}{x^2-1} $$
Алгоритм приведения алгебраических дробей к общему знаменателю
- Разложить все знаменатели на множители (коэффициенты, степени переменных, двучлены, трехчлены, многочлены)
- Найти наименьшее общее кратное знаменателей – это будет общий знаменатель.
- Найти дополнительные множители для каждой из дробей.
- Умножить числитель каждой из дробей на её дополнительный множитель, записать результат с общим знаменателем.
Например: привести к общему знаменателю $frac{1}{xy^2}, frac{x}{y}, frac{-4}{x}$
Шаг 1. Наименьшее общее кратное: $xy^2$
Шаг 2. Дополнительные множители
$$ frac{1}{xy^2}, frac{x^{xy}}{y}, -frac{4^{y2}}{x}$$
Шаг 3. Результат:
$$ frac{1}{xy^2}, frac{x^2 y}{xy^2}, -frac{4y^2}{xy^2} $$
Перемена знака у члена дроби
Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:
$$ frac{x}{y} = frac{-x}{-y} $$
Дробь также не изменится, если провести следующие перемены знаков:
$$ frac{x}{y} = frac{-x}{y} = -frac{x}{-y} $$
Ещё несколько полезных формул, связанных с переменой знаков:
$$ frac{a-b}{b-a} = -1, frac{(a-b)^2}{(b-a)^2} = 1, frac{1}{a-b} = -frac{1}{b-a}, frac{1}{(a-b)^2} = frac{1}{(b-a)^2} $$
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
а)$ frac{5}{a^2-4}$
$ a^2-4 neq 0 iff (a-2)(a+2) neq 0 iff a neq pm 2$
${a| a in Bbb R, a neq pm 2}$ – все действительные числа, кроме $pm 2$
б)$ frac{7x+y}{3x-1}$
$ 3x-1 neq 0 iff x neq frac{1}{3}$
${x|x in Bbb R, x neq frac{1}{3}}$ – все действительные числа, кроме $frac{1}{3}$
в)$ frac{k^2-1}{k+1}$
$k+1 neq 0 iff k neq -1 $
${k|k in Bbb R, k neq -1}$ – все действительные числа, кроме -1
Обратите внимание: несмотря на то, что дробь сокращается $frac{k^2-1}{k+1} = frac{(k+1)(k-1)}{k+1} = k-1$ требование $k neq -1$ сохраняется.
г) $ frac{5}{x^2+6x+9}$
$x^2+6x+9 neq 0 iff (x+3)^2 neq 0 iff x neq -3 $
$ {x|x in Bbb R, x neq -3}$ – все действительные числа, кроме -3
д)*$ frac{1}{x-frac{4}{x}} $
$$ x- frac{4}{x} neq 0 iff frac{x^2-4}{x} neq 0 iff {left{ begin{array}{c} x^2-4 neq 0 \ x neq 0 end{array} right.} iff x neq {0; pm2}$$
${x|x in Bbb R, x neq {0;pm2}}$ – все действительные числа, кроме $0,pm2$
е)*$ frac{5}{y^2-3|y|} $
$ y^2-3|y| neq 0 iff |y|(|y|-3) neq 0 iff {left{ begin{array}{c} |y| neq 0 \ |y| neq 3 end{array} right.} iff y neq {0; pm3} $
${y|y in Bbb R, y neq {0; pm3} }$ – все действительные числа, кроме $0, pm3$
Пример 2. Сократите дроби:
а) $$ frac{a^2-9}{2a+6} = frac{(a-3)(a+3)}{2(a+3)} = frac{a-3}{2}$$
б)$$ frac{x^2+2x+1}{x^2-1} = frac{(x+1)^2}{(x+1)(x-1)} = frac{x+1}{x-1}$$
в) $$ frac{12x^2-8xy}{3xy-2y^2} = frac{4x(3x-2y)}{y(3x-2y)} = frac{4x}{y} $$
г) $$ frac{b+5}{b^3-125} = frac{b+5}{(b+5)(b^2-5b+25)} = frac{1}{b^2-5b+25} $$
Пример 3. Упростите выражение:
а) $$ frac{a-b}{(b-a)^2} = frac{a-b}{(a-b)^2} = frac{1}{a-b}$$
б) $$ frac{(-a-b)^2}{a+b} = frac{(-1)^2 (a+b)^2}{a+b} = a+b $$
в) $$ frac{(-a-b)^2}{(a+b)^2} = frac{(a+b)^2}{(a+b)^2} = 1 $$
г) $$ frac{(a-b)^2}{b-a} = frac{(b-a)^2}{b-a} = b-a $$
Пример 4. Постройте график функции:
(О графике линейной функции – см. §38 справочника для 7 класса)
$а) y(x) = frac{x^2-4}{2x+4}$
$$ y(x) = frac{(x-2)(x+2)}{2(x+2)} = {left{ begin{array}{c} frac{x-2}{2} \ x neq -2 end{array} right.} $$
График – прямая y(x) = 0,5x-1, кроме точки (-2;-2), т.к. $x neq -2$.
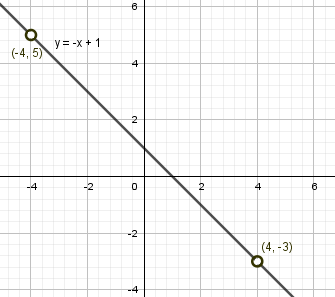
$б) y(x) = frac{x^3-16x}{x^2-16}-2x+1$
$$ y(x) = frac{x(x^2-16)}{x^2-16}-2x+1 = {left{ begin{array}{c} -x+1 \ x neq pm 4 end{array} right.} $$
График – прямая y(x) = -x+1, кроме точек (-4;5) и (4;-3), т.к. $x neq pm 4$.
Любое выражение с переменной в алгебре (математике) имеет свою область допустимых значений (или ОДЗ), где оно существует. ОДЗ – это то, что необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как найти ОДЗ (ОДЗ логарифма, ОДЗ корня), использовать на примерах
(без необходимости искать готовые решения онлайн). Также будет рассмотрена важность указания ОДЗ при решении домашних заданий, гдз и прочих случаях.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1:а, если а=0, тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут подробно ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда можно уже определять более полно
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Для примера рассмотрим выражение вида 1x-y+z, где имеются три переменные. Иначе можно записать, как x=0, y=1, z=2, другая же запись имеет вид (0,1,2). Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 10-1+2=11=1. Отсюда видим, что (1,1,2) недопустимы. Подстановка дает в результате деление на ноль, то есть 11-2+1=10.
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Если имеем выражение вида 5z-3, тогда ОДЗ имеет вид (−∞, 3)∪(3, +∞). Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.
Если имеется выражения вида zx-y, тогда видно, что x≠y, z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f(x).
Как найти ОДЗ? Примеры, решения
Поиск определенного ОДЗ означает поиск всех допустимых значений, подходящих для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Как находить ОДЗ? Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Как решать ОДЗ? Существуют выражения, где их вычисление невозможно:
- если имеется деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого показателя – только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения тангенса π2+π·k, k∈Z и котангенса π·k, k∈Z;
- нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [-1; 1].
Все это говорит о том, как важно наличие ОДЗ.
Найти ОДЗ выражения x3+2·x·y−4.
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Найти ОДЗ выражения 13-x+10.
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅.
Найти ОДЗ заданного выражения x+2·y+3-5·x.
Решение
Наличие квадратного корня (квадрат корня) говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x+2·y+3≥0. То есть это и есть искомая область допустимых значений.
Ответ: множество x и y, где x+2·y+3≥0.
Определить ОДЗ выражения вида 1x+1-1+logx+8(x2+3).
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x+1-1≠0 . Выражение под корнем всегда имеет смысл, когда больше или равно нулю, то есть x+1≥0. Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x2+3>0. Основание логарифма также должно иметь положительное значение и отличное от 1, тогда добавляем еще условия x+8>0 и x+8≠1. Отсюда следует, что искомое ОДЗ примет вид:
x+1-1≠0,x+1≥0,x2+3>0,x+8>0,x+8≠1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [−1, 0)∪(0, +∞).
Ответ: [−1, 0)∪(0, +∞)
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
Тождественные преобразования:
- могут не влиять на ОДЗ;
- могут привести к расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Если имеем выражение вида x2+x+3·x, тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Если взять пример выражения x+3x−3x, то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид (−∞, 0)∪(0, +∞). Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Если имеется x-1·x-3, тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства (x−1)·(x−3)≥0. Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид (−∞, 1]∪[3, +∞). После преобразования x-1·x-3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x-1≥0,x-3≥0. При ее решении получаем, что [3, +∞). Значит, ОДЗ полностью записывается так: (−∞, 1]∪[3, +∞).
Нужно избегать преобразований, которые сужают ОДЗ.
Рассмотрим пример выражения x-1·x-3, когда х=-1. При подстановке получим, что -1-1·-1-3=8=22. Если это выражение преобразовать и привести к виду x-1·x-3, тогда при вычислении получим, что 2-1·2-3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Рассмотрим на примере дроби вида xx3+x. Если сократить на x, тогда получаем, что 1×2+1. Тогда ОДЗ расширяется и становится (−∞ 0)∪(0, +∞). Причем при вычислении уже работаем со второй упрощенной дробью.
В случае нахождения ОДЗ для логарифмов дело обстоит немного иначе. Вот пример нахождения ОДЗ для логарифма.
Если имеется выражение вида ln x+ln(x+3), его заменяют на ln(x·(x+3)), опираясь на свойство логарифма. Отсюда видно, что ОДЗ с (0, +∞) до (−∞, −3)∪(0, +∞). Поэтому для определения ОДЗ ln(x·(x+3)) необходимо производить вычисления на ОДЗ, то есть (0, +∞) множества.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Колягин Ю.М. Ткачева М.В. Федорова Н.Е
УЧЕБНИК ДЛЯ 7 КЛАССА
гдз решебник алгебра 7 класс
учебник ответы готовые домашние задания
УСТНЫЕ ВОПРОСЫ И ЗАДАНИЯ (параграф 24)
OCR перевод условия
устные вопросы и задания параграф 24
учебник по алгебре Колягин 7 класс
§ 24. Алгебраическая дробь. Сокращение дробей
Нужно вспомнить: • понятие обыкновенной дроби; • основное свойство обыкновенной дроби; • решение линейных уравнений; • условие равенства нулю произведения двух и более чисел; • способы разложения многочлена на множители; • понятие числа, обратного данному числу; • понятие числа, противоположного данному числу; • понятие модуля числа.
Устные вопросы и задания 1. Чем являются числитель и знаменатель алгебраической дроби?
2. Что называют значением алгебраической дроби?
3. Что такое допустимые значения букв, входящих в алгебраическую дробь?
4. Как найти допустимые значения букв, входящих в алгебраическую дробь?
5. Сформулировать основное свойство дроби.
6. Как сократить алгебраическую дробь?
Калькулятор расчета монолитного плитного фундамента тут obystroy.com
Как снять комнату в коммунальной квартире здесь
Дренажная система водоотвода вокруг фундамента – stroidom-shop.ru