Конспект
Целые выражения – это такие выражения, которые состоят из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля.

Дробные выражения – это выражения, которые помимо действий сложения, вычитания, умножения и деления на число, отличное от нуля, содержат деление на выражение с переменными.

Целые и дробные выражения вместе называют рациональными выражениями.
Дробь – это выражение вида ![]() .
.
Целое выражение имеет смысл при любых значениях входящих в него переменных, потому что действия для нахождения значения целого выражения, всегда возможны.
Дробное выражение при некоторых значениях переменной может не иметь смысла.
Примеры
Дробные выражения имеют смысл при любых значениях входящих в них переменных, кроме тех, что обращают знаменатель в нуль.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями.
Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.
Примеры

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Чтобы найти допустимые значения переменных в дроби, необходимо:
-
• Приравнять знаменатель, содержащий переменные, к нулю.
• Решить полученное уравнение. Корни этого уравнения будут являться теми значениями переменных, которые обращают знаменатель в нуль.
• Исключить эти значения из всех действительных чисел.
Пример 1.
Найти допустимые значения переменной в дроби  .
.
1) x(x + 1) = 0
2) x = 0 или x + 1 = 0
x = 0 или x = –1.
Корни уравнения 0 и – 1.
3) Допустимыми значениями x являются все числа, кроме 0 и –1.
Пример 2.
Найти значения x, при которых дробь  равна нулю.
равна нулю.
 , когда x2 – 1 = 0 и x + 1 ≠ 0.
, когда x2 – 1 = 0 и x + 1 ≠ 0.
1) x2 – 1 = 0
2) (x – 1)(x + 1) = 0
x = ±1
3) x + 1 ≠ 0
x ≠ –1.
 при x = 1.
при x = 1.
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
- Подробности
- Категория: Алгебра 7-9 классы
Рациональные дроби и их свойства
1. Рациональные выражения
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла
при а = 0. При всех остальных значениях а это выражение имеет
смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида называется, как известно, дробью.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдем допустимые значения переменной в дроби
Чтобы найти, при каких значениях а знаменатель дроби обращается в нуль, нужно решить уравнение а(а – 9) = 0.
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Пример 2. При каком значении х значение дроби равно нулю ?
Дробь равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.
Числители дроби равен нулю, если
, т.е.
или
. Итак, числитель дроби равен нулю при x = 7 и x= -3. Знаменатель данной дроби не равен нулю, если x ≠ -3. Значит, данная дробь равна нулю при x = 7.
2. Основное свойство дроби. Сокращение дробей
Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство
Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.
Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :
На основании сочетательного и переместительного свойств умножения имеем:
Так как bс ≠ 0, то по определению частного
Значит,
Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство
Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.
Равенство (1) выражает основное свойство рациональной дроби:
если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Например,
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.
Пример 1. Приведем дробь к знаменателю
Так как то, умножив числитель и знаменатель дроби
на
, получим:
Множитель называют дополнительным множителем к числителю и знаменателю дроби
Пример 2. Приведем дробь к знаменателю
Для этого числитель и знаменатель данной дроби умножим на -1:
Дробь можно заменить тождественно равным выражением
, поставив знак “минус” перед дробью и заменив знак в числителе:
Вообще
если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.
Пример 3. Сократим дробь
Разложим числитель и знаменатель дроби на множители:
Сократим полученную дробь на общий множитель a + 3:
Итак,
Пример 4. Построим график функции
Область определения функции -множество всех чисел, кроме числа 4. Сократим дробь
Графиком функции является прямая, а графиком функции
но с “выколотой” точкой (4 ; 4) (рис. 1.)
Допустимые
значения переменных,
входящих в дробное выражение
Цели:
формировать умение находить допустимые значения переменных, входящих в дробные
выражения.
Ход урока
I. Организационный момент.
II. Устная работа.
– Подставьте вместо * какое-нибудь число и
назовите полученную дробь:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г)
![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з)
![]() .
.
III. Объяснение нового
материала.
Объяснение нового материала
происходит в т р и э т а п а:
1. Актуализация знаний
учащихся.
2. Рассмотрение вопроса о том,
всегда ли рациональная дробь имеет смысл.
3. Вывод правила нахождения
допустимых значений переменных, входящих в рациональную дробь.
При актуализации знаний
учащимся можно задать следующие
в о п р о с ы:
– Какую дробь называют
рациональной?
– Всякая ли дробь является дробным
выражением?
– Как найти значение рациональной дроби
при заданных значениях входящих в неё переменных?
Для выяснения вопроса о допустимых значениях
переменных, входящих в рациональную дробь, можно предложить учащимся выполнить
задание.
З а д а н и е. Найдите
значение дроби при указанных значениях переменной:
![]() при х = 4; 0; 1.
при х = 4; 0; 1.
Выполняя данное задание,
учащиеся понимают, что при х = 1 невозможно найти значение
дроби. Это позволяет им сделать следующий в ы в о д: в рациональную дробь
нельзя подставлять числа, которые обращают её знаменатель в нуль (этот вывод
должен быть сформулирован и произнесён вслух самими учащимися).
После этого учитель сообщает учащимися, что все
значения переменных, при которых рациональное выражение имеет смысл, называют
допустимыми значениями переменных.
Далее ставится вопрос: как находить
допустимые значения переменных? При поиске ответа на этот вопрос учащиеся
должны сформулировать р я д в о п р о с о в:
1) Если выражение является
целым, то все значения входящих в него переменных будут допустимыми.
2) Чтобы найти допустимые значения
переменных дробного выражения, нужно проверить, при каких значениях знаменатель
обращается в нуль. Найденные числа не будут являться допустимыми значениями.
IV. Формирование умений и навыков.
1. № 10, № 11.
Ответ на вопрос о допустимых значениях
переменных, входящих в дробное выражение, может звучать по-разному. Например,
рассматривая рациональную дробь ![]() , можно сказать, что допустимыми значениями
, можно сказать, что допустимыми значениями
переменной являются все числа, кроме х = 4, или что в допустимые
значения переменной не входит число 4, то есть х ≠ 4.
И та и другая формулировки являются
верными, главное – следить за правильностью оформления.
О б р а з е ц о ф о р м л е н и я:
№ 11.
г) 
4х (х + 1) = 0
|
4х = 0 или х = 0 |
х + 1 = 0 х = –1 |
О т в е т: х ≠ 0 и х
≠ 1 (или все числа, кроме 0 и –1).
2. № 13.
3. № 14 (а, в), № 15.
При выполнении этих заданий следует
обратить внимание учащихся на необходимость учёта допустимых значений
переменных.
№ 15.
г) ![]()
|
х (х х = |
2х + 6 ≠ 0 х = |
О т в е т: х = 0.
4. № 17.
Следить за обоснованием всех рассуждений.
В классе с высоким уровнем
подготовки можно дополнительно выполнить № 18 и № 20.
№ 18.
Р е ш е н и е
а) ![]() .
.
Из всех дробей с одинаковым положительным
числителем большей будет та, у которой знаменатель является наименьшим. То есть
необходимо найти, при каком значении а выражение а2 +
5 принимает наименьшее значение.
Поскольку выражение а2
не может быть отрицательным ни при каких значениях а, то выражение а2
+ 5 будет принимать наименьшее значение при а = 0.
О т в е т: а = 0.
б)  .
.
Рассуждая аналогично, получим, что
необходимо найти то значение а, при котором выражение (а – 3)2
+ 1 принимает наименьшее значение.
О т в е т: а = 3.
№ 20.
Р е ш
е н и е
 .
.
Для
ответа на вопрос предварительно нужно преобразовать выражение, стоящее в
знаменателе дроби.
 .
.
Дробь
будет принимать наибольшее значение, если выражение (2х +
+ у)2 + 9 принимает наименьшее значение. Поскольку (2х
+ у)2 не может принимать отрицательные значения, то
наименьшее значение выражения (2х + у)2 + 9 равно 9.
Тогда
значение исходной дроби равно ![]() = 2.
= 2.
V.
Итоги урока.
В
о п р о с ы у ч а щ и м с я:
–
Какие значения называются допустимыми значениями переменных, входящих в
выражение?
–
Каковы допустимые значения переменных целого выражения?
–
Как найти допустимые значения переменных дробного выражения?
–
Существуют ли рациональные дроби, для которых все значения переменных являются
допустимыми? Приведите примеры таких дробей.
Домашнее
задание: № 12,
№ 14 (б, г), № 212.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Рациональные выражения
- Рациональные дроби
Ранее мы познакомились с целыми выражениями, то есть выражениями, составленными из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля. Так, например, к целым выражениям относятся выражения
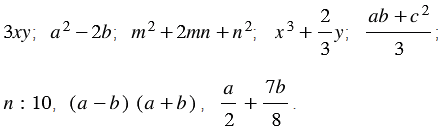
Теперь рассмотрим дробные выражения.
Дробные выражения – это выражения, которые кроме действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Так, например, к дробным выражениям относятся выражения
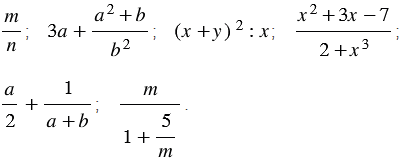
Целые и дробные выражения называют рациональными выражениями.
Если в целом выражении заменить переменные числами, то получим числовое выражение, которое всегда имеет смысл, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Если в дробном выражении заменить переменные числами, то получим числовое выражение, которое может не иметь смысла, если эта замена приводит к делению на нуль, т.к. на нуль делить нельзя.
Например, выражение  при
при 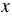 = 3 не имеет смысла, то есть не существует числового значения этого выражения при
= 3 не имеет смысла, то есть не существует числового значения этого выражения при 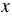 = 3. При всех остальных значениях
= 3. При всех остальных значениях 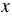 это выражение имеет смысл.
это выражение имеет смысл.
Определение:
Допустимыми значениями переменных, входящих в рациональное выражение, называют все значения переменных, при которых это выражение имеет смысл.
Так, в рассмотренном выше выражении допустимыми значениями переменной 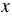 являются все числа, кроме 3.
являются все числа, кроме 3.
Допустимыми значениями переменных, входящих в целое выражение, являются все числа.
Среди рациональных выражений можно выделить отдельный вид выражений – рациональные дроби или еще их называют алгебраические дроби.
Рациональная дробь (алгебраическая дробь) – это дробь, числитель и знаменатель которой – многочлены. При этом помним то, что числа и одночлены считают отдельным видом многочленов.
Примерами рациональных дробей служат дроби
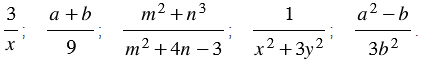
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
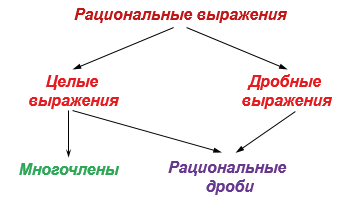
Схематично связь между рациональными выражениями, многочленами, целыми выражениями, дробными выражениями и рациональными дробями можно изобразить так:
Пример. Найдите допустимые значения переменной, входящей в выражение 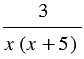 .
.
Решение:
Чтобы найти, при каких значениях 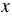 знаменатель рассматриваемого выражения обращается в нуль, т.е. значения переменной, при которых выражение не имеет смысла, нужно решить уравнение
знаменатель рассматриваемого выражения обращается в нуль, т.е. значения переменной, при которых выражение не имеет смысла, нужно решить уравнение 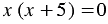 . Учитывая то, что произведение равно нулю, если хотя бы один из множителей равен нулю, это уравнение имеет два корня
. Учитывая то, что произведение равно нулю, если хотя бы один из множителей равен нулю, это уравнение имеет два корня 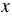 = 0 и
= 0 и 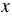 =
= 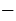 5, т.к.
5, т.к. 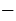 5 + 5 = 0.
5 + 5 = 0.
Следовательно, допустимыми значениями переменной 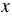 в рассматриваемом выражении являются все числа, кроме 0 и
в рассматриваемом выражении являются все числа, кроме 0 и 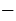 5.
5.
Советуем посмотреть:
Основное свойство рациональной дроби
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями
Умножение и деление рациональных дробей. Возведение рациональной дроби в степень
Равносильные уравнения. Рациональные уравнения
Степень с целым отрицательным показателем
Свойства степени с целым показателем
Функция y=k/x и её график.
Рациональные выражения
Правило встречается в следующих упражнениях:
8 класс
Номер 7,
Мерзляк, Полонский, Якир, Учебник
Номер 87,
Мерзляк, Полонский, Якир, Учебник
Номер 89,
Мерзляк, Полонский, Якир, Учебник
Номер 100,
Мерзляк, Полонский, Якир, Учебник
Номер 104,
Мерзляк, Полонский, Якир, Учебник
Номер 109,
Мерзляк, Полонский, Якир, Учебник
Номер 118,
Мерзляк, Полонский, Якир, Учебник
Номер 159,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
Номер 369,
Мерзляк, Полонский, Якир, Учебник
Целые выражения – это выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля.
Дробные выражения допускают также деление на выражение с переменными.
Целые и дробные выражения называют рациональными выражениями.
Допустимые значения переменных – это те значения переменных, при которых выражение имеет смысл.
Рациональная дробь – это дробь, числителем и знаменателем которой являются многочлены.
Основное свойство дроби: если числитель и знаменатель некоторой рациональной дроби умножить на один и тот же многочлен, не равный тождественно нулю, то получится дробь, равная исходной.
Тождество – это равенство, которое верно при всех допустимых значениях переменных, входящих в это равенство.
Свойства действий с рациональными дробями:
Если а, b, с — многочлены, причем многочлен c не равен нулю тождественно, то верно:
-
$frac{a}{c}+frac{b}{c} = frac{a+b}{c}$
-
$frac{a}{c}-frac{b}{c} = frac{a-b}{c}$
Если a, b,c,d- многочлены, причем многочлены b и d тождественно не равны нулю, то верно:
-
$frac{a}{b}cdot frac{c}{d} = frac{ac}{bd}$
-
$(frac{a}{b})^n = frac{a^n}{b^n}$
Если a, b, с, d – многочлены, причем многочлены b, с и d тождественно не равны нулю, то верно:
-
$frac{a}{b} : frac{c}{d} = frac{ad}{bc}$
Пример 1. Сократите дробь $frac{x^2-2xy+y^2-1}{x-y+1}$
Решение:
$frac{x^2-2xy+y^2-1}{x-y+1} = frac{(x-y)^2-1}{x-y+1} = frac{(x-y-1)(x-y+1)}{x-y+1} = x-y-1 $
Ответ: х-у-1.
Пример 2. Упростите выражение $frac{2x^2-5}{(x-5)^3} – frac{45}{(x-5)^3}$
Решение:
$frac{2x^2-5}{(x-5)^3} – frac{45}{(x-5)^3} = frac{2x^2-5-45}{(x-5)^3} = frac{2(x^2-25)}{(x-5)^3} = frac{2(x^2-5^2)}{(x-5)^3} = $
$= frac{2(x-5)(x+5)}{(x-5)(x^2+5x+25)} = frac{2(x+5)}{x^2+5x+25} = frac{2x+10}{x^2+5x+25}$
Ответ: $frac{2x+10}{x^2+5x+25}$
Пример 3. Упростите выражение $(frac{3a^2}{a-b} – frac{3b^2}{a+b}) cdot frac{a^2-b^2}{4(a+b)^2}$
Решение:
$(frac{3a^2}{a-b} – frac{3b^2}{a+b}) cdot frac{a^2-b^2}{4(a+b)^2} = frac{3a^2(a+b) – 3b^2(a-b)}{a^2-b^2}cdot frac{a^2-b^2}{4(a+b)^2} =$
$= frac{3a^3+3a^2b-3ab^2-3b^3}{4(a+b)^2} = frac{3(a^3-b^3)+3ab(a-b)}{4(a+b)^2} = frac{3(a-b)(a^2+ab+b^2)+3ab(a-b)}{4(a+b)^2} =$
$= frac{3(a-b)(a^2+2ab+b^2)}{4(a+b)^2} = frac{3}{4}a – frac{3}{4}b = 0,75(a-b)$
Ответ: 0,75(a-b)
Пример 4. Выполните деление: $frac{x^2-3x}{2y^2} : frac{x-3}{4y}$
Решение:
$frac{x^2-3x}{2y^2} : frac{x-3}{4y} = frac{x(x-3)cdot 4y}{2y^2(x-3)} = frac{2x}{y}$
Ответ: $frac{2x}{y}$
