Загрузить PDF
Загрузить PDF
Искать выход из лабиринта очень весело, если только ваше умение ориентироваться не стремится к нулю. В таком случае вы можете почувствовать себя в тупике. Однако можно воспользоваться несколькими приемами, чтобы легко пройти через лабиринт. Правда, тогда вы лишите себя азарта от самостоятельного поиска выхода. В простых лабиринтах, где все стены соединены, можно воспользоваться правилом правой руки. А вот для любого другого лабиринта подойдет алгоритм Люка-Тремо.
-

1
Положите руку на правую стену от входа в лабиринт. Чтобы эта техника сработала, важно начать на входе. Очень часто люди пытаются использовать этот метод только после того, как заблудились в лабиринте. Однако попытка сделать это в середине лабиринта не поможет вам выбраться.[1]
-

2
Начните идти вдоль правой стены. Всегда ведите рукой вдоль стены в качестве ориентира. Идите вперед, прочь от выхода, пока не наткнетесь на перекресток или тупик.
-

3
Продолжайте идти вдоль правой стены через перекрестки и вокруг тупиков. Благодаря этому методу вам даже не нужно думать о том, как выйти из перекрестка или тупика. На перекрестках вы, как правило, будете идти по ближайшему пути справа от вас. А оказавшись в тупике и шагая вдоль правой стены, вы обернетесь вокруг и выйдите из него.
- При условии, что вы будете держать руку на правой стене и идти вперед, вы найдете выход.
Реклама
-

1
Найдите вещь, которую можно использовать, чтобы помечать каждую тропу. Важно, чтобы выбранное приспособление подходило для того, чтобы делать пометки на полу лабиринта. Например, на твердой поверхности, такой как дерево или бетон, можно использовать мел. В случае других поверхностей подумайте, что вы можете оставить после себя, например, хлебные крошки или камешки.
- Какой бы предмет вы ни использовали, у вас должна быть возможность сделать два разных вида маркировки. Вам нужно различать пути: какие вы прошли один раз, а какие — два.
-

2
Выберите случайную тропу и следуйте по ней до следующего перекрестка. У каждого лабиринта своя планировка на старте. Некоторые могут начинаться с перекрестка, а в других будет только одна тропа. В любом случае выберите любую тропу и идите вперед, пока не достигнете перекрестка или тупика.
-

3
Отмечайте тропы по мере их прохождения. Чтобы алгоритм Люка-Тремо сработал, очень важно отслеживать, какие тропы вы уже прошли. Обязательно отмечайте начало и конец каждой тропы любым выбранным для этого способом.
- Если вы идете по тропе в первый раз, вам нужно сделать на ней одну пометку. Если вы пользуетесь мелом, достаточно начертить одну простую линию. Если вы используете предметы, например, горсть камешков, оставляйте по камешку в начале и в конце тропы.
- Если вы идете по тропе во второй раз, отметьте ее еще раз. При использовании мела нарисуйте вторую линию, а в случае с предметами просто оставьте второй позади.
- Если вы зашли в тупик, пометьте тропу, чтобы распознать ее как тупиковую. Например, если вы используете мел, пометьте тропу буквой «Т». Сделайте эту пометку рядом с перекрестком, к которому ведет тропа.
-

4
На перекрестках отдавайте предпочтение тропам без пометок. Всякий раз выходя на перекресток, выделяйте минутку, чтобы осмотреть пометки на каждой тропе. Некоторые из них могут быть без пометок, в то время как другие покажут, что вы выбирали их уже один раз (или два). Стоит отдавать предпочтение тропам без пометок. Так вы с большей вероятностью будете продвигаться вперед. Если все тропы отмечены по одному разу, выберите одну наугад.
-

5
Избегайте троп, отмеченных дважды. Если вы вынуждены идти по тропе, которую вы уже отметили один раз, вам стоит отметить ее и во второй раз. Согласно алгоритму Люка-Тремо, тропа с двойной пометкой не приведет вас к выходу. Если вы нашли перекресток, где одна тропа отмечена дважды, всегда выбирайте другой путь, даже если это будет означать, что придется возвращаться назад.[2]
-

6
Вернитесь назад, если наткнулись на тупик. Если вы зашли в тупик, вам нужно вернуться к последнему перекрестку, который вы пересекли. Не забудьте пометить тропу, чтобы помнить, что она ведет в тупик. Как только доберетесь до перекрестка, выберите среди оставшихся троп одну и продолжайте пересекать лабиринт.[3]
-

7
Продолжайте идти по тропам, которые не отмечены больше одного раза. Если вы будете систематично это делать, в конечном итоге, вы найдете выход. Обратите внимание — не факт, что вы найдете самый простой или самой прямой путь из лабиринта, но вы гарантированно из него выберетесь. Алгоритм Люка-Тремо по сути дает вам возможность проверить большое количество троп, используя систему для вычисления тех из них, которые определенно не ведут к выходу. В результате вы сможете выбраться из любого лабиринта.
Реклама
Советы
- Не сдавайтесь. Выход есть (если только лабиринт не очень сложный), и настойчивость поможет вам его найти.
- Имейте в виду, что эти методы по сути предназначены для того, чтобы «смухлевать» в лабиринте, — используя их, искать выход будет не так весело.
- Если вы пытаетесь выбраться из лабиринта командой, ни в коем случае не разделяйтесь. Найти друг друга будет почти невозможно.
Реклама
Об этой статье
Эту страницу просматривали 43 942 раза.
Была ли эта статья полезной?
Как найти выход из любого лабиринта: советы, которые помогут вам не заблудиться
Мало ли когда вам пригодится это знание, но все же уметь выбираться из лабиринта — важная способность.

Чтобы выйти из лабиринта не обязательно долго бродить и натыкаться на тупики. Вот несколько способов быстро отыскать выход
Лабиринт – это структура, состоящая из одного или нескольких извилистых путей, ведущих от входа к цели. С давних времен лабиринты несут в себе ощущение тайны. Одним из самых известных был лабиринт Минотавра, и он играет важную роль в древнегреческой мифологии. В современном мире такие лабиринты являются объектами развлечения. В парках и садах есть запутанные лабиринты из живых изгородей, а также зеркальные и снежные лабиринты. Но как легко найти выход из лабиринта и не заблудиться?
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Правила поиска выхода из лабиринта
Правило левой или правой руки
Этот метод хорош для «простых» лабиринтов, где все стены соединены вместе, и нет путей, которые пересекают друг друга мостами или образуют петли. Однако этот метод не сработает, если начало и конечная точка расположены в центре лабиринта.
Как воспользоваться этим методом:
- Войдите в лабиринт и немедленно положите руку (правую или левую) на стену лабиринта у входа.
- Идите, держа руку в контакте со стеной. В конце концов, вы выберетесь из лабиринта.
Если вы начнете применять этот метод не с начала лабиринта, вы можете попасть в ловушку из-за отдельной стоячей стены, которая огибает сама себя и не имеет входов или выходов. Если это так, попробуйте как-нибудь отметить свою позицию. Если вы снова наткнетесь на начальную точку, то переключитесь на другую стену, вдоль которой еще не шли.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Алгоритм Тремо (Trémaux)
Существуют сложные лабиринты, из которых невозможно выбраться, используя метод «руки на стене», например, лабиринты с множеством мостов.
Как воспользоваться этим методом:
- Вы должны взять с собой что-нибудь, что поможет вам отмечать пройденные участки. Если стены лабиринта сделаны из твердых поверхностей, таких как бетон, кирпич или дерево, тогда вы можете использовать мел. В других случаях вы можете оставить камешки или хлебные крошки, как в «Гензель и Гретель».
- Каждый раз, когда вы входите в проход, ставьте пометку, будь то мел, камешек или немного панировочных сухарей. Если вы используете камешки, положите их близко к стене, чтобы другие люди, проходящие по лабиринту, случайно не пнули или не сдвинули их.
- Когда вы выйдете из прохода, также поставьте отметку в конце стены.
- Если вы подходите к перекрестку в лабиринте, где ни один из проходов не обозначен, выберите именно такой (неважно, какой). Не забудьте отметить его у входа и выхода.
- Если это приведет вас к другому перекрестку, где один путь будет для вас новым, а другой — нет, выберите новый путь.
- Если вы оказались в тупике, вернитесь и поставьте вторую отметку. Это будет означать, что этот путь пройден дважды, туда и обратно. Вам больше не нужно ходить по нему.
- Если вам нужно выбрать между 2 путями, один из которых использовался один раз, а другой уже использовался 2 раза, выберите путь, который использовался 1 раз, и оставьте там вторую отметку. Никогда не выбирайте путь, на котором уже есть 2 метки.
Этот метод, несомненно, поможет вам выбраться из любого лабиринта. Но он не гарантирует, что вы найдете самый короткий и быстрый маршрут.

Прежде чем узнать, как найти выход из лабиринта, интересный вопрос!
А вы много знаете о лабиринтах? ПРАВДА или ВЫМЫСЕЛ, что в Китае некоторые входы в здания строят в виде нескольких изгибов наподобие лабиринта?
Узнать ответ и проверить себя вы сможете в конце статьи.
Лабиринт представляет собой сеть запутанных коридоров и ходов. Задача попавшего в него человека- найти выход. В большинстве своём он находится там же, где и вход.
Подробнее об истории возникновения и видах лабиринтов мы поговорим в следующих статьях. А пока давайте поймём, как выбраться из почти любого лабиринта, используя хитрые методы и теорию вероятности.
Смотрим на стены
И первое, что нам нужно сделать, это определить вид лабиринта. А именно, является он односвязным или многосвязным.
- Односвязный лабиринт имеет одну сплошную извилистую стену или перегородку. То есть если бы мы решили повторить его очертания на бумаге, нам не пришлось бы отрывать карандаш от листа.
- У многосвязного лабиринта всё сложнее. Есть отдельно стоящие перегородки различной формы, как если бы фигурки из тетриса кто-нибудь рассыпал на пол.
Конечно, если лабиринт находится в двухмерном пространстве, то есть нарисован на земле, полу или бумаге, проще понять к какому виду он относится.
Однако с высокими стенами, которые могут быть намного выше человеческого роста, вряд ли получится сделать это сразу.
Выход из односвязного лабиринта
Итак, предположим мы определили, что лабиринт имеет одну связную перегородку на протяжении всего пути.
В поиске выхода нам поможет правило одной руки. Выбираем любую руку и кладём её на стену лабиринта. По мере продвижения вперёд на протяжении всего пути, выбранная рука не должна отрываться от стены.
Так, скользя рукой по стене, если изначально правильно был определён тип лабиринта, вы рано или поздно найдёте выход.
Но, если вдруг вы осознали, что уже три и более раза проходите одну и ту же стену, значит вы столкнулись с лабиринтом второго типа-многосвязным.
Выход из многосвязного лабиринта

Для прохождения многосвязных лабиринтов существует специальный алгоритм.
Разработал его математик по фамилии Тремо. А позже, другой математик по фамилии Люк, доработал его идеи и описал их в своей книге. Отсюда описанный далее способ прохождения носит название «алгоритм Люка-Тремо».
Итак, для поиска выхода из многосвязного лабиринта нам понадобится некий реквизит, чтобы помечать дорогу. Это может быть карандаш или камешки, или любые другие предметы в большом количестве, чтобы отмечать пройденные места.
Секрет кроется в том, чтобы не ходить в одни и те же коридоры более двух раз. Что это значит:
- Двигаясь по коридору от перекрёстка до перекрёстка, помечайте начало и конец прохода выбранным способом (например, рисуем на земле крестики).
- Дойдя до перекрёстка (развилки), всегда поворачивайте туда, где ещё нет крестиков. Если метки стоят на всех возможных поворотах, то сворачивайте в любую сторону.
Не забывайте помечать дважды пройденный путь вторым крестом. А, также, обозначать тупики, чтобы не зайти в них снова.
- По мере прохождения лабиринта, вам придётся проходить многие коридоры дважды, это тоже часть алгоритма. Самое главное, на перекрёстке всегда сворачивать туда, где ноль или только один крест, а не два.
Алгоритм работает таким образом, что коридоры с двойными метками точно не приводят к выходу.
Так, отдавая предпочтение проходам, где вы ещё не были, можно выйти из многосвязного лабиринта.
Как итог
Конечно, интересно попробовать найти выход из лабиринта самостоятельно, не прибегая к хитростям.
Но, также, не менее интересно и попробовать выше названые способы в действии и проверить, действительно ли возможно при помощи алгоритмов выбраться из лабиринта.
А теперь вернёмся с вами к нашему вопросу: ПРАВДА или ВЫМЫСЕЛ, что в Китае некоторые входы в здания строят в виде нескольких изгибов наподобие лабиринта?
ПРАВДА
Китайцы верят, что злые духи могут ходить и летать только прямо. Следовательно, они не смогут попасть в дом с извилистым ломаным коридором в виде лабиринта.
А какой способ найти выход выбрали бы вы, оказавшись в лабиринте?
Алгоритм поиска путей в лабиринте
Время на прочтение
5 мин
Количество просмотров 124K
Доброго времени суток, уважаемое сообщество.
Предыстория
В один прекрасный день, гуляя просторами интернета, был найден лабиринт. Интересно стало узнать его прохождение и погуляв еще по сети, я так и не нашел, рабочей программной реализации, решения лабиринта.
Вот собственно и он:

Рабочий день был скучный, настроение было отличное. Цель, средства и желание имеются. Вывод очевиден, будем проходить.
История
Для удобного решения, необходимо имеющееся изображение лабиринта, привести к типу двумерного массива. Каждый элемент которого может принять одно из 3-ех значений:
const
WALL=-1;
BLANK=-2;
DEADBLOCK=-3;
Наперед, хочу показать функции для сканирования изображения лабиринта с последующей записью данных в массив, и функцию генерации нового изображения, на основании данных из массива:
Сканирование изображения:
...
var
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
...
var bit:TBitmap;
i,j:integer;
begin
bit:=TBitmap.Create;
If OpenDialog1.Execute then
begin
bit.LoadFromFile(OpenDialog1.FileName);
for i:=0 to N do
for j:=0 to N do
if bit.Canvas.Pixels[j,i]=clWhite then
LABIRINT[j,i]:=BLANK else LABIRINT[j,i]:=WALL;
bit.Free;
...
end;
end;
...
Генерация изображения:
...
var
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
...
procedure genBitmap;
var bit:TBitmap;
i,j:Integer;
begin
bit:=TBitmap.Create;
bit.Width:=N+1;
bit.Height:=N+1;
for i:=0 to N do
for j:=0 to N do
begin
if LABIRINT[i,j]=BLANK then bit.Canvas.Pixels[i,j]:=clWhite //
else
if LABIRINT[i,j]=WALL then bit.Canvas.Pixels[i,j]:=clBlack
else bit.Canvas.Pixels[i,j]:=clRed;
end;
bit.SaveToFile('tmp.bmp');
bit.Free;
end;
...
Для начала, необходимо пересохранить изображение, как монохромный bmp, для того, чтоб иметь 2 цвета белый или черный. Если присмотреться к лабиринту, то он имеет стенку толщиной в 2 пикселя, а дорогу толщиной в 4 пикселя. Идеально было бы сделать, чтоб толщина стенки и дороги была 1 пиксель. Для этого необходимо перестроить изображение, разделить изображение на 3, то есть удалить каждый 2рой и 3тий, ряд и столбик пикселей из рисунка (на правильность и проходимость лабиринта это не повлияет).
Подготовленный рисунок:
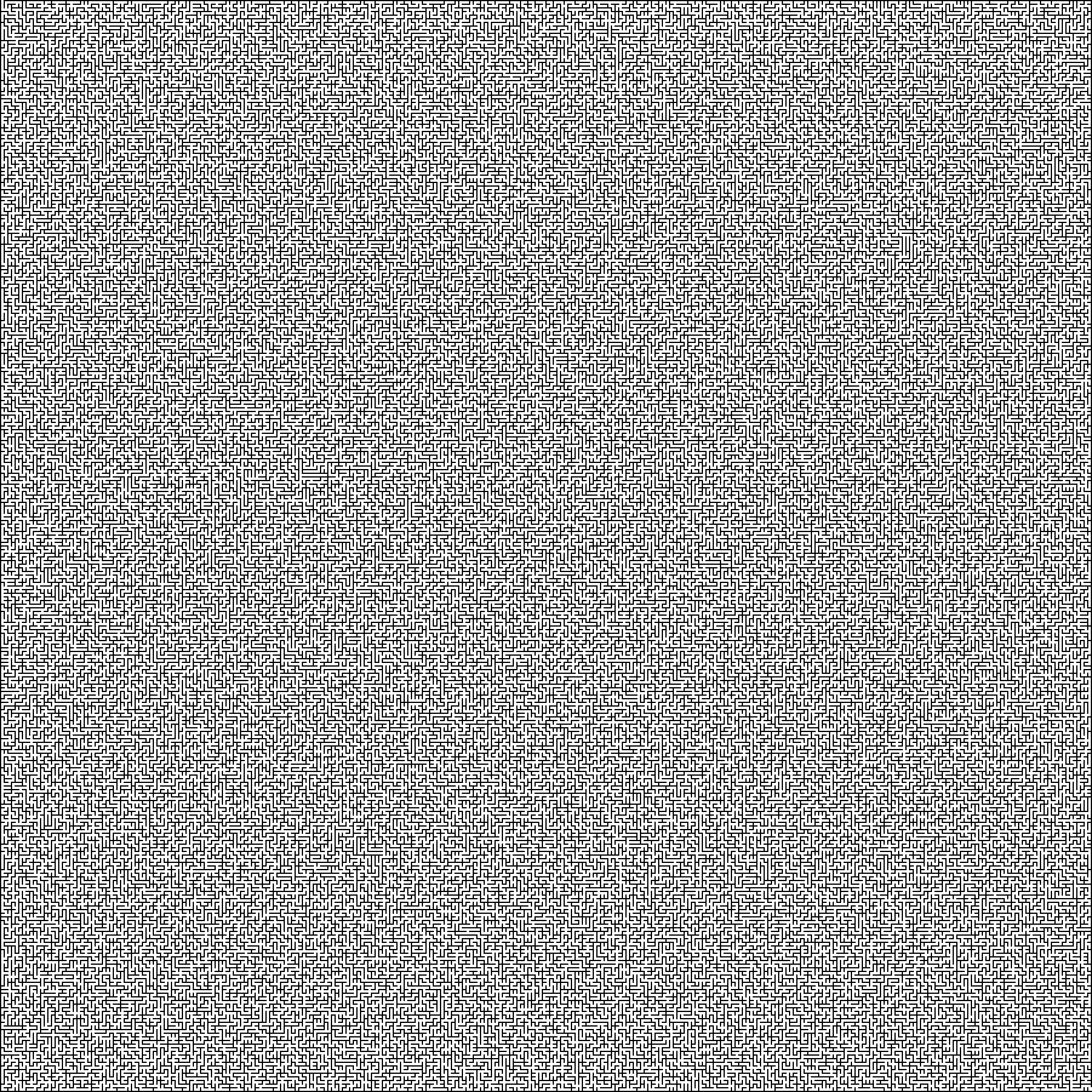
Ширина и высота изображения: 1802 пикселя.
1. Используем функцию сканирования изображения.
2. Перестраиваем изображение:
...
var
N:integer=1801;
LABIRINT:array[0..1801,0..1801] of integer;
...
procedure rebuildArr2;
var i,j:integer;
begin
for i:=0 to ((N div 3) ) do
for j:=0 to ((N div 3) ) do
LABIRINT[i,j]:=LABIRINT[i*3,j*3];
N:=N div 3;
end;
...
3. Генерируем перестроенное изображение.
Результат работы процедуры:

Ширина и высота изображения: 601 пиксель.
И так, у нас есть изображение лабиринта нужного вида, теперь самое интересное, поиск всех вариантов прохождения лабиринта. Что у нас есть? Массив с записанными значениями WALL — стена и BLANK — дорога.
Была одна неудачная попытка найти прохождение лабиринта с помощью волнового алгоритма. Почему неудачная, во всех попытках данный алгоритм приводил к ошибке «Stack Overflow». Я уверен на 100%, что используя его, можно найти прохождение, но появился запал придумать что-то более интересное.
Идея пришла не сразу, было несколько реализаций прохождения, которые по времени, работали приблизительно по 3 минуты, после чего пришло озарение: «а что, если искать не пути прохождения, а пути которые не ведут к прохождению лабиринта и помечать их как тупиковые».
Алгоритм такой:
Выполнять рекурсивную функцию по всем точкам дорог лабиринта:
1. Если мы стоим на дороге и вокруг нас 3 стены, помечаем место где мы стоим как тупик, в противном случае выходим из функции;
2. Переходим на место которое не является стенкой из пункта №1, и повторяем пункт №1;
Программная реализация:
...
var
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
...
procedure setBlankAsDeadblockRec(x,y:integer);
var k:integer;
begin
k:=0;
if LABIRINT[x,y]=blank then
begin
if LABIRINT[x-1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y-1]<>BLANK then k:=k+1;
if LABIRINT[x+1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y+1]<>BLANK then k:=k+1;
if k=4 then LABIRINT[x,y]:=DEADBLOCK;
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y);
if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y);
if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1);
end;
end;
end;
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
setBlankAsDeadblockRec(i,j);
end;
...
Заключение
Я получил «полный» рабочий алгоритм, который можно использовать для поиска всех прохождений лабиринта. Последний по скорости работы превзошел все ожидания. Надеюсь моя маленькая работа, принесет кому-то пользу или подтолкнет к новым мыслям.
Программный код и пройденный лабиринт:
//Прошу не бить ногами за использованный язык программирования.
unit Unit1;
interface
uses
Windows, Graphics, Forms, Dialogs, ExtCtrls, StdCtrls, Controls, Classes;
const
WALL=-1;
BLANK=-2;
DEADBLOCK=-3;
type
TForm1 = class(TForm)
Button1: TButton;
OpenDialog1: TOpenDialog;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
N:integer=600;
LABIRINT:array[0..600,0..600] of integer;
implementation
{$R *.dfm}
procedure genBitmap;
var bit:TBitmap;
i,j:Integer;
begin
bit:=TBitmap.Create;
bit.Width:=N+1;
bit.Height:=N+1;
for i:=0 to N do
for j:=0 to N do
begin
if LABIRINT[i,j]=BLANK then bit.Canvas.Pixels[i,j]:=clWhite //
else
if LABIRINT[i,j]=WALL then bit.Canvas.Pixels[i,j]:=clBlack
else bit.Canvas.Pixels[i,j]:=clRed;
end;
bit.SaveToFile('tmp.bmp');
bit.Free;
end;
procedure rebuildArr2;
var i,j:integer;
begin
for i:=0 to ((N div 3) ) do
for j:=0 to ((N div 3) ) do
LABIRINT[i,j]:=LABIRINT[i*3,j*3];
N:=N div 3;
end;
procedure setBlankAsDeadblockRec(x,y:integer);
var k:integer;
begin
k:=0;
if LABIRINT[x,y]=blank then
begin
if LABIRINT[x-1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y-1]<>BLANK then k:=k+1;
if LABIRINT[x+1,y]<>BLANK then k:=k+1;
if LABIRINT[x,y+1]<>BLANK then k:=k+1;
if k=4 then LABIRINT[x,y]:=DEADBLOCK;
if k=3 then
begin
LABIRINT[x,y]:=DEADBLOCK;
if LABIRINT[x-1,y]=BLANK then setBlankAsDeadblockRec(x-1,y);
if LABIRINT[x,y-1]=BLANK then setBlankAsDeadblockRec(x,y-1);
if LABIRINT[x+1,y]=BLANK then setBlankAsDeadblockRec(x+1,y);
if LABIRINT[x,y+1]=BLANK then setBlankAsDeadblockRec(x,y+1);
end;
end;
end;
procedure setDeadblock;
var i,j:integer;
begin
for i:=1 to N-1 do
for j:=1 to N-1 do
setBlankAsDeadblockRec(i,j);
end;
procedure TForm1.Button1Click(Sender: TObject);
var bit:TBitmap;
i,j:integer;
begin
bit:=TBitmap.Create;
If OpenDialog1.Execute then
begin
bit.LoadFromFile(OpenDialog1.FileName);
for i:=0 to N do
for j:=0 to N do
if bit.Canvas.Pixels[j,i]=clWhite then
LABIRINT[j,i]:=BLANK else LABIRINT[j,i]:=WALL;
bit.Free;
setDeadblock;
genBitmap;
end;
end;
end.

Для поиска кратчайшего пути, планируется применить волновой алгоритм к найденным прохождениям лабиринта. Было-бы интересно услышать, какие еще алгоритмы можно применить, для быстрого поиска пути в большом лабиринте?
Учитывая лабиринт в виде двоичной прямоугольной матрицы найти длину кратчайшего пути в лабиринте от заданного источника до заданного пункта назначения. Путь можно построить только из ячеек со значением 1, и в любой момент мы можем двигаться только на один шаг в одном из четырех направлений.
Допустимые ходы:
Go Top: (x, y) ——> (x – 1, y)
Go Left: (x, y) ——> (x, y – 1)
Go Down: (x, y) ——> (x + 1, y)
Go Right: (x, y) ——> (x, y + 1)
Например, рассмотрим следующую бинарную матрицу. Если источник = (0, 0) и пункт назначения = (7, 5), кратчайший путь от источника к месту назначения имеет длину 12.
[ 1 1 1 1 1 0 0 1 1 1 ]
[ 0 1 1 1 1 1 0 1 0 1 ]
[ 0 0 1 0 1 1 1 0 0 1 ]
[ 1 0 1 1 1 0 1 1 0 1 ]
[ 0 0 0 1 0 0 0 1 0 1 ]
[ 1 0 1 1 1 0 0 1 1 0 ]
[ 0 0 0 0 1 0 0 1 0 1 ]
[ 0 1 1 1 1 1 1 1 0 0 ]
[ 1 1 1 1 1 0 0 1 1 1 ]
[ 0 0 1 0 0 1 1 0 0 1 ]
Потренируйтесь в этой проблеме
Чтобы найти кратчайший путь в лабиринте, ищите все возможные пути в лабиринте от начальной позиции до конечной позиции, пока не будут исчерпаны все возможности. Мы можем легко достичь этого с помощью Backtracking. Идея состоит в том, чтобы начать с данной исходной ячейки в матрице и исследовать все четыре возможных пути и рекурсивно проверить, приведут ли они к месту назначения или нет. Затем обновляйте минимальную длину пути всякий раз, когда достигается ячейка назначения. Если путь не достигает пункта назначения или не изучены все возможные маршруты из текущей ячейки, выполните возврат. Чтобы убедиться, что путь прост и не содержит циклов, отслеживайте ячейки, участвующие в текущем пути, в матрице, и перед исследованием любой ячейки игнорируйте ячейку, если она уже покрыта текущим путем.
Ниже приведена реализация этой идеи на C++, Java и Python:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 |
#include <iostream> #include <vector> #include <climits> #include <cstring> using namespace std; // Проверяем, можно ли перейти в (x, y) из текущей позиции. // функция возвращает false, если ячейка имеет значение 0 или уже посещена bool isSafe(vector<vector<int>> &mat, vector<vector<bool>> &visited, int x, int y) { return (x >= 0 && x < mat.size() && y >= 0 && y < mat[0].size()) && mat[x][y] == 1 && !visited[x][y]; } // Находим кратчайший путь в матрице `mat` из исходной ячейки (i, j) // в ячейку назначения (x, y). // `min_dist` передается по ссылке и хранит длину самого длинного пути // от источника к месту назначения, найденному до сих пор, и `dist` поддерживает длину // пути от исходной ячейки к текущей ячейке (i, j). void findShortestPath(vector<vector<int>> &mat, vector<vector<bool>> &visited, int i, int j, int x, int y, int &min_dist, int dist) { // если место назначения найдено, обновить `min_dist` if (i == x && j == y) { min_dist = min(dist, min_dist); return; } // установить (i, j) ячейку как посещенную visited[i][j] = true; // переходим в нижнюю ячейку if (isSafe(mat, visited, i + 1, j)) { findShortestPath(mat, visited, i + 1, j, x, y, min_dist, dist + 1); } // переходим в правую ячейку if (isSafe(mat, visited, i, j + 1)) { findShortestPath(mat, visited, i, j + 1, x, y, min_dist, dist + 1); } // переходим в верхнюю ячейку if (isSafe(mat, visited, i – 1, j)) { findShortestPath(mat, visited, i – 1, j, x, y, min_dist, dist + 1); } // переходим в левую ячейку if (isSafe(mat, visited, i, j – 1)) { findShortestPath(mat, visited, i, j – 1, x, y, min_dist, dist + 1); } // возврат: удалить (i, j) из посещенной матрицы visited[i][j] = false; } // Обертка над функцией findShortestPath() int findShortestPathLength(vector<vector<int>> &mat, pair<int, int> &src, pair<int, int> &dest) { // базовый случай: неверный ввод if (mat.size() == 0 || mat[src.first][src.second] == 0 || mat[dest.first][dest.second] == 0) { return –1; } // Матрица `M × N` int M = mat.size(); int N = mat[0].size(); // строим матрицу `M × N` для отслеживания посещенных ячеек vector<vector<bool>> visited; visited.resize(M, vector<bool>(N)); int min_dist = INT_MAX; findShortestPath(mat, visited, src.first, src.second, dest.first, dest.second, min_dist, 0); if (min_dist != INT_MAX) { return min_dist; } return –1; } int main() { vector<vector<int>> mat = { { 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 }, { 0, 1, 1, 1, 1, 1, 0, 1, 0, 1 }, { 0, 0, 1, 0, 1, 1, 1, 0, 0, 1 }, { 1, 0, 1, 1, 1, 0, 1, 1, 0, 1 }, { 0, 0, 0, 1, 0, 0, 0, 1, 0, 1 }, { 1, 0, 1, 1, 1, 0, 0, 1, 1, 0 }, { 0, 0, 0, 0, 1, 0, 0, 1, 0, 1 }, { 0, 1, 1, 1, 1, 1, 1, 1, 0, 0 }, { 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 }, { 0, 0, 1, 0, 0, 1, 1, 0, 0, 1 }, }; pair<int, int> src = make_pair(0, 0); pair<int, int> dest = make_pair(7, 5); int min_dist = findShortestPathLength(mat, src, dest); if (min_dist != –1) { cout << “The shortest path from source to destination “ “has length “ << min_dist; } else { cout << “Destination cannot be reached from a given source”; } return 0; } |
Скачать Выполнить код
результат:
The shortest path from source to destination has length 12
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 |
class Main { // Проверяем, можно ли перейти в (x, y) из текущей позиции. // функция возвращает false, если ячейка недействительна, имеет значение 0 или уже посещена private static boolean isSafe(int[][] mat, boolean[][] visited, int x, int y) { return (x >= 0 && x < mat.length && y >= 0 && y < mat[0].length) && mat[x][y] == 1 && !visited[x][y]; } // Находим кратчайший путь в матрице `mat` из исходной ячейки (i, j) // в ячейку назначения (x, y). // `min_dist` хранит длину самого длинного пути от источника до места назначения // пока найдено, а `dist` поддерживает длину пути от исходной ячейки // в текущую ячейку (i, j). public static int findShortestPath(int[][] mat, boolean[][] visited, int i, int j, int x, int y, int min_dist, int dist) { // если место назначения найдено, обновить `min_dist` if (i == x && j == y) { return Integer.min(dist, min_dist); } // установить (i, j) ячейку как посещенную visited[i][j] = true; // переходим в нижнюю ячейку if (isSafe(mat, visited, i + 1, j)) { min_dist = findShortestPath(mat, visited, i + 1, j, x, y, min_dist, dist + 1); } // переходим в правую ячейку if (isSafe(mat, visited, i, j + 1)) { min_dist = findShortestPath(mat, visited, i, j + 1, x, y, min_dist, dist + 1); } // переходим в верхнюю ячейку if (isSafe(mat, visited, i – 1, j)) { min_dist = findShortestPath(mat, visited, i – 1, j, x, y, min_dist, dist + 1); } // переходим в левую ячейку if (isSafe(mat, visited, i, j – 1)) { min_dist = findShortestPath(mat, visited, i, j – 1, x, y, min_dist, dist + 1); } // возврат: удалить (i, j) из посещенной матрицы visited[i][j] = false; return min_dist; } // Обертка над функцией findShortestPath() public static int findShortestPathLength(int[][] mat, int i, int j, int x, int y) { // базовый случай: неверный ввод if (mat == null || mat.length == 0 || mat[i][j] == 0 || mat[x][y] == 0) { return –1; } // Матрица `M × N` int M = mat.length; int N = mat[0].length; int min_dist; // строим матрицу `M × N` для отслеживания посещенных ячеек boolean[][] visited = new boolean[M][N]; min_dist = findShortestPath(mat, visited, i, j, x, y, Integer.MAX_VALUE, 0); if (min_dist != Integer.MAX_VALUE) { return min_dist; } return –1; } public static void main(String[] args) { int mat[][] = { { 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 }, { 0, 1, 1, 1, 1, 1, 0, 1, 0, 1 }, { 0, 0, 1, 0, 1, 1, 1, 0, 0, 1 }, { 1, 0, 1, 1, 1, 0, 1, 1, 0, 1 }, { 0, 0, 0, 1, 0, 0, 0, 1, 0, 1 }, { 1, 0, 1, 1, 1, 0, 0, 1, 1, 0 }, { 0, 0, 0, 0, 1, 0, 0, 1, 0, 1 }, { 0, 1, 1, 1, 1, 1, 1, 1, 0, 0 }, { 1, 1, 1, 1, 1, 0, 0, 1, 1, 1 }, { 0, 0, 1, 0, 0, 1, 1, 0, 0, 1 }, }; int min_dist = findShortestPathLength(mat, 0, 0, 7, 5); if (min_dist != –1) { System.out.println(“The shortest path from source to destination “ + “has length “ + min_dist); } else { System.out.println(“Destination cannot be reached from source”); } } } |
Скачать Выполнить код
результат:
The shortest path from source to destination has length 12
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
import sys # Проверить, можно ли перейти к (x, y) из текущей позиции. # Функция # возвращает false, если ячейка недействительна, имеет значение 0 или уже посещена def isSafe(mat, visited, x, y): return 0 <= x < len(mat) and 0 <= y < len(mat[0]) and not (mat[x][y] == 0 or visited[x][y]) # Найти кратчайший возможный маршрут в матрице `mat` из исходной ячейки (i, j) # в ячейку назначения `dest`. # `min_dist` хранит длину самого длинного пути от источника до пункта назначения. # найден до сих пор, а `dist` поддерживает длину пути от исходной ячейки до # текущая ячейка (i, j). def findShortestPath(mat, visited, i, j, dest, min_dist=sys.maxsize, dist=0): #, если место назначения найдено, обновить `min_dist` if (i, j) == dest: return min(dist, min_dist) # устанавливает ячейку (i, j) как посещенную visited[i][j] = 1 # перейти в нижнюю ячейку if isSafe(mat, visited, i + 1, j): min_dist = findShortestPath(mat, visited, i + 1, j, dest, min_dist, dist + 1) # перейти в правую ячейку if isSafe(mat, visited, i, j + 1): min_dist = findShortestPath(mat, visited, i, j + 1, dest, min_dist, dist + 1) # перейти в верхнюю ячейку if isSafe(mat, visited, i – 1, j): min_dist = findShortestPath(mat, visited, i – 1, j, dest, min_dist, dist + 1) # перейти в левую ячейку if isSafe(mat, visited, i, j – 1): min_dist = findShortestPath(mat, visited, i, j – 1, dest, min_dist, dist + 1) # Возврат #: удалить (i, j) из посещаемой матрицы visited[i][j] = 0 return min_расстояние # Обертка над функцией findShortestPath() def findShortestPathLength(mat, src, dest): # получить исходную ячейку (i, j) i, j = src # получить ячейку назначения (x, y) x, y = dest # Базовый вариант if not mat or len(mat) == 0 or mat[i][j] == 0 or mat[x][y] == 0: return –1 # Матрица `M × N` (M, N) = (len(mat), len(mat[0])) # создает матрицу `M × N` для отслеживания посещенных ячеек. visited = [[False for _ in range(N)] for _ in range(M)] min_dist = findShortestPath(mat, visited, i, j, dest) if min_dist != sys.maxsize: return min_dist else: return –1 if __name__ == ‘__main__’: mat = [ [1, 1, 1, 1, 1, 0, 0, 1, 1, 1], [0, 1, 1, 1, 1, 1, 0, 1, 0, 1], [0, 0, 1, 0, 1, 1, 1, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1, 1, 0, 1], [0, 0, 0, 1, 0, 0, 0, 1, 0, 1], [1, 0, 1, 1, 1, 0, 0, 1, 1, 0], [0, 0, 0, 0, 1, 0, 0, 1, 0, 1], [0, 1, 1, 1, 1, 1, 1, 1, 0, 0], [1, 1, 1, 1, 1, 0, 0, 1, 1, 1], [0, 0, 1, 0, 0, 1, 1, 0, 0, 1] ] src = (0, 0) dest = (7, 5) min_dist = findShortestPathLength(mat, src, dest) if min_dist != –1: print(“The shortest path from source to destination has length”, min_dist) else: print(“Destination cannot be reached from source”) |
Скачать Выполнить код
результат:
The shortest path from source to destination has length 12
Временная сложность приведенного выше решения для поиска с Backtracking будет выше, поскольку необходимо пройти все пути. Однако, поскольку это задача о кратчайшем пути, Поиск в ширину (BFS) будет идеальным выбором. Если для решения этой проблемы используется BFS, мы путешествуем уровень за уровнем. Таким образом, первое вхождение целевого узла дает нам результат, и мы можем остановить наш поиск там. Обсуждается подход BFS здесь.
