Различные
статистики, получаемые в результате
вычислений, представляют собой точечные
оценки соответствующих параметров
генеральной совокупности.
Если
из генеральной совокупности извлечь
некоторое количество выборок и для
каждой
из них найти интересующие нас статистики,
то вычисленные значения будут представлять
собой случайные величины, которые
распределены по нормальному закону и
имеющие некоторый разброс вокруг
оцениваемого параметра.
Но,
как правило, в результате эксперимента
в распоряжении исследователя имеется
одна выборка. Поэтому значительный
интерес представляет получение
интервальной
оценки,
т.е. получение некоторого интервала,
внутри которого, как можно предположить,
лежит истинное значение параметра.
Вероятности,
признанные достаточными для уверенных
суждений о параметрах генеральной
совокупности на основании статистик,
называются доверительными.
Для
примера рассмотрим
как оценку параметра
.
Доказано,
что если выборки извлекаются из
генеральной совокупности с параметрами:
то
распределение выборочных средних
будет приближаться к нормальному закону
распределения и иметь среднее, равное,
дисперсию,
среднее квадратическое,
где– объем выборки.
Для
такого распределения, как мы показали
раньше,
наблюдений лежат в интервале
,
т.е.,
в интервале
и
в интервале
.
В общем случае, вместо конкретных цифрможно взять некоторый параметрt
и записать:
(5.7)
где
γ
– процент наблюдений, которые попадают
в интервал
.
С
другой стороны величина γ
равна,
как мы знаем,
(см. ф. (3.16)).
Или
говорят, с надежностью
доверительный интервал
покрывает неизвестный параметр
с точностью
.
Здесь,
наоборот, мы задаемся надежностью (или
доверительной вероятностью)
,
а знаяпо таблицам для функции Лапласа находим
параметри далее – доверительный интервал.
Но для
этого нам необходимо знать истинное
значение параметра генеральной
совокупности
,
которое нам неизвестно.
Поэтому
на практике вместо параметра
используют выборочное среднее
квадратическое отклонение.
То есть доверительный интервал
определяется выражением
(5.8)
Но при
этом параметр
это ужепараметр
распределения Стьюдента,
который находится по соответствующим
таблицам при данных
и
,
где– задаваемая надежность, или доверительный
интервал. Этот интервал покрывает
неизвестный параметрс надежностью
,
гдеи
находятся по формулам (5,3), (5.4) и (5.5),
(5.6) соответственно.
Пример.
Найти доверительный интервал для оценки
математического ожидания
нормальной случайной величины с
надежностью,
зная выборочную среднюю,
объем выборки,
среднее квадратическое отклонение.
Решение.
Имеем
.
Отсюда.
По таблице значений функции Лапласа
находим.
Отсюда
5. Применение критерия Стьюдента для сравнения двух генеральных совокупностей.
Пусть
нам надо оценить эффективность действия
рекламы какого-то товара.
До
запуска рекламы продажа товара по
неделям (в шт.) имела следующий вид:
После
выпуска рекламы продажа этого же товара
по неделям стала иметь вид:
Следовательно,
доверительный интервал с надежностью
для первой выборки равен
А для
второй
Т
образом, если по средним мы можем сделать
положительный вывод о влиянии рекламы
товара, то по доверительным интервалам
мы вправе сомневаться: уж очень велики
интервалы, и они значительно перекрывают
друг друга (см. рис. 5.3).
Однако
нам необходимо со всей определенностью
истолковать результаты эксперимента.
Мы
можем высказать два предположения
(статистические гипотезы).
1.
Нулевая гипотеза. Между генеральными
совокупностями с параметрами
и
,
и
разница равна нулю, т.е.
.
Следовательно, разница между выборочными
среднимивозникла случайно, в процессе группировки
данных.
2.
Альтернативная гипотеза, т.е.
противоположная.
Для
проверки этих гипотез существуют
специальные параметры, которые
табулированы и приводятся в соответствующих
справочниках.
В
частности, если сравниваемые генеральные
совокупности имеют нормальный закон
распределения, то сравнение выборочных
средних проводят с помощью
иликритерия
Стьюдента:
где

Согласно
нулевой гипотезе
,
отсюда:
(5.9)
Нулевая
гипотеза (разницы нет) отвергается, если
для заданной надежности и числа (степеней
свободы).
Здесь– фактический коэффициент Стьюдента,
найденный по формуле (5.9), а– теоретический коэффициент, найденный
по специальным таблицам.
Для
нашего примера
,
.
Следовательно,.
По таблицам, для надежностии числа
,
находим.
Итак,и нулевая гипотеза сохраняется: разница
между результатами опыта и контроля
оказалась статистически недостоверной.
Таблица
Стьюдента.
|
k |
Уровни |
||
|
95 |
99 |
99,9 |
|
|
7 |
2,37 |
3,50 |
5,51 |
|
8 |
2,31 |
3,36 |
5,04 |
|
9 |
2,26 |
3,25 |
4,78 |
|
10 |
2,23 |
3,17 |
4,59 |
Соседние файлы в папке 9.ТеорВер
- #
- #
- #
- #
- #
- #
- #
- #
19.05.20151.3 Mб35~WRL1476.tmp
- #
- #
- #
Как рассчитать достоверность
Чтобы сравнить две выборки, взятые из одной генеральной совокупности, либо два различных состояния одной и той же совокупности, используется метод Стьюдента. С его помощью можно рассчитать достоверность различий, то есть узнать, можно ли доверять проведенным измерениям.

Инструкция
Для того чтобы правильно выбрать формулу расчета достоверности, определите величину групп выборок. Если количество измерений больше 30, такая группа будет считаться большой. Таким образом, возможно три варианта: обе группы малые, обе группы большие, одна группа малая, вторая – большая.
Кроме того, вам понадобится знать, зависимы ли измерения первой группы с измерениями второй. Если каждая i-ая варианта первой группы противопоставлена i-ой варианте второй группы, то они называются попарно-зависимыми. Если же варианты внутри группы можно менять местами, такие группы называются группами с попарно-назависимыми вариантами.
Для сравнения групп с попарно-независимыми вариантами (хотя бы одна из них должна быть большой), воспользуйтесь формулой, представленной на рисунке. С помощью формулы вы сможете найти критерий Стьюдента, именно по нему определяют доверительную вероятность различия двух групп.

Чтобы определить критерий Стьюдента для групп небольшого размера с попарно-независимыми вариантами, применяйте другую формулу, она представлена на втором рисунке. Число степеней свободы рассчитывается так же, как и в первом случае: сложите объемы двух выборок и вычтите число 2.
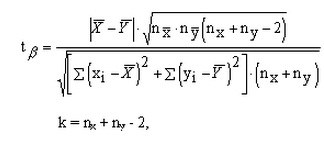
Сравнить две малые группы с попарно-зависимыми результатами можно при помощи двух формул, на ваш выбор. При этом число степеней свободы рассчитывается иначе, по формуле k=2*(n-1).
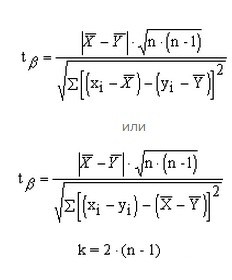
Далее определите доверительную вероятность по таблице t-критериев Стьюдента. При этом учтите, чтобы выборка была достоверной, доверительная вероятность должна быть не менее 95%. То есть найдите в первом столбце свое значение числа степеней свободы, а в первой строке – рассчитанный критерий Стьюдента и оцените, меньше или больше полученная вероятность 95%.
Например, вы получили t=2,3; k=73. По таблице определите доверительную вероятность, она больше 95%, следовательно, различия выборок достоверны. Другой пример: t=1,4; k=70. По таблице, чтобы получить минимальное значение достоверности 95%, для k=70, t должно быть равно хотя бы 1,98. У вас же оно меньше – всего 1,4, поэтому различие выборок недостоверно.
Источники:
- достоверность формулы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику – среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 – n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае – двойной средней ошибки) – 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 – практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше – по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | – | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni – количество извлекаемых единиц для выборки из i-й типической группы;
n – общий объем выборки;
Ni – количество единиц генеральной совокупности, составивших i-ю типическую группу;
N – общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при “больших” выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения – распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.














 ) при использовании типического отбора, пропорционального объему типических групп
) при использовании типического отбора, пропорционального объему типических групп















