Как найти доверительные границы погрешности измерения

     9.1
Доверительные границы погрешности
оценки измеряемой величины находят
путем построения композиции распределений
случайных погрешностей и НСП,
рассматриваемых как случайные величины
в соответствии с 8.3. Если доверительные
границы случайных погрешностей найдены
в соответствии с разделом 7, границы
погрешности оценки измеряемой величины
(без учета знака)
вычисляют по формуле

,
                                                      (12)
где
– коэфф, зависящий
от соотношения случайной составляющей
погрешности и НСП.
     Суммарное
среднее квадратическое отклонениеоценки измеряемой
величины вычисляют по формуле

,
                                              (13)  
где
– среднее
квадратическое отклонение НСП, которое
оценивают в зависимости от способа
вычисления НСП по формуле

,
                                                    (14)     
где
– границы НСП,
которые определяют по одной из формул
(7), (9), (10) или

,
                                                 (15)
где
–
доверительные границы НСП, которые
определяют из формул (8), (11);– коэффициент, определяемый принятой
доверительной вероятностью Рд,
числом составляющих НСП и их соотношением
между собой.
     
     Коэффициент
для подстановки
в формулу (12) в зависимости от числа НСП
определяют по эмпирическим формулам
соответственно(16)

10 Форма записи оценки измеряемой величины

     10.1
Оформление записи оценок измеряемых
величин проводят в соответствии с
правилами по межгосударственной
стандартизации [2].

     10.2
Округление при обработке результатов
измерений выполняют в соответствии с
приложением Е.    

     10.3
При симметричных доверительных границах
погрешности оценку измеряемой величины
представляют в форме

,
,
                                                    (17)      
где– оценка измеряемой
величины.
     
     Числовое
значение оценки измеряемой величины
должно оканчиваться цифрой того разряда,
что и значение погрешности.

Приложение
А (справочное). Критические значения
для критерия Граббса

Таблица
А.1
– Критические значения
для критерия
Граббса

	Одно наибольшее или одно наименьшее значение при уровне значимости
	Свыше 1%	Свыше 5%
3	1,155	1,155
4	1,496	1,481
5	1,764	1,715
6	1,973	1,887
7	2,139	2,020
8	2,274	2,126
9	2,387	2,215
10	2,482	2,290
11	2,564	2,355
12	2,636	2,412
13	2,699	2,462
14	2,755	2,507
15	2,806	2,549
16	2,852	2,585
17	2,894	2,620
18	2,932	2,651
19	2,968	2,681
20	3,001	2,709
21	3,031	2,733
22	3,060	2,758
23	3,087	2,781
24	3,112	2,802
25	3,135	2,822
26	3,157	2,841
27	3,178	2,859
28	3,199	2,876
29	3,218	2,893
30	3,236	2,908
31	3,253	2,924
32	3,270	2,938
33	3,286	2,952
34	3,301	2,965
36	3,330	2,991
38	3,356	3,014
40	3,381	3,036

Приложение
Б
(справочное). Проверка гипотезы о
нормальности распределения результатов
измерений при числе результатов измерений
15 < n меньше или равно 50
Проверка
гипотезы о нормальности распределения
результатов измерений при числе
результатов измерений 15
< n< 50

          При
числе результатов измерений n
<
50 нормальность
их распределения проверяют с помощью
составного критерия.

        Б.1
Критерий
          Вычисляют
отношение
(Б.1)
        где– смещенное среднее
квадратическое отклонение, вычисляемое
по формуле

.
                                         (Б.2)
     Результаты
измерений в ряду считают распределенными
нормально, если

,
                                 
 (Б.3)
где
и– квантили
распределения, получаемые из таблицы
Б.1 по,и,
причем– заранее выбранный
уровень значимости (1%, 5%, 99% или 95%).Таблица
Б.1
– Квантили
ираспределения

	·100%	·100%
	1%	5%	99%	95%
16	0,9137	0,8884	0,6829	0,7236
21	0,9001	0,8768	0,6950	0,7304
26	0,8901	0,8686	0,7040	0,7360
31	0,8826	0,8625	0,7110	0,7404
36	0,8769	0,8578	0,7167	0,7440
41	0,8722	0,8540	0,7216	0,7470
46	0,8682	0,8508	0,7256	0,7496
51	0,8648	0,8481	0,7291	0,7518

Б.2
Критерий 2
     
     Считают,
что результаты измерений принадлежат
нормальному распределению, если не
более
разностейпревысили
значение,
    где– среднее
квадратическое отклонение, вычисляемое
по формуле (3);
      –
верхний квантиль распределения
нормированной функции Лапласа, отвечающий
вероятности.
     
     Значения
вероятностиP
определяют из таблицы Б.2 по выбранному
уровню значимости
, %, и числу
результатов измеренийn.
Зависимость P
от n
приведена в таблице Б.3.
     

Таблица
Б.2
– Значения Р для вычисления

		·100%
n		1%	2%	5%
10	1	0,98	0,98	0,96
11-14	1	0,99	0,98	0,97
15-20	1	0,99	0,99	0,98
21-22	2	0,98	0,97	0,96
23	2	0,98	0,98	0,96
24-27	2	0,98	0,98	0,97
28-32	2	0,99	0,98	0,98
33-35	2	0,99	0,98	0,98
36-49	2	0,99	0,99	0,98

     
     

Таблица
Б.3
– Значения

0,96	2,06
0,97	2,17
0,98	2,33
0,99	2,58

     
   При
уровне значимости, отличном от
предусмотренных в таблице Б.2, значение
находят путем
линейной интерполяции.
     
     При
несоблюдении хотя бы одного из критериев
считают, что распределение результатов
измерений группы не соответствует
нормальному.

Приложение
В
(справочное). Проверка гипотезы о
нормальности распределения результатов
измерений при числе измерений n ≥50

     
Проверка
гипотезы о нормальности распределения
результатов измерений при числе измерений
n
≥50

     В.1
При числе результатов измерений
50 для проверки
критерия согласия теоретического
распределения с практическим чаще всего
используют критерий К.Пирсона.
Рекомендуемые числа интерваловв зависимости от
числа результатов измерений приведены
в таблице В.1. Вычисления сводят в таблицу
В.2, в которой приведен алгоритм вычислений
для проверки гипотезы о нормальности
распределения результатов измерений.
При этом группируют результаты измерений.
Группирование – разделение результатов
измерений от наименьшегодо наибольшегонаинтервалов.

Таблица В.1
– Рекомендуемые числа интервалов в
зависимости от числа результатов
измерений

Число результатов измерений	Рекомендуемое число интервалов
40-100	7-9
100-500	8-12
500-1000	10-16
1000-10000	12-22

 

Таблица
В.2
– Вспомогательная таблица для проверки
распределения результатов измерений

Номер интервала	Середина интервала	Число результатов измерений в интервал

     
     Ширину
интервала
выбирают постоянной и
вычисляют по формуле

.
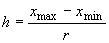                                                (В.1)

     В.2
Установив границы интервалов, подсчитывают
число результатов измерений
, попавших в каждый
интервал. Далее вычисляют: середины
интервалов, среднее
арифметическоеи среднее
квадратическое отклонение результатов
измерений. Определяют число
результатов измерений, которое должно
было бы находиться в интервале, если бы
распределение результатов измерений
было нормальным,

по
формуле
,
                                               (В.2)
где– плотность
нормального распределения;– вероятность попадания результатов
измерении в-й интервал.

     В.3
Для каждого интервала вычисляют критерий
К.Пирсона
.
Просуммировавпо всеминтервалам,
получаютс
определенным числом степеней свободы. Для нормального
распределения.

     В.4
Выбрав уровень значимости
по таблицам
распределения, находят нижнееи верхнее(значения-процентных точек
для распределенияприведены в таблице
В.3).
     
     Выбрав
уровень значимости критерия, определяют
квантилии. Квантиль, вычисленный по
результатам измерений, должен находиться
междуи.

Таблица
В.3
– Значения
-процентных точекдля распределения

	Число степеней свободы
	4	6	8	10	12	14	16	18
99,0	0,30	0,87	1,65	2,56	3,57	4,66	5,81	7,02
95,0	0,71	1,64	2,73	3,94	5,23	6,57	7,96	9,39
90,0	1,06	2,20	3,49	4,86	6,30	7,79	9,31	10,89
10,0	7,78	10,64	13,36	15,99	18,55	21,06	23,54	25,99
5,0	9,49	12,59	15,51	18,31	21,03	23,68	26,30	28,87
1,0	13,28	16,81	20,09	23,21	26,22	29,14	32,00	34,80

Приложение
Г (справочное).
Проверка гипотезы о нормальности
распределения результатов измерений
при числе измерений n больше или равно
50, критерий “омега(2)
Проверка
гипотезы о нормальности распределения
результатов измерений при числе измерений
50, критерий

     Г.1
Критерий Мизеса-Смирнова
использует
статистику, имеющую вид

,   
где
– теоретическая
функция распределения;– эмпирическая функция распределения;– весовая функция, область определения
которой представляет собой область
значений функции.
      
    Конкретный
вид статистики(или, точнее,) зависит от вида
весовой функции. Как правило, используют
весовые функции двух видов:,
при которой все значения функции
распределения обладают одинаковым
весом, и,
при которой вес результатов измерений
увеличивается на “хвостах”
распределений. В приведенном критерии
использована весовая функция второго
вида, поскольку на практике различия
между распределениями наиболее отчетливы
в области крайних значений. Однако почти
всегда малое число результатов измерений
имеется как раз в области крайних
значений. Поэтому целесообразно придать
этим результатам больший вес.
     
     Если
принять весовую функцию второго вида,
то статистикапосле выполнения
интегрирования имеет вид

(Г.1)
где
–
значение функции теоретического
распределения при значении аргумента,
равном(1,
…,);– результаты измерений, упорядоченные
по значению.
     
     Результаты
измеренийрекомендуется
свести в таблицу, аналогичную таблице
Г.1 расчетного примера применения
критерия, а соответствующие
им значениявнести
в третий столбец таблицы, аналогичной
таблице Г.2 этого же примера.
     
     Статистикаподчиняется
асимптотическому (при)
распределению

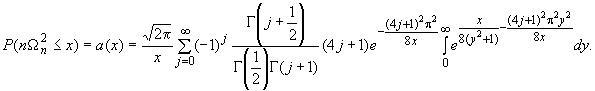
     Значения
функции распределения
для 02,6
с шагом 0,01 приведены в таблице
Г.3.

     Г.2
Применение критерия
требует выполнения
большого объема вычислительных операций,
но этот критерий более мощный, чем
критерий Пирсона. Число результатов
измерений при использовании этого
критерия должно быть более 50.

     Г.3
При использовании критерия
вычисления проводят
в следующем порядке:

     Г.3.1
Вычисляют значение статистики
по формуле
(Г.1).
     
     Промежуточные
вычисления по формуле (Г.1) рекомендуется
сводить в таблицу, аналогичную таблице
Г.2 примера. После заполнения таблицы
суммируют значения, внесенные в ее
последний столбец. Значение величинынаходят, подставляя
полученную сумму в формулу (Г.1).

     Г.3.2
По таблице Г.3 находят значение функции
распределения
для, равного вычисленному
значению.

     Г.3.3
Задают уровень значимости
. Рекомендуется
выбирать значение, равное 0,1 или
0,2.

     Г.3.4
Если
,
то гипотезу о согласии эмпирического
и теоретического распределений отвергают,
если,
то гипотезу принимают.

Пример
применения критерия
Пример
составлен при малом количестве данных
в целях иллюстрации сложного вычислительного
процесса при использовании критерия.
     Результаты
измерений приведены в таблице Г.

.

Таблица
Г.1 – Результаты измерений

Номер результата измерений	Результат измерений
1	15,61
2	20,71
3	21,68
4	22,28
5	23,22
6	24,14
7	24,59
8	26,18
9	26,23
10	27,59
11	27,88
12	28,74
13	29,34
14	30,86
15	32,08

Требуется
проверить гипотезу о том, что группа
результатов измерений не противоречит
нормальному распределению. Среднее
арифметическое значение и среднее
квадратическое отклонение результатов
измерений, представленных в таблице
Г.1, равные соответственно
25,4087 и4,3241, приняты в
качестве параметров нормального
распределения, значения функции
распределения которогопредставлены
в третьем столбце таблицы Г.2.
      Результаты
дальнейших вычислений также приведены
в таблице Г.2.

Таблица
Г.2
– Результаты промежуточных
вычислений . значения статистики
по формуле (Г.1)

1	0,033	0,011726	-2,14336	-0,07145	0,9667	0,882740	0,12472	-0,12057	-0,19201
2	0,100	0,136321	1,99274	-0,19927	0,9000	0,863679	0,14655	-0,13190	-0,33117
3	0,167	0,194344	1,63813	-0,27302	0,8333	0,805656	0,21610	-0,18008	-0,45310
4	0,233	0,234533	1,45016	-0,33837	0,7667	0,765467	0,26727	-0,20491	-0,54328
5	0,300	0,306428	1,18277	-0,35483	0,7000	0,693572	0,36590	-0,25613	-0,61096
6	0,367	0,384761	0,95513	-0,35022	0,6333	0,615239	0,48574	-0,30764	-0,65785
7	0,433	0,425046	-0,85556	-0,37074	0,5667	0,574954	0,55346	-0,31363	-0,68437
8	0,500	0,570639	0,56100	-0,28050	0,5000	0,429361	0,84546	-0,42273	-0,70323
9	0,567	0,575345	0,55279	-0,31325	0,4333	0,424655	0,85648	-0,37114	-0,68439
10	0,633	0,692869	0,36691	-0,23238	0,3667	0,307131	1,18048	-0,43284	-0,66522
11	0,700	0,716339	0,33360	-0,23352	0,3000	0,283661	1,25998	-0,37799	-0,61151
12	0,766	0,729350	0,31560	-0,24196	0,2333	0,270650	1,30693	-0,30495	-0,54691
13	0,833	0,818325	0,20050	-0,16708	0,1667	0,181675	1,70554	-0,28426	-0,45134
14	0,900	0,896346	0,10943	-0,09849	0,1000	0,103654	2,26670	-0,22667	-0,32516
15	0,966	0,938585	0,06338	-0,06127	0,0333	0,061415	2,79010	-0,09300	-0,15427
Примечания      1 В первой строке заголовочной части таблицы приведена нумерация столбцов со 2-го по 10-й заглавными буквами латинского алфавита (,, …,).      2 Во второй строке заголовочной части таблицы для столбцов с 4-го по 10-й (столбцы, …,) приведены формулы для вычисления значений в строках, имеющих номер(1,…, 15), использующие значения (, …,), указанные на пересечении соответствующих столбцов и строк с номерами.      3 Для вычисления значенийво втором столбце таблицы (столбец) число измерений15.

Сумма
значений, приведенных в столбце 10 таблицы
Г.2, равна минус 7,61478. Тогда результат
вычисления по формуле (Г.1) будет
.
Значение функции, в соответствии
с таблицей Г.3, для0,23
равно 0,016. Это значение достаточно мало
(0,016<0,8<0,9), следовательно, в соответствии
с Г.4, гипотеза о том, что выборка
принадлежит нормально распределенной
генеральной совокупности, не может быть
отвергнута.Таблица
Г.3
– Значения функции

Значение	0	1	2	3	4	5	6	7	8	9
0,0	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000
0,1	0,000	0,000	0,000	0,000	0,000	0,001	0,001	0,002	0,003	0,005
0,2	0,007	0,010	0,013	0,016	0,020	0,025	0,030	0,035	0,041	0,048
0,3	0,055	0,062	0,070	0,078	0,086	0,095	0,104	0,113	0,122	0,132
0,4	0,141	0,151	0,161	0,171	0,181	0,192	0,202	0,212	0,222	0,233
0,5	0,243	0,253	0,263	0,274	0,284	0,294	0,304	0,313	0,323	0,333
0,6	0,343	0,352	0,361	0,371	0,380	0,389	0,398	0,407	0,416	0,424
0,7	0,433	0,441	0,449	0,458	0,466	0,474	0,482	0,489	0,497	0,504
0,8	0,512	0,519	0,526	0,533	0,540	0,547	0,554	0,560	0,567	0,573
0,9	0,580	0,586	0,592	0,598	0,604	0,610	0,615	0,621	0,627	0,632
1,0	0,637	0,643	0,648	0,653	0,658	0,663	0,668	0,673	0,677	0,682
1,1	0,687	0,691	0,696	0,700	0,704	0,709	0,713	0,717	0,721	0,725
1,2	0,729	0,732	0,736	0,740	0,744	0,747	0,751	0,754	0,758	0,761
1,3	0,764	0,768	0,771	0,774	0,777	0,780	0,783	0,786	0,789	0,792
1,4	0,795	0,798	0,800	0,803	0,806	0,809	0,811	0,814	0,816	0,819
1,5	0,821	0,824	0,826	0,828	0,831	0,833	0,835	0,837	0,839	0,842
1,6	0,844	0,846	0,848	0,850	0,852	0,854	0,856	0,858	0,859	0,861
1,7	0,863	0,865	0,867	0,868	0,870	0,872	0,873	0,875	0,877	0,878
1,8	0,880	0,881	0,883	0,884	0,886	0,887	0,889	0,890	0,892	0,893
1,9	0,894	0,896	0,897	0,898	0,900	0,901	0,902	0,903	0,905	0,906
2,0	0,907	0,908	0,909	0,910	0,912	0,913	0,914	0,915	0,916	0,917
2,1	0,918	0,919	0,920	0,921	0,922	0,923	0,924	0,925	0,926	0,927
2,2	0,928	0,929	0,929	0,930	0,931	0,932	0,933	0,934	0,934	0,935
2,3	0,936	0,937	0,938	0,938	0,939	0,940	0,941	0,941	0,942	0,943
2,4	0,943	0,944	0,945	0,945	0,946	0,947	0,947	0,948	0,949	0,949
2,5	0,950	0,951	0,952	0,952	0,953	0,953	0,954	0,954	0,955	0,956

Приложение
Д (справочное).
Значения коэффициентов t для случайной
величины Y, имеющей распределение
Стьюдента с n-1 степенями свободы

     
Значения
коэффициентов
для случайной
величины,
имеющей распределение
Стьюдента сстепенями свободы

Таблица
Д.1 – Значения коэффициентов Стьюдента

	0,95	0,99
3	3,182	5,841
4	2,776	4,604
5	2,571	4,032
6	2,447	3,707
7	2,365	2,998
8	2,306	3,355
9	2,262	3,250
10	2,228	3,169
12	2,179	3,055
14	2,145	2,977
16	2,120	2,921
18	2,101	2,878
20	2,086	2,845
22	2,074	2,819
24	2,064	2,797
26	2,056	2,779
28	2,048	2,763
30	2,042	2,750
	1,960	2,576

Приложение
Е (обязательное).
Правила округления при обработке
результатов измерений     

 Е.1
Точность результатов измерений и
точность вычислений при обработке
результатов измерений должны быть
согласованы с требуемой точностью
получаемой оценки измеряемой величины.     

     Е.2
Погрешность оценки измеряемой величины
следует выражать не более чем двумя
значащими цифрами.
     

Две
значащие цифры в погрешности оценки
измеряемой величины сохраняют:
     –
при точных измерениях;   
     –
если первая значащая цифра не более
трех.
     

     Е.3
Число цифр в промежуточных вычислениях
при обработке результатов измерений
должно быть на две больше, чем в
окончательном результате.
     

     Е.4
Погрешность при промежуточных вычислениях
должна быть выражена не более чем тремя
значащими цифрами.
     

     Е.5
Сохраняемую значащую цифру в погрешности
оценки измеряемой величины при округлении
увеличивают на единицу, если отбрасываемая
цифра неуказываемого младшего разряда
больше либо равна пяти, и не изменяют,
если она меньше пяти.
     
     

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Р 50.2.038-2004

РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ

Государственная
система обеспечения
единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ
ОДНОКРАТНЫЕ

Оценивание погрешностей и
неопределенности
результата измерений

ГОССТАНДАРТ РОССИИ

Москва

Предисловие

1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием
Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева
Госстандарта России (ФГУП ВНИИМ им. Д.И. Менделеева)

ВНЕСЕНЫ Управлением метрологии Госстандарта России

2 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по
техническому регулированию и метрологии от 27 октября 2004 г. № 43-ст

3 ВЗАМЕН МИ 1552-86

СОДЕРЖАНИЕ

РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ

Государственная система
обеспечения единства измерений

ИЗМЕРЕНИЯ ПРЯМЫЕ ОДНОКРАТНЫЕ

Оценивание погрешностей и неопределенности
результата измерений

State system for ensuring the uniformity of
measurements.
Direct single measurements. Estimation of errors and uncertainty of
measurements result

Дата введения 2005-01-01

1 Область применения

Настоящие рекомендации распространяются
на нормативные, конструкторские, технические и другие документы,
устанавливающие методики выполнения измерений (МВИ), и содержат методы
оценивания характеристик погрешности и неопределенности результатов прямых
однократных измерений. Разрабатываемые МВИ должны соответствовать требованиям ГОСТ Р 8.563.

Пример оценивания
погрешности однократного измерения приведен в приложении А.

2 Нормативные ссылки

В настоящих рекомендациях
использованы ссылки на следующие нормативные документы:

ГОСТ
8.207-76 Государственная система обеспечения единства измерений. Прямые
измерения с многократными наблюдениями. Методы обработки результатов
наблюдений. Основные положения

ГОСТ
8711-93 ( МЭК
51-2-84) Приборы аналоговые показывающие электроизмерительные прямого
действия и вспомогательные части к ним. Часть 2. Особые требования к
амперметрам и вольтметрам

ГОСТ Р 8.563-96 Государственная
система обеспечения единства измерений. Методики выполнения измерений

РМГ
43-2001 Государственная система обеспечения единства измерений. Применение
«Руководства по выражению неопределенности измерений»

РД
50-453-84 Характеристики погрешности средств измерений в реальных условиях
эксплуатации. Методы расчета

МИ
1317-86 Государственная система обеспечения единства измерений. Результаты
и характеристики погрешности измерений. Формы представления. Способы
использования при испытаниях образцов продукции и контроле их параметров

3 Термины, определения, обозначения и сокращения

3.1 В настоящих рекомендациях применяют следующие термины с
соответствующими определениями:

границы неисключенной
систематической погрешности измерений: Границы интервала, внутри которого находится
неисключенная систематическая погрешность измерений.

однократное измерение: Измерение, выполненное один
раз.

неопределенность
(измерений): Параметр,
связанный с результатом измерений и характеризующий рассеяние значений, которые
могли бы быть обоснованно приписаны измеряемой величине (по РМГ 43).

стандартная неопределенность
и (измерений): Неопределенность результата измерений, выраженная в виде среднего квадратического
отклонения (по РМГ
43).

Примечания

1 Стандартную
неопределенность, оцениваемую по типу А, u_A вычисляют по формуле

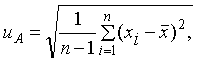                                        (1)

где  – среднее
арифметическое экспериментальных данных, полученных при измерении (по РМГ
43).

2 Стандартную
неопределенность, оцениваемую по типу В, u_B вычисляют по
формуле

                                                     (2)

где Θ – неисключенная систематическая погрешность, заданная
границами ±Θ (по РМГ
43).

суммарная стандартная
неопределенность u_c (измерений): Стандартная неопределенность ре зультата измерений, равная положительному
квадратному корню суммы дисперсий (по РМГ
43).

расширенная неопределенность
U (измерений): Границы интервала, в
пределах которого нахо дится большая часть распределения значений, которые могли бы быть
приписаны измеряемой величине.

3.2 В настоящих
рекомендациях использованы следующие сокращения:

– СИ – средство измерений;

– НСП – неисключенная систематическая погрешность;

– СКО – среднее
квадратическое отклонение.

3.3 В настоящих
рекомендациях использованы следующие обозначения:

à – результат однократного
измерения;

x_i – i -е
экспериментальное данное, полученное при измерении;

 – среднее арифметическое
значение экспериментальных данных;

и – стандартная неопределенность
измерений;

u_A – стандартная
неопределенность, оцениваемая по типу А;

u_B – стандартная неопределенность,
оцениваемая по типу В;

u_c – суммарная стандартная
неопределенность;

U
– расширенная
неопределенность;

U (Р)
– расширенная неопределенность для уровня доверия Р;

k –
поправочный коэффициент при суммировании НСП, определяемый принятой доверительной
вероятностью Р и числом т составляющих
Θ _j ;

k _о –
коэффициент охвата;

К – коэффициент, используемый
при суммировании систематической и случайной составляющих погрешности;

S (Ã)
– СКО случайной погрешности результата измерений;

S –
СКО единичного измерения при многократных измерениях;

D ( Р ) – доверительные границы суммарной погрешности результата измерений для
доверительной вероятности Р ;

z_{P /2} – квантиль нормального распределения для доверительной
вероятности Р ;

Θ – границы неисключенной
систематической погрешности;

Θ(Р) – доверительные
границы систематической погрешности измерения для доверительной вероятности Р ;

п – число экспериментальных
данных;

т – число суммируемых НСП;

e (Р) –
доверительные границы случайных погрешностей.

4 Общие положения

4.1 За результат
однократного измерения Ã принимают значение величины, полученное
при измерении.

4.2 На этапе перехода от
погрешности к неопределенности целесообразно указывать характеристики и погрешности,
и неопределенности результата измерения.

Составляющие погрешности
результата измерения должны быть известны до проведения измерения.
Предполагают, что известные систематические погрешности исключены (внесены
поправки на все известные источники неопределенности, имеющие систематический
характер).

4.3 Полагают, что
распределение случайных погрешностей не противоречит нормальному распределению,
а неисключенные систематические погрешности, представленные заданными границами
±Θ, распределены равномерно.

Неопределенность результата
измерений понимают как неполное знание значения измеряемой величины, и для
количественного выражения этой неполноты вводят распределение вероятностей
возможных значений измеряемой величины – параметр, который количественно характеризует
точность результата измерений. Полагают, что распределение вероятностей
возможных значений измеряемой величины не противоречит нормальному
распределению.

В целях количественного
выражения неопределенности результата измерения, представленной в виде границ
отклонения значения величины от ее оценки [- Θ; + Θ] (неполное знание
о значении величины), полагают, что распределение возможных значений измеряемой
величины в указанных границах не противоречит равномерному распределению.

4.4 Выполнение однократных
измерений обосновывают следующими факторами:

– производственной
необходимостью (разрушение образца, невозможность повторения измерения,
экономическая целесообразность и т.д.);

– возможностью пренебрежения
случайными погрешностями;

– случайные погрешности
существенны, но доверительная граница погрешности результата измерения не
превышает допускаемой погрешности измерений;

– стандартная
неопределенность, оцениваемая по типу А, существенна, но расширенная неопределенность
не превышает заданного предела.

Примечания

1 Случайные
погрешности считают пренебрежимо малыми по сравнению с неисключенными
систематическими, если

Θ/S(Ã) > 8,                                                                                        (3)

где Θ – граница НСП
результата измерения;

S( Ã) – СКО
случайных погрешностей результата измерения.

2
Неопределенность, оцениваемую по типу А, считают пренебрежимо малой по
сравнению с неопределенностью, оцениваемой по типу В, если выполняется условие

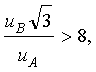                                                                           (4)

где u_A
и u_B – стандартные неопределенности, оцениваемые по
типам А и В соответственно.

4.5 При определении доверительных границ погрешности или расширенной
неопределенности для уровня доверия Р результата измерения принимают
вероятность, равную 0,95.

В особых случаях, например
при измерениях, которые нельзя повторить, допускается указывать доверительные
границы или расширенную неопределенность для уровня доверия Р и более
высоких вероятностей.

4.6 При вычислениях следует
пользоваться правилами округления в соответствии с МИ
1317. Доверительные границы погрешности (характеристики погрешности) и
расширенная неопределенность (расширенная неопределенность для уровня доверия Р)
результата измерения должны быть представлены не более чем двумя значащими
цифрами.

5 Составляющие погрешности и неопределенности результата
измерения

5.1 Составляющими
погрешности результата однократного измерения являются погрешности СИ, метода,
оператора, а также погрешности, обусловленные изменением условий измерения.

5.2 Погрешность результата
однократного измерения чаще всего представлена НСП и случайными погрешностями.

Неопределенность результата
однократного измерения может быть представлена стандартными неопределенностями,
оцениваемыми по типам А и В.

5.3 Характеристикой НСП
могут быть:

– границы ±Θ;

– доверительные границы ± Θ (Р).

5.4 Характеристикой
случайных погрешностей могут быть:

– СКО S ;

–
доверительные
границы ± e (Р).

5.5 Погрешность СИ
определяют на основании их метрологических характеристик, которые должны быть
указаны в нормативных и технических документах, и в соответствии с РД
50-453.

5.6 Погрешности метода и
оператора должны быть определены при разработке и аттестации конкретной МВИ.

6
Оценивание неисключенной систематической погрешности и стандартной
неопределенности, оцениваемой по типу В, результата измерения

6.1 НСП результата измерения
выражают границами этой погрешности, если среди составляющих погрешности
результата измерения в наличии одна НСП.

При указанном выше условии
стандартную неопределенность u_B , обусловленную неисключенной систематической погрешностью, заданной
своими границами ±Θ, оценивают по формуле ( 2).

6.2 Доверительные границы НСП
результата измерения вычисляют следующим образом.

6.2.1
При наличии нескольких НСП, заданных своими границами ±Θ _j , доверительную границу НСП
результата измерения Θ(Р) (без учета знака) вычисляют по
формуле

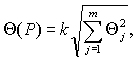                                                     (5)

где k – поправочный коэффициент,
определяемый принятой доверительной вероятностью и числом т составляющих
Θ _j .

При доверительной
вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.

При доверительной
вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если
число суммируемых составляющих т > 4. Если же число составляющих
равно четырем (т = 4), то поправочный коэффициент k
≈ 1,4;
при т = 3 k ≈ 1,3; при т = 2 k
≈
1,2. Более точное значение k для доверительной
вероятности Р = 0,99 при числе составляющих т £ 4 в зависимости от
соотношения составляющих l
определяют по графику [ k = f ( m ,
l )] в соответствии с требованиями ГОСТ
8.207.

Примечание – Погрешность, возникающая при использовании
формулы ( 5)
для суммирования НСП и при нахождении поправочного коэффициента k для доверительной вероятности Р = 0,99
по графику [ k ⁼ f( m,
l)], не
превышает 5 %.

При условии, указанном в 6.2.1,
суммарную стандартную неопределенность, оцениваемую по типу В, и_с,
B вычисляют по формуле

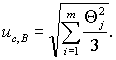                                                         (6)

6.2.2 При наличии нескольких
НСП, заданных доверительными границами Θ _j (Р _i ), рассчитанными по
формуле ( 5),
доверительную границу НСП результата однократного измерения вычисляют по
формуле

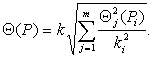                                                    (7)

При условии, указанном выше,
суммарную стандартную неопределенность, оцениваемую по типу В, вычисляют по
формуле

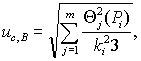                                                   (8)

где Θ_j ( P_i ) – доверительная
граница j -й НСП, соответствующая
доверительной вероятности Р _i ;

k и k_i – коэффициенты, соответствующие доверительным
вероятностям Р и Р _i .

Значения коэффициентов k и k_i определяют в соответствии с требованиями 6.2.1.

7
Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по
типу А, результата измерения

7.1 Доверительные границы
случайной погрешности и стандартную неопределенность, оцениваемую по типу А,
результата измерения вычисляют следующим образом.

7.1.1
Если случайные погрешности представлены несколькими СКО S_i , то СКО результата
однократного измерения S( Ã) вычисляют по формуле

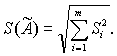                                                              (9)

Учитывая условия 7.1.1,
стандартную неопределенность, оцениваемую по типу А, результата однократного
измерения и _A вычисляют по формуле

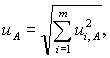
                                                         (10)

где т – число составляющих случайных
погрешностей;

u_i,_A = S_i.

Доверительную границу
случайной погрешности результата измерения e (Р) вычисляют
по формуле

e (P) = Z_P/2S(Ã),                                                           (11)

где Z_{P /2} – Р/2 точка
нормированной функции Лапласа, отвечающая вероятности Р. При
доверительной вероятности Р = 0,95 Z _0,95/2 принимают равным 2, при Р
= 0,99 Z _0,99/2 = 2,6.

7.1.2 Если случайные
погрешности представлены доверительными границами e _i ( Р ) , соответствующими одной и той же вероятности, доверительную границу
случайной погрешности результата однократного измерения вычисляют по формуле

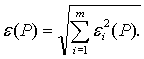                                                  (12)

7.1.3 Если случайные
погрешности представлены доверительными границами, соответствующими разным
вероятностям, сначала определяют СКО результата измерения по формуле

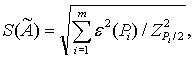                                        (13)

а затем вычисляют доверительные границы случайной
погрешности результата измерения по формуле ( 11).

8
Оценивание погрешности и расширенной неопределенности результата измерения

8.1 Если погрешности метода
и оператора пренебрежимо малы по сравнению с погрешностью используемых СИ (не
превышают 15 % погрешности СИ),
то за погрешность результата измерения принимают погрешность используемых СИ.

8.2 Если , то НСП или стандартной неопределенностью, оцениваемой по
типу В, пренебрегают и принимают в качестве погрешности или неопределенности
результата измерения доверительные границы случайных погрешностей или
расширенную неопределенность для уровня доверия Р, вычисляемую по
формуле U ( P ) = k _о и_А.

Если , то случайными погрешностями или стандартной
неопределенностью, оцениваемой по типу А, пренебрегают и принимают в качестве
погрешности или неопределенности результата измерения границы НСП или
расширенную неопределенность для уровня доверия Р, вычисляемую по
формуле U ( P ) = k _о и _B .

8.3 Если , то доверительную границу погрешности результата измерений D ( Р ) вычисляют по формуле

D (P) = K[Θ(P) + e (P)],                                                  (14)

где К – коэффициент, значение которого для
доверительной вероятности 0,95 равно 0,76; для доверительной вероятности 0,99
значение коэффициента K
равно 0,83.

Расширенную неопределенность
для уровня доверия Р вычисляют по формуле

                                            (15)

где k_o – коэффициент охвата
(коэффициент, используемый как множитель суммарной неопределенности для
получения расширенной неопределенности). Значение коэффициента охвата для
доверительной вероятности Р = 0,95 считают равным 2, для доверительной
вероятности Р = 0,99 – равным 3.

9 Форма представления
результата измерения

9.1 Форма представления
результатов однократных измерений должна соответствовать МИ
1317.

9.2 При симметричной
доверительной погрешности результат однократного измерения представляют в форме
Ã; ± D (Р); Р или Ã;
± D (Р), или Ã; U (Р).

Значение результата
измерения должно оканчиваться цифрами того же разряда, что и значение
погрешности или расширенной неопределенности для уровня доверия.

ПРИЛОЖЕНИЕ А
(справочное)

Расчет погрешности измерения
напряжения показывающим прибором

Однократное измерение
напряжения на участке электрической цепи сопротивлением R =
4 Ом.

А.1 Априорные данные об
исследуемом объекте

Участок электрической цепи
представляет собой соединение нескольких резисторов, имеющих стабильное
сопротивление. Ток в цепи – постоянный. Измерение выполняют в сухом
отапливаемом помещении температурой до 30 ° С при магнитном поле до 400
А/м. Предполагаемое падение напряжения на участке цепи, не превышающее 1,5 В,
постоянно.

Для измерения выбирают
вольтметр класса точности 0,5 по ГОСТ
8711 (приведенная погрешность 0,5 %) с верхним пределом диапазона измерений
U _{п p} = 1,5 В. Вольтметр имеет
магнитный экран. Некоторый запас по точности средства измерений необходим из-за
возможного наличия дополнительных погрешностей, погрешности метода и т.д.

Инструментальная
составляющая погрешности определяется основной и дополнительной погрешностями.

Основная погрешность прибора
указана в приведенной форме. Следовательно,
предел допускаемой основной погрешности вольтметра

Дополнительная погрешность
из-за влияния магнитного поля не превышает 1,5 % нормирующего значения прибора
и равна ±0,0225 В (0,015 · 1,5). Дополнительная температурная погрешность,
обусловленная отклонением температуры от нормальной (20 °С) на 10 °С, не
превышает 60 % предела
допускаемой основной погрешности, эта дополнительная погрешность равна ±0,0045
В (0,0075 · 0,6).

А.2
Оценивание погрешности результата измерения

Погрешность метода
определяется соотношением между сопротивлением участка цепи R и
сопротивлением вольтметра R_V . Сопротивление вольтметра
известно: R_V = 1000 Ом. При подсоединении
вольтметра к цепи исходное напряжение U_x изменяется на

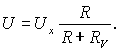
Отсюда методическая
погрешность D _M
в абсолютной форме

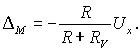
Методическая погрешность
δ_м в относительной форме

Оцененная методическая
погрешность является систематической составляющей погрешности измерений и
должна быть внесена в результат измерения в виде поправки  В. Тогда результат
измерения Ã с учетом поправки на
систематическую погрешность

à = 0,90 + 0,004 = 0,904 В.

Находят границы погрешности
результата измерения.

Поскольку основная
погрешность применяемого средства измерений и его дополнительные погрешности
заданы границами, следует рассматривать эти погрешности как неисключенные систематические.
Воспользовавшись формулой ( 5), находят доверительную границу неисключенной
систематической погрешности результата измерения при доверительной вероятности Р
= 0,95:

Результат измерения в
соответствии с разделом 9 следует представить в форме

à = 0,904 В; D (Р) = ±0,027 В; Р = 0,95
или (0,904 ± 0,027) В; Р = 0,95.

Ключевые слова: результат измерения,
однократные измерения, среднее квадратическое отклонение, стандартная
неопределенность, оцениваемая по типу А и по типу В, доверительная погрешность,
расширенная неопределенность, коэффициент охвата, неисключенная систематическая
погрешность

Все полученные отклонения результатов измерений должны у Вас попасть в рассчитанные пределы. Если отклонения результата измерений от заданного эталоном значения превысили допустимые пределы, то бракуйте СИ. Поскольку по теории вероятности вероятность такого результата возможна при числе опытов более 2000 (грубо), а не 5.

Т.е. я должен пересмотреть все результаты измерений и оценить “попадание” в доверительные границы?

Указанная Вами процедура в прочитанной мной методике не упоминается. Разработчик или предполагает, что поверитель должен это знать и применять на практике автоматически, или сам плохо представляет как этим пользоваться, т.к. далее по тексту он оперирует только средними величинами, сравнивает их с “требуемыми” и ни о каких границах даже не упоминает. Вот у меня и возник вопрос, а зачем их считать и что с ними делать?

P.S. Спасибо за ликбез!

Разработчика “легко” обидеть. Надо до конца с ГОСТ Р 8.736-2011 разобраться.

“4.2 При статистической обработке группы результатов прямых многократных независимых измерений выполняют следующие операции:

– исключают известные систематические погрешности из результатов измерений;

– вычисляют оценку измеряемой величины;

– вычисляют среднее квадратическое отклонение результатов измерений;

– проверяют наличие грубых погрешностей и при необходимости исключают их;

– проверяют гипотезу о принадлежности результатов измерений нормальному распределению;

– вычисляют доверительные границы случайной погрешности (доверительную случайную погрешность) оценки измеряемой величины;

– вычисляют доверительные границы (границы) неисключенной систематической погрешности оценки измеряемой величины;

– вычисляют доверительные границы погрешности оценки измеряемой величины. “

Вот для подтверждения закона распределения погрешности необходимо провести как минимум 17 (или 21 уж по памяти) опытов. Никак не 5.

Вот : “7.2 При числе результатов измерений n<=15 принадлежность их к нормальному распределению не проверяют. При этом вычисление доверительных границ случайной погрешности оценки измеряемой величины по методике, предусмотренной настоящим стандартом, допускается только в том случае, если заранее известно, что результаты измерений принадлежат нормальному распределению.”

Значит нормальнее некуда и определено на этапе проведения испытаний СИ до нас :)/>

Далее СКО умножаем на коэф. Стьюдента из приложения Д: при n=5 и вероятности 0,95 он равен 2,776. Получили доверительные границы случайной погрешности. Осталась систематика.

С НСП немного сложнее. Поэтому думаю если ошибусь, то коллеги помогут Вам. В сущности это отклонение среднего значения результатов от значения заданного эталоном. Переход в ГОСТ от конкретного значения НСП к количеству составляющих мягко говоря “размыт” . Критерий того, что “пренебрежительно мал” не раскрыт: “В качестве границ составляющих НСП принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.” Пренебрежительно -это на порядок или как?

Если природа составляющих НСП известна, то вы геометрически суммируете составляющие с учетом коэф. влияния составляющей и умножаете на 1,1. Получили -доверительные границы НСП оценки измеряемой величины .

Далее по формулам 12 и 13 находите доверительные границы погрешности.

Вот формула 16 опять ставит меня в тупик- где взять число составляющих НСП (опять).

Изменено 2 Мая 2014 пользователем libra