Как найти доверительные границы среднего значения

Определяя
для средней арифметической (или
относительной) величины два крайних
значения: минимально возможное и
максимально возможное, находят пределы,
в которых может быть искомая величина
генерального
параметра. Эти
пределы называют доверительными
границами.

Доверительные
границы – границы
средних (или относительных) величин,
выход за пределы которых вследствие
случайных колебаний имеет незначительную
вероятность.

Вероятность
попадания средней или относительной
величины в доверительный интервал
называется доверительной
вероятностью.

Доверительные
границы средней
арифметической генеральной совокупности
определяют по формуле:

М_ген
= М_выб
±
t
· m_M

Доверительные
границы относительной величины в
генеральной совокупности определяют
по следующей формуле:

Р_ген
= Рвыб ± t
· m_р

Где:
М_ген
и Р_ген
– значения средней и
относительной величин, полученных для
генеральной совокупности;

М_выб
и Р_выб
– значения средней и
относительной величин, полученных для
выборочной совокупности;

m_M
и m_р
– ошибки
репрезентативности выборочных величин;

t
– доверительный критерий,
который зависит от величины безошибочного
прогноза, устанавливаемого при
планировании исследования.

Произведение
t
· m
(Δ)
– предельная ошибка показателя, полученного
при данном выборочном исследовании.

Размеры
предельной ошибки зависят от коэффициента
t,
который избирает сам
исследователь, исходя из заданной
вероятности безошибочного прогноза.

Величина
критерия t
связана с вероятностью
безошибочного прогноза (Р)
и числом наблюдений в
выборочной совокупности (табл. 4.1).

Таблица
4.1

Зависимость
доверительного критерия t
от степени

вероятности
безошибочного прогноза
Р (при n
> 30)

Степень вероятности безошибочного прогноза (Р %)	Доверительный критерий t
95,0	2
99,0	2,6
99,9	3,3

Для большинства
медико-биологических и социальных
исследований достоверными считаются
доверительные границы, установленные
с вероятностью безошибочного прогноза
= 95% и более.

Чтобы
найти критерий t
при числе наблюдений
(n) < 30,
необходимо пользоваться специальной
таблицей Н.А.Плохинского (табл. 4.2), в
которой слева показано число наблюдений
– единица (n
– 1), а сверху (Р)
– степень вероятности
безошибочного прогноза.

При
определении доверительных границ
сначала надо решить вопрос о том, с какой
степенью вероятности безошибочного
прогноза необходимо представить
доверительные границы средней или
относительной величины. Избрав
определенную степень вероятности,
соответственно этому находят величину
доверительного критерия t
при данном числе
наблюдений. Таким образом, доверительный
критерий устанавливается заранее, при
планировании исследования.

Таблица 4.2

Значение
критерия t
для трех степеней
вероятности (по Н.А.Плохинскому)

Р n = n-1	95%	99%	99,9%
1	12,7	63,7	37,0
2	4,3	9,9	31,6
3	3,2	5,8	12,9
4	2,8	4,6	8,6
5	2,6	4,0	6,9
6	2,4	3,7	6,0
7	2,4	3,5	5,3
8	2,3	3,4	5,0
9	2,3	3,3	4,8
10	2,2	3,2	4,6
11	2,2	3,1	4,4
12	2,2	3,1	4,3
13	2,3	3,0	4,1
14-15	2,1	3,0	4,1
16-17	2,1	2,9	4,0
18-20	2,1	2,9	3,9
21-24	2,1	2,8	3,8
25-29	2,0	2,8	3,7

Любой параметр
(средняя или относительная величина)
может оцениваться с учетом доверительных
границ, полученных при расчете.

Например:требуется определить доверительные
границы среднего уровня пепсина у
больных гипертериозом с 95% вероятностью
безошибочного прогноза. Если известно,
что:

n
= 49;

М_выб
=1г%;

m_м
= ± 0,05г%

1.Определение
доверительных границ средней величины
в генеральной совокупности:

М_ген
= М_выб
±
t
· m_M
= 1г% ± 2 ·
0,05г%

1г%
+ 0,1г% = 1,1 г%

М_ген
=

1г%
– 0,1г% = 0,9 г%

Заключение:
установлено с вероятностью безошибочного
прогноза 95%, что средний уровень пепсина
в генеральной совокупности у больных
гипертериозом находится в пределах от
1,1 г% до 0,9 г%.

Как видно,
доверительные границы зависят от размера
доверительного интервала.

Анализ
доверительных интервалов указывает,
что при заданных степенях вероятности
и n
> 30 – t
имеет неизменную величину
и при этом доверительный интервал
зависит от величины ошибки репрезентативности.

С уменьшением
величины ошибки суживаются доверительные
границы средних и относительных величин,
полученных на выборочной совокупности,
т.е. уточняются результаты исследования,
которые приближаются к соответствующим
величинам генеральной совокупности.
Если ошибка большая, то получают для
выборочной величины большие доверительные
границы, которые могут противоречить
логической оценке искомой величины в
генеральной совокупности. В подобном
случае надо искать резервы сокращения
размаха доверительных границ в размере
величины ошибки репрезентативности.

Доверительные
границы М_выб
и Р_выб
зависят не только от
средних ошибок этих величин, но и от
избранной исследователем степени
вероятности безошибочного прогноза.
При большой степени вероятности размах
доверительных границ увеличивается.

3.
Определение достоверности разности
средних (или относительных) величин (по
критерию t
– Стъюдента).

В медицине и
здравоохранении по разности параметров
оценивают средние и относительные
величины, полученные для разных групп
населения по полу, возрасту, а также
групп больных и здоровых и т.д. Во всех
случаях при сопоставлении двух
сравниваемых величин возникает
необходимость не только определить
их разность, но и оценить ее достоверность.

Достоверность
разности величин, полученных при
выборочных исследованиях, означает,
что вывод об их различии может быть
перенесен на соответствующие генеральные
совокупности.

Достоверность
разности выборочной совокупности
измеряется доверительным критерием,
который рассчитывается по специальным
формулам для средних и относительных
величин.

Формула оценки
достоверности разности сравниваемых
средних величин:

M₁
– M₂

t
= ——————

m₁²
+ m₂²

Для относительных
величин:

Р₁
– Р₂

t
= ——————

m₁²
+ m₂²

Где:
M₁;
M₂
; Р₁;
Р₂
– параметры,
полученные при выборочных исследованиях;

m₁;
m₂
– их средние ошибки;

t
– критерий достоверности
(Стъюдента).

Разность
статистически достоверна при t
≥ 2, что соответствует
вероятности безошибочного прогноза,
равной 95% и более.

Для большинства
исследований, проводимых в медицине и
здравоохранении, такая степень вероятности
является вполне достаточной.

При
величине критерия достоверности t
< 2 степень вероятности
безошибочного прогноза составляет Р <
95%. При такой степени
вероятности нельзя утверждать, что
полученная разность показателей
достоверна с достаточной степенью
вероятности. В этом случае необходимо
получить дополнительные данные, увеличив
число наблюдений.

Иногда при увеличении
численности выборки разность продолжает
оставаться не достоверной. Если при
повторных исследованиях разность
остается недостоверной, можно считать
доказанным, что между сравниваемыми
совокупностями не обнаружено различий
по изучаемому признаку.

Например:требуется определить, достоверны ли
различия в уровне пепсина в желудочном
соке больных гипертериозом и здоровых
лиц. Обследуются на пепсин две группы:
49 больных гипертериозом и 50 здоровых
людей (контрольная группа). Результаты
представлены в таблице 4.3.

Таблица
4.3

Сравнение среднего
уровня пепсина в желудочном соке больных
гипертериозом и здоровых лиц

Сравниваемые группы	N	М (г%)	m (г%)	t	Уровень вероятности безошибочного прогноза (Р)
Больные гипертериозом	49	1,0	± 0,3	10,0	< 99,9
Здоровые (контрольная группа)	50	4,0	± 0,1

M₁
– M₂

t
= ——————

m₁²
+ m₂²

4
– 1

t
= —————- = 10,0

0,3²
+ 0,1²

Заключение:
при гипертериозе наблюдается снижение
уровня пепсина, что подтверждается с
большой степенью вероятности безошибочного
прогноза (Р > 99,9%).
Следовательно, снижение уровня пепсина
может быть использовано в качестве
одного из симптомов для подтверждения
диагностики гипертериоза.

Подобным же образом
оценивают достоверность разности
сравниваемых относительных величин.

Указанная методика
оценки достоверности и разности
результатов исследования позволяет
проводить только сравнение групп по
парам, при обязательном наличии обобщающих
параметров – средних арифметических
или относительных величин и их средних
ошибок.

Соседние файлы в папке По вопросам

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.

Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.

Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.

Определение доверительного интервала.

Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 – alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.

Этот интервал часто упоминается как (100 (1 – alpha)% ) доверительный интервал для параметра.

Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).

В этом чтении, мы имеем дело только с двусторонними доверительными интервалами – доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.

Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.

При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.

При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.

Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.

Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.

На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.

Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.

Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.

Построение доверительных интервалов.

Доверительный интервал (100 (1 – alpha)% ) для параметра имеет следующую структуру.

Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.

Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.

Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.

Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).

Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).

Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.

Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.

В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.

---

Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 – alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.

Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:

( sigma_{overline X} = 20 Big / sqrt{100} = 2 )

Доверительный интервал, таким образом, имеет нижний предел:

( overline X – 1.96 sigma_{overline X} ) = 25 – 1.96(2) = 25 – 3.92 = 21.08.

Верхний предел доверительного интервала равен:

( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92

95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.

Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).

Доверительный интервал (100 (1 – alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:

( Large dst overline X pm z_{alpha /2}{sigma over sqrt n}  ) (Формула 4)

Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.

Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.

Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:

Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.

«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»

см. Freund и Williams (1977), стр. 266.

На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.

Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.

---

Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).

Распределение статистики (t) называется t-распределением Стьюдента (англ. “Student’s t-distribution”) из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.

В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.

Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, – это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).

В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).

Доверительные интервалы для среднего по совокупности – z-альтернатива (большая выборка, дисперсия совокупности неизвестна).

Доверительный интервал (100 (1 – alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:

( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)

Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.

Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.

Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.

[см. также: CFA – Коэффициент Шарпа]

Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.

Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.

---

Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).

Доверительный интервал будет равен:

( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495   end{aligned} )

Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.

В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.

Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.

Концепция степеней свободы.

Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.

Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.

Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.

t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.

Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.

Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n – 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.

Мы также используем ( n – 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.

---

Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?

При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.

Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n – 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.

Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.

t-распределение Стьюдента.

Предположим, что мы делаем выборку из нормального распределения.

Коэффициент (z = (overline X – mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X – mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n – 1) степеней свободы.

Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.

Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.

На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.

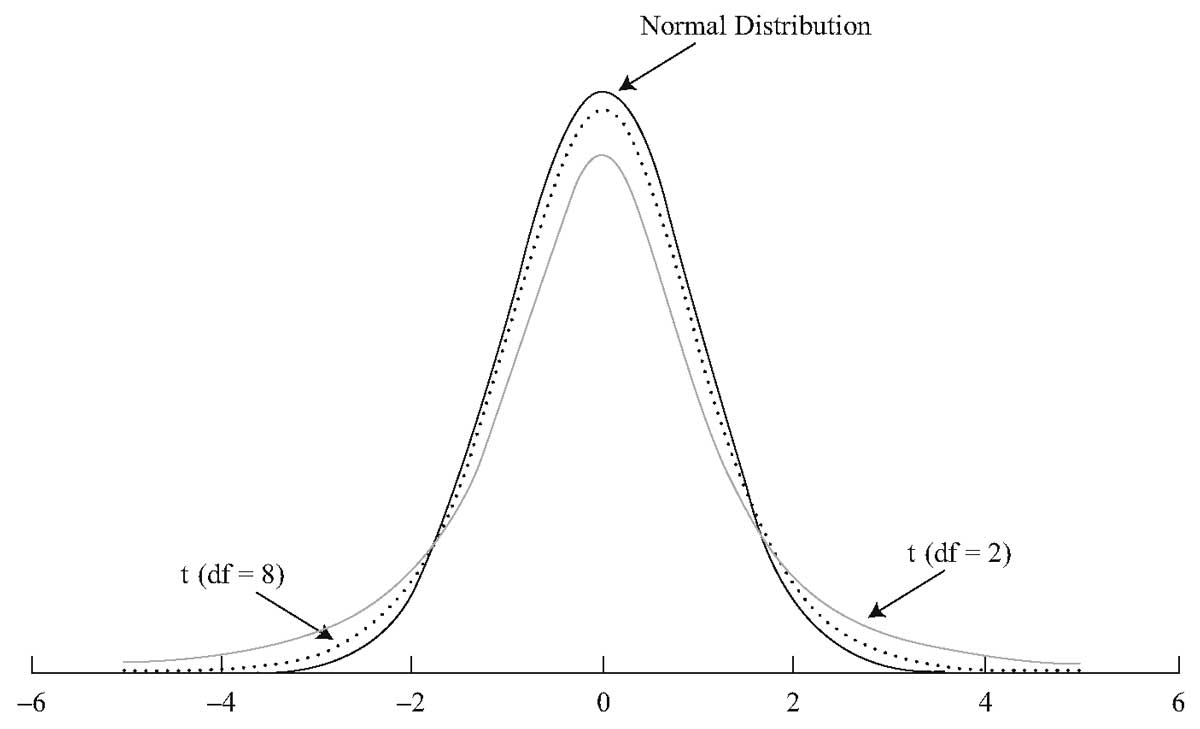Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.

Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.

По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.

Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.

t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.

Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.

Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.

Например,

Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.

Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) – t-распределение.

Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:

• выборка является большой, или
• выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,

то доверительный интервал (100 (1 – alpha)% ) для среднего совокупности ( mu ) задается формулой:

Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.

Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.

Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.

Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение – 0.30.

Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.

Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.

Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.

Доверительный интервал будет:

( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \  &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498   end{aligned} )

Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.

В Таблице 3 приведены различные факторы надежности, которые мы использовали.

Таблица 3. Основы для расчета факторов надежности.

Выборка из:	Статистика для выборки малого размера	Статистика для выборки большого размера
Нормальное распределение с известной дисперсией	(z)	(z)
Нормальное распределение с неизвестной дисперсией	(t)	(t)*
Ненормальное распределение с известной дисперсией	недоступно	(z)
Ненормальное распределение с неизвестной дисперсией	недоступно	(t)*

* Использование (z) также приемлемо.

Доверительный интервал для среднего

Построим в MS EXCEL доверительный интервал для оценки среднего значения распределения в случае известного значения дисперсии.

В статье

Статистики, выборочное распределение и точечные оценки в MS EXCEL

дано определение

точечной оценки

параметра распределения (point estimator). Однако, в силу случайности выборки,

точечная оценка

не совпадает с оцениваемым параметром и более разумно было бы указывать интервал, в котором может находиться неизвестный параметр при наблюденной выборке х

₁

, x

₂

, …, х

_n

. Поэтому цель использования

доверительных интервалов

состоит в том, чтобы по возможности избавиться от неопределенности и сделать как можно более полезный

статистический вывод

.

Примечание

: Процесс обобщения данных

выборки

, который приводит к

вероятностным

утверждениям обо всей

генеральной совокупности

, называют

статистическим выводом

(statistical inference).

СОВЕТ

: Для построения

Доверительного интервала

нам потребуется знание следующих понятий:

• дисперсия и стандартное отклонение

  ,

• выборочное распределение статистики

  ,

• уровень доверия/ уровень значимости

  ,

• стандартное нормальное распределение

  и

  его квантили

  .

К сожалению, интервал, в котором

может

находиться неизвестный параметр, совпадает со всей возможной областью изменения этого параметра, поскольку соответствующую

выборку

, а значит и

оценку параметра

, можно получить с ненулевой вероятностью. Поэтому приходится ограничиваться нахождением границ изменения неизвестного параметра с некоторой заданной наперед вероятностью.

Определение

:

Доверительным интервалом

называют такой интервал изменения случайной величины

,

которыйс заданной вероятностью

,

накроет истинное значение оцениваемого параметра распределения.

Эту заданную вероятность называют

уровнем доверия

(или

доверительной вероятностью

).

Обычно используют значения

уровня доверия

90%; 95%; 99%, реже 99,9% и т.д. Например,

уровень

доверия

95% означает, что дополнительное событие, вероятность которого 1-0,95=5%, исследователь считает маловероятным или невозможным.

Примечание

:

Вероятность этого дополнительного события называется

уровень значимости

или

ошибка первого рода

. Подробнее см. статью

Уровень значимости и уровень надежности в MS EXCEL

.

Разумеется, выбор

уровня доверия

полностью зависит от решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.

Примечание

:

Построение

доверительного интервала

в случае, когда

стандартное отклонение

неизвестно, приведено в статье

Доверительный интервал для оценки среднего (дисперсия неизвестна) в MS EXCEL

. О построении других

доверительных интервалов

см. статью

Доверительные интервалы в MS EXCEL

.

Формулировка задачи

Предположим, что из

генеральной совокупности

имеющей

нормальное распределение

взята

выборка

размера n. Предполагается, что

стандартное отклонение

этого распределения известно. Необходимо на основании этой

выборки

оценить неизвестное

среднее значение распределения

(μ,

математическое ожидание

) и построить соответствующий

двухсторонний

доверительный интервал

.

Точечная оценка

Как известно из

Центральной предельной теоремы

,

статистика

(обозначим ее

Х

_ср

) является

несмещенной оценкой среднего

этой

генеральной совокупности

и имеет распределение N(μ;σ

²

/n).

Примечание

:

Что делать, если требуется построить

доверительный интервал

в случае распределения, которое

не является

нормальным?

В этом случае на помощь приходит

Центральная предельная теорема

, которая гласит, что при достаточно большом размере

выборки

n из распределения

не являющемся

нормальным

,

выборочное распределение статистики Х

_ср

будет

приблизительно

соответствовать

нормальному распределению

с параметрами N(μ;σ

²

/n).

Итак,

точечная оценка

среднего

значения распределения

у нас есть – это

среднее значение выборки

, т.е.

Х

_ср

. Теперь займемся

доверительным интервалом.

Построение доверительного интервала

Обычно, зная распределение и его параметры, мы можем вычислить вероятность того, что случайная величина примет значение из заданного нами интервала. Сейчас поступим наоборот: найдем интервал, в который случайная величина попадет с заданной вероятностью. Например, из свойств

нормального распределения

известно, что с вероятностью 95%, случайная величина, распределенная по

нормальному закону

, попадет в интервал примерно +/- 2

стандартных отклонения

от

среднего значения

(см. статью про

нормальное распределение

). Этот интервал, послужит нам прототипом для

доверительного интервала

.

Теперь разберемся,знаем ли мы распределение

,

чтобы вычислить этот интервал? Для ответа на вопрос мы должны указать форму распределения и его параметры.

Форму распределения мы знаем – это

нормальное распределение

(напомним, что речь идет о

выборочном распределении

статистики

Х

_ср

).

Параметр μ нам неизвестен (его как раз нужно оценить с помощью

доверительного интервала

), но у нас есть его оценка

Х

_ср

,

вычисленная на основе

выборки,

которую можно использовать.

Второй параметр –

стандартное отклонение выборочного среднего

будем считать известным

, он равен σ/√n.

Т.к. мы не знаем μ, то будем строить интервал +/- 2

стандартных отклонения

не от

среднего значения

, а от известной его оценки

Х

_ср

. Т.е. при расчете

доверительного интервала

мы НЕ будем считать, что

Х

_ср

попадет в интервал +/- 2

стандартных отклонения

от μ с вероятностью 95%, а будем считать, что интервал +/- 2

стандартных отклонения

от

Х

_ср

с вероятностью 95% накроет μ

– среднее генеральной совокупности,

из которого взята

выборка

. Эти два утверждения эквивалентны, но второе утверждение нам позволяет построить

доверительный интервал

.

Кроме того, уточним интервал: случайная величина, распределенная по

нормальному закону

, с вероятностью 95% попадает в интервал +/- 1,960

стандартных отклонений,

а не+/- 2

стандартных отклонения

. Это можно рассчитать с помощью формулы

=НОРМ.СТ.ОБР((1+0,95)/2)

, см.

файл примера Лист Интервал

.

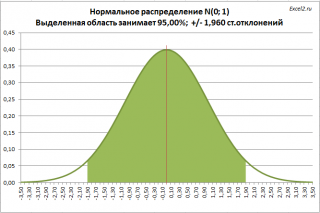
Теперь мы можем сформулировать вероятностное утверждение, которое послужит нам для формирования

доверительного интервала

: «Вероятность того, что

среднее генеральной совокупности

находится от

среднего выборки

в пределах 1,960 «

стандартных отклонений выборочного среднего»

, равна 95%».

Значение вероятности, упомянутое в утверждении, имеет специальное название

уровень доверия

, который связан с

уровнем значимости α (альфа) простым выражением

уровень доверия

=

1

-α

.

В нашем случае

уровень значимости

α

=1-0,95=0,05

.

Теперь на основе этого вероятностного утверждения запишем выражение для вычисления

доверительного интервала

:

где Z

_α/2

–

верхний α/2-квантиль

стандартного

нормального распределения

(такое значение случайной величины

z

,

что

P

(

z

>=

Z

_α/2

)=α/2

).

Примечание

:

Верхний α/2-квантиль

определяет ширину

доверительного интервала

в

стандартных отклонениях

выборочного среднего.

Верхний α/2-квантиль

стандартного

нормального распределения

всегда больше 0, что очень удобно.

В нашем случае при α=0,05,

верхний α/2-квантиль

равен 1,960. Для других уровней значимости α (10%; 1%)

верхний α/2-квантиль

Z

_α/2

можно вычислить с помощью формулы

=НОРМ.СТ.ОБР(1-α/2)

или, если известен

уровень доверия

,

=НОРМ.СТ.ОБР((1+ур.доверия)/2)

.

Обычно при построении

доверительных интервалов для оценки среднего

используют только

верхний α

/2-

квантиль

и не используют

нижний α

/2-

квантиль

. Это возможно потому, что

стандартное

нормальное распределение

симметрично относительно оси х (

плотность его распределения

симметрична относительно

среднего, т.е. 0

)

.

Поэтому, нет нужды вычислять

нижний α/2-квантиль

(его называют просто α

/2-квантиль

), т.к. он равен

верхнему α

/2-

квантилю

со знаком минус.

Напомним, что, не смотря на форму распределения величины х, соответствующая случайная величина

Х

_ср

распределена

приблизительно

нормально

N(μ;σ

²

/n) (см. статью про

ЦПТ

). Следовательно, в общем случае, вышеуказанное выражение для

доверительного интервала

является лишь приближенным. Если величина х распределена по

нормальному закону

N(μ;σ

²

/n), то выражение для

доверительного интервала

является точным.

Расчет доверительного интервала в MS EXCEL

Решим задачу.

Время отклика электронного компонента на входной сигнал является важной характеристикой устройства. Инженер хочет построить доверительный интервал для среднего времени отклика при уровне доверия 95%. Из предыдущего опыта инженер знает, что стандартное отклонение время отклика составляет 8 мсек. Известно, что для оценки времени отклика инженер сделал 25 измерений, среднее значение составило 78 мсек.

Решение

: Инженер хочет знать время отклика электронного устройства, но он понимает, что время отклика является не фиксированной, а случайной величиной, которая имеет свое распределение. Так что, лучшее, на что он может рассчитывать, это определить параметры и форму этого распределения.

К сожалению, из условия задачи форма распределения времени отклика нам не известна (оно не обязательно должно быть

нормальным

).

Среднее, т.е. математическое ожидание

, этого распределения также неизвестно. Известно только его

стандартное отклонение

σ=8. Поэтому, пока мы не можем посчитать вероятности и построить

доверительный интервал

.

Однако, не смотря на то, что мы не знаем распределение

времени

отдельного отклика

, мы знаем, что согласно

ЦПТ

,

выборочное распределение

среднего времени отклика

является приблизительно

нормальным

(будем считать, что условия

ЦПТ

выполняются, т.к. размер

выборки

достаточно велик (n=25))

.

Более того,

среднее

этого распределения равно

среднему значению

распределения единичного отклика, т.е. μ. А

стандартное отклонение

этого распределения (σ/√n) можно вычислить по формуле

=8/КОРЕНЬ(25)

.

Также известно, что инженером была получена

точечная оценка

параметра μ равная 78 мсек (Х

_ср

). Поэтому, теперь мы можем вычислять вероятности, т.к. нам известна форма распределения (

нормальное

) и его параметры (Х

_ср

и σ/√n).

Инженер хочет знать

математическое ожидание

μ распределения времени отклика. Как было сказано выше, это μ равно

математическому ожиданию выборочного распределения среднего времени отклика

. Если мы воспользуемся

нормальным распределением

N(Х

_ср

; σ/√n), то искомое μ будет находиться в интервале +/-2*σ/√n с вероятностью примерно 95%.

Уровень значимости

равен 1-0,95=0,05.

Наконец, найдем левую и правую границу

доверительного интервала

. Левая граница:

=78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)

=

74,864

Правая граница:

=78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136

или так

Левая граница:

=НОРМ.ОБР(0,05/2; 78; 8/КОРЕНЬ(25))

Правая граница:

=НОРМ.ОБР(1-0,05/2; 78; 8/КОРЕНЬ(25))

Ответ

:

доверительный интервал

при

уровне доверия 95% и σ

=8

мсек

равен

78+/-3,136 мсек.

В

файле примера на листе Сигма

известна создана форма для расчета и построения

двухстороннего

доверительного интервала

для произвольных

выборок

с заданным σ и

уровнем значимости

.

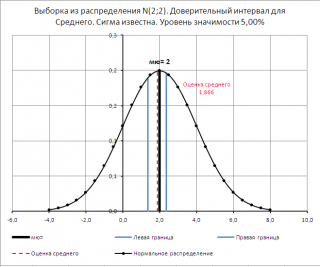
Функция

ДОВЕРИТ.НОРМ()

Если значения

выборки

находятся в диапазоне

B20:B79

, а

уровень значимости

равен 0,05; то формула MS EXCEL:

=СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79))

вернет левую границу

доверительного интервала

.

Эту же границу можно вычислить с помощью формулы:

=СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))

Примечание

: Функция

ДОВЕРИТ.НОРМ()

появилась в MS EXCEL 2010. В более ранних версиях MS EXCEL использовалась функция

ДОВЕРИТ()

.

Предположим что мы рассчитывали бы такой показатель для каждого из выборочных средних. Пусть зеленый столбик выборочное среднее равняется

x1x_1

, если бы мы рассчитали интервал для такого выборочного среднего

x1±1.96sex_1 pm 1.96se

, то как видим, этот интервал включил бы в себя среднее ГС. Если бы мы рассчитали такой интервал для среднего

x2x_2

, то такой интервал также включил в себя среднее ГС. Таким образом 95% процентов всех выборочных средних включили бы в себя среднее ГС, если бы рассчитывали такой интервал и только те выборочные средние, которые очень далеко отклонились от среднего ГС например

x4x_4

и не включили бы в свой 95% интервал среднее ГС.