Конечной целью
моделирования является оценка или
прогнозирование показателя Y
в зависимости
от значений X.
Прогноз подразделяется
на точечный и интервальный и обычно
осуществляется не более чем на одну
треть размаха:
 ,
,
где
 – точка прогноза.
– точка прогноза.
В точечном прогнозе
показателя Y
для
 определяется лишь одно число, которое
определяется лишь одно число, которое
представляет условное среднее и (при
выполнении предпосылок регрессионного
анализа) наиболее вероятное значение
с точки зрения закономерности, отраженной
в модели. В таком прогнозе не учитываются
отклонения от закономерностей в
результате воздействия случайных и
неучтенных факторов.
В интервальном
прогнозе отклонения от закономерностей
в результате случайных воздействий
определяются границами доверительных
интервалов.
Доверительным
интервалом называется такой интервал,
которому с заданной степенью вероятности
(называемой доверительной) принадлежат
истинные значения показателя при
условии, что закономерности, отраженные
в модели, не противоречат развитию как
на участке наблюдения, так и на участке
оценки (или в периоде упреждения
прогноза).
Случайные отклонения
от модели проявляются в виде ошибок.
Поэтому при определении границ,
доверительных интервалов необходимо
определить из чего складываются возможные
ошибки моделирования, оценки и
прогнозирования. При условии, что модель
адекватна, и возможные ошибки носят
случайный характер, следует различать
два основных источника ошибок:
-
ошибки аппроксимации
(рассеяние наблюдений относительно
модели); -
ошибки оценок
параметров модели.
Наличие ошибок
первого типа очевидно даже визуально.
Величина ошибок аппроксимации
характеризуется остаточной дисперсией
 или средней квадратической ошибкой
или средней квадратической ошибкой .
.
Распределение этих ошибок для адекватных
моделей – нормально (нормальность
ошибок – одно из условий адекватности).
Ошибки оценок
параметров модели обусловлены тем, что
их параметры, фиксированные в модели
как однозначные, в действительности
являются случайными величинами, так
как они оцениваются на основе фактических
данных, в которых присутствует как
закономерная, так и случайная составляющие.
Средние значения этих оценок при
выполнении предпосылок регрессионного
анализа соответствует истинным значениям
параметров, а их дисперсии зависят от
остаточной дисперсии, числа наблюдений
и вида модели.
Общее среднее
квадратическое отклонение истинных
значений от расчетных может быть
представлено как:
 (87)
(87)
а в точке прогноза:

(88)
Исходя из предпосылки
нормального распределения остатков
границы доверительных интервалов
определяются по формулам:

(89)
Анализ выражений
(88, 89) позволяет для моделей парной
регрессии сделать вывод, что доверительные
интервалы тем шире, чем:
– больше остаточная
дисперсия (менее точна модель);
– значение
 больше удалено от среднего значения
больше удалено от среднего значения (см.
(см.
рис. 7.5);
– сложнее форма
модели;
– больше заданная
доверительная вероятность.
Обобщая полученные
результаты, можно сделать вывод, что
построенная модель обладает хорошим
качеством, т.е. она достаточно точна и
адекватна исследуемому процессу по
всем перечисленным ранее критериям.
Учитывая еще и нормальность ряда остатков
можно осуществлять точечный и интервальный
прогнозы. В связи с этим табл. 7.5 приведены
данные для построения доверительных
интервалов.
Массив
![]() дополнен двумя значениями:
дополнен двумя значениями:![]() и
и![]() ,
,
которые выделены жирным шрифтом.
Значения: –
–
ширина доверительного интервала; –
–
нижняя граница доверительного интервала; –
–
верхняя граница доверительного интервала
вычислены по формулам (87 – 89) с доверительной
вероятностью 0,975 и соответствующим ей
коэффициентом доверия Стьюдента 2,317.
Выбор распределения Стьюдента обусловлен
не большим объёмом анализируемой
совокупности.
График доверительных
интервалов и график их ширины приведены
на рис. 6 и 7.

Рис. 6. График
доверительных интервалов

Рис. 7. График
ширины доверительных интервалов
С учетом нормального
распределения остатков при среднем
значении ВТО фирм равном 1067,43 млн. долл.
с вероятностью 0,975 прогнозируемые
таможенные платежи в бюджет составят
от 27,61 до 31,37 млн. долл., при этом условное
среднее (наиболее вероятный объём
поступлений) ожидается 29,49 млн. долл.
ЛИТЕРАТУРА
-
Андронов А.М.,
Копытов Е.А., Гринглаз Л.Я. Теория
вероятностей и математическая статистика:
Учебник для вузов. – СПб: Питер. 2004. –
461 с.: ил. – (серия «Учебник для вузов»). -
Боровиков В.
STATISTICA.
Искусство анализа данных на компьютере:
Для профессионалов. 2-е изд. (+ CD).
– СПб.: Питер. 2003. – 688 с.: ил. -
Козлов А.Ю., Мхитарян
В.С., Шишов В.Ф. Статистический анализ
данных в MS
EXCEL:
Учеб. Пособие.- М.: ИНФРА-М, 2012, – 320 с.-
(Высшее образование). -
Громыко Г.Л. Теория
статистики: Практикум. – 3-е изд., доп.
и перераб. – М.: ИНФРА – М, 2006. – 205 с. –
(Высшее образование). -
Елисеева И.И.,
Юзбашев М.М. Общая теория статистики:
Учебник/ Под ред. И.И. Елисеевой. – 5-е
изд., перераб. и доп. – М.: Финансы и
статистика. 2004. – 656 с.: ил. -
Ефимова М.Р.,
Петрова Е.В., Румянцев В.Н. Общая теория
статистики: Учебник. – 2-е изд., испр. и
доп. – М.: ИНФРА – М, 2005. – 416 с. – (Высшее
образование). -
Макарова Н.В.,
Трофимец В.Я. Статистика в Excel:
Учебное пособие. – М.: Финансы и
статистика, 2002. – 368 с.: ил. -
Салманов О.Н.
Математическая экономика с применением
Mathcad
и Ecxel.
– СПб.: БХВ – Петербург, 2003. – 464 с.: ил. -
Скучалина Л.М.,
Павлова С.А. Статистические методы
анализа, моделирования и прогнозирования
внешнеторговых потоков на основе данных
таможенной статистики: Учеб. пособие.
– Люберцы: РИО РТА, 2000. – 67 с.: ил.
10. Сигел, Эндрю.
Практическая бизнес-статистка: Пер с
англ. – М.: Издательский дом «Вильямс»,
2004. – 1056 с.: ил. – Парал. Тит. англ.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В примерах в данной статье данные генерятся при каждой загрузке страницы. Если Вы хотите посмотреть пример с другими значениями –
обновите страницу .
Параметры дискретного закона распределения
В статье описано как найти среднее значение и стандартное отклонение. Вы узнаете, что такое квантиль и каких он бывает видов, а также,
как построить доверительный интервал.
Математическое описание
Смотря на закон распределения, мы можем понять, какова вероятность того или иного события,
можем сказать, какова вероятность, что произойдёт группа событий, а в этой статье мы рассмотрим, как наши выводы “на глаз” перевести
в математически обоснованное утверждение.
Крайне важное определение: математическое ожидание – это площадь под графиком распределения. Если мы говорим о дискретном распределении –
это сумма событий умноженных на соответсвующие вероятности, также известно как момент:
(2) E(X) = Σ(pi•Xi) E – от английского слова Expected (ожидание)
Для математического ожидания справедливы равенства:(3) E(X + Y) = E(X) + E(Y)
(4) E(X•Y) = E(X) • E(Y)
Момент степени k:
(5) νk = E(Xk)
Центральный момент степени k:
(6) μk = E[X – E(X)]k
Среднее значение
Среднее значение (μ) закона распределения – это математическое ожидание случайной величины
(случайная величина – это событие), например, сколько в среднем посетителей заходит в магазин в час:
| Кол-во посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Количество наблюдений | 33 | 8 | 107 | 48 | 8 | 93 | 103 |
| Таблица 1. Количество посетителей в час |
График 1. Количество посетителей в час
Чтобы найти среднее значение всех результатов необходимо сложить всё вместе и разделить на количество результатов:
μ = (33 • 0 + 8 • 1 + 107 • 2 + 48 • 3 + 8 • 4 + 93 • 5 + 103 • 6) / 400 = 1481/400 = 3.7
То же самое мы можем проделать используя формулу 2:
μ = M(X) = Σ(Xi•pi) = 0 • 0.08 + 1 • 0.02 + 2 • 0.27 + 3 • 0.12 + 4 • 0.02 + 5 • 0.23 + 6 • 0.26 = 3.7 Момент первой степени, формула (5)
Собственно, формула 2 представляет собой среднее арифметическое всех значений
Итог: в среднем, 3.7 посетителя в час
| Количество посетителей | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность (%) | 8.3 | 2 | 26.8 | 12 | 2 | 23.3 | 25.8 |
| Таблица 2. Закон распределения количества посетителей |
Отклонение от среднего
Посмотрите на это распределение, можно предположить, что в среднем случайная величина равна 100±5, поскольку
кажется, что таких значений несравнимо больше чем тех, что меньше 95 или больше 105:
График 2. График функции вероятности. Распределение ≈ 100±5
Среднее значение по формуле (2): μ = 99.95, но как посчитать, насколько далеко все значения находятся от среднего? Вам должна быть
знакома запись 100±5. Что бы получить это значение ±, нам необходимо определить диапазон значений вокруг среднего. И мы могли бы
использовать в качестве меры удалённости “разность” между средним и случайными величинами:
(7) xi – μ
но сумма таких расстояний, а следовательно и любое производное от этого числа, будет равно нулю, поэтому в качестве меры выбрали квадрат разниц
между величинами и средним значением:
(8) (xi – μ)2
Соответственно, среднее значение удалённости – это математическое ожидание квадратов удалённости:
(9) σ2 = E[(X – E(X))2]
Поскольку вероятности любой удалённости равносильны – вероятность каждого из них – 1/n, откуда:
(10) σ2 = E[(X – E(X))2] = ∑[(Xi – μ)2]/n
Она же формула центрального момента (6) второй степени
σ возведена в квадрат, поскольку вместо расстояний мы взяли квадрат расстояний. σ2 называется дисперсией. Корень из дисперсии
называется средним квадратическим отклонением, или среднеквадратическим отклоненим, и его используют в качестве меры разброса:
(11) μ±σ
(12) σ = √(σ2) = √[∑[(Xi – μ)2]/n]
Возвращаясь к примеру, посчитаем среднеквадратическое отклонение для графика 2:
σ = √(∑(x-μ)2/n) = √{[(90 – 99.95)2 + (91 – 99.95)2 + (92 – 99.95)2 + (93 – 99.95)2 + (94 – 99.95)2 + (95 – 99.95)2 + (96 – 99.95)2 + (97 – 99.95)2 + (98 – 99.95)2 + (99 – 99.95)2 + (100 – 99.95)2 + (101 – 99.95)2 + (102 – 99.95)2 + (103 – 99.95)2 + (104 – 99.95)2 + (105 – 99.95)2 + (106 – 99.95)2 + (107 – 99.95)2 + (108 – 99.95)2 + (109 – 99.95)2 + (110 – 99.95)2]/21} = 6.06
Итак, для графика 2 мы получили:
X = 99.95±6.06 ≈ 100±6 , что немного отличается от полученного “на глаз”
Квантиль
График 3. Функция распределения. Медиана
График 4. Функция распределения. 4-квантиль или квартиль
График 5. Функция распределения. 0.34-квантиль
Для анализа функции распределения ввели понятие квантиль. Квантиль – это случайная величина при заданном уровне вероятности, т.е.:
квантиль для уровня вероятности 50% – это случайная величина на графике плотности вероятности, которая имеет вероятность 50%.
На примере с графиком 3, квантиль уровня 0.5 = 99 (ближайшее значение, поскольку распределение дискретно и события со значением 99.3 просто не существует)
- 2-квантиль – медиана
- 4-квантиль – квартиль
- 10-квантиль – дециль
- 100-квантиль – перцентиль
То есть, если мы говорим о дециле (10-квантиле), то это означает, что мы разбили график на 10 частей, что соответствует девяти линяям,
и для каждого дециля нашли значение случайной величины.
Также, используется обозначение x-квантиль, где х – дробное число, например, 0.34-квантиль, такая запись означает значение случайной величины при
p = 0.34.
Для дискретного распределения квантиль необходимо выбирать следующим образом: квантиль гарантирует вероятность, поэтому, если рассчитанный
квантиль не совпадает с одним и значений, необходимо выбирать меньшее значение.
Построение интервалов
Квантили используют для построения доверительных интервалов, которые необходимы для исследования статистики не одного конкретного события (например,
интерес – случайное число = 98), а для группы событий (например, интерес – случайное число между 96 и 99). Доверительный интервал бывает двух видов:
односторонний и двусторонний. Параметр доверительного интервала – уровень доверия. Уровень доверия означает процент событий, которые можно считать успешными.
Двусторонний доверительный интервал
Двусторонний доверительный интервал строится следующим образом: мы задаёмся уровнем значимости, например, 10%, и выделяем область на графике так, что 90% всех
событий попадут в эту область. Поскольку интервал двусторонний, то мы отсекаем по 5% с каждой стороны, т.е. мы ищем 5й перцентиль, 95й перцентиль и значения
случайной величины между ними будут являться доверительной областью, значения за пределами доверительной области называются “критическая область”
График 6. Плотность вероятности
График 7. Функция распределения с 5 и 95 перцентилями. Цветом выделен доверительный интервал с уровнем доверия 0.9
График 8. Функция вероятности и двусторонний доверительный интервал с уровнем доверия 90%
Доверительный интервал
Левосторонний и правосторонний доверительные интервалы строятся аналогично двустороннему: для левостороннего интервала мы находим перцентиль уровня
[‘один’ минус ‘уровень значимости’]. Таким образом, для построения доверительного левостороннего интервала уровня значимости 4% нам необходимо найти четвёртый перцентиль
и всё, что справа – доверительный интервал, всё что слева – критическая область.
График 9. Левосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал
График 10. Правосторонний доверительный интервал с уровнем значимости 4%. Заливкой выделен доверительный интервал
Итого
Среднее значение – математическое ожидание случайной величины, находится по формуле:
μ = E(X) = Σ(pi•Xi)
Среднеквадратичное отклонение – математическое ожидание удалённости значений от среднего, находится по формуле:
σ = √(σ2) = √[∑[(Xi – μ)2]/n]
n-квантиль – разделение функции распределения на n равных отрезков, основные типы квантилей:
- 2-квантиль – медиана
- 4-квантиль – квартили
- 10-квантиль – децили
- 100-квантиль – перцентили
Доверительный интервал уровня α – участок функции вероятности, содержащий α всех возможных значений. Двусторонний доверительный
интервал строится отсечением (1-α)/2 справа и слева. Левосторонний и правосторонний доверительные интервалы строятся отсечением
области (1-α) слева и справа соответственно.
Построить ряд распределения
Предположим, мы имеем 100 значений и все разные, например: масса тела Сомалийских пиратов.
Такой набор данных обрабатывать неудобно, мы даже не можем представить их на обычном графике.
Поэтому нам необходимо категоризировать имеющиеся данные и для этого мы делаем следующее:
Запишем наши данные в таблицу:
| 114 | 133 | 62 | 133 | 55 | 70 | 80 | 71 | 133 | 110 |
| 110 | 82 | 130 | 64 | 103 | 117 | 113 | 62 | 128 | 81 |
| 118 | 102 | 57 | 107 | 108 | 66 | 113 | 109 | 52 | 94 |
| 70 | 78 | 77 | 54 | 90 | 136 | 87 | 80 | 137 | 62 |
| 59 | 135 | 66 | 86 | 53 | 65 | 126 | 130 | 72 | 118 |
| 74 | 87 | 130 | 115 | 125 | 90 | 119 | 66 | 68 | 124 |
| 116 | 125 | 63 | 63 | 92 | 70 | 128 | 56 | 60 | 114 |
| 77 | 60 | 124 | 112 | 109 | 87 | 137 | 125 | 122 | 75 |
| 85 | 67 | 61 | 62 | 137 | 82 | 51 | 134 | 74 | 80 |
| 71 | 71 | 115 | 124 | 66 | 129 | 126 | 110 | 113 | 61 |
| Таблица 3. Вес сомалийских пиратов |
Данные разобьём на группы, для начала предлагаю разбить на девять интервалов:
Узнаём максимальное и минимальное значения, вычитаем их друг из друга и делим на количество
интервалов – получили отрезки:
Максимальное значение: 137
Минимальное значение: 51
Разница: 137 – 51 = 86
Длина интервала: 86 / 9 = 9.56
Теперь посчитаем количество пиратов (весов, я имею ввиду) в каждом интервале:
| # | Интервал | Количество элементов |
|---|---|---|
| 1. | 51 – 60.56 | 10 |
| 2. | 60.56 – 70.12 | 19 |
| 3. | 70.12 – 79.68 | 10 |
| 4. | 79.68 – 89.24 | 11 |
| 5. | 89.24 – 98.8 | 4 |
| 6. | 98.8 – 108.36 | 4 |
| 7. | 108.36 – 117.92 | 15 |
| 8. | 117.92 – 127.48 | 12 |
| 9. | 127.48 – 137.04 | 15 |
| Таблица 4. Количество элементов в интервалах |
Вуа-ля, наше распределение на графике:
График 11. Ряд распределения массы тела сомалийских пиратов
Бонус
Интервалы лучше брать целыми числами, поэтому, если с выбранным количеством интервалов
размер выходит нецелым, то можно раздвинуть диапазон значений, пример:
Значение интервала равно 9.56, число не является целым, поэтому
отодвигаем верхнюю границу:
Остаток от деления: [(137 – 51) / 9] = 5
Подвинуть на: 4
Новый диапазон: [51;141]
Диапазон можно двигать как вверх, так и вниз, но лучше в обе стороны.
Совет
Принято делить распределение на 7-8 интервалов, но в каждой конкретной ситуации
Вы можете выбрать отличное количество интервалов, впрочем, как и сделать их
различной длины.
Список параметров
Итак, вот список основных параметров дискретного закона распределения:
| Название | Символ | Формула |
|---|---|---|
| Математическое ожидание (среднее) | E(X) | Σ(pi•Xi) |
| Центральный момент (среднеквадратичное отклонение) |
σx | σ = √(σ2) = √[∑[(Xi – μ)2]/n] |
| Длина интервала | R | max(x) – min(x) |
| Мода | mo | max P(x = mo) |
| 1й квантиль | – | F(x) = 0.25 |
| Медиана | me | F(x) = 0.5 |
| Дециль | – | F(x) = 0.1 |
| Таблица 5. Основные параметры дискретного закона распределения |
Шаблон гистограммы в OpenOffice Calc
Файл histogram_mock.ods содержит шаблон
построения гистограммы.
Вам понравилась статья?
/
Просмотров: 16 000
Бутстреп и А/Б тестирование
Время на прочтение
10 мин
Количество просмотров 25K
Привет, Хабр! В этой статье разберёмся, как с помощью бутстрепа оценивать стандартное отклонение, строить доверительные интервалы и проверять гипотезы. Узнаем, когда бутстреп незаменим, и в чём его недостатки.

Продолжаем писать серию статей по А/Б тестированию, это наша вторая статья. Первую можно посмотреть тут: Стратификация. Как разбиение выборки повышает чувствительность A/B теста.
Метрики и точность их оценки
Давайте представим, что мы работаем аналитиками в сервисе по доставке заказов онлайн-магазина. Нам поставили задачу оценить, как быстро мы выполняем заказы. У нас есть данные со временем выполнения каждого заказа, осталось выбрать метрику и оценить её значение. В этой статье положим, что мы работаем с независимыми одинаково распределенными случайными величинами. Случай зависимых случайных величин будет разобран в последующих статьях.
Самый простой вариант метрики – среднее время выполнения заказа. Для оценки среднего времени выполнения заказа можно взять все заказы за какой-то промежуток времени, например, за последний месяц, и вычислить среднее время их выполнения.
Допустим, мы получили оценку среднего времени доставки, равную 90 минутам. Насколько ей можно верить? Понятно, что это, скорее всего, не истинное значение среднего времени доставки. Если мы подождём ещё месяц и повторим вычисление, то получим чуть большее или чуть меньшее значение. Важно оценить стандартное отклонение полученной оценки, чтобы понять, насколько она точна, так как 90±1 минута и 90±30 минут – совсем разные ситуации.
Для среднего оценка стандартного отклонения вычисляется по формуле:
где – размер выборки,
– случайные величины времени доставки,
– выборочное среднее времени доставки.
Рассмотрим пример вычисления оценки среднего и стандартного отклонения. Допустим, что у нас есть информация о 1000 доставках. Распределение времени доставки в реальной жизни может быть произвольным. В примере будем генерировать время доставки из нормального распределения со средним 90 и стандартным отклонением 20. Сгенерируем выборку, оценим среднее и стандартное отклонение среднего.
import numpy as np
n = 1000
values = np.random.normal(90, 20, n)
mean = values.mean()
std = values.std() / np.sqrt(n)
print(f'Оценка среднего времени доставки: {mean:0.2f}')
print(f'Оценка std для среднего времени доставки: {std:0.2f}')Оценка среднего времени доставки: 90.23
Оценка std для среднего времени доставки: 0.64Получилось, что в нашем примере 1000 наблюдений оказалось достаточно, чтобы стандартное отклонение оценки среднего было меньше минуты.
Квантили
Мы оценили среднее время выполнения заказа. Это хорошо, но это всего лишь “среднее по больнице”. Кто-то получает заказы быстрее, кто-то медленнее. Мы хотим, чтобы подавляющее большинство клиентов получали заказы достаточно быстро. Оценить, за сколько доставляется бОльшая часть заказов можно, например, с помощью 90% квантиля. Какой физический смысл квантиля? Если 90% квантиль равен 2 часам, то 90% заказов доставляются не более, чем за 2 часа.

Мы легко можем оценить 90% квантиль по данным, но как оценить стандартное отклонение полученной оценки? Простой универсальной теоретической формулы для оценки стандартного отклонения квантиля нет.
Было бы хорошо, если у нас было 100 параллельных вселенных. Мы бы в каждой вселенной собрали данные, посчитали 100 квантилей и оценили стандартное отклонения по полученным значениям. Но у нас нет 100 параллельных вселенных.

Кто-то может предложить разбить наши данные из 1000 наблюдений на 10 частей по 100 значений в каждом. В каждой части посчитать значение квантиля и оценить стандартное отклонение по этим 10 значениям. Такой подход даст неверный результат, так как стандартное отклонение оценки зависит от количества наблюдений, используемых при оценке значения квантиля. Чем больше данных, тем точнее оценка и меньше стандартное отклонение.
Что же делать? Оказывается, есть способ, который позволяет оценить стандартное отклонение произвольной статистики, в том числе квантиля. Он называется бутстреп.
Бутстреп
Бутстреп (bootstrap) – это метод для оценки стандартных отклонений и нахождения доверительных интервалов статистических функционалов.
Разберёмся, как работает бутстреп. Напомним, что мы хотим оценить стандартное отклонение произвольной статистики. В статье мы будет оценивать стандартное отклонение оценки 90% квантиля.
Если бы мы могли получать данные из исходного распределения, то могли бы сгенерировать из этого распределения 100 выборок, посчитать по ним 100 квантилей и оценить стандартное отклонение. Истинного распределения мы не знаем, но можем его оценить по имеющимся данным.
В качестве оценки функции распределения будем использовать эмпирическую функцию распределения (ЭФР). ЭФР является несмещённой оценкой и сходится к истинной ФР при увеличении размера выборки.
Определение ФР и ЭФР


Заметим, что ЭФР – это ФР дискретной СВ, которая получается в предположении, что элементы выборки независимы и одинаково распределены. Действительно, давайте каждому наблюдению придадим вес 1/n
|
Значение |
X_1 |
X_2 |
… |
X_n |
|
Вероятность |
1/n |
1/n |
… |
1/n |
Данное табличное распределение и есть распределение ЭФР.
Теоремы сходимости ЭФР к ФР

Посмотрим как визуально выглядит ЭФР для данных разного размера из стандартного нормального распределения.
Код
import matplotlib.pyplot as plt
from scipy import stats
def plot_ecdf(values, label, xlim):
"""Построить график ЭФР."""
X_ = sorted(set(values))
Y_ = [np.mean(values <= x) for x in X_]
X = [xlim[0]] + sum([[v, v] for v in X_], []) + [xlim[1]]
Y = [0, 0] + sum([[v, v] for v in Y_], [])
plt.plot(X, Y, label=label)
# Генерируем данные и строим ЭФР
for size in [20, 200]:
values = np.random.normal(size=size)
plot_ecdf(values, f'ЭФР, size={size}', [-3, 3])
# Строим ФР
X = np.linspace(-3, 3, 1000)
Y = stats.norm.cdf(X)
plt.plot(X, Y, '--', color='k', label='ФР')
plt.title('ФР и ЭФР стандартного нормального распределения')
plt.legend()
plt.show()
На графике видно, что при увеличении размера выборки ЭФР лучше приближает истинную функцию распределения. Если увеличить размер выборки до нескольких тысяч, то ЭФР визуально будет сложно отличить от истинной функции распределения.
Так как нам известно, что ЭФР “хорошо” приближает истинную ФР, давайте генерировать данные из неё! Как это сделать?
Сгенерировать подвыборку размера из ЭФР – это тоже самое, что выбрать случайно с возвращением
элементов из исходной выборки. Это можно сделать одной строчкой кода
np.random.choice(values, size=n, replace=True)Теперь мы можем оценить стандартное отклонение оценки квантиля. Для этого 1000 раз сгенерируем подвыборки из ЭФР, вычислим значение статистики в каждой подвыборке и оценим стандартное отклонение получившихся значений.
n = 1000 # размер исходной выборки
B = 1000 # количество генерируемых подвыборок
values = np.random.normal(90, 20, n)
quantile = np.quantile(values, 0.9)
bootstrap_quantiles = []
for _ in range(B):
bootstrap_values = np.random.choice(values, n, True)
bootstrap_quantiles.append(np.quantile(bootstrap_values, 0.9))
std = np.std(bootstrap_quantiles)
print(f'Оценка 90% квантиля: {quantile:0.2f}')
print(f'Оценка std для 90% квантиля: {std:0.2f}')Оценка 90% квантиля: 115.24
Оценка std для 90% квантиля: 1.56Мы только что применили бутстреп для оценки стандартного отклонения 90% квантиля.
Обратим внимание на два момента:
-
Чтобы оценка стандартного отклонения была несмещённой, необходимо генерировать выборки такого же размера, как и размер исходной выборки;
-
Количество итераций бутстрепа рекомендуется брать в диапазоне от 1000 до 10000. Этого, как правило, хватает для получения достаточно точных результатов.
Доверительные интервалы
Мы научились оценивать стандартное отклонение оценки статистики. Зная стандартное отклонение, можно интуитивно понять насколько достоверны полученные результаты. Для получения более точных результатов можно построить доверительный интервал.
Доверительный интервал (ДИ) – это интервал, который покрывает оцениваемый параметр с заданной вероятностью.
Строгое определение ДИ

Вероятность следует понимать в том смысле, что если бы мы провели эксперимент множество раз, то в среднем для 95% доверительного интервала в 95 экспериментах из 100 истинный параметр принадлежал бы доверительному интервалу.
В строгом смысле доверительный интервал – это случайный вектор. В реальности же мы имеем дело с реализацией доверительного интервала (не со случайными величинами) и говорить о вероятности отличной от 0 или 1 не приходится (истиный параметр или принадлежит интервалу, или не принадлежит). Но для простоты мы пишем “доверительный интервал” вместо “реализация доверительного интервала” так же, как часто говорим “выборка” вместо “реализация выборки”.
Вернёмся к примеру с доставкой из онлайн-магазина и построим ДИ среднего времени доставки. В нашей статье будем использовать 95% доверительный интервал. Если данных много, то, независимо от распределения исходных данных (предполагается, что дисперсия существует и не равна нулю), по центральной предельной теореме среднее будет распределено нормально. Для нормально распределённых статистик ДИ можно вычислить по формуле
где – квантиль стандартного нормального распределения,
– уровень значимости. Для 95% доверительного интервала уровень значимости равен 0.05.

Для построения ДИ квантиля мы, как вы наверное уже догадались, будем использовать бутстреп. ДИ с помощью бутстрепа можно построить тремя способами.
Первый способ аналогичен тому, как мы строили ДИ для среднего. Для его вычисления нужно выполнить следующие три шага:
-
оценить значение квантиля по исходным данным;
-
с помощью бутстрепа оценить стандартное отклонение оценки квантиля;
-
по формуле вычислить ДИ
,
где
– это точечная оценка (point estimation).
Такой ДИ называется нормальным доверительным интервалом.
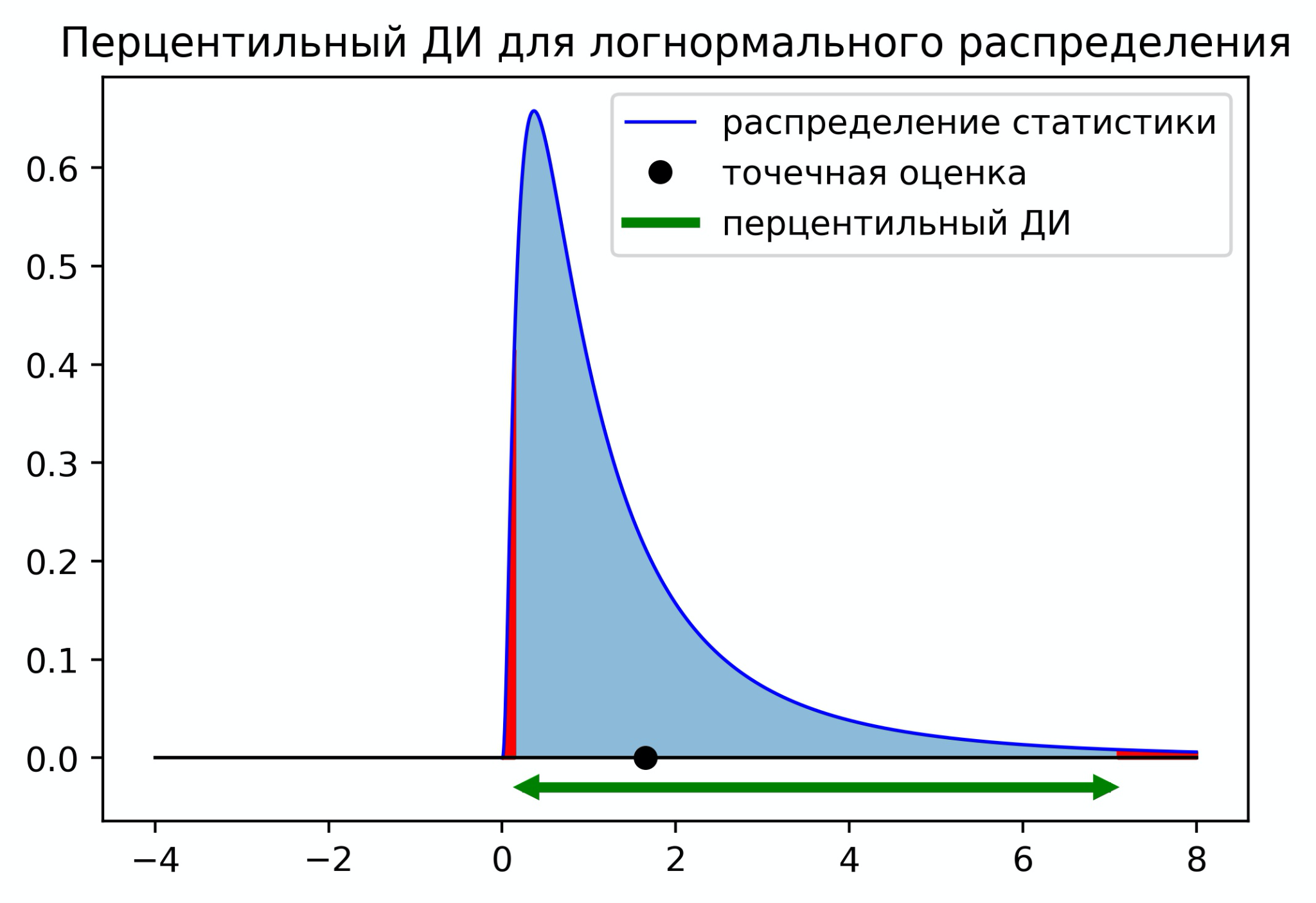
Нормальный доверительный интервал отлично подходит, когда распределение статистики близко к нормальному распределению. Если распределение статистики несимметричное, то нормальный доверительный интервал может давать странный результат. На графике ниже изображена ситуация, когда граница доверительного интервала выходит за минимальное значение распределения.

В случае несимметричных распределений мы можем использовать перцентильный доверительный интервал. Чтобы построить перцентильный ДИ, нужно отрезать с каждой стороны по площади распределения. Для 95% ДИ нужно отрезать по 2.5%. На практике для вычисления границ ДИ нужно оценить квантиль
и
по значениям статистик полученных с помощью бутстрепа. Доверительный интервал будет иметь следующий вид
Существует ещё один вариант – центральный доверительный интервал. Его границы равны
На первый взгляд этот доверительный интервал кажется нелогичным, но он имеет под собой строгое математическое обоснование.

Центральный ДИ для логнормального распределения смещён в сторону с нулевой плотностью. Это можно интерпретировать как стремление перестраховаться на случай, если у нас неполная информация о распределении, и левее нуля на самом деле могут быть значения.
Мы познакомились с тремя способами построения доверительных интервалов с помощью бутстрепа. Ниже приведён пример кода построения этих ДИ.
Код
import seaborn as sns
def get_normal_ci(bootstrap_stats, pe, alpha):
"""Строит нормальный доверительный интервал."""
z = stats.norm.ppf(1 - alpha / 2)
se = np.std(bootstrap_stats)
left, right = pe - z * se, pe + z * se
return left, right
def get_percentile_ci(bootstrap_stats, pe, alpha):
"""Строит перцентильный доверительный интервал."""
left, right = np.quantile(bootstrap_stats, [alpha / 2, 1 - alpha / 2])
return left, right
def get_pivotal_ci(bootstrap_stats, pe, alpha):
"""Строит центральный доверительный интервал."""
left, right= 2 * pe - np.quantile(bootstrap_stats, [1 - alpha / 2, alpha / 2])
return left, right
n = 1000
B = 10000
alpha = 0.05
values = np.random.normal(90, 20, n)
quantile = np.quantile(values, 0.9)
bootstrap_quantiles = np.quantile(np.random.choice(values, (B, n), True), 0.9, axis=1)
normal_ci = get_normal_ci(bootstrap_quantiles, quantile, alpha)
percentile_ci = get_percentile_ci(bootstrap_quantiles, quantile, alpha)
pivotal_ci = get_pivotal_ci(bootstrap_quantiles, quantile, alpha)
sns.kdeplot(bootstrap_quantiles, label='kde статистики')
plt.plot([quantile], [0], 'o', c='k', markersize=6, label='точечная оценка')
plt.plot([109, 120], [0, 0], 'k', linewidth=1)
d = 0.02
plt.plot(normal_ci, [-d, -d], label='нормальный ДИ')
plt.plot(percentile_ci, [-d*2, -d*2], label='перцентильный ДИ')
plt.plot(pivotal_ci, [-d*3, -d*3], label='центральный ДИ')
plt.title('Доверительные интервалы для 90% квантиля')
plt.legend()
plt.show()
Бутстреп и А/Б тестирование
Мы научились строить доверительные интервалы. С помощью доверительного интервала можно не только получать дополнительную информацию о значении метрики, но и проверять статистические гипотезы. Чтобы проверить гипотезу о равенстве квантилей на уровне значимости 5% достаточно построить 95% доверительный интервал для разности квантилей между группами. Если ноль находится вне доверительного интервала, то отличия статистически значимы, иначе нет.

Опишем ещё раз алгоритм проверки гипотез о равенстве двух произвольных метрик с помощью бутстрепа:
-
Генерируем пару подвыборок того же размера из исходных данных контрольной и экспериментальной групп;
-
Считаем метрики (реализация оценки метрики) для каждой из групп;
-
Вычисляем разность метрик, сохраняем полученное значение;
-
Повторяем шаги 1-3 от 1000 до 10000 раз;
-
Строим доверительный интервал с уровнем значимости
;
-
Если 0 не принадлежит ДИ, то отличия статистически значимы на уровне значимости
, иначе нет.
Посмотрим, как этот алгоритм можно реализовать в коде. Для примера, при генерации данных в экспериментальной группе уменьшим дисперсию, это приведёт к уменьшению значения 90% квантиля.
n = 1000
B = 10000
alpha = 0.05
values_a = np.random.normal(90, 20, n)
values_b = np.random.normal(90, 15, n)
pe = np.quantile(values_b, 0.9) - np.quantile(values_a, 0.9)
bootstrap_values_a = np.random.choice(values_a, (B, n), True)
bootstrap_metrics_a = np.quantile(bootstrap_values_a, 0.9, axis=1)
bootstrap_values_b = np.random.choice(values_b, (B, n), True)
bootstrap_metrics_b = np.quantile(bootstrap_values_b, 0.9, axis=1)
bootstrap_stats = bootstrap_metrics_b - bootstrap_metrics_a
ci = get_percentile_ci(bootstrap_stats, pe, alpha)
has_effect = not (ci[0] < 0 < ci[1])
print(f'Значение 90% квантиля изменилось на: {pe:0.2f}')
print(f'{((1 - alpha) * 100)}% доверительный интервал: ({ci[0]:0.2f}, {ci[1]:0.2f})')
print(f'Отличия статистически значимые: {has_effect}')Значение 90% квантиля изменилось на: -6.69
95.0% доверительный интервал: (-9.66, -3.41)
Отличия статистически значимые: TrueПолучилось, что 90% квантиль статистически значимо уменьшился.
В данном примере для построения ДИ использовался перцентильный ДИ. На практике все три способа построения ДИ зачастую дают схожие по точности результаты. Однако могут быть и исключения, результат будет зависеть от природы данных и сравниваемых метрик. Чтобы понять какой способ лучше работает в вашей ситуации, нужно оценить ошибки первого и второго рода по историческим данным. Как это сделать можно прочитать в нашей прошлой статье Стратификация. Как разбиение выборки повышает чувствительность A/B теста.
Ограничения бутстрепа
Бутстреп является весьма универсальным методом. Он позволяет численно исследовать свойства распределений произвольных статистик, а не только квантиля. Это делает его незаменимым для построения доверительных интервалов и проверки гипотез с нетривиальными метриками.
Если бутстреп так хорош, то почему его не используют во всех задачах? Основной недостаток бутстрепа – его скорость работы. Применение бутстрепа является вычислительно трудоёмкой процедурой. Это становится ощутимо, когда приходится работать с большими объёмами данных и многократно применять бутстреп. Вычисления могут занимать часы, дни и даже недели.
Обратим внимание, что во всех примерах выше предполагалось, что мы имеем дело с независимыми одинаково распределёнными случайными величинами. В таких ситуациях для генерации подвыборок можно случайно выбирать значения из исходной выборки. Если же исходные данные зависимы и имеют сложную природу, то при генерации подвыборок нужно это учесть, иначе оценка распределения статистики с помощью бутстрепа может плохо приближать истинное распределение.
Важно не забывать про качество исходных данных, с которыми работает бутстреп. Если эти данные нерепрезентативны и плохо отражают реальное состояние, то достоверных результатов ожидать не стоит.
Заключение
Мы разобрали статистический метод, позволяющий получать оценки стандартного отклонения и строить доверительные интервалы самых нетривиальных статистик. Обсудили, как применять бутстреп для проверки гипотез, когда он незаменим и в чём его недостатки.
Полезные материалы: Larry Wasserman. All of Statistics: A Concise Course in Statistical Inference.
Авторы: Николай Назаров, Александр Сахнов
17 авг. 2022 г.
читать 2 мин
Доверительный интервал представляет собой диапазон значений, который может содержать некоторый параметр генеральной совокупности с определенным уровнем достоверности.
В этом руководстве объясняется, как отображать доверительные интервалы на линейчатых диаграммах в Excel.
Пример 1. Нанесение доверительных интервалов на гистограмму
Предположим, у нас есть следующие данные в Excel, которые показывают среднее значение четырех различных категорий вместе с соответствующей погрешностью для 95% доверительных интервалов:

Чтобы создать гистограмму для визуализации средних значений категорий, выделите ячейки в диапазоне A1:B5 , а затем щелкните вкладку « Вставка » на верхней ленте. Затем нажмите « Вставить столбец или гистограмму» в группе «Диаграммы».
Это создаст следующую гистограмму:

Чтобы добавить полосы доверительного интервала, нажмите знак «плюс» (+) в правом верхнем углу гистограммы, затем нажмите « Полосы ошибок » и « Дополнительные параметры »:

В появившемся справа окне нажмите кнопку « Пользовательский » внизу. В появившемся новом окне выберите =Sheet1!$C$2:$C$5 как для положительного, так и для отрицательного значения ошибки. Затем нажмите ОК .

Это создаст следующие полосы доверительного интервала на гистограмме:

Не стесняйтесь также менять цвет столбцов, чтобы полосы доверительного интервала было легче увидеть:
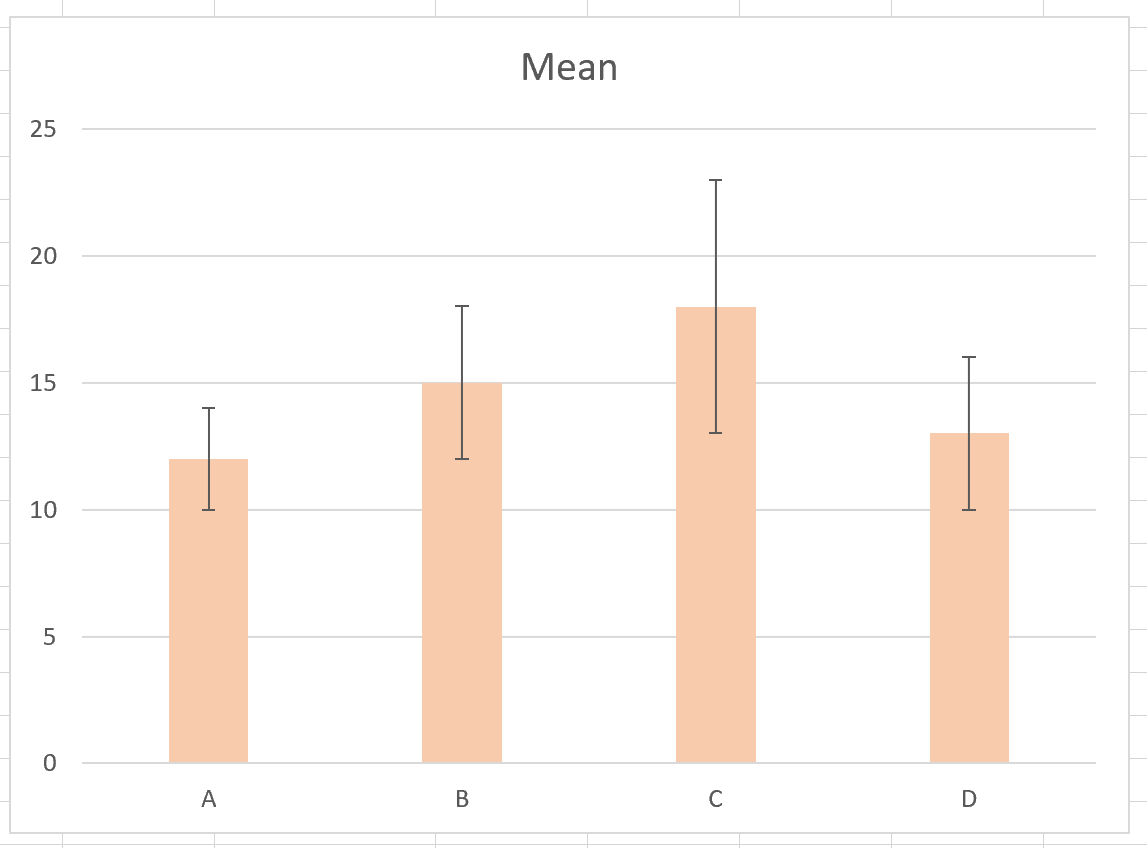
Верхняя часть столбца представляет среднее значение для каждой категории, а столбцы ошибок показывают диапазон доверительного интервала для каждого среднего значения.
Например:
- Среднее значение для категории А равно 12, а 95% доверительный интервал для этого среднего колеблется от 10 до 14.
- Среднее значение для категории B равно 15, а 95% доверительный интервал для этого среднего колеблется от 12 до 18.
- Среднее значение для категории C равно 18, а 95% доверительный интервал для этого среднего колеблется от 13 до 23.
- Среднее значение для категории D равно 13, а 95% доверительный интервал для этого среднего колеблется от 10 до 16.
Дополнительные ресурсы
Введение в доверительные интервалы
Как рассчитать доверительные интервалы в Excel
Погрешность и доверительный интервал: в чем разница?
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 – alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.
Этот интервал часто упоминается как (100 (1 – alpha)% ) доверительный интервал для параметра.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
В этом чтении, мы имеем дело только с двусторонними доверительными интервалами – доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Доверительный интервал (100 (1 – alpha)% ) для параметра имеет следующую структуру.
Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка
где
- Точечная оценка = точечная оценка параметра (значение выборочной статистики).
- Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 – alpha)) для доверительного интервала.
- Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.
Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).
Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 – alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:
( sigma_{overline X} = 20 Big / sqrt{100} = 2 )
Доверительный интервал, таким образом, имеет нижний предел:
( overline X – 1.96 sigma_{overline X} ) = 25 – 1.96(2) = 25 – 3.92 = 21.08.
Верхний предел доверительного интервала равен:
( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Доверительный интервал (100 (1 – alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:
( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
- 90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
- 95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
- 99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58
На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.
Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
Распределение статистики (t) называется t-распределением Стьюдента (англ. “Student’s t-distribution”) из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, – это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Доверительные интервалы для среднего по совокупности – z-альтернатива (большая выборка, дисперсия совокупности неизвестна).
Доверительный интервал (100 (1 – alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:
( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
[см. также: CFA – Коэффициент Шарпа]
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).
Доверительный интервал будет равен:
( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n – 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.
Мы также используем ( n – 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n – 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент (z = (overline X – mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X – mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n – 1) степеней свободы.
Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
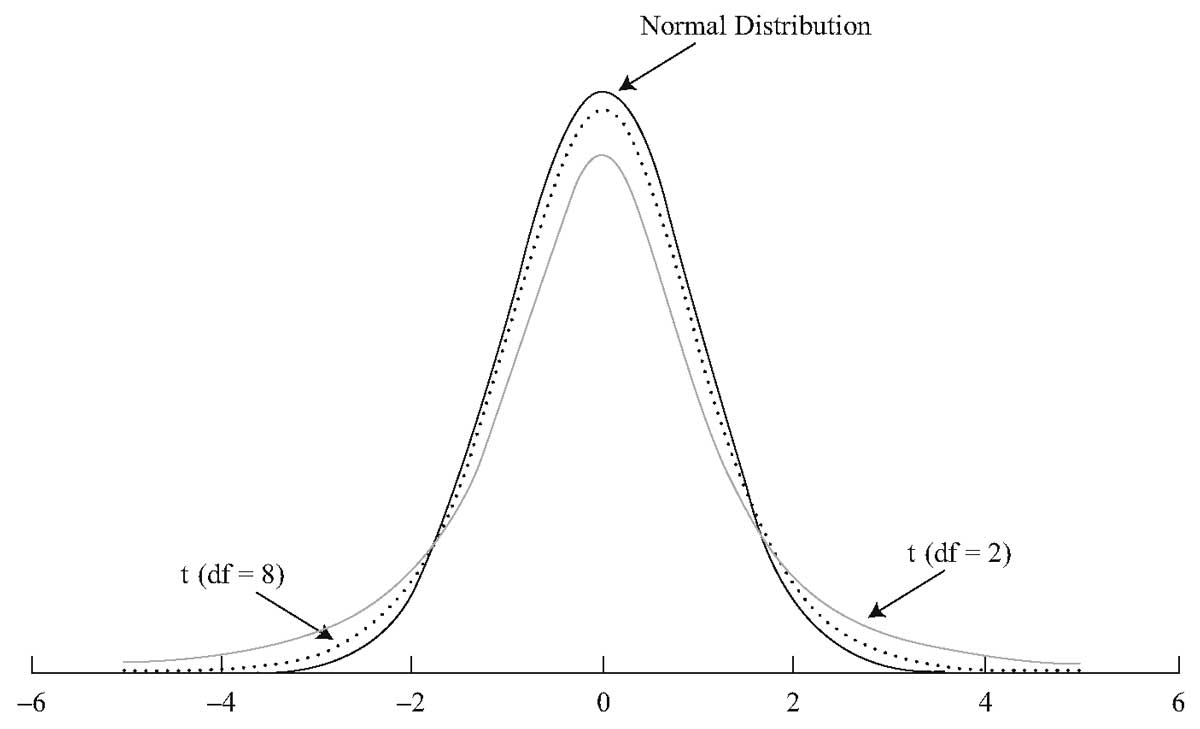 Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.
Например,
для DF = 30,
(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) – t-распределение.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
- выборка является большой, или
- выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,
то доверительный интервал (100 (1 – alpha)% ) для среднего совокупности ( mu ) задается формулой:
( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)
где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) – это размер выборки.
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение – 0.30.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \ &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.
|
Выборка из: |
Статистика для выборки малого размера |
Статистика для выборки большого размера |
|---|---|---|
|
Нормальное распределение с известной дисперсией |
(z) |
(z) |
|
Нормальное распределение с неизвестной дисперсией |
(t) |
(t)* |
|
Ненормальное распределение с известной дисперсией |
недоступно |
(z) |
|
Ненормальное распределение с неизвестной дисперсией |
недоступно |
(t)* |
* Использование (z) также приемлемо.
