Чтобы
найти границы доверительного интервала
выполняют действия в
следующем порядке:
-
Формируют
выборку. -
Вычисляют
объем выборки n,
среднюю арифметическую
и стандартное отклонение S. -
По
формуле n
=
n-1
определяется
число степеней свободы. -
Выбирается
стандартный уровень надежности или
значимости. Для вычисленного числа
степеней
свободы n
и выбранного уровня надежности 1-α
или значимости α
определяют значение критерия tst
( критерия Стьюдента
). -
Определяют
ошибку репрезентативности требуемой
характеристики
соответственно формулам этих ошибок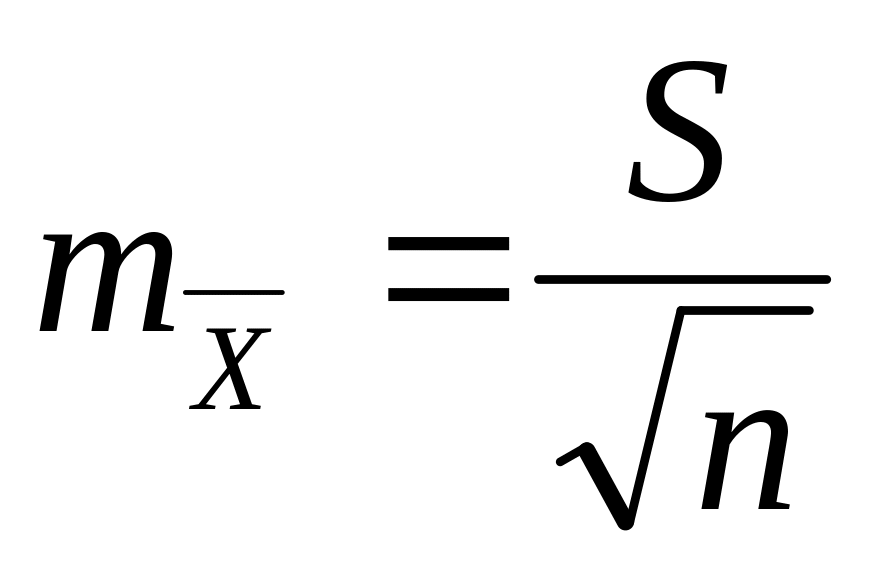
,
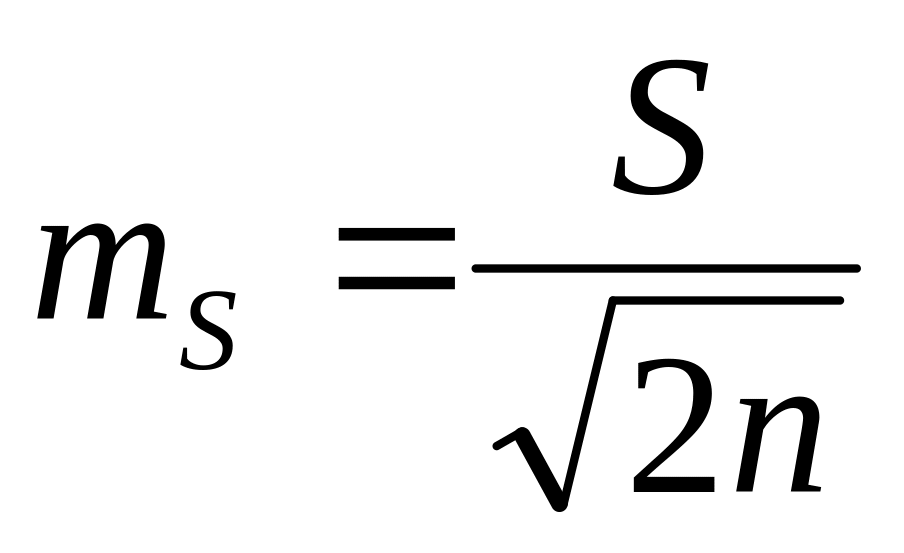
,
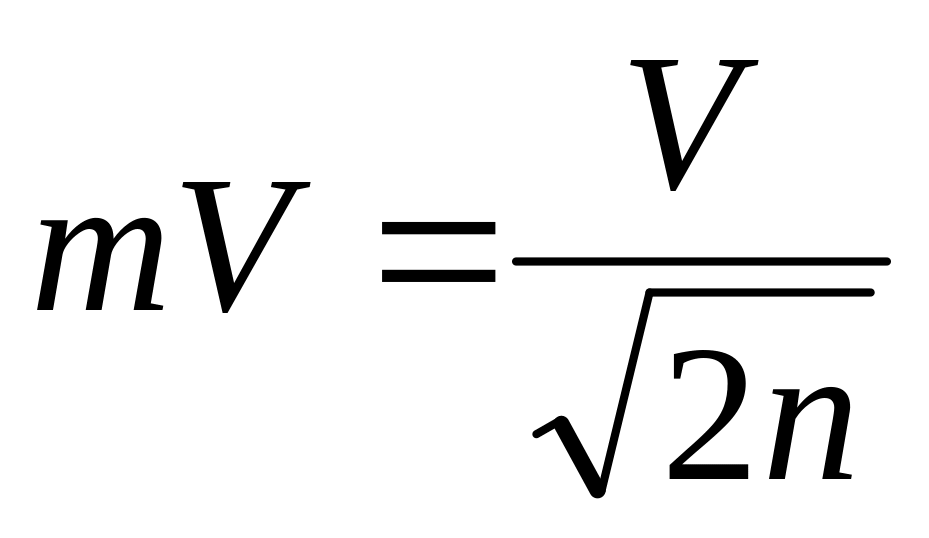
. -
Определяют
нижнюю границу доверительного интервала
по формуле
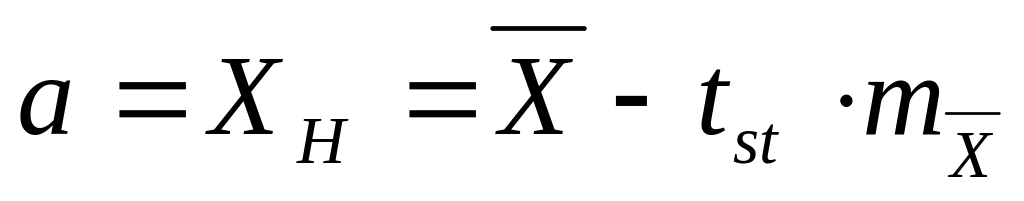
. -
Определяют
верхнюю границу доверительного интервала
по формуле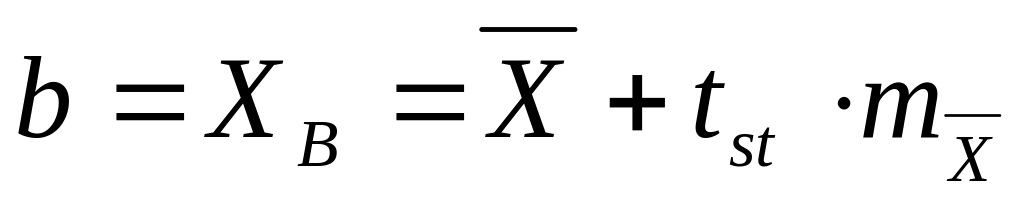
. -
Записывают
полный доверительный интервал для
параметра генеральной совокупности
соответственно выражению:
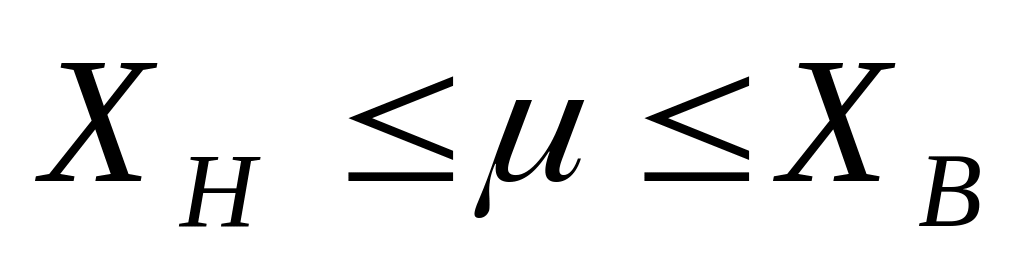
.
Интервал
можно записать следующим образом:
![]()
![]()
.
Пример:
Имеется выборка объемом 26 вариантов,
средняя арифметическая которой равна
10, а стандартное отклонение 2. Необходимо
определить доверительный интервал для
средней арифметической
генеральной совокупности при уровне
надежности равном 0,95.
-
Выборка
26 вариант; -
n
=
26,
= 10,
S
=
2; -
n
=
n-1=26-1=25; -
По
таблице находим для n=25
и 1-α=0,95
или α=0,05
значение критерия Стьюдента tst=
2,06; -
Определяем
ошибку репрезентативности средней
арифметической
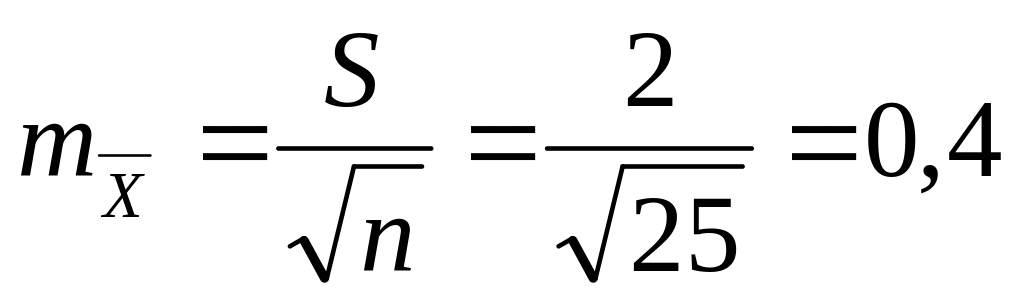
; -
Определяем
нижнюю границу доверительного интервала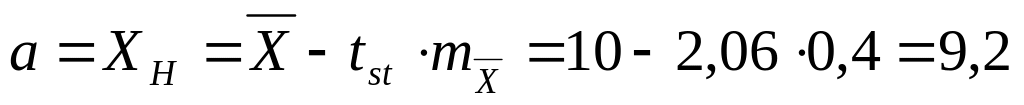
-
Определяем
верхнюю границу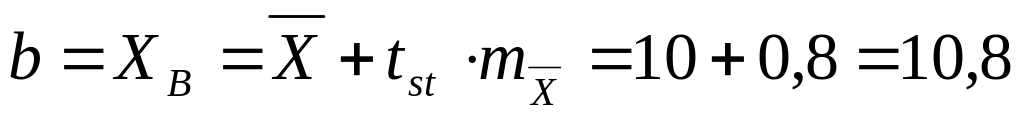
-
Записываем
полный доверительный интервал
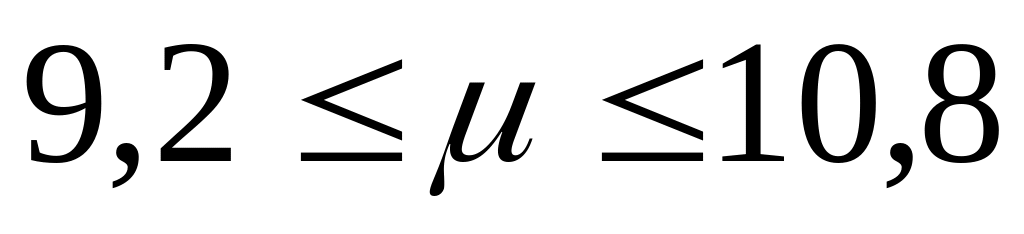
Вывод:
с надежностью 0,95 средняя арифметическая
генеральной совокупности будет находиться
в интервале с границами 9,2-10,8 или 10 ±
0,8.
5. Способы определения принадлежности варианты к совокупности и их характеристика
Способы
определения принадлежности варианты
к совокупности используются
тогда, когда в выборках встречаются
варианты, которые по
своему числовому значению значительно
отличаются от остальных. Такие
варианты называются «выскакивающими»
вариантами.
Чтобы решить
вопрос об их включении в совокупность
применяют специальные статические
критерии.
В
медицинских исследования наиболее
часто используют способ «трех стандартных
отклонений» и способ «тэ-критерия».
Способ
трех стандартных отклонений.
Сущность
способа:
Варианта
xмакс
принадлежит к совокупности, если ее
числовое
значение отличается от значения средней
арифметической не более,
чем на три стандартных отклонения. При
несоблюдении этого условия варианту
считают «выскакивающей». Условия
сохранения варианты в выборке: /xмакс
–
/
![]()
3S.
Алгоритм
способа:
-
Измерить
все варианты и выбрать из них варианту
с максимальным числовым
значением xмакс. -
Вычислить
среднюю арифметическую выборки
.
-
Вычислить
стандартное отклонение S
и его утроенное значение 3S. -
Определить
разность /xмакс
–/
-
Сравнить
результат разности с утроенным
стандартным отклонением.
Если выполняется условие /xмакс
–/
3S,
то варианту
оставляют в совокупности. Если
/xмакс
–/
>
3S
варианту
считают «выскакивающей» и
отбрасывают.
Способ
«тэ-критерия».
Данный
способ применяют для выборок с количеством
вариантов не более 30и
при условии, что распределение подчиняется
закону нормального распределения.
Сущность
способа
состоит в том, что варианту исключают
из
выборки, если вычисленное значение
«тэ-критерия» больше его табличного
значения.
Алгоритм
способа.
-
Для
данной выработки измерить все значения
вариант и подсчитать
объем /n/. -
Выбрать
варианту с максимальным числовым
значением /xмакс/.
Она
будет предположительно «выскакивающей»
вариантой. -
Вычислить
среднюю арифметическую /
/
и стандартное отклонение /S/
выборки. -
Получить
разность /xмакс
–/
и
вычислить значение фактического
«тау -критерия» по формуле
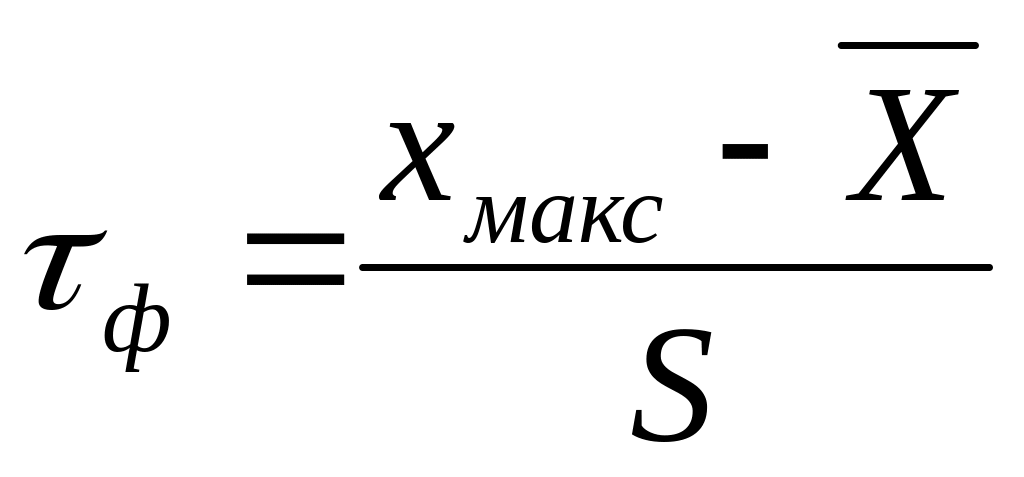
-
Обратиться
к таблице с «тэ-критериями» и для данного
объема выборки
/n/
и уровня значимости /α=0,05 или 0т01/
найти табличное
значение критерия. -
Сопоставить
вычисленный фактический и табличный
критерии и сделать
вывод. Варианта
сохраняется если значение фактического
критерия меньше
или равно табличному
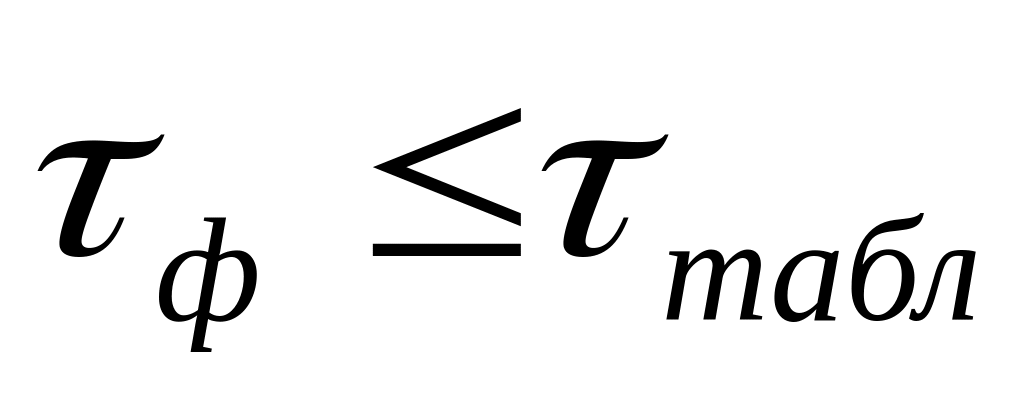
.
Варианта
отбрасывается, если значение фактического
критерия
больше, чем табличного
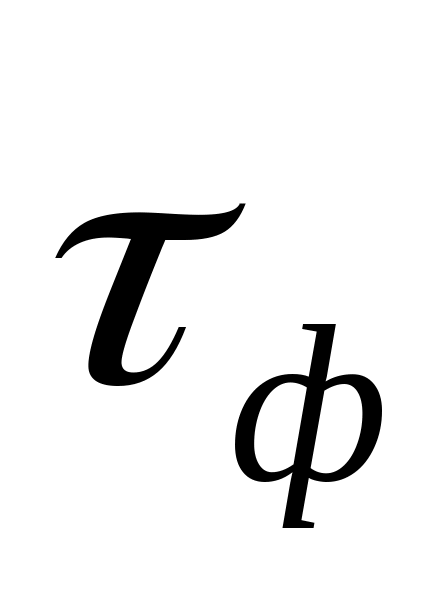
>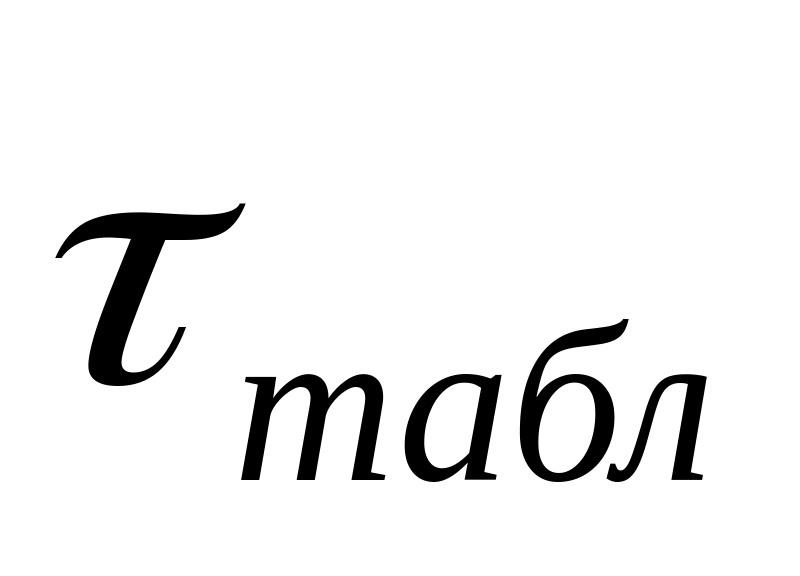
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Способы расчета доверительного интервала

21 апреля 2016
Часто оценщику приходится анализировать рынок недвижимости того сегмента, в котором располагается объект оценки. Если рынок развит, проанализировать всю совокупность представленных объектов бывает сложно, поэтому для анализа используется выборка объектов. Не всегда эта выборка получается однородной, иногда требуется очистить ее от экстремумов – слишком высоких или слишком низких предложений рынка. Для этой цели применяется доверительный интервал. Цель данного исследования – провести сравнительный анализ двух способов расчета доверительного интервала и выбрать оптимальный вариант расчета при работе с разными выборками в системе estimatica.pro.
Способы расчета доверительного интервала
Доверительный интервал – вычисленный на основе выборки интервал значений признака, который с известной вероятностью содержит оцениваемый параметр генеральной совокупности.
Смысл вычисления доверительного интервала заключается в построении по данным выборки такого интервала, чтобы можно было утверждать с заданной вероятностью, что значение оцениваемого параметра находится в этом интервале. Другими словами, доверительный интервал с определенной вероятностью содержит неизвестное значение оцениваемой величины. Чем шире интервал, тем выше неточность.
Существуют разные методы определения доверительного интервала. В этой статье рассмотрим 2 способа:
- через медиану и среднеквадратическое отклонение;
- через критическое значение t-статистики (коэффициент Стьюдента).
Этапы сравнительного анализа разных способов расчета ДИ:
1. формируем выборку данных;
2. обрабатываем ее статистическими методами: рассчитываем среднее значение, медиану, дисперсию и т.д.;
3. рассчитываем доверительный интервал двумя способами;
4. анализируем очищенные выборки и полученные доверительные интервалы.
Этап 1. Выборка данных
Выборка сформирована с помощью системы estimatica.pro. В выборку вошло 91 предложение о продаже 1 комнатных квартир в 3-ем ценовом поясе с типом планировки «Хрущевка».
Таблица 1. Исходная выборка
|
№ |
Цена 1 кв.м., д.е. |
|
1 |
50943 |
|
2 |
35000 |
|
3 |
51613 |
|
4 |
50645 |
|
5 |
49841 |
|
… |
… |
|
86 |
58772 |
|
87 |
70714 |
|
88 |
53393 |
|
89 |
54876 |
|
90 |
52542 |
|
91 |
56140 |
Рис.1. Исходная выборка

Этап 2. Обработка исходной выборки
Обработка выборки методами статистики требует вычисления следующих значений:
1. Среднее арифметическое значение

2. Медиана – число, характеризующее выборку: ровно половина элементов выборки больше медианы, другая половина меньше медианы
![]() (для выборки, имеющей нечетное число значений)
(для выборки, имеющей нечетное число значений)
3. Размах – разница между максимальным и минимальным значениями в выборке

4. Дисперсия – используется для более точного оценивания вариации данных

5. Среднеквадратическое отклонение по выборке (далее – СКО) – наиболее распространённый показатель рассеивания значений корректировок вокруг среднего арифметического значения.

6. Коэффициент вариации – отражает степень разбросанности значений корректировок

7. коэффициент осцилляции – отражает относительное колебание крайних значений цен в выборке вокруг средней

Таблица 2. Статистические показатели исходной выборки
|
Показатель |
Значение |
|
Ср. значение |
54970 |
|
Медиана |
53934 |
|
Размах |
39194 |
|
Дисперсия |
45126821 |
|
СКО |
6755 |
|
Коэф. вариации |
12,29% |
|
Коэф. осциляции |
71,30% |
Коэффициент вариации, который характеризует однородность данных, составляет 12,29%, однако коэффициент осцилляции слишком велик. Таким образом, мы можем утверждать, что исходная выборка не является однородной, поэтому перейдем к расчету доверительного интервала.
Этап 3. Расчёт доверительного интервала
Способ 1. Расчёт через медиану и среднеквадратическое отклонение.
Доверительный интервал определяется следующим образом: минимальное значение – из медианы вычитается СКО; максимальное значение – к медиане прибавляется СКО.
Формула доверительного интервала:

Таким образом, доверительный интервал (47179 д.е.; 60689 д.е.)
Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 20 объектов, что составило 22% выборки.
Рис. 2. Значения, попавшие в доверительный интервал 1.

Способ 2. Построение доверительного интервала через критическое значение t-статистики (коэффициент Стьюдента)
С.В. Грибовский в книге «Математические методы оценки стоимости имущества» описывает способ вычисления доверительного интервала через коэффициент Стьюдента. При расчете этим методом оценщик должен сам задать уровень значимости ∝, определяющий вероятность, с которой будет построен доверительный интервал. Обычно используются уровни значимости 0,1; 0,05 и 0,01. Им соответствуют доверительные вероятности 0,9; 0,95 и 0,99. При таком методе полагают истинные значения математического ожидания и дисперсии практически неизвестными (что почти всегда верно при решении практических задач оценки).
Формула доверительного интервала:

n – объем выборки;
![]() – критическое значение t- статистики (распределения Стьюдента) с уровнем значимости ∝,числом степеней свободы n-1,которое определяется по специальным статистическим таблицам либо с помощью MS Excel (
– критическое значение t- статистики (распределения Стьюдента) с уровнем значимости ∝,числом степеней свободы n-1,которое определяется по специальным статистическим таблицам либо с помощью MS Excel (![]() →”Статистические”→ СТЬЮДРАСПОБР);
→”Статистические”→ СТЬЮДРАСПОБР);
∝ – уровень значимости, принимаем ∝=0,01.

Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 62 объекта, что составило 68% выборки.
Рис. 2. Значения, попавшие в доверительный интервал 2.

Этап 4. Анализ разных способов расчета доверительного интервала
Два способа расчета доверительного интервала – через медиану и коэффициент Стьюдента – привели к разным значениям интервалов. Соответственно, получилось две различные очищенные выборки.
Таблица 3. Статистические показатели по трем выборкам.
|
Показатель |
Исходная выборка |
1 вариант |
2 вариант |
|
Среднее значение |
54970 |
53593 |
54750 |
|
Медиана |
53934 |
53425 |
54688 |
|
Размах |
39194 |
12888 |
3677 |
|
Дисперсия |
45126821 |
8919645 |
1228707 |
|
СКО |
6755 |
3008 |
1128 |
|
Коэф. вариации |
12,29% |
5,61% |
2,06% |
|
Коэф. осциляции |
71,30% |
24,05% |
6,72% |
|
Количество выбывших объектов, шт. |
20 |
62 |
На основании выполненных расчетов можно сказать, что полученные разными методами значения доверительных интервалов пересекаются, поэтому можно использовать любой из способов расчета на усмотрение оценщика.
Однако мы считаем, что при работе в системе estimatica.pro целесообразно выбирать метод расчета доверительного интервала в зависимости от степени развитости рынка:
- если рынок неразвит, применять метод расчета через медиану и среднеквадратическое отклонение, так как количество выбывших объектов в этом случае невелико;
- если рынок развит, применять расчет через критическое значение t-статистики (коэффициент Стьюдента), так как есть возможность сформировать большую исходную выборку.
При подготовке статьи были использованы:
1. Грибовский С.В., Сивец С.А., Левыкина И.А. Математические методы оценки стоимости имущества. Москва, 2014 г.
2. Данные системы estimatica.pro
Читайте также:
Расчет корректировок методом парных продаж
Статью подготовили: Наталья Ничкова и Михаил Филимонов
17 авг. 2022 г.
читать 3 мин
Доверительный интервал — это диапазон значений, который может содержать параметр генеральной совокупности с определенным уровнем достоверности. Он рассчитывается по следующей общей формуле:
Доверительный интервал = (точечная оценка) +/- (критическое значение) * (стандартная ошибка)
Эта формула создает интервал с нижней границей и верхней границей, который, вероятно, содержит параметр совокупности с определенным уровнем достоверности:
Доверительный интервал = [нижняя граница, верхняя граница]
В этом руководстве объясняется, как рассчитать следующие доверительные интервалы в Excel:
1. Доверительный интервал для среднего
2. Доверительный интервал для разницы в средних значениях
3. Доверительный интервал для пропорции
4. Доверительный интервал для разницы в пропорциях
Давайте прыгать!
Пример 1: Доверительный интервал для среднего
Мы используем следующую формулу для расчета доверительного интервала для среднего значения :
Доверительный интервал = x +/- z*(s/√n)
куда:
- x : выборочное среднее
- z: выбранное значение z
- s: стандартное отклонение выборки
- n: размер выборки
Пример: Предположим, мы собираем случайную выборку черепах со следующей информацией:
- Размер выборки n = 25
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
На следующем снимке экрана показано, как рассчитать 95% доверительный интервал для истинного среднего веса популяции черепах:
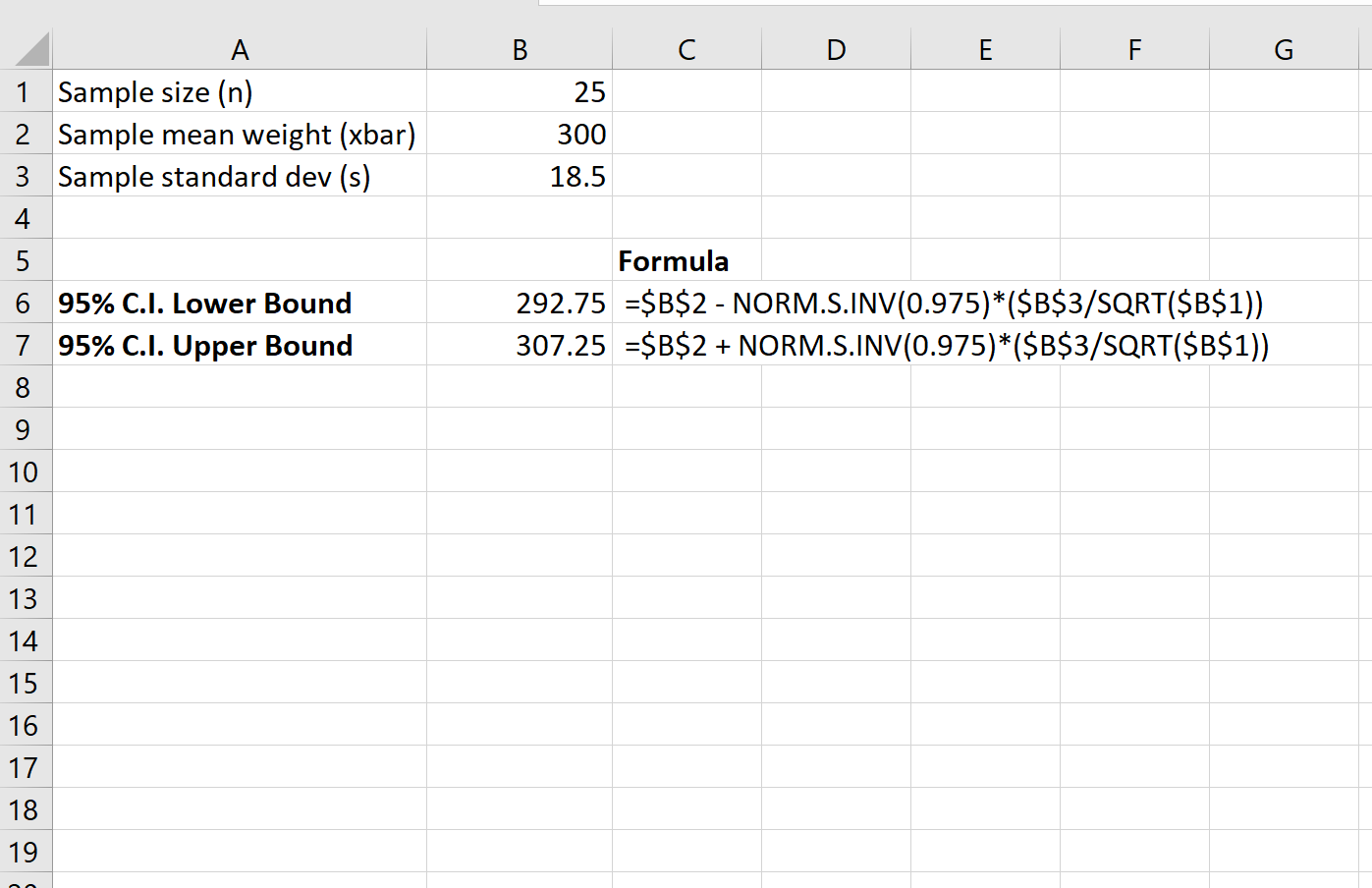
95% доверительный интервал для истинного среднего веса популяции черепах составляет [292,75, 307,25] .
Пример 2: Доверительный интервал для разницы в средних значениях
Мы используем следующую формулу для расчета доверительного интервала для разницы в средних значениях генеральной совокупности :
Доверительный интервал = ( x 1 – x 2 ) +/- t * √ ((s p 2 /n 1 ) + (s p 2 /n 2 ))
куда:
- x 1 , x 2 : среднее значение для образца 1, среднее значение для образца 2
- t: t-критическое значение, основанное на доверительном уровне и (n 1 +n 2 -2) степенях свободы
- s p 2 : объединенная дисперсия, рассчитанная как ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 ) / (n 1 +n 2 -2)
- t: t-критическое значение
- n 1 , n 2 : размер выборки 1, размер выборки 2
Пример: Предположим, мы хотим оценить разницу в среднем весе между двумя разными видами черепах, поэтому мы собираем случайную выборку из 15 черепах из каждой популяции. Вот сводные данные для каждого образца:
Образец 1:
- х 1 = 310
- с 1 = 18,5
- п 1 = 15
Образец 2:
- х 2 = 300
- с 2 = 16,4
- п 2 = 15
На следующем снимке экрана показано, как рассчитать 95% доверительный интервал для истинной разницы в средних значениях населения:
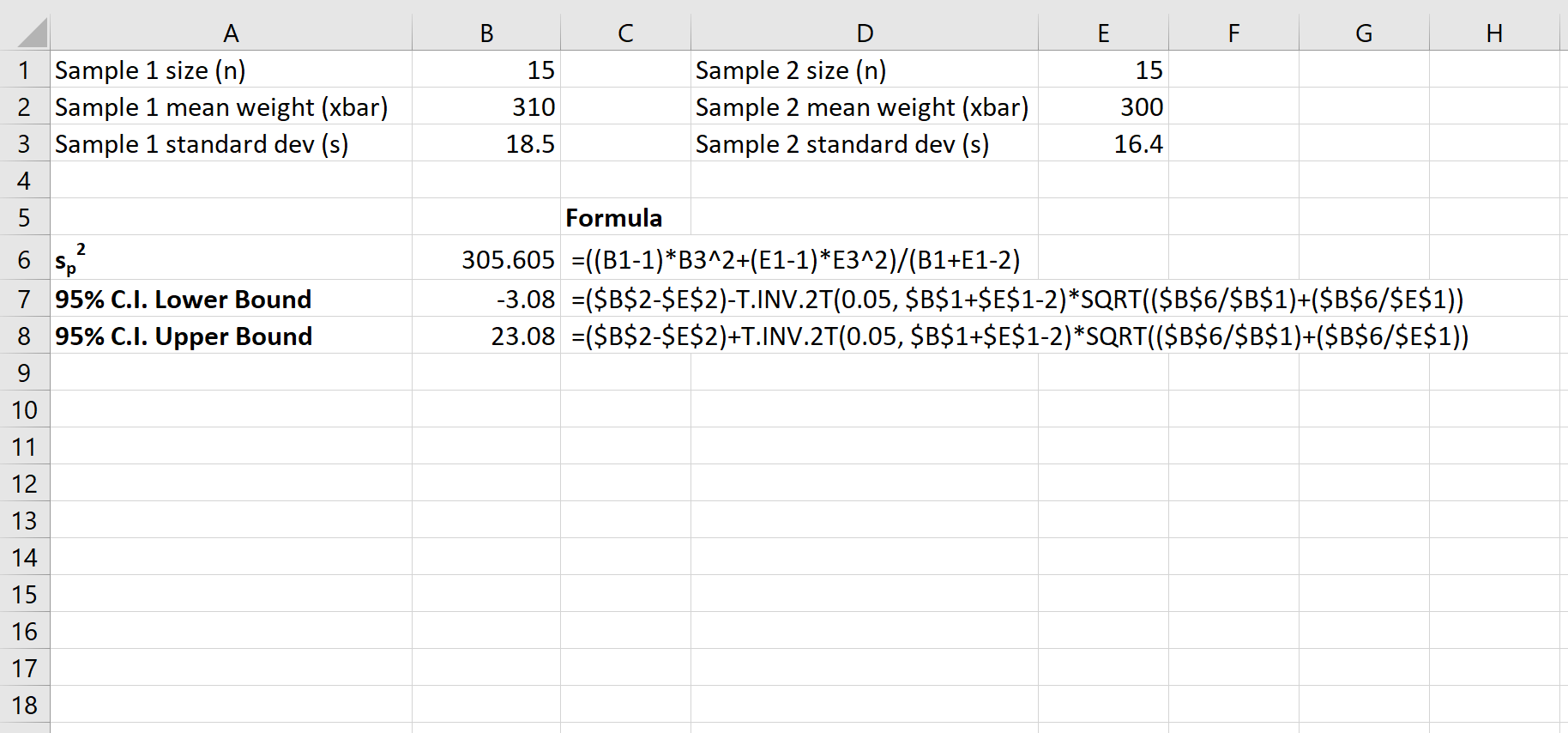
95% доверительный интервал для истинной разницы в средних значениях населения составляет [-3,08, 23,08] .
Пример 3: Доверительный интервал для пропорции
Мы используем следующую формулу для расчета доверительного интервала для пропорции :
Доверительный интервал = p +/- z * √ p (1-p) / n
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
На следующем снимке экрана показано, как рассчитать 95-процентный доверительный интервал для истинной доли жителей всего округа, поддерживающих закон:
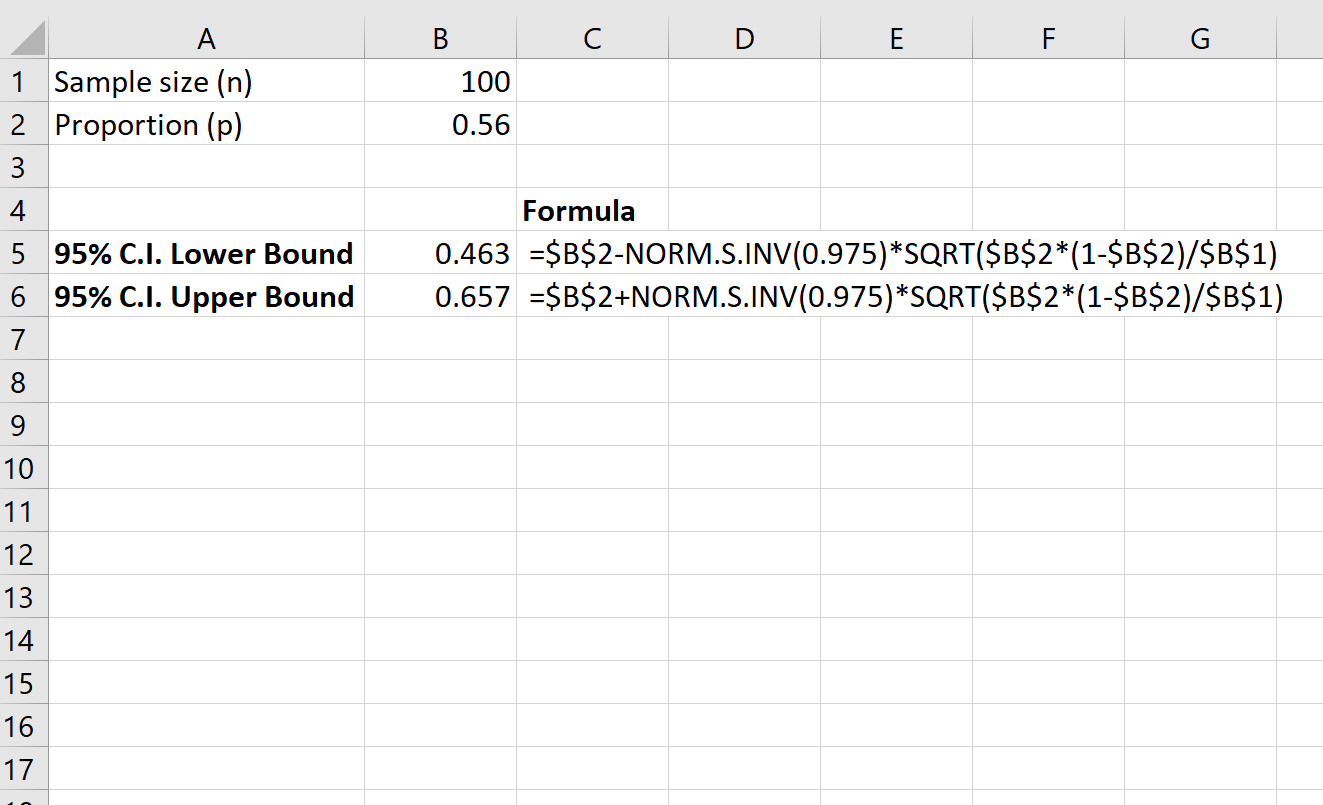
95-процентный доверительный интервал для истинной доли жителей всего округа, поддерживающих закон, составляет [0,463, 0,657] .
Пример 4: Доверительный интервал для разницы в пропорциях
Мы используем следующую формулу для расчета доверительного интервала для разницы в пропорциях :
Доверительный интервал = (p 1 –p 2 ) +/- z*√(p 1 (1-p 1 )/n 1 + p 2 (1-p 2 )/n 2 )
куда:
- p 1 , p 2 : доля образца 1, доля образца 2
- z: z-критическое значение, основанное на доверительном уровне
- n 1 , n 2 : размер выборки 1, размер выборки 2
Пример. Предположим, мы хотим оценить разницу в доле жителей, поддерживающих определенный закон в округе А, по сравнению с долей жителей, поддерживающих закон в округе Б. Вот сводные данные для каждой выборки:
Образец 1:
- п 1 = 100
- p 1 = 0,62 (т.е. 62 из 100 жителей поддерживают закон)
Образец 2:
- п 2 = 100
- p 2 = 0,46 (т.е. 46 из 100 жителей поддерживают закон) На следующем снимке экрана показано, как рассчитать 95% доверительный интервал для истинной разницы в доле жителей, поддерживающих закон, между округами:
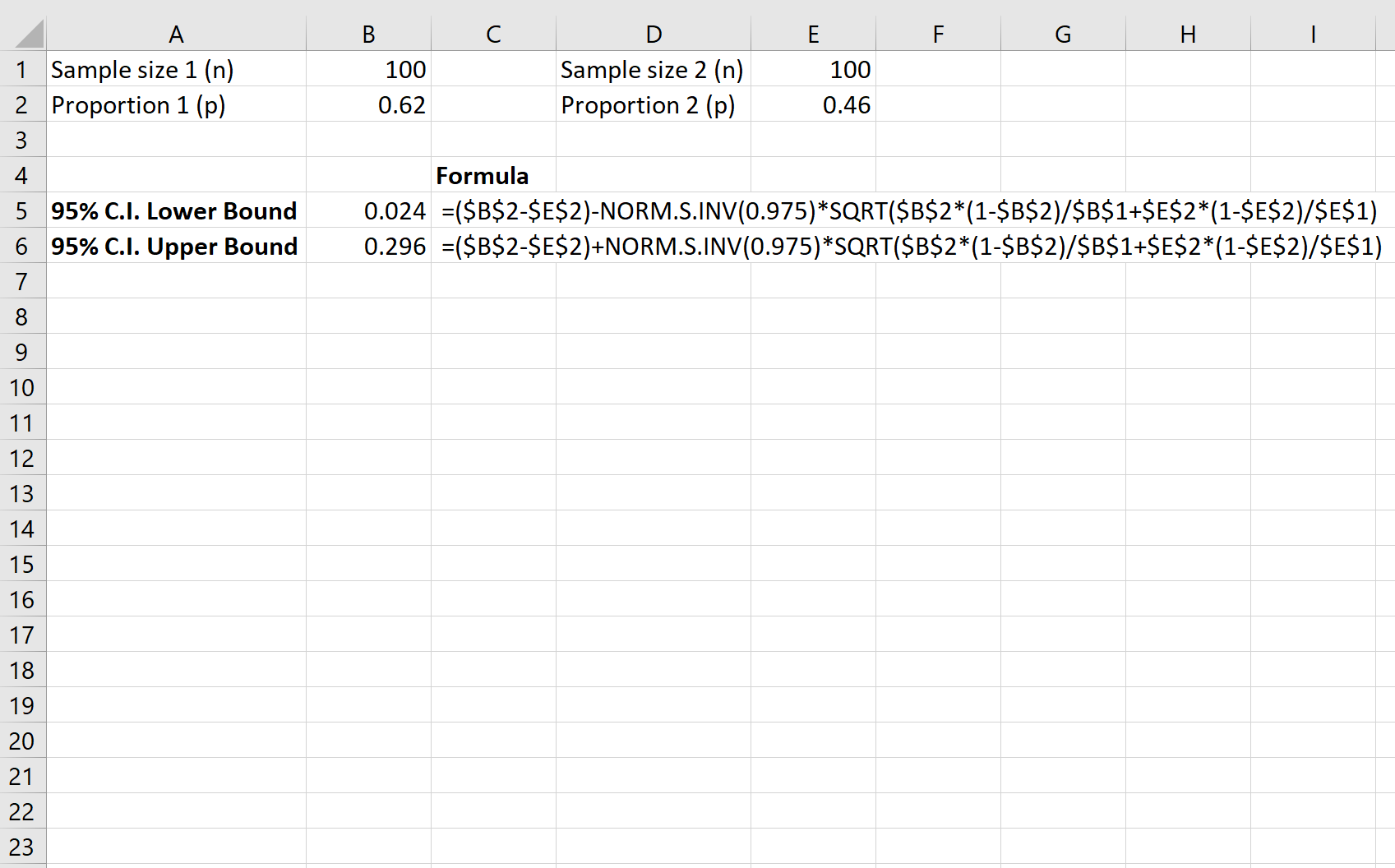
Доверительный интервал 9,5% для истинной разницы доли жителей, поддерживающих закон, между округами составляет [0,024, 0,296] .
Вы можете найти больше учебников по Excel здесь .
Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.
Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.
Содержание
- Вычисление доверительного интервала
- Метод 1: оператор ДОВЕРИТ.НОРМ
- Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
- Заключение
Вычисление доверительного интервала
Доверительный интервал нужен для того, чтобы дать интервальную оценку каким-либо статическим данным. Основная цель этой операции – убрать неопределенности точечной оценки.
В Microsoft Excel существует два метода выполнения данной задачи:
- Оператор ДОВЕРИТ.НОРМ – применяется в случаях, когда дисперсия известна;
- Оператор ДОВЕРИТ.СТЬЮДЕНТ– когда дисперсия неизвестна.
Ниже мы пошагово разберем оба метода на практике.
Метод 1: оператора ДОВЕРИТ.НОРМ
Данная функция впервые была внедрена в арсенал программы в редакции Эксель 2010 года (до этой версии ее заменял оператор “ДОВЕРИТ”). Оператор входит в категорию “статистические”.
Формула функции ДОВЕРИТ.НОРМ выглядит так:
=ДОВЕРИТ.НОРМ(Альфа;Станд_откл;Размер)
Как мы видим, у функции есть три аргумента:
- “Альфа” – это показатель уровня значимости, который берется за основу при расчете. Доверительный уровень считается так:
1-"Альфа". Это выражение применимо в случае, если значение “Альфа” представлено в виде коэффициента. Например, 1-0,7=0,3, где 0,7=70%/100%.(100-"Альфа")/100. Применятся это выражение, если мы считаем доверительным уровень со значением “Альфа” в процентах. Например, (100-70)/100=0,3.
- “Стандартное отклонение” — соответственно, стандартное отклонение анализируемой выборки данных.
- “Размер” – объем выборки данных.
Примечание: У данной функции наличие всех трех аргументов является обязательным условием.
Оператор “ДОВЕРИТ”, который применялся в более ранних редакциях программы, содержит такие же аргументы и выполняет те же самые функции.
Формула функции ДОВЕРИТ выглядит следующим образом:
=ДОВЕРИТ(Альфа;Станд_откл;Размер)
Отличий в самой формуле нет никаких, лишь название оператора иное. В редакциях приложения Эксель 2010 года и последующих этот оператор находится в категории “Совместимость”. В более же старых версиях программы он находится в разделе статических функций.
Граница доверительного интервала определяется следующей формулой:
X+(-)ДОВЕРИТ.НОРМ
где Х – это среднее значение по заданному диапазону.
Теперь давайте разберемся, как применять эти формулы на практике. Итак, у нас есть таблица с различными данными 10-ти проведенных замеров. При этом, стандартное отклонение совокупности данных равняется 8.

Перед нами стоит задача – получить значение доверительного интервала с 95%-ым уровнем доверия.
- Первым делом выбираем ячейку для вывода результата. Затем кликаем по кнопке “Вставить функцию” (слева от строки формул).

- Откроется окно Мастера функций. Кликнув по текущей категории функций, раскрываем список и щелкаем в нем по строке “Статистические”.

- В предложенном перечне кликаем по оператору “ДОВЕРИТ.НОРМ”, затем жмем OK.

- Перед нами появится окно с настройками аргументов функции, заполнив которые нажимаем кнопку OK.
- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
(100-95)/100. Пишем его в поле аргумента (или можно сразу написать результат вычисления, равный 0,05). - в поле “Станд_откл” согласно нашим условия, пишем цифру 8.
- в поле “Размер” указываем количество исследуемых элементов. В нашем случае было проведено 10 замеров, значит пишем цифру 10.

- в поле “Альфа” указываем уровень значимости. В нашей задаче предполагается 95%-ый уровень доверия. Подставив данное значение в формулу расчета, которую мы рассматривали выше, получаем выражение:
- Чтобы при изменении данных не пришлось заново настраивать функцию, можно автоматизировать ее. Для это применим функцию “СЧЁТ”. Ставим указатель в область ввода информации аргумента “Размер”, затем щелкаем по значку треугольника с левой стороны от строки формул и кликаем по пункту “Другие функции…”.

- В результате откроется еще одно окно Мастера функций. Выбрав категорию “Статистические”, кликаем по функции “СЧЕТ”, затем – OK.

- На экране отобразится еще одно окно с настройками аргументов функции, которая применяется для определения числа ячеек в заданном диапазоне, в которых находятся числовые данные.
Формула функции СЧЕТ пишется так:=СЧЁТ(Значение1;Значение2;...).
Количество доступных аргументов этой функции может достигать 255 штук. Здесь можно прописать, либо конкретные числа, либо адреса ячеек, либо диапазоны ячеек. Мы воспользуемся последним вариантом. Для этого кликаем по области ввода информации для первого аргумента, затем зажав левую кнопку мыши выделяем все ячейки одного из столбцов нашей таблицы (не считая шапки), после чего жмем кнопку OK.
- В результате проделанных действий в выбранной ячейке будет выведено результат расчетов по оператору ДОВЕРИТ.НОРМ. В нашей задаче его значение оказалось равным 4,9583603.

- Но это еще не конечный результат в нашей задаче. Далее требуется рассчитать среднее значение по заданному интервалу. Для этого потребуется применить функцию “СРЗНАЧ”, которая выполняет задачу по вычислению среднего значения в пределах указанного диапазона данных.
Формула оператора пишется так:=СРЗНАЧ(число1;число2;...).
Выделяем ячейку, куда планируем вставить функцию и жмем кнопку “Вставить функцию”.
- В категории “Статистические” выбираем нудный оператор “СРЗНАЧ” и кликаем OK.

- В аргументах функции в значении аргумента “Число” указываем диапазон, в который входят все ячейки со значениями всех замеров. Затем кликаем OK.

- В результате проделанных действий среднее значение будет автоматически подсчитано и выведено в ячейку с только что вставленной функцией.

- Теперь нам нужно рассчитать границы ДИ (доверительного интервала). Начнем с расчета значения правой границы. Выбираем ячейку, куда хотим вывести результат, и выполняем в ней сложение результатов, полученных с помощью операторов “СРЗНАЧ” и “ДОВЕРИТ.НОРМ”. В нашем случае формула выглядит так:
A14+A16. После ее набора жмем Enter.
- В результате будет произведен расчет и результат немедленно отобразится в ячейке с формулой.

- Затем аналогичным способом выполняем расчет для получения значения левой границы ДИ. Только в этом случае значение результата “ДОВЕРИТ.НОРМ” нужно не прибавлять, а вычитать из результата, полученного при помощи оператора “СРЗНАЧ”. В нашем случае формула выглядит так:
=A16-A14.
- После нажатия Enter мы получим результат в заданной ячейке с формулой.

Примечание: В пунктах выше мы постарались максимально подробно расписать все шаги и каждую применяемую функцию. Однако все прописанные формулы можно записать вместе, в составе одной большой:
- Для определения правой границы ДИ общая формула будет выглядеть так:
=СРЗНАЧ(B2:B11)+ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)). - Точно также и для левой границы, только вместо плюса нужно поставить минус:
=СРЗНАЧ(B2:B11)-ДОВЕРИТ.НОРМ(0,05;8;СЧЁТ(B2:B11)).
Метод 2: оператор ДОВЕРИТ.СТЬЮДЕНТ
Теперь давайте познакомимся со вторым оператором для определения доверительного интервала – ДОВЕРИТ.СТЬЮДЕНТ. Данная функция была внедрена в программу относительно недавно, начиная с версии Эксель 2010, и направлена на определение ДИ выбранной совокупности данных с применением распределения Стьюдента, при неизвестной дисперсии.
Формула функции ДОВЕРИТ.СТЬЮДЕНТ выглядит следующим образом:
=ДОВЕРИТ.СТЬЮДЕНТ(Альфа;Cтанд_откл;Размер)
Давайте разберем применение данного оператора на примере все той же таблицы. Только теперь стандартное отклонение по условиям задачи нам неизвестно.
- Сначала выбираем ячейку, куда планируем вывести результат. Затем кликаем по значку “Вставить функцию” (слева от строки формул).

- Откроется уже хорошо знакомое окно Мастера функций. Выбираем категорию “Статистические”, затем из предложенного списка функций щелкаем по оператору “ДОВЕРИТ.СТЬЮДЕНТ”, после чего – OK.

- В следующем окне нам нужно настроить аргументы функции:.
- В выбранной ячейке отобразится значение доверительного интервала согласно заданным нами параметрам.

- Далее нам нужно рассчитать значения границ ДИ. А для этого потребуется получить среднее значение по выбранному диапазону. Для этого снова применим функцию “СРЗНАЧ”. Алгоритм действий аналогичен тому, что был описан в первом методе.

- Получив значение “СРЗНАЧ”, можно приступать к расчетам границ ДИ. Сами формулы ничем не отличаются от тех, что использовались с оператором “ДОВЕРИТ.НОРМ”:
- Правая граница ДИ=СРЗНАЧ+ДОВЕРИТ.СТЬЮДЕНТ
- Левая граница ДИ=СРЗНАЧ-ДОВЕРИТ.СТЬЮДЕНТ

Заключение
Арсенал инструментов Excel невероятно большой, и наряду с распространенными функциями, программа предлагает большое разнообразие специальных функций, которые помогут существенно облегчить работу с данными. Возможно, описанные выше шаги некоторым пользователям, на первый взгляд, могут показаться сложными. Но после детального изучения вопроса и последовательности действий, все станет намного проще.
Содержание
- Процедура вычисления
- Способ 1: функция ДОВЕРИТ.НОРМ
- Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
- Вопросы и ответы

Одним из методов решения статистических задач является вычисление доверительного интервала. Он используется, как более предпочтительная альтернатива точечной оценке при небольшом объеме выборки. Нужно отметить, что сам процесс вычисления доверительного интервала довольно сложный. Но инструменты программы Эксель позволяют несколько упростить его. Давайте узнаем, как это выполняется на практике.
Читайте также: Статистические функции в Экселе
Процедура вычисления
Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.
В Экселе существуют два основных варианта произвести вычисления с помощью данного метода: когда дисперсия известна, и когда она неизвестна. В первом случае для вычислений применяется функция ДОВЕРИТ.НОРМ, а во втором — ДОВЕРИТ.СТЮДЕНТ.
Способ 1: функция ДОВЕРИТ.НОРМ
Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.
Его синтаксис выглядит следующим образом:
=ДОВЕРИТ.НОРМ(альфа;стандартное_откл;размер)
«Альфа» — аргумент, указывающий на уровень значимости, который применяется для расчета доверительного уровня. Доверительный уровень равняется следующему выражению:
(1-«Альфа»)*100
«Стандартное отклонение» — это аргумент, суть которого понятна из наименования. Это стандартное отклонение предлагаемой выборки.
«Размер» — аргумент, определяющий величину выборки.
Все аргументы данного оператора являются обязательными.
Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:
=ДОВЕРИТ(альфа;стандартное_откл;размер)

Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.
Граница доверительного интервала определяется при помощи формулы следующего вида:
X+(-)ДОВЕРИТ.НОРМ
Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.
Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.
- Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».
- Появляется Мастер функций. Переходим в категорию «Статистические» и выделяем наименование «ДОВЕРИТ.НОРМ». После этого клацаем по кнопке «OK».
- Открывается окошко аргументов. Его поля закономерно соответствуют наименованиям аргументов.
Устанавливаем курсор в первое поле – «Альфа». Тут нам следует указать уровень значимости. Как мы помним, уровень доверия у нас равен 97%. В то же время мы говорили, что он рассчитывается таким путем:(1-«Альфа»)*100Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:
(1-уровень доверия)/100То есть, подставив значение, получаем:
(1-97)/100Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.
Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.
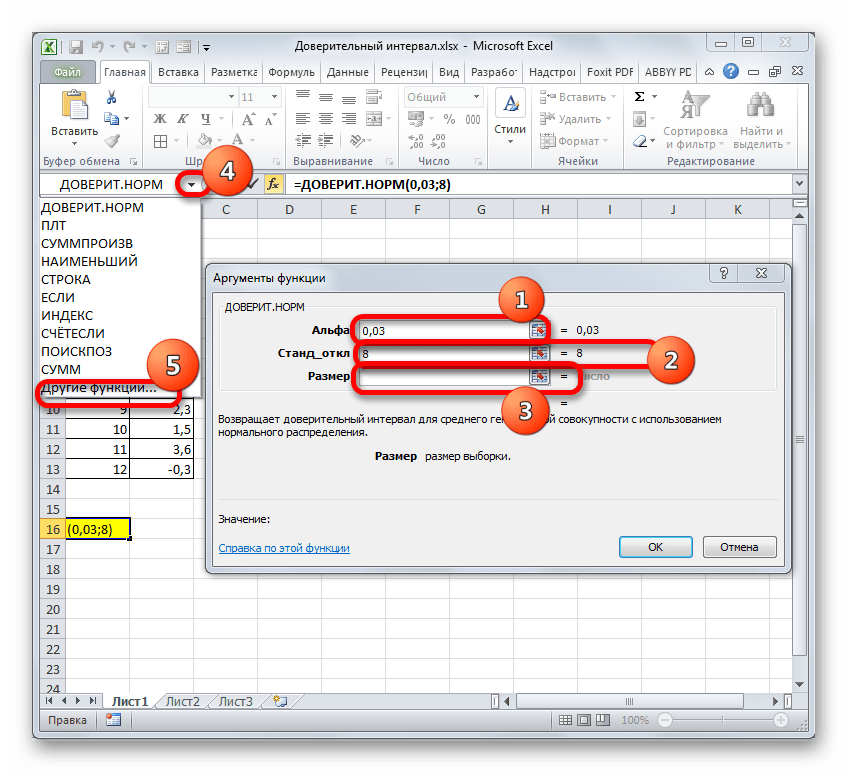
В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.
Появляется список недавно применяемых функций. Если оператор СЧЁТ применялся вами недавно, то он должен быть в этом списке. В таком случае, нужно просто кликнуть по его наименованию. В обратном же случае, если вы его не обнаружите, то переходите по пункту «Другие функции…».
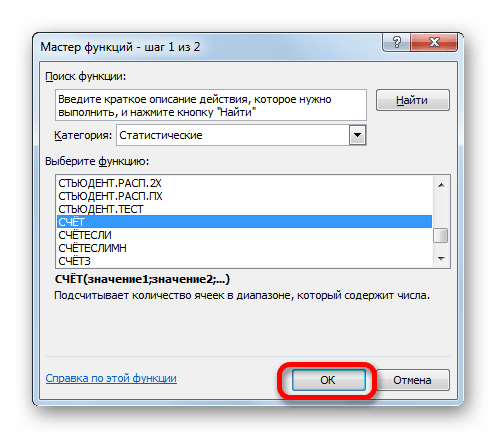
- Появляется уже знакомый нам Мастер функций. Опять перемещаемся в группу «Статистические». Выделяем там наименование «СЧЁТ». Клацаем по кнопке «OK».
- Появляется окно аргументов вышеуказанного оператора. Данная функция предназначена для того, чтобы вычислять количество ячеек в указанном диапазоне, которые содержат числовые значения. Синтаксис её следующий:
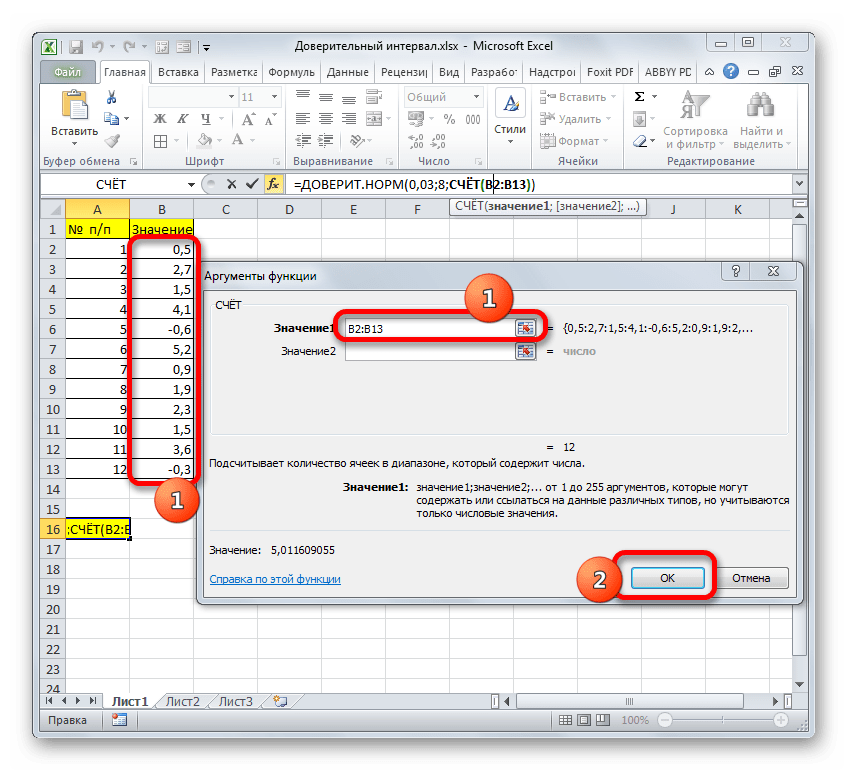
=СЧЁТ(значение1;значение2;…)Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.
Устанавливаем курсор в поле «Значение1» и, зажав левую кнопку мыши, выделяем на листе диапазон, который содержит нашу совокупность. Затем его адрес будет отображен в поле. Клацаем по кнопке «OK».
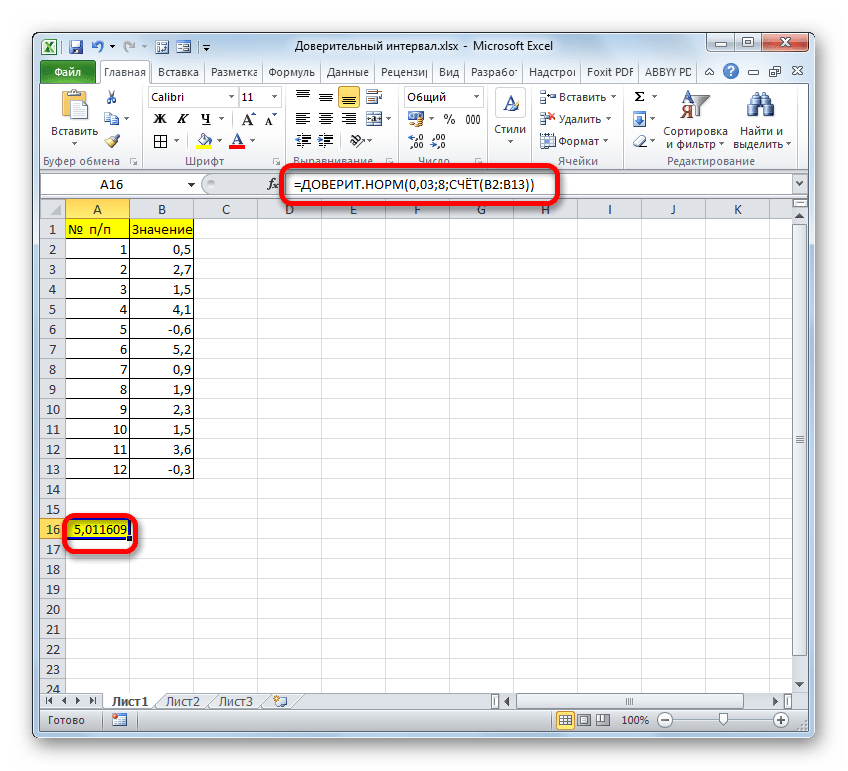
- После этого приложение произведет вычисление и выведет результат в ту ячейку, где она находится сама. В нашем конкретном случае формула получилась такого вида:
=ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))Общий результат вычислений составил 5,011609.
- Но это ещё не все. Как мы помним, граница доверительного интервала вычисляется путем сложения и вычитания от среднего выборочного значения результата вычисления ДОВЕРИТ.НОРМ. Таким способом рассчитывается соответственно правая и левая граница доверительного интервала. Само среднее выборочное значение можно рассчитать при помощи оператора СРЗНАЧ.
Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:
=СРЗНАЧ(число1;число2;…)Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.
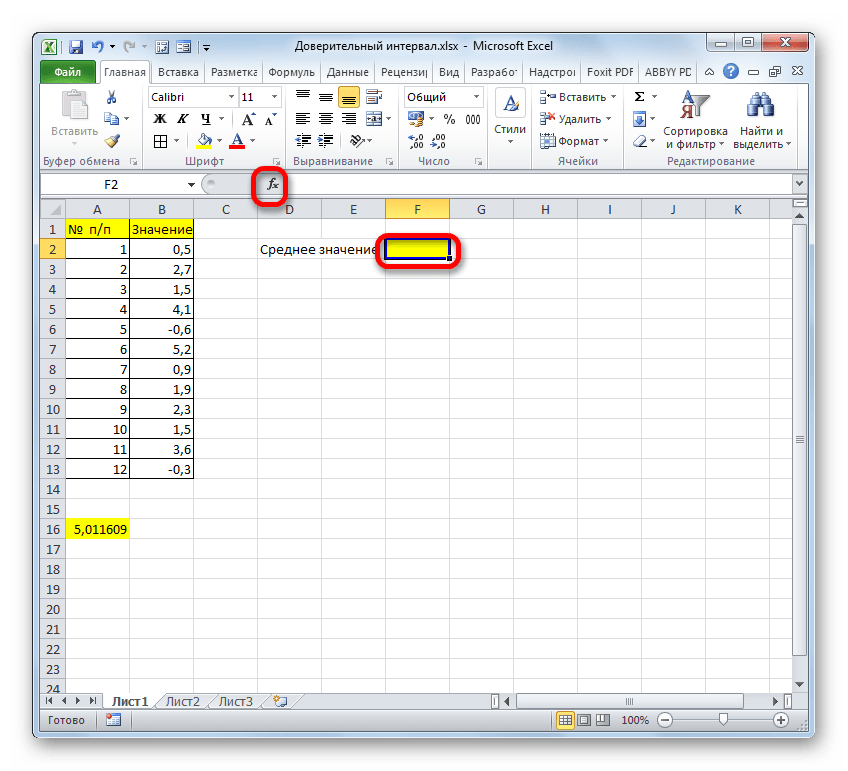
Итак, выделяем ячейку, в которую будет выводиться расчет среднего значения, и щелкаем по кнопке «Вставить функцию».
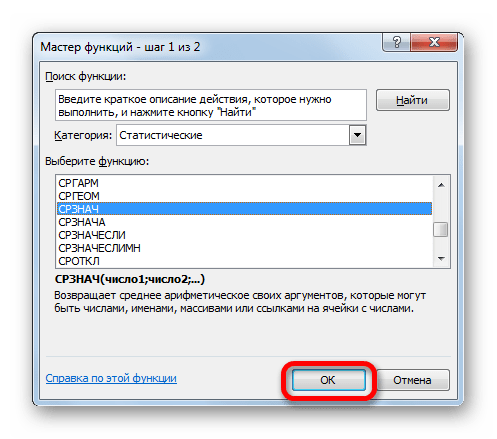
- Открывается Мастер функций. Снова переходим в категорию «Статистические» и выбираем из списка наименование «СРЗНАЧ». Как всегда, клацаем по кнопке «OK».
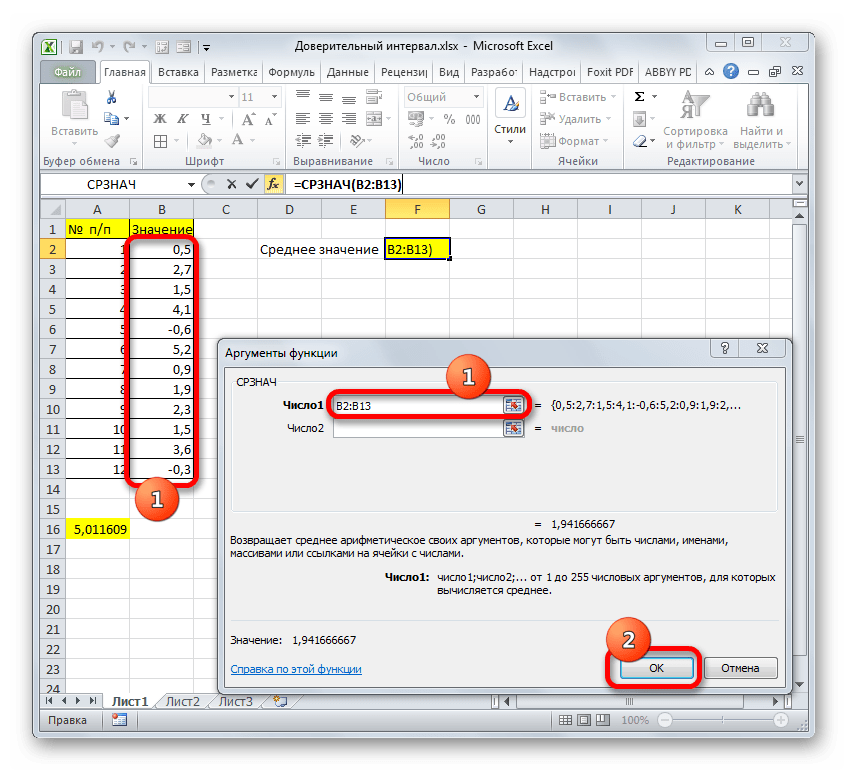
- Запускается окно аргументов. Устанавливаем курсор в поле «Число1» и с зажатой левой кнопкой мыши выделяем весь диапазон значений. После того, как координаты отобразились в поле, клацаем по кнопке «OK».
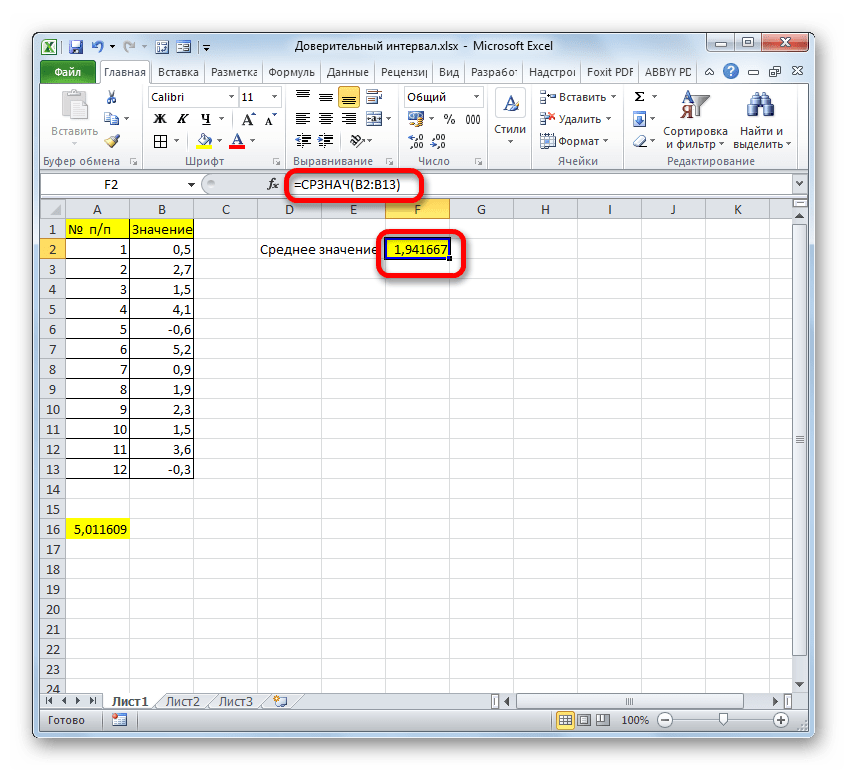
- После этого СРЗНАЧ выводит результат расчета в элемент листа.
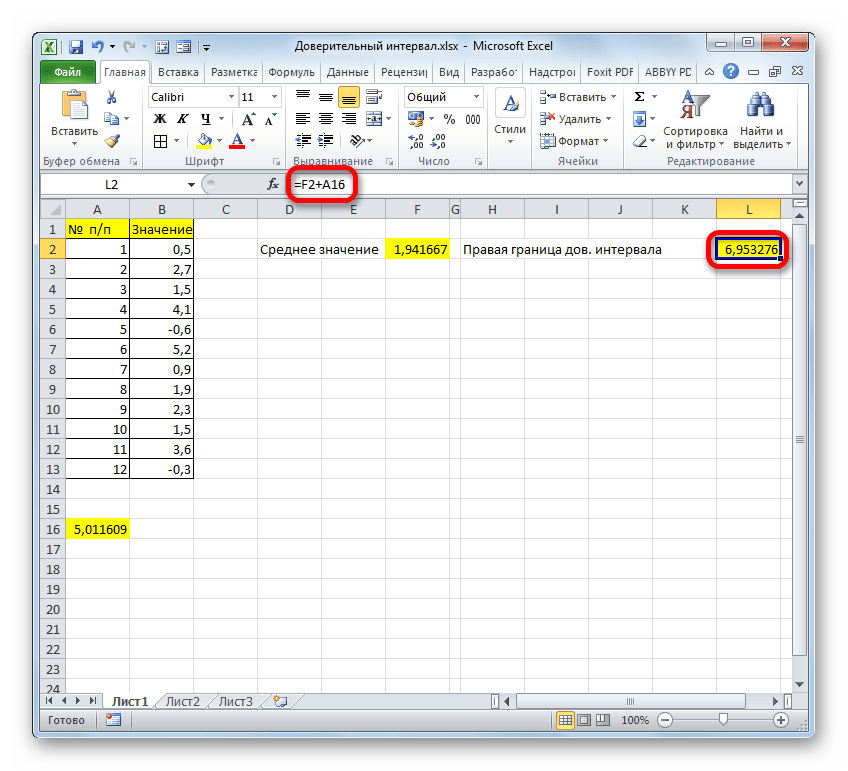
- Производим расчет правой границы доверительного интервала. Для этого выделяем отдельную ячейку, ставим знак «=» и складываем содержимое элементов листа, в которых расположены результаты вычислений функций СРЗНАЧ и ДОВЕРИТ.НОРМ. Для того, чтобы выполнить расчет, жмем на клавишу Enter. В нашем случае получилась следующая формула:
=F2+A16Результат вычисления: 6,953276
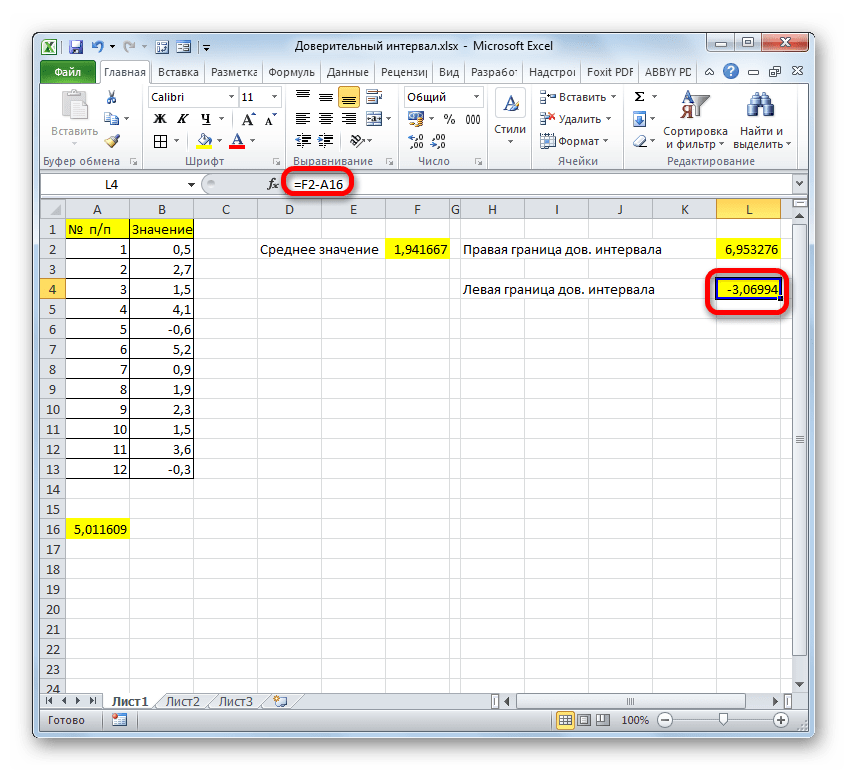
- Таким же образом производим вычисление левой границы доверительного интервала, только на этот раз от результата вычисления СРЗНАЧ отнимаем результат вычисления оператора ДОВЕРИТ.НОРМ. Получается формула для нашего примера следующего типа:
=F2-A16Результат вычисления: -3,06994
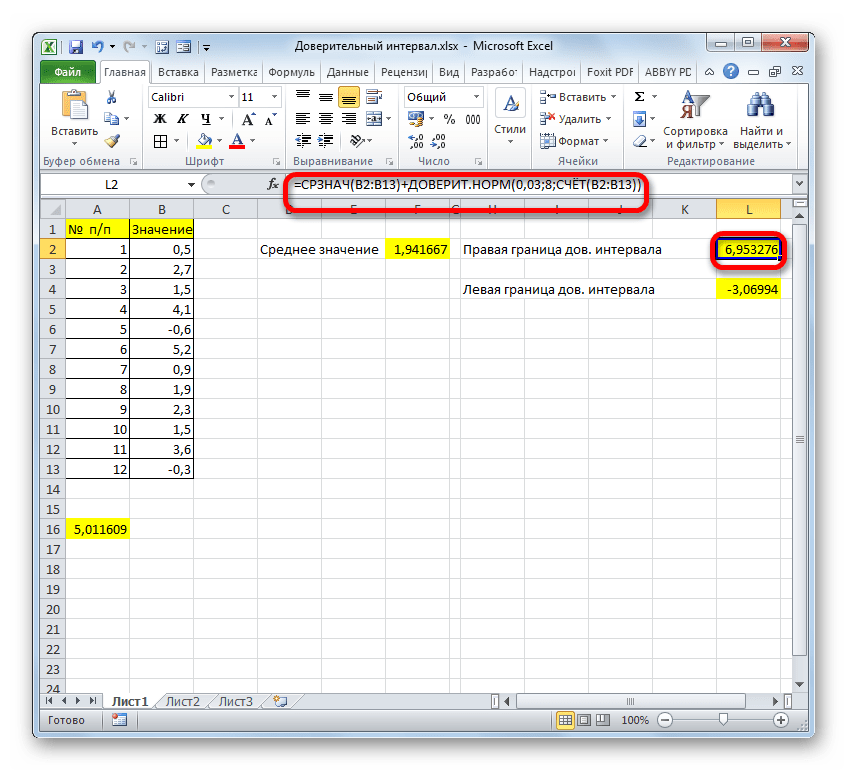
- Мы попытались подробно описать все действия по вычислению доверительного интервала, поэтому детально расписали каждую формулу. Но можно все действия соединить в одной формуле. Вычисление правой границы доверительного интервала можно записать так:
=СРЗНАЧ(B2:B13)+ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13)) - Аналогичное вычисление левой границы будет выглядеть так:
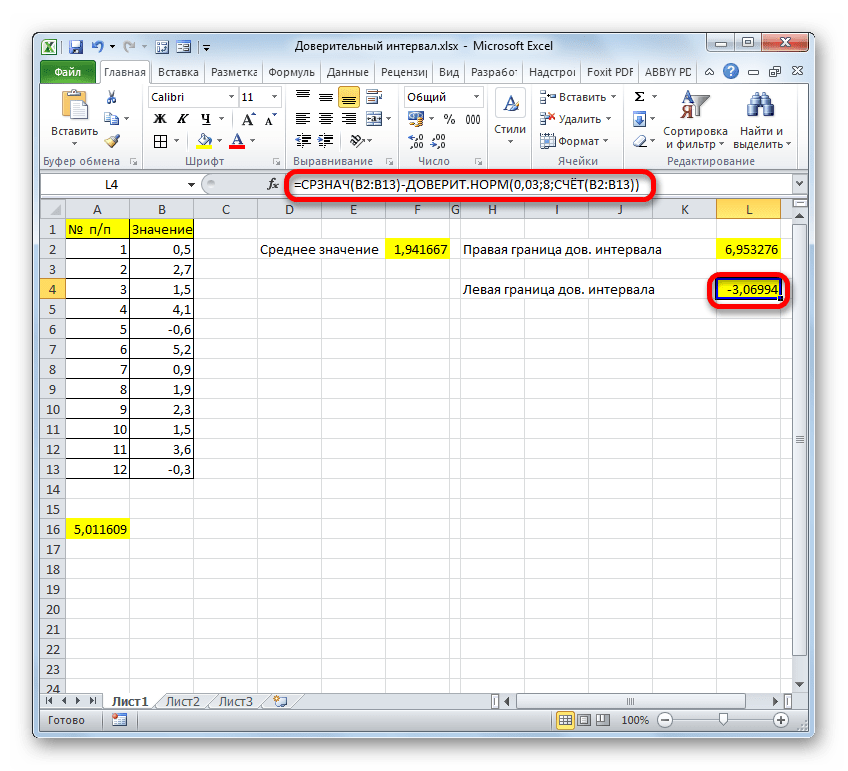
=СРЗНАЧ(B2:B13)-ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))
Способ 2: функция ДОВЕРИТ.СТЮДЕНТ
Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:
=ДОВЕРИТ.СТЬЮДЕНТ(альфа;стандартное_откл;размер)
Как видим, наименования операторов и в этом случае остались неизменными.
Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.
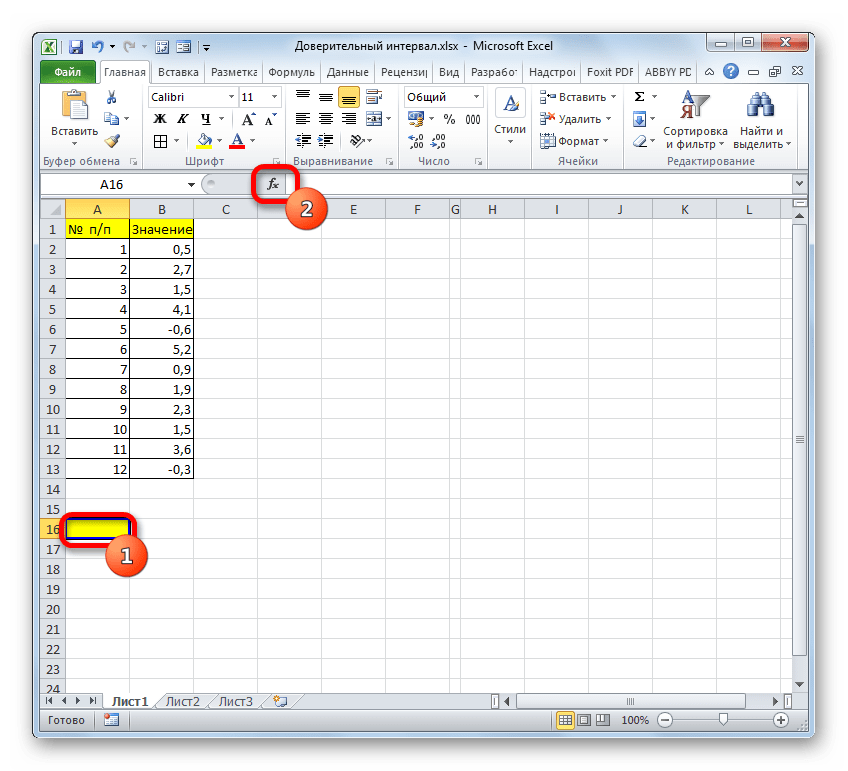
- Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».
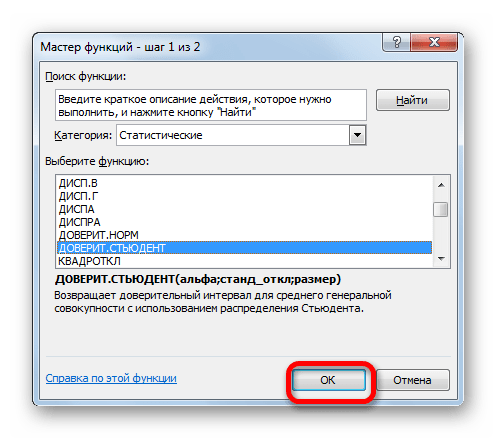
- В открывшемся Мастере функций переходим в категорию «Статистические». Выбираем наименование «ДОВЕРИТ.СТЮДЕНТ». Клацаем по кнопке «OK».
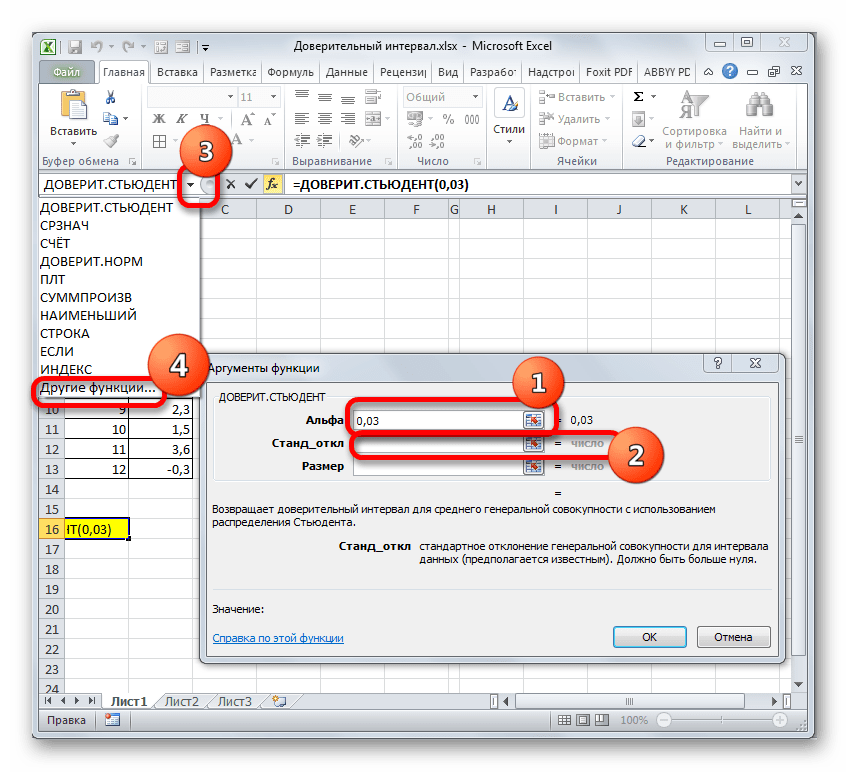
- Производится запуск окна аргументов указанного оператора.
В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.
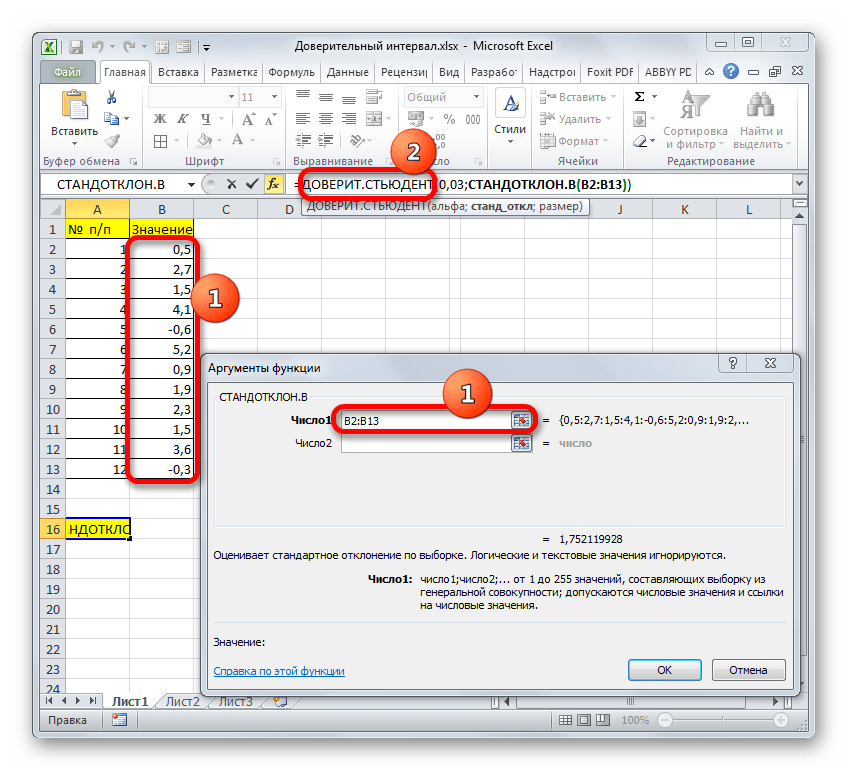
После этого устанавливаем курсор в поле «Стандартное отклонение». На этот раз данный показатель нам неизвестен и его требуется рассчитать. Делается это при помощи специальной функции – СТАНДОТКЛОН.В. Чтобы вызвать окно данного оператора, кликаем по треугольнику слева от строки формул. Если в открывшемся списке не находим нужного наименования, то переходим по пункту «Другие функции…».
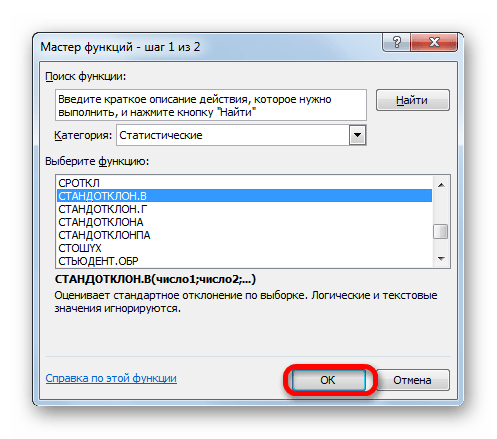
- Запускается Мастер функций. Перемещаемся в категорию «Статистические» и отмечаем в ней наименование «СТАНДОТКЛОН.В». Затем клацаем по кнопке «OK».
- Открывается окно аргументов. Задачей оператора СТАНДОТКЛОН.В является определение стандартного отклонения при выборке. Его синтаксис выглядит так:
=СТАНДОТКЛОН.В(число1;число2;…)Нетрудно догадаться, что аргумент «Число» — это адрес элемента выборки. Если выборка размещена единым массивом, то можно, использовав только один аргумент, дать ссылку на данный диапазон.
Устанавливаем курсор в поле «Число1» и, как всегда, зажав левую кнопку мыши, выделяем совокупность. После того, как координаты попали в поле, не спешим жать на кнопку «OK», так как результат получится некорректным. Прежде нам нужно вернуться к окну аргументов оператора ДОВЕРИТ.СТЮДЕНТ, чтобы внести последний аргумент. Для этого кликаем по соответствующему наименованию в строке формул.
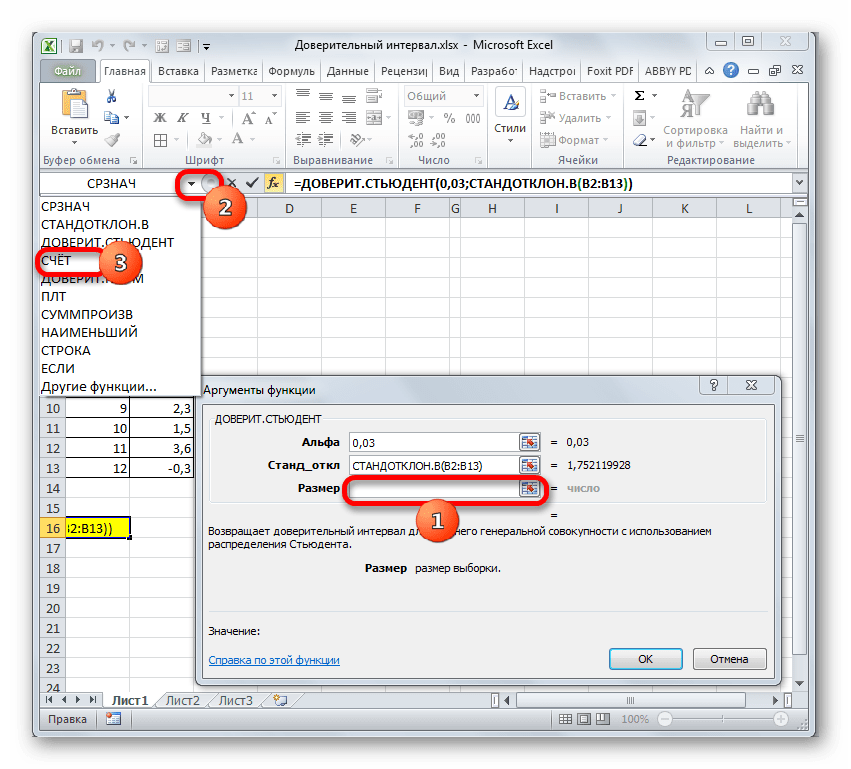
- Снова открывается окно аргументов уже знакомой функции. Устанавливаем курсор в поле «Размер». Опять жмем на уже знакомый нам треугольник для перехода к выбору операторов. Как вы поняли, нам нужно наименование «СЧЁТ». Так как мы использовали данную функцию при вычислениях в предыдущем способе, в данном списке она присутствует, так что просто щелкаем по ней. Если же вы её не обнаружите, то действуйте по алгоритму, описанному в первом способе.
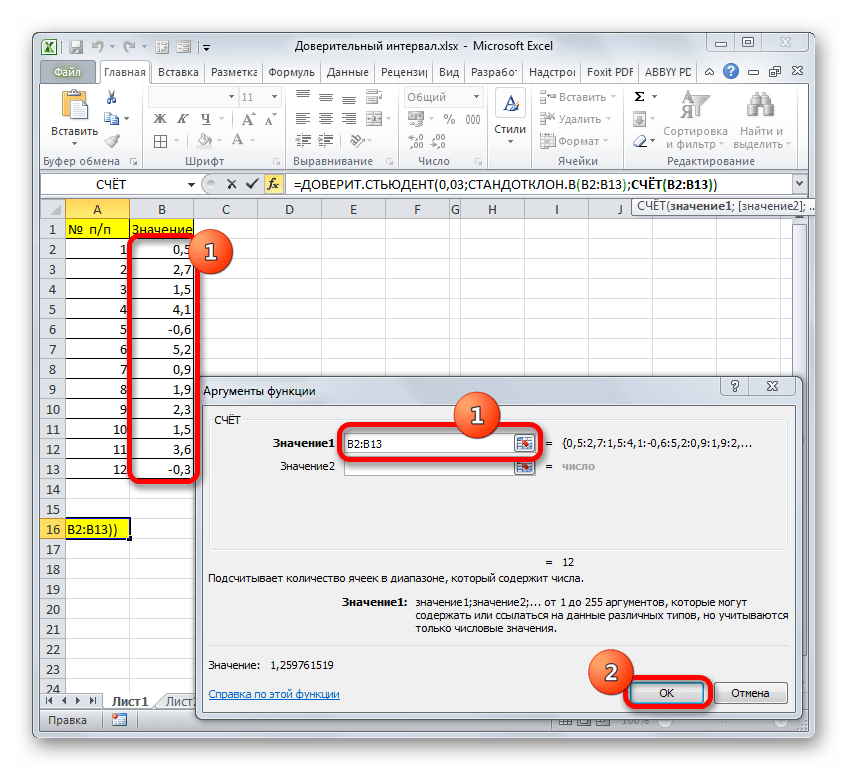
- Попав в окно аргументов СЧЁТ, ставим курсор в поле «Число1» и с зажатой кнопкой мыши выделяем совокупность. Затем клацаем по кнопке «OK».
- После этого программа производит расчет и выводит значение доверительного интервала.
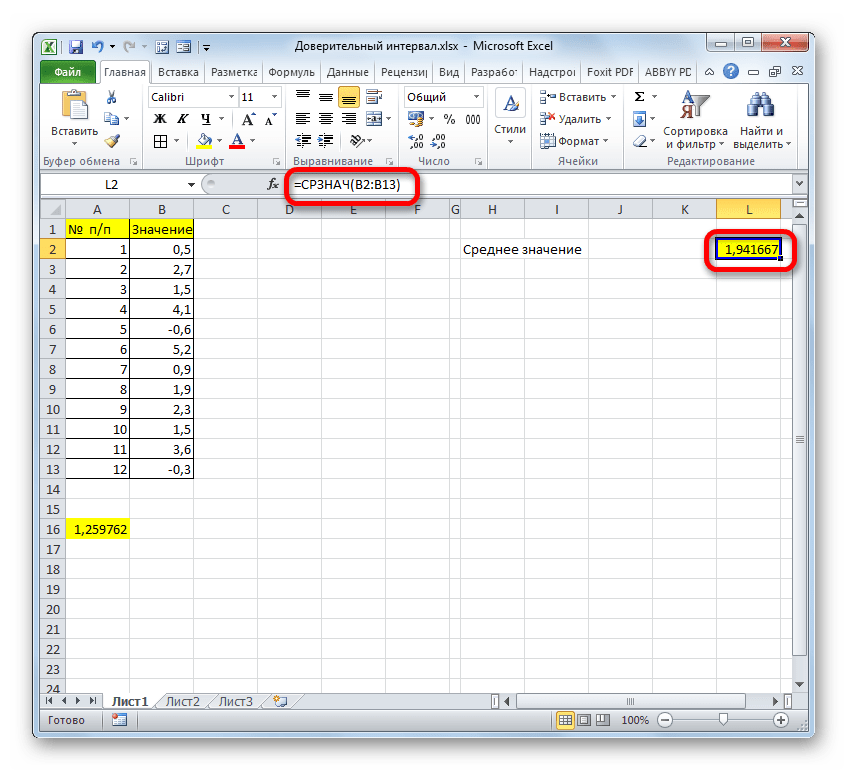
- Для определения границ нам опять нужно будет рассчитать среднее значение выборки. Но, учитывая то, что алгоритм расчета при помощи формулы СРЗНАЧ тот же, что и в предыдущем способе, и даже результат не изменился, не будем на этом подробно останавливаться второй раз.
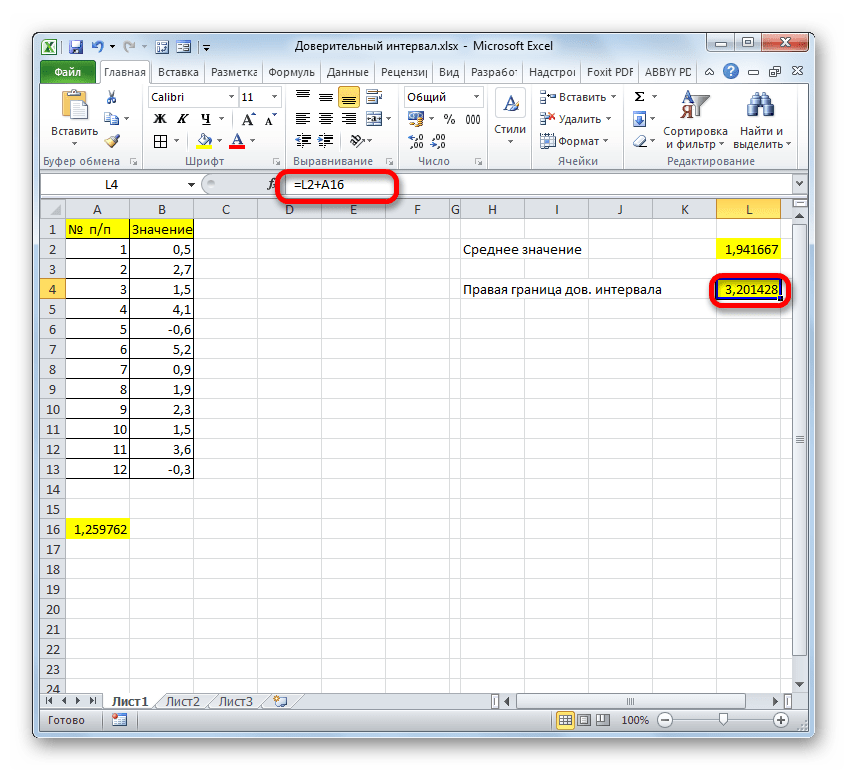
- Сложив результаты вычисления СРЗНАЧ и ДОВЕРИТ.СТЮДЕНТ, получаем правую границу доверительного интервала.
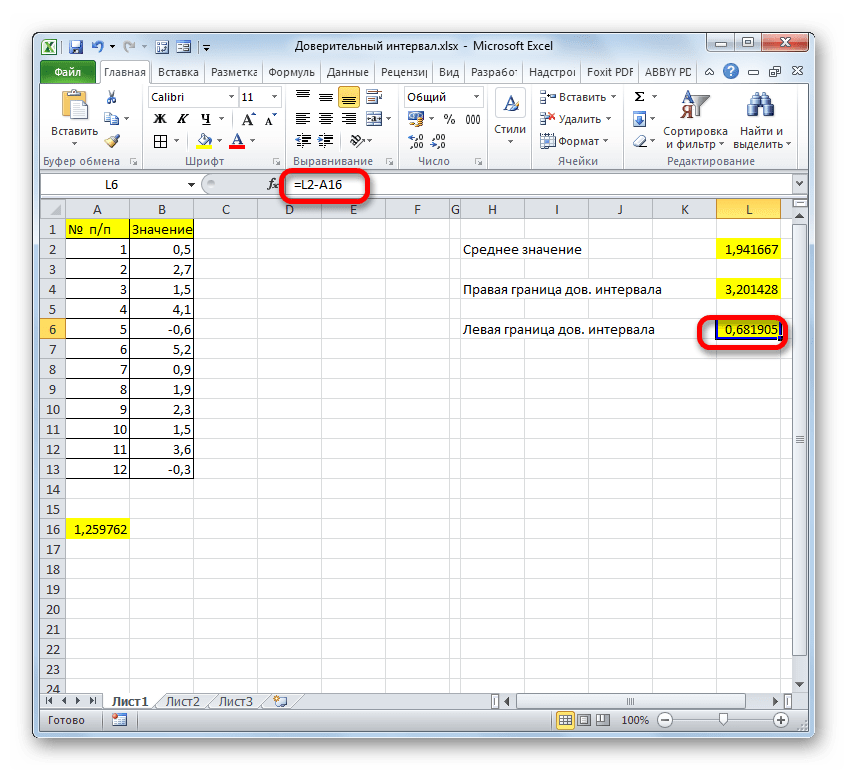
- Отняв от результатов расчета оператора СРЗНАЧ результат расчета ДОВЕРИТ.СТЮДЕНТ, имеем левую границу доверительного интервала.
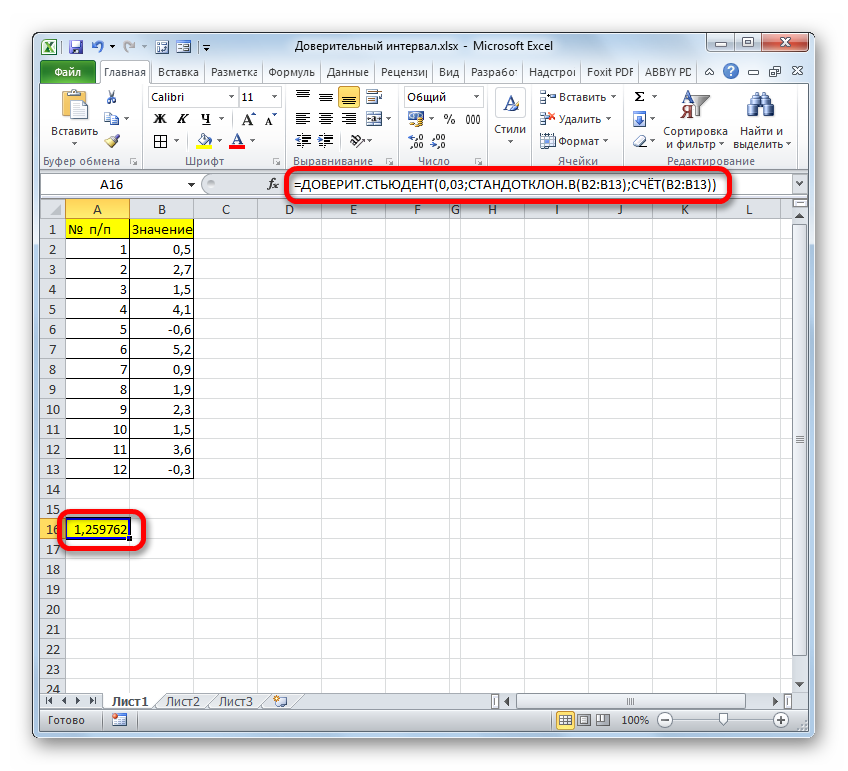
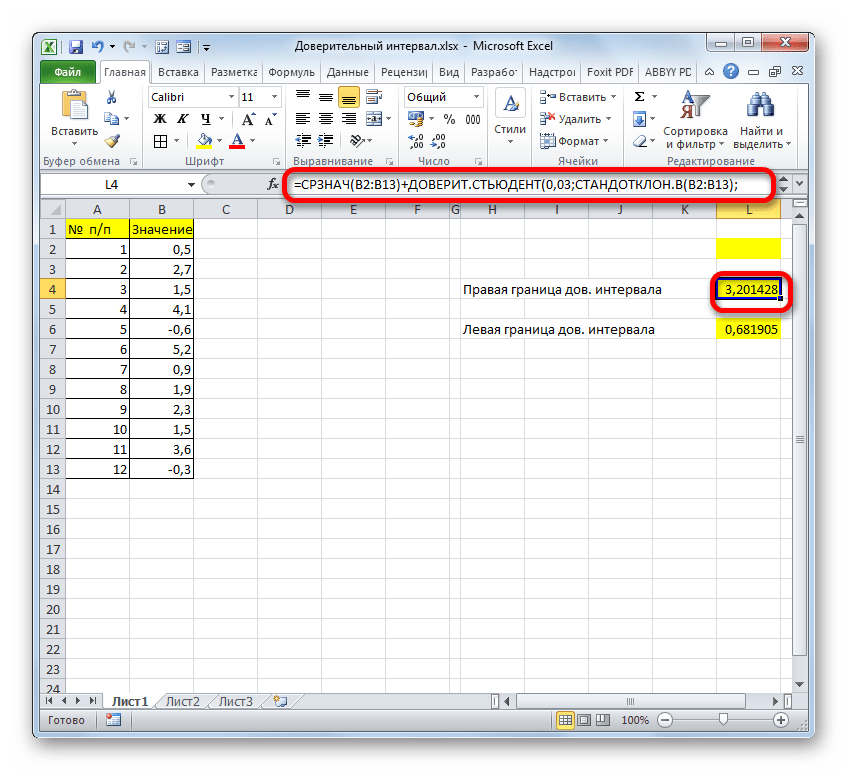
- Если расчет записать одной формулой, то вычисление правой границы в нашем случае будет выглядеть так:
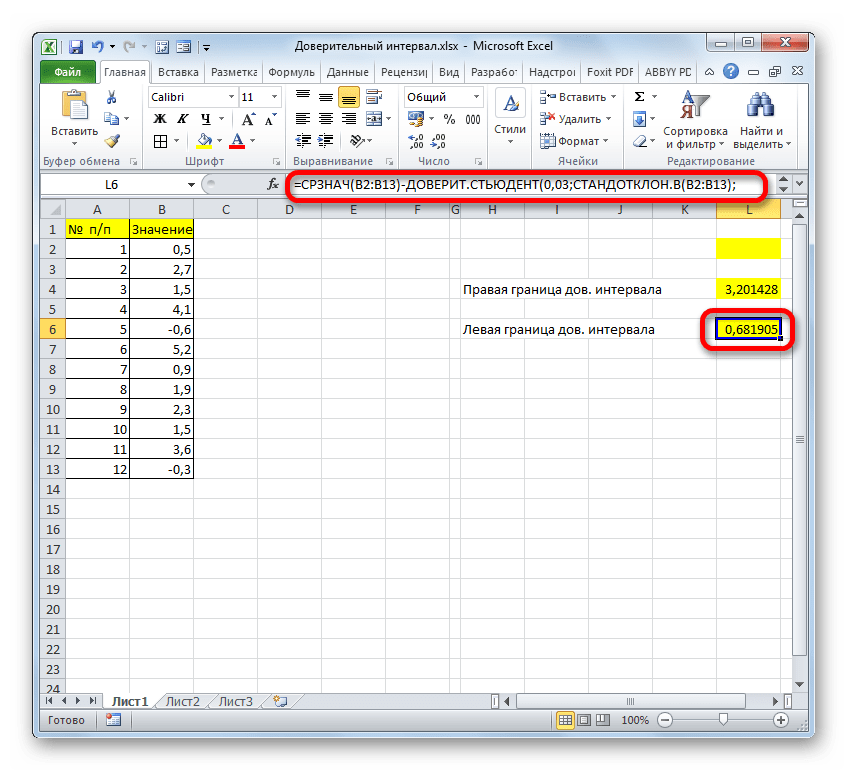
=СРЗНАЧ(B2:B13)+ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13)) - Соответственно, формула расчета левой границы будет выглядеть так:
=СРЗНАЧ(B2:B13)-ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))
Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.

