Способы расчета доверительного интервала

21 апреля 2016
Часто оценщику приходится анализировать рынок недвижимости того сегмента, в котором располагается объект оценки. Если рынок развит, проанализировать всю совокупность представленных объектов бывает сложно, поэтому для анализа используется выборка объектов. Не всегда эта выборка получается однородной, иногда требуется очистить ее от экстремумов – слишком высоких или слишком низких предложений рынка. Для этой цели применяется доверительный интервал. Цель данного исследования – провести сравнительный анализ двух способов расчета доверительного интервала и выбрать оптимальный вариант расчета при работе с разными выборками в системе estimatica.pro.
Способы расчета доверительного интервала
Доверительный интервал – вычисленный на основе выборки интервал значений признака, который с известной вероятностью содержит оцениваемый параметр генеральной совокупности.
Смысл вычисления доверительного интервала заключается в построении по данным выборки такого интервала, чтобы можно было утверждать с заданной вероятностью, что значение оцениваемого параметра находится в этом интервале. Другими словами, доверительный интервал с определенной вероятностью содержит неизвестное значение оцениваемой величины. Чем шире интервал, тем выше неточность.
Существуют разные методы определения доверительного интервала. В этой статье рассмотрим 2 способа:
- через медиану и среднеквадратическое отклонение;
- через критическое значение t-статистики (коэффициент Стьюдента).
Этапы сравнительного анализа разных способов расчета ДИ:
1. формируем выборку данных;
2. обрабатываем ее статистическими методами: рассчитываем среднее значение, медиану, дисперсию и т.д.;
3. рассчитываем доверительный интервал двумя способами;
4. анализируем очищенные выборки и полученные доверительные интервалы.
Этап 1. Выборка данных
Выборка сформирована с помощью системы estimatica.pro. В выборку вошло 91 предложение о продаже 1 комнатных квартир в 3-ем ценовом поясе с типом планировки «Хрущевка».
Таблица 1. Исходная выборка
|
№ |
Цена 1 кв.м., д.е. |
|
1 |
50943 |
|
2 |
35000 |
|
3 |
51613 |
|
4 |
50645 |
|
5 |
49841 |
|
… |
… |
|
86 |
58772 |
|
87 |
70714 |
|
88 |
53393 |
|
89 |
54876 |
|
90 |
52542 |
|
91 |
56140 |
Рис.1. Исходная выборка

Этап 2. Обработка исходной выборки
Обработка выборки методами статистики требует вычисления следующих значений:
1. Среднее арифметическое значение

2. Медиана – число, характеризующее выборку: ровно половина элементов выборки больше медианы, другая половина меньше медианы
![]() (для выборки, имеющей нечетное число значений)
(для выборки, имеющей нечетное число значений)
3. Размах – разница между максимальным и минимальным значениями в выборке

4. Дисперсия – используется для более точного оценивания вариации данных

5. Среднеквадратическое отклонение по выборке (далее – СКО) – наиболее распространённый показатель рассеивания значений корректировок вокруг среднего арифметического значения.

6. Коэффициент вариации – отражает степень разбросанности значений корректировок

7. коэффициент осцилляции – отражает относительное колебание крайних значений цен в выборке вокруг средней

Таблица 2. Статистические показатели исходной выборки
|
Показатель |
Значение |
|
Ср. значение |
54970 |
|
Медиана |
53934 |
|
Размах |
39194 |
|
Дисперсия |
45126821 |
|
СКО |
6755 |
|
Коэф. вариации |
12,29% |
|
Коэф. осциляции |
71,30% |
Коэффициент вариации, который характеризует однородность данных, составляет 12,29%, однако коэффициент осцилляции слишком велик. Таким образом, мы можем утверждать, что исходная выборка не является однородной, поэтому перейдем к расчету доверительного интервала.
Этап 3. Расчёт доверительного интервала
Способ 1. Расчёт через медиану и среднеквадратическое отклонение.
Доверительный интервал определяется следующим образом: минимальное значение – из медианы вычитается СКО; максимальное значение – к медиане прибавляется СКО.
Формула доверительного интервала:

Таким образом, доверительный интервал (47179 д.е.; 60689 д.е.)
Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 20 объектов, что составило 22% выборки.
Рис. 2. Значения, попавшие в доверительный интервал 1.

Способ 2. Построение доверительного интервала через критическое значение t-статистики (коэффициент Стьюдента)
С.В. Грибовский в книге «Математические методы оценки стоимости имущества» описывает способ вычисления доверительного интервала через коэффициент Стьюдента. При расчете этим методом оценщик должен сам задать уровень значимости ∝, определяющий вероятность, с которой будет построен доверительный интервал. Обычно используются уровни значимости 0,1; 0,05 и 0,01. Им соответствуют доверительные вероятности 0,9; 0,95 и 0,99. При таком методе полагают истинные значения математического ожидания и дисперсии практически неизвестными (что почти всегда верно при решении практических задач оценки).
Формула доверительного интервала:

n – объем выборки;
![]() – критическое значение t- статистики (распределения Стьюдента) с уровнем значимости ∝,числом степеней свободы n-1,которое определяется по специальным статистическим таблицам либо с помощью MS Excel (
– критическое значение t- статистики (распределения Стьюдента) с уровнем значимости ∝,числом степеней свободы n-1,которое определяется по специальным статистическим таблицам либо с помощью MS Excel (![]() →”Статистические”→ СТЬЮДРАСПОБР);
→”Статистические”→ СТЬЮДРАСПОБР);
∝ – уровень значимости, принимаем ∝=0,01.

Значения, содержащиеся в исходной выборке и не попадающие в доверительный интервал, удаляем. Удалено 62 объекта, что составило 68% выборки.
Рис. 2. Значения, попавшие в доверительный интервал 2.

Этап 4. Анализ разных способов расчета доверительного интервала
Два способа расчета доверительного интервала – через медиану и коэффициент Стьюдента – привели к разным значениям интервалов. Соответственно, получилось две различные очищенные выборки.
Таблица 3. Статистические показатели по трем выборкам.
|
Показатель |
Исходная выборка |
1 вариант |
2 вариант |
|
Среднее значение |
54970 |
53593 |
54750 |
|
Медиана |
53934 |
53425 |
54688 |
|
Размах |
39194 |
12888 |
3677 |
|
Дисперсия |
45126821 |
8919645 |
1228707 |
|
СКО |
6755 |
3008 |
1128 |
|
Коэф. вариации |
12,29% |
5,61% |
2,06% |
|
Коэф. осциляции |
71,30% |
24,05% |
6,72% |
|
Количество выбывших объектов, шт. |
20 |
62 |
На основании выполненных расчетов можно сказать, что полученные разными методами значения доверительных интервалов пересекаются, поэтому можно использовать любой из способов расчета на усмотрение оценщика.
Однако мы считаем, что при работе в системе estimatica.pro целесообразно выбирать метод расчета доверительного интервала в зависимости от степени развитости рынка:
- если рынок неразвит, применять метод расчета через медиану и среднеквадратическое отклонение, так как количество выбывших объектов в этом случае невелико;
- если рынок развит, применять расчет через критическое значение t-статистики (коэффициент Стьюдента), так как есть возможность сформировать большую исходную выборку.
При подготовке статьи были использованы:
1. Грибовский С.В., Сивец С.А., Левыкина И.А. Математические методы оценки стоимости имущества. Москва, 2014 г.
2. Данные системы estimatica.pro
Читайте также:
Расчет корректировок методом парных продаж
Статью подготовили: Наталья Ничкова и Михаил Филимонов
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Доверительный интервал (англ. ‘confidence interval’) представляет собой диапазон, для которого можно утверждать, с заданной вероятностью (1 – alpha ), называемой степенью доверия (или степенью уверенности, англ. ‘degree of confidence’), что он будет содержать оцениваемый параметр.
Этот интервал часто упоминается как (100 (1 – alpha)% ) доверительный интервал для параметра.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
В этом чтении, мы имеем дело только с двусторонними доверительными интервалами – доверительные интервалами, для которых мы вычисляем и нижние и верхние пределы.
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Доверительный интервал (100 (1 – alpha)% ) для параметра имеет следующую структуру.
Точечная оценка (pm) Фактор надежности (times) Стандартная ошибка
где
- Точечная оценка = точечная оценка параметра (значение выборочной статистики).
- Фактор надежности (англ. ‘reliability factor’) = коэффициент, основанный на предполагаемом распределении точечной оценки и степени доверия ((1 – alpha)) для доверительного интервала.
- Стандартная ошибка = стандартная ошибка выборочной статистики, значение которой получено с помощью точечной оценки.
Величину (Фактор надежности) (times) (Cтандартная ошибка) иногда называют точностью оценки (англ. ‘precision of estimator’). Большие значения этой величины подразумевают более низкую точность оценки параметра совокупности.
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как (Z). Обозначение (z_alpha ) обозначает такую точку стандартного нормального распределения, в которой (alpha) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем ( z_{0.05} = 1.65 ).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией (sigma^2) = 400 (значит, (sigma) = 20).
Мы рассчитываем выборочное среднее как ( overline X = 25 ). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Таким образом, ( z_{0.025} = 1.96) является фактором надежности для этого 95%-ного доверительного интервала. Обратите внимание на связь (100 (1 – alpha)% ) для доверительного интервала и (z_{alpha/2}) для фактора надежности.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна:
( sigma_{overline X} = 20 Big / sqrt{100} = 2 )
Доверительный интервал, таким образом, имеет нижний предел:
( overline X – 1.96 sigma_{overline X} ) = 25 – 1.96(2) = 25 – 3.92 = 21.08.
Верхний предел доверительного интервала равен:
( overline X + 1.96sigma_{overline X} ) = 25 + 1.96(2) = 25 + 3.92 = 28.92
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Доверительный интервал (100 (1 – alpha)% ) для среднего по совокупности ( mu ), когда мы делаем выборку из нормального распределения с известной дисперсией ( sigma^2 ) задается формулой:
( Large dst overline X pm z_{alpha /2}{sigma over sqrt n} ) (Формула 4)
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
- 90%-ные доверительные интервалы: используется (z_{0.05}) = 1.65
- 95%-ные доверительные интервалы: используется (z_{0.025}) = 1.96
- 99%-ные доверительные интервалы: используется (z_{0.005}) = 2.58
На практике, большинство финансовых аналитиков используют значения для (z_{0.05}) и (z_{0.005}), округленные до двух знаков после запятой.
Для справки, более точными значениями для (z_{0.05}) и (z_{0.005}) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала (z_{0.025}) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
Распределение статистики (t) называется t-распределением Стьюдента (англ. “Student’s t-distribution”) из-за псевдонима «Студент» (Student), использованного британским математиком Уильямом Сили Госсеттом, который опубликовал свою работу в 1908 году.
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
Второй подход к доверительным интервалам для среднего по совокупности, основанного на стандартном нормальном распределении, – это z-альтернатива (англ. ‘z-alternative’). Он может быть использован только тогда, когда размер выборки является большим (в общем случае, размер выборки 30 или больше, можно считать большим).
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки (s) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Доверительные интервалы для среднего по совокупности – z-альтернатива (большая выборка, дисперсия совокупности неизвестна).
Доверительный интервал (100 (1 – alpha)% ) для среднего по совокупности ( mu ) при выборке из любого распределения с неизвестной дисперсией, когда размер выборки большой, задается формулой:
( Large dst overline X pm z_{alpha /2}{s over sqrt n} ) (Формула 5)
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
[см. также: CFA – Коэффициент Шарпа]
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет ( z_{0.05} = 1.65 ).
Доверительный интервал будет равен:
( begin{aligned} & overline X pm z_{0.05}{s over sqrt n } \ &= 0.45 pm 1.65{0.30 over sqrt {100}} \ &= 0.45 pm 1.65(0.03) = 0.45 pm 0.0495 end{aligned} )
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности (t) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности (z). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Формула 3 дает несмещенную оценку выборочной дисперсии, которую мы используем. Выражение в знаменателе, ( n – 1 ), означающее размер выборки минус 1, это число степеней свободы при расчете дисперсии совокупности с использованием Формулы 3.
Мы также используем ( n – 1 ) как число степеней свободы для определения факторов надежности на основе распределения Стьюдента. Термин «степени свободы» используются, так как мы предполагаем, что в случайной выборке наблюдения отобраны независимо друг от друга. Числитель выборочной дисперсии, однако, использует выборочное среднее.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Учитывая, что мы должны сначала вычислить выборочное среднее от общего числа (n) независимых наблюдений, только (n – 1) наблюдений могут быть отобраны независимо друг от друга для расчета выборочной дисперсии.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент (z = (overline X – mu) Big / (sigma big / sqrt n) ) нормально распределен со средним значением 0 и стандартным отклонением 1, однако, коэффициент (t = (overline X – mu) Big / (s big / sqrt n) ) следует t-распределению со средним 0 и (n – 1) степеней свободы.
Коэффициент (t) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
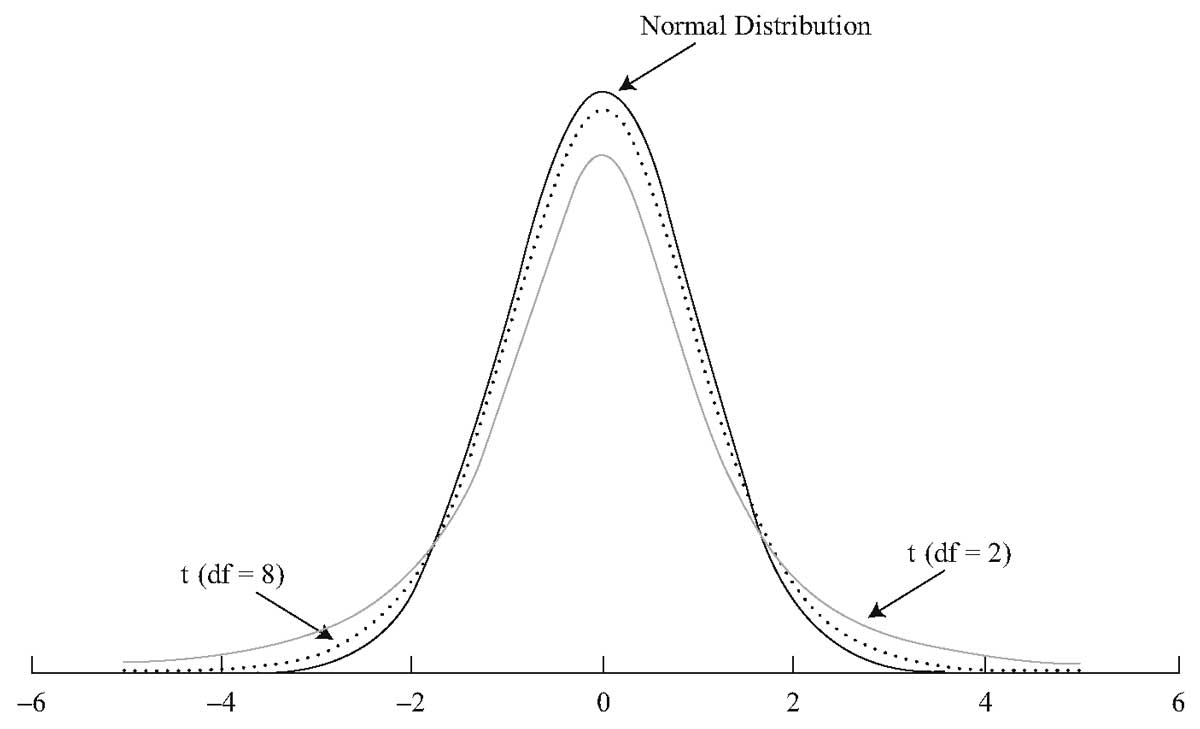 Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Рисунок (1) t-распределение Стьюдента по сравнению со стандартным нормальным распределением.
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Значения (t_{0.10}), (t_{0.05}), (t_{0.025}), (t_{0.01}) и (t_{0.005}) также называют односторонними критическими значениями t на значимых уровнях 0.10, 0.05, 0.025, 0.01 и 0.005, для указанного числа степеней свободы.
Например,
для DF = 30,
(t_{0.10}) = 1.310,
(t_{0.05}) = 1.697,
(t_{0.025}) = 2.042,
(t_{0.01}) = 2.457,
(t_{0.005}) = 2.750.
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Доверительные интервалы для среднего по совокупности (дисперсия совокупности неизвестна) – t-распределение.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
- выборка является большой, или
- выборка небольшая, но совокупность имеет нормальное распределение, или приблизительно нормально распределена,
то доверительный интервал (100 (1 – alpha)% ) для среднего совокупности ( mu ) задается формулой:
( Large dst overline X pm t_{alpha /2}{s over sqrt n} ) (Формула 6)
где число степеней свободы для ( t_{alpha /2}) равно ( n-1 ), а ( n ) – это размер выборки.
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Выборочное среднее коэффициентов Шарпа составляет 0.45, а выборочное стандартное отклонение – 0.30.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что (t_{0.05}) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности (z_{0.05}) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
( begin{aligned} & overline X pm t_{0.05}{s over sqrt n } \ &= 0.45 pm 1.66{0.30 over sqrt {100}} \ &= 0.45 pm 1.66(0.03) = 0.45 pm 0.0498 end{aligned} )
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.
|
Выборка из: |
Статистика для выборки малого размера |
Статистика для выборки большого размера |
|---|---|---|
|
Нормальное распределение с известной дисперсией |
(z) |
(z) |
|
Нормальное распределение с неизвестной дисперсией |
(t) |
(t)* |
|
Ненормальное распределение с известной дисперсией |
недоступно |
(z) |
|
Ненормальное распределение с неизвестной дисперсией |
недоступно |
(t)* |
* Использование (z) также приемлемо.
Различные
статистики, получаемые в результате
вычислений, представляют собой точечные
оценки соответствующих параметров
генеральной совокупности.
Если
из генеральной совокупности извлечь
некоторое количество выборок и для
каждой
из них найти интересующие нас статистики,
то вычисленные значения будут представлять
собой случайные величины, которые
распределены по нормальному закону и
имеющие некоторый разброс вокруг
оцениваемого параметра.
Но,
как правило, в результате эксперимента
в распоряжении исследователя имеется
одна выборка. Поэтому значительный
интерес представляет получение
интервальной
оценки,
т.е. получение некоторого интервала,
внутри которого, как можно предположить,
лежит истинное значение параметра.
Вероятности,
признанные достаточными для уверенных
суждений о параметрах генеральной
совокупности на основании статистик,
называются доверительными.
Для
примера рассмотрим
![]() как оценку параметра
как оценку параметра![]() .
.
Доказано,
что если выборки извлекаются из
генеральной совокупности с параметрами:
![]()
то
распределение выборочных средних
![]() будет приближаться к нормальному закону
будет приближаться к нормальному закону
распределения и иметь среднее, равное![]() ,
,
дисперсию![]() ,
,
среднее квадратическое![]() ,
,
где![]() – объем выборки.
– объем выборки.
Для
такого распределения, как мы показали
раньше,
![]() наблюдений лежат в интервале
наблюдений лежат в интервале![]() ,
,
т.е.![]() ,
,![]() в интервале
в интервале![]() и
и![]() в интервале
в интервале![]() .
.
В общем случае, вместо конкретных цифр![]() можно взять некоторый параметрt
можно взять некоторый параметрt
и записать:
![]() (5.7)
(5.7)
где
γ
– процент наблюдений, которые попадают
в интервал
![]() .
.
С
другой стороны величина γ
равна,
как мы знаем,
![]() (см. ф. (3.16)).
(см. ф. (3.16)).
Или
говорят, с надежностью
![]() доверительный интервал
доверительный интервал![]() покрывает неизвестный параметр
покрывает неизвестный параметр![]() с точностью
с точностью![]() .
.
Здесь,
наоборот, мы задаемся надежностью (или
доверительной вероятностью)
![]() ,
,
а зная![]() по таблицам для функции Лапласа находим
по таблицам для функции Лапласа находим
параметр![]() и далее – доверительный интервал.
и далее – доверительный интервал.
Но для
этого нам необходимо знать истинное
значение параметра генеральной
совокупности
![]() ,
,
которое нам неизвестно.
Поэтому
на практике вместо параметра
![]() используют выборочное среднее
используют выборочное среднее
квадратическое отклонение![]() .
.
То есть доверительный интервал
определяется выражением
![]() (5.8)
(5.8)
Но при
этом параметр
![]() это ужепараметр
это ужепараметр
распределения Стьюдента,
который находится по соответствующим
таблицам при данных
![]() и
и![]() ,
,
где![]() – задаваемая надежность, или доверительный
– задаваемая надежность, или доверительный
интервал. Этот интервал покрывает
неизвестный параметр![]() с надежностью
с надежностью![]() ,
,
где![]() и
и![]() находятся по формулам (5,3), (5.4) и (5.5),
находятся по формулам (5,3), (5.4) и (5.5),
(5.6) соответственно.
Пример.
Найти доверительный интервал для оценки
математического ожидания
![]() нормальной случайной величины с
нормальной случайной величины с
надежностью![]() ,
,
зная выборочную среднюю![]() ,
,
объем выборки![]() ,
,
среднее квадратическое отклонение![]() .
.
Решение.
Имеем
![]() .
.
Отсюда![]() .
.
По таблице значений функции Лапласа
находим![]() .
.
Отсюда

5. Применение критерия Стьюдента для сравнения двух генеральных совокупностей.
Пусть
нам надо оценить эффективность действия
рекламы какого-то товара.
До
запуска рекламы продажа товара по
неделям (в шт.) имела следующий вид:
![]()
После
выпуска рекламы продажа этого же товара
по неделям стала иметь вид:
![]()
Следовательно,
доверительный интервал с надежностью
![]() для первой выборки равен
для первой выборки равен
![]()
А для
второй
![]()
Т аким
аким
образом, если по средним мы можем сделать
положительный вывод о влиянии рекламы
товара, то по доверительным интервалам
мы вправе сомневаться: уж очень велики
интервалы, и они значительно перекрывают
друг друга (см. рис. 5.3).
Однако
нам необходимо со всей определенностью
истолковать результаты эксперимента.
Мы
можем высказать два предположения
(статистические гипотезы).
1.
Нулевая гипотеза. Между генеральными
совокупностями с параметрами
![]() и
и![]() ,
,![]() и
и![]() разница равна нулю, т.е.
разница равна нулю, т.е.![]() .
.
Следовательно, разница между выборочными
средними![]() возникла случайно, в процессе группировки
возникла случайно, в процессе группировки
данных.
2.
Альтернативная гипотеза, т.е.
противоположная.
Для
проверки этих гипотез существуют
специальные параметры, которые
табулированы и приводятся в соответствующих
справочниках.
В
частности, если сравниваемые генеральные
совокупности имеют нормальный закон
распределения, то сравнение выборочных
средних проводят с помощью
![]() иликритерия
иликритерия
Стьюдента:
![]()
где
 .
.
Согласно
нулевой гипотезе
![]() ,
,
отсюда:
![]() (5.9)
(5.9)
Нулевая
гипотеза (разницы нет) отвергается, если
![]() для заданной надежности и числа (степеней
для заданной надежности и числа (степеней
свободы)![]() .
.
Здесь![]() – фактический коэффициент Стьюдента,
– фактический коэффициент Стьюдента,
найденный по формуле (5.9), а![]() – теоретический коэффициент, найденный
– теоретический коэффициент, найденный
по специальным таблицам.
Для
нашего примера
![]() ,
,![]() .
.
Следовательно,![]() .
.
По таблицам, для надежности![]() и числа
и числа![]() ,
,
находим![]() .
.
Итак,![]() и нулевая гипотеза сохраняется: разница
и нулевая гипотеза сохраняется: разница
между результатами опыта и контроля
оказалась статистически недостоверной.
Таблица
![]() Стьюдента.
Стьюдента.
|
k |
Уровни |
||
|
95 |
99 |
99,9 |
|
|
7 |
2,37 |
3,50 |
5,51 |
|
8 |
2,31 |
3,36 |
5,04 |
|
9 |
2,26 |
3,25 |
4,78 |
|
10 |
2,23 |
3,17 |
4,59 |
Соседние файлы в папке 9.ТеорВер
- #
- #
- #
- #
- #
- #
- #
- #
19.05.20151.3 Mб35~WRL1476.tmp
- #
- #
- #
| Распределение Стьюдента | |
|---|---|
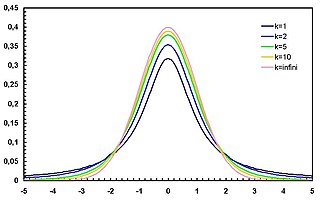 Плотность вероятности Плотность вероятности |
|
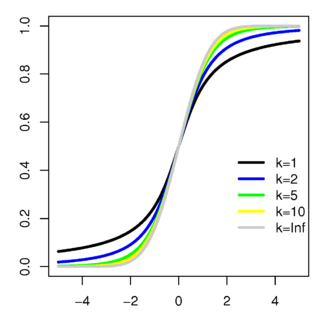 Функция распределения Функция распределения |
|
| Обозначение |
 |
| Параметры |
 — число степеней свободы — число степеней свободы |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
  где где  — гипергеометрическая функция — гипергеометрическая функция |
| Математическое ожидание |
 , если , если  |
| Медиана |
 |
| Мода |
 |
| Дисперсия |
 , если , если  |
| Коэффициент асимметрии |
 , если , если  |
| Коэффициент эксцесса |
 , если , если  |
| Дифференциальная энтропия |
|
| Производящая функция моментов | не определена |
Распределе́ние Стью́дента (
Распределение Стьюдента играет важную роль в статистическом анализе и используется, например, в t-критерии Стьюдента для оценки статистической значимости разности двух выборочных средних, при построении доверительного интервала для математического ожидания нормальной совокупности при неизвестной дисперсии, а также в линейном регрессионном анализе. Распределение Стьюдента также появляется в байесовском анализе данных, распределённых по нормальному закону.
График плотности распределения Стьюдента, как и нормального распределения, является симметричным и имеет вид колокола, но с более «тяжёлыми» хвостами, то есть реализациям случайной величины, имеющей распределение Стьюдента, более свойственно сильно отличаться от математического ожидания. Это делает его важным для понимания статистического поведения определённых типов отношений случайных величин, в которых отклонение в знаменателе увеличено и может производить отдалённые величины, когда знаменатель соотношения близок к нулю.
Распределение Стьюдента — частный случай обобщённого гиперболического распределения.
История и этимология[править | править код]
В статистике t-распределение было впервые получено как апостериорное распределение в 1876 году Фридрихом Гельмертом[1][2][3] и Якобом Люротом[en][4][5][6].
В англоязычной литературе распределение берёт название из статьи Уильяма Госсета в журнале Пирсона «Биометрика», опубликованной под псевдонимом «Стьюдент»[7][8].
Госсет работал в пивоварне Гиннесс в Дублине, Ирландия, и применял свои знания в области статистики как при варке пива, так и на полях — для выведения самого урожайного сорта ячменя. Исследования были обращены к нуждам пивоваренной компании и проводились на малом количестве наблюдений, что послужило толчком для развития методов, работающих на малых выборках.
Госсету пришлось скрывать свою личность при публикации из-за того, что ранее другой исследователь, работавший на Гиннесс, опубликовал в своих материалах сведения, составлявшие коммерческую тайну компании, после чего Гиннесс запретил своим работникам публикацию любых материалов, независимо от содержавшейся в них информации.
Статья Госсета описывает распределение как «Частотное распределение стандартных отклонений выборок, извлечённых из генеральной совокупности». Оно стало известным благодаря работе Роналда Фишера, который называл распределение «распределением Стьюдента», а величину — буквой t[9].
Определение[править | править код]
Пусть 


называется распределением Стьюдента с 

Это распределение абсолютно непрерывно с плотностью:
,
где 
для чётных
и соответственно
для нечётных
.
Также плотность распределения Стьюдента можно выразить воспользовавшись бета-функцией Эйлера 
.
График функции плотности t-распределения симметричен, а его форма напоминает форму колокола, как у стандартного нормального распределения, но он ниже и шире.
Следующие графики отражают плотность t-распределения при увеличении числа 

|
1 степень свободы |
2 степени свободы |
3 степени свободы |
|
5 степеней свободы |
10 степеней свободы |
30 степеней свободы |
Функция распределения[править | править код]
Функция распределения может быть выражена через регуляризованную неполную бета-функцию 
Для 
где
[10]
Для 
Другая формула верна для 
,
где 2F1 является частным случаем гипергеометрической функции.
Частные случаи[править | править код]
- Распределение Стьюдента с одной степенью свободы (
) это стандартное распределение Коши.
-
- Функция распределения:
- Плотность вероятности:
- Функция распределения:
- Распределение Стьюдента с двумя степенями свободы (
):
-
- Функция распределения:
- Плотность вероятности:
;
- Функция распределения:
- Распределение Стьюдента с тремя степенями свободы (
):
-
- Плотность вероятности:
- Плотность вероятности:
- Распределение Стьюдента с бесконечным числом степеней свободы (
):
-
- Плотность вероятности
- Плотность вероятности
совпадает с плотностью вероятности стандартного нормального распределения.
Свойства распределения Стьюдента[править | править код]
-
, если
нечётно;
, если
чётно. В частности,
Характеристики[править | править код]
Распределение Стьюдента с 

,
где
Пусть, 


– несмещённая оценка дисперсии.
Тогда случайная величина
имеет распределение хи-квадрат с 
Случайная величина 





Подставим получившиеся величины в величину
,
которая имеет распределение Стьюдента и отличается от 






Распределение статистики критерия 

Как возникает t-распределение[править | править код]
Выборочная дисперсия[править | править код]
Распределение Стьюдента возникает в связи с распределением выборочной дисперсии.
Пусть 



.
С этим фактом связано использование распределения Стьюдента в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего выборки из нормального распределения.
Байесовская статистика[править | править код]
В байесовской статистике, нецентральное t-распределение встречается как маргинальное распределение коэффициента 

Зависимость неизвестной дисперсии выражается через:
где 

Когда данные неинформативны из теоремы Байеса следует
нормальное распределение и масштабированное обратное хи-квадрат распределение, где
.
Маргинализованный интеграл в таком случае имеет вид
после замены 

получим 
и оценку 


это нестандартизированное t-распределение.
С помощью замены 
Дифференцирование выше было представлено для случая неинформативной априорной вероятности для 



Обобщения распределения Стьюдента[править | править код]
Нестандартизированное распределение Стьюдента[править | править код]
Распределение Стьюдента можно обобщить до семейства функций с тремя параметрами, включающими коэффициент сдвига 

или
,
где 

Плотность нестандартизированного распределения Стьюдента представляет собой репараметризованное распределение Пирсона типа VII и определяется следующим выражением[13]
Здесь 


В байесовском выводе предельное распределение неизвестного среднего значения 







Такое распределение является результатом комбинации распределения Гаусса (нормального распределения) со средним значением 


Эквивалентно, это распределение является результатом комбинации распределения Гаусса с масштабированным обратным хи-квадрат распределением с параметрами 


Альтернативная параметризация на основании обратного параметра масштабирования λ[14] (аналогично тому, как мера точности обратна дисперсии), определенная отношением 
тогда плотность определяется как
Свойства:





Это распределение является результатом комбинации распределения Гаусса со средним 


Нецентральное распределение Стьюдента[править | править код]
Нецентральное распределение Стьюдента, это один способов обобщения стандартного распределения Стьюдента, включающий дополнительный коэффициент сдвига (параметр нецентральности) 

В нецентральном распределении Стьюдента медиана не совпадает с модой, т.е. оно не симметрично (в отличие от нестандартизированного).
Это распределение важно для изучения статистической мощности t-критерия Стьюдента.
Дискретное распределение Стьюдента[править | править код]
Дискретное распределение Стьюдента имеет следующую функцию распределения с r пропорциональным:[15]
Где a, b, и k – параметры. Такое распределение возникает при работе с системами из дискретных распределений, таких как распределение Пирсона.[16]
Связь с другими распределениями[править | править код]
Обобщение распределения Гаусса[править | править код]
Мы можем получить выборку с t-распределением, взяв отношение величин из нормального распределения и квадратный корень из распределения хи-квадрат.
где 


Если мы вместо нормального распределения, возьмём например, Ирвин-Холл, получится симметричное распределение с 4 параметрами, которое включает в себя нормальное, равномерное, треугольное, а также распределения Стьюдента и Коши; таким образом, это обобщение более гибкое, чем многие другие симметричные обобщения распределения Гаусса.
Применение распределения Стьюдента[править | править код]
Проверка гипотезы[править | править код]
Некоторые статистики могут иметь распределение Стьюдента на выборках небольшого размера, поэтому распределение Стьюдента формирует основу критериев значимости. Например, тест ранговой корреляции Спирмена ρ, в нулевом случае (нулевая корреляция) хорошо аппроксимируется распределением Стьюдента при размере выборки больше 20.
Построение доверительного интервала[править | править код]
Распределение Стьюдента может быть использовано для оценки того, насколько вероятно, что истинное среднее находится в каком-либо заданном диапазоне.
Предположим, что число A выбрано так, что

Тогда T имеет t-распределение с n–1 степенями свободы. В силу симметрии распределения, это равноценно утверждению, что А удовлетворяет



что эквивалентно

таким образом, интервал с доверительным пределом в точках 
Такой подход применяется в t-критерии Стьюдента: если разность между средними значениями выборок из двух нормальных распределений сама может быть нормально распределена, распределение Стьюдента может быть использовано для исследования того, можно ли с большой долей вероятности полагать эту разность равной нулю.
Для нормально распределённых выборок односторонний (1−a) верхний доверительный предел (UCL) среднего значения равен

Полученный в результате верхний доверительный предел будет наибольшим средним значением для данного доверительного интервала и размера выборки. Другими словами, если 

Построение интервала-предиктора[править | править код]
Распределение Стьюдента может быть использовано для получения интервала-предиктора для ненаблюдаемой выборки из нормального распределения с неизвестным средним и дисперсией.
В байесовской статистике[править | править код]
Распределение Стьюдента, особенно нецентральное, часто возникает в байесовской статистике как результат связи с нормальным распределением.
Действительно, если нам неизвестна дисперсия нормально распределенной случайной величины, но известно сопряженное априорное распределение, можно будет подобрать такое гамма-распределение, что полученные в результате величины будут обладать распределением Стьюдента.
Эквивалентные конструкции с теми же результатами включают сопряжённое масштабированное обратное хи-квадратное распределение. Если некорректное априорное распределение, пропорциональное 
Параметрическое моделирование, устойчивое к нарушениям исходных предпосылок[править | править код]
Распределение Стьюдента часто используется в качестве альтернативы нормальному распределению для модели данных.[18] Это происходит из-за того, что довольно часто настоящие данные имеют более тяжелые хвосты, чем позволяет нормальное распределение. Классический подход заключается в определении выбросов и их исключении (или понижении их веса). Однако не всегда легко определить выброс (особенно в задачах с большой размерностью), и распределение Стьюдента является естественным выбором, обеспечивающим параметрический подход к робастной статистике.
Ланж и другие исследовали использование распределения Стьюдента для робастного (устойчивого к нарушениям исходных предпосылок) моделирования данных. Байесовский расчет обнаруживается у Гельмана и др.
Количество степеней свободы контролирует эксцесс распределения и коррелируется с параметром масштабирования.
Некоторые другие свойства распределения Стьюдента[править | править код]
Пусть, 

Функция 
Это используется например, в T-критерии Стьюдента. Для t-распределения с 


где Ix – регуляризированная неполная бета функция (a, b).
При статистической проверки гипотез эта функция используется для построения р-значения.
Выборка по методу Монте-Карло[править | править код]
Есть разные подходы к получению случайных величин из распределения Стьюдента. Всё зависит от того, требуются независимые выборки, или они могут быть построены путём применения обратной функции распределения над выборкой с однородным распределением.
В случае с независимой выборкой легко применить расширение метода Бокса-Мюллера в его полярной (тригонометрической) форме[19]. Преимущество этого метода в том, что он одинаково относится ко всем положительным степеням свободы 

Плотность распределения Стьюдента через решение дифференциального уравнения[править | править код]
Плотность распределения Стьюдента можно получить, решив следующее дифференциальное уравнение:

Процентили[править | править код]
Таблицы значений[править | править код]
Многие учебники по статистике включают в себя таблицы распределения Стьюдента.
В наши дни лучший способ узнать полностью точное критическое значение t или кумулятивную вероятность — это использование статистической функции, встроенной в электронные таблицы (Office Excel, OpenOffice Calc и т.д.), или интерактивного веб-калькулятора. Нужные функции электронных таблиц — TDIST и TINV.
Таблица ниже включает в себя значения некоторых значений для распределений Стьюдента с v степенями свободы для ряда односторонних или двусторонних критических областей.
В качестве примера того, как читать эту таблицу, возьмём четвёртый ряд, который начинается с 4; это означает, что v, количество степеней свободы, равно 4 (и если мы работаем, как это показано выше, с n величин с фиксированной суммой, то n = 5). Возьмём пятое значение в колонке 95% для односторонних(90% для двусторонних). Значение это равно “2.132”. Значит, вероятность, что T меньше 2.132 равна 95% или Pr(−∞ <T< 2.132) = 0.95; это также означает, что Pr(−2.132 <T< 2.132) = 0.9.
Это может быть вычислено по симметрии распределения,
- Pr(T < −2.132) = 1 − Pr(T > −2.132) = 1 − 0.95 = 0.05,
получаем
- Pr(−2.132 < T < 2.132) = 1 − 2(0.05) = 0.9.
Обратите внимание, что последний ряд также даёт критические точки: распределение Стьюдента с бесконечным количеством степеней – это нормальное распределение.
Первая колонка отображает число степеней свободы.
| односторонний | 75% | 80% | 85% | 90% | 95% | 97.5% | 99% | 99.5% | 99.75% | 99.9% | 99.95% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| двусторонний | 50% | 60% | 70% | 80% | 90% | 95% | 98% | 99% | 99.5% | 99.8% | 99.9% |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.080 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
| ∞ | 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
Например, если нам дана выборка с выборочной дисперсией 2 и выборочным средним 10, взятая из выборочного набора 11 (10 степеней свободы), используя формулу

Мы можем определить с 90% уровнем доверия, что истинное среднее таково:

(то есть, в среднем, в 90% случаев верхний предел превышает истинное среднее)
и, всё также с 90% уверенностью, мы находим истинное среднее значение, превышающее

(В среднем, в 90% случаев нижний предел меньше истинного среднего)
Так что с 80% уверенностью (1-2*(1-90%) = 80%), мы находим истинное значение, лежащее в интервале

Другими словами, в 80% случаев истинное среднее ниже верхнего предела и выше нижнего предела.
Это не эквивалентно утверждению, что с 80% вероятностью истинное среднее лежит между определенной парой верхних и нижних пределов.
Обобщение[править | править код]
Обобщением распределения Стьюдента является обобщённое гиперболическое распределение.
Примечания[править | править код]
- ↑ Helmert, F. R. (1875). “Über die Bestimmung des wahrscheinlichen Fehlers aus einer endlichen Anzahl wahrer Beobachtungsfehler”. Z. Math. Phys., 20, 300–3.
- ↑ Helmert, F. R. (1876a). “Über die Wahrscheinlichkeit der Potenzsummen der Beobachtungsfehler und uber einige damit in Zusammenhang stehende Fragen”. Z. Math. Phys., 21, 192–218.
- ↑ Helmert, F. R. (1876b). “Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers directer Beobachtungen gleicher Genauigkeit”, Astron. Nachr., 88, 113–32.
- ↑ Lüroth, J. Vergleichung von zwei Werten des wahrscheinlichen Fehlers (нем.) // Astron. Nachr. : magazin. — 1876. — Bd. 87, Nr. 14. — S. 209—220. — doi:10.1002/asna.18760871402. — Bibcode: 1876AN…..87..209L.
- ↑ Pfanzagl, J.; Sheynin, O. A forerunner of the t-distribution (Studies in the history of probability and statistics XLIV) (англ.) // Biometrika : journal. — 1996. — Vol. 83, no. 4. — P. 891—898. — doi:10.1093/biomet/83.4.891.
- ↑ Sheynin, O. Helmert’s work in the theory of errors (англ.) // Arch. Hist. Exact Sci. : journal. — 1995. — Vol. 49. — P. 73—104. — doi:10.1007/BF00374700.
- ↑ “Student” [William Sealy Gosset]. The probable error of a mean (англ.) // Biometrika : journal. — 1908. — March (vol. 6, no. 1). — P. 1—25. — doi:10.1093/biomet/6.1.1.
- ↑ “Student” (William Sealy Gosset), original Biometrika paper as a scan Архивная копия от 5 марта 2016 на Wayback Machine
- ↑ 1 2 Рональд Фишер. Applications of “Student’s” distribution (англ.) // metron. — 1925. — Vol. 5. — P. 90—104. Архивировано 5 марта 2016 года.
- ↑ 1 2 3 Johnson, N.L., Kotz, S., Balakrishnan, N. глава 28 // Continuous Univariate Distributions, Volume 2, 2nd Edition.. — 1995. — ISBN 0-471-58494-0.
- ↑ Hogg & Craig (1978, Sections 4.4 and 4.8.)
- ↑ W. G. Cochran. The distribution of quadratic forms in a normal system, with applications to the analysis of covariance // Mathematical Proceedings of the Cambridge Philosophical Society. — 1934-04-01. — Т. 30, вып. 02. — С. 178—191. — ISSN 1469-8064. — doi:10.1017/S0305004100016595.
- ↑ Simon Jackman. Bayesian Analysis for the Social Sciences. — Wiley. — 2009. — С. 507.
- ↑ Bishop C.M. Pattern recognition and machine learning. — Springer. — 2006.
- ↑ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (Table 5.1)
- ↑ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (Chapter 5)
- ↑ Королюк, 1985, с. 134.
- ↑ Kenneth L. Lange, Roderick J. A. Little, Jeremy M. G. Taylor. Robust Statistical Modeling Using the t Distribution // Journal of the American Statistical Association. — 1989-12-01. — Т. 84, вып. 408. — С. 881—896. — ISSN 0162-1459. — doi:10.1080/01621459.1989.10478852.
- ↑ 1 2 Ralph W. Bailey. Polar Generation of Random Variates with the t-Distribution // Mathematics of Computation. — 1994-01-01. — Т. 62, вып. 206. — С. 779—781. — doi:10.2307/2153537. Архивировано 3 апреля 2016 года.
Литература[править | править код]
- Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).
Распределение Стьюдента
Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ2. Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией
![]()
Тогда случайная величина
![]()
имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.
Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:
![]()
где
![]()
Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96sx̅. Другими словами, являются ли распределения случайных величин
![]()
и
![]()
эквивалентными.
Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.
Собрав математическое обоснование и рассчитав значения функции обнаруженного им распределения, химик из Дублина Уильям Госсет написал заметку, которая была опубликована в мартовском выпуске 1908 года журнала «Биометрика» (главред – Карл Пирсон). Гиннесс строго-настрого запретил выдавать секреты пивоварения, и Госсет подписался псевдонимом Стьюдент.
Несмотря на то что, К. Пирсон уже изобрел распределение Хи-квадрат, все-таки всеобщее представление о нормальности еще доминировало. Никто не собирался думать, что распределение выборочных оценок может быть не нормальным. Поэтому статья У. Госсета осталась практически не замеченной и забытой. И только Рональд Фишер по достоинству оценил открытие Госсета. Фишер использовал новое распределение в своих работах и дал ему название t-распределение Стьюдента. Критерий для проверки гипотез, соответственно, стал t-критерием Стьюдента. Так произошла «революция» в статистике, которая шагнула в эру анализа выборочных данных. Это был краткий экскурс в историю.
Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:
![]()
Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.
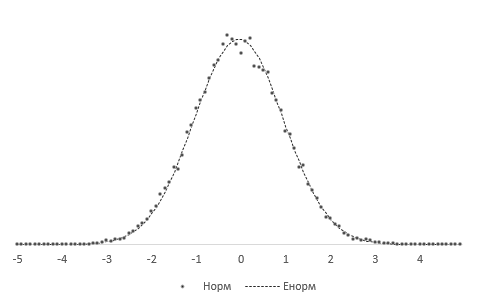
Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.
Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.
![]()
Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.
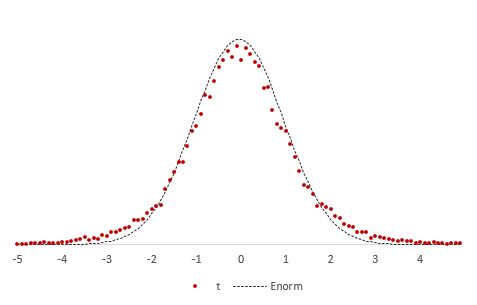
Видно, что распределения на этот раз не очень-то и совпадают. Близки, да, но не одинаковы. Хвосты стали более «тяжелыми».
У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина
![]()
зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.
Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:
1. средняя X̅ и выборочная дисперсия s2 являются независимыми величинами;
2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ2(хи-квадрат) с таким же количеством степеней свободы, т.е.
![]()
где k – количество степеней свободы (на английском degrees of freedom (d.f.))
Вернемся к распределению средней. Разделим числитель и знаменатель выражения
![]()
на σX̅. Получим
![]()
Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.
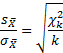
Тогда исходное выражение примет вид
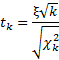
Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.
Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.
Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин
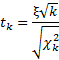
где ξ распределена по стандартному нормальному закону, а χ2k подчиняется распределению χ2 c k степенями свободы.
Таким образом, формула критерия Стьюдента для средней арифметической
![]()
есть частный случай стьюдентова отношения
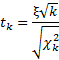
Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.
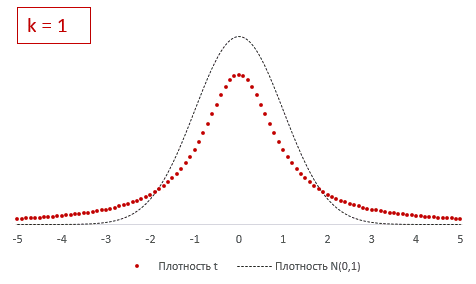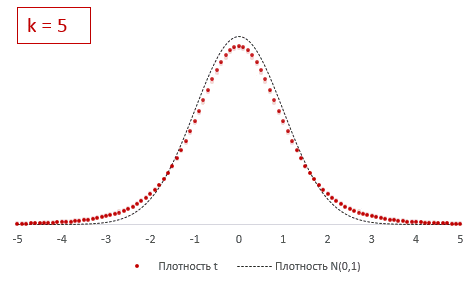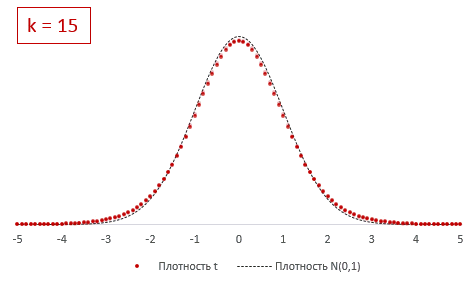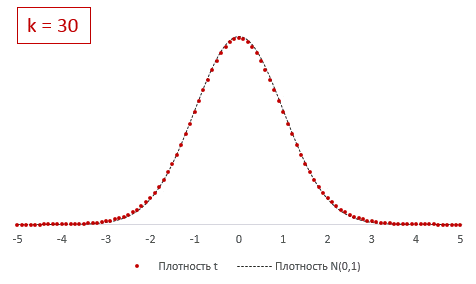
При k > 30 t-критерий практически не отличается от стандартного нормального распределения.
В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.
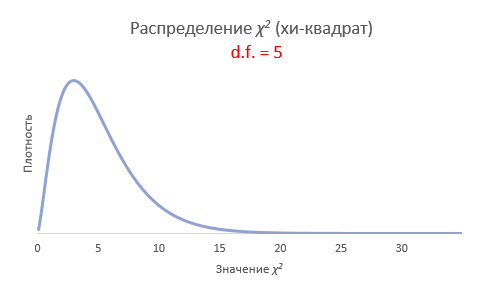
Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
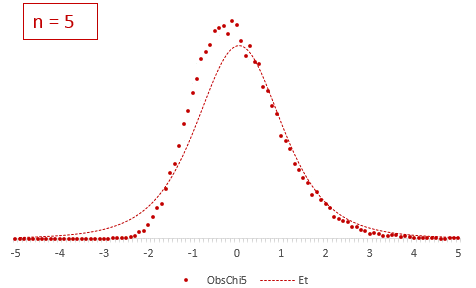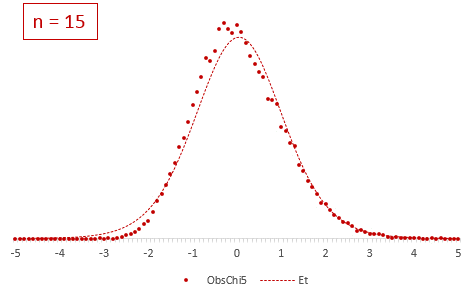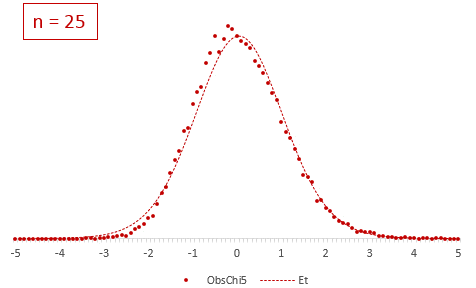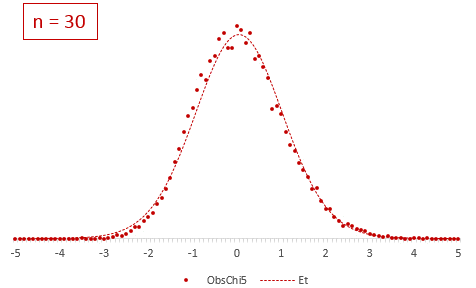
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.
Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.
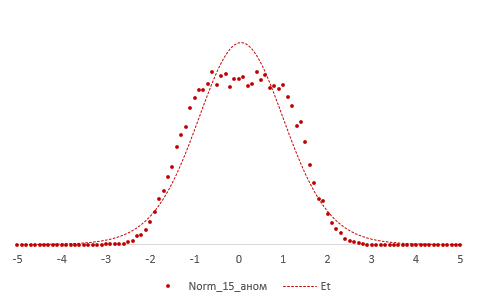
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel
В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.
СТЬЮДЕНТ.РАСП – «классическое» левостороннее t-распределение Стьюдента. На вход подается значение t-критерия, количество степеней свободы и опция (0 или 1), определяющая, что нужно рассчитать: плотность или значение функции. На выходе получаем, соответственно, плотность или вероятность того, что случайная величина окажется меньше указанного в аргументе t-критерия, т.е. левосторонний p-value.
СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).
СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.
СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.
СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058
СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.
ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.
Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.
Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.
Краткое условие в обще принятых обозначениях выглядит так.
H0: μ = 50 кг
Ha: μ ≠ 50 кг
Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.
Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:
![]()
Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).
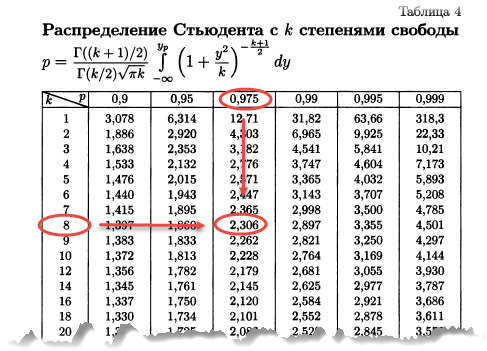
По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.
Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H0 о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.
Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.
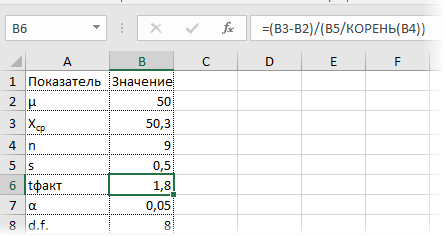
Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.
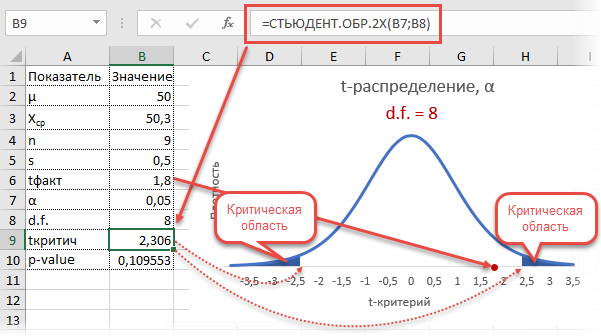
Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.
Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.
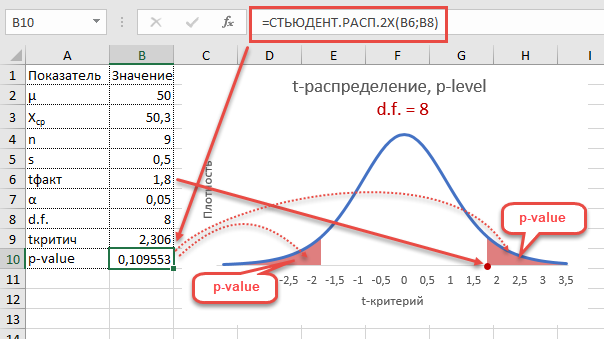
P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.
Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.
Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.
![]()
Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.
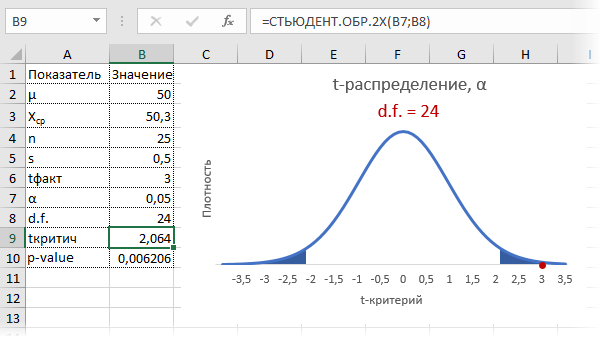
Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.
Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel
С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.
Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.
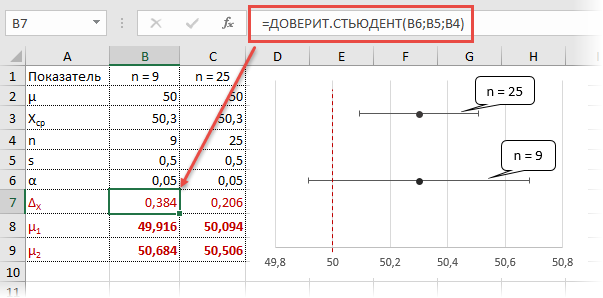
Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.
Таким образом, мы решили одну и ту же задачу тремя способами:
1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.
Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.
Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.
Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.
Скачать файл с примером.
Всего доброго, будьте здоровы.
Поделиться в социальных сетях:
![{begin{matrix}{frac {n+1}{2}}left[psi ({frac {1+n}{2}})-psi ({frac {n}{2}})right]\[0.5em]+log {left[{sqrt {n}}B({frac {n}{2}},{frac {1}{2}})right]}end{matrix}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd3fdc61973f68042141bd52ef3b36cd233e8a0)

























