Тип лекции: ключевая; Время чтения: 15 минут;
Цель: понять, что такое дробь, где применяется и как с ней работать.
Узнаем, что такое наибольший общий делитель, наименьшее общее кратное и применяется. Обсудим, почему при делении на дробь её нужно перевернуть и умножить, а также почему при делении на 0 получается бесконечность. Разберем пару простых задач на процент и как решать их в одно действие.
Что такое дробь
В лекции про числа обсуждали, что существуют исчисляемые предметы, такие как дом, автомобиль, велосипед и другие. При делении этих предметов они теряют свои свойства: автомобиль без колес не поедет, а жить в доме без крыши – некомфортно. С другой стороны существуют неисчисляемые предметы, которые не потеряют свои свойства при делении: вода, воздух, пицца, молоко и очарование =)
Дроби – способ описать части неисчисляемого предмета.
Возьмем пиццу, пицца – неисчисляемый предмет, потому что ее можно разделить на кусочки и каждый кусочек будет обладать вкусом.
Например, пицца – состоит из 8 кусочков, 1 кусочек забрали, как описать это на языке математики?
Пицца – это 7/8, где 8 – сколько кусочков в целом предмете, 7 – сколько кусочков сейчас.
Дробь – это другая запись деления, имеет тот же смысл.
Определение дроби
Дробь – это запись из двух чисел, разделенных чертой. Верхнее число называют числителем, нижнее – знаменателем. Это понадобится, чтобы понимать математические определения.
Обратите внимание, что знаменатель не может быть равен нулю, мы поговорим об этом ниже, на самом деле делить на 0 можно и это будет равно бесконечности. Если можно делить на 0, значит может быть и дробь со знаменателем 0.
Читается дробь как “числитель знаменательных”: 3/4 – “три четвертых”; 2/3 – “две третьих”; 1/2 – “одна вторая” и т.д.
Дробь можно представить в виде круга поделенного на сектора: нижнее число (знаменатель) показывает на сколько секторов поделен целый круг, верхнее число (числитель) показывает сколько секторов круга взяли.
Обратите внимание, когда числитель больше знаменателя, значит взяли больше чем 1 круг. Здесь подошли к понятию правильной и неправильной дроби.
Дроби бывают правильные и неправильные.
Правильные дроби – в которых знаменатель больше числителя.
Неправильные дроби – в которых числитель больше знаменателя. Неправильная дробь выражает число больше единицы и ее можно представить в виде правильной дроби, для этого нужно вычислить целую часть, а остаток представить в виде дроби.
Действия с дробями
Дроби можно преобразовывать в разный вид, это нужно для того, чтобы сравнивать и складывать их. Преобразование дроби строится на свойствах умножения и деления: a × 1 = a; b/b = 1;
Сначала возьмем свойство a × 1 = a, вместо а подставим дробь 2/3, потому а – это переменная и можно подставить вместо нее все что угодно, получим: 2/3 × 1 = 2/3.
Теперь вместо 1 подставим деление любого числа самого на себя, для начала возьмем 2/2; 1 = 2/2;
Подставим в выражение: 2/3 × 2/2 = 2/3; Пока от такой записи мало пользы, но что если 2/2 представить в виде действий умножения и деления?
2/3 × 2 ÷ 2;
Разберемся сначала с умножением: 2/3 × 2 – то есть у нас есть 2 части, неважно третьих или автомобиля, просто две каких то части, что будет, когда мы возьмем их дважды? Будет 4 части, в нашем случае 4 третьих части: 2/3 × 2 = 4/3;
Теперь поговорим о делении: в выражении осталось 4/3 ÷ 2; Не важно что, что-то разделили на 3 части, а затем каждую получившуюся часть разбили еще на 2 части, то есть всего получилось 6 частей. Отсюда 4/3 ÷ 2 = 4/6;
Именно отсюда следует закон: при умножении дробей числители перемножаются и знаменатели перемножаются. Чуть ниже мы покажем как это выглядит графически, пока продолжим разговор про преобразование дробей.
Выражение 2/3 × 2/2 = 2/3 можно представить как 2/3 × 2/2 = 4/6;
То есть 2/3 = 4/6; Это одно и то же количество, просто представленное разными размерами кусочков. Ниже можно наглядно рассмотреть, как происходит изменение размера кусочков при умножении на разные числа.
Умножение дробей
Выше мы разобрали, почему при перемножении дробей числители перемножаются между собой и знаменатели перемножаются между собой. Графически умножение дробей можно представить так:
Вот так выглядит неполное преобразование или умножение дробей.
Сложение и сравнение дробей
Дробь – это части, чтобы их сравнить или сложить, нужно привести их к одинаковому размеру: “привести к общему знаменателю”
Выше разбирали, как происходит изменение размеров дробей. Технически нужно числитель и знаменатель одной дроби умножить на знаменатель другой дроби и наоборот. Так дроби будут состоять из одинаковых частей. Когда получили части одинакового размера, их легко можно складывать, вычитать и сравнивать.
Есть проблема, если попытаться сложить 1/231 и 1/84 получатся громоздкие, неудобные числа:
1/231 + 1/84 = ?;
1/231 × 84/84 = 84/19404;
1/84 × 231/231 = 231/19404;
84/19404 + 231/19404 = 315/25200;
Но можно проще:
1/231 + 1/84 = 4/924 + 11/924 = 15/924 = 5/308;
Это возможно благодаря наибольшему общему делителю (НОД) и наименьшему общему кратному (НОК), о них мы поговорим ниже.
Наибольший общий делитель (НОД) и Наименьшее общее кратное (НОК)
Все целые числа подразделяются на простые числа и составные числа.
Простые числа – делятся только на самих себя и на единицу: 2, 3, 5, 7, 11, 13 и так далее. Нет конца простым числам, они нам нужны для поиска НОД и НОК, но также участвуют в алгоритмах генерации псевдослучайных чисел, в алгоритмах шифрования.
Составные числа – получаются путем перемножения простых чисел.
Чтобы найти НОД и НОК, нужно разложить числа на множители.
Как раскладывать на множители
Возьмем дробь 84/231, до этого мы преобразовывали дроби в сторону увеличения числителя и знаменателя, но как преобразовать дробь в сторону уменьшения числителя и знаменателя? В этом поможет наибольший общий делитель.
Нужно разложить на множители все интересующие нас числа: 84 и 231. Поочередно делим число на простые числа. Если не делится без остатка, берем следующее простое число, иначе использованное простое число – множитель нашего числа. Результат деления по этому же механизму делим на простые числа.
Разложим 84 на множители:
- 84 делится на 2? – да, добавляем 2 в список множителей. 84 ÷ 2 = 42;
- 42 делится на 2? – да, добавляем 2 в список множителей. 42 ÷ 2 = 21;
- 21 делится на 2? – нет, на 3? – да, добавляем 3 в список множителей.
21 ÷ 3 = 7; - 7 – это простое число, то есть делится только само на себя и на единицу. Добавляем 7 в список множителей и завершаем.
Получилось: 84 = 2 × 2 × 3 × 7;
Разложим 231 на множители:
- 231 делится на 2? – нет, на 3? – да, добавляем 3 в список множителей.
231 ÷ 3 = 77; - 77 делится на 2? – нет, на 3? – нет, на 5? – нет, на 7? – да, добавляем 7 в список множителей. 77 ÷ 7 = 11;
- 11 – это простое число, то есть делится только само на себя и на единицу. Добавляем 11 в список множителей и завершаем.
Получилось: 231 = 3 × 7 × 11;
Даже большие числа без труда раскладываются на множители.
Как найти НОД на основе множителей
Наибольший общий делитель – самое больше число, которое без остатка поделит указанные числа.
Технически НОД – это произведение общих множителей.
231 = 3 × 7 × 11; 84 = 2 × 2 × 3 × 7; Общие множители: 3 и 7;
НОД(84, 231) = 3 × 7 = 21;
Графически это выглядит так:
Как найти НОК на основе множителей
НОК – это произведение всех множителей, но общие множители берутся единожды.
Хотим сложить две дроби: 1/231 и 1/84, нужно найти общий знаменатель. Для этого возьмем наименьшее число, которое делится на оба знаменателя. Точнее возьмем наименьшее общее кратное.
231 = 3 × 7 × 11; 84 = 2 × 2 × 3 × 7; Общие множители: 3 и 7, значит их возьмем только единожды;
НОК(84, 231) = 3 × 7 × 2 × 2 × 11 = 924;
Каждую дробь умножим на множители, которых нет в текущем числе, но есть в другом числе.
Графически это выглядит так:
НОД и НОК – это инструменты для преобразования дробей. Однако это не единственная область применения.
Почему при делении дробь переворачивается
Существует 2 объяснения.
Графический способ
Деление можно представить в виде вопроса: “если разобьем по столько то, сколько получим”.
Например, возьмем число 6, если разобьем
- по 3 кусочка, получим 2 части;
- по 2 кусочка, получим 3 части;
- по 1 кусочку, получим 6 частей;
- по половинке кусочка (1/2), получим 12 частей; то есть в 2 раза больше, чем изначальное число (6), или 6 ÷ 1/2 = 6 × 2;
Переформулирование вопроса
Действие это вопрос, помните? Сколько будет если число разделить на другое число, например 6 ÷ 3; Здесь ответ очевиден: 2.
Но здесь 6 ÷ 1/2 неочевидно, что должно получиться. Давайте переформулируем вопрос: сколько раз нужно взять половинку (1/2), чтобы получилось 6?
1/2 × ? = 6; Теперь ответ очевиден: 12
Вспоминайте взаимосвязь умножения и деления из лекции про базовые математические операции и их свойства
Почему на 0 делить нельзя или почему при делении на 0 получается бесконечность?
Результат неочевиден: 1 ÷ 0 = ? Можно делить единицу на числа приближающиеся к нулю и заметить закономерность.
Для начала возьмем число меньше единицы, например 1/10:
1 ÷ 1/10 дробь при делении переворачивается 1 × 10/1 = 10;
- 1/100:
1 ÷ 1/100 → 1 × 100/1 = 100; - 1/1000:
1 ÷ 1/1000 → 1 × 1000/1 = 1000; - 1/10000:
1 ÷ 1/10000 → 1 × 10000/1 = 10000;
Закономерность очевидна: чем меньше число, на которое делим, тем больше результат, потому при делении на 0, результат будет где-то невообразимо далеко.
Процент и промилле
Процент и промилле – это те же дроби и они подчиняются тем же правилам, что и обычные дроби.
Один процент (%) – это 1/100;
Один промилле (‰) – это 1/1000;
Задачи на процент
Разберем пару задач с использованием процентов.
Задача 1. Сколько процентов от прибыли
Прибыль компании за неделю 180 000 рублей, а за день составила 28 800 рублей, сколько процентов от прибыли в неделю сделали за день.
- Надо узнать сколько составляет 1%: 180 000 – это то, с чем сравниваем, значит это 100%. 1% = 180 000/100 = 1 800.
- Нужно целевую сумму (28 800) разделить на размер 1%, чтобы узнать сколько процентов в этой сумме: 28 800 / 1% = 28 800 / 1 800 = 16%
Ответ: 28 800 это 16% от 180 000
Запишем в одно действие:
28 800 ÷ (180 000 / 100) = 28 800 × 100 / 180 000 = 28 800 / 180 000 × 100;
Можно отбросить × 100 и получим 28 800 ÷ 180 000 = 0,16
0,16 – это называют процентом в виде доли.
Таким образом задача на процент сократилась до одного действия.
Задача 2. Сколько прибыли по проценту
На счете в банке 12 334 рублей, за год банк выплатил 11,4% от суммы счета. Каков размер счета на конец года?
- Узнаем сколько составляет 1%: 12 334 / 100 = 123,34
- Умножим сумму одного процента на размер выплаты в %:
123,34 × 11,4% = 1 406,07 - Прибавляем сумму на начало года и сумму процентов:
12 334 + 1 406,07 = 13 740,07
Ответ: 12 334 + 11,4% = 13 740,07
Запишем в одно действие:
12 334 + 12 334 / 100 × 1,4; создадим скобку:
12 334 + 12 334 / 100 × 1,4 = 1 (12 334+ 12 334 / 100 × 1,4);
вынесем 12 334 за скобку:
1 (12 334 + 12 334 / 100 × 1,4) = 12 334 (1 + 1/100 × 1,4) =
12 334 (1 + 1,4/100) = 12 334 (1 + 0,014) =
12 334 × 1,014
Снова пришли к решению в одно действие.
Закономерность: чтобы узнать результат после увеличения числа на %, достаточно число × (1 + % в виде доли):
100 увеличили на 24% = 100 × (1 + 0,24) = 100 × 1,24 = 124;
100 увеличили на 5% = 100 × (1 + 0,05) = 100 × 1,05 = 105;
100 увеличили на 275% = 100 × (1 + 2,75) = 100 × 3,75 = 375;
Закономерность: чтобы узнать результат после уменьшения числа на %, достаточно число × (1 – % в виде доли):
100 уменьшили на 24% = 100 × (1 – 0,24) = 100 × 0,76 = 76;
100 уменьшили на 5% = 100 × (1 – 0,05) = 100 × 0,95 = 95;
100 уменьшили на 54% = 100 × (1 – 0,54) = 100 × 0,46 = 46;
Задача 3. С подвохом
Товар стоит 100 рублей, накрутка продавца составляет 15%. Сколько процентов составила накрутка от результирующей стоимости товара?
Важный момент: процент берется от какой-то величины, вначале это
100 рублей, то есть результирующая стоимость товара по закономерностям из предыдущих задач: 100 × (1 + 0,15) = 100 × 1,15 = 115;
А накрутка 15% = 100 × 0,15 = 15 рублей.
Сколько процентов составила накрутка от результирующей стоимости товара?
15 / 115 ≈ 0,13 = 13%
Ответ: накрутка от результирующей стоимости товара составила 13%
Вывод
Процент и промилле – это те же дроби и они подчиняются тем же правилам, что и обычные дроби.
Многие задачи можно решать в одно действие, достаточно представить процент в виде доли.
Процент и промилле можно выразить в виде доли:
например, 45% (45 процентов) – это 0,45, а 45‰ (45 промилле) – это 0,045.
Заключение
Дроби – способ описать части неисчисляемого предмета. Технически, дробь – это запись из двух чисел, разделенных чертой. Верхнее число называют числителем, нижнее – знаменателем. Это понадобится, чтобы понимать математические определения. Знаменатель – это размер частей, числитель – количество частей.
Правильные дроби – в которых знаменатель больше числителя.
Неправильные дроби – в которых числитель больше знаменателя.
Дробь – это части, чтобы их сравнить или сложить, нужно привести их к одинаковому размеру: “привести к общему знаменателю”.
Умножение дробей можно представить в виде поочередных операций умножения и деления. При делении на дробь ее нужно перевернуть и умножить на получившуюся дробь.
Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) – инструменты для преобразования дробей. Чтобы найти НОД и НОК, нужно разложить число на простые множители.
Простые числа – делятся только на самих себя и на единицу.
Составные числа – получаются путем перемножения простых чисел.
Процент и промилле – это те же дроби и они подчиняются тем же правилам, что и обычные дроби.
Один процент (%) – это 1/100;
Один промилле (‰) – это 1/1000;
Если есть вопросы, задавайте в комментариях. Ставьте палец вверх, если понравилось.
Копирование приветствуется и вознаграждается по закону кармы. Пусть знания будут доступны каждому человеку.
Фото автора Polina Tankilevitch: Pexels
#математика просто #математика #дроби #наибольший общий делитель #нод #наименьшее общее кратное #нок #сложение дробей #умножение дробей #деление дробей
Деление дробей онлайн
Чтобы разделить дробь на дробь нужно умножить первую дробь на дробь обратную второй.
Правила деления дробей
Чтобы разделить дробь на дробь, нужно делимое умножить на дробь обратную делителю
Как делить обыкновенные дроби
Чтобы разделить обыкновенную дробь на обыкновенную дробь, нужно вторую дробь сделать обратной затем умножить на вторую дробь по правилам умножения дробей.
Разберём пример: разделим дробь 1/4 на 1/3. Для этого развернём вторую дробь 3/1. Получится выражение 1/4 × 3/1. Перемножим числители 1 × 3 = 3 и знаменатели 4 × 1 = 4 в итоге у нас получится дробь 3/4
Как разделить натуральное число на дробь
Чтобы разделить натуральное число на дробь, нужно сделать дробь обратной. Числитель обратной дроби умножить на натуральное число а знаменатель обратной дроби останется без изменения.
Как разделить смешанную дробь на целое число
Чтобы разделить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем целое число представить в виде обратной дроби и умножить на неправильную дробь. После чего выполнить умножение обыкновенных дробей.
Разберём пример: разделим смешанную дробь 3 целые 3/4 на целое число 7.
Перед делением нужно смешанную дробь перевести в неправильную 3 целые 3/4 = 15/4. Представим целое число в виде обратной дроби7 это 1/7. Умножим дроби 15/4 и 1/7. Перемножим числители 15*1 = 15, перемножим знаменатели4*7 = 28
Как разделить смешанную дробь на смешанную дробь
Для деления смешанной дроби ра смешанную дробь нужно обе дроби представить в виде неправильных. Затем вторую дробь преобразовать в обратную. После чего перемножить обе дроби по правилам умножения обыкновенных дробей.
Разберём пример: разделим смешанную дробь 2 целые 3/5 на смешанную дробь 3 целые 1/2
Преобразуем обе дроби в неправильные
Развернём вторую дробь и изменим знак деления на умножение
Перемножим дроби по правилам умножения обыкновенных дробей
Похожие калькуляторы
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя – верхней части, и знаменателя – нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 1114, 1714, 914 имеют одинаковый знаменатель 14. Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 45 и 34 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 45 на 4, а числитель и знаменатель дроби 34 умножим на 5. Вместо дробей 45 и 34 получим соответственно 1620 и 1520.
Приведение дробей к общему знаменателю – это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель дробей – это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 16 и 35. Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5. Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Можно ди дроби 13, 216, 512 привести к общему знаменателю, который равен 150?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3, 6, 12. Другими словами, число 150 должно без остатка делиться на 3, 6, 12. Проверим:
150÷3=50, 150÷6=25, 150÷12=12,5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель дробей – это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел – это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Нужно найти наименьший общий знаменатель для дробей 110 и 12728.
Ищем НОК чисел 10 и 28. Разложим их на простые множители и получим:
10=2·528=2·2·7НОК(15, 28)=2·2·5·7=140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Есть дроби 314 и 518. Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14=2·718=2·3·3НОК(14, 18)=2·3·3·7=126
Вычисляем дополнительные множители для каждой дроби. Для 314 дополнительный множитель находится как 126÷14=9, а для дроби 518 дополнительный множитель будет равен 126÷18=7.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3·914·9=27126, 5·718·7=35126.
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Привести дроби 32, 56,38 и 1718 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
НОК(2, 6)=6НОК(6, 8)=24НОК(24, 18)=72НОК(2, 6, 8, 18)=72
Далее вычислим дополнительные множители для каждой дроби.
Для 32 дополнительный множитель равен 72÷2= 36, для 56 дополнительный множитель равен 72÷6= 12, для 38 дополнительный множитель равен 72÷8= 9, наконец, для 1718 дополнительный множитель равен 72÷18= 4.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
32·36=1087256·12=607238·9=27721718·4=6872
Как привести дробь к наименьшему общему знаменателю (пример)

![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание
- Как решать дроби. Решение дробей.
- Как решать дроби. Примеры.
- Приведение дроби к общему знаменателю
- Обыкновенные дроби
- Доля целого
- Понятие дроби
- Как устроена обыкновенная дробь
- Как устроена десятичная дробь
- Свойства дробей
- Действия с дробями
- Сравнение дробей
- Сокращение дробей
- Сложение и вычитание дробей
- Умножение и деление дробей
Как решать дроби. Решение дробей.
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
Дроби имеют вид : ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.
- Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
- Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
- Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.
Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20 Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Должна признаться, что решать дроби — это мое самое любимое математическое действие. Это тема, которую я понимаю без вопросов. Можно сказать, хлебом не корми, дай только дроби порешать )))
Дроби я тоже люблю. Умножать и делить их — милое дело. Вообще мне кажется, что с решением дробей мало у кого могут быть проблемы, потому что все довольно просто. Есть в математике огромное количество гораздо более сложных вещей, чем дроби решать.
Я вообще не умею решать дроби, но понятие немного есть. И поэтому стараюсь как можно скорее научиться решать дроби как дважды два четыре. Мне легче с формулами сложные примеры решить чем решать дроби!
говорит та самая красотка которая не навидит дроби
Источник
Обыкновенные дроби

О чем эта статья:
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Виды дробей:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 — 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x — y). Значение дроби зависит от данных значений букв.
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
 где a, b, k — натуральные числа.
где a, b, k — натуральные числа.
- Дробь не имеет значения, при условии, если делитель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
- Приведем дроби к общему знаменателю:
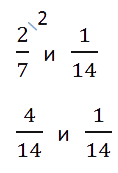
- Сравним дроби с одинаковыми знаменателями:
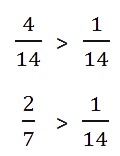
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю (НОЗ);
- сравнить полученные дроби.
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
- Найдем наименьшее общее кратное для определения единого делителя.
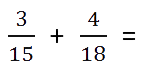
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
Полученные числа запишем справа сверху над числителем.
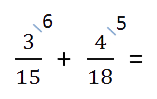
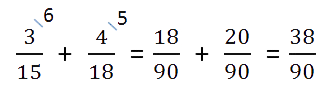
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
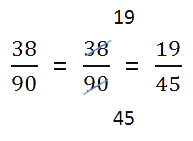
Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
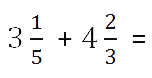
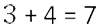
- Сложить дробные части.
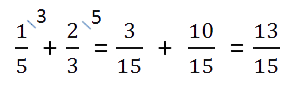
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
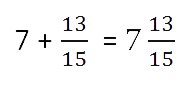
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
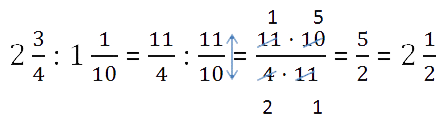
Источник
Adblock
detector
Это правило позволяет легко и быстро устно найти наименьший общий знаменатель дробей.
Правило нахождения наименьшего общего знаменателя для двух или нескольких дробей:
1) Выбираем из всех знаменателей наибольшее число и проверяем, делится ли оно на остальные. Если делится, то это число и есть наименьший общий знаменатель (НОЗ) этих дробей.
2) Если наибольший знаменатель не делится на все остальные, умножаем его на 2 и проверяем, делится ли полученное число на все остальные. Если делится, то это новое число и есть НОЗ.
3) Если после умножения на два новое число не делится на все остальные, наибольший из знаменателей умножаем на 3,4,5 и так далее до тех пор, пока новое число не будет делиться на все остальные. Это новое число и есть наименьший общий знаменатель.
Примеры.
Найти общий знаменатель дробей:
![]()
Выбираем бОльший знаменатель и проверяем, делится ли он на меньший. 12 на 4 делится. Значит, наименьший общий знаменатель этих дробей равен 12.
![]()
Выбираем больший знаменатель и проверяем, делится ли он на меньший. 15 на 10 не делится. Умножаем бОльший знаменатель на 2 и проверяем, делится ли новое число на меньший знаменатель. 15∙2=30, 30 на 10 делится. Значит, наименьший общий знаменатель этих дробей равен 30.
![]()
Выбираем большее число и проверяем, делится ли оно на остальные. 20 на 15 и 12 не делится. Большее число умножаем на 2 и проверяем, делится ли новое число на остальные. 20∙2=40. 40 на 15 и 12 не делится. Значит, большее число 20 надо умножить на 3 и проверить, будет ли делиться результат на остальные. 20∙3=60. 60 делится и на 15, и на 12. Поэтому 60 — наименьший общий знаменатель этих дробей.
![]()
Большее — 18. Оно не делится на меньшее — 15. Умножаем большее на 2: 18∙2=36. 36 на 15 не делится. Умножаем большее на 3: 18 ∙3=54. 54 на 15 не делится. Умножаем большее на 4: 18∙4=72. 72 на 15 не делится. Умножаем большее на 5: 18∙5=90. 90 на 15 делится. Значит, наименьший общий знаменатель этих дробей равен 90.
В следующий раз мы посмотрим, как это правило применять при сложении и вычитании дробей с разными знаменателями.
