Математика
5 класс
Урок №80
Представление дробей на координатном луче
Перечень рассматриваемых вопросов
– изображение дробей на координатном луче;
– запись координаты дроби;
– решение текстовых задач с опорой на смысл понятия координаты числа;
– применение дроби для выражения единиц измерения длины, массы, времени в более крупных единицах.
Тезаурус
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Координатная ось – это прямая, с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта.
Координата данной точки – это число, которое соответствует данной точке на координатной оси.
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Обязательная литература
1. Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС//С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямую с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта называют координатным лучом.
Начало отсчёта – точка 0.
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Координатный луч обычно располагают горизонтально и направляют вправо.
На координатном луче можно изобразить дробь.
Изобразим дробь 
Для этого единичный отрезок разделим на q частей.
Возьмём  часть и отложим p раз на координатном луче от точки 0.
часть и отложим p раз на координатном луче от точки 0.

Точку, изображающую на координатном луче дробь p/q, называют точкой с координатой p/q или короче – точкой p/q
Например, точка А имеет координату три пятых. Пишем A (3/5).
Точка В имеет координату семь пятых, выраженную неправильной дробью или одна целая две пятых, выраженную смешанным числом. Пишем В (7/8) или В(1 2/5)

Положительные дроби называют ещё положительными рациональными числами, а точки, изображающие их на луче, называют положительными рациональными точками.
3/5, 7/5,1 2/5 – положительные дроби, или положительные рациональные числа.

Если а и с – два положительных рациональных числа и с > a, то:
- точка c на координатном луче находится правее точки а;
- расстояние между точками а и c равно c – а;
- точка (a + c) : 2 является серединой отрезка, соединяющего точки а и с.

Докажем, что точка (a + c) : 2 является серединой отрезка, соединяющего точки а и с:

Рассмотрим задачу.
Найдём длину отрезка, соединяющего точки:

и с = 1, и координату середины этого отрезка.

Решение
3/7 < 1, поэтому точка 1 находится правее 3/7.
Значит, длина отрезка, соединяющего точки а и с, равна:

Середина этого отрезка будет иметь координату:

Таким способом можно вычислить координату середины отрезка, соединяющего любые две рациональные точки.
Т. е. между любыми двумя рациональными точками находится ещё хотя бы одна рациональная точка.
Число (a + c) : 2 называется средним арифметическим чисел а и с.
Например:

Если необходимо вычислить среднее арифметическое нескольких чисел, нужно найти частное от деления суммы этих чисел на число слагаемых.
Например:

Рассмотрим, как применять дроби для выражения единиц измерения длины, массы и времени в более крупных единицах.
Известно, что для измерения массы используют единицы измерения: граммы, килограммы, центнеры, тонны. Если масса тела небольшая, используют г или кг. Если тело более крупное, то массу измеряют в тоннах.
Мы знаем, что 1 кг = 1000 г. А как узнать, сколько килограмм в грамме? Для этого нужно один разделить на тысячу, получим одну тысячную, т. е. в одном грамме содержится одна тысячная килограмма.

Рассмотрим единицы измерения времени. Время измеряют в секундах, минутах, часах. Вы знаете, что в одном часе шестьдесят минут, следовательно, минута будет равна одной шестидесятой часа.


Рассмотрим единицы измерения длины.
Длину измеряют в метрах, километрах, сантиметрах.

Тренировочные задания
№ 1. Подставьте к изображению координаты середин отрезков АВ, ВС и СК.

Варианты ответов:
Координаты середины отрезка определяются по формуле (a + c) : 2, где а и с – координаты концов отрезка.
Найдём середину отрезка АВ. Для этого сложим координаты точки А и В, поделим на два и получим:

Значит, 1 – это середина отрезка АВ.
Найдём середину ВС. Для этого сложим координаты точки В и С, поделим на два и получим:

Значит, 2 – это середина отрезка ВС.
Найдём середину СК. Для этого сложим координаты точки С и К, поделим на два и получим:

Значит, 3 – это середина отрезка СК.
№ 2. Найдите среднее арифметическое чисел 11, 14 и 17. В ответе напишите только число: __
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
У нас три слагаемых, значит, сложим числа 11, 14 и 17 и полученную сумму разделим на 3.
(11 + 14 + 17) : 3 = 42 : 3 = 14
Правильный ответ:14.
Также, как и на координатном луче, изображение дроби на координатной прямой начинается с выбора единичного отрезка.
Самый удобный вариант — единичный отрезок взять из такого количества клеточек, каков знаменатель дроби.
Например, требуется на координатной прямой отметить точки, координаты которых — смешанные числа и дроби со знаменателем 3. В качестве единичного берем отрезок длиной три клеточки. В этом случае одна клеточка соответствует дроби 1/3, две клеточки — 2/3, а три клеточки — 1.
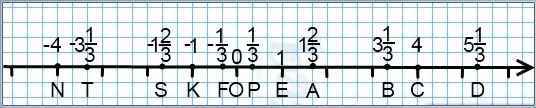
![]()
![]()
Если требуется изобразить на координатной прямой дроби со знаменателем 4, удобно в качестве единичного взять отрезок длиной 4 клеточки:
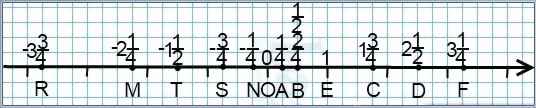
![]()
![]()
![]()
Если знаменатель равен 6, для изображения дроби на координатной прямой берем единичный отрезок длиной шесть клеточек:
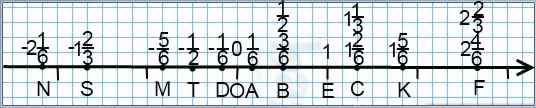
![]()
![]()
![]()
Причем в этом случае удобно изображать не только дроби со знаменателем 6, но также дроби со знаменателем 3 и 2 (так как в этом случае 6 — их наименьший общий знаменатель).
Для изображения дроби на координатной прямой:
1) разбиваем единичный отрезок на столько частей, каков знаменатель;
2) берем из них столько частей, каков числитель.
You can graph a fraction in three different ways. The first is if you need to find out where a fraction exists on a number line; the second is if you’re graphing coordinates that have fractional values. If you’ve ever read a ruler, you already have an intuitive grasp of the concepts you’ll need for those two missions. The third option is when you’re using slope, which is usually expressed as a fraction, to draw the graph of a line. If you’ve already mastered basic graphing, you already know everything you need for that particular challenge.
Graphing Fractions on a Number Line
Graphing or drawing fractions in the right place on a number line is a lot like reading a ruler – except that you have to draw the ruler yourself.
-
You can write the fraction in any form you want, but reducing it to lowest terms will save you a lot of labor when it comes to drawing the number line.
-
Counting the number of subdivisions in your number line is just like counting the subdivisions on a ruler.
Reduce the fraction to lowest terms by canceling common factors from the numerator and denominator. For example, if you’ve been asked to graph 10/15 on a number line, you could factor 5 out of both the numerator and denominator, leaving yourself with 2/3.
Tips
Locate the integers that would be to either side of the fraction on the number line. In this case, the next whole number larger than 2/3 is 1, and the next smaller number is 0. Mark those numbers on the number line, leaving enough room for several subdivisions between them.
Note the denominator of your fraction; continuing the example, the denominator is 3. Mark that many subdivisions between the integers from Step 2. So in this case, you’d mark out three subdivisions between 0 and 1.
Count out the subdivisions, starting from the lower integer you mapped out and moving toward the larger number. Stop when you’ve counted as many subdivisions as the numerator of the fraction. So in this case, because the fraction is 2/3, you’d stop after counting two of the three subdivisions. The place you stopped is where you place a mark for the fraction; make sure you remember to label it.
Tips
Graphic Coordinates That Involve Fractions
A two-dimensional graph is just a pair of number lines set perpendicular to each other, so much of what you learned in the previous example can be put to work for graphing in two dimensions, too.
Reduce any fractional parts of the coordinate set(s) to lowest terms if this hasn’t been done already. In this case, imagine that you’ve been asked to graph the coordinate set (2, 3/7). The fraction is already in lowest terms, so continue to the next step.
Note the number in the denominator of the fraction. Once again, this is the number of subdivisions you should make between integers. But this time, you must also look at the other coordinates you’re being asked to graph.
If there are fractions with other denominators, you’ll need to either approximate their placement or find a common denominator between all the fractions involved. Also, the scale of each axis must be large enough that even the most extreme values from your set of coordinates will still appear on the graph.
Label each axis with its units of measure (if appropriate) and then label along the axes to show their scale, just as you would with any number line.
Plot your points in the graph, using the same “count and mark” method laid out in the previous example to precisely place the fractional values.
Graphing a Line Using Fractional Slope
If you’re an algebra student learning to graph lines, you’ve probably already run into the concept of slope. Simply put, slope tells you how steeply a line tilts up or down. It’s often expressed as a fraction, with the numerator showing the change in the y coordinate and the denominator showing the change in the x coordinate.
In order for the slope of the line to be useful, you must also know the coordinates for at least one point on the line. Whatever those coordinates are, graph them.
Starting from the point that you just graphed, count up the number units that are in the numerator of the fraction that represents your slope. So if the fraction is 4/5, you’d count up four units. (If the fraction were -4/5, you’d count down four units.)
Starting from where you ended up in Step 2, count across the same number of units that are in the denominator of your slope. Continuing the example, if the fraction is 4/5, you’d count 5 units in the positive (rightward) direction. If the slope were 4/(-5), you’d count 5 units in the negative (leftward) direction.
The point you’ve just arrived at is on your line; mark it. You can continue as necessary to graph more points on the line, starting the process over from the last marked point every time.
Нарисуем линию и обозначим на ней точку O, которую назовем началом отсчета координат. После этого выберем направление и единичный отрезок. В этом случае можно сказать, что у нас есть координатная прямая с точкой ноль и началом отсчета координат. Справа от нуля располагается положительное направление слева – отрицательное.
Каждое натуральное число или дробь можно представить на этой прямой. Каждая точка на прямой может быть связана только с единственной координатой. Например, как найти координату (5)? Нужно от (0) отложить пять единиц вправо – вот это и есть представление точки на координатной прямой.
Отметьте координаты дробных чисел: (-1frac{3}{8})(,-frac{7}{8},frac{3}{8},frac{5}{8}.)
Решение: требуется изобразить на координатной прямой дроби со знаменателем 8, поэтому мы разделим единичный отрезок на 8 равных частей:
— это прямая с указанными на ней началом отсчета, направлением и единичным отрезком.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Также как и натуральные числа обыкновенные дроби можно сравнивать.
Рассмотрим две неравные дроби на числовой оси. Меньшая дробь будет располагаться левее, а большая — правее.
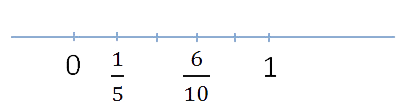
Равные дроби соответствует одной и той же точке на числовой оси.
На рисунке хорошо видно, что
<
.
Но необязательно пользоваться числовой осью, чтобы
сравнивать дроби.
Сравнение дробей с одинаковыми знаменателями
Запомните!
![]()
Из двух дробей с одинаковыми знаменателями больше та, у которой
числитель больше.
Пример. Сравним
и
.
В обеих дробях одинаковый знаменатель равный 5.
В первой дроби числитель равен 1 и он меньше числителя второй дроби,
который равен 4.
Поэтому первая дробь
меньше второй
.
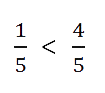
Сравнение дробей с одинаковыми числителями
Запомните!
![]()
Из двух дробей с одинаковыми числителями больше та, у которой
знаменатель меньше.
Пример. Сравним
и
. Ответ:
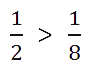
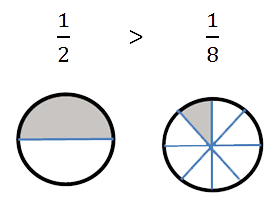
Правило выше легче понять, если представить, что у вас в руках куски торта. В первом случае
торт разделили на 2 части (знаменатель дроби равен 2), и у вас в руках
половина торта, а во втором — торт поделили на
8 частей, и у вас в руках маленькая часть торта.
Сравнение дробей с разными знаменателями
Запомните!
![]()
Чтобы сравнить дроби с разными знаменателями, нужно привести
дроби к общему знаменателю.
После приведения дробей к общему знаменателю, дроби сравниваются по правилу сравнения дробей
с одинаковыми знаменателями.
Пример. Сравним
и
.
- Приводим дроби к общему знаменателю.
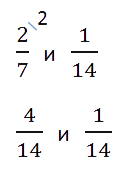
- Сравниваем дроби с одинаковыми знаменателями.
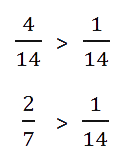
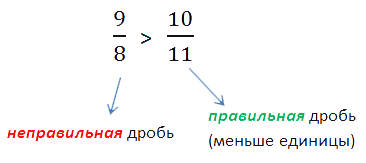
Это объясняется тем, что неправильная дробь всегда больше или равна 1, а правильная дробь
всегда меньше 1.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
24 августа 2016 в 14:24
Альбина Королева

Профиль
Благодарили: 0
Сообщений: 2

Альбина Королева
Профиль
Благодарили: 0
Сообщений: 2
и 0.21
как сравнить это и пожалусто объясните![]()
0
Спасибо
Ответить
25 августа 2016 в 10:08
Ответ для Альбина Королева
Борис Гуров

Профиль
Благодарили: 1
Сообщений: 28

Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Переведите десятичную дробь 0,21 в обыкновенную и далее сравните дроби по правилам сравнения обыкновенных дробей.
Правила сравнения обыкновенных дробей есть в этом уроке.
0
Спасибо
Ответить
25 августа 2016 в 10:28
Ответ для Альбина Королева
Альбина Королева

Профиль
Благодарили: 0
Сообщений: 2

Альбина Королева
Профиль
Благодарили: 0
Сообщений: 2
спасибо за объяснение![]()
0
Спасибо
Ответить
3 августа 2016 в 14:09
Карина Терентьева

Профиль
Благодарили: 0
Сообщений: 1

Карина Терентьева
Профиль
Благодарили: 0
Сообщений: 1
Найдите две дроби, каждаяиз которых меньше
и больше
0
Спасибо
Ответить
5 августа 2016 в 2:11
Ответ для Карина Терентьева
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
и .
0
Спасибо
Ответить
30 сентября 2016 в 14:53
Ответ для Карина Терентьева
Ольга Чикалова-Елисеева

Профиль
Благодарили: 0
Сообщений: 2

Ольга Чикалова-Елисеева
Профиль
Благодарили: 0
Сообщений: 2
Доброго времени суток. Помогите пожалуйста, я в тупике.
Суть вопроса: плоскости примыкают друг другу под углом 45 градусов. Сами плоскости имеют наклон 5 градусов от внутреннего угла к внешнему. При таком условии градус примыкания должен измениться. Как рассчитать точный градус примыкания?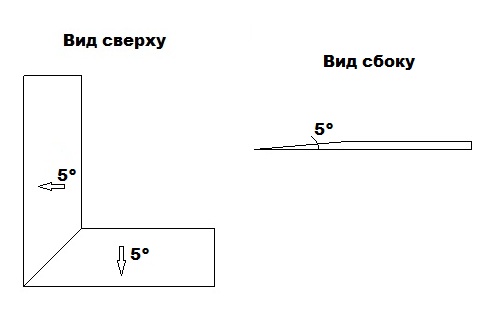
0
Спасибо
Ответить
