Лучший ответ
Елена Кухарева
Профи
(904)
13 лет назад
умножить число (или дробь) на эту дробь. Например 1/3 от 27 это 27*1/3=9 или 1/2 от 2/3, это 2/3*1/2=2/6
Остальные ответы
Кира
Ученик
(151)
13 лет назад
Чтобы найти дробь от числа, надо эту дробь умножить на число. 2.Чтобы найти число по его дроби, надо это число разделить на данную дробь.
Mari
Мастер
(1036)
13 лет назад
Чтобы найти дробь от числа нужно умножить число на эту дробь.
вишня ярмоловна
Ученик
(153)
7 лет назад
Чтобы найти дробь (часть) от числа, нужно это число умножить на данную дробь
Источник: голова и учебник
Алексей Волков
Ученик
(148)
7 лет назад
чтобы найти дробь от числа надо число умножить на верхнее число а на нижние разделить
Макс Миленин
Ученик
(109)
7 лет назад
мда
Иван Пушнаренко
Ученик
(139)
6 лет назад
сколько пятых долей 2целых двух пятых
Ульяна Павлова
Знаток
(403)
6 лет назад
а как найти дробь от дроби?
виталий герасимов
Знаток
(287)
6 лет назад
про батя
Вика Рейн
Ученик
(114)
6 лет назад
как
В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
-
Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
В 5 классе на уроках математики ученики знакомятся с дробями и процентами. В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.
Обыкновенная дробь – это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу
Пример 1.1.
В самолёте 120 пассажиров. $frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
2. Чему равны $frac{2}{5}$ (две пятых) от 120?
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $frac{3}{25}$ – школьники. Сколько в городе школьников?
Решение
1. Чему равна $frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель
Пример 1.3.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $frac{2}{7}$:
$14cdot frac{2}{7} = frac{14cdot 2}{7} = 2cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.
Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($frac{2}{5}$) от общего количества пассажиров в салоне. Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров – это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $frac{2}{7}$:
$4: frac{2}{7} = frac{4cdot 7}{2} = 2cdot 7 = 14$
Ответ: 14 автомобилей завезли в салон.
И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего
Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$frac{48}{120}=frac{24}{60}$
Сократим ещё раз на 2:
$frac{24}{60} = frac{12}{30}$
И ещё раз:
$frac{12}{30} = frac{6}{15}$
Теперь можно сократить на 3:
$frac{6}{15} = frac{2}{5}$
Больше сокращать не на что – это и можно записать как окончательный ответ задачи.
Ответ: $frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель – эти числа, а затем сократить её.
Обратите внимание, что дробь $frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников. Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$frac{180000}{1500000}=frac{18}{150}=frac{9}{75}=frac{3}{25}$
Ответ: школьники составляют $frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $frac{4}{14}$ и сокращаем:
$frac{4}{14}=frac{2}{7}$
Ответ: продали $frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе “Математика в школе”.
- Категория: Математика
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на числитель. Чтобы найти число по его дроби, нужно число разделить на числитель и умножить на знаменатель.
Разберем на примере задачи нахождение дроби от числа.
От дома до школы 560 м. Саша прошел 2/5 этого пути. Сколько метров прошел Саша?
Весь путь – это 5 частей или одно целое (5/5). Найдем одну часть:
1) 560 : 5 = 112 (м) – составляет одна часть Сашиного пути. А он прошел 2 таких части
2) 112 * 2 = 224 (м) – составляет 2/5 пути.
Ответ: 224 м.
А теперь ту же задачу превратим в нахождение числа по его дроби.
Саша прошел 224 м, что составляет 2/5 всего пути от дома до школы. Найди расстояние от дома до школы?
224 м – это часть пути, значит весь путь будет больше. Эта информация нужна для самопроверки. Найдем сначала 1/5 пути
1) 224 : 2 = 112 (м) – составляет 1/5 пути
2) 112 * 5 = 560 (м) – составляет весь путь
Ответ: 560 м.
Проверим себя. При нахождении дроби от числа результат будет меньше этого числа, если у нас правильная дробь, и больше, если неправильная (то есть целое + еще какая-то часть).
При нахождении числа от дроби – все наоборот, результат будет больше этого числа, если у нас правильная дробь, и меньше, если неправильная.
Калькулятор на нахождения дроби от числа и числа по его дроби
Этот урок будет интересным и познавательным. Мы научимся применять дроби для различных жизненных случаев.
Нахождение дроби от числа
Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, 
от пиццы это половина пиццы:
Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет от десяти сантиметров:
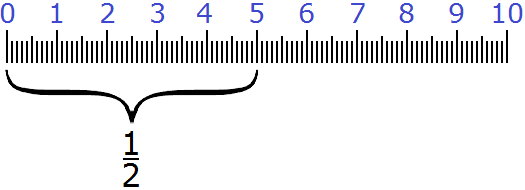
Как вы уже догадались от десяти сантиметров составляют пять сантиметров. Ведь это простейшая дробь, которая означает половину от чего-то. У нас было десять сантиметров. Мы разделили эти десять сантиметров пополам и получили пять сантиметров.
Попробуем узнать, сколько составляет от одного часа. Вспоминаем, что час это 60 минут. Нам нужно найти (половину) от 60 минут. Нетрудно догадаться, что половина от 60 минут это 30 минут. Значит от одного часа составляет 30 минут или полчаса.
Попробуем найти от одного центнера. Центнер это 100 кг. Требуется найти (половину) от 100 кг. Нетрудно догадаться, что половина от 100 кг это 50 кг. Значит от одного центнера составляют 50 кг.
Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём от числа 12.
Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит числа 12 составляет число 6.
Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:
Пусть требуется найти от этих десяти сантиметров. Читаем первую часть правила:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби
Итак, делим десять сантиметров на знаменатель дроби . Знаменатель этой дроби равен числу 2. Поэтому делим десять сантиметров на 2
10 см : 2 = 5 см
Читаем вторую часть правила:
и полученный результат умножить на числитель дроби
Итак, умножаем пять сантиметров на числитель дроби . Числитель дроби в данном случае единица. Поэтому умножаем пять сантиметров на единицу:
5 см × 1 = 5 см
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют пять сантиметров:
Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.
В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби , мы тем самым указали, что берем одну часть из двух.
Пример 2. Найти 
от 10 см.
Применим правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Сначала делим 10 сантиметров на знаменатель дроби
10 см : 5 = 2 см
Получили два сантиметра. Этот результат нужно умножить на числитель дроби
2 см × 2 = 4 см
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют четыре сантиметра.
Весь процесс решения можно увидеть на следующем рисунке:
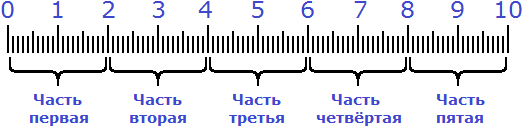
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:
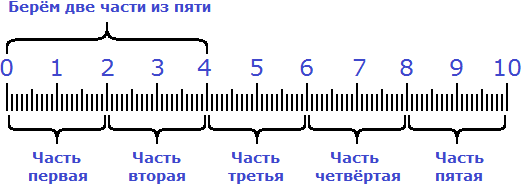
Пример 3. Найти 
от числа 56.
Чтобы найти от числа 56, нужно это число разделить на знаменатель дроби 
, и полученный результат умножить на числитель дроби .
Итак, сначала делим число 56 на знаменатель дроби
56 : 8 = 7
Теперь умножаем полученное результат на числитель дроби
7 × 3 = 21
Получили ответ 21. Значит от числа 56 составляет 21.
Пример 4. Найти 
от одного часа.
Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.
Сначала разделим 60 минут на знаменатель дроби
60 мин : 4 = 15 мин
Теперь умножим полученные 15 минут на числитель дроби
15 мин × 2 = 30 мин
Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.
Пример 5. Найти 
от одного метра.
Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби
100 см : 5 = 20 см
Теперь умножим полученные 20 см на числитель дроби
20 см × 4 = 80 см
Получили ответ 80 см. Значит от одного метра составляют 80 см.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
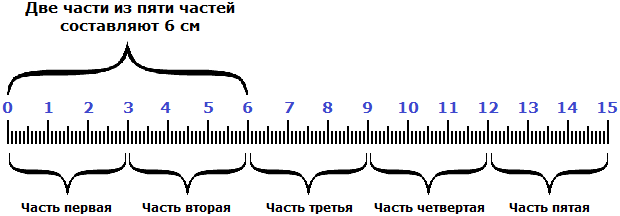
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
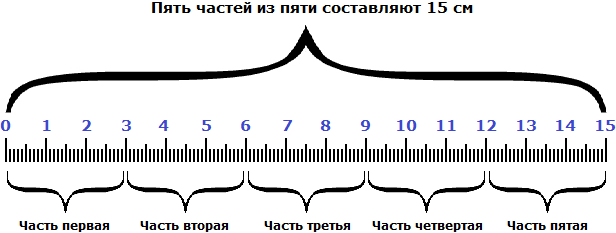
Видно, что пять частей из пяти или 
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это от всего числа. Найдите это число.
Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
20 : 4 = 5
Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
5 × 5 = 25
Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это 
времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
времени приготовления. Для этого 10 нужно разделить на числитель дроби
10 мин : 2 = 5 мин
Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли 
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. 
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти 
массы мешка. Для этого 30 надо разделить на числитель дроби .
30кг : 2 = 15кг
Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
15кг × 4 = 60кг
Мы нашли 
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Деление меньшего числа на большее
В жизни часто возникают ситуации, когда требуется разделить меньшее число на большее. Например, представим ситуацию. Имеется трое друзей:
И требуется поровну разделить между ними два яблока. Как это сделать? Друзей трое, а яблок всего два. Мы попали в ситуацию в которой требуется разделить меньшее число на большее (два яблока на троих).
Для таких случаев предусмотрено следующее правило:
При делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Давайте применим это правило. Оно говорит, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе делитель. Делимое у нас это два яблока. Записываем в числителе число 2:
А делитель у нас это трое друзей (вспоминаем, что делитель показывает на сколько частей надо разделить делимое). Записываем тройку в знаменателе нашей дроби:
Забавно, но дробь 
это ответ к нашей задаче. Каждому другу достанется яблока. Почему так произошло?
Чтобы разделить два яблока на троих, надо разрезать ножом каждое яблоко на три части и раскидать поровну эти куски между тремя друзьями:
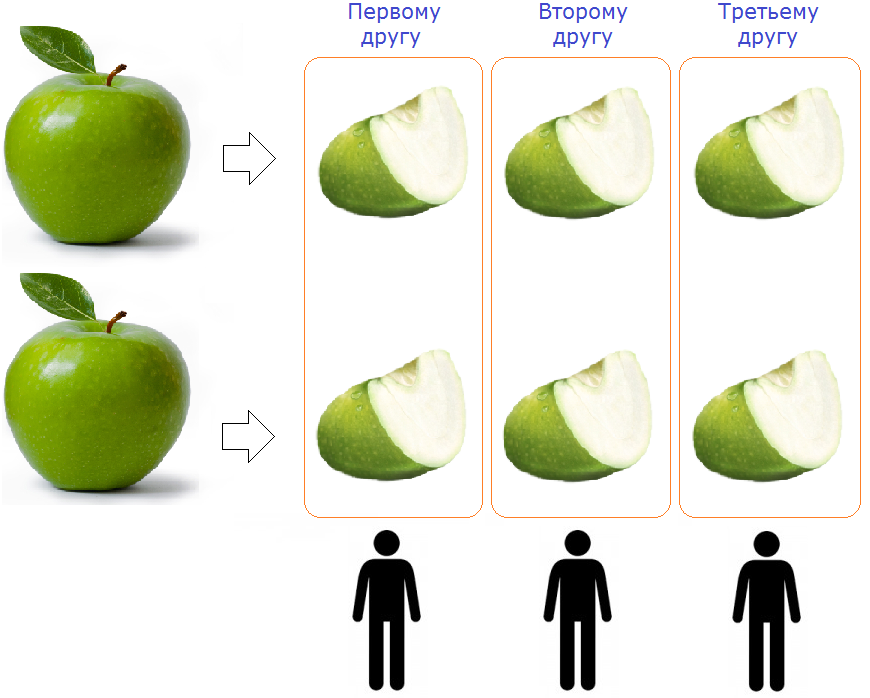
Как видно на рисунке, каждое яблоко было разделено на три части и раскидано поровну на троих друзей. Каждому другу досталось яблока (два кусочка из трёх).
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь 
.
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
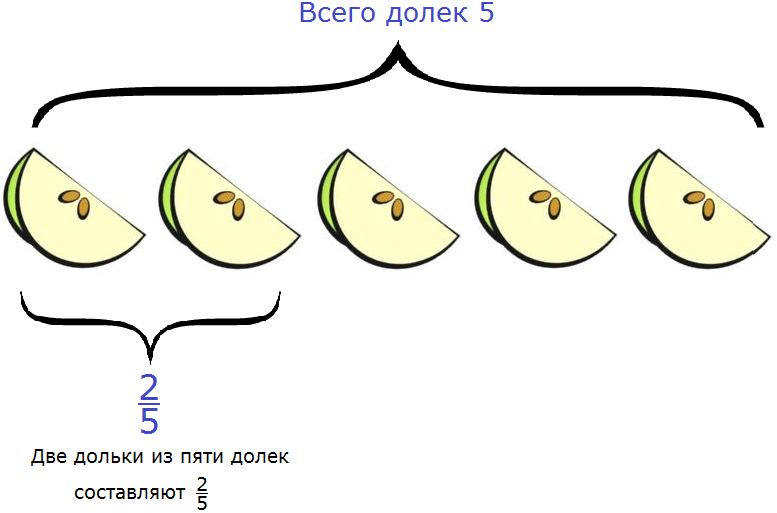
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь 
. Значит число 2 от числа 10 составляет (две десятых).
Дробь означает, что число 10 разделено на десять частей, и от этих десяти частей взято две части.
Также, эту дробь можно сократить на 2. После сокращения дроби на 2 получаем дробь 
.
Дробь тоже может послужить ответом к задаче. Она будет означать, что число 10 разделено на пять частей, и от этих пяти частей взята одна часть.
Таким образом, число 2 составляет (одну пятую) от числа 10.
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь 
. Эту дробь можно сократить на 5
Получили аккуратную дробь 
. Значит ответ будет выглядеть следующим образом:
Число 5 составляет (одну третью) от числа 15.
Это можно даже проверить. Для этого нужно найти от числа 15. Если мы всё сделали правильно, то должны получить число 5.
Итак, найдём от числа 15. Как находить дробь от числа мы уже знаем
15 : 3 = 5
5 × 1 = 5
Получили ответ 5. Значит задача была решена правильно.
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь 
. Эту дробь можно сократить на 3
Получили ответ 
. Значит 3 см составляют (одну четвёртую) от 12 см.
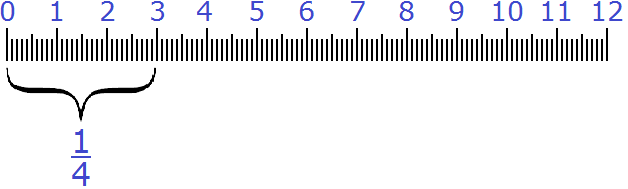
Проверим правильно ли мы решили эту задачу. Для этого найдём от 12 см. Если мы всё сделали правильно, то должны получить 3 см.
Делим 12 на знаменатель дроби
12 см : 4 = 3 см
Умножаем полученные 3 см на числитель дроби
3 см × 1 = 3 см
Получили ответ 3 см. Значит задача была решена правильно.
Задания для самостоятельного решения
Задание 1. Найдите от числа 30.
Задание 2. Найдите от числа 30.
Задание 3. Найдите от числа 30.
Задание 4. Найдите 
от числа 48.
Задание 5. Найдите 
от числа 48.
Задание 6. Найдите от 120 см.
120 см : 3 = 40 см
40 см × 2 = 80 см
Задание 7. Найдите от 150 см.
150 см : 3 = 50 см
50 см × 2 = 100 см
Задание 8. Найдите целое число по дроби, если известно, что этого числа составляет число 16.
Задание 9. Найдите целое число по дроби, если известно, что этого числа составляет число 32.
Задание 10. Найдите целое число по дроби, если известно, что этого числа составляет число 150.
150 : 5 = 30
30 × 8 = 240
Задание 11. Найдите длину пути от дома до школы, если известно, что этого пути составляют 4 км.
4 км : 2 = 2 км
2 км × 3 = 6 км
Задание 12. Найдите длину рулетки, если известно, что этой рулетки составляют 100 см.
100 см : 5 = 20 см
20 см × 8 = 160 см
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
