|
Для того чтобы время выразить в виде десятичной дроби, нужно помнить, что в одном часе содержится 60 минут. То есть:
Разберем перевод времени на конкретном примере. У нас имеется время: 3 часа 9 минут. Оставим пока имеющиеся 3 часа в сторонке и займемся преобразованием минут. Наши 9 минут переведем в часы, для чего умножаем эти минуты на 1/60: 9 х 1/60 = 9/60 = 0,15 (часов). А теперь складываем найденные нами минуты в часах с исходным значением часов: 0,15 + 3 = 3,15 (часов). То есть: 3 часа 9 минут = 3,15 (часов). Действуя аналогично, можно любое время, данное в часах и минутах, перевести в десятичную дробь. автор вопроса выбрал этот ответ лучшим
андрей4100 5 лет назад Для перевода часов и минут в десятичную дробь на нужно: Например нам нужно перевести 1 час 39 минут в десятичную дробь. Часы всегда записываем как целое число-1,; Для перевода минут нам нужно 39 разделить 60(60 минут в одном часе); Считаем: 1 час 39 мин=1,(39/60)=1,65.
Очень просто, знаменателем обычной дроби всегда будет число шестьдесят, а числителем количество минут. Для перевода в десятичные дроби надо просто количество минут разделить на шестьдесят и получится число меньше единицы. Вот целое количество часов ставим до запятой а после запятой, то число которое получилось у нас при делении, получаем десятичную дробь. Давайте разберем на примере: Требуется записать десятичной дробью выражение 3 часа 45 минут. Берем число 3 за цело число, а 45 делим на 60, получаем 0,75. Теперь соединяем целое и доли, получаем 3,75. Или, 00 часов 34 минуты. У нас изначально получается 0 целых, далее 34 делим на 60 получаем все вместе 0,56.
Эл Лепсоид 4 года назад Перевод длинной записи, выраженной в виде часов и минут (например, 5 часов и 24 минуты), в более компактную запись, в которой указанное время выражено в виде числа с десятичной дробью (например, 2,7 часа), надо просто имеющиеся минуты разделить на 60 (поскольку в часе как-раз 60 минут) и полученную простую дробь округлить до дроби десятичной, а количество часов останется неизменным – они будут всегда указывать целое количество имеющихся часов. Беря в качестве примера то время, что я указал выше, получаем: 24/60 = 4/10 = 0,4. В итоге получаем: 5 часов 24 минуты – это 5,4 часа. Несколько сложнее, если минуты на 60 делятся с остатком: переведем в часы 4 часа и 13 минут – 13/60 преобразуется в десятичную дробь, как 0,21(6). Поэтому 4 часа 13 минут будут приблизительно равны 4,22 часа.
127771 4 года назад Достаточно простой вопрос для меня. Чтобы ответить на этот вопрос необходимо знать, что в одном часе шестьдесят минут. Сначала перейдем к простому как сантиметры перевести в метры. В одном метре 100 сантиметров. Значит, если нам нужно перевести 60 сантиметров в метры, мы 60 делим на 100 и получаем 0,6 метров. Теперь необходимо будет тоже самое проделать с минутами. Итак нам дано тридцать минут, нужно перевести в часы. Нужно 30 разделить на 60 и получаем 0,5 часов. Теперь посложнее, переведем 3 часа 15 минут в десятичный формат, 15 делим на 60 и получаем 3,25 часа. Теперь выводим формулу: часы (в десятичном формате) = минуты делим на 60.
-Irinka- 4 года назад Прежде всего нужно помнить, исходить из того, что в одном часе всего 60 минут. Рассмотрим на примере. Допустим заданное время, которое необходимо перевести это 4 часа 15 минут – 4:15. Переводим минуты в часы, для этого их необходимо поделиться на 60: 15 ? 60 = 0,25 часа. Теперь суммирум часы (4 часа) с полученным значением: 4 + 0,25 = 4,25 часа. 4 часа 15 минут в десятичной дроби будет равняться 4,25 часа. Аналогичное вычисление можно произвести с любым временем.
RIOLIt 5 лет назад Такой камень преткновения случается у младших школьников, но каждая пятиминутка двенадцатая часть часа, каждая шестиминутка- десятая, десятиминутка- шестая часть, а- каждые пятнадцать минут, часы отбивают четверти, вот отсюда и исходить следует, переводя часы и минуты в дроби,( где понятнее- десятичная, а где- то и простая лучше…)
Бархатные лапки 4 года назад На самом деле это не так и сложно. Используем такую формулу:
Теперь, чтобы было понятнее переводим на примере часы в десятичную дробь. К примеру берем 2 часа 30 минут. Часы у нас будут записываться как целое число, в данном случае это 2. Теперь разберемся с минутами. 30 разделим на 60. 30/60=0,5. В результате получаем – 2,5.
Viridi 4 года назад Для того чтобы выполнить это математическое действие, нужно вспомнить сколько же минут содержится в одном часу. Конечно же 60. Для наглядности перевода возьмём например 6 часов и 24 минуты. Поскольку количество часов нам уже известно цифру 6 оставляем без изменений, а вот с минутами нужно будет провести некоторые вычисления, а именно 24 делим на 60 в итоге получим 0,4. То есть 24 минуты – это 0,4 часа. Производим действие сложения: 6 + 0,4 = 6,4. таким образом 6 часов и 24 минуты = 6,4 ч.
vdtest 5 лет назад Чтобы перевести часы и минуты в часы надо помнить, что значение до десятичной запятой (или точки) это количество часов, а значение после десятичного разделителя равно число минут деленное на 60 Пример 15-30 15 часов 30 минут это 30/60=0.5 часов получаем десятичную дробь 15,5
lanita-67 5 лет назад Один час – это 60 минут. Чтобы перевести минуты в десятичную дробь, то нужно составить уравнение. 60(мн)= одно целое 1(мн) = Х Х=1:60=1/60= 0,166666667 Допустим интересует сколько будет 5 минут. 60(мн)= 1 5 = Х Х=5:60=5/60= 0, 08333(3) В скобках 3 в периоде Знаете ответ? |
Содержание материала
- Правильная и неправильная дробь
- Видео
- Дроби
- Нахождение части от целого (дроби от числа)
- Вычитание дробей
- Нахождение целого числа по дроби
- Как перевести десятичную дробь в обыкновенную или смешанную
- Применение нахождения дроби от числа для решения задач
- Нахождение числа по значению дроби
Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.
Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.
Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.
Дроби
Дроби вида $frac{n}{m}$ называют «обыкновенные дроби». В дроби $frac{n}{m}$ число над чертой называют числителем дроби, а число под чертой – знаменателем дроби.
Знаменатель показывает, на сколько долей делят, а числитель — сколько таких долей взято.
Таким образом, если нам нужно обозначить не один «кусочек» числа, а больше, мы просто пишем в верхней части дроби не единицу, а другое число, например, так:
Дроби нужно уметь читать правильно: числитель читается как количественное числительное женского рода (одна, две и т.д.), а знаменатель как порядковое числительное (вторая, пятая) и согласуется с первым числительным.Например: $frac{1}{2}$ — одна вторая, $frac{2}{5}$ — две пятых, $frac{6}{11}$ — шесть одиннадцатых.
На рисунке 6 изображён отрезок АВ, его длина 10 см, то есть 1 дм. Длина отрезка АС будет 1 см.
А какую долю составит сантиметр от метра?
Показать ответ
Скрыть
$frac{1}{100}$
А грамм от килограмма?
Показать ответ
Скрыть
$frac{1}{1000}$
Видео
Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
- Перевести смешанные дроби в обыкновенные (избавиться от целой части).
- Привести дроби к общему знаменателю. Для этого нужно числитель и знаменатель первой дроби умножить на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой дроби.
- Вычесть одну дробь из другой, путем вычитания числителя второй дроби из числителя первой.
- Найти наибольший общий делитель (НОД) числителя и знаменателя и сократить дробь, поделив числитель и знаменатель на НОД.
- Если числитель итоговой дроби больше знаменателя, то выделить целую часть.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 
длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби 
. Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби 
. Известно, что 
длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 
это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби 
это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или 
длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
от всего числа. Найдите это число.
Знаменатель дроби 
показывает, что число, которое мы должны найти, разделено на пять частей. Если 
этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти 
(одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби 
20 : 4 = 5
Мы нашли 
от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби 
5 × 5 = 25
Мы нашли 
от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это 
времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби 
показывает, что общее время приготовления каши разделено на три части. Если 
времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
времени приготовления. Для этого 10 нужно разделить на числитель дроби 
10 мин : 2 = 5 мин
Мы нашли 
времени приготовления каши. 
времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби 
5 мин × 3 = 15 мин
Мы нашли 
времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. 
массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби 
показывает, что общая масса мешка разделена на четыре части. Если 
массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти 
массы мешка. Для этого 30 надо разделить на числитель дроби 
.
30кг : 2 = 15кг
Мы нашли 
массы мешка. 
массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби 
15кг × 4 = 60кг
Мы нашли 
массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
- Записать дробь в виде десятичная дробь1
- Умножать числитель и знаменатель на 10 до тех пор, пока числитель не станет целым числом.
- Найти наибольший общий делитель и сократить дробь.
Например, переведем 0.36 в обыкновенную дробь:
- Записываем дробь в виде: 0.361
- Умножаем на 10 два раза, получим 36100
- Сокращаем дробь 36100 = 925
Применение нахождения дроби от числа для решения задач
В начале урока мы уже разобрали пример с тортом, сейчас посмотрим на другие примеры.
Задача 1
Остап зарабатывает 40 000 рублей в месяц.
Из них (mathbf{frac{1}{4}}) это подработка.
Сколько рублей Остапу приносит подработка?
Решение:
В данной случае числом будет являться сумма заработка за месяц — 40 000
Ну а дробью, очевидно, будет (mathbf{frac{1}{4}}).
Тогда, чтобы найти прибыль от подработки, надо просто умножить дробь на число.
(mathbf{40000cdotfrac{1}{4}=frac{40000}{4}=10000})
Ответ: 10 000 рублей.
Теперь рассмотрим что-нибудь посложнее.
Задача 2
Порфирий живет в комнате площадью 18 квадратных метров.
3 кровати занимают (mathbf{frac{1}{3}}) площади комнаты.
Какую площадь занимает одна кровать?
Решение:
Сначала найдем, какую площадь занимают 3 кровати, затем разделим это число на 3, чтобы получить площадь одной кровати.
1) (mathbf{18cdotfrac{1}{3}=frac{18}{3}=6}) (квадратных метров) занимают 3 кровати
2) (mathbf{6div3=2}) (квадратных метра) занимает одна кровать
Ответ: 2 квадратных метра.
Теперь посмотрим, как в задачах применяются проценты.
Задача 3
Пересвет работает на заводе и производит 100 деталей в день.
Начальник Елисей пообещал Пересвету выдать премию, если он будет делать на 20% деталей больше.
Сколько деталей в день должен делать Пересвет, чтобы получить премию?
Решение:
Для начала надо понять, на сколько в количественном измерении больше деталей нужно выпустить Пересвету, чтобы получить премию.
Для этого домножим текущее количество деталей на процент или долю, учитывая, что 20% — это 20 частей из 100, или иначе 0,20, и получим искомую прибавку.
1) (mathbf{20%=20div100=0.2})
2) (mathbf{100cdot0.2=20}) (деталей)- то, насколько больше деталей нужно производить
Теперь, чтобы найти общее количество деталей, надо прибавить эту прибавку к тому, что Пересвет производит уже сейчас.
3) (mathbf{100+20=120}) (деталей) в день нужно производить для получения премии
Ответ: 120 деталей.
В некоторых задачах нужно несколько раз применять нахождение процентов от числа.
Задача 4
Глубина реки в начале мая была равна 10 метрам, к началу июня она обмелела на 10%, а к началу июля еще на 15% относительно показателей начала июня. Вычислите, какая глубина реки была в начале июля.
Решение:
Исходное число- 10 метров, дробь задана в виде процентов.
Первым действием нужно будет найти глубину реки в начале июня.
Здесь можно пойти двумя разными путями:
I. Посчитаем, на сколько метров опустился уровень воды, а затем вычтем это из исходных показателей.
0) (mathbf{10%=10div100=0.1})
1) (mathbf{10-10cdot0.1=10-1=9}) (метров)- глубина реки в начале июня
II. Можно вместо того, чтобы считать разницу и вычитать ее, посчитать сколько процентов останется и найти сразу именно эту часть от исходного числа.
Учитывая, что всего у нас 100%, да если глубина уменьшилась на 10%, то осталось 90%.
0) (mathbf{100-10=90}) (процентов) останется
1) (mathbf{90%=90div100=0.9})
2) (mathbf{10cdot0.9=9}) (метров)- глубина реки в начале июня
Как мы видим, эти два подхода дают одинаковый результат.
Поэтому вы можете выбирать любой из них в зависимости от задачи и ваших предпочтений.
Таким образом, мы посчитали глубину в начале июня. Теперь нужно понять, какая будет глубина в начале июля, когда глубина уменьшится еще на 15 процентов.
Используем в этом случае второй способ.
3) (mathbf{100-15=85}) (процентов) останется в июле от уровня июня
4) (mathbf{85%=85div100=0.85})
5) (mathbf{0.85cdot9=7.65}) (метров) составит глубина реки в начале июля
Ответ: 7.65 метра.
Пройти тест Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации Вход Регистрация
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
m = m : a / b
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет2 / 5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :2 / 5
= 20 ⋅5 / 2
=20 ⋅ 5 / 2
= 50
Теги
В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Цели:
- Продолжить формирование умений решать задачи на движение в соединении с темой «Дроби».
- Производить соответствующие записи и вычисления.
- Развивать логическое мышление и внимание.
- Развивать умение анализировать и обобщать.
- Учить изменять условия задачи.
Ход урока
1. Орг. момент
– Что изучаем? (Дробные числа).
– Какого типа задачи учимся решать? (На движение).
– Какие 3 величины там обязательно должны быть (S, V, t).
– Сегодня мы попробуем соединить эти две темы.
– Как и где это возможно сделать? (В задачах на движение).
– Это мы попробуем сделать позже, а сначала немного повторим.
2. Устный счет.
Учитель пишет на доске.
– Найти: 1/2 от 48, 1/2 от 96, 1/2 от 78.
– Какая разница. Находим доли от числа и числа по доле.
– Объясните, как вы находили. На сколько частей делим?
– Как можно по-другому назвать 1/2.
– Найти 1/4 от 60 мин, 1/7 от 84.
– А если взять ⅔, то сколько частей надо взять.
– Сколько раз надо взять по 1/10 круга, чтобы получить целый круг?
– Сколько раз содержится в 1 круге по 1/2 .
– А по 1/4 , а по 1/10, а по 1/8.
От города до деревни 20км. Асфальтом покрыто 4/5.
Выбери схему, которая соответствует данному решению.
3. Подготовка к решению задач.
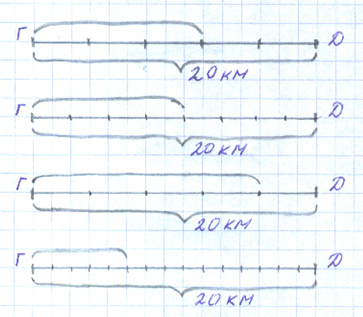
– Найдите её и докажите, что это так (у нас дробь 4/5, этот отрезок разделён на 5 частей и мы взяли 4 части).
– Почему не подходят все остальные схемы и какие дроби на них получились? (Подписываем над отрезками).
– Какое же количество асфальта покрыто в 3 задаче? Как узнать?
20:5 • 4 = 16 км
Сколько же действий нам потребовалось, чтобы найти 4/5 (2).
– Какие? (Деление и умножение).
– Почему? (Делили на части, а потом брали их).
4. Решение задач.
Итак, мы с вами решили, что дробные числа можно применять в задачах на движение. Давайте подумаем и приведем примеры, как это возможно.
Задача. На путь из одного города в другой почтовый голубь затратил 8 часов. Из них ⅟4 он отдыхал, а остальное время летел со скоростью 10км/ч. На каком расстоянии находятся друг от друга города?
– На какую тему эта задача? (На движение).
– Какие три величины всегда есть в таких задачах? (v, t, s).
– Чертим таблицу. Читаем задачу по частям и постепенно заполняем таблицу.
|
T |
V |
S |
|
Всего 8 ч. Отдых ? 1/4 часть Остальное – ? ч. |
10км/ч |
?км |
Читаем 1 предложение.
– Что такое 8 часов? (Время).
– Читаем 2 предложение (в какую графу пишем?)
– Какое время он летел? (Остальное).
– (1 ученик по таблице рассказывает еще раз условие).
– Нам нужно узнать расстояние. Какие два данных нужны, чтобы ответить на вопрос (t и v).
– Какую знаем уже? (Cкорость).
– Какова же она? (10 км/ч)
– Какое данное неизвестно? (Время).
– Смотрим на 1 графу и выделяем 1 простую задачу.
1. 8 : 4 × 1 = 2ч он отдыхал.
Рассуждаем дальше:
Сколько времени он потратил непосредственно при перелёте из одного города в другой?
Формулируем вторую простую задачу.
2. 8 – 2 = 6ч он летел (время в пути).
Рассуждаем дальше.
Формулируем 3 простую задачу. (Записываем формулу) S = v × t
3. 10 = 60км расстояние между городами.
Записываем ответ.
– Как изменить условие задачи так, чтобы решение стало короче? Что для этого нужно изменить в таблице (время).
– Как? (Просто записать количество часов).
Записываем.
Сформулируем задачу.
Как узнаем (это последнее действие предыдущей задачи).
– Решаем, пишем формулу.
– Как изменить условие задачи, чтобы решение стало длиннее?
– Что нужно сделать? (оставить условие, усложнив его).
– В какую графу можно добавить новые данные (если дети затрудняются).
– А голубь всегда с одной и той же скоростью летает?
|
T |
V |
S |
|
Всего – 8 ч. Отдых 1/4 часть 4 ч Остальные |
10км/ч 15км/ч |
?км |
На путь из одного города в другой почтовый голубь затратил 8 часов. Из них ⅟4 часть он отдыхал. 4 часа летел со скоростью 10км/ч, а остальное время со скоростью 15км/ч. На каком расстоянии находятся друг от друга города?
- 8 : 4 × 1 = 2ч отдыхал
- 8 – 2 = 6ч он летел
- 6 – 4 = 2ч остальное
- 10 × 4 = 40км за 4 часа
- 15 × 2 = 30км за 2 часа
- 40 + 30 = 70км – весь путь
- Логическая задача.
Выходные дни составляют недели. Сколько выходных дней в году?
- 365 : 7 = 52 (ост . 1) недели в году.
- 7 : 7 × 2 = 2 выходных дня в неделе.
- 2 × 52 = 104 выходных дня в году.
Сколько же от года отдыхаем в дробях (примерно ).
6. Итог.
Над чем на уроке работали? Что нового узнали? Какие темы соединяли?
Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Пример
Задание. Найти
$frac{7}{20}$ от 40.
Решение. В рассматриваемом примере 40 – это заданное число, $frac{7}{20}$ – дробь, задающая искомую часть.
Тогда, согласно правилу, имеем:
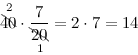
Итак, получили, что $frac{7}{20}$ от 40 равно 14 – искомая часть данного числа.
Ответ. $frac{7}{20}$ от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В классе 12 мальчиков, что составляет $frac{4}{5}$ части всех учеников класса.
Сколько всего человек учится в классе?
Решение. Искомое количество учеников
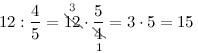
Ответ. Всего в классе учится 15 человек.
Читать следующую тему: десятичные дроби.
