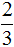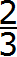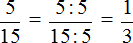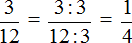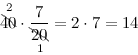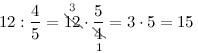В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
|
Нужно привести эти дроби к общему знаменателю. 1/5 = 3/15; 1/3 = 5/15 Между ними лежит число 4/15. Если нужно больше чисел в промежутке, то увеличиваем знаменатель. 1/5 = 3/15 = 6/30; 1/3 = 5/15 = 10/30 Между ними будут числа 7/30, 8/30 = 4/15 и 9/30 = 3/10 автор вопроса выбрал этот ответ лучшим Андрей А-ч 5 лет назад Для того чтобы найти другие дроби между двумя какими то известными дробями математически, можно например сотавить уравнение в котором неизвестной будет общий знаменатель при известной разнице в числителях. Знаете ответ? |
При нахождении наименьшего общего знаменателя при сложении (вычитании) обыкновенных дробей учащиеся часто поступают нерационально, принимая в качестве общего знаменателя произведение знаменателей исходных дробей.
Можно использовать следующий прием, использующий навык сокращения дробей
Пример 1. Найти сумму дробей с разными знаменателями
Составили дробь из знаменателей дробей слагаемых и после ее сокращения на 7 получили дополнительные множители к дробям слагаемым:
2 – дополнительный множитель к дроби со знаменателем 21,
3 – дополнительный множитель к дроби со знаменателем 14
Т.е. дополнительные множители соответствуют исходным знаменателям “крест-накрест”
Пример 2. Найти разность дробей с разными знаменателями
Составили дробь из знаменателей, сократили ее и получили дополнительные множители, которые соответствуют исходным знаменателям “крест-накрест”, как в пропорции
Способ можно применять для нахождения наименьшего общего кратного двух чисел (это очевидно, т.к. наименьший общий знаменатель является наименьшим общим кратным исходных знаменателей)
Пример 3. Найти наименьшее общее кратное
Составили дробь из чисел, для которых надо найти наименьшее общее кратное, сократили ее последовательно (сначала на 2, потом на 7, потом на 3) – получили несократимую дробь.
Числитель составленной дроби умножаем на знаменатель дроби после сокращения (84 умножаем на 3).
Знаменатель составленной дроби умножаем на числитель дроби после сокращения (126 умножаем на 2).
В обоих случаях получаем наименьшее общее кратное при условии, что получена именно несократимая дробь.
Алгоритм усложняется, если надо найти общий знаменатель трех и более дробей. В этом случае надо найти общий знаменатель первых двух дробей, потом найти общий знаменатель результата и следующей дроби и т.д.
Алгоритм можно применять также при сложении (вычитании) алгебраических дробей.
Содержание
- Как найти дробь от числа
- Применение дробей
- Нахождение дроби от числа
- Нахождение целого числа по дроби
- Деление меньшего числа на большее
- Какую часть одно число составляет от другого
Как найти дробь от числа
Одна из простой, но интересной темы – это как найти дробь от целого (от числа).
Как найти часть от целого? У нас есть какое-то значение и нам нужно найти долю или дробь от этого значения.
К примеру, пицца весит 540 г. Сколько весит кусок пиццы, если ее разделили на 6 одинаковых кусков?
Пиццу разрезали на 6 одинаковых кусков, значит, один кусок – это 1/6 от всей пиццы.
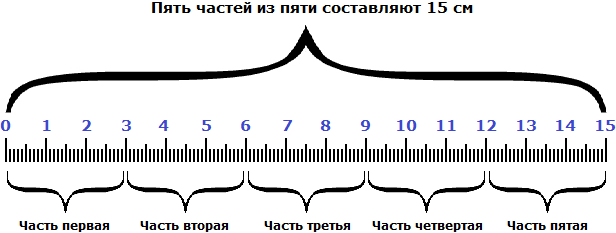
Начертим схему: чертим отрезок, разделим его на 6 равных частей. Удобнее начертить отрезок длиной 6 или 12 см (см. статью здесь).
Если пиццу разрезали, то и весь вес надо разделить: 540:6=90 (г)
Если нужно узнать вес двух кусков, т.е. 2/6
то эти 90 взять 2 раза: 90х2= 180 (г)
В итоге, 540 : 6 х 2, или, зная правила работы с дробями — 540 х 2/6.
Видим, что для того, чтобы найти 2/6 от целой пиццы нужно просто умножить общий вес на значение этой части — 2/6.
Как-то странно. Не правда ли? И, тем не менее: чтобы найти часть, мы умножаем, а не делим. Потому что если вспомнить, что дробь, вернее, горизонтальная черта дроби — это деление. Итак:
7/8 от 24 — 24:8х7=21
3/5 от 60 – 60:5х3=45
3/4 от 12 – 12:4х3=9
7/8 от 64 – 64:8х7=56
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 70
Источник
Применение дробей
Этот урок будет интересным и познавательным. Мы научимся применять дроби для различных жизненных случаев.
Нахождение дроби от числа
Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, 
Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет 
Как вы уже догадались 

Попробуем узнать, сколько составляет 


Попробуем найти 


Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём 
Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит 
Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
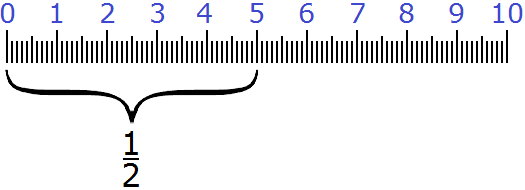
Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:
Пусть требуется найти 
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби 
Итак, делим десять сантиметров на знаменатель дроби 
Читаем вторую часть правила:
и полученный результат умножить на числитель дроби
Итак, умножаем пять сантиметров на числитель дроби 
Мы нашли 

Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.
В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби 
Пример 2. Найти 
Применим правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
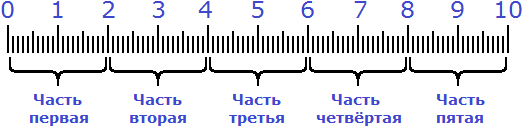
Сначала делим 10 сантиметров на знаменатель дроби
Получили два сантиметра. Этот результат нужно умножить на числитель дроби
Мы нашли 

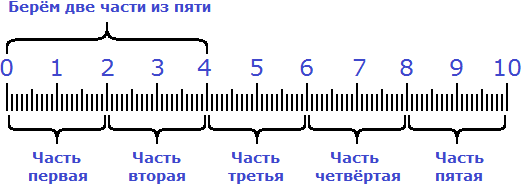
Весь процесс решения можно увидеть на следующем рисунке:
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:
Пример 3. Найти 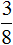
Чтобы найти 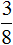
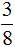
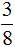
Итак, сначала делим число 56 на знаменатель дроби
Теперь умножаем полученное результат на числитель дроби
Получили ответ 21. Значит 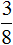
Пример 4. Найти от одного часа.
Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.
Сначала разделим 60 минут на знаменатель дроби
60 мин : 4 = 15 мин
Теперь умножим полученные 15 минут на числитель дроби
15 мин × 2 = 30 мин
Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.
Пример 5. Найти 
Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби
100 см : 5 = 20 см
Теперь умножим полученные 20 см на числитель дроби
20 см × 4 = 80 см
Получили ответ 80 см. Значит 
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если 

Требуется найти длину всей линейки по дроби 

Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби 

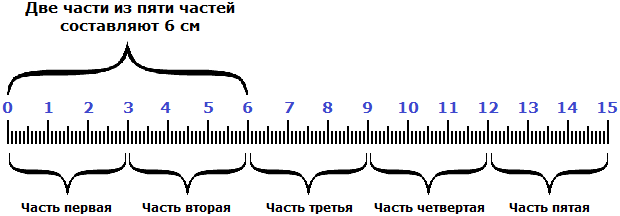
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
Итак, мы нашли длину одной части. Одна часть из пяти или 
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или 
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это 
Знаменатель дроби 


Мы нашли 
Мы нашли 
Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти 
10 мин : 2 = 5 мин
Мы нашли 

5 мин × 3 = 15 мин
Мы нашли 
Пример 4. 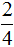
Знаменатель дроби 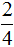
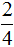
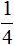
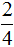
Мы нашли 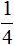
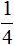
Мы нашли 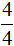
Деление меньшего числа на большее
В жизни часто возникают ситуации, когда требуется разделить меньшее число на большее. Например, представим ситуацию. Имеется трое друзей:
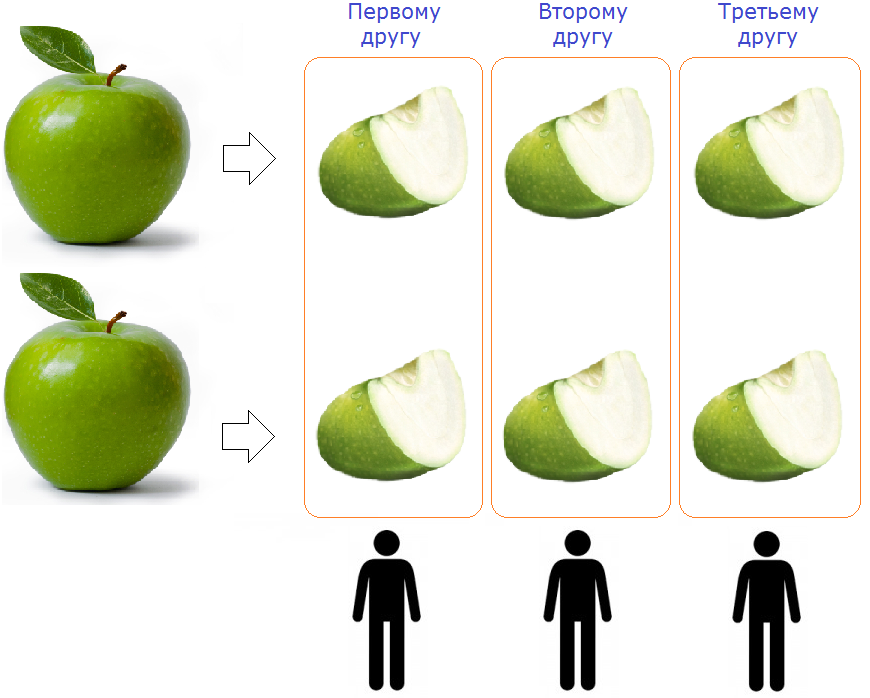
И требуется поровну разделить между ними два яблока. Как это сделать? Друзей трое, а яблок всего два. Мы попали в ситуацию в которой требуется разделить меньшее число на большее (два яблока на троих).
Для таких случаев предусмотрено следующее правило:
При делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Давайте применим это правило. Оно говорит, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе делитель. Делимое у нас это два яблока. Записываем в числителе число 2:
А делитель у нас это трое друзей (вспоминаем, что делитель показывает на сколько частей надо разделить делимое). Записываем тройку в знаменателе нашей дроби:
Забавно, но дробь 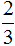
Чтобы разделить два яблока на троих, надо разрезать ножом каждое яблоко на три части и раскидать поровну эти куски между тремя друзьями:
Как видно на рисунке, каждое яблоко было разделено на три части и раскидано поровну на троих друзей. Каждому другу досталось 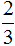
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
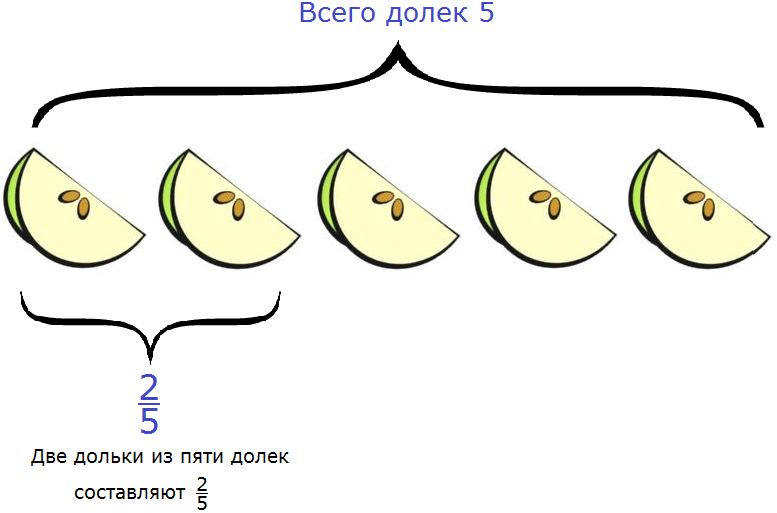
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь 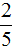
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь 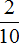
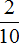
Дробь 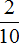
Также, эту дробь можно сократить на 2. После сокращения дроби 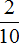
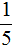
Дробь 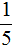
Таким образом, число 2 составляет 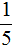
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь 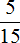
Получили аккуратную дробь 
Число 5 составляет 
Это можно даже проверить. Для этого нужно найти 
Итак, найдём 
Получили ответ 5. Значит задача была решена правильно.
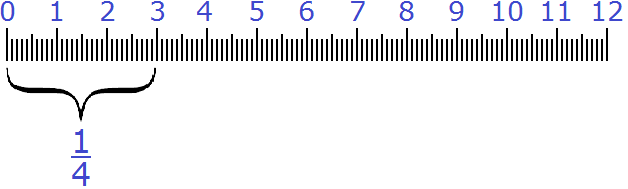
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь 
Получили ответ 

Проверим правильно ли мы решили эту задачу. Для этого найдём 
Делим 12 на знаменатель дроби
Умножаем полученные 3 см на числитель дроби
Получили ответ 3 см. Значит задача была решена правильно.
Источник
Существует ряд задач, в которых необходимо найти часть или дробь
некоторого числа. Такие задачи решаются умножением на основании следующего правила:
Чтобы найти дробь от заданного числа, нужно это число умножить на дробь.
Пример
Задание. Найти
$frac{7}{20}$ от 40.
Решение. В рассматриваемом примере 40 – это заданное число, $frac{7}{20}$ – дробь, задающая искомую часть.
Тогда, согласно правилу, имеем:
Итак, получили, что $frac{7}{20}$ от 40 равно 14 – искомая часть данного числа.
Ответ. $frac{7}{20}$ от 40 равно 14.
Иногда требуется по известной части числа и дроби, которая выражает эту часть, определить все число. Подобные задачи решаются делением.
Чтобы найти число, по известной величине его дроби, надо заданную величину поделить на дробь.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В классе 12 мальчиков, что составляет $frac{4}{5}$ части всех учеников класса.
Сколько всего человек учится в классе?
Решение. Искомое количество учеников
Ответ. Всего в классе учится 15 человек.
Читать следующую тему: десятичные дроби.