Как найти дроби которые можно представить

Как найти дроби которые можно представить

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно  рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название  элементарных дробей.

Типы дробей

Дроби различают:

  1.  Ax-a;
  2. A(x-a)n;
  3. Mx+Nx2+px+q;
  4. Mx+N(x2+px+q)n.

A, M, N, a, p, q из которых являются числами, а дискриминант дробей 3 и 4 меньше нуля, то есть корней не имеет выражение.

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Например, если необходимо брать интеграл от дробно-рациональной функции вида ∫2×3+3×3+xdx.  После чего необходимо произвести разложение подынтегральной функции на простейшие дроби. Все это к формированию простых интегралов. Получаем, что

∫2×3+3×3+xdx=∫2+2x-3x+2×2+1dx==∫2dx+∫3xdx-∫3x+2×2+1dx==2x+3lnx-32∫d(x2+1)x2+1-2∫dxx2+1==2x+3lnx-32lnx2+1-2arctan(x)+C

Пример 1

Произвести разложение дроби вида -2x+3×3+x.

Решение

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

Типы дробей

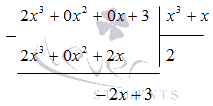
Отсюда следует, что дробь примет вид

2×3+3×3+x=2+-2x+3×3+x

Значит, такое разложение приведет к тому, что результат будет равен -2x+3×3+x.

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

  • Произвести разложение на множители. можно применять вынесение за скобки, формулы сокращенного умножения, подбор корня. Имеющийся пример x3+x=xx2+1 для упрощения выносят х за скобки.
  • Разложение дроби на простейшие дроби с неопределенными коэффициентами.

Рассмотрим на нескольких примерах:

Пример 2

Когда в знаменателе имеется  выражение вида (x-a)(x-b)(x-c)(x-d), количество множителей не имеет значения, дробь можно представить в виде дроби первого типа Ax-a+Bx-b+Cx-c+Dx-d, где a, b, c и d являются числами, A, B, C и D – неопределенными коэффициентами.

Пример 3

Когда знаменатель имеет выражение (x-a)2(x-b)4(x-c)3, количество множителей также не имеет значения, причем саму дробь необходимо привести ко второму или первому типу вида:

A2x-a2+A1x-a+B4x-b4+B3x-b3+B2x-b2+B1x-b++C3x-c3+C2x-c2+C1x-c

где имеющиеся a, b, c являются числами, а A1, A2, B1, B2, B3, B4, C1, C2, C3 – неопределенными коэффициентами. Какова степень многочлена, такое количество слагаемых имеем.

Пример 4

Когда знаменатель имеет вид типа x2+px+qx2+rx+s, тогда количество квадратичных функций значения не имеет,  а дробь принимает вид третьего типа Px+Qx2+px+q+Rx+Sx2+rx+s,где имеющиеся p, q, r и s являются числами, а P, Q, R и S – определенными коэффициентами.

Пример 5

Когда знаменатель имеет вид x2+px+q4x2+rx+s2, количество множителей значения не имеет также , как и их степени, дробь представляется в виде третьего и четверного типов вида

P4x+Q4(x2+px+q)4+P3x+Q3(x2+px+q)3+P2x+Q2(x2+px+q)2+P1x+Q1x2+px+q++R2x+S2(x2+rx+s)2+R1x+S1x2+rx+s

где имеющиеся p, q, r и s являются числами, а P1,P2,P3,P4,R1,R2,S1,S2 – неопределенными коэффициентами.

Пример 6

Когда имеется знаменатель вида (x-a)(x-b)3(x2+px+q)(x2+rx+s)2, тогда дробь необходимо представить в виде четвертого типа

Ax-a+B3x-b3+В2x-b2+В1x-b++Px+Qx2+px+q+R2x+S2x2+rx+s2+R1x+S1x2+rx+s

Рассмотрим на примере дроби. Когда дробь раскладывается  в сумму третьим типом вида 2x-3×3+x=2x-3x(x2+1)=Ax+Bx+Cx2+1, где A, B и C являются неопределенными коэффициентами.

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

2x-3×3+x=2x-3x(x2+1)=Ax+Bx+Cx2+1==A(x2+1)+(Bx+C)xx(x2+1)=Ax2+A+Bx2+Cxx(x2+1)==x2(A+B)+xC+Ax(x2+1)

Когда х отличен от 0, тогда решение сводится к приравниванию двух многочленов. Получаем 2x-3=x2(A+B)+xC+A. Многочлены считаются равными тогда, когда совпадают коэффициенты при одинаковых степенях.

  • Приравнивание коэффициентов с одинаковыми степенями х. Получим, что система линейных уравнений при наличии определенных коэффициентов:
    A+B=0C=2A=-3
  • Решение полученной системы при помощи любого способа для нахождения неопределенных коэффициентов: A+B=0C=2A=-3⇔A=-3B=3C=2
  • Производим запись ответа:
    2×3+3×3+x=2-2x-3×3+x=2-2x-3x(x2+1)==2-Ax+Bx+Cx2+1=2–3x+3x+2×2+1=2+3x-3x+2×2+1

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

2+3x-3x+2×2+1=2x(x2+1)-(3x+2)xx(x2+1)=2×3+3×3+x

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

x-ax-bx-cx-d.

Пример 7

Произвести разложение дроби 2×2-x-7×3-5×2+6x.

Решение

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти  к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

x3-5×2+6x=x(x2-5x+6)

Квадратный трехчлен x2-5x+6 имеет корни, которые находим не по дискриминанту, а по теореме Виета. Получим:

x1+x2=5×1·x2=6⇔x1=3×2=2

Запись трехчлена может быть в виде x2-5x+6=(x-3)(x-2).

Тогда изменится знаменатель:x2-5×2+6x=x(x2-5x+6)=x(x-3)(x-2)

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

2×2-x-7×3-5×2+6x=2×2-x-7x(x-3)(x-2)=Ax+Bx-3+Cx-2

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

2×2-x-7×3-5×2+6x=2×2-x-7x(x-3)(x-2)=Ax+Bx-3+Cx-2==A(x-3)(x-2)+Bx(x-2)+Cx(x-3)x(x-3)(x-2)

После упрощения придем к неравенству вида

2×2-x-7x(x-3)(x-2)=A(x-3)(x-2)+Bx(x-2)+Cx(x-3)x(x-3)(x-2)⇒⇒2×2-x-7=A(x-3)(x-2)+Bx(x-2)+Cx(x-3)

Теперь переходим к нахождению неопределенных коэффициентов. Нужно подставлять полученные значения в равенство для того, чтобы знаменатель обратился в ноль, то есть значения х=0, х=2 и х=3.

Если х=0, получим:

2·02-0-7=A(0-3)(0-2)+B·0·(0-2)+C·0·(0-3)-7=6A⇒A=-76

Если x=2, тогда

2·22-2-7=A(2-3)(2-2)+B·2·(2-2)+C·2·(2-3)-1=-2C⇒C=12

Если x=3, тогда

2·32-3-7=A(3-3)(3-2)+B·3·(3-2)+C·3·(3-3)8=3B⇒B=83

Ответ: 2×2-x-7×3-5×2+6x=Ax+Bx-3+Cx-2=-76·1x+83·1x-3+12·1x-2

Метод коэффициентов и метод частных значений  отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

Пример 8

Произвести разложение выражения x4+3×3+2x-11(x-1)(x+1)(x-3)3 на простейшие дроби.

Решение

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

x4+3×3+2x-11(x-1)(x+1)(x-3)3=Ax-1+Bx+1+C(x-3)3+C(x-3)2+Cx-3

Производим приведение к общему знаменателю. Имеем, что

x4+3×3+2x-11(x-1)(x+1)(x-3)3=Ax-1+Bx+1+C(x-3)3+C(x-3)2+Cx-3==A(x+1)(x-3)3+B(x-1)(x-3)3(x-1)(x+1)(x-3)3++C3(x-1)(x+1)+C2(x-1)(x+1)(x-3)+C1(x-1)(x+1)(x-3)2(x-1)(x+1)(x-3)3

Приравняем числители и получим, что

x4+3×3+2x+11==A(x+1)(x-3)3+B(x-1)(x-3)3++C3(x-1)(x+1)+C2(x-1)(x+1)(x-3)+C1(x-1)(x+1)(x-3)2

Из выше написанного понятно, что нули знаменателя – это х=1, х=-1 и х=3. Тогда применим метод частных решений. Для этого подставим значения х. получим, что если х=1:

-5=-16A⇒A=516

Если х=-1

-15=128B⇒B=-15128

Если х=3

157=8C3⇒C3=1578

Отсюда следует, что нужно найти значения C1 и C3.

Поэтому подставим полученный значения  в числитель, тогда

x4+3×3+2x-11==516(x+1)(x-3)3-15128(x-1)(x-3)3+1578(x-1)(x+1)++C2(x-1)(x+1)(x-3)+C1(x-1)(x+1)(x-3)2

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

x4+3×3+2x-11=x425128+C1+x3-8564+C2-6C1++x267332-3C2+8C1+x40564-C2+6C1+3C2-9C1-3997128

Необходимо приравнять соответствующие коэффициенты с одинаковыми степенями, тогда сможем найти искомое значение C1 и C3.  Теперь необходимо решить систему:

25128+C1=1-8564+C2-6C1=367332-3C2+8C1=040564-C2+6C1=23C2-9C1-3997128=11

Первое уравнение дает возможность найти C1=103128, а второе C2=3+8564+6C1=3+8564+6·103128=29332.

Итог решения – это искомое разложение дроби на простейшие вида:

x4+3×3+2x-11(x-1)(x+1)(x-3)3=Ax-1+Bx+1+C3x-33+C2x-32+C1x-3==5161x-1-151281x+1+1578·1x-33+293321x-32+1031281x-3

Примечание

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Среди данных дробей выберите те, которые можно представить в виде дроби со знаменателем 4, и покажите, как это сделать:

12
20

;

4
16

;

24
32

;

8
12

;

32
40

;

33
44

.

reshalka.com

ГДЗ учебник по математике 5 класс Зубарева. § 21. Основное свойство дроби. Номер №354

Решение

4
16

=

4
∗
1

4
∗
4

=

1
4

24
32

=

8
∗
3

8
∗
4

=

3
4

33
44

=

11
∗
3

11
∗
4

=

3
4

Источник

Разложение рациональной дроби на простейшие ― представление рациональной дроби в виде суммы многочлена и простейших дробей. Разложение на простейшие используется во многих задачах, например для интегрирования[1], разложения в ряд Лорана[2], расчёта обратного преобразования Лапласа рациональных функций[3].

Определение[править | править код]

Рациональная дробь называется простейшей если её знаменатель представляет собой степень некоторого неприводимого многочлена и степень её числителя меньше степени этого неприводимого многочлена.[4]

Представление дроби в виде {displaystyle {frac {P(x)}{Q(x)}}=G(x)+sum _{i=1}^{n}{frac {P_{i}(x)}{Q_{i}(x)}}}, где G(x) ― многочлен, а дроби {displaystyle {frac {P_{i}(x)}{Q_{i}(x)}}} ― простейшие, называется разложением дроби {displaystyle {frac {P(x)}{Q(x)}}} на простейшие.

Такое представление существует для любой рациональной дроби над полем и единственно с точностью до перестановки слагаемых.

Способы разложения[править | править код]

Выделение целой части[править | править код]

Любую рациональную дробь над полем можно единственным образом представить в виде суммы многочлена (называемого целой частью дроби) и правильной дроби (называемой дробной частью).[5] В свою очередь любая правильная дробь раскладывается в сумму одних только простейших дробей без слагаемого многочлена. Таким образом, задача разложения дроби на простейшие может быть решена в два этапа: сначала разложить в сумму целой и дробной части (эта процедура называется выделением целой части), а зачем разложить дробную часть в сумму простейших.

Выделение целой части происходит с помощью деления многочлена в числителе на многочлен в знаменателе в столбик. Полученное в результате неполное частное ― это целая часть, а остаток делённый на делимое ― дробная.

Алгоритм деления в столбик на каждой итерации получает новое значение остатка и частного. Перед началом положим значение остатка равным делимому, а значение частного равным 0.

  1. Если степень остатка меньше степени делителя, то алгоритм завершается.
  2. Пусть {displaystyle ax^{n}} ― член остатка со старшей степенью, {displaystyle bx^{m}} ― член делителя со старшей степенью. Тогда к частному прибавляем {displaystyle {frac {a}{b}}x^{n-m}}, а из остатка вычитаем {displaystyle {frac {a}{b}}x^{n-m}Q(x)} и переходим к шагу 1.[6]

Таким образом в конце мы получим неполное частное G(x) и остаток R(x). В итоге {displaystyle {frac {P(x)}{Q(x)}}=G(x)+{frac {R(x)}{Q(x)}}}, где {displaystyle {frac {P(x)}{Q(x)}}} ― правильная дробь, раскладывающаяся в сумму простейших дробей. Задача свелась к разложению в сумму простейших правильной дроби.

Несмотря на то, что большинство методов разложения правильной дроби на простейшие могут быть применены и к неправильной, все эти методы существенно сложнее деления многочленов в столбик. Предварительное нахождение коэффициентов целой части делением в столбик уменьшает количество коэффициентов, которые придётся искать «сложными» методами, тем самым упрощая вычисления.

Метод неопределённых коэффициентов[править | править код]

Метод неопределённых коэффициентов состоит в том, чтобы записать разложение на простейшие с неизвестными коэффициентами, составить систему уравнений на эти коэффициенты и решить ее. Пусть {displaystyle {frac {P(x)}{Q(x)}}} ― правильная дробь в несократимой записи, {displaystyle Q(x)=(Q_{i_{1}}(x))^{m_{1}}...(Q_{i_{n}}(x))^{m_{n}}} ― разложение знаменателя Q(x) на неприводимые множители. Тогда разложение на простейшие имеет вид {displaystyle {frac {P(x)}{Q(x)}}=sum _{i=1}^{n}sum _{j=1}^{m_{i}}{frac {A_{ij}}{(Q_{i}(x))^{j}}}}.
Умножим обе части равенства на Q(x). Получим равенство многочленов {displaystyle P(x)=sum _{i=1}^{n}sum _{j=1}^{m_{i}}A_{ij}(Q_{1}(x))^{m_{1}}...(Q_{i-1}(x))^{m_{i-1}}(Q_{i}(x))^{m_{i}-j}(Q_{i+1}(x))^{m_{i+1}}...(Q_{n}(x))^{m_{n}}}.
Многочлены равны тогда, когда их коэффициенты при одинаковых степенях равны. Приравняв их получим систему линейных алгебраических уравнений над A_{{ij}} с n уравнениями и n неизвестными. Решив её, получим искомые значения A_{{ij}}.[7]

Получающиеся таким способом уравнения часто довольно громоздки. Поэтому на практике подстановкой стараются получить более простые уравнения. Общая схема этого приёма такова: равенство {displaystyle {frac {P(x)}{Q(x)}}=sum _{i=1}^{n}sum _{j=1}^{m_{i}}{frac {A_{ij}}{(Q_{i}(x))^{j}}}} умножают на некоторый многочлен, а затем подставляют в него вместо x какое-то определённое значение.
Чаще всего умножают на Q(x) и подставляют его корень. Таким образом, почти все слагаемые зануляются и получается довольно простое уравнение, позволяющее почти сразу вычислить один из коэффициентов. Этот приём позволяет находить коэффициенты при старших степенях линейных множителей.[8]
В качестве подставляемого корня можно даже использовать корень не принадлежащий основному полю. Например, в действительных числах часто используют подстановку комплексного корня, а затем приравнивают действительную и мнимую часть уравнения. Аналогично можно сделать и над произвольным полем. Впрочем, это приравнивание не обязательно, недостающие уравнения можно получить и другими способами.
Также иногда используют подстановку бесконечности: умножают на один из линейных многочленов, входящих в разложение Q(x), и подставляют бесконечность (тут правильность дроби {displaystyle {frac {P(x)}{Q(x)}}} становится существенна). Данный приём позволяет просто находить коэффициенты при первой степени линейных множителей.[9]
В общем преобразование уравнения и последующая подстановка может быть какой угодно, важно лишь то, чтобы эта подстановка имела смысл и не превращала слагаемые в бесконечности. Например при подстановке корня знаменателя нужно предварительно умножить уравнение на многочлен, избавляющий от деления на 0, а при подстановке бесконечности смотреть, чтобы нигде не получилось целое слагаемое, содержащее x.

Решение системы линейных алгебраических уравнений довольно трудоёмкий процесс, из-за чего на практике используют менее универсальные, но более простые методы.

Метод прикрытия Хевисайда[править | править код]

Метод Хевисайда состоит в прямом вычислении коэффициентов с помощью следующей формулы. Пусть в разложении Q(x) на неприводимые множители есть линейный множитель x-a, m ― его кратность. В разложении на простейшие содержатся слагаемые вида {displaystyle {frac {B_{j}}{(x-a)^{j}}}}, где {displaystyle 1leq jleq m}. Тогда

{displaystyle B_{m}={frac {P(x)(x-a)^{m}}{Q(x)}}{Bigr |}_{x=a}} ― формула Хевисайда[10]

Формула Хевисайда позволяет без каких-либо затруднений сразу же получить большую часть коэффициентов, из-за чего она очень широко применяется на практике. В случае если знаменатель дроби раскладывается на линейные множители, методом Хэвисайда можно получить всё разложение сразу. Если же нет, то вычисление оставшихся коэффициентов требует использования иных методов, например метода неопределённых коэффициентов.

Метод Лагранжа[править | править код]

Метод Лагранжа предлагает другую формулу для вычисления коэффициентов. Пусть a ― корень знаменателя кратности 1. Тогда коэффициент A при {displaystyle {frac {1}{x-a}}} равен

{displaystyle A={frac {P(x)}{Q'(x)}}{Bigr |}_{x=a}} ― формула Лагранжа. [11]

Аналогично методу Хевисайда метод Лагранжа позволяет сразу найти разложение на простейшие в случае если знаменатель раскладывается на линейные множители.

Обобщение формулы Лагранжа[править | править код]

Формулу Лагранжа можно обобщить для корня кратности m:

{displaystyle A_{m}=m!{frac {P(x)}{Q^{(m)}(x)}}{Bigr |}_{x=a}}, где A_{m} ― коэффициент при {displaystyle {frac {1}{(x-a)^{m}}}}.[12]

Таким образом, любой коэффициент, который может быть найден с помощью этой формулы, может быть найден с помощью формулы Хевисайда, и наоборот.

Вынесение повторяющихся множителей[править | править код]

Один из способов нахождения остальных коэффициентов без применения метода неопределённых коэффициентов ― вынесение повторяющихся множителей.[13] Рассмотрим его на примере.

Пусть нужно разложить дробь {displaystyle {frac {1}{(s+1)^{2}(s+2)}}}. Вынесем повторяющиеся множители.
{displaystyle {frac {1}{s+1}}left({frac {1}{(s+1)(s+2)}}right)}. Правый множитель состоит только из линейных множителей, а значит, его можно разложить по методу Хэвисайда или Лагранжа. Разложим.
{displaystyle {frac {1}{s+1}}left({frac {1}{s+1}}-{frac {1}{s+2}}right)}. Раскроем скобки.
{displaystyle {frac {1}{(s+1)^{2}}}-{frac {1}{(s+1)(s+2)}}}. Разложение правой дроби на простейшие мы уже знаем.
{displaystyle {frac {1}{(s+1)^{2}}}-{frac {1}{s+1}}+{frac {1}{s+2}}} ― искомое разложение.

Рекурсивный метод[править | править код]

Метод заключается в том, чтобы найти все старшие простейшие слагаемые со старшей степенью при помощи метода Хевисайда (или обобщённого Лагранжа), затем вычесть из первоначальной дроби и повторить эту процедуру для получившейся дроби.[14]

Пусть нужно разложить дробь {displaystyle {frac {1}{(x-1)^{2}(x-2)^{3}}}}. Найдём старшие простейшие слагаемые:
{displaystyle -{frac {1}{(x-1)^{2}}},{frac {1}{(x-2)^{3}}}}. Вычтем их из первоначальной дроби.
{displaystyle {frac {1}{(x-1)^{2}(x-2)^{3}}}+{frac {1}{(x-1)^{2}}}-{frac {1}{(x-2)^{3}}}={frac {x-4}{(x-2)^{2}(x-1)}}}. Полученная дробь это сумма оставшихся простейших дробей, а значит эти оставшиеся дроби есть ни что иное как разложение полученной дроби на простейшие. Вновь находим старшие простейшие слагаемые.
{displaystyle -{frac {2}{(x-2)^{2}}},-{frac {3}{x-1}}}. Вычитаем.
{displaystyle {frac {x-4}{(x-2)^{2}(x-1)}}+{frac {2}{(x-2)^{2}}}+{frac {3}{x-1}}={frac {3}{x-2}}}. Получилась правильная дробь, а значит все слагаемые разложения найдены.
{displaystyle {frac {1}{(x-1)^{2}(x-2)^{3}}}={frac {1}{(x-2)^{3}}}-{frac {1}{(x-1)^{2}}}-{frac {2}{(x-2)^{2}}}-{frac {3}{x-1}}+{frac {3}{x-2}}}.

Наибольшую сложность в этом методе представляет вычитание дробей с последующим её сокращением. Для упрощения этого шага выполняют следующий приём.

Пусть нужно найти {displaystyle {frac {R(x)}{D(x)}}={frac {P(x)}{Q(x)}}-sum _{i=1}^{n}{frac {A_{i}}{(x-x_{i})_{i}^{m}}}}.
Знаменатель дроби D(x) нам и так известен: это Q(x), поделенный на произведение {displaystyle (x-x_{i})} (без учёта кратности). Поэтому задача состоит в том, чтобы найти R(x). Для этого умножим всё равенство на D(x). Получим, что R(x) равен сумме дробей. Но, так как сумма правильных дробей вновь правильная дробь, сумма дробных частей этих дробей будет равна 0, а сам многочлен будет равен сумме целых частей. Таким образом, достаточно найти лишь неполное частное от деления этих дробей, а на остатки не обращать внимания. С данной модификацией этот метод называется методом отбрасывания остатков.[15]

Рассмотрим на примере сверху.
{displaystyle {frac {1}{(x-1)^{2}(x-2)^{3}}}+{frac {1}{(x-1)^{2}}}-{frac {1}{(x-2)^{3}}}}. Умножим на D(x)
{displaystyle {frac {1}{(x-1)(x-2)}}+{frac {(x-2)^{2}}{x-1}}-{frac {x-1}{x-2}}}. Первое слагаемое правильное, значит его можно отбросить. Считаем целую часть второго слагаемого. Поделим {displaystyle (x-2)^{2}} на x-1 в столбик. Получим {displaystyle x-3}. Аналогично целая часть последнего слагаемого ― −1. Складываем их и получаем искомый многочлен ― {displaystyle x-4}.

Простые преобразования[править | править код]

Иногда разложение на простейшие можно получить просто преобразовывая выражения.[16]

{displaystyle {frac {x^{2}-1}{x(x^{2}+1)^{2}}}={frac {x^{2}-(x^{2}+1)+x^{2}}{x(x^{2}+1)^{2}}}={frac {2x}{(x^{2}+1)^{2}}}-{frac {1}{x(x^{2}+1)}}={frac {2x}{(x^{2}+1)^{2}}}-{frac {(x^{2}+1)-x^{2}}{x(x^{2}+1)}}={frac {2x}{(x^{2}+1)^{2}}}-{frac {1}{x}}+{frac {x}{x^{2}+1}}}

Метод вычетов[править | править код]

Формула Хевисайда может быть обобщена для произвольного коэффициента.

Пусть в разложении Q(x) на неприводимые множители есть линейный множитель x-a, m ― его кратность. В разложении на простейшие содержатся слагаемые вида {displaystyle {frac {B_{k}}{(x-a)^{k}}}}, где {displaystyle 1leq kleq m}. Тогда:

{displaystyle B_{k}={frac {1}{(m-k)!}}left({frac {P(x)(x-a)^{m}}{Q(x)}}right)^{(m-k)}{Bigr |}_{x=a}}[12]

Для множителей высокой кратности данная формула требует подсчёта производной рациональной дроби высокого порядка, что является достаточно трудоёмкой операцией.

Коэффициенты у многочленов старших степеней[править | править код]

Если в знаменателе простейшей дроби стоит неприводимый многочлен выше первой степени, то для нахождения её числителя из всех перечисленных методов можно использовать только метод неопределённых коэффициентов. Однако этой проблемы можно избежать, если найти разложение на простейшие в алгебраическом замыкании поля (или, точнее, в любом расширении, содержащим поле разложения знаменателя), а затем сложить слагаемые с сопряжёнными знаменателями. Такой способ очень часто используется для нахождения разложения на простейшие над полем действительных чисел.[17]

Рассмотрим пример. Пусть нужно найти разложение
{displaystyle {frac {1}{(x^{2}+1)(x+1)}}}. Перейдём в поле комплексных чисел и разложим знаменатель на линейные множители.
{displaystyle {frac {1}{(x+i)(x-i)(x+1)}}}. Воспользуемся методом Хэвисайда.
{displaystyle {frac {displaystyle {frac {1}{2}}}{x+1}}+{frac {displaystyle {frac {1}{2i(i+1)}}}{x-i}}-{frac {displaystyle {frac {1}{2i(-i+1)}}}{x+i}}}. Теперь сложим дроби с сопряжёнными знаменателями.
{displaystyle {frac {displaystyle {frac {1}{2}}}{x+1}}+{frac {displaystyle {frac {1}{2}}(1-x)}{x^{2}+1}}} ― искомое разложение.

Комбинации методов[править | править код]

Приведённые методы дают способы вычисления отдельных коэффициентов, однако они не требуют вычисления остальных именно этим методом. Таким образом, можно как угодно комбинировать эти методы: один коэффициент посчитать методом Хевисайда, другой методом Лагранжа, а оставшиеся методом неопределённых коэффициентов, который уже будет значительно проще, чем если бы все коэффициенты были неизвестны. Использование в нужных случаях подходящих методов даст возможность просто и эффективно находить разложение.

Вариации и обобщения[править | править код]

В евклидовом кольце[править | править код]

Понятие простейшей дроби можно очевидным образом обобщить для поля частных евклидова кольца. Назовём правильной дробью дробь, если евклидова норма её числителя меньше евклидовой нормы её знаменателя. Правильную дробь назовём простейшей, если в её знаменателе стоит неприводимый элемент в некоторой степени. Тогда разложение дроби на простейшие определяется как представление в виде суммы некоторого элемента из евклидова кольца и простейших дробей.

Для любой дроби из поля частных евклидова кольца существует разложение на простейшие, однако не для любого евклидова кольца оно всегда будет единственным.[18] Например над целыми числами с дроби могут иметь несколько разложений: {displaystyle {frac {1}{4}}={frac {1}{2}}-{frac {1}{4}}} (здесь евклидова норма ― модуль целого числа, {frac {1}{4}} ― простейшая дробь, поэтому она является разложением на простейшие самой себя, но при этом мы смогли получить ещё одно разложение).

Разложение на простейшие единственно для всех элементов поля частных евклидова кольца тогда и только тогда, когда это кольцо либо поле, либо изоморфно кольцу многочленов над полем (при этом евклидова норма эквивалентна степени многочлена).[19].

В целых числах[править | править код]

Для целых чисел можно рассмотреть альтернативное определение разложения на простейшие. Потребуем, чтобы все простейшие слагаемые были положительными. Тогда для любого рационального числа существует и единственно разложение на простейшие.[20]

Например, {displaystyle {frac {77}{12}}=5+{frac {1}{2}}+{frac {1}{4}}+{frac {2}{3}}} ― единственное разложение на простейшие с положительными простейшими слагаемыми. Если разрешить отрицательные простейшие слагаемые, то, как уже было показано выше, разложение перестанет быть единственным.

См. также[править | править код]

  • Разложение дробей при интегрировании
  • Метод неопределённых коэффициентов
  • Ряд Лорана

Примечания[править | править код]

  1. ↑ Зорич, 2019, с. 292.
  2. ↑ Краснов, 1971, с. 51.
  3. ↑ Краснов, 1971, с. 125.
  4. ↑ Фаддеев, 1984, с. 187.
  5. ↑ Фаддеев, 1984, с. 184.
  6. ↑ Фаддеев, 1984, с. 168.
  7. ↑ Brazier, 2007, с. 2.
  8. ↑ Gustafson, 2008, с. 2.
  9. ↑ Gustafson, 2008, с. 5.
  10. ↑ Gustafson, 2008, с. 3.
  11. ↑ Hazra, 2016, с. 28.
  12. ↑ 1 2 Bauldry, 2018, с. 429.
  13. ↑ Gustafson, 2008, с. 4.
  14. ↑ Man, 2009, с. 809.
  15. ↑ Brazier, 2007, с. 809.
  16. ↑ Кудрявцев, 2003, с. 502.
  17. ↑ Bauldry, 2018, с. 430.
  18. ↑ Bradley, 2012, с. 1526.
  19. ↑ Bradley, 2012, с. 1527.
  20. ↑ Bradley, 2012, с. 1528.

Литература[править | править код]

  • Зорич В. А. Математический анализ. Часть 1. — 10-е изд. — М.: МЦНМО, 2019. — 564 p.
  • Краснов М. Л., Киселёв А. И., Макаренко Г. И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. — М.: Наука, 1971. — 256 p.
  • Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — 416 p.
  • Bauldry W.C. Partial Fractions via Calculus (англ.) // Daniel Alpay Problems, Resources, and Issues in Mathematics Undergraduate Studies : журнал. — 2018. — 9 May (vol. 28, iss. 5). — P. 425–437. — ISSN 1051-1970. — doi:10.1080/10511970.2017.1388312.
  • Gustafson G. B. Heviside’s Method (англ.) (pdf). Grant B. Gustafson at math.utah.edu (2008). Дата обращения: июль 2021.
  • Brazier R. A., Boman E. C. How to Compute the Partial Fraction Decomposition Without Really Trying (англ.) // AMATYC Review : журнал. — 2007. — Vol. 21, no. 1. — P. 20–29. — ISSN 0740-8404.
  • Hazra M. Decomposition of Partial Fractions Using Lagrange Method (англ.) // Research Journal Of Pure Science : журнал. — 2016. — Vol. 5, no. 2. — P. 27–32. — ISSN 2348-5361.
  • Yiu-Kwong Man. An improved Heaviside approach to partial fraction expansion and its applications (англ.) // International Journal of MathematicalEducation in Science and Technology : журнал. — 2009. — 4 August (vol. 40, iss. 6). — P. 808–814. — doi:10.1080/00207390902825310.
  • Bradley W. T., Cook W. J. Two Proofs of the Existence and Uniqueness of the Partial Fraction Decomposition (англ.) // International Mathematical Forum : журнал. — 2012. — Vol. 7, no. 31. — P. 1517–1535.
  • Кудрявцев Л. Д. Курс математического анализа. В 3-х томах. Том 1. Дифференциальное и интегральное исчисления функций многих переменных. — М.: Дрофа, 2003. — 704 p.
Источник

Содержание:

  • Основные понятия и определения
  • Разложении правильной рациональной дроби

Основные понятия и определения

Определение

Простыми дробями называются рациональные дроби вида
$frac{A}{(x-a)^{n}}$,
$frac{B x+C}{left(x^{2}+p x+qright)^{m}}$, где
$n,m geq 1$,
$p^2-4q < 0$.

Теорема

(О разложении многочлена на элементарные множители)

Многочлен $n$-ой степени может быть разложен на произведение сомножителей следующим образом:

$P_{n}(x)=a_{0}left(x-x_{1}right)left(x-x_{2}right) ldotsleft(x-x_{n}right)$

Здесь $x_{i}, i=overline{1 ; n}$ – корни многочлена
$P_{n}x$, а
$a_0$ – коэффициент при старшей степени
$x^n$ указанного многочлена.

Квадратный трехчлен можно разложить на множители следующим образом:

$$a x^{2}+b x+c=aleft(x-x_{1}right)left(x-x_{2}right)$$

если $b^{2}-4 a c geq 0$ . Здесь
$x_1,x_2$ – корни многочлена
$ax^2+bx+c$ .

Пример

Задание. Разложить на множители многочлен $f(x)=x^2+5x-6$

Решение. Найдем вначале корни многочлена, для этого решим уравнение
$f(x)=0$ :

$$f(x)=0 Rightarrow x^{2}+5 x-6=0$$

Находим дискриминант:

$$D=b^{2}-4 a c=5^{2}-4 cdot 1 cdot(-6)=25+24=49$$
$$sqrt{D}=sqrt{49}=7$$

Тогда

$$x_{1,2}=frac{-b pm sqrt{D}}{2 a}=frac{-5 pm 7}{2 cdot 1}=frac{-5 pm 7}{2}={1 ;-6}$$

Таким образом,

$$f(x)=x^{2}+5 x-6=1 cdot(x-1)(x-(-6))=(x-1)(x+6)$$

Можете проверить решение на нашем онлайн калькуляторе – решение квадратных уравнений.

Ответ. $f(x)=(x-1)(x+6)$

Многочлен третьей степени:

$$a x^{3}+b x^{2}+c x+d=aleft(x-x_{1}right)left(x-x_{2}right)left(x-x_{3}right)$$

или 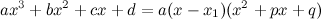, если
$a x^{3}+b x^{2}+c x+d=aleft(x-x_{1}right)left(x^{2}+p x+qright),$ ecли $p^{2}-4 q< 0$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Разложить на множители кубический многочлен
$f(x)=x^3-x^2-4x-6$

Решение. Найдем корни данного многочлена. Известно, что если многочлен имеет корни, то они являются делителем
свободного коэффициента, то есть в данном случае 6, а это ±1,±2,±3,±6.
Подставляем указанные значения в заданный многочлен:

$$begin{array}{c}
f(1)=1^{3}-1^{2}-4 cdot 1-6=-10 neq 0 \
f(-1)=(-1)^{3}-(-1)^{2}-4 cdot(-1)-6=-4 neq 0 \
f(2)=2^{3}-2^{2}-4 cdot 2-6=-10 neq 0 \
f(-2)=(-2)^{3}-(-2)^{2}-4 cdot(-2)-6=-10 neq 0 \
f(3)=3^{3}-3^{2}-4 cdot 3-6=0
end{array}$$

Итак, один корень найден, это $x_1=3$ .

Для нахождения остальных двух корней поделим заданный многочлен
$f(x)$ на двучлен
$x-3$ в столбик (уголком):

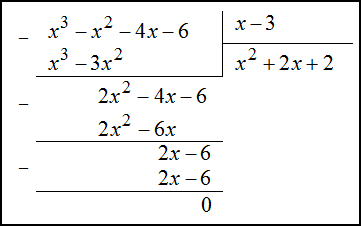
Тогда

$$f(x)=x^{3}-x^{2}-4 x-6=(x-3)left(x^{2}+2 x+2right)$$

Находим теперь корни квадратного трехчлена $x^2+2x+2$ . Для
этого приравниваем его к нулю и находим дискриминант:

$$x^{2}+2 x+2=0 Rightarrow D=2^{2}-4 cdot 1 cdot 2=4-8=-4<0$$ lt p>Таким образом, трехчлен $x^2+2x+2$ действительных корней не имеет.

Итак, искомое разложение

$$f(x)=(x-3)left(x^{2}+2 x+2right)$$

Ответ. $f(x)=(x-3)left(x^{2}+2 x+2right)$

Разложении правильной рациональной дроби

Теорема

(О разложении правильной рациональной дроби на сумму простых дробей)

Каждая рациональная дробь $frac{P_{m}(x)}{Q_{n}(x)}$,
знаменатель которой имеет вид $Q_{n}(x)=left(x-x_{1}right)^{n}left(x-x_{2}right)^{m} ldotsleft(x^{2}+p_{1} x+q_{1}right)^{k} ldots$ , может быть разложена
и притом единственным образом на сумму простых дробей по правилу

$$begin{aligned}
frac{P_{m}(x)}{Q_{n}(x)}=& frac{A_{1}}{x-x_{1}}+ldots+frac{A_{n}}{left(x-x_{1}right)^{n}}+frac{B_{1}}{x-x_{2}}+ldots+frac{B_{m}}{left(x-x_{2}right)^{m}}+\
&+frac{C_{1} x+D_{1}}{x^{2}+p_{1} x+q_{1}}+ldots+frac{F_{k} x+G_{k}}{left(x^{2}+p_{1} x+q_{1}right)^{k}}+ldots
end{aligned}$$

где $A_{1}, ldots, A_{n} ; B_{1}, ldots, B_{m} ; C_{1}, ldots, C_{k}: D_{1}, ldots, D_{k}$ – действительные постоянные числа,
часть которых в разложении может обратиться в нуль.

В частности, если в знаменателе правильной рациональной дроби стоит квадратный трехчлен, то

$$frac{P_{1}(x)}{left(x-x_{1}right)left(x-x_{2}right)}=frac{A}{x-x_{1}}+frac{B}{x-x_{2}}$$

Пример

Задание. Представить в виде суммы простейших дробей дробь
$frac{x+1}{x^{2}+3 x-4}$ . Коэффициенты разложения находить ненужно.

Решение. Знаменатель рассматриваемой дроби можно разложить на множители следующим образом:

$$x^{2}+3 x-4=(x-1)(x+4)$$

то есть

$$frac{x+1}{x^{2}+3 x-4}=frac{x+1}{(x-1)(x+4)}=frac{A}{x-1}+frac{B}{x+4}$$

Ответ. $frac{x+1}{x^{2}+3 x-4}=frac{A}{x-1}+frac{B}{x+4}$

Если многочлен третей степени, то в зависимости от числа и кратности действительных корней разложение будет иметь вид:

$$frac{P_{2}(x)}{left(x-x_{1}right)left(x-x_{2}right)left(x-x_{3}right)}=frac{A}{x-x_{1}}+frac{B}{x-x_{2}}+frac{C}{x-x_{3}}$$

или

$$frac{P_{2}(x)}{left(x-x_{1}right)left(x-x_{2}right)^{2}}=frac{A}{x-x_{1}}+frac{B}{x-x_{2}}+frac{C}{left(x-x_{2}right)^{2}}$$

или

$$frac{P_{2}(x)}{left(x-x_{1}right)left(x^{2}+p x+qright)}=frac{A}{x-x_{1}}+frac{B x+C}{x^{2}+p x+q}$$

Читать дальше: метод неопределенных коэффициентов.

Источник
Автор статьи

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение обыкновенной дроби

Определение 1

Обыкновенные дроби используют для описания числа долей. Рассмотрим пример, с помощью которого можно дать определение обыкновенной дроби.

Яблоко разделили на $8$ долей. В этом случае каждая доля представляет одну восьмую долю целого яблока, т. е. $frac{1}{8}$. Две доли обозначаются $frac{2}{8}$, три доли — $frac{3}{8}$ и т.д., а $8$ долей — $frac{8}{8}$. Каждая из представленных записей называется обыкновенной дробью.

Приведем общее определение обыкновенной дроби.

Определение 2

Обыкновенной дробью называется запись вида $frac{m}{n}$, где $m$ и $n$– любые натуральные числа.

Часто можно встретить следующую запись обыкновенной дроби: $m/n$.

Пример 1

Примеры обыкновенных дробей:

[{3}/{4}, frac{101}{345}, {23}/{5}, frac{15}{15}, {111}/{81}.]

Замечание 1

Числа $frac{sqrt{2}}{3}$, $-frac{13}{37}$, $frac{4}{frac{2}{7}}$, $frac{2,4}{8,3}$ не являются обыкновенными дробями, т.к. не подходят под вышеприведенное определение.

Числитель и знаменатель

Обыкновенная дробь состоит из числителя и знаменателя.

Определение 3

Числителем обыкновенной дроби $frac{m}{n}$ называется натуральное число $m$, которое показывает количество взятых равных долей из единого целого.

Определение 4

Знаменателем обыкновенной дроби $frac{m}{n}$ называется натуральное число $n$, которое показывает, на сколько равных долей разделено единое целое.

«Обыкновенные дроби» 👇

Рисунок 1.

Числитель располагается над дробной чертой, а знаменатель –под дробной чертой. Например, числителем обыкновенной дроби $frac{5}{17}$ является число $5$, а знаменателем — число $17$. Знаменатель показывает, что предмет разделен на $17$ долей, а числитель — что взято $5$ таких долей.

Натуральное число как дробь со знаменателем 1

Знаменателем обыкновенной дроби может быть единица. В таком случае считают, что предмет неделим, т.е. представляет собой единое целое. Числитель такой дроби показывает, сколько целых предметов взято. Обыкновенная дробь вида $frac{m}{1}$ имеет смысл натурального числа $m$. Таким образом получаем обоснованное равенство $frac{m}{1}=m$.

Если переписать равенство в виде $m=frac{m}{1}$, то оно даст возможность любое натуральное число $m$ представить в виде обыкновенной дроби. Например, число $5$ можно представить в виде дроби $frac{5}{1}$, число $123 456$ — это дробь $frac{123 456}{1}$.

Таким образом, любое натуральное число $m$ можно представить в виде обыкновенной дроби со знаменателем $1$, а любую обыкновенную дробь вида $frac{m}{1}$ можно заменить натуральным числом $m$.

Дробная черта как знак деления

Представление предмета в виде $n$ долей является делением на $n$ равных частей. После деления предмета на $n$ долей его можно разделить поровну между $n$ людьми — каждый получит по одной доле.

Пусть имеется $m$ одинаковых предметов, разделенных на $n$ долей. Эти $m$ предметов можно поровну разделить между $n$ людьми, если раздать каждому человеку по одной доле от каждого из $m$ предметов. При этом каждый человек получит $m$ долей $frac{1}{n}$, которые дают обыкновенную дробь $frac{m}{n}$. Получаем, что обыкновенная дробь $frac{m}{n}$ может применяться для обозначения деления $m$ предметов между $n$ людьми.

Связь между обыкновенными дробями и делением выражается в том, что дробную черту можно понимать как знак деления, т.е. $frac{m}{n}=m:n$.

Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.

Пример 2

Например, результат деления $7$ яблок на $9$ человек можно записать как $frac{7}{9}$, т.е. каждый получит семь девятых долей яблока: $7:9=frac{7}{9}$.

Равные и неравные обыкновенные дроби, сравнение дробей

Результатом сравнения двух обыкновенных дробей может быть или их равенство, или их не равенство. При равенстве обыкновенных дробей их называют равными, в другом случае обыкновенные дроби называют неравными.

Обыкновенные дроби $frac{a}{b}$ и $frac{c}{d}$ называют равными, если справедливым является равенство $acdot d=bcdot c$.

Обыкновенные дроби $frac{a}{b}$ и $frac{c}{d}$ называют неравными, если равенство $acdot d=bcdot c$ не выполняется.

Пример 3

Выяснить, являются ли равными дроби $frac{1}{3}$ и $frac{2}{6}$.

Проверим, выполняется ли равенство $acdot d=bcdot c$:

[1cdot 6=3cdot 2.]

Равенство выполняется, значит, дроби $frac{1}{3}$ и $frac{2}{6}$ являются равными: $frac{1}{3}=frac{2}{6}$.

Данный пример можно рассмотреть на примере яблок: одно из двух одинаковых яблок разделено на три равные доли, второе — на $6$ долей. При этом видно, что две шестых доли яблока составляют $frac{1}{3}$ долю.

Пример 4

Проверить, являются ли равными обыкновенные дроби $frac{3}{17}$ и $frac{4}{13}$.

Проверим, выполняется ли равенство $acdot d=bcdot c$:

[3cdot 13ne 17cdot 4;] [39ne 58.]

Равенство не выполняется, значит, дроби $frac{3}{17}$ и $frac{4}{13}$ не равны: $frac{3}{17}ne frac{4}{13}$.

При сравнении двух обыкновенных дробей, если выясняется, что они не равны, можно узнать, какая из них больше, а какая — меньше другой. Для этого используют правило сравнения обыкновенных дробей: нужно привести дроби к общему знаменателю и затем сравнить их числители. У какой дроби числитель будет больше, та дробь и будет являться большей.

Дроби на координатном луче

Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче.

Чтобы на координатном луче отметить точку, которая соответствует дроби $frac{m}{n}$, необходимо от начала координат в положительном направлении отложить $m$ отрезков, длина которых составляет $frac{1}{n}$ долю единичного отрезка. Такие отрезки получают при делении единичного отрезка на $n$ равных частей.

Чтобы отобразить на координатном луче дробное число, нужно единичный отрезок разделить на части.

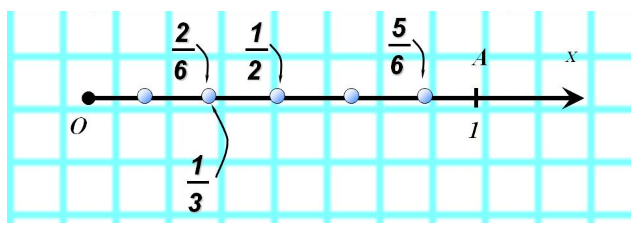
Рисунок 2.

Равные дроби описываются одним и тем же дробным числом, т.е. равные дроби представляют собой координаты одной и той же точки на координатном луче. Например, координатами $frac{1}{3}$, $frac{2}{6}$, $frac{3}{9}$, $frac{4}{12}$ описывается одна и та же точка на координатном луче, так как все записанные дроби равны.

Если точка описывается координатой с большей дробью, то она будет находится правее на горизонтальном направленном вправо координатном луче от точки, координатой которой является меньшая дробь. Например, т.к. дробь $frac{5}{6}$ больше дроби $frac{2}{6}$, то и точка с координатой $frac{5}{6}$ находится правее точки с координатой $frac{2}{6}$.

Аналогично, точка с меньшей координатой будет лежать левее точки с большей координатой.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Добавить комментарий