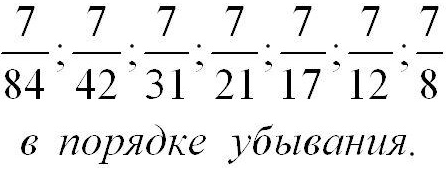Тема дроби объяснение.
Чему равна дробь, числитель которой равен знаменателю? Как сравнивать, складывать, вычитать и умножать дроби с одинаковыми числителем и знаменателем?
Рассмотрим на примерах дроби с одинаковыми числителем и знаменателем.
Проработайте примеры дробей внимательно.
Чему равна дробь, числитель которой равен знаменателю?
Дробь числитель которой равен знаменателю равна единице.
Пример.
Почему дробь, числитель которой равен знаменателю, равна единице?
Дробь – это другой способ записи деления. Смотрите в Дроби объяснение.
Значит дробь мы можем представить в виде деления:
Сравнение дробей с одинаковыми числителями и знаменателями
Дроби с одинаковыми числителями и знаменателями всегда равны.
Сложение дробей с одинаковыми знаменателями и числителями
Сложение дробей с одинаковыми знаменателями и числителями делается так: числители складываются, а знаменатель остается неизменным.
Пример.
| 5 | + | 5 | = | 5 + 5 | = | 10 | = 2 |
|---|---|---|---|---|---|---|---|
| 5 | 5 | 5 | 5 |
Вычитание дробей с одинаковыми числителями и знаменателями
Вычитание дробей с одинаковыми числителями и знаменателями всегда дает ноль.
Пример.
Умножение дробей с одинаковыми знаменателями и числителями
Умножение дробей с одинаковыми знаменателями и числителями всегда дает единицу.
Пример.
Сравнивать дроби очень легко на примере предметов.
Например: апельсин и мандарин разделим на одинаковое количество долек.
Возьмем одну дольку апельсина и одну дольку мандарина.
Дольки будут одинаковые по размеру? (Разные). Почему?
Да, потому что целый апельсин больше, чем мандарин.
Вывод: чтобы сравнить доли, надо чтобы целые предметы, которые мы делим на части, были равные по размеру.
Точно также мы поступаем и с дробями: мы умеем легко сравнивать дроби с разными числителями (см. статью здесь).
А как же сравнивать дроби, если знаменатели разные?
Сегодня мы будем учиться сравнивать дроби с разными знаменателями, но с ОДИНАКОВЫМИ ЧИСЛИТЕЛЯМИ.
Итак, начнем.
Пример 1. Мама испекла торт. К нам в гости могут прийти 5 или 8 человек. Если придут 5 человек, то мы разрежем торт на 5 равных частей, а если придут 8 человек, то разделим на 8 равных частей.
В каком случаем на один гость съест кусок торта большего размера?
Конечно, когда придут 5 человек, кусок торта будет больше.
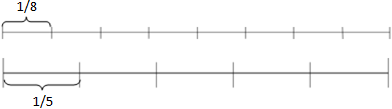
Начертим схему к данной задаче:
На схеме хорошо видно, что отрезок 1/8 меньше отрезка 1/5, а отрезок 1/5 больше отрезка 1/8.
Значит: 1/5 > 1/8, а 1/5 > 1/8.
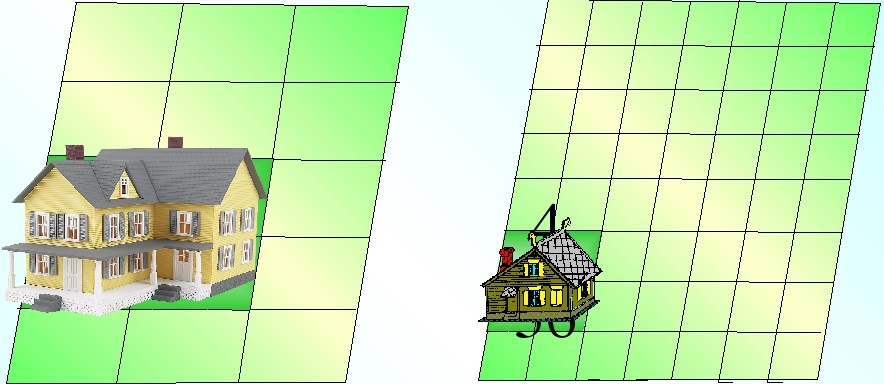
Пример 2. На двух одинаковых участках земли построили дома. Один дом занял 4/15 части участка, а второй — 4/56 участка.
Какой дом больше? Какая часть участка под домом меньше?
Ответ: первый дом занял 4/15 участка, а второй 4/56. Мы видим на рисунке, что первый дом больше, а второй – меньше. Значит, 4/15 > 4/56.
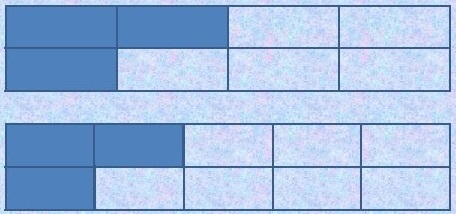
Пример 3. Вырежем из бумаги два одинаковых прямоугольника.
Первый прямоугольник разделим на 8 равных частей. Второй – на 10 равных части. В первом и во втором прямоугольниках по 3 части раскрасим синим цветом.
В каком прямоугольнике раскрашена большая часть? В каком – меньшая?
Мы видим, что в первом прямоугольнике раскрашена большая часть, а во втором – меньшая часть.
Сравним дроби 3/8 и 3/10.
3/8 > 3/10, a 3/10< 3/8.
Итак, мы сравнивали дроби: 1/5 и 1/8; 4/15 и 4/56, 3/8 и 3/10.
Чем похожи дроби в каждой паре?
В каждой паре дроби с одинаковыми числителями.
Мы наглядно увидели, что, оказывается, больше та дробь, где знаменатель был меньше; а меньше та дробь, где знаменатель был больше.
Вывод:
А теперь — потренируемся:
1. Сравните дроби: 2/12 и 2/6; 6/18 и 6/21; 7/15 и 7/20; 8/13 и 8/11.
Проверка:
2/12 и 2/6. Числители у дробей одинаковые, сравниваем знаменатели: 12 больше, чем 6. Мы знаем правило: чем больше знаменатель, тем дробь меньше. Значит: 2/12< 2/6.
6/18 и 6/21. Числители у дробей одинаковые, сравниваем знаменатели: 18 меньше, чем 21. Мы знаем правило: чем меньше знаменатель, тем дробь больше. Значит: 6/18 > 6/21.
7/15 и 7/20. Числители у дробей одинаковые, сравниваем знаменатели: 15 меньше, чем 20. Мы знаем правило: чем меньше знаменатель, тем дробь больше. Значит: 7/15 > 7/20.
8/13 и 8/11. Числители у дробей одинаковые, сравниваем знаменатели: 13 больше, чем 11. Мы знаем правило: чем больше знаменатель, тем дробь меньше. Значит: 8/13< 8/11.
2. Расставить дроби
Проверка:
Нам нужно расставить дроби в порядке убывания, значит, первая дробь должна быть самой большой. Числитель у дробей одинаковый, сравниваем знаменатель: самая большая дробь та, у которой самый маленький знаменатель.
Значит: 7/8, 7/12, 7/17, 7/21, 7/31, 7/42, 7/84.
Похожие статьи
Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.
Сравнение дробей с одинаковыми знаменателями.
Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.
Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.
Рассмотрим пример:
Сравните дроби (frac{7}{26}) и (frac{13}{26}).
Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:
(frac{7}{26} < frac{13}{26})
Сравнение дробей с равными числителями.
Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.
Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.
Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.
(frac{20}{4} > frac{20}{10})
Если мы до решаем эти дроби, то получим числа (frac{20}{4} = 5) и (frac{20}{10} = 2). Получаем, что 5 > 2
В этом и заключается правило сравнения дробей с одинаковыми числителями.
Рассмотрим еще пример.
Сравните дроби с одинаковым числителем (frac{1}{17}) и (frac{1}{15}) .
Так как числители одинаковые, больше та дробь, где знаменатель меньше.
(frac{1}{17} < frac{1}{15})
Сравнение дробей с разными знаменателями и числителями.
Чтобы сравнить дроби с разными знаменателями, необходимо дроби привести к общему знаменателю, а потом сравнить числители.
Пример:
Сравните дроби (frac{2}{3}) и (frac{5}{7}).
Сначала найдем общий знаменатель дробей. Он будет равен числу 21.
(begin{align}&frac{2}{3} = frac{2 times 7}{3 times 7} = frac{14}{21}\\&frac{5}{7} = frac{5 times 3}{7 times 3} = frac{15}{21}\\ end{align})
Потом переходим к сравнению числителей. Правило сравнения дробей с одинаковыми знаменателями.
(begin{align}&frac{14}{21} < frac{15}{21}\\&frac{2}{3} < frac{5}{7}\\ end{align})
Сравнение неправильной и правильной дроби.
Неправильная дробь всегда больше правильной. Потому что неправильная дробь больше 1, а правильная дробь меньше 1.
Пример:
Сравните дроби (frac{11}{13}) и (frac{8}{7}).
Дробь (frac{8}{7}) неправильная и она больше 1.
(1 < frac{8}{7})
Дробь (frac{11}{13}) правильная и она меньше 1. Сравниваем:
(1 > frac{11}{13})
Получаем, (frac{11}{13} < frac{8}{7})
Вопросы по теме:
Как сравнить дроби с разными знаменателями?
Ответ: надо привести к общему знаменателю дроби и потом сравнить их числители.
Как сравнивать дроби?
Ответ: сначала нужно определиться к какой категории относятся дроби: у них есть общий знаменатель, у них есть общий числитель, у них нет общего знаменателя и числителя или у вас правильная и неправильная дробь. После классификации дробей применить соответствующее правило сравнения.
Что такое сравнение дробей с одинаковыми числителями?
Ответ: если у дробей одинаковые числители, та дробь больше у которой знаменатель меньше.
Пример №1:
Сравните дроби (frac{11}{12}) и (frac{13}{16}).
Решение:
Так как нет одинаковых числителей или знаменателей, применяем правило сравнения с разными знаменателями. Нужно найти общий знаменатель. Общий знаменатель будет равен 96. Приведем дроби к общему знаменателю. Первую дробь (frac{11}{12}) умножим на дополнительный множитель 8, а вторую дробь (frac{13}{16}) умножим на 6.
( begin{align}&frac{11}{12} = frac{11 times 8}{12 times 8} = frac{88}{96}\\&frac{13}{16} = frac{13 times 6}{16 times 6} = frac{78}{96}\\ end{align})
Сравниваем дроби числителями, та дробь больше у которой числитель больше.
( begin{align}&frac{88}{96} > frac{78}{96}\\&frac{11}{12} > frac{13}{16}\\ end{align})
Пример №2:
Сравните правильную дробь с единицей?
Решение:
Любая правильная дробь всегда меньше 1.
Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?
Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac{5}{10} ).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac{3}{5} ).
Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.
(begin{align}&frac{3}{5} = frac{3 times 2}{5 times 2} = frac{6}{10}\\&frac{5}{10} < frac{6}{10}\\&frac{5}{10} < frac{3}{5}\\ end{align})
Ответ: у папы результат лучше.
В данной публикации мы рассмотрим, какие дроби являются равными, а также как сравнить две дроби с одинаковыми числителями/знаменателями или с разными знаменателями.
- Равные дроби
-
Сравнение простых дробей
- С одинаковыми знаменателями
- С одинаковыми числителями
- С разными знаменателями
- Другие правила сравнения дробей
Равные дроби
Две дроби являются равными, если их числители и знаменатели соответственно равны (пропорционально равны).
Пример: дроби
4/5
и
8/10
равны, т.к. числитель и знаменатель первой дроби в два раза меньше числителя и знаменателя второй дроби.
Равные дроби соответствует:
- одной и той же точке на числовой оси;
- одной и той же десятичной дроби, которая вычисляется путем деления числителя на знаменатель. В нашем случае 4/5 = 8/10 = 0,8.
Сравнение простых дробей
С одинаковыми знаменателями
Из двух дробей с одинаковыми знаменателями, больше та, у которой числитель больше.
Пример:
5/7
>
3/7
, т.к. 5>3.
С одинаковыми числителями
Из двух дробей с одинаковыми числителями, больше та, у которой знаменатель меньше.
Пример:
6/4
>
6/11
, т.к. 4<11.
С разными знаменателями
Для того, чтобы иметь возможность сравнить дроби с разными знаменателями, для начала их нужно привести к общему знаменателю, после чего их уже можно сравнить по одинаковому знаменателю.
Пример: сравним дроби
3/8
и
2/16
.
В данном случае нам нужно представить первую дробь со знаменателем 16 путем умножения числителя и знаменателя на число 2.
Теперь у нас имеются две дроби с одинаковыми знаменателями, которые мы можем сравнить по соответствующему правилу, рассмотренному выше.
Другие правила сравнения дробей
1. Любая правильная дробь меньше 1.
2. Любая неправильная дробь больше 1.
Пример:
8/3
>1, т.к.
8/3
=2
2/3
>1.
3. Любая неправильная дробь всегда больше правильной, что следует из правил 1 и 2 выше.
Рассмотрим случай сравнения дробей, у которых одинаковые числители..
Чем больше частей, на которые делим предмет, тем каждая часть получается меньше.
Например,
18>112
. То есть при делении на (8) части получаются больше, чем при делении на (12). Значит (5) бо՛льших частей больше, чем пять меньших частей:
58>512
.
| Пиццу разделили на (10) равных частей. | Пиццу разделили на (6) равных частей. |
 |
 |
|
(3) части составляют меньше половины пиццы. |
(3) части составляют половину пиццы. |
 |
 |
Если дроби имеют одинаковые числители, то из них меньше дробь с большим знаменателем (и, наоборот, больше дробь с меньшим знаменателем).
Обрати внимание!
При сравнении дробей с одинаковыми числителями сравнивают знаменатели!