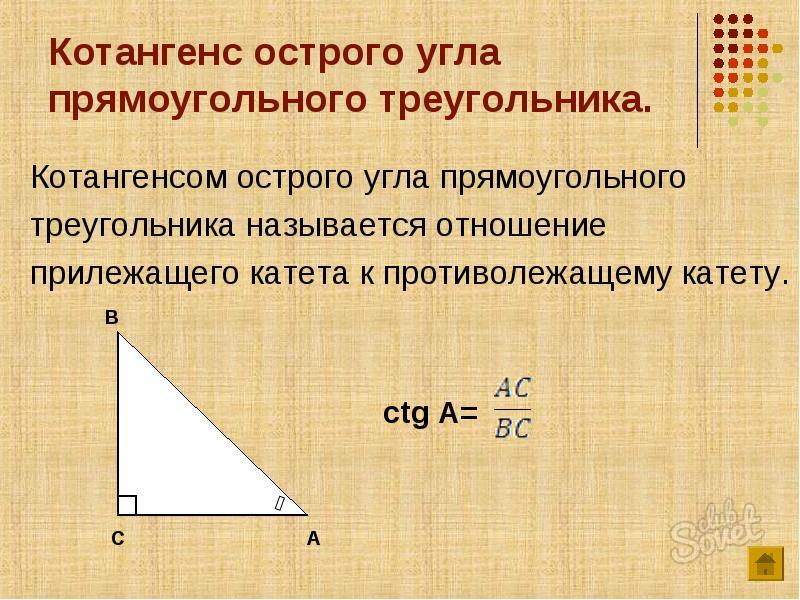
Как найти стороны прямоугольного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как найти стороны прямоугольного треугольника
Чтобы посчитать стороны прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Катет a =
Катет b =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
c² = a² + b²
следовательно: c = √a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √3² + 4² = √9 + 16 = √25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
c = a/cos(β) = b/cos(α)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) =
Гипотенуза c =
0
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
c = a/sin(α) = b/sin(β)
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Гипотенуза c =
Катет (известный) =
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
a = √c² – b²
b = √c² – a²
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √5² – 4² = √25 – 16 = √9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Гипотенуза c =
Угол (прилежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
a = c ⋅ cos(β)
b = c ⋅ cos(α)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Гипотенуза c =
Угол (противолежащий катету) = °
Катет =
0
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
a = c ⋅ sin(α)
b = c ⋅ sin(β)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Катет (известный) =
Угол (прилежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
a = b ⋅ tg(α)
b = a ⋅ tg(β)
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Катет (известный) =
Угол (противолежащий известному катету) = °
Катет (искомый) =
0
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
a = b / tg(β)
b = a / tg(α)
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см
См. также
Это смотря какие данные нам даны для решения.
Например есть теорема Пифагора:
по ней, если катеты a и b, а гипотенуза c, то:
a²+b²=c²
Отсюда можно найти катет, зная длину гипотенузы и второго катета:
a²=c²-b²
a=√(c²-b²)
Также находим и b:
b=√(c²-a²)
Ещё можно найти катет через тригонометрические функции, то есть зная угол через синусы, косинусы, тангенсы, котангенсы и т.д.
Если представить треугольник как вписанный в круг, то зная угол и размер гипотенузы можно найти катеты.
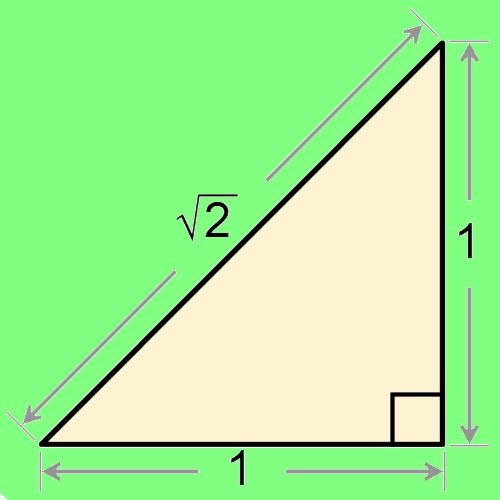
В рассматриваемом треугольнике, вписанном в круг, гипотенуза будет радиусом круга и приравнивается к 1 (к единице). А катеты – это синус и косинус, они меньше единицы.
Допустим зная угол α можно вычислить sin(α) и cos(α).
Синус соответствует вертикальному катету, а косинус горизонтальному.
Теперь, чтобы найти длины этих катетов, нужно перевести их из коэффициентов, которые меньше единицы, в реальные длины. Для этого их нужно домножить на длину гипотенузы:
Если:
Y – вертикальный катет, а X – горизонтальный катет (см. картинку) a Z – гипотенуза, то:
Y=Z*sin(α)
X=Z*cos(α)
Можно найти катет и зная лишь длину второго катета, а также угол.
Допустим знаем Y и угол α.
Тогда запросто находим гипотенузу, выражая её из предыдущей формулы:
Z=sin(α)/Y
А затем уже находим второй катет: X=Z*cos(α)
Если же наоборот знаем только X катет (горизонтальный, относительно приведённого рисунка), то находим гипотенузу так:
Z=X/cos(α)
А затем уже находим катет Y: Y=Z*sin(α)
Как найти неизвестный катет
Катет – это сторона прямоугольного треугольника, прилегающая к прямому углу. Найти его можно, используя теорему Пифагора или тригонометрические отношения в прямоугольном треугольнике. Для этого нужно знать другие стороны или углы этого треугольника.
Вам понадобится
- – теорема Пифагора;
- – тригонометрические соотношения в прямоугольном треугольнике;
- – калькулятор.
Инструкция
Если в прямоугольном треугольнике известна гипотенуза и один из катетов, то второй катет найдите, используя теорему Пифагора. Поскольку сумма квадратов катетов a и b, равна квадрату гипотенузы c (c²=a²+b²), то, произведя несложное преобразование, получите равенство для нахождения неизвестного катета. Обозначьте неизвестный катет как b. Для того чтобы найти его, найдите разность квадратов гипотенузы и известного катета, а из результата выделите корень квадратный b=√(c²-a²).
Пример. Гипотенуза прямоугольного треугольника равна 5 см, а один из катетов 3 см. Найдите, чему равен второй катет. Подставьте значения в выведенную формулу и получите b=√(5²-3²)=√(25-9) =√16=4 см.
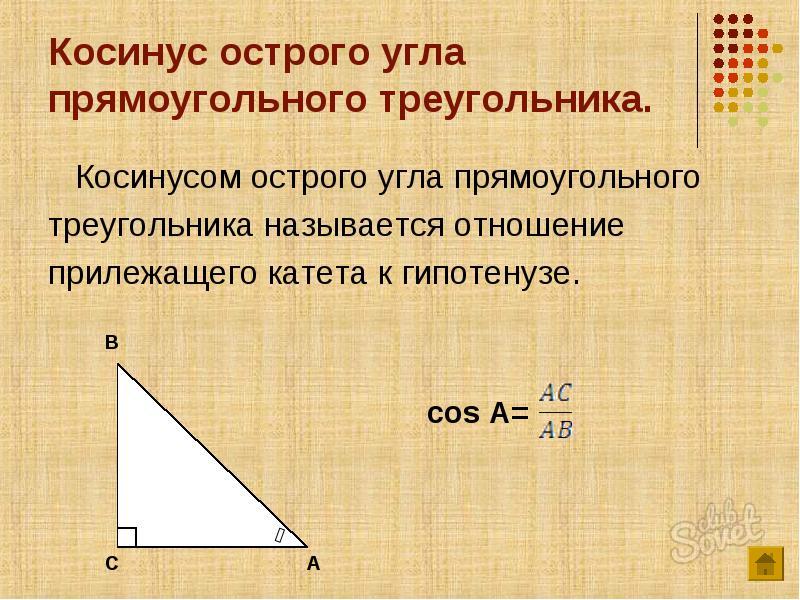
Если в прямоугольном треугольнике известна длина гипотенузы и один из острых углов, используйте свойства тригонометрических функций для того, чтобы найти нужный катет. Если нужно найти катет, прилежащий к известному углу, чтобы найти его, используйте одно из определений косинуса угла, которое гласит, что он равен отношению прилежащего катета a к гипотенузе c (cos(α)=a/c). Тогда чтобы найти длину катета, умножьте гипотенузу на косинус прилежащего к данному катету угла a=c∙cos(α).
Пример. Гипотенуза прямоугольного треугольника равна 6 см, а его острый угол 30º. Найдите длину катет, прилежащего к этому углу. Этот катет будет равен a=c∙cos(α)=6∙cos(30º)=6∙√3/2≈5,2 см.
Если нужно найти катет противолежащий острому углу, используйте ту же методику расчета, только косинус угла в формуле поменяйте на его синус (a=c∙sin(α)). Например, используя условие предыдущей задачи, найдите длину катета, противолежащего острому углу 30º. Использовав предложенную формулу, получите: a=c∙sin(α)= 6∙sin(30º)= 6∙1/2=3 см.
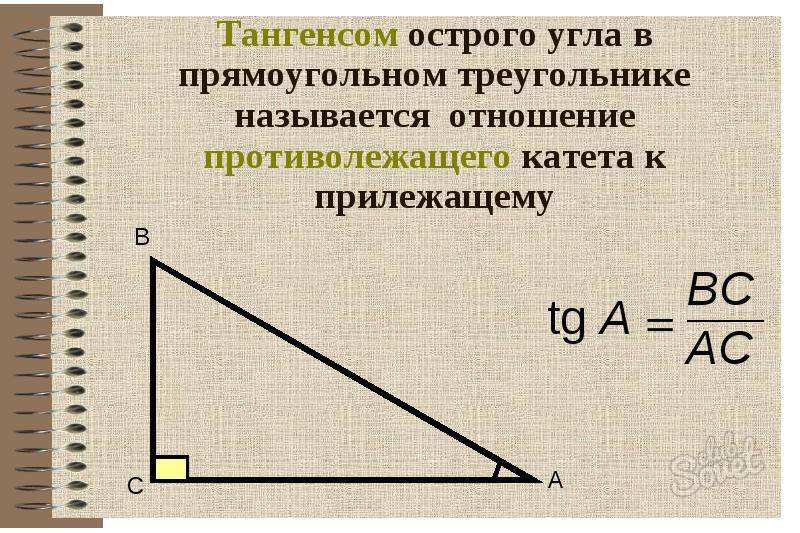
Если известен один из катетов и острый угол, то для расчета длины другого используйте тангенс угла, который равен отношению противолежащего катета к прилежащему. Тогда, если катет a является прилежащим к острому углу, найдите его, поделив противолежащий катет b на тангенс угла a=b/tg(α). Если катет a противолежит острому углу, то он равен произведению известного катета b на тангенс острого угла a=b∙tg(α).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание материала
- Онлайн калькулятор
- Пример
- Найти гипотенузу по катету и прилежащему к нему острому углу
- Пример
- Найти гипотенузу по катету и противолежащему к нему острому углу
- Пример
- Найти катет по гипотенузе и катету
- Пример
- Найти катет по гипотенузе и прилежащему к нему острому углу
- Пример
- Найти катет по гипотенузе и противолежащему к нему острому углу
- Пример
- Найти катет по второму катету и прилежащему к нему острому углу
- Пример
- Найти катет по второму катету и противолежащему к нему острому углу
- Пример
- Видео
- Как найти катет прямоугольного треугольника
- Тригонометрические формулы
- Свойства сторон в прямоугольном треугольнике
- Задачи и решения
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² — 4² = √ 25 — 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Как найти катет прямоугольного треугольника
С задачками по геометрии сталкиваются все в средней школе. Кому-то такие задачки даются сложно, а кто-то их щелкает, как орешки. На самом деле эти задачи не особо сложные, просто нужно вникнуть и понять определенный алгоритм решения. Давайте подробнее разберем, как найти катет прямоугольного треугольника.
Видео
Тригонометрические формулы
Для нахождения длины катета прямоугольного треугольника используют простые формулы. Для их применения нужно знать значение любой из сторон и величину разворота произвольной вершины. Существует четыре способа, позволяющих найти катет с использованием тригонометрических правил:
- В основе лежит аксиома, что синус находится из отношения противолежащего катета к гипотенузе. Например, пусть известно что длина гипотенузы составляет 100 сантиметров, а вершина A имеет разворот равный 30 градусам. Используя тригонометрические таблицы, можно утверждать, что синус угла A составляет ½. Учитывая преобразованное выражение, находят катет: a = 100 / 2 =50 (см). Таким образом, синус острого угла численно равен отношению одного из катетов, деленного на гипотенузу: sin A = BC/AB.
- Используется правило, что косинус в прямоугольнике представляет собой отношение прилежащего катета к прямому углу и гипотенузе: cosA = AC/AB. Например, пусть разворот вершины C равен 60 градусам, а гипотенуза равна 100 сантиметрам. Согласно тригонометрической таблице, угол в 60 градусов равен ½. Подставив это значение в формулу, можно найти значение катета: a=cos∠C*a; b=½*100=50 сантиметров.
- Тангенс угла можно вычислить, разделив значение длины противолежащего катета к прилежащему. Математическая формула этого утверждения имеет вид: tg = BC/AC. Катет многоугольника может быть найден как b = tg * a. Например, известно, что у фигуры один из углов равен 45 градусов, а длина гипотенузы составляет 100 сантиметров. Так как тангенс 45 градусов равен единице, то ответом на задачу будет: a = 1*100 = 100 сантиметров.
- Котангенс определяется из соотношения прилежащего катета к противолежащему. Фактически это величина, обратная тангенсу: ctg = AC/BC. Например, пусть разворот угла A составляет 30 градусов, а длина катета, находящегося напротив него, равняется 50 сантиметрам. Котангенс 30 градусов соответствует корню из трёх. Подставив в формулу известные данные, можно вычислить неизвестный катет: b =50√3 сантиметров.
Зная, как выглядят тригонометрические формулы и содержание двух теорем, вычислить значение катета можно будет в большинстве поставленных задач.
Свойства сторон в прямоугольном треугольнике
Гипотенуза всегда больше каждого из катетов.
BC>AC; BC>AB
Сторона, которая находится напротив угла равного 30 градусов, равна половине величины гипотенузы.
К прямоугольному треугольнику можно применить теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
AC2+AB2=BC2
Задачи и решения
Задача 1. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетов равна 26.4см. Найдите гипотенузу треугольника.
Решение. Обозначим через b− меньший катет, а через c− гипотенузу. Из условия задачи имеем: c+b=26.4см.
Так как один из острых углов прямоугольного треугольника равен 60°, то другой острый угол равен 90°−60°=30°. Как известно, против угла 60° лежит большая сторона (катет), а против угла 30° − меньшая. Из свойства 2 следует, что меньшая сторона равна половине гипотенузы :


Ответ: 17.6 см.
Задача 2. В треугольниках ABC и A1B1C1, углы A и A1 прямые, BD и B1D1 −биссектрисы. Докажите, что 

Доказательство. Так как BD и B1D1 −биссектрисы и 




Тогда 








Теги
Как найти катет прямоугольного треугольника
В жизни нам часто придется сталкиваться с математическими задачами: в школе, в университете, а затем помогая своему ребенку с выполнением домашнего задания. Люди определенных профессий будут сталкиваться с математикой ежедневно. Поэтому полезно запоминать или вспоминать математические правила. В этой статье мы разберем одно из них: нахождение катета прямоугольного треугольника.
1
Что такое прямоугольный треугольник
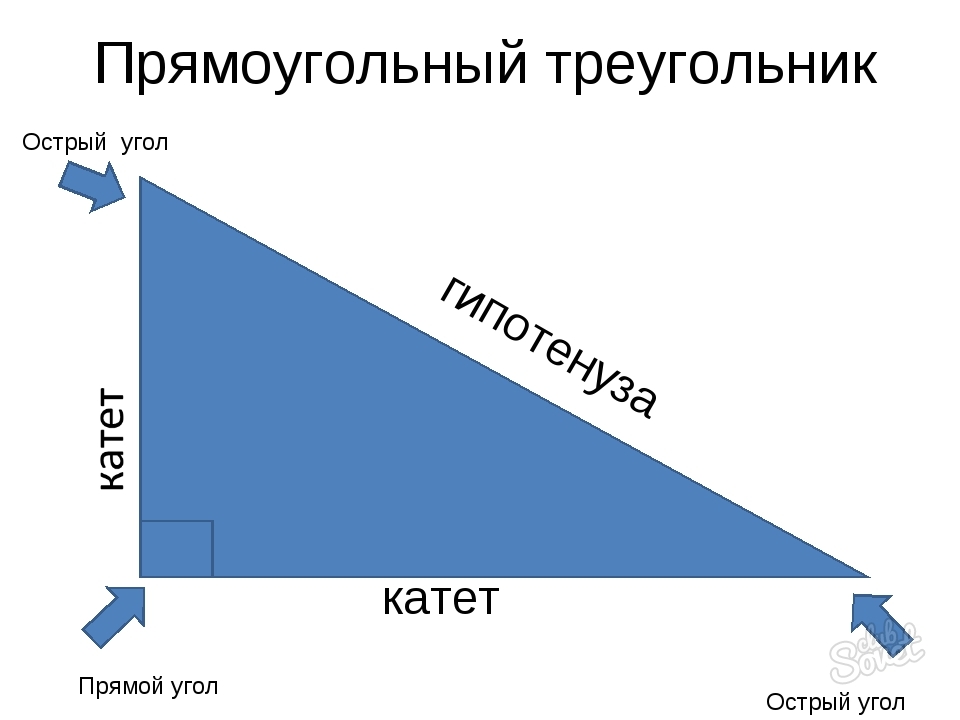
Для начала вспомним, что такое прямоугольный треугольник. Прямоугольный треугольник – это геометрическая фигура из трех отрезков, которые соединяют точки, не лежащие на одной прямой, и один из углов этой фигуры равен 90 градусам. Стороны, образующие прямой угол, называются катетами, а сторона, которая лежит напротив прямого угла – гипотенузой.
2
Находим катет прямоугольного треугольника
Существует несколько способов, позволяющих узнать длину катета. Хотелось бы рассмотреть бы их подробнее.
Теорема Пифагора, чтобы найти катет прямоугольного треугольника
Если нам известны гипотенуза и катет, то мы можем найти длину неизвестного катета по теореме Пифагора. Звучит она так: “Квадрат гипотенузы равен сумме квадратов катетов”. Формула: c²=a²+b², где c – гипотенуза, a и b – катеты. Преобразовываем формулу и получаем: a²=c²-b².
Пример. Гипотенуза равна 5 см, а катет – 3 см. Преобразовываем формулу: c²=a²+b² → a²=c²-b². Далее решаем: a²=5²-3²; a²=25-9; a²=16; a=√16; a=4 (см).
Тригонометрические соотношения, чтобы найти катет прямоугольного треугольника
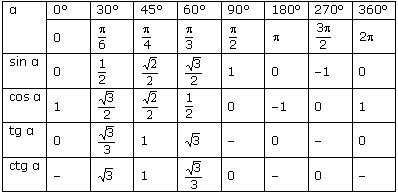
Также можно найти неизвестный катет, если известны любая другая сторона и любой острый угол прямоугольного треугольника. Есть четыре варианта нахождения катета при помощи тригонометрических функций: по синусу, косинусу, тангенсу, котангенсу. Для решения задач нам поможет таблица, которая находится чуть ниже. Рассмотрим эти варианты.
Найти катет прямоугольного треугольника при помощи синуса
Синус угла (sin) – это отношение противолежащего катета к гипотенузе. Формула: sin=a/c, где а – катет, лежащий против данного угла, а с – гипотенуза. Далее преобразуем формулу и получаем: a=sin*c.
Пример. Гипотенуза равна 10 см, угол А равен 30 градусов. По таблице вычисляем синус угла А, он равен 1/2. Затем по преобразованной формуле решаем: a=sin∠А*c; a=1/2*10; a=5 (см).
Найти катет прямоугольного треугольника при помощи косинуса
Косинус угла (cos) – это отношение прилежащего катета к гипотенузе. Формула: cos=b/c, где b – катет, прилежащий к данному углу, а с – гипотенуза. Преобразуем формулу и получим: b=cos*c.
Пример. Угол А равен 60 градусов, гипотенуза равна 10 см. По таблице вычисляем косинус угла А, он равен 1/2. Далее решаем: b=cos∠A*c; b=1/2*10, b=5 (см).
Найти катет прямоугольного треугольника при помощи тангенса
Тангенс угла (tg) – это отношение противолежащего катета к прилежащему. Формула: tg=a/b, где а – противолежащий к углу катет, а b – прилежащий. Преобразуем формулу и получаем: a=tg*b.
Пример. Угол А равен 45 градусов, гипотенуза равна 10 см. По таблице вычисляем тангенс угла А, он равен Решаем: a=tg∠A*b; a=1*10; a=10 (см).
Найти катет прямоугольного треугольника при помощи котангенса
Котангенс угла (ctg) – это отношение прилежащего катета к противолежащему. Формула: ctg=b/a, где b – прилежащий к углу катет, а – противолежащий. Иначе говоря, котангенс – это “перевернутый тангенс”. Получаем: b=ctg*a.
Пример. Угол А равен 30 градусов, противолежащий катет равен 5 см. По таблице тангенс угла А равен √3. Вычисляем: b=ctg∠A*a; b=√3*5; b=5√3 (см).
Итак, теперь вы знаете, как находить катет в прямоугольном треугольнике. Как видите, это не так уж и сложно, главное – запомнить формулы.