95
|
1 |
(10)4 |
3 |
||||||||
|
(12)12 |
(8) 8 |
(22)7 |
(10) |
(11)11 |
||||||
|
(14)9 |
||||||||||
|
s |
17 |
12 |
||||||||
|
(18) |
(12)12 |
10 |
(12) |
(10)10 |
||||||
|
(12) |
(17)17 |
|||||||||
|
( 9)5 |
||||||||||
|
2 |
4 |
|||||||||
Рисунок 10.15.
|
1 |
(10)4 |
3 |
|||
|
(12)12 |
(8) 8 |
(22)7 |
(10) |
(11)11 |
|
|
s |
|||||
|
(14)9 |
5 |
6 |
(10)10 |
||
|
(18)17 |
(12)12 |
t |
|||
|
( |
(12)12 |
||||
|
(17)17 |
|||||
|
( 9)5 |
|||||
|
2 |
4 |
||||
Рисунок 10.16.
7.Выполнив действия, связанные с увеличением допустимого потока в сети (рисунки 10.1 –10.16) от вершины s к вершине t , переходим
кпостроению минимального разреза сети Т.
96
8.1. Процедура “пометок вершин “
Начальное состояние: ¾ все вершины не имеют пометок.
Вершине s приписывается пометка.
Всем вершинам xi Î {Gs}, для которых дуга (s, xi) не насыщена:
¾
с si > j si присваиваются пометки.
Всем вершинам xk Î {G xi}, для которых дуга (xi , xk,) не насыщена:
¾
сij > j ij присваиваются пометки.
Входе присвоения пометок вершинам сети возможны две
ситуации:¾
1. Удалось присвоить пометку вершине t, из чего следует, что в сети есть путь от вершины s к вершине t, все дуги которого не насыщены. Следовательно, поток на сети может быть увеличен за счёт его увеличения на пути s,…, t (с помощью рассмотренного выше алгоритма).
2. Не удалось присвоить пометку вершине t. Следовательно, на сети получен максимальный поток и, для его вычисления, возможно, построить минимальный разрез.
На рисунке 10.17 приведён результат пометок вершин для рассматриваемой сети:
|
1 |
(10)4 |
3 |
|||
|
(12)12 |
(8) 8 |
(22)7 |
(10) |
(11)11 |
|
|
(14)9 |
5 |
(12)10 |
6 |
(10)10 |
|
|
(18)17 |
(12)12 |
t |
|||
|
( |
(12)12 |
(17)17 |
|||
Рисунок 10.17.
97
8.2. Определение дуг минимального разреза
По результату алгоритма пометок, когда не возможно пометить вершину t (сток), определяем дуги минимального разреза: ¾ это дуги, начала которых находятся в помеченных вершинах, а концы – в не
|
помеченных вершинах. |
|||||||
|
В наше примере это дуги us,1 ; u5,6 |
; u2,6 |
; u3,t ; u4,t (см. рисунок 10.18). |
|||||
|
Таким образом минимальный разрез данной сети Т = (us,1 ; u5,6 ; |
|||||||
|
u2,6 |
; |
A=(1, 6, t) |
u3,t ; u4,t ). |
||||
|
9. |
1 |
(10)4 |
3 |
||||
|
(12)12 |
(8) 8 |
(22)7 |
(10) |
(11)11 |
|||
|
s |
(14)9 |
5 |
(12)10 |
6 |
(10)10 |
t |
|
|
(18)17 |
(12)12 |
(12)12 |
|||||
|
( |
(17)17 |
||||||
Рисунок 10.18.
Вычисление величины максимального потока Фmax:
|
Фmax = сs,1 + |
с5,6 + с4,t + с2,6 + с3,t = 12+10+17+12+ 11 = 62. |
|
|
Допустимый поток максимальной величины на заданной сети G ¾ |
||
|
найден. |
||
|
Упражнения |
||
|
1. Для сети |
G = (X,U, С), где | X | = 6, |
| U | = 10 и U = {(x1, x2), |
|
(x1, x3), (x2, x4), (x2, |
x5), (x3, x2), (x3, x5), (x4, x3), |
(x5, x4), (x4, x6), (x5, x6)}, |
|
определить: ¾ является G насыщенной, т.е. |
в G задан максимальный |
98
допустимый поток, или G ненасыщенная, если известно, что дуги сети
|
(x1, x2), (x4, x6), (x3, x5), (x2, x4), (x5, x4) ¾ насыщенные. |
|||||
|
2. |
Определить максимальный поток в сети G = (X,U, С), где | X | = 6, |
||||
|
| U | = 10, пропускные |
способности |
дуг |
равны: ¾ |
c12 =7, |
|
|
c13 =5, c24 = 4, c25 =10, c32 = 8, |
c35 = 6, c43 = 5, |
c45 =3, |
c46 = 11, c56 = 6. |
||
|
3. |
Определить минимальный разрез в |
сети G = (X,U, С), |
где |
||
|
| X | = 6, |
U = {(x1, x2), (x1, x3), (x2, x4), (x2, x5), (x3, x2), (x3, x5), (x4, x3), (x4, |
||||
|
x5), (x4, x6), (x5, x6)} , если известно, что дуги сети |
(x1, x2), (x4, x6), |
(x3, x5), |
|||
|
(x2, x4), (x4, x5) , (x5, x6) ¾ насыщенные. |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти минимальный разрез в сети
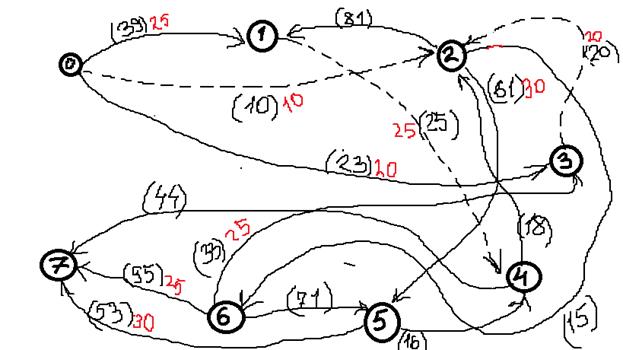
Решить задачу нахождения максимального потока в транспортной сети с помощью алгоритма Форда—Фалкерсона, и построить разрез сети S.
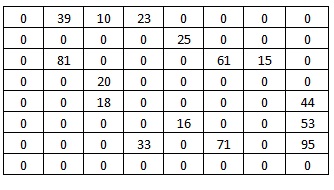
Исходные данные:
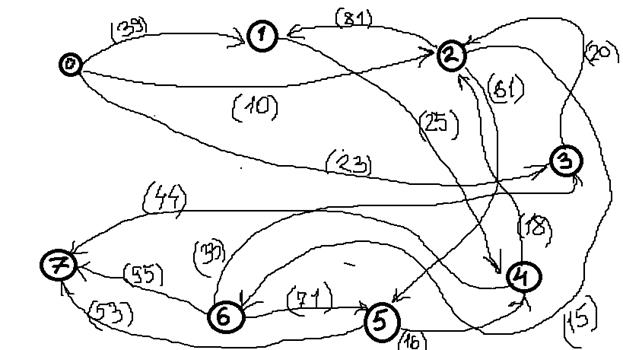
Дана сеть S(X,U) 
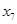
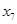
Значения пропускных способностей дуг 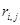
r[0,1] = 39; r[4,7] = 44; r[6,3] = 33; r[5,7] = 53; r[0,2] = 10;
r[4,2] = 18; r[6,7] = 95; r[5,4] = 16; r[0,3] = 23; r[2,5] = 61;
r[2,1] = 81; r[6,5] = 71; r[1,4] = 25; r[2,6] = 15; r[3,2] = 20
1. Зададим на сети нулевой поток (на всех дугах величина потока 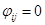
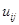
2. Выбираем на сети (произвольно) путь, ведущий из вершины x0 в вершину x7:
X0-X1-X4-X6-X7
3. Находим 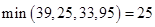
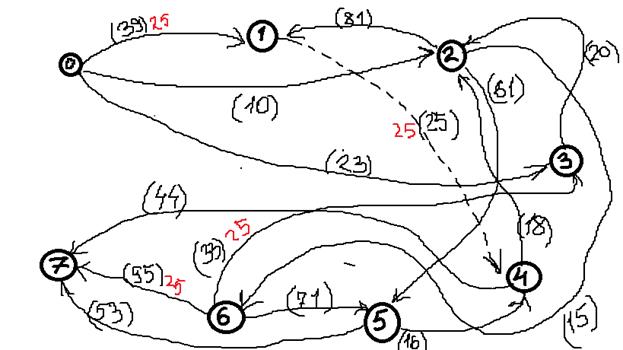
4. Выбираем еще один путь, например: Х0-Х2-Х5-Х7, находим 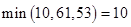
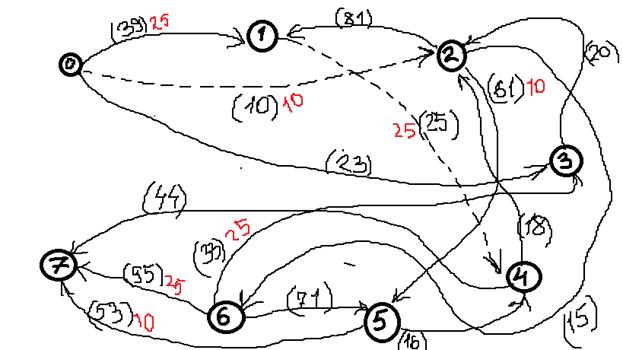
5. Выбираем еще один путь, например: Х0-Х3-Х2-Х5-Х7, находим 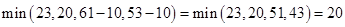
6. Более путей от Х0 до Х7 нет, суммируем увеличения потока: 25+10+20=55.
Вывод: максимальный поток равен 55.
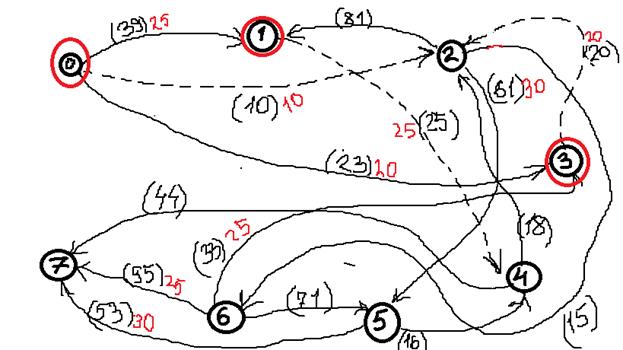
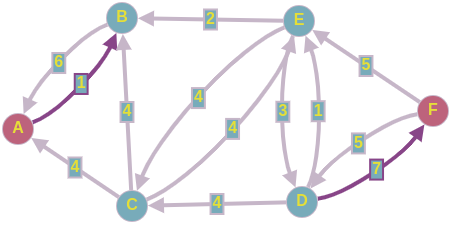
2) Построить разрез сети S.
Процедура «пометок вершин».
Начальное состояние: все вершины не имеют пометок.
Вершине Х0 приписывается пометка. Всем вершинам 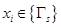
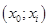
Определяем дуги минимального разреза: это дуги, начала которых находятся в помеченных вершинах, а концы — в непомеченных вершинах.
Это дуги:
Таким образом, минимальный разрез данной сети
Вычисление величины максимального потока
Алгоритм Форда-Фалкерсона
Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.
При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
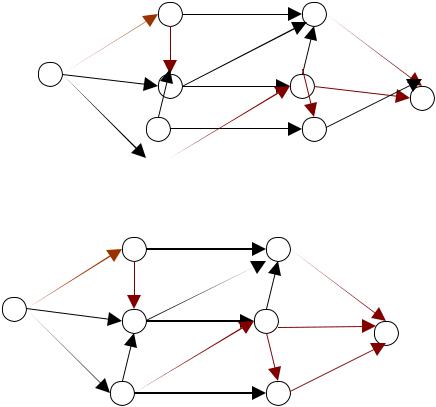
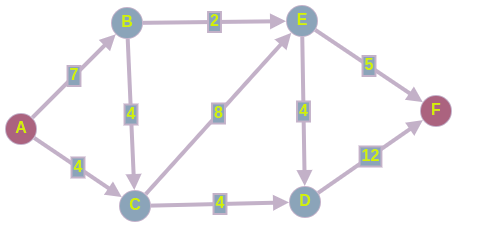
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток.
Исходный граф
Как работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
Отправлять определенное количество потока из текущей вершины в соседние.
Возвращать определенное количество потока из соседних вершин в текущую.
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
Допустим наш алгоритм нашел следующий путь из вершинывнашей остаточной сети, которая на момент начала, совпадает с исходным графом.
Сколько потока можем провести по этому пути.
— Больше 2 ед. мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в .
Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:
Пропускаем 3 ед . потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:
На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:
Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
На 4-ой итерации находим следующий путь в остаточной сети:
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
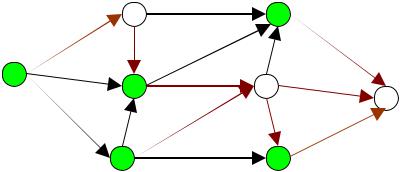
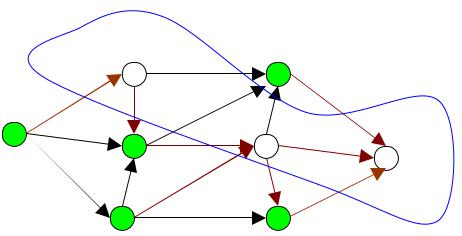
Получим следующую картину:
Итоговая остаточная сеть
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Максимальный поток и минимальный разрез
Теорема Форда-Фалкерсона 1 (о максимальном потоке и минимальном разрезе).
В любой сети существует максимальный поток. Величина максимального потока равна пропускной способности минимального разреза.
Теорема Форда-Фалкерсона 2.
Поток, вычисленный с помощью алгоритма Форда-Фалкерсона имеет максимальную величину, а разрез , где -множество вершин, помеченных при последнем помечивании, имеет минимальную пропускную способность.
Нахождение максимального потока и построение минимального разреза в сети с использованием алгоритма Форда-Фалкерсона
В данной задаче основным параметром на дугах сети является – пропускная способность. Пропускная способность показывает, сколько единиц потока может быть передано по дугам сети. Таким образом, потоком в сетиD = [N, M] называется неотрицательная вещественная функция, удовлетворяющая условиям:
1. ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги ;
2. сохранения: суммарный поток, заходящий в любую вершину сети (кроме истока и стока), равен суммарному потоку, выходящему из этой вершины.
Дуга сети называется насыщенной, если поток по этой дуге равен пропускной способности этой дуги, т. е. .
Разрезом сетиназывается множество дуг, удаление которых из сети приводит к тому, что исток и сток оказываются несвязанными.
Пропускной способностью разрезаназывается число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.
Отыскание минимального разреза – одна из основных задач анализа транспортных сетей. В силу конечности графа минимальный разрез может быть найден перебором всех разрезов, но этот путь, конечно, неприемлем для достаточно больших графов.
Минимальный разрез можно отыскать при помощи теоремы Форда – Фалкерсона: в любой транспортной сети величина любого максимального потокаравна пропускной способности любого минимального разреза.
Для нахождения максимального потока в сети разработан алгоритм Форда – Фалкерсона. Перед началом выполнения алгоритма все вершины сети нумеруются произвольным образом, кроме источника и стока (источник получает минимальный номер 1, сток – максимальный , где – число узлов).
Алгоритм состоит из следующих основных шагов:
1. Определить начальный поток в сети, сложив потоки по дугам, выходящим из источника.
2. Вершинам сети присвоить целочисленные метки, а дугам – знаки «+» и «–» по следующим правилам:
а) вершине-истоку присвоить метку ;
б) находим непомеченнуювершину , смежную помеченнойвершине . Если поток по соединяющей вершины дуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершина является образомпомеченной вершины , то происходит прямое помечивание (дуга в прямом направлении допустима): вершина получает метку, равную номеру вершины , соединяющая вершины дуга получает метку «+», переходим к рассмотрению следующей вершины. Если вершина не имеет ни одного помеченного прообраза, поток по дуге в прямом направлении больше 0, то происходит обратное помечивание (дуга допустима в обратном направлении): вершина получает метку, равную номеру вершины (являющейся в данном случае ее образом), соединяющая вершины дуга получает метку «–», происходит переход к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.
3. Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток – максимальный, переход к шагу 5. В противном случае перейти к пункту 4.
4. Рассмотреть последовательность вершин L, метка каждой из которых равна номеру следующей за ней вершины, и множество дуг МL, соединяющих соседние вершины из L.
Построение нового потока по схеме:
а) Если дуга принадлежит множеству МL (смотри выше) и имеет знак «+», то новый поток по этой дуге = старый поток по этой дуге + Δ (схему нахождения смотри далее).
б) Если дуга принадлежит множеству МL и имеет знак «–», то новый поток по этой дуге = старый поток по этой дуге – Δ.
в) Если дуга не принадлежит множеству МL, то поток по дуге оставляем без изменения.
I. , где для нахождения рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «+», и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге ( ). Затем из этих значений разностей выбирается минимальное значение и присваивается .
II. Для нахождения рассматриваются все дуги, принадлежащие множеству МL и имеющие знак «–». Затем из этих дуг выбирается дуга с минимальным потоком ( ), и значение потока по этой дуге присваивается .
Перейти к шагу 2.
5. Определяем максимальный поток, складывая начальный поток и все полученные изменения потока.
В оптимальном решении, т. е. когда найден максимальный поток, минимальный разрез образуется насыщенными дугами.
Дата добавления: 2019-02-22 ; просмотров: 5017 ; Мы поможем в написании вашей работы!
Слайды презентации
Слайд 1
Потоки в сетях
Теорема о максимальном потоке
и минимальном разрезе
Лекция 6
Слайд 2
Сеть
•
Ориентированный граф G с пропускными
способностями дуг u
: E ( G ) → R
+ и
две
выделенные вершины s ( источник ) и
t ( сток ).
•
Четверка ( G , u , s , t ) называется сетью .
•
Главная задача ― транспортировать так
много единиц продукта, как возможно,
одновременно из s в t . Решение этой задачи
назовем максимальным потоком.
Слайд 3
Поток
•
Определение 6 .1. Дан орграф G с
пропускными
способностями (вместимостями) u : E (
G ) → R
+ ,
потоком называется функция
f : E ( G ) → R
+ с
f ( e ) ≤ u ( e ) для всех e E ( G ). Будем говорить, что f
удовлетворяет закону сохранения в вершине v ,
если
Поток, удовлетворяющий закону сохранения в
каждой вершине называется циркуляцией .
.
veve efef
Слайд 4
s-t- Поток
•
Да на сеть ( G , u ,
s , t ), s – t – потоком
называется
поток, удовлетворяющий закону сохранения во
всех вершинах
кроме s и t. Определим величину
s – t – потока функцией
.:value
sese efeff
Слайд 5
Задача « Максимальный Поток »
•
Дано : Сеть (
G , u , s , t ) .
•
Найти
s – t – поток максимальной
величины .
Слайд 6
s – t- Разрез
•
s-t – разрез в графе
― разрез X для
некоторого
X V ( G ) с
s X и t V ( G ) X .
•
пропускной способностью s – t – разреза
называется сумма вместимостей его дуг
(ребер) . Под минимальным s – t – разрезом в
( G , u , s , t ) мы понимаем s – t – разрез с
минимальной пропускной способностью
( относительно u ) в G.
Слайд 7
s – t – Поток и s –
t – разрез
•
Лемма 6 . 2
Для
всех A V ( G ) таких,
что s A , t ∉ A ,
и любого s – t – потока f.
.value b) .value a)
Ae AeAe
euf efeff
Величина максимального потока не превосходит
пропускной способности минимального разреза.
Слайд 8
Доказательство (а)
.
value
AeAe Av
veve sese
efef efef
efeff
Слайд 9
s – t – Поток и s –
t – разрез
•
Лемма 6 . 2
Для
всех A V ( G ) таких,
что s A , t ∉ A ,
и любого s – t – потока f.
.value b) .value a)
Ae AeAe
euf efeff
Слайд 10
Обратные дуги и остаточные
пропускные способности
•
Определение 6
. 3
Для орграфа G определим Ğ:=(
V ( G ), E ( G ) U {ĕ:
e E ( G ) }),
где для каждого e = ( v , w ) E ( G ) определим ĕ как новое
ребро из w в v . Назовем ĕ обратной дугой к e и, наоборот.
Заметим, что если e = ( v , w ) , e ′ = ( w , v ), то ĕ и e ′ два
параллельных ребра в Ğ .
Дан орграф G с вместимостями u : E ( G ) → R
+ и поток f ,
определим остаточные пропускные способности u
f
: E ( Ğ ) → R
+ как u
f ( e ):= u ( e ) − f ( e ) и u
f (ĕ) := f ( e ) для всех
e E ( G ) .
Остаточным графом G
f называется граф
( V ( G ), {e E ( Ğ ): u
f ( e ) > 0 }) .
Слайд 11
Остаточный граф
S t5
5 5
514
3 25
1
S t1
2 5
314
3
2G
G
f
Слайд 12
Увеличивающий Путь
Даны поток f и
путь (или цикл) P в G
f , увеличение
f
вдоль P на γ означает следующее для каждой
e E ( P ) :
•
если e E ( G ) , то увеличим f ( e ) на γ ,
•
если e = ĕ
0 , e
0 E ( G ) , то уменьшим f ( e
0 ) на γ .
Дана сеть ( G , u , s , t ) и s – t – поток f , f –увеличивающим
путем называется s – t – путь в остаточном графе G
f .
Слайд 13
Увеличивающий Путь
S t5
5 5
514
3 25
1
S t1
2 5
314
3
2G
G
f
S
t5
5 5
515
3 35
Слайд 14
Алгоритм Форда-Фалкерсона
Input: Сеть ( G, u, s, t ).
Output:
s – t – поток f
максимальной величины .
1. Положим f ( e ) = 0
для всех e E ( G ) .
2. Найти f – увеличивающий путь P .
If такого пути нет then stop .
3. Вычислить
Увеличить f вдоль P на γ и go to 2.
.min: eu
f
PEe
Слайд 15
Замечание
•
Найти увеличивающий путь легко (любой
s – t – путь в G
f ).
•
Если
выбирать произвольный увеличивающий
путь в G
f , то
–
Существует пример
с иррациональными
вместимостями дуг, когда алгоритм никогда не
остановится.
–
Существует пример с целыми вместимостями дуг, на
котором алгоритм производит экспоненциальное от
размера входа число увеличений.
Слайд 16
Пример c бесконечным числом итераций
( все линии представляют ребра,
то есть поток может идти в оба
направления )
S
t
u
( x
1 , y
1 )=1, u ( x
2 , y
2
)= σ , u ( x
3 , y
3 )= u ( x
4 , y
4 )= σ 2x
1
y
1
x
2
x
3
x
4 y
2
y
3
y
4
Пропускная способность остальных ребер 1 /(1- σ ). 2 15
Слайд 17
Упражнение 6.1
•
Показать, что для сети из предыдущего
примера алгоритм Форда-Фалкерсона
может работать бесконечно долго.
Слайд 18
Целочисленный пример c
экспоненциальным числом итераций
S tR
R R
R1
2 R итераций
. Длина входа ― O(log R ).
Слайд 19
Характеризация максимального
потока
Теорема 6 . 4
s-t-
Поток f является максимальным
тогда и только тогда,
когда в G
f не
существует f – увеличивающ
его пути .
Слайд 20
Доказательство
•
Пусть в G
f не существует f –
увеличивающ его пути .
t не
достижимо в G
f из s .
•
Пусть R множество вершин,
достижимых из s в G
f .
•
По определению G
f имеем f ( e ) = u ( e ) для всех e +
( R ),
и f ( e ) = 0 для всех e –
( R ) .
•
Лемма 6.2 a)
•
Лемма 6.2 b) f ― максимальный поток.
. value
R e
e u f
Слайд 21
Замечание
•
В частности, из доказательства следует, что
каждому максимальному потоку соответствует
s – t – разрез, пропускная способность которого
равна величине потока.
•
Вместе с леммой 6.2 b) это влечет центральный
результат теории потоков в сети.
Слайд 22
Максимальный поток и
минимальный разрез
Теорема
6 . 5 ( Форд , Фалкерсон [1956],
Элиас
, Файнштайн , Шэннон [1956] )
Величина максимального s-t
– потока
равна пропускной способности
минимального s-t – разреза .
Слайд 23
Теорема о целочисленном потоке
Следствие 6 .
6
Если пропускные способности
дуг в сети
целые числа, то существует целочисленный
максимальный поток.
Слайд 24
Упражнение 6. 2
•
По c троить пример сети, в которой
вместимости
дуг целые числа, и существует
нецелочисленный максимальный поток.
Слайд 25
Теорема о Декомпозиции Потока
Теорема 6 . 7 ( Фалкерсон
[1962] )
Пусть ( G, u, s,
t ) ― сеть и f ― s-t –
поток в G. Тогда
существует семейство P s-t- путей и семейство C
циклов в G с весами w : P U C → R
+ таких, что
f ( e ) = Σ
P P U C : e E ( P ) w ( P ) для всех e E ( G ),
Σ
P P w ( P ) = value( f ), и | P | + | C | ≤ | E ( G ) |. Более
того , если f ― целочисленный поток, то w может
быть выбрано целочисленным .
Слайд 26
Доказательство
•
Построим P , C и w индукцией по
числу
дуг с ненулевым потоком. Пусть e = (
v
0 , w
0 )
дуга с f ( e )
> 0. Если w
0 ≠ t , то должна быть
дуга ( w
0 , w
1 ) c ненулевым потоком.
•
Положим i = 1. Если w
0
{ t , v
0 , w
0 ,…, w
i – 1 } ,
то STOP. Иначе i = i + 1 и продолжаем.
•
Если процесс завершится в t , то проделаем
тоже самое в обратном направлении,
стартуя с v
0 .
Слайд 27
Иллюстрация доказательства
ts
v
0 w
0 w
1 w
2
w
3
ts
v
0 w
0 w
1 w
2
w
3v
1
v
2
Слайд 28
Доказательство
•
Пусть P будет цикл или путь, найденный в
результате описанной
процедуры.
•
w ( P ) = min
e E ( P
) f ( e )
•
Положим
f ‘ ( e ) = f ( e ) – w ( P ) для e E ( P )
и f ‘ ( e ) = f ( e ) для e E ( P ) .
•
По крайней мере, одна дуга обнулилась и
добавился ровно один путь или цикл.
•
Величина потока вдоль дуг из P уменьшилась
на величину w ( P ) .
•
Если P цикл, то величина s-t – потока не изменилась.
•
Если P путь, то величина s-t – потока уменьшилась на w ( P ) .
Слайд 29
Теорема о Декомпозиции Потока
Теорема 6 . 7 ( Фалкерсон
[1962] )
Пусть ( G, u, s,
t ) ― сеть и f ― s-t –
поток в G. Тогда
существует семейство P s-t- путей и семейство C
циклов в G с весами w : P U C → R
+ таких, что
f ( e ) = Σ
P P U C : e E ( P ) w ( P ) для всех e E ( G ),
Σ
P P w ( P ) = value( f ), и | P | + | C | ≤ | E ( G ) |. Более
того , если f ― целочисленный поток, то w может
быть выбрано целочисленным .
Слайд 30
Упражнение 6.2
•
Доказать следующую теорему
Теорема (Хоффман 1960)
Задан орграф G
и нижние и верхние оценки на
пропускные способности
дуг l, u : E ( G ) → R
+
c l ( e ) ≤ u ( e ) для всех e E ( G ). В орграфе G
существует циркуляция f с l ( e ) ≤ f ( e ) ≤ u ( e ) для
всех e E ( G ) тогда и только тогда, когда
. , G V X e u e l
XeXe
Чтобы скачать презентацию – поделитесь ей с друзьями с помощью
социальных кнопок.
Недавно, на Geektimes я опубликовал статью, где привёл немного поверхностной статистики из серии книг «Песнь льда и пламени». Но я не стал углубляться в самую интересную часть, в граф социальных связей, ибо тема заслуживает отдельного внимания. В этой статье я продемонстрирую как теория графов может помочь при анализе подобных данных и приведу реализации алгоритмов, которыми я пользовался.
Всем кому интересно, добро пожаловать под кат.
Из опроса вышеупомянутой статьи, я сделал вывод, что больше трети аудитории Geektimes ознакомлено с книгой фентези романа, а больше половины с сюжетом из сериала. Я надеюсь, аудитории Geektimes и Habrahabr пересекаются и вам возможно будут интересны не только использованные алгоритмы, но и результаты.
Данные
Начнём, конечно же, с главного — данных. У нас есть граф социальной активности:
На нём изображены персонажи из мира престолов в вершинах графа, где размер вершины зависит от сказанных им слов, и диалогов персонажей на ребрах графа, где толщина ребра зависит от количества состоявшихся разговоров.
Общие сведения о графе:
Граф неориентированный.
Вершин (читай персонажей): 1105
Рёбер (читай диалогов): 3505
Это всё хорошо, но кто же составил список всех разговоров, да еще и определил их принадлежность спросите вы меня (в 5ти книгах ведь почти 2 миллиона слов). Метод условных случайных полей, отвечу я. Да, для сбора данных было привлечено машинное обучение и, как заявляет «тренер» модели, точность определения принадлежности разговора составляет около 75%. Я добавлю опросник в конце статьи, чтобы узнать стоит ли переводить эту статью о том как метод условных случайных полей был применен.
Итак, формат входных данных для всех алгоритмов будет одинаковый:
Первая строка содержит V и E, количество вершин и ребер в графе соответственно.
Далее идут V строк с ID персонажа и его именем. После этого E строк вида u v w — описание рёбер. Означает, что между u и v есть ребро с весом w, где u и v это ID персонажа. Напомню, что вес означает количество диалогов между соответствующими персонажами. Вес самих вершин учитываться нигде не будет, т.к. не нашёл достойного ему применения. Ах да, код алгоритмов будет представлен на языке C++.
Нам, конечно же, нужно считать данные. Для этого я создал файлы definitions.h и definitions.cpp. Далее я везде буду подключать definitions.h чтобы кода было меньше и код читался легче. Каждый последующий алгоритм реализован как отдельная функция и вызывается в функции main.
defenitions.h
#ifndef DEF_H
#define DEF_H
#define _CRT_SECURE_NO_DEPRECATE
#include <cstdio>
#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <algorithm>
#include <queue>
#include <set>
#include <iterator>
#include <functional>
using namespace std;
extern int reverseID[];
extern vector<int> id;
extern vector< vector<int> > weight, edge;
extern map<int, string> name;
extern int V, E;
void read_data();
#endif
definitions.cpp
#include "definitions.h"
int reverseID[3000];
vector<int> id; // origin ID of characters
vector< vector<int> > weight; // weights of edges
vector< vector<int> > edge; // the graph's edges
map<int, string> name; // names of characters
int V, E; // amount of vertices and edges
void read_data() {
freopen("input.in", "r", stdin); // read from the input file
cin >> V >> E;
id.resize(V);
weight.resize(V);
edge.resize(V);
int u;
char s[100];
for (int i = 0; i < V; i++) { // read the names
scanf("%d %[^n]", &u, s);
name[i] = string(s);
id[i] = u; // origin ID by assigned ID
reverseID[u] = i; // assigned ID by origin ID
}
int a, b, w;
for (int i = 0; i < E; i++) { // read the edges and weights
cin >> a >> b >> w;
edge[reverseID[a]].push_back(reverseID[b]);
edge[reverseID[b]].push_back(reverseID[a]);
weight[reverseID[a]].push_back(w);
weight[reverseID[b]].push_back(w);
}
}
main.cpp
#include "definitions.h"
#include "degree.h"
#include "dfsbfs.h"
#include "bridges_articulations.h"
#include "cliques.h"
#include "spanning.h"
#include "cut.h"
int main() {
read_data();
degree();
count_components();
calculate_diameter();
find_cliques();
get_spanning_tree();
find_bridges_and_articulations();
find_cut();
}
Степень вершины
Для начала, попробуем реализовать что нибудь очень простое, что даже стыдно назвать алгоритмом, но будет интересно читателю/зрителю. Найдём степень каждой вершины. Степень вершины — это количество рёбер, инцидентных (примыкающих к) вершине. Этот параметр в контексте графа, который мы имеем, покажет нам сколько же «друзей» у персонажа.
Это можно сделать за один проход и сложность этого алгоритма О(V+E). Если применить и сортировку результата, как это сделал я, то сложность будет O(E+V*log(V)).
Алгоритм определения степени вершин
#include "definitions.h"
void degree() {
freopen("degree.txt", "w", stdout); // output file
vector< pair<int,int> > degree(V);
for (int i = 0; i < V; i++) {
degree[i] = make_pair(edge[i].size(), i);
}
stable_sort(degree.begin(), degree.end());
for (int i = V-1; i >= 0; i--) {
cout << name[degree[i].second] << ": " << degree[i].first << endl;
}
}
Топ 10 многосвязных персонажей:
- Тирион Ланнистер: 168
- Джон Сноу: 128
- Арья Старк: 104
- Джейми Ланнистер: 102
- Серсея Ланнистер: 86
- Кейтилин Старк: 85
- Теон Грейджой: 76
- Дайнерис Таргариен: 73
- Бриенна: 71
- Санса Старк: 69
Весь список
Интересно то, что в топе не оказалось того, кто знаком со многими и по занимаемой должности обязан поддерживать контакт с людьми, Вариса (он на 25ом месте). А вот, казалось бы, второстепенный персонаж Бриенна, от имени которой главы еще нет, на 9ом месте.
Обход графа
Итак, теперь перейдем к простым алгоритмам, а именно к поиску в глубину (Depth-first search) и поиску в ширину (Breadth-first search). Оба алгоритма очень похожи, различаются только способом обхода графа. Они применяются, когда требуется пройти по рёбрам от заданной вершины в графе до другой. В случае поиска в глубину, граф проходится начиная от вершины и поочередно в максимальную глубину по одному из исходящих рёбер. В случае же с поиском в ширину граф обходится сначала по всем своим соседним вершинам, далее по соседям соседних вершин и так пока не пройденных вершин не останется. Оба алгоритма имеют сложность O(V+E).
Связность графа
Найдём компоненты связности нашего графа. Компонента связности это подграф, у которого все вершины имеют путь до любой другой вершины компоненты. Для этого запустим алгоритм поиска в глубину по одному из вершин, а после завершения, в следующей, не помеченной алгоритмом, вершине. Таким образом каждый запуск поиска будет означать новую компоненту связности.
Код подсчёта компонент связности
#include "definitions.h"
vector<bool> useddfs;
vector<int> comp;
void dfs(int u) {
useddfs[u] = true;
comp.push_back(u);
for (vector<int>::iterator i = edge[u].begin(); i != edge[u].end(); i++)
if (!useddfs[*i])
dfs(*i);
}
void count_components() {
freopen("components.txt", "w", stdout); // output file
int comp_num = 0;
useddfs.resize(V, false);
for (int i = 0; i < V; i++) {
if (!useddfs[i]) {
comp.clear();
dfs(i);
comp_num++;
}
}
cout << comp_num;
}
Было бы крайне странно, если бы граф был не связным и в нём было больше одной компоненты, не правда ли? Но к моему удивлению в графе оказалось аж 3 компоненты! Но посмотрев на них я увидел, что присутствовала одна большая компонента, и 2 другие, в которых было по одному персонажу (Это были улыбающийся старик (A smiley old man), который разговаривал с Арьей возле Божьего ока (God’s eye). И повар (A Cook), который играл с Тирионом на корабле). Ничего необычного, у них нет имён и удивительно, что участники разговора вообще определились правильно. Я, конечно же, добавил недостающие рёбра и в результате весь граф получился связным.
Теория рукопожатий
Следующее что мы найдем с помощью алгоритма поиска уже в ширину — максимальное число рукопожатий в графе, другими словами диаметр графа, т.е наидлиннейший из кратчайших путей между всеми вершинами графа. Как оказалось, максимальное количество рукопожатий это 8. Неплохой результат для произведения о «средневековых веках», если учитывать Теорию 6ти рукопожатий. Для примера, одна из таких цепочек связи:
Матушка Кротиха (Mother Mole) — Репейница (Thistle) — Варамир (Varamyr) — Джон Сноу (Jon Snow) — Эддард Старк (Ned Stark) — Барристан Селми (Barristan Selmy) — Квентин Мартелл (Quentyn Martell) — Принц-Оборванец (The Tattered Prince) — Льюис Ланстер (Lewis Lanster)
Такой алгоритм работает за O(V*V+V*E). Так как нужно запустить алгоритм BFS из каждой вершины графа. Будь этот граф деревом, то потребовалось бы только 2 раза запустить BFS. Сначала из любой вершины графа, а затем из самой отдалённой от неё вершины. И наибольшая глубина последнего запуска и была бы диаметром графа.
А раз я нашёл самые длинные пути для всех вершин графа, то можно вычислить и среднее значение, а так же составить распределение максимальных путей. Среднее значение для длины максимальных путей оказалось 6,16 (в среднем вполне вписывается в теорию о 6ти рукопожатиях), а общее среднее расстояние 3,6, для сравнения у фейсбука этот параметр 4.57.
Распределение длин максимальных путей:
Если взглянуть на распределение то мы видим что 77 персонажей находятся «в центре» графа, иными словами они могут связаться с любым другим персонажем не более чем через 4х других. Среди них все основные персонажи истории, кроме Дайнерис Таргариен и Сансы Старк, а среди тех, кому в книгах посвящено меньше пяти глав попали в список Барристан Селми, Джон Коннингтон и Мелисандра.
Весь результат
Код нахождения приведённых параметров
#include "definitions.h"
vector<bool> usedbfs;
void bfs(int u, vector<int> &distance, vector<int> &path) {
queue<int> q;
q.push(u);
usedbfs[u] = true;
path[u] = -1;
while (!q.empty()) {
int u = q.front();
q.pop();
for (vector<int>::iterator i = edge[u].begin(); i != edge[u].end(); i++) {
int to = *i;
if (!usedbfs[to]) {
usedbfs[to] = true;
q.push(to);
distance[to] = distance[u] + 1;
path[to] = u;
}
}
}
}
void calculate_diameter() {
freopen("diameter.txt", "w", stdout); // output file
int diameter = 0;
int current_max = 0;
double average_max = 0;
double average_average = 0;
vector< vector<int> > distribution(V, vector<int> (0));
vector< vector<int> > max_path;
vector<int> farthest_node;
for (int i = 0; i < V; i++) {
vector<int> distance_to(V, 0);
vector<int> path(V,-1);
usedbfs.clear();
usedbfs.resize(V, false);
bfs(i, distance_to, path);
current_max = 0;
for (int j = 0; j < V; j++) {
average_average += distance_to[j];
if (distance_to[j] > current_max)
current_max = distance_to[j];
if (distance_to[j] > diameter) {
diameter = distance_to[j];
farthest_node.clear();
max_path.clear();
max_path.push_back(path);
farthest_node.push_back(j);
} else if (distance_to[j] == diameter){
max_path.push_back(path);
farthest_node.push_back(j);
}
}
average_max += current_max;
distribution[current_max].push_back(i);
}
average_max /= V;
average_average /= V*V;
cout << "Diameter: " << diameter << endl;
cout << "Average path: " << average_average << endl;
cout << "Average farthest path: " << average_max << endl;
vector < vector<int> > farthest_path;
for (int i = 0; i < farthest_node.size(); i++) {
farthest_path.push_back(vector<int>());
for (int u = farthest_node[i]; u != -1; u = max_path[i][u])
farthest_path[i].push_back(u);
}
cout << "Farthest paths:" << endl;
for (int i = 0; i < farthest_path.size(); i++) {
cout << i+1 << ": ";
for (vector<int>::iterator j = farthest_path[i].begin(); j != farthest_path[i].end(); j++)
cout << name[*j] << ". ";
cout << endl;
}
int minimum = V;
cout << "Farthest paths distribution:" << endl;
for (int i = 0; i <= diameter; i++) {
if (distribution[i].size() != 0 && i < minimum)
minimum = i;
cout << i << ": " << distribution[i].size() << endl;
}
cout << "Characters with minimum farthest path:" << endl;
for (vector<int>::iterator i = distribution[minimum].begin(); i != distribution[minimum].end(); i++) {
cout << name[*i] << endl;
}
}
Клики в графе
Алгоритм Брона-Кербоша позволяет найти максимальные клики в графе, иными словами подмножества вершин, любые две из которых связаны ребром. В контексте рассматриваемого графа это позволит найти сильно связанные компании, которые общались между собой в истории. Сложность алгоритма линейна относительно количества клик в графе, но в худшем случае она экспоненциальна O(3V/3), алгоритм решает NP полную задачу всё таки. Сам по себе алгоритм представляет рекурсивную функцию, которая для каждой вершины находит максимальную клику, т.е. такую, в которую нельзя добавить ни одной другой вершины. Итак, результаты:
Распределение размеров клик:
Как видно, максимальная клика размером в 9 персонажей. К примеру одна из таких — компания Ланнистеров: Тирион, Джейми, Серсея, Варис, Тайвин, Кеван, Пицель, Петир и Мейс Тирелл. Что интересно, все клики размера 8 и 9 сформированы в Королевской Гавани или вблизи неё. А максимальная клика с Дайнерис размера 5.
Весь результат
Код нахождения клик
#include "definitions.h"
vector < vector<int> > cliques;
bool compare_vectors_by_size(const vector<int> &i, const vector<int> &j)
{
return (i.size() > j.size());
}
void bron_kerbosch(set <int> R, set <int> P, set <int> X) { // where R is probable clique, P - possible vertices in clique, X - exluded vertices
if (P.size() == 0 && X.size() == 0) { // R is maximal clique
cliques.push_back(vector<int>(0));
for (set<int>::iterator i = R.begin(); i != R.end(); i++) {
cliques.back().push_back(*i);
}
}
else {
set <int> foriterate = P;
for (set<int>::iterator i = foriterate.begin(); i != foriterate.end(); i++) {
set <int> newR;
set <int> newP;
set <int> newX;
newR = R;
newR.insert(*i);
set_intersection(P.begin(), P.end(), edge[*i].begin(), edge[*i].end(), inserter(newP, newP.begin()));
set_intersection(X.begin(), X.end(), edge[*i].begin(), edge[*i].end(), inserter(newX, newX.begin()));
bron_kerbosch(newR, newP, newX);
P.erase(*i);
X.insert(*i);
}
}
}
void find_cliques() {
freopen("cliques.txt", "w", stdout); // output file
set <int> P;
for (int i = 0; i < V; i++) {
P.insert(i);
stable_sort(edge[i].begin(), edge[i].end());
}
bron_kerbosch(set<int>(), P, set<int>());
stable_sort(cliques.begin(), cliques.end(), compare_vectors_by_size);
cout << "Distribution:" << endl;
int max_size = 0;
int max_counter = 0;
for (int i = cliques.size()-1; i >= 0 ; i--) {
if (cliques[i].size() > max_size) {
if (max_counter > 0) {
cout << max_size << ": " << max_counter << endl;
}
max_size = cliques[i].size();
max_counter = 0;
}
max_counter++;
}
if (max_counter > 0) {
cout << max_size << ": " << max_counter << endl;
}
cout << "Cliques:" << endl;
for (int i = 0; i < cliques.size(); i++) {
cout << i + 1 << "(" << cliques[i].size() << "): ";
for (int j = 0; j < cliques[i].size(); j++) {
cout << name[cliques[i][j]] << ". ";
}
cout << endl;
}
}
Остовное дерево
А теперь немного упростим наш граф связей, оставив в нём только «костяк», так называемое остовное дерево, т.е. наиболее важные рёбра связи и при этом превратив граф в дерево со всеми исходными вершинами. Поможет нам в этом алгоритм Крускала. Алгоритм жадный, для его осуществления нужно всего лишь отсортировать все рёбра по их весу и поочередно добавлять каждое ребро, если оно связывает две компоненты. Если использовать правильную структуру данных (обычно используют систему непересекающихся множеств), то сложность алгоритма получится O(E(logE)+V+E) = O(E(logV)). Ниже приведен результат графа, который подвергся этим манипуляциям. Я так же для читаемости удалил рёбра с весом 1.
картинка кликабельна
Итак, из этого графа можно увидеть главных героев и их связь между собой. Как я и ожидал, Тирион Ланнистер находится в «центре» всех связей, от него исходят 4 большие ветки: Серсея Ланнистер, Джон Сноу, Санса Старк и Джорах Мормонт (ветка Дайнерис). Последние в свою очередь герои следующего уровня по связям. Вполне ожидаемый результат, не правда ли?
Весь результат
Код построения остовного дерева
#include "definitions.h"
vector<int> p;
int dsu_get(int v) {
return (v == p[v]) ? v : (p[v] = dsu_get(p[v]));
}
void dsu_unite(int u, int v) {
u = dsu_get(u);
v = dsu_get(v);
if (rand() & 1)
swap(u, v);
if (u != v)
p[u] = v;
}
void get_spanning_tree() {
freopen("spanning.txt", "w", stdout); // output file
vector < pair < int, pair<int, int> > > edges_weights, result;
vector < vector<bool> > used;
for (int i = 0; i < V; i++) {
used.push_back(vector<bool>(V, false));
}
for (int i = 0; i < V; i++) {
for (int j = 0; j < edge[i].size(); j++) {
int cur_v = edge[i][j];
if (!used[i][cur_v]) {
edges_weights.push_back(make_pair(weight[i][j], make_pair(i, cur_v)));
used[i][cur_v] = true;
used[cur_v][i] = true;
}
}
}
sort(edges_weights.begin(), edges_weights.end(), greater< pair < int, pair<int, int> > >());
for (int i = 0; i < V; i++) {
p.push_back(i);
}
for (int i = 0; i < E; i++) {
int u = edges_weights[i].second.first;
int v = edges_weights[i].second.second;
int w = edges_weights[i].first;
if (dsu_get(u) != dsu_get(v)) {
result.push_back(edges_weights[i]);
dsu_unite(u, v);
}
}
for (vector < pair < int, pair<int, int> > >::iterator i = result.begin(); i != result.end(); i++) {
cout << id[(i->second).first] << " " << id[(i->second).second] << " " << i->first << endl;
}
}
А вот сколько всего остовных деревьев, включая не только максимальные можно построить? Неимоверно много в данном графе, разумеется. Но их можно подсчитать используя теорему Кирхгофа. Теорема говорит, что если построить матрицу, где все элементы матрицы смежности будут заменены на противоположные, а на главной диагонали будут стоять степени соответствующих вершин, то все алгебраические дополнения полученной матрицы будут равны и это значение будет количеством остовных деревьев графа.
Мосты и шарниры
Мостами в графе называют рёбра, при удалении которых, количество компонент связности увеличивается. Аналогичное определение и у шарниров, только в отличии от мостов, шарниры это вершины, при удалении которых количество компонент связности возрастает. В данном графе, наличие мостов будет означать что в мире престолов существуют связи, которые являются единственным источником коммуникации между отдельными группами персонажей. Шарниры же, это герои, которые являются единственным посредником к группе других персонажей. Мосты и шарниры искать не очень тяжело. Для этого нам понадобится знакомый нам алгоритм поиска в глубину, но слегка модифицированный. Нужно использовать, так называемое, время входа в вершину и функцию времени выхода (fout) на вершине, которая будет принимать значения минимума времени входа и значений fout вершины в которую поиск в глубину пройден, таким образом, если при проходе ребра окажется, что значение функции fout на вершине больше чем время захода в неё, то это будет мостом, а так же и шарниром, а если равно, то только шарниром. Иными словами мы проверяем, возвращаемся ли мы после обхода в то же самое ребро/вершину и только в неё при обходе части графа, если да, то это и будет искомым мостом либо шарниром.
Как и ожидалось, все шарниры и мосты охватывали только малозначимых персонажей. Количество вершин в компонентах, которые получилось бы изолировать, удалением шарниров и мостов, не превышает 4х. Это означает, что нет героя, которым бы невозможно было пожертвовать. Все связаны между собой как минимум через двух других персонажей.
Весь результат
Код поиска мостов и шарниров
#include "definitions.h"
vector<bool> used, usedcnt;
int timer = 0;
vector<int> tin, fout, articulations;
vector < pair<int,int> > bridges;
int count_rec(int v, int skip) {
int cnt = 1;
usedcnt[v] = true;
for (int i = 0; i < edge[v].size(); i++) {
int to = edge[v][i];
if(to == skip || usedcnt[to])
continue;
cnt += count_rec(to, skip);
}
return cnt;
}
int count_from(int v, int skip, bool clean = true){
usedcnt.resize(V, false);
if (clean) {
for (int i = 0; i < usedcnt.size(); i++)
usedcnt[i] = false;
}
return count_rec(v, skip);
}
void dfs(int v, int prev = -1) {
used[v] = true;
tin[v] = fout[v] = timer++;
int root_calls = 0;
bool in_ar_list = false;
for (int i = 0; i < edge[v].size(); i++) {
int to = edge[v][i];
if (to == prev) continue;
if (used[to])
fout[v] = min(fout[v], tin[to]);
else {
dfs(to, v);
fout[v] = min(fout[v], fout[to]);
if (fout[to] > tin[v]) {
bridges.push_back(make_pair(v, to));
}
if (fout[to] >= tin[v] && prev != -1 && !in_ar_list) {
articulations.push_back(v);
in_ar_list = true;
}
root_calls++;
}
}
if (prev == -1 && root_calls > 1)
articulations.push_back(v);
}
void find_bridges_and_articulations() {
freopen("bridges_and_articulations.txt", "w", stdout); // output file
used.resize(V, false);
tin.resize(V);
fout.resize(V);
for (int i = 0; i < V; i++)
if (!used[i])
dfs(i);
cout << "Bridges:" << endl;
for (int i = 0; i < bridges.size(); i++) {
cout << name[bridges[i].first] << " (" << count_from(bridges[i].first, bridges[i].second) << ") - " << name[bridges[i].second] << " (" << count_from(bridges[i].second, bridges[i].first) <<")" << endl;
}
cout << endl << "Articulation points:" << endl;
for (int i = 0; i < articulations.size(); i++) {
int cur = articulations[i];
cout << name[cur];
for (int i = 0; i < usedcnt.size(); i++)
usedcnt[i] = false;
for (int j = 0; j < edge[cur].size(); j++) {
if (!usedcnt[edge[cur][j]]) {
int comp_size = count_from(edge[cur][j], cur, false);
cout << " (" << comp_size << ")";
}
}
cout << endl;
}
}
Минимальный разрез
Но всё же интересно узнать, сколько героев требуется «убить» чтобы полностью исключить контакт двух самых популярных (по вышеизложенной статистике) персонажей, скажем, Тириона Ланнистера и Арью Старк, либо Джона Сноу и Серсею Ланнистер. Для этого будем использовать алгоритм Диница. Для начала разберёмся как работает алгоритм.
По теореме Форда-Фалкерсона следует, что величина максимального потока в графе путей равна величине пропускной способности его минимального разреза. Иными словами, мы можем найти минимальный разрез между двумя вершинами (сток и исток) если найдём максимальный поток между этими вершинами. Алгоритм Диница как раз позволяет найти величину максимального потока и, собственно, сам поток. Я не буду разбирать подробно сам алгоритм и предоставлю вам возможность самим разобраться в нём. Для понимания полученного результата достаточно знать, что поток — это некая функция, которая для каждого ребра лежащего на пути от истока к стоку, определяет положительную величину, не превышающую пропускную способность этого ребра. Для упрощения можно представить систему труб с водой, где объем воды протекающей от истока к стоку в момент t и есть величина потока.
Поставленная мною задача слегка отличается от той, что решает алгоритм. Дело в том, что поток определяется на рёбрах, и если мы найдём минимальный разрез, то он «разрежет» граф по рёбрам, т.е. связям в графе, но нам ведь нужно разрезать граф не по рёбрам, а вершинам, т.е. персонажам. Чтобы решить эту задачу нужно подвергнуть граф небольшим изменениям. Раздвоим каждую вершину в графе, скажем вместо вершины v у нас получатся вершины v1 и v2, далее если между двумя вершинами v и u было ребро, то перенаправим v1 в u2, а u1 в v2, вместо ребра (u, v) получатся рёбра (v1, u2) и (u1, v2). И между каждыми раздвоенными вершинами v1 и v2 проведём ребро (v2, v1). В полученном, уже ориентированном, графе, все связи сохранятся, но там где раньше были вершины, появятся рёбра. Если вес этих ребер будет 1, а у всех остальных, скажем бесконечность (на практике можно использовать количество вершин в графе), то ребро между раздвоенными вершинами будет слабым звеном в графе и по принципу «предохранителя» не позволит пройти бОльшему потоку через себя, что даст возможность узнать количество вершин, которые нужно удалить, чтобы граф стал несвязным. А дальше запустим алгоритм Диница на полученном графе.
Сложность алгоритма O(n2m). Поэтому мы будем искать величину максимального потока не по всем парам вершин, а только по персонажам, которые имеют наибольшее количество связей, иначе для данного графа сложность получится O(n5), где n=1000 и работать всё будет много часов. Ниже я приведу результаты по топ 100 персонажам по связям.
Я немного удивился результатам. Оказалось, что в топ 100, разрезать граф можно избавившись от минимум 6ти персонажей. Все такие связи при этом содержат либо Джона Коннингтона либо Эурона Грейджоя в качестве стока/истока. Но это не основные персонажи. Что интересно, в топ 10ти, в основном минимальный поток равен около 45ти. Например между Тирионом и Арьей поток равен 53, а между Джоном Сноу и Серсеей 42. Но есть и персонаж, которого можно отделить, удалив 16 других персонажей. Это Дайнерис Таргариен, не удивительно, ведь она наиболее удалённая героиня на карте престолов.
Ещё интересно было бы узнать, кто же наиболее «важный» герой в потоках. Т.е. через кого чаще всего протекает максимальный поток. Тут есть чему удивиться. Топ 10 важных персонажей в потоках (в скобках соответствующее количество вхождений в потоки):
- Тирион Ланнистер (4109)
- Джейми Ланнистер (3067)
- Арья Старк (3021)
- Джон Сноу (2883)
- Эддард Старк (2847)
- Серсея Ланнистер (2745)
- Теон Грейджой (2658)
- Бриенна (2621)
- Сандор Клегане (2579)
- Санса Старк (2573)
Во первых, Эддард Старк был важным персонажем и их, к несчастью (или к счастью) не жалеют. Во вторых, Сандор Клегане, от имени которого не написано ни одной главы, всё же важный персонаж. В третьих, топ 10 персонажей весьма живучи, во всяком случае пока, но самое интересное, что следующие 10 персонажей это:
11. Джофрей Ланнистер
12. Робб Старк
13. Ренли Баратеон
14. Кейтилин Старк
15. Русе Болтон
16. Йорен
17. Сэм
18. Мелисандра
19. Бран Старк
20. Варис
где из верхних 6ти персонажей в книге уже убиты 5. Не позавидуешь этой десятке. Кто же следующий?
Так же, благодаря потокам, удалось вычислить «лишние» вершины, авторов реплик которых не удалось правильно распознать, поэтому они были связаны со многими персонажами, с которыми не должны были пересекаться. Ими оказались Человек (A Man) и Страж (A Guard). В следствии чего, я удалил эти вершины и пересчитал всю статистику заново.
Весь результат
Код нахождения минимального разреза по вершинам
#include "definitions.h"
const int INF = 1000000000;
struct edge_s{
int a, b, c, flow; // a->b, c-capacity, flow=0
edge_s(int a, int b, int c, int flow) : a(a), b(b), c(c), flow(flow) {}
};
vector< pair<int, int> > top_degree;
vector< pair<int, int> > top_flow;
vector<int> dis;
vector<int> ptr;
vector<edge_s> edgelist;
vector< vector<int> > edges_dup;
bool compare_pairs_by_second(const pair<int, int> &i, const pair<int, int> &j)
{
return (i.second > j.second);
}
bool bfs_dinic(int s, int t) {
queue<int> q;
q.push(s);
dis[s] = 0;
while (!q.empty() && dis[t] == -1) {
int v = q.front();
q.pop();
for (int i = 0; i < edges_dup[v].size(); i++) {
int ind = edges_dup[v][i],
next = edgelist[ind].b;
if (dis[next] == -1 && edgelist[ind].flow < edgelist[ind].c) {
q.push(next);
dis[next] = dis[v] + 1;
}
}
}
return dis[t] != -1;
}
int dfs_dinic(int v, int t, int flow) {
if (!flow) {
return 0;
}
if (v == t) {
return flow;
}
for (; ptr[v] < (int) edges_dup[v].size(); ptr[v]++) {
int ind = edges_dup[v][ptr[v]];
int next = edgelist[ind].b;
if (dis[next] != dis[v] + 1) {
continue;
}
int pushed = dfs_dinic(next, t, min(flow, edgelist[ind].c - edgelist[ind].flow));
if (pushed) {
edgelist[ind].flow += pushed;
edgelist[ind ^ 1].flow -= pushed;
return pushed;
}
}
return 0;
}
long long dinic_flow(int s, int t) {
long long flow = 0;
while (true) {
fill(dis.begin(), dis.end(), -1);
if (!bfs_dinic(s, t)) {
break;
}
fill(ptr.begin(), ptr.end(), 0);
while (int pushed = dfs_dinic(s, t, INF)) {
flow += pushed;
}
}
return flow;
}
void dinic_addedge(int a, int b, int c) {
edges_dup[a].push_back((int) edgelist.size());
edgelist.push_back(edge_s(a, b, c, 0));
edges_dup[b].push_back((int) edgelist.size());
edgelist.push_back(edge_s(b, a, 0, 0));
}
void find_cut() {
freopen("cut_min.txt", "w", stdout); // output file
dis.resize(2 * V, 0);
ptr.resize(2 * V, 0);
edges_dup.resize(2 * V, vector<int>(0));
const int top = min(10, V);
for (int i = 0; i < V; i++)
top_flow.push_back(make_pair(0, i));
for (int i = 0; i < V; i++) {
top_degree.push_back(make_pair(edge[i].size(), i));
for (int j = 0; j < edge[i].size(); j++) {
int to = edge[i][j];
dinic_addedge(i, to + V, V);
}
dinic_addedge(i + V, i, 1);
}
stable_sort(top_degree.rbegin(), top_degree.rend());
cout << "Minimum cut between characters:" << endl;
for (int i = 0; i < top; i++) {
for (int j = i + 1; j < top; j++) {
vector<int>::iterator p = find(edge[top_degree[i].second].begin(), edge[top_degree[i].second].end(), top_degree[j].second);
if (p != edge[top_degree[i].second].end())
continue;
int flow = dinic_flow(top_degree[i].second, top_degree[j].second + V);
cout << name[top_degree[i].second] << " -> " << name[top_degree[j].second] << " = " << flow << endl;
for (int k = 0; k < edgelist.size(); k++) {
if ((edgelist[k].a == (edgelist[k].b + V)) && (edgelist[k].flow == 1)) {
top_flow[edgelist[k].b].first++;
}
edgelist[k].flow = 0;
}
}
}
stable_sort(top_flow.rbegin(), top_flow.rend());
cout << endl << "Top involved characters in the flows:" << endl;
for (int i = 0; i < top; i++) {
cout << name[top_flow[i].second] << " (" << top_flow[i].first << ")" << endl;
}
}
На этом всё. Напоследок можно отметить, что Тирион Ланнистер очень важный персонаж в мире престолов. Надеюсь, статься оказалась для вас интересной, а возможно и полезной. Исходный код всех алгоритмов есть так же и на GitHub, ссылки ниже.
Ссылки:
Проект на GitHub
Исходный социальный граф
Программа Gephi, с помощью которого можно открыть проект
Автор фото заголовка — Adam Foster
В конце, как и обещал, опросник: стоит ли переводить статью о том, как были определены авторы диалогов в книгах?
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Переводить статью?
Проголосовали 380 пользователей.
Воздержались 95 пользователей.
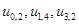
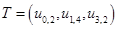
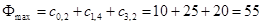
























![Презентация на тему Лекция 6. Потоки в сетях. Теорема о максимальном потоке и минимальном разрезе Теорема о Декомпозиции Потока Теорема 6 . 7 ( Фалкерсон Теорема о Декомпозиции Потока Теорема 6 . 7 ( Фалкерсон [1962] )](https://slaidy.com/files/685/684817/page-25.jpg)



![Презентация на тему Лекция 6. Потоки в сетях. Теорема о максимальном потоке и минимальном разрезе Теорема о Декомпозиции Потока Теорема 6 . 7 ( Фалкерсон Теорема о Декомпозиции Потока Теорема 6 . 7 ( Фалкерсон [1962] )](https://slaidy.com/files/685/684817/page-29.jpg)