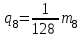Длина дуги меридиана от экватора до точки
Длина дуги (Х)
меридиана от экватора (В=00)
до точки (или до параллели) с широтой
(В)
вычисляется по формуле:
![]() (4.1)
(4.1)
где
![]()
![]()
![]()
Задание 4.2
Вычислить длины дуг меридиана от
экватора до точек с широтами B1
= 31°00′
(широта нижней рамки трапеции) и B2
= 31°20′
(широта верхней рамки трапеции).
Для рассматриваемого
примера имеем:
ХoB1
= 3431035,2629
ХoB2
= 3467993,3550
Для контроля длины
дуг меридиана от экватора до точек с
широтами B1,
и B2
можно также вычислить по формуле:
![]() (4.2)
(4.2)
где:
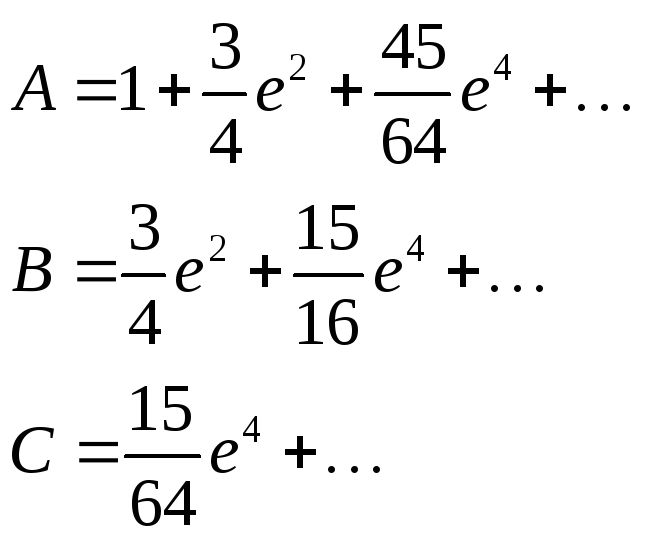
Для рассматриваемого
примера имеем:
ХoB1
= 3431035,2689
ХoB2
= 3467993,3605
Лабораторная работа № 5 Вычисление размеров съёмочной трапеции.
Длина дуги (ΔX)
меридиана между параллелями с широтами
В1
и В2
вычисляется по формуле:
![]() (5.1)
(5.1)
где ΔB=В2-В1
– приращение
широты (в угловых секундах);
![]() – средняя широта;
– средняя широта;
ρ”
= 206264,8” – количество секунд в радиане;
М1,
М2
и
Мm
– радиусы
кривизны меридиана в точках с широтами
В1,
В2
и
Вm.
Задание 5.1 Вычислить
радиусы кривизны меридиана, первого
вертикала и средний радиус кривизны
для точек с широтами
B1
=
31°00′ (широта нижней рамки трапеции), B2
=
31°20′ (широта верхней рамки трапеции) и
и Bm,=
(B1
+ B2)/2
(средняя
широта трапеции)
Для рассматриваемого
примера имеем:
|
В1 |
31° |
M1 |
6352463,644 |
N1 |
6383914,9 |
R1 |
6368169,865 |
|
В2 |
31° |
M2 |
6352792,871 |
N2 |
6384025,2 |
R2 |
6368389,890 |
|
Вm |
31° |
Mm |
6352628,003 |
Nm |
6383970,0 |
Rm |
6368279,708 |
Задание 5.2 Вычислить
длину дуги меридиана между точками с
широтами
B1
=
31°00′ (широта нижней рамки трапеции), B2
=
31°20′ (широта верхней рамки трапеции) на
местности и на карте масштаба 1 : 100 000 .
Решение.
Вычисление длины
дуги меридиана между точками
с геодезическими широтами B1,
и B2
по формуле 5.1даёт
результат на местности:
ΔХ
= 36958,092 м.,
на
карте масштаба 1:100 000 :
ΔХ
= 36958,09210м. : 100000 = 0,3695809210м. ≈ 369,58мм.
Для контроля длину
дуги меридиана ΔХ
между точками
с геодезическими широтами B1,
и B2
можно вычислить по формуле:
ΔХ = Хo
B2
–Хo
B1
(5.2)
где Х0В1
и Х0В2
– длины дуги меридиана от экватора до
параллелей с широтами В1
и В2
что даёт результат на местности:
ΔХ = 3467993,3550 –
3431035,2629 = 36958,0921м.,
на карте масштаба
1:100000 :
ΔХ = 36957,6715 м.м. :
100000 = 0,369575715м. ≈ 369,58мм.
Длина дуги параллели
Длина дуги параллели
вычисляется по формуле:
![]()
(5.3)
где N
– радиус кривизны первого вертикала в
точке с широтой В;
ΔL=L2
– L1
– разность
долгот двух меридианов (в угловых
секундах);
ρ” = 206264,8” –
количество секунд в радиане.
Задание 5.3 Вычислить
длины дуг параллелей на
геодезических широтах B1=31°00′
и B2=31°20′
между меридианами с долготами L1=66°00′
и L2=66°30′.
Решение.
Вычисление длины
дуги параллели на
геодезических широтах B1,
и B2
между точками
с долготами L1‘
и L2
по формуле
5.3 даёт результат на местности:
ΔУН
= 47 752,934 м., ΔУВ
= 47 586,020 м.
на
карте масштаба 1:100 000 :
ΔУН
= 47 752,934м. : 100000 = 0, 47752934 м. ≈ 477,53мм.
ΔУВ
= 47 586,020м. : 100000 = 0, 47586020м м. ≈ 475,86мм.
Вычисление
площади съемочной трапеции.
Площадь съемочной
трапеции вычисляется по
формуле:

(5.4)
Задание 5.4 Вычислить
площадь съёмочной трапеции ограниченной
параллелями с широтами
B1=31°00′
и B2=31°20′
и меридианами с долготами L1=66°00′
и L2=66°30′.
Решение
Вычисление
площади съёмочной трапеции по формуле
5.4 даёт результат:
Р = 1761777864,9 м2.
= 176177,7865 га. = 1761,778 км2.
Для грубого
контроля
площадь съемочной
трапеции можно вычислить по
приближённой формуле:
![]() (5.5)
(5.5)
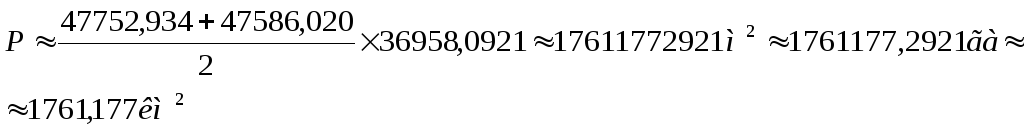
Вычисление
диагонали съемочной трапеции.
Д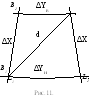 иагональ
иагональ
съемочной трапециивычисляют
по формуле:
![]() (5.6)
(5.6)
где:
d
– длина диагонали трапеции,
ΔYН
– длина
дуги параллели нижней рамки, ΔYВ–
длина дуги параллели верхней рамки
трапеции,
ΔХ
– длина
дуги меридиана левой (правой) рамки.
Задание 5.4 Вычислить
диагональ съёмочной трапеции ограниченной
параллелями с широтами
B1=31°00′
и B2=31°20′
и меридианами с долготами L1=66°00′
и L2=66°30′.
Решение
![]()
Соседние файлы в папке литература ВГ
- #
- #
Подборка по базе: КР ЛА Прыжок в длину способом %22согнув ноги%22 у женщин.docx, Практическая работа по теме Вычисление интегралов.pdf, № 10 – Зайка – длиные уши.docx, Самостоятельная работа по математике _Окружность. Круг. Длина ок, 5. Длинноволосая звезда.docx, метрические единицы длины.doc, контр раб по геом 9Б кл Длина окр и площад круга.docx, конспект урока математики в 1 классе Дециметр – единица длины.do, Практическая работа №4 Вычисление проиводных.docx, ТЕОРИЯ ДЛИННЫХ ЦИКЛОВ.pptx
Задание № 1: Вычисление длин дуг меридианов и параллелей
- Определить длины рамок (меридиан и параллели) трапеций масштаба 1:100000
Определение исходных данных для задачи:
1. Параметры эллипсоида в таблице № 1 приложения 1.
2. Широтный пояс трапеции масштаба 1: 1000000 выбирается по номеру десятка из номера учетного шифра (разделить номер на 10 и округлить вверх) в таблице № 3 приложения 1;
3. Номер номенклатуры листа масштаба 1:100000 – номер пояса выбираем по номеру единиц в номере учетного шифра (например, в номере 23 единицы – 3) в таблице № 2 приложения 1.
4. Номер зоны для листа трапеции масштаба 1:1000000 – 7.
Длины дуг меридианов и параллелей
Вычисление длины дуги меридиана (от экватора) выполняют степенными функциями,
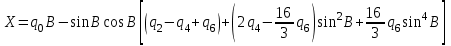 ; ; |
(1) |
Коэффициенты, являющиеся постоянными величинами имеют вид:
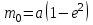 ; ; 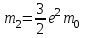 ; ; 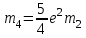 ; ; 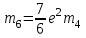 ; ; 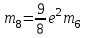 ; ; 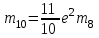 |
(2) |
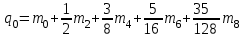 ; ; 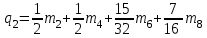 ; ;
|
(3) |
где – 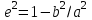 – квадрат первого эксцентриситета; а — большая или экваториальная полуось эллипсоида, b — малая или полярная полуось.
– квадрат первого эксцентриситета; а — большая или экваториальная полуось эллипсоида, b — малая или полярная полуось.
Параллель представляет собой окружность радиуса 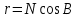 . Поэтому длину дуги параллели на широте В между меридианами
. Поэтому длину дуги параллели на широте В между меридианами 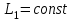 и
и 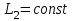 найдем по формуле
найдем по формуле
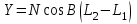 . . |
(4) |
Примечание: разности долгот дуг параллелей 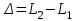 на разных широтах, будут иметь разную длину, так как радиус параллели
на разных широтах, будут иметь разную длину, так как радиус параллели 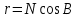 зависит от широты.
зависит от широты.
Приложение
Таблица 1 Параметры эллипсоидов №1 и №2
Параметры эллипсоидов №1 и №2
| №
п/п |
Эллипсоид №1 | Эллипсоид №2 | ||
| Semi-major axis (a)
(большая полуось) |
Semi-minor axis (b)
(малая полуось) |
Semi-major axis (a)
(большая полуось) |
Semi-minor axis (b)
(малая полуось) |
|
|
|
6378710,30 | 6357912,84 | 6378680,99 | 6357136,87 |
|
|
6378867,89 | 6357861,02 | 6378594,67 | 6357637,74 |
|
|
6378993,02 | 6358280,07 | 6379007,45 | 6358231,37 |
|
|
6378752,70 | 6357392,21 | 6379223,72 | 6358272,15 |
|
|
6378500,46 | 6357116,07 | 6378658,75 | 6358296,08 |
|
|
6378493,95 | 6358206,17 | 6378840,88 | 6356927,17 |
|
|
6378620,19 | 6356866,35 | 6378253,19 | 6357588,85 |
|
|
6379168,58 | 6358049,97 | 6378586,03 | 6357512,86 |
|
|
6378489,19 | 6357273,72 | 6378816,95 | 6358257,39 |
|
|
6378737,34 | 6357806,17 | 6378473,77 | 6358231,49 |
|
|
6379094,29 | 6357715,74 | 6378635,22 | 6358009,89 |
|
|
6378511,67 | 6358218,05 | 6379190,32 | 6358061,73 |
|
|
6378388,36 | 6358137,66 | 6379025,63 | 6357106,67 |
|
|
6378458,99 | 6357820,51 | 6379089,76 | 6357417,77 |
|
|
6378323,83 | 6357815,04 | 6378481,17 | 6357484,03 |
|
|
6378955,44 | 6357595,87 | 6378471,29 | 6357025,38 |
|
|
6378282,08 | 6357926,56 | 6378511,35 | 6357065,68 |
|
|
6378751,49 | 6357590,01 | 6378768,73 | 6357233,71 |
|
|
6378660,73 | 6357898,73 | 6378801,62 | 6358252,67 |
|
|
6379242,20 | 6357800,09 | 6378492,08 | 6358212,93 |
|
|
6378502,04 | 6357734,33 | 6379226,78 | 6357545,29 |
|
|
6378777,08 | 6358128,76 | 6378776,23 | 6358122,05 |
|
|
6378729,95 | 6357989,39 | 6378307,70 | 6358316,65 |
|
|
6379162,00 | 6357907,86 | 6379059,95 | 6358235,46 |
|
|
6378815,15 | 6358325,65 | 6379061,01 | 6358195,27 |
|
|
6378449,30 | 6358323,53 | 6378887,26 | 6357447,32 |
|
|
6378383,95 | 6357153,31 | 6379204,23 | 6357357,52 |
|
|
6378346,26 | 6357117,57 | 6378986,70 | 6357691,28 |
|
|
6379030,87 | 6357352,07 | 6378330,83 | 6358127,19 |
|
|
6378767,60 | 6356927,84 | 6378730,97 | 6356905,98 |
|
|
6378956,61 | 6358295,07 | 6379072,73 | 6358104,30 |
|
|
6379121,92 | 6357400,46 | 6379153,71 | 6357051,50 |
|
|
6378395,04 | 6357456,20 | 6379209,42 | 6357984,32 |
|
|
6378333,16 | 6356931,07 | 6379116,94 | 6358238,00 |
|
|
6378866,84 | 6357151,60 | 6378931,26 | 6357288,63 |
|
|
6378933,53 | 6357580,68 | 6379180,46 | 6357406,84 |
|
|
6378261,59 | 6357981,85 | 6378954,47 | 6357771,94 |
|
|
6379082,11 | 6356937,30 | 6378672,41 | 6358185,66 |
|
|
6379058,35 | 6357036,98 | 6379121,44 | 6358011,58 |
|
|
6378722,09 | 6357025,88 | 6379087,98 | 6357765,99 |
|
|
6378508,06 | 6356988,29 | 6378810,40 | 6358037,12 |
|
|
6378312,18 | 6357797,24 | 6378983,99 | 6358204,78 |
|
|
6378491,60 | 6357451,85 | 6379116,91 | 6357196,32 |
|
|
6378319,53 | 6358255,46 | 6379220,13 | 6358350,67 |
|
|
6378667,43 | 6356970,45 | 6378882,23 | 6357183,68 |
|
|
6378920,30 | 6357507,32 | 6378538,88 | 6356927,61 |
|
|
6378523,50 | 6357097,81 | 6378749,91 | 6358353,74 |
|
|
6378661,11 | 6357816,50 | 6378972,32 | 6357263,63 |
|
|
6379147,61 | 6358124,40 | 6378961,84 | 6357646,52 |
|
|
6378321,46 | 6358264,98 | 6379049,40 | 6357892,03 |
|
|
6378814,43 | 6357161,26 | 6378953,31 | 6357660,64 |
|
|
6378907,17 | 6357832,22 | 6378456,76 | 6357396,95 |
|
|
6378781,67 | 6357717,56 | 6379037,61 | 6358072,25 |
|
|
6379017,70 | 6357730,89 | 6378852,68 | 6358037,54 |
|
|
6378458,25 | 6357175,11 | 6378715,82 | 6357767,29 |
|
|
6379013,51 | 6357972,98 | 6378657,74 | 6357924,99 |
|
|
6378340,02 | 6358006,87 | 6378821,36 | 6358246,50 |
|
|
6378972,69 | 6356896,72 | 6378536,72 | 6358141,07 |
|
|
6379148,39 | 6358219,95 | 6378414,76 | 6357525,50 |
|
|
6378953,77 | 6356945,79 | 6378289,90 | 6357050,44 |
|
|
6378304,77 | 6357680,55 | 6378286,99 | 6356926,47 |
|
|
6378317,84 | 6357548,59 | 6379034,07 | 6357852,63 |
|
|
6378667,31 | 6357804,86 | 6379117,85 | 6357939,94 |
|
|
6378900,45 | 6357532,03 | 6378457,19 | 6356900,45 |
|
|
6378394,84 | 6358028,27 | 6378608,57 | 6357648,55 |
|
|
6378515,75 | 6358361,44 | 6378787,33 | 6358115,06 |
|
|
6378766,72 | 6357465,39 | 6379117,68 | 6356952,52 |
|
|
6378508,44 | 6357416,77 | 6378857,54 | 6357212,00 |
|
|
6379098,87 | 6357811,31 | 6378487,82 | 6357829,34 |
|
|
6378488,54 | 6357189,41 | 6378582,89 | 6357891,47 |
|
|
6378711,13 | 6358335,84 | 6378594,44 | 6357993,37 |
|
|
6379235,58 | 6358281,47 | 6379004,51 | 6356912,79 |
|
|
6378382,46 | 6357942,59 | 6379222,58 | 6358192,63 |
|
|
6378817,23 | 6357234,82 | 6379137,69 | 6357946,83 |
|
|
6378330,61 | 6358131,43 | 6378505,70 | 6357801,16 |
|
|
6379036,26 | 6357198,58 | 6379101,71 | 6358307,72 |
|
|
6378762,90 | 6357840,00 | 6378303,20 | 6357533,95 |
|
|
6378395,42 | 6357337,30 | 6378260,31 | 6357941,43 |
|
|
6379130,20 | 6358082,25 | 6379082,50 | 6358316,93 |
|
|
6378506,22 | 6357059,11 | 6378723,53 | 6358169,84 |
|
|
6378371,17 | 6357190,72 | 6378466,50 | 6358064,28 |
|
|
6378704,21 | 6358097,62 | 6378548,03 | 6357747,62 |
|
|
6379119,17 | 6357820,19 | 6379176,42 | 6357351,77 |
|
|
6378911,22 | 6357298,01 | 6378297,29 | 6357583,66 |
|
|
6379133,69 | 6358217,61 | 6378450,66 | 6357242,87 |
|
|
6378966,17 | 6358357,33 | 6378483,15 | 6357744,68 |
|
|
6378745,90 | 6357549,83 | 6378955,53 | 6358124,75 |
|
|
6378726,15 | 6357215,99 | 6378392,05 | 6357119,27 |
|
|
6379192,96 | 6357890,19 | 6378882,64 | 6357937,43 |
|
|
6379008,09 | 6357217,88 | 6379073,53 | 6357567,74 |
|
|
6378823,95 | 6357629,85 | 6378781,98 | 6357915,50 |
|
|
6378832,34 | 6357385,68 | 6378452,46 | 6357492,28 |
|
|
6378479,93 | 6357515,36 | 6378691,41 | 6358123,24 |
|
|
6378458,43 | 6357750,01 | 6378692,84 | 6357034,74 |
|
|
6378275,79 | 6357261,83 | 6378495,91 | 6358202,42 |
|
|
6378944,04 | 6358031,52 | 6378861,30 | 6358164,09 |
|
|
6378684,47 | 6358122,67 | 6378421,11 | 6357045,91 |
|
|
6378753,10 | 6357045,44 | 6378888,50 | 6357492,95 |
|
|
6378947,50 | 6358268,48 | 6378540,60 | 6357840,45 |
|
|
6378459,63 | 6357021,75 | 6378278,32 | 6358212,97 |
С помощью карты можно определять расстояние между точками на земной поверхности, но точность таких вычислений невысока.
Ситуация относительно проста, если точки лежат на одном меридиане. Все меридианы имеют одинаковую длину. Можно подсчитать, что одному градусу широты соответствует примерно 111,3 км реальной длины. Поэтому надо найти разницу в долготе между точками и умножить ее на 111,3 км. Например, если точка А находится на северной широте 50°, а Б располагается на северной широте 32°, и при этом у них совпадает долгота, то расстояние между ними составит.
111,3х(50° – 32°) = 111,3х16 = 1780,8 км
Ситуация меняется, когда одна точка имеет северную, а другая – южную широту. В этом случае широты уже надо складывать. Так, если бы точка Б из предыдущего примера располагалась бы на южной широте 32°, то расстояние от А до Б составило бы:
111,3х(50° + 32°) = 111,3х82 = 9126,6 км
Ситуация усложняется, когда точки находятся на разных меридианах, но на одной параллели. Если у обеих точек долгота западная (или, наоборот, восточная), то сначала надо найти разницу их долгот. Если же одна точка имеет восточную, а другая западную долготу, то их надо суммировать. Далее результат надо умножить на длину 1° параллели. Эта длина у параллелей различна и зависит от их широты. Можно воспользоваться таблицей ниже:
| Широта параллели | Длина ее дуги величиной в 1° |
|---|---|
| 0° | 111,3 |
| 5° | 110,9 |
| 10° | 109,6 |
| 15° | 107,6 |
| 20° | 104,6 |
| 25° | 102,1 |
| 30° | 96,5 |
| 35° | 91,3 |
| 40° | 85,4 |
| 45° | 78,8 |
| 50° | 71,7 |
| 55° | 64,0 |
| 60° | 55,8 |
| 65° | 47,2 |
| 70° | 38,2 |
| 75° | 28,9 |
| 80° | 19,4 |
| 85° | 9,7 |
| 90° | 0 |
Например, нужно найти расстояние между точками, имеющими координаты:
А – 60° с. ш, 39° з. д.
Б – 60° с. ш, 25° з. д.
Широты у них одинаковы, поэтому смотрим на долготу. Она у обеих точек западная, поэтому надо найти их разницу:
39° – 25° = 14°
Полученный результат надо умножить на длину 1° параллели, широта которой составляет 60°. По табличке определяем, что на широте 60° дуга в 1° имеет длину 55,8 км. Перемножаем два числа:
14°х 55,8 км = 781,2 км
Список использованных источников
• https://www.yaklass.ru/p/geografiya/5-klass/izobrazheniia-zemnoi-poverkhnosti-i-ikh-ispolzovanie-131512/geograficheskie-koordinaty-161116/re-d77ff3cc-0858-4fd8-aabd-69f1fdffb41d • https://interneturok.ru/lesson/geografy/5-klass/plan-i-karta/gradusnaya-setka-geograficheskaya-dolgota-i-shirota

Гугломаг
Спрашивай! Не стесняйся!
Задать вопрос
Не все нашли? Используйте поиск по сайту
Есть у нас калькулятор, вычисляющий длину дуги меридиана в зависимости от широты, а точнее, длину дуги меридиана размером в одну минуту, более известной как морская миля. Для полноты решил написать калькулятор, рассчитывающий размер длины дуги параллели в зависимости от широты. Из достаточно очевидных соображений, чем больше широта, то есть, чем ближе мы к тому или иному полюсу, тем меньше размер дуги, скажем, в 1 градус, в метрах. Калькулятор ниже и считает размер этой дуги на заданной широте по заданному угловому размеру дуги. Для справки, на экваторе размер дуги параллели в один градус будет максимальным (широта равна нулю) и составит 111 км 319 метров (приближенно). Как это считается, описано под калькулятором.
![]()
Длина дуги параллели
Длине дуги параллели в градусах равной
соответствует длина дуги параллели в метрах
Точность вычисления
Знаков после запятой: 2
Длина дуги параллели
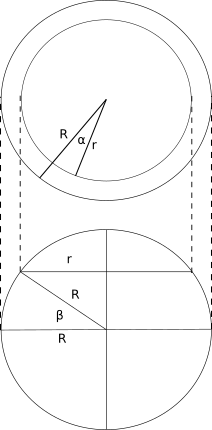
Расчет достаточно простой, и выполняется из общих геометрических соображений. Землю мы конечно приближенно представляем сферой (хотя она геоид).
Чтобы найти длину дуги окружности по углу дуги α, достаточно радиус окружности r умножить на угол дуги в радианах
Для длины дуги в 360 градусов, или 2π радиан, формула превращается в известную всем формула длины окружности
Как видно из рисунка, на определенной широте нас интересует радиус окружности r, полученной при отсечении части сферы плоскостью, параллельной плоскости экватора. На самом экваторе радиус совпадает с радиусом земли R. Выразим интересующий нас радиус через радиус Земли R и заданную широту β:
Соответственно, финальная формула
Ну и в качестве радиуса Земли берем значение, определенное в стандарте WGS-84, а именно, 6378137м. Вот и всё.
Скачать с Depositfiles

1.10 Вычисление длины дуги параллели
Параллель на эллипсоиде вращения является окружностью, поэтому вычис-
ление дуги параллели не представляет особой сложности и сводится к опреде-
лению дуги окружности с центральным углом, равным разности долгот конечных
точек дуги. Радиус параллели r определяется по формулам (1.13) и (1.18)
r = N cos B =
a cos B
1 − e2 sin2 B
=
a cos B
.
W
Длина дуги параллели ∆Y, имеющей широту B и разность долгот конечных
точек дуги l, очевидно, определится формулой
∆Y = N cos B
l ′′
.
ρ′′
(1.32)
Можно решить и обратную задачу, т.е. зная расстояние между точками, рас-
положенными на одной параллели с широтой B, найти разность долгот
1. Геометрия земного эллипсоида
23
l ′′ =
∆Y
sec B ρ′′ .
N
(1.33)
1.11 Вычисление длины дуги меридиана
Сложнее обстоит дело с вычислением длины дуги меридиана, т.к. сечение
меридиана представляет собой эллипс, радиус кривизны которого постоянно
изменяется.
Возьмем на меридианном эллипсе две точки Q1 и Q2 соответственно с широ-
dX (рис.1.14.). В этом случае дугу
dX можно рассматривать как дугу окружности радиуса M
dX = ( B 2 − B1)M = M dB .
(1.34)
тами B1 и B2 на бесконечно малом расстоянии
Длина дуги меридиана между конечными точками, имеющими широты B1 и
B2, определится следующим интегралом
∆X =
B2
∫
B1
(
)
a 1 − e2 dB
(1 − e
Рис.1.14
2
sin2 B
)
3
(
= a 1− e
2
B2
)∫(
B1
1 − e2 sin2 B
)
−3 2
dB .
(1.35)
Этот интеграл является эллиптиче-
ским и в элементарных функциях не бе-
рется. Для его нахождения используют 2
способа:
1. Раскладывают подынтегральную
функцию в степенной ряд, ограничиваясь
определенным числом членов разложе-
ния, и выполняют почленное интегриро-
вание, которое, таким образом сводится к
интегрированию в элементарных функци-
ях.
2. Применяют численное интегриро-
вание методами, известными в вычисли-
тельной математике.
1 способ.
Разложение подынтегральной функции в быстросходящийся ряд позволяет
получить общую формулу для вычисления дуги меридиана
Ю.Н.Гавриленко — Основы сфероидической геодезии
24
(
)
a
a
∆X = a 1 − e2 a0 ( B 2 − B1) − 2 ( sin 2 B 2 − sin 2 B1) + 4 ( sin 4 B 2 − sin 4 B1) −
2
4
a
(1.36)
− 6 ( sin 6B 2 − sin 6B1)+ … ,
6
где (B2- B1 ) — разность широт выраженная в радианах,
3
45
175 6 11025 8
a0 = 1 + e2 + e4 +
e +
e + … ;
4
64
256
16384
3 2 15 4 525 6 2205 8
a2 =
e + e +
e +
e + … ;
4
16
512
2048
15
105 6 2205 8
a4 =
+ e4 +
e +
e + … ;
64
256
4096
35 6 315 8
a6 =
+
e +
e + … .
512
2048
Формула (1.36), как уже отмечалось, является общей для дуги меридиана.
Она может быть преобразована в зависимости от ее назначения и от длины дуги
меридиана.
1. Если принять B1=0, то получим формулу для длины дуги меридиана от эк-
ватора до точки с заданной широтой B
(
)
B ′′ a2
a
a
X = a 1 − e2 a0
− sin 2 B + 4 sin 4 B − 6 sin 6B + … .
4
6
ρ′′ 2
(1.37)
Эта формула используется для вычисления плоских прямоугольных коорди-
нат в проекции Гаусса-Крюгера по заданным геодезическим координатам.
2. Для вычисления длин дуг меридианов протяженностью до 400 километров
с точностью до одного миллиметра в формуле (1.36) достаточно удерживать
слагаемые, содержащие множитель e2, и тогда получим следующую формулу
∆X = M m
( B 2 − B1) 1 + ( B 2 − B1)2 e2 cos 2 B
ρ
8ρ2
m ,
(1.38)
где Mm -вычисляется по средней широте Bm =(B1+B2 )/2.
3. Для вычислений в триангуляции, когда стороны незначительны и редко
превышают 40-50 километров, приведем более простую и удобную формулу
∆X = M m
( B 2 − B1 ) .
ρ
(1.39)
Следовательно, при длине дуги менее 45 км ее можно рассматривать как
сферическую с центральным углом, равным разности широт конечных точек, и
1. Геометрия земного эллипсоида
25
описанную радиусом меридианного сечения, соответствующим средней широте
дуги.
Нахождение широты B по заданной длине дуги меридиана от экватора явля-
ется обратной задачей. Из формулы (1.37) может быть записана следующая
формула для определения широты
BX по заданной длине дуги меридиана про-
извольной длины X
BX
a4
a6
1
X
a2
=
+ sin 2 B X −
sin 4 B X +
sin 6 B X
a0 a 1 − e 2 2
4
6
(
)
(1.40)
Вычисление широты производят методом последовательных приближений,
принимая в первом приближении
I
BX =
(
X
a0 a 1 − e 2
)
Последующие приближения выражаются следующими формулами:
II
I
BX = BX +
III
I
BX = BX +
IV
I
BX = BX +
1 a2
1a
I
I
sin 2 B X − 4 sin 4 B X ;
2 a0
4 a0
1 a2
1a
1a
II
II
II
sin 2 B X − 4 sin 4 B X + 6 sin 6 B X ;
2 a0
4 a0
6 a0
1 a2
1a
1a
III
III
III
sin 2 B X − 4 sin 4 B X + 6 sin 6 B X .
2 a0
4 a0
6 a0
Окончательное значение выражается следующей формулой
I
BX = BX +
1 a2
1a
1a
IV
IV
IV
sin 2 B X − 4 sin 4 B X + 6 sin 6 B X .
2 a0
4 a0
6 a0
2 способ.
При численном интегрировании удобно использовать наиболее простую и
достаточно точную формулу Симпсона (формулу парабол). Разделим интервал
интегрирования на 2 равные части. Тогда можно записать
∆B
(1.41)
( M 1 + 4M m + M 2 ) .
6
В данной формуле радиус кривизны M определяется в трех точках искомой
∆X =
дуги меридиана: в начальной, конечной и средней, соответственно по широтам
Ю.Н.Гавриленко — Основы сфероидической геодезии
26
B1, B2, Bm. При расстояниях между точками до 500 километров формула (1.41)
обеспечивает точность вычислений 1-2 см.
Для контроля и повышения точности длину дуги меридиана можно вычис-
B2
Bm
Bm
Bm
B1
Экватор
Рис.1.15
лить как сумму нескольких дуг. На рис.1.15. показано нахождение дуги меридиа-
на между точками с широтами B1 и B2 как сумму двух дуг
∆X 1 и ∆X 2 :
∆X = ∆X 1 + ∆X 2 ;
(Bm − B1 )′′ (M + 4M ′ + M )
∆X 1 =
m
m
1 ;
6 ρ ′′
(B2 − Bm )′′ (M + 4M ′′ + M )
∆X 2 =
2
m
m .
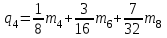 ;
;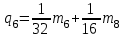 ;
;