Как найти дугу окружности если известен радиус

Как найти дугу окружности если известен радиус

Длина дуги окружности

{L = dfrac{pi R alpha}{180degree}}

Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.

Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.

Содержание:
  1. калькулятор длины дуги окружности
  2. формула длины дуги окружности через радиус и угол
  3. формула длины дуги окружности по формуле Гюйгенса
  4. примеры задач

Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:

  • Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.

    Полная окружность

  • Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.

    Полуокружность

  • Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.

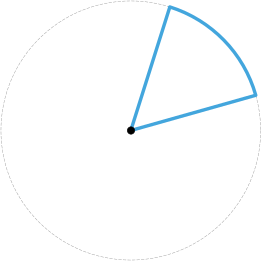
    Сектор окружности

Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.

Формула длины дуги окружности через радиус и угол

Длина дуги окружности через радиус и угол

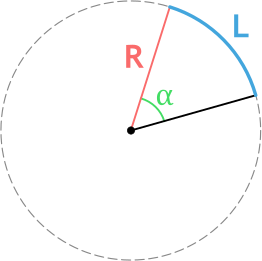
{L = dfrac{pi R alpha}{180degree}}

R – радиус окружности

α – центральный угол (угол между радиусами) в градусах

{L = R alpha}

R – радиус окружности

α – центральный угол (угол между радиусами) в радианах

Формула длины дуги окружности по формуле Гюйгенса

Длина дуги окружности по формуле Гюйгенса

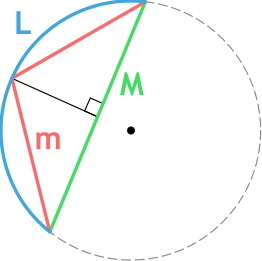
{L approxeq 2m + dfrac{2m-M}{3}}

m – длина хорды m

M – длина хорды M

Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.

Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.

Примеры задач на нахождение длины дуги

Задача 1

Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.

Решение

Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:

L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.

Ответ: {pi : см approx 3.14 : см.}

Введем известные значения в калькулятор для проверки полученного ответа.

Задача 2

Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.

Решение

Задача аналогична предыдущей. Также воспользуемся первой формулой.

L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.

Ответ: {2.5 pi : см approx 7.85398 : см.}

В проверке ответа нам снова поможет калькулятор .

Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.

Источник

Как рассчитать длину дуги окружности

На данной странице калькулятор поможет рассчитать длину дуги окружности онлайн. Для расчета задайте радиус, угол между радиусами.

Чтобы найти длину дуги, когда не известен радиус, например, на чертеже или у предмета, то используют формулу Гюйгенса. При расчете по этой формуле есть погрешность, примерно от 0,5% до 0,02%.

Дуга окружности – это часть окружности ограниченная двумя точками.

Через радиус и угол

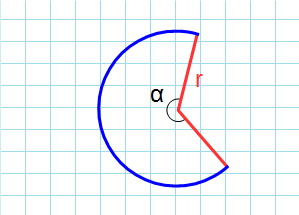
Длина дуги

Формула для нахождения площади сектора круга:

π – константа равная (3.14); α – угол сектора круга; r – радиус окружности.

По формуле Гюйгенса

Длина дуги по формуле Гюйгенса

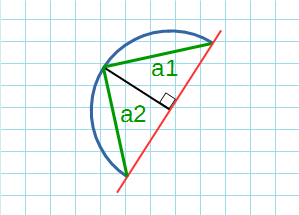
Формула Гюйгенса для нахождения длины дуги окружности:

a1, a2 – хорды.

Источник

Длина дуги

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Длина дуги

Чтобы найти длину дуги окружности воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Длина дуги
Чему равна длина дуги, если:

радиус r =
угол α =

Ответ: L =

0

Округление числа π: Округление ответа:

Просто введите радиус и угол α, и получите ответ.

Теория

Чему равна длина дуги окружности L если её радиус r, а угол между двумя прямыми, проведёнными от центра окружности к конечным точкам дуги – центральный угол α?

Формула

Если угол в градусах:

L = π ⋅ r ⋅ α ⁄ 180

Если угол в радианах:

L = r ⋅ α

Пример

Для примера посчитаем чему равна длина дуги окружности с радиусом r = 2 см и центральным углом α = 45° :

L = 3.14 ⋅ 2 ⋅ 45/180 = 6.28 ⋅ 0.25 = 1.57 см

См. также

Источник

Дуга окружности – это фрагмент окружности. Если на окружности отметить две точки A И B, то она разобьётся на 2 части, называемые дугами окружности.

Для того, чтобы найти длину дуги окружности, необходимо использовать значение центрального угла, измеряемого в радианах или градусах.

Существует 2 формулы длины дуги окружности:

1) Если дан центральный угол в радианах: l = R*α, где R – радиус, α – величина угла AOB в радианах.

2) Если дан центральный угол в градусах: l = R*π*C/180, где R – радиус, C – величина угла AOB в градусах.

Пример

Дано:

1) радиус окружности R = 6 дм.

2) центральный угол AOB = 45°.

Найти:

Длину дуги AB.

Решение:

l = 6*3,14*1/4 дм. = 4,71 дм.

Источник


Загрузить PDF


Загрузить PDF

Дуга – это некоторая часть окружности.[1]
 Длина дуги равна расстоянию между двумя точками, которые лежат на окружности. Чтобы вычислить длину дуги, необходимо иметь некоторое представление о геометрии окружности. Так как дуга представляет собой часть окружности, нужно найти величину центрального угла (в градусах или радианах), а затем вычислить длину дуги.

  1. Изображение с названием Find Arc Length Step 1

    1

    Запишите формулу для вычисления длины дуги. Формула: L=2pi (r)({frac {theta }{360}}), где r – радиус окружности, theta – центральный угол, измеренный в градусах.[2]

  2. Изображение с названием Find Arc Length Step 2

    2

    В формулу подставьте радиус окружности. Как правило, значение радиуса дается в задаче; в противном случае просто измерьте его. Значение радиуса подставляется вместо r.

    • Например, если радиус окружности равен 10 см, формула запишется так: L=2pi (10)({frac {theta }{360}}).

  3. Изображение с названием Find Arc Length Step 3

    3

    В формулу подставьте центральный угол. Как правило, значение центрального угла дается в задаче; в противном случае просто измерьте его. В указанную формулу подставьте центральный угол, измеренный в градусах (а не в радианах). Значение центрального угла подставляется вместо theta .

    • Например, если центральный угол равен 135 градусов, формула запишется так: L=2pi (10)({frac {135}{360}}).

  4. Изображение с названием Find Arc Length Step 4

    4

    Радиус умножьте на 2pi . Если нет калькулятора, воспользуйтесь следующим приблизительным значением: pi =3,14. Перепишите формулу, подставив в нее полученное значение, которое равно длине окружности.[3]

  5. Изображение с названием Find Arc Length Step 5

    5

    Разделите центральный угол на 360. Так как в круге 360 градусов, это вычисление позволит определить, какую часть круга представляет сектор. Благодаря полученной информацию можно найти часть окружности, которую представляет дуга.

  6. Изображение с названием Find Arc Length Step 6

    6

    Перемножьте два числа. Получится длина дуги.

    Реклама

  1. Изображение с названием Find Arc Length Step 7

    1

    Запишите формулу для вычисления длины дуги. Формула: L=theta (r), где r – радиус окружности, theta – центральный угол, измеренный в радианах.[4]

  2. Изображение с названием Find Arc Length Step 8

    2

    В формулу подставьте радиус окружности. Чтобы воспользоваться этим методом, нужно знать радиус. Значение радиуса подставляется вместо r.

    • Например, если радиус окружности равен 10 см, формула запишется так: L=theta (10).

  3. Изображение с названием Find Arc Length Step 9

    3

    В формулу подставьте центральный угол. В указанную формулу подставляйте центральный угол, измеренный в радианах. Если угол измеряется в градусах, этим методом пользоваться нельзя.

    • Например, если центральный угол равен 2,36 радиан, формула запишется так: L=2,36(10).

  4. Изображение с названием Find Arc Length Step 10

    4

    Умножьте радиус на центральный угол (измеренный в радианах). Получится длина дуги.

    Реклама

Советы

  • Если известен диаметр окружности, можно найти длину дуги. Приведенные выше формулы для вычисления длины дуги включают радиус окружности. Радиус равен половине диаметра, поэтому чтобы вычислить радиус, нужно просто разделить диаметр на 2.[5]
     Например, диаметр окружности равен 14 см; чтобы найти радиус, разделите 14 на 2:
    14div 2=7.
    Таким образом, радиус окружности равен 7 см.

Реклама

Об этой статье

Эту страницу просматривали 89 770 раз.

Была ли эта статья полезной?

Источник

Добавить комментарий