Как найти длину дуги окружности ?
r – радиус окружности
α – угол AOB, в градусах
Формула длины дуги ( L ):
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Как найти дугу окружности зная другую дугу
Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга

Часть окружности, расположенная между двумя точками окружности
Круг

Конечная часть плоскости, ограниченная окружностью
Сектор

Часть круга, ограниченная двумя радиусами
Сегмент

Часть круга, ограниченная хордой
Правильный многоугольник

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:

Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула |
| Площадь круга |  |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Площадь круга |
 |
 ,
,
где R – радиус круга, D – диаметр круга
Площадь сектора

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь сегмента

 ,
,
если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула |
| Длина окружности |  |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга
Длина дуги

если величина угла α выражена в радианах
 ,
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .






Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности



то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:

откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.

В случае, когда величина α выражена в градусах, справедлива пропорция

из которой вытекает равенство:

В случае, когда величина α выражена в радианах, справедлива пропорция

из которой вытекает равенство:

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем



В случае, когда величина α выражена в в радианах, получаем
Как найти длину дуги окружности ?
r — радиус окружности
α — угол AOB, в градусах
Формула длины дуги ( L ):
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
Длина дуги
На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
[spoiler title=”источники:”]
http://mnogoformul.ru/dlina-dugi
http://b4.cooksy.ru/articles/kak-nayti-dugu-okruzhnosti-znaya-druguyu-dugu
[/spoiler]
Дуга окружности – это фрагмент окружности. Если на окружности отметить две точки A И B, то она разобьётся на 2 части, называемые дугами окружности.

Для того, чтобы найти длину дуги окружности, необходимо использовать значение центрального угла, измеряемого в радианах или градусах.
Существует 2 формулы длины дуги окружности:
1) Если дан центральный угол в радианах: l = R*α, где R – радиус, α – величина угла AOB в радианах.
2) Если дан центральный угол в градусах: l = R*π*C/180, где R – радиус, C – величина угла AOB в градусах.
Пример
Дано:
1) радиус окружности R = 6 дм.
2) центральный угол AOB = 45°.
Найти:
Длину дуги AB.
Решение:
l = 6*3,14*1/4 дм. = 4,71 дм.

{L = dfrac{pi R alpha}{180degree}}
Длина дуги окружности – важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности – через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.
Содержание:
- калькулятор длины дуги окружности
- формула длины дуги окружности через радиус и угол
- формула длины дуги окружности по формуле Гюйгенса
- примеры задач
Если обобщить, то дуга окружности – это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:
-
Полная окружность – это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r – радиус окружности.

-
Полуокружность – это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
-
Сектор окружности – это область, ограниченная дугой окружности и двумя ее радиусами.
Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.
Формула длины дуги окружности через радиус и угол
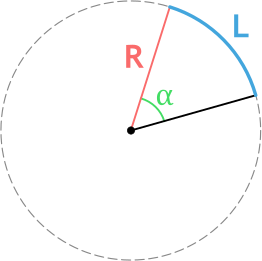
{L = dfrac{pi R alpha}{180degree}}
R – радиус окружности
α – центральный угол (угол между радиусами) в градусах
{L = R alpha}
R – радиус окружности
α – центральный угол (угол между радиусами) в радианах
Формула длины дуги окружности по формуле Гюйгенса
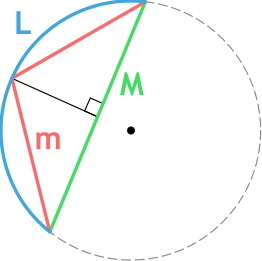
{L approxeq 2m + dfrac{2m-M}{3}}
m – длина хорды m
M – длина хорды M
Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак “равно или почти равно”, который записывается так – «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.
Примеры задач на нахождение длины дуги
Задача 1
Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.
Решение
Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.
Ответ: {pi : см approx 3.14 : см.}
Введем известные значения в калькулятор для проверки полученного ответа.
Задача 2
Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.
Решение
Задача аналогична предыдущей. Также воспользуемся первой формулой.
L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.
Ответ: {2.5 pi : см approx 7.85398 : см.}
В проверке ответа нам снова поможет калькулятор .
Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.
 Свойство касательных.
Свойство касательных.
Свойства касательных и секущих.
Свойства хорд.
Углы окружности.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
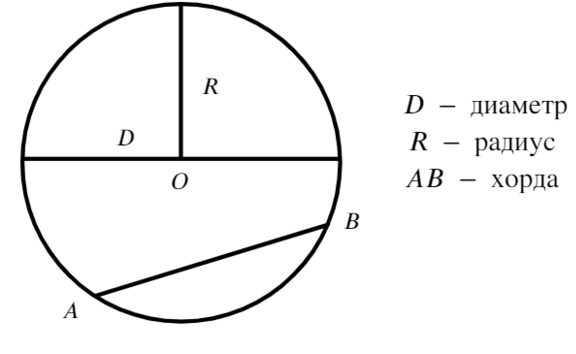
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
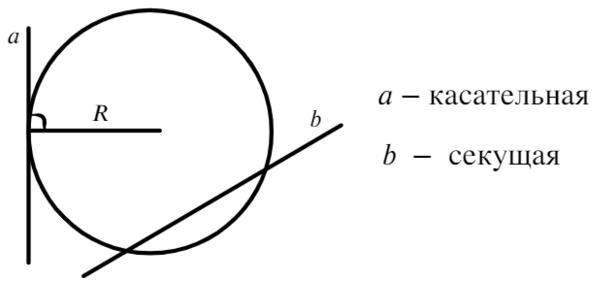
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
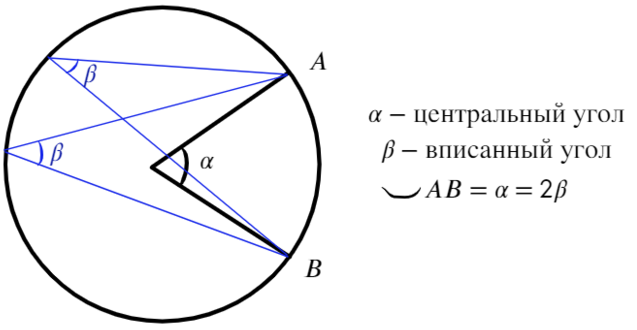
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
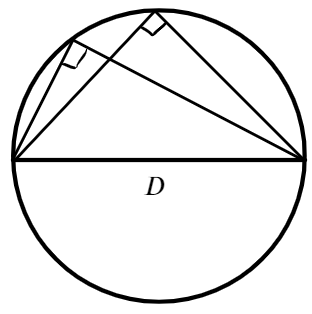
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
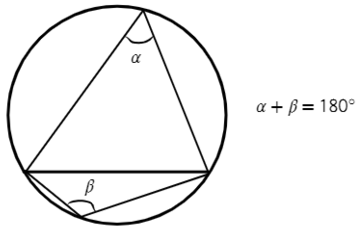
Запишем основные свойства углов в окружности:
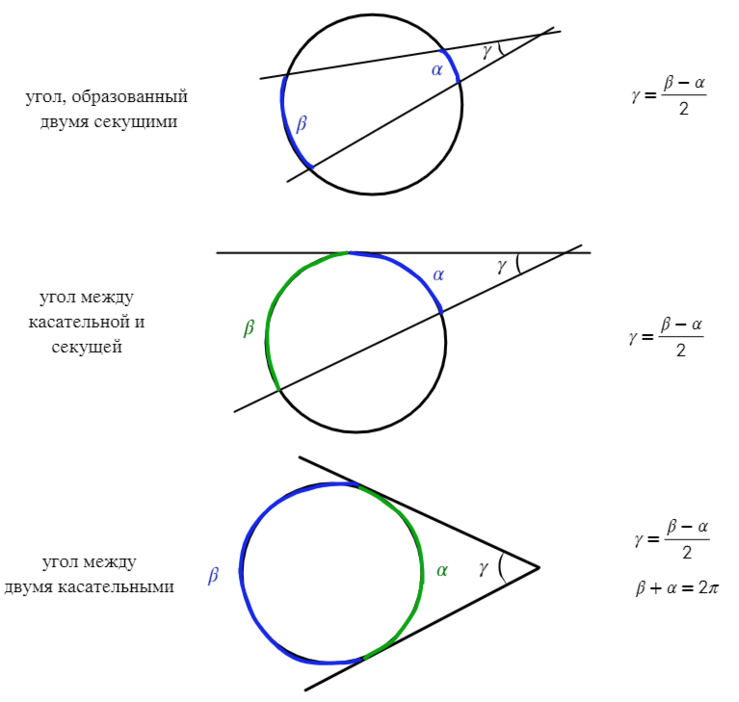
Нашел что-то общее?
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
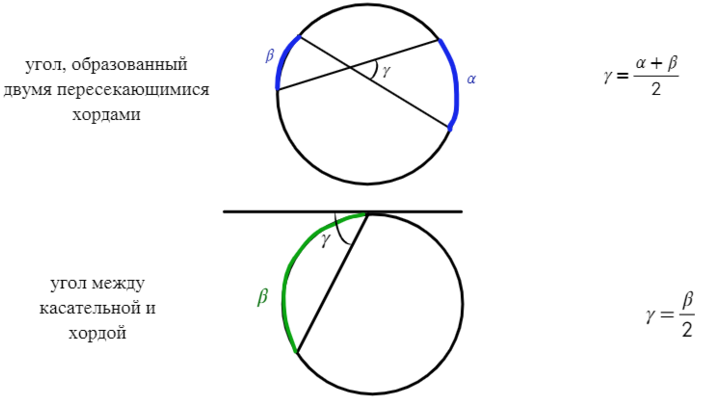
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
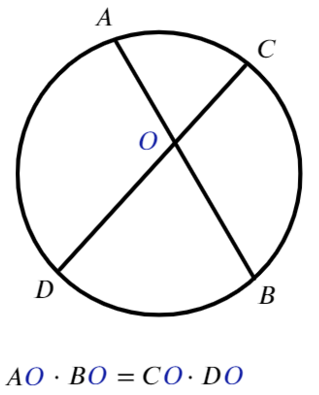
Отношение отрезков:
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
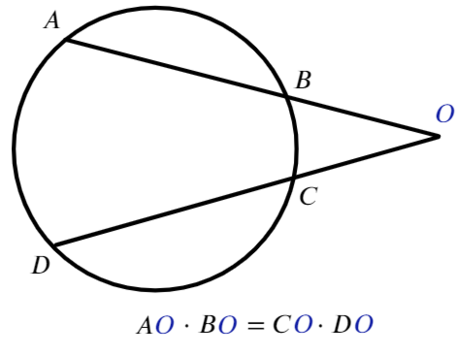
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
Если из точки, лежащей вне окружности, проведены касательная и секущая:
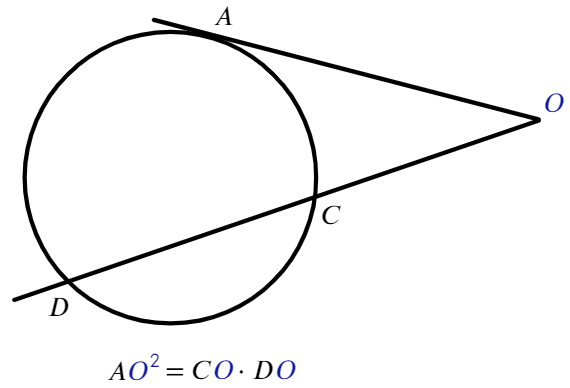
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
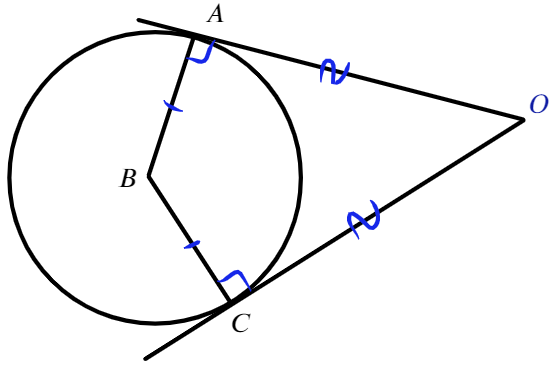
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
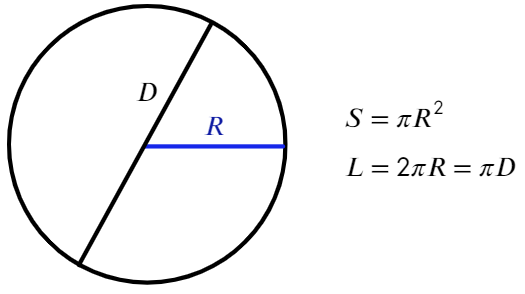
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
Задача №1. Дано на рисунке:
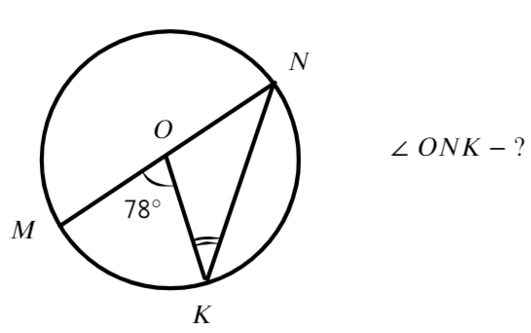
Достаточно вспомнить свойства центральных и вписанных углов.

Ответ: 39°
Задача №2. Дано на рисунке:
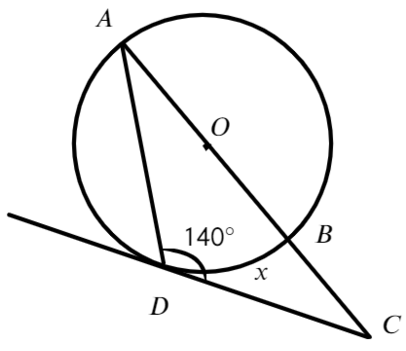
Найти нужно меньшую дугу BD
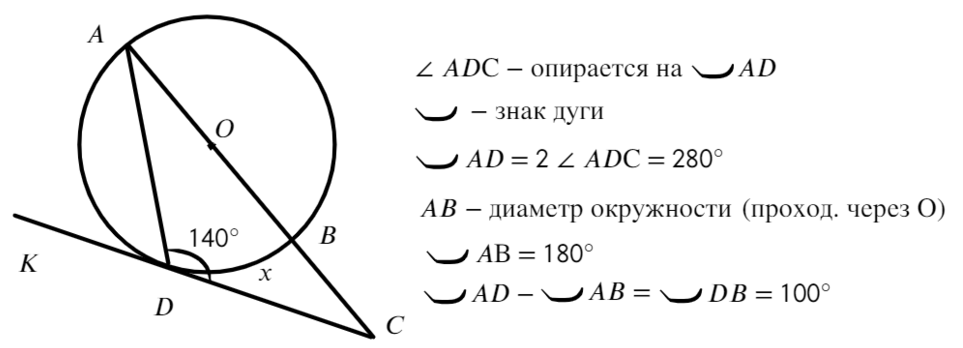
Ответ: 100°Задача №3. Дано на рисунке:
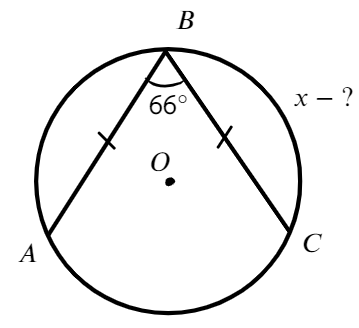
Найти меньшую дугу ВС
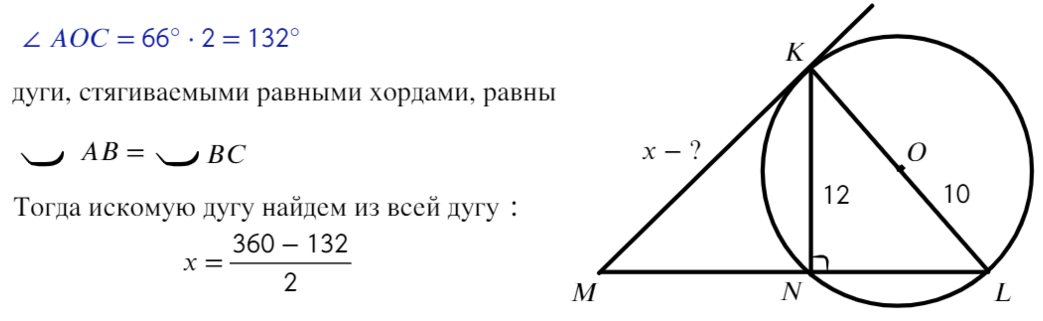
Ответ: 114°
Задача №4. Дано на рисунке:
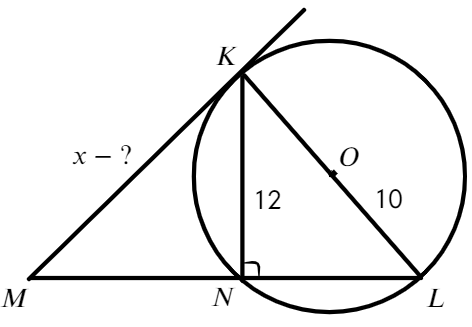
Найти отрезок МК
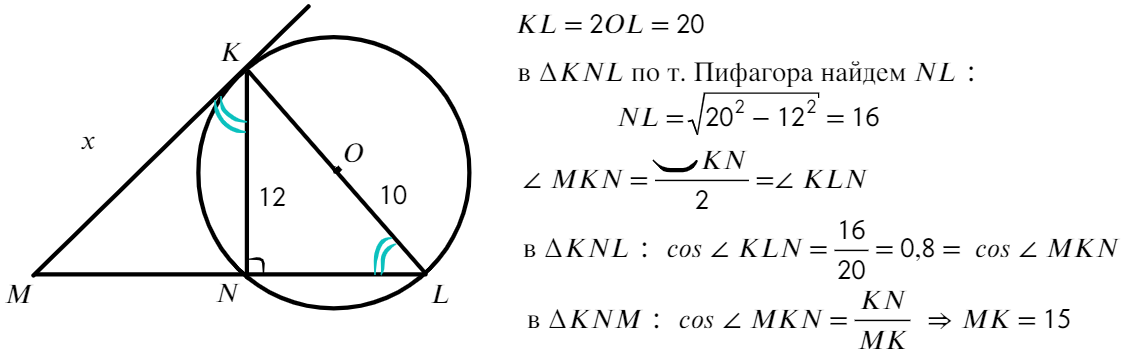
Ответ: МК = 15.
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники

Ответ: 6
Задача №5. Дано на рисунке:
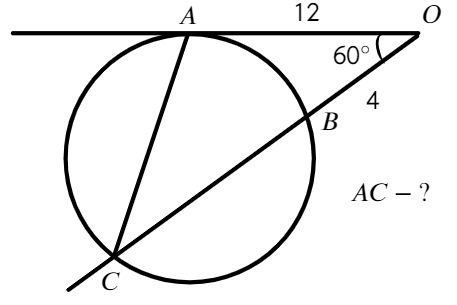
Без свойства секущей и касательной здесь будет тяжело
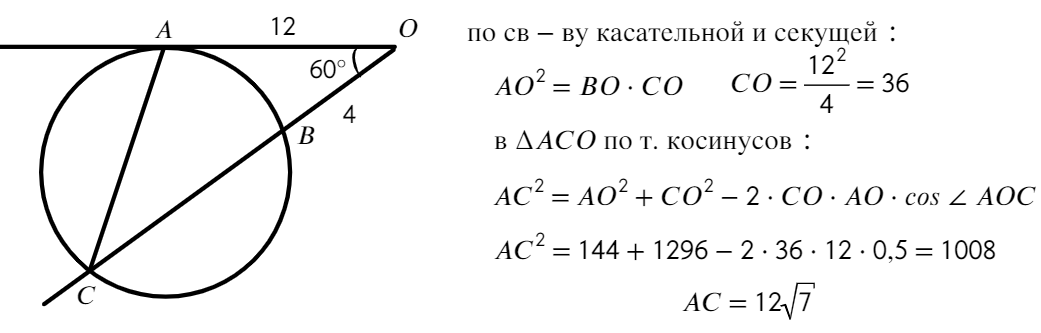
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
Попробуй эти задачи с подсказками.
О треугольниках
О четырехуголникахp.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
Длина дуги
Лариса Семеновна Петрова
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
Из этой статьи вы узнаете, как выглядит формула длины дуги окружности через угол, а также научитесь определять длину дуги сектора по формуле Гюйгенса. Также на страницу добавлены онлайн-калькуляторы для вычисления по данным формулам.
Определение 1
Дугой окружности (сектора) называют часть окружности, ограниченную двумя точками.
Чтобы определить длину дуги окружности, введите заданные данные в поля для ввода онлайн-калькулятора.
Длина дуги через радиус и угол

Для определения длины дуги можно воспользоваться формулой:
$l = π cdot R cdot frac{α}{180°}$, где
$R$ — радиус окружности;
$α$ — угол, которым характеризуется дуга;
$π$ — константа.
Рассмотрим пример на использование этой формулы.
Пример 1
Задача
Угол, ограничивающий дугу, составляет $50°$, а радиус окружности равен $9$ см. Рассчитайте, чему равна длина дуги.
Решение:
$l = 3.14 cdot 9 cdot frac{50}{180} = 7.85$ см.
Проверим длину дуги окружности с помощью онлайн-калькулятора. Результат совпадает, значит ответ верный.
Длина дуги по формуле Гюйгенса

По формуле Гюйгенса длина дуги рассчитывается следующим образом:
$l ≈ 2 cdot AB + frac13 cdot ( 2 cdot AB – AC)$, здесь
$AC$ — хорда, соединяющая концы дуги;
$AB$ — хорда, соединяющая середину дуги, расположенную в точке $B$ и конец дуги $A$.
Формула Гюйгенса не является точной. Для угла в $60°$ погрешность по этой формуле будет составлять около $0.5%$, однако для меньших значений угла погрешность уменьшается.
Также посмотрим, как использовать формулу Гюйгенса.
Пример 2
Задача
Длина хорды $AC$ равна $3.51$ см, а хорды $AB$ $2.19$ см. Чему равна длина дуги $l$?
Решение:
$l = 2 cdot 2.19 + frac13 cdot (2 cdot 2.19 — 3.51) = 4.67$ см.
Результат совпадает, а значит, ответ — верный.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 27.06.2019