Как найти дугу описанного квадрата

Как найти дугу описанного квадрата

Как найти длину дуги окружности ?

r – радиус окружности

α – угол AOB, в градусах

Формула длины дуги ( L ):

Калькулятор для расчета длины дуги окружности :

Формулы для окружности и круга:

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

  • Длины всех сторон квадрата равны.
  • Все углы квадрата прямые.
  • Диагонали квадрата равны.
  • Диагонали пересекаются под прямым углом.
  • Диагонали квадрата являются биссектрисами углов.
  • Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

Из равенства (1) найдем d:

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

Из формулы (5) найдем R:

или, умножая числитель и знаменатель на , получим:

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Длина дуги

На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между ними и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькуляторов, которые используют эти формулы.

Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.

[spoiler title=”источники:”]

http://matworld.ru/geometry/kvadrat.php

http://mnogoformul.ru/dlina-dugi

[/spoiler]

Источник

Здравствуйте, уважаемые читатели. Продолжаем разбор заданий с окружностью. В этой статье рассмотрим задачи на вписанную окружность в квадрат и описанную около квадрата.

1. Центральные и вписанные углы.

2.Касательная, хорда, секущая.

3.Вписанная и описанная окружность (треугольник)

4. Вписанная и описанная окружность (квадрат)

Все задачи такого типа достаточно простые. Приступим сразу же к решению задач.

Задача №1

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Решение:

Радиус окружности – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

Решение к этой задачи представлю в виде картинки.

Решение к задаче №1
Решение к задаче №1

О – центр окружности, r – радиус окружности. В этой задаче радиус окружности равен половине стороны квадрата. Ответ 8.

Задача №2

Найдите площадь квадрата, описанного вокруг окружности радиуса 9

Решение:

Задача обратная той, что мы решили выше. Так как радиус окружности равен 9, то сторона квадрата равна 18. Площадь квадрата равна:

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Задача №3

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Решение:

В предыдущих задачах мы определили, что если известен радиус вписанной окружности в квадрат, то сторона квадрата будет равна удвоенному значению радиуса.

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Зная сторону квадрата, диагональ квадрата найдем, используя теорему Пифагора.

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Задача №4

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Решение:

Эта задача, включает в себя все этапы, которые были разобраны выше. Задачу можно разбить на действия:

1) Найдем сторону квадрата.

2) Найдем диагональ квадрата.

3) Найдем радиус описанной окружности, разделив диагональ квадрата пополам.

d - диагональ квадрата, r - радиус вписанной окружности, R - радиус описанной окружности
d – диагональ квадрата, r – радиус вписанной окружности, R – радиус описанной окружности

1) Найдем сторону квадрата:

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

2) Найдем диагональ квадрата используя теорему Пифагора:

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

3) Найдем радиус описанной окружности, разделив диагональ квадрата пополам.

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ

Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Вписанная и описанная окружность (квадрат) Задание №16 ОГЭ
Источник

Квадрат вписанный в окружность

Обновлено 28.02.2022

Содержание

  1. Определение
  2. Формулы
  3. Радиус вписанной окружности в квадрат
  4. Радиус описанной окружности около квадрата
  5. Сторона квадрата
  6. Площадь квадрата
  7. Периметр квадрата
  8. Диагональ квадрата
  9. Свойства

Определение

Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.

На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.
Квадрат вписанный в окружность

Формулы

Радиус вписанной окружности в квадрат

  1. Радиус вписанной окружности в квадрат, если известна сторона:

    [ r=frac{a}{2} ]

  2. Радиус вписанной окружности в квадрат, если известен периметр:

    [ r=frac{P}{8} ]

  3. Радиус вписанной окружности в квадрат, если известна площадь:

    [ r=frac{sqrt S}{2} ]

  4. Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:

    [ r=frac{ R}{sqrt 2} ]

  5. Радиус вписанной окружности в квадрат, если известна диагональ:

    [ r=frac{ d}{2sqrt 2} ]

Радиус описанной окружности около квадрата

  1. Радиус описанной окружности около квадрата, если известна сторона:

    [ R=afrac{sqrt 2}{ 2} ]

  2. Радиус описанной окружности около квадрата, если известен периметр:

    [ R=frac{ P}{4 sqrt 2} ]

  3. Радиус описанной окружности около квадрата, если известна площадь:

    [ R=frac{sqrt 2S}{ 2} ]

  4. Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:

    [ R= r sqrt2 ]

  5. Радиус описанной окружности около квадрата, если известна диагональ:

    [ R=frac{d}{2} ]

Сторона квадрата

  1. Сторона квадрата вписанного в окружность, если известна площадь:

    [ a=sqrt S ]

  2. Сторона квадрата вписанного в окружность, если известна диагональ:

    [ a=frac{ d}{sqrt 2} ]

  3. Сторона квадрата вписанного в окружность, если известен периметр:

    [ a=frac{ P}{4} ]

Площадь квадрата

  1. Площадь квадрата вписанного в окружность, если известна сторона:

    [ S=a^2 ]

  2. Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:

    [ S=4r^2 ]

  3. Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:

    [ S=2R^2 ]

  4. Площадь квадрата вписанного в окружность, если известен периметр:

    [ S=frac{ P^2}{ 16} ]

  5. Площадь квадрата вписанного в окружность, если известна диагональ:

    [ S=frac{ d^2}{ 2} ]

Периметр квадрата

  1. Периметр квадрата вписанного в окружность, если известна сторона:

    [ P=4a ]

  2. Периметр квадрата вписанного в окружность, если известна площадь:

    [ P=4sqrt S ]

  3. Периметр квадрата вписанного в окружность, если известен радиус вписанной окружности:

    [ P=8r ]

  4. Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:

    [ P=4Rsqrt 2 ]

  5. Периметр квадрата вписанного в окружность, если известна диагональ:

    [ P=2dsqrt 2 ]

Диагональ квадрата

  1. Диагональ квадрата вписанного в окружность, если известна сторона:

    [ d=asqrt 2 ]

  2. Диагональ квадрата вписанного в окружность, если известна площадь:

    [ d=sqrt 2S ]

  3. Диагональ квадрата вписанного в окружность, если известен периметр:

    [ d=frac{ P}{2 sqrt 2} ]

  4. Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:

    [ d=2rsqrt 2 ]

  5. Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:

    [ d=2R ]

Свойства

  1. Все углы в квадрате прямые.
  2. Все стороны квадрата равны.
  3. Сумма всех углов квадрата 360°.
  4. Диагонали квадрата одновременно равны, пересекаются под прямым углом и являются биссектрисами углов.
  5. Точка пересечения диагоналей квадрата является центром вписанной и описанной окружности.
  6. Диагонали квадрата перпендикулярны, точкой пересечения делятся пополам.
  7. Квадрат обладает симметрией.
Источник

В публикации представлены онлайн-калькуляторы и формулы для расчета радиуса описанной около квадрата окружности через сторону фигуры или ее диагональ.

  • Расчет радиуса окружности

    • Через сторону квадрата

    • Через диагональ квадрата

Расчет радиуса окружности

Квадрат ABCD с описанной вокруг окружностью

Инструкция по использованию: введите сторону квадрата (a) или его диагональ (d), затем нажмите кнопку “Рассчитать”. В результате будет вычислен радиус (R) окружности, описанной описанной вокруг фигуры.

Через сторону квадрата

Формула расчета

Формула расчета радиуса описанной около квадрата окружности через длину его стороны

Через диагональ квадрата

Формула расчета

Формула расчета радиуса описанной около квадрата окружности через длину его диагонали

Источник

Радиус описанной окружности квадрата, формула

Радиус описанной окружности квадрата
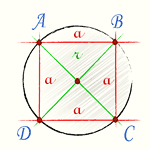
Формула радиуса описанной окружности квадрата выходит из теоремы Пифагора поскольку диагональ квадрата является диаметром описанной окружности.

[R=frac{sqrt{a^2+a^2}}{2}=frac{a}{sqrt{2}}]

(a – сторона квадрата; R – радиус описанной окружности квадрата)

Вычислить, найти радиус описанной окружности квадрата по формуле (1)

a (сторона квадрата) 

Вычислить

нажмите кнопку для расчета

Радиус описанной окружности квадрата

 стр. 248
Источник

Добавить комментарий