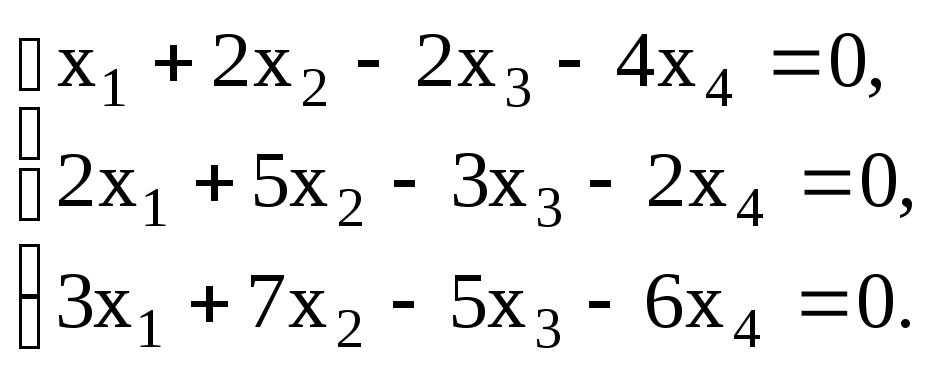Как найти два базиса системы векторов

Алгоритм нахождения базиса системы векторов

Для того чтобы найти базис системы векторов A_v А₂. А , необходимо:

1) составить соответствующую системе векторов однородную систему уравнений

2) привести эту систему к равносильной разрешенной системе вида

• 3) записать базис системы векторов Б = (А_рА₂, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
• 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора

в разрешенной системе уравнений, т.е.

Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.

Пример 3.3. Найти ранг и базис системы векторов

разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.

Решение. Составим систему уравнений A _t ay + А₂х₂ + . + А„х_п = 0, которая в координатной записи имеет вид

Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.

Разрешенная система имеет вид

В базис системы векторов включаем 1-й и 2-й векторы Б_: = (A_VA₂), которые соответствуют разрешенным неизвестным х₁ и х₂. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.

Запишем разложения векторов по базису. Коэффициентами разложения вектора А₃ являются координаты вектора А’₃ = (3, -2), т.е. коэффициенты при х₃ в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х₃ А₃ = ЗЛ₁ – 2А_г Аналогично, коэффициентами разложения вектора А₄ являются координаты вектора А’₄ = (4, 1) А₄ = 4А_у + 1 А_т

Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я₉₄ = 1.

Как найти базис данной системы векторов

Определение базиса.Система векторов образует базис, если:

1) она линейно-независима,

2) любой вектор пространства через нее линейно выражается.

Пример 1.Базис пространства : .

2. В системе векторов базисом являются векторы: , т.к. линейно выражается через векторы .

Замечание.Чтобы найти базис данной системы векторов необходимо:

1) записать координаты векторов в матрицу,

2) с помощью элементарных преобразований привести матрицу к треугольному виду,

3) ненулевые строки матрицы будут являться базисом системы,

4) количество векторов в базисе равно рангу матрицы.

Теорема Кронекера-Капелли

Теорема Кронеккера–Капелли дает исчерпывающий ответ на вопрос о совместности произвольной системы линейных уравнений с неизвестными

Теорема Кронеккера–Капелли. Система линейных алгебраических урав­нений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы, .

Алгоритм отыскания всех решений совместной системы линейных уравнений вытекает из теоремы Кронеккера–Капелли и следующих теорем.

Теорема. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.

Теорема. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.

Алгоритм решения произвольной системы линейных уравнений:

1. Найдем ранги основной и расширенной матриц системы. Если они не равны ( ), то система несовместна (не имеет решений). Если ранги равны ( , то система совместна.

2. Для совместной системы найдем какой-нибудь минор, порядок которого определяет ранг матрицы (такой минор называют базисным). Составим новую систему из уравнений, в которых коэффициенты при неизвестных, входят в базисный минор (эти неизвестные называют главными неизвестными), остальные уравнения отбросим. Главные неизвестные с коэффициентами оставим слева, а остальные неизвестных (их называют свободными неизвестными) перенесем в правую часть уравнений.

3. Найдем выражения главных неизвестных через свободные. Получаем общее решение системы.

4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образомнаходим частные решения исходной системы уравнений.

Линейное программирование. Основные понятия

Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующихсистему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называетсядопустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁ , х₂ , … х_n ) и функция этих переменных f(x) = f (х₁ , х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что
а) функция f(x) является линейной функцией переменных х₁ , х₂ , … х_n
б) область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в себя:

Базис векторов и линейные действия над векторами аналитическим путём (теория и решение задач)

Базис – это неопределённое количество векторов в векторном пространстве, и абсолютно любой из этих векторов может создавать линейную комбинацию.

Базис векторов

Так, согласно доказательству (3), произвольные три некомпланарные векторы , , , образуют в трёхмерном пространстве базис, по которому, согласно формуле (2) можно единственным образом разложить произвольный вектор пространства. Векторы , , , которые образуют базис называются базисными.

Будем считать, что базисные векторы , , сведены к точке .

Числ , про которые упоминалось в разделах “линейно зависимая и линейно независимые системы векторов”, называют координатами вектора в заданном базисе, и пишут:

.

Аналогично, на плоскости базис образуют какие-то два неколлинеарные векторы, а любой некомпланарный с ними может быть разложен по этому базису.

Базисным вектором на прямой линии может быть любой ненулевой вектор.Согласно свойствам линейных операций над векторами, следует, что при сложении и вычитании векторов в данном базисе прибавляются и отнимаются их соответствующие координаты, а при умножении вектора на число умножаются не это число координаты вектора, то есть:

1. .
2. .
3. .

Линейные действия над векторами аналитическим путём

Если раньше линейные действия над векторами осуществлялись графически, то теперь эти операции можно выполнять аналитически, не пользуясь рисунком. Давайте вспомним и сформулируем линейные действия:

Чтобы прибавлять (отнимать) два вектора, необходимо прибавить (отнять) их соответствующие координаты, то есть:

Найти сумму векторов и , заданных на плоскости .

Решение:

Согласно правилу 1 у нас получается:

= (6, 3).

Построим эти векторы: .

Мы видим, что четырёхугольник OABC – параллелограмм. Координаты вектора мы сначала получили путём вычислений (аналитически), без помощи рисунка. Рисунок только подтверждает правило параллелограмма при прибавлении векторов, поэтому дальше рисунками будем пользоваться для наглядности.

Чтобы умножить вектор на число, необходимо каждую из его координат умножить на это число:

Дан вектор Найти

Решение:

Согласна правилу 2 у нас получается:

Геометрическое изображение смотрите на рис. 4.

Два вектора равны, если у них равны соответствующие координаты:

.

Теперь вы понимаете, как получить координаты вектора не только графическим путём, но и аналитическим. В дальнейшем у вас не возникнет сложностей по этому поводу.

Как найти базис вектора, пример

В некотором базисе заданы своими координатами векторы и Разложить вектор по базису, который образовался из векторов и

Решение:

Разложение вектора по базису и имеет такой вид:

где числа и – неизвестные. Чтобы их найти, подставим в последнее равенство координаты векторов и , а тогда воспользуемся свойствами 1 и 2:

Согласно свойству 3 про равенство векторов, получим систему уравнений:

Первое равенство умножаем на 1, а второе на (- 2) и в итоге у на получается:

.

Значит, ответ у нас выходит:

[spoiler title=”источники:”]

http://megaobuchalka.ru/10/21983.html

http://nauchniestati.ru/spravka/bazis-vektorov/

[/spoiler]

Линейной
комбинацией векторов
называется вектор,
где λ₁, … , λ_m– произвольные коэффициенты.

Система
векторов
называется
линейно зависимой, если существует ее
линейная комбинация, равная,
в которой есть хотя бы один ненулевой
коэффициент.

Система
векторов
называется
линейно независимой, если в любой ее
линейной комбинации, равной,
все коэффициенты нулевые.

Базисом
системы векторов
называется
ее непустая линейно независимая
подсистема, через которую можно выразить
любой вектор системы.

П р
и м е р 2. Найти базис системы векторов=
(1, 2, 2, 4),=
(2, 3, 5, 1),=
(3, 4, 8, -2),=
(2, 5, 0, 3) и выразить остальные векторы
через базис.

Р е
ш е н и е. Строим матрицу, в которой
координаты данных векторов располагаем
по столбцам. Приводим ее к ступенчатому
виду.

~~~.

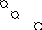
Базис
данной системы образуют векторы
,,,
которым соответствуют ведущие элементы
строк, выделенные кружками. Для выражения
векторарешаем уравнениеx₁+x₂+
x₄=.
Оно сводится к системе линейных
уравнений, матрица которой получается
из исходной перестановкой столбца,
соответствующего,
на место столбца свободных членов.
Поэтому для решения системы используем
полученную матрицу в ступенчатом виде,
сделав в ней необходимые перестановки.

Последовательно
находим:

x₄
= 0;

x₂
= 2;

x₁
+ 4 = 3, x₁
= -1;

=
–+2.

Замечание
1. Если требуется выразить через базис
несколько векторов, то для каждого из
них строится соответствующая система
линейных уравнений. Эти системы будут
отличаться только столбцами свободных
членов. Поэтому для их решения можно
составить одну матрицу, в которой будет
несколько столбцов свободных членов.
При этом каждая система решается
независимо от остальных.

Замечание
2. Для выражения любого вектора достаточно
использовать только базисные векторы
системы, стоящие перед ним. При этом
нет необходимости переформировывать
матрицу, достаточно поставить вертикальную
черту в нужном месте.

У п
р а ж н е н и е 2. Найти базис системы
векторов и выразить остальные векторы
через базис:

а)
=
(1, 3, 2, 0),=
(3, 4, 2, 1),=
(1, -2, -2, 1),=
(3, 5, 1, 2);

б)
=
(2, 1, 2, 3),=
(1, 2, 2, 3),=
(3, -1, 2, 2),=
(4, -2, 2, 2);

в)
=
(1, 2, 3),=
(2, 4, 3),=
(3, 6, 6),=
(4, -2, 1);=
(2, -6, -2).

1. 3. Фундаментальная система решений

Система
линейных уравнений называется однородной,
если все ее свободные члены равны нулю.

Фундаментальной
системой решений однородной системы
линейных уравнений называется базис
множества ее решений.

Пусть
дана неоднородная система линейных
уравнений. Однородной системой,
ассоциированной с данной, называется
система, полученная из данной заменой
всех свободных членов на нули.

Если
неоднородная система совместна и
неопределенна, то ее произвольное
решение имеет вид f_н
+ ₁f_о1+
… + _kf_оk
,гдеf_н– частное
решение неоднородной системы иf_о1,
… , f_оk–
фундаментальная система решений
ассоциированной однородной системы.

П р
и м е р 3. Найти частное решение
неоднородной системы из примера 1 и
фундаментальную систему решений
ассоциированной однородной системы.

Р е
ш е н и е. Запишем решение, полученное
в примере 1, в векторном виде и разложим
получившийся вектор в сумму по свободным
параметрам, имеющимся в нем, и фиксированным
числовым значениям:

= (x₁,
x₂,
x₃,
x₄) =
(–2a + 7b –
2, a, –2b + 1, b) = (–2a,
a, 0, 0) + (7b, 0, –2b, b) + +(–
2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (–
2, 0, 1, 0).

_­­Получаемf_н=(–
2, 0, 1, 0), f_о1= (-2, 1, 0,
0), f_о2= (7, 0, -2, 1).

Замечание.
Аналогично решается задача нахождения
фундаментальной системы решений
однородной системы.

У п
р а ж н е н и е 3.1 Найти фундаментальную
систему решений однородной системы:

а)

б)

в)
2x₁ –
x₂
+3x₃=
0.

У п
р а ж н е н и е 3.2. Найти частное решение
неоднородной системы и фундаментальную
систему решений ассоциированной
однородной системы:

а)

б)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Может кто-нибудь пояснить как найти все базисы системы векторов a1 = (1,2,3,4), a2 = (2,3,4,5), a3 = (3,4,5,6), a4 = (4,5,6,7). Я понимаю, что нужно составить матрицу 4×4 и привести ее к ступенчатому виду, тогда у меня получаются две ненулевые строки (1 2 3 4) и (0 -1 -2 -3), следовательно ранг системы векторов равен двум, как и число векторов в базисе этой системы. Но я не могу понять как нужно искать сами базисы этой системы, на основе чего это делается? Пока что дошел до того, что нужно просто выбрать все комбинации a1-a4 по 2 элемента такие, что один вектор невыразим через другой умноженный на какой-то скаляр, так как векторы базиса неколлинеарны. И в итоге в этом задании получится 6 разных базисов. Но есть ли какие-нибудь другие способы найти все базисы, кроме перебора? Ведь если ранг будет равен 4 и количество векторов системы будет больше, перебирать будет весьма затруднительно.

В статье о n-мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n-мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n-векторов. Размерность его соответственно равна n. Возьмем систему из n-единичных векторов:

e(1)=(1, 0,…,0)e(2)=(0, 1,…,0)e(n)=(0, 0,…,1)

Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n. Ранг этой матрицы равен n. Следовательно, векторная система e(1), e(2),…, e(n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы e(1), e(2),…, e(n) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n-мерных векторов, в которой число векторов меньше n, не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e(2), e(1),…, e(n). Она также будет являться базисом n-мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n. Система e(2), e(1),…, e(n) линейно независима и является базисом n-мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n-мерного векторного пространства.

Рассмотрим применение данной теории на конкретных примерах.

Разложение вектора по базису

Примем, что произвольные векторы e(1), e(2),…, e(n) являются базисом векторного n-мерного пространства. Добавим к ним некий n-мерный вектор x→: полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.

Доказанная теория делает понятным выражение «задан n-мерный вектор x=(x1, x2,…, xn)»: рассматривается вектор x→ n-мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n-мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n-мерного векторного пространства задана система из n линейно независимых векторов

e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))

а также задан вектор x=(x1, x2,…, xn).

Векторы e1(1), e2(2),…, en(n) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x→ в базисе e1(1), e2(2),…, en(n), обозначаемые как x~1, x~2,…, x~n.

Вектор x→ будет представлен следующим образом:

x=x~1·e(1)+x~2·e(2)+…+x~n·e(n)

Запишем это выражение в координатной форме:

(x1, x2,…, xn)=x~1·(e(1)1, e(1)2,…, e(1)n)+x~2·(e(2)1, e(2)2,…, e(2)n)+…++x~n·(e(n)1, e(n)2,…, e(n)n)==(x~1e1(1)+x~2e1(2)+…+x~ne1(n), x~1e2(1)+x~2e2(2)++…+x~ne2(n), …, x~1en(1)+x~2en(2)+…+x~nen(n))

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x~1, x~2,…, x~n:

x1=x~1e11+x~2e12+…+x~ne1nx2=x~1e21+x~2e22+…+x~ne2n⋮xn=x~1en1+x~2en2+…+x~nenn

Матрица этой системы будет иметь следующий вид:

e1(1)e1(2)⋯e1(n)e2(1)e2(2)⋯e2(n)⋮⋮⋮⋮en(1)en(2)⋯en(n)

Пусть это будет матрица A, и ее столбцы – векторы линейно независимой системы векторов e1(1), e2(2),…, en(n). Ранг матрицы – n, и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x~1, x~2,…, x~n вектора x→ в базисе e1(1), e2(2),…, en(n).

Применим рассмотренную теорию на конкретном примере.

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c(1)=(c1(1), c2(1),…, cn(1))c(2)=(c1(2), c2(2),…, cn(2))⋮c(n)=(c1(n), e2(n),…, cn(n))

И

e(1)=(e1(1), e2(1),…, en(1))e(2)=(e1(2), e2(2),…, en(2))⋮e(n)=(e1(n), e2(n),…, en(n))

Указанные системы являются также базисами заданного пространства.

Пусть c~1(1), c~2(1),…, c~n(1) – координаты вектора c(1) в базисе e(1), e(2),…, e(3), тогда связь координат будет задаваться системой линейных уравнений:

с1(1)=c~1(1)e1(1)+c~2(1)e1(2)+…+c~n(1)e1(n)с2(1)=c~1(1)e2(1)+c~2(1)e2(2)+…+c~n(1)e2(n)⋮                                                           сn(1)=c~1(1)en(1)+c~2(1)en(2)+…+c~n(1)en(n)

В виде матрицы систему можно отобразить так:

(c1(1), c2(1),…, cn(1))=(c~1(1), c~2(1),…, c~n(1))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

Сделаем по аналогии такую же запись для вектора c(2):

(c1(2), c2(2),…, cn(2))=(c~1(2), c~2(2),…, c~n(2))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

И, далее действуя по тому же принципу, получаем:

(c1(n), c2(n),…, cn(n))=(c~1(n), c~2(n),…, c~n(n))·e1(1)e2(1)…en(1)e1(2)e2(2)…en(2)⋮⋮⋮⋮e1(n)e2(n)…en(n)

Матричные равенства объединим в одно выражение:

c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)=c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e(1), e(2),…, e(3) через базис c(1), c(2),…, c(n):

e1(1)e2(1)⋯en(1)e1(2)e2(2)⋯en(2)⋮⋮⋮⋮e1(n)e2(n)⋯en(n)=e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c1(1)c2(1)⋯cn(1)c1(2)c2(2)⋯cn(2)⋮⋮⋮⋮c1(n)c2(n)⋯cn(n)

Дадим следующие определения:

Из этих равенств очевидно, что

c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)·e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1e~1(1)e~2(1)⋯e~n(1)e~1(2)e~2(2)⋯e~n(2)⋮⋮⋮⋮e~1(n)e~2(n)⋯e~n(n)·c~1(1)c~2(1)⋯c~n(1)c~1(2)c~2(2)⋯c~n(2)⋮⋮⋮⋮c~1(n)c~2(n)⋯c~n(n)=10⋯001⋯0⋮⋮⋮⋮00⋯1 

т.е. матрицы перехода взаимообратны.

Рассмотрим теорию на конкретном примере.