Содержание:
- Линейные преобразования. Собственные векторы и собственные числа линейного оператора
- Собственные векторы и собственные числа линейного оператора: определение, свойства
- Нахождение собственных чисел и собственных векторов
- Базис пространства из собственных векторов линейного оператора
- Линейная модель обмена (модель международной торговли)
Линейные преобразования. Собственные векторы и собственные числа линейного оператора
Линейные преобразования (линейные операторы). Матрица линейного преобразования
Пусть задано 


этого же пространства, говорится, что в векторном пространстве 


Вектор 



Преобразование 


То есть линейный оператор преобразует пространство 
Примерами простейших линейных преобразований являются:
тождественное преобразование: 

нулевой оператор 

Линейное преобразование 





Рассмотрим задачу об отыскании координат образа вектора 
Пусть в пространстве 







Но образы 

где 


С учетом (5.5) соотношение (5.4) принимает вид:
Группируя члены правой части относительно векторов базиса, имеем:
С другой стороны, если 


Сопоставляем (5.8) из (5.7) и получаем координаты вектора 
Следовательно, при линейном преобразовании:
координаты образа вектора являются линейными комбинациями координат прообраза, коэффициенты при которых составляют матрицу 

Матрица 




Каждый – 






Обратите внимание, что 

Каждому линейном оператору 



Например, с помощью оператора линейных преобразований можно описать поворот произвольного вектора с пространства 





где 


точки 

По соотношению (5.12) матрица линейного преобразования} 


а матрица обратного линейного преобразования 


Теорема 5.1 (о связи между матрицами оператора в различных базисах).
Матрицы 




где 
Доказательство. Пусть линейный оператор 








Умножим равенство (5.14) слева на матрицу 


Сравнив соотношение 

Две квадратные матрицы 




Соответствующие линейные операторы называются преобразованиями сходства.
Подобные матрицы описывают то же линейное преобразование, но в разных базисах, а матрица 
Подобные матрицы имеют те же ранги, суммы элементов главной диагонали и определители.
В базисе 


Определим матрицу 




Предоставим расписание векторов нового базиса по векторам исходного базиса: 
Ее определитель 

По теореме 5.1 определяем матрицу оператора 
Обратите внимание, что в новом базисе матрица оператора 
Собственные векторы и собственные числа линейного оператора: определение, свойства
Рассмотрим 



Ненулевой вектор 



Скаляр 


Согласно определениями собственного числа и собственного вектора имеем:
1) Если 




2) любой ненулевой 



Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы
Поставим задачу нахождения собственных чисел и собственных векторов заданной матрицы
Запишем матричное уравнение (5.17) в развернутом виде:
Таким образом, задача сводится к решению однородной системы 

Раскрытие определителя в соотношении (5.19) дает многочлен степени 




По основной теореме алгебры уравнения 





Множество всех собственных чисел матрицы называют спектром матрицы. Если в спектре матрицы то же собственное число повторяется 

Теорема 5.2 (о единственности собственного чucлa, что соответствует собственному вектору). Если 



Доказательство. Предположим, что кроме собственного числа 
скаляр 




Согласно теореме 5.2 говорят, что собственный вектор 


Теорема 5.3 (о множестве собственных векторов, принадлежащих собственному числу). Если матрица имеет собственный вектор, принадлежащий собственному числу 
Доказательство базируется на определении собственного вектора и свойствах ассоциативности и коммутативности операции умножения матрицы на скаляр.
Действительно, пусть 







Поскольку равенство (5.19) выполняется для произвольного 
Теорема 5.4 (критерий существования собственного вектора 






Доказательство сводится к тождественных преобразований матричных уравнений.
Необходимость уже доказано переходом от соотношения 

Достаточность. На основании свойств действий над матрицами с учетом условия 

Теорема 5.5 (пpo линейную независимость собственных векторов). Собственные векторы, принадлежащие различным собственным числам, является линейно независимыми.
Доказательство проведем методом от противного. Пусть 





Предположим обратное. Пусть (5.23) выполняется при условии, что одно из чисел 
Умножим левую и правую части (5.23) на собственное число 
Левую и правую части равенства (5.23) умножим на матрицу 
Сравним (5.25) и (5.24). Получаем:
По условию теоремы 




Если есть более двух собственных векторов, принадлежащих попарно различным собственным числам, доведение аналогичное (с использованием метода математической индукции).
Заметим, что собственные векторы, принадлежащих различным собственным числам, можно использовать как базисные векторы пространства 
Теорема 5.6 (пpo сумму и произведение собственных чисел). Если 

1) сумма собственных чисел равна сумме элементов главной диагонали матрицы 
2) произведение собственных чисел равна определителю матрицы 
Доказательство основывается на формулах Виета, которые описывают соотношение между корнями и коэффициентами многочлена 
Рассмотрим простейший случай 
С (5.29) по теореме Виета (для квадратного уравнения) имеем:
Сумму всех диагональных элементов матрицы называют следом (от нем. spur – след) этой матрицы и обозначают 
Для квадратной матрицы произвольного порядка 
при этом собственное число 
Нахождение собственных чисел и собственных векторов
Рассмотрим алгоритм нахождения собственных чисел матрицы 
Согласно соотношениями (5.18) и (5.19) имеем такой порядок отыскания собственных чисел и собственных векторов матрицы.
1. Составляем по исходной матрицей 
2. Подставляем поочередно каждое собственное число в систему (5.18) и находим все ее нетривиальные решения, что и дает множество собственных векторов, принадлежащих соответствующему собственному числу.
Замечания. Множество всех собственных векторов, принадлежащих определенному собственному числу, можно представить как линейную комбинацию фундаментальных решений однородной системы уравнений согласно (4.19), гл. 4.
Найдем собственные числа и собственные векторы матрицы
Характерным уравнением этой матрицы является квадратное уравнение:
Решив его, получим собственные числа 
Теперь описываем множества 

Для этого в матрицу 

Предоставляя параметру 

Теорема 5.7 (про собственные числа и собственные векторы симметричной матрицы).
Симметричная матрица 
Теорема приводим без доказательства.
Проиллюстрируем прав выводов данной теоремы на примере.
Пусть имеем симметричную матрицу
Найдем собственные числа и собственные векторы этой матрицы и докажем ортогональность собственных векторов, соответствующих различным собственным числам.
1. Составим характеристическое уравнение матрицы
2. Найдем корни полученного кубического уравнения относительно 

Нахождение других двух корней сводится к решению квадратного уравнения:
3. Опишем множества 

Для этого в матрицу 

Аналогично находим собственные векторы 
Система векторов 

Убеждаемся, что векторы 

Для этого определим их скалярные произведения:
Поскольку скалярные произведения векторов равны нулю, то векторы попарно ортогональны.
Если в выражениях (5.31-5.33) положить 
которая использовалась как базис пространства 





Теорема 5.8 (о преобразовании матрицы к диагональному виду). Матрица линейного оператора 


Теорему наводим без доказательств
Заметим, что при нахождении собственных чисел для заданной матрицы самой задачей является решение алгебраического уравнения 
Следующий пример был решен в пакете MatLab, в котором конечный результат вычислений предоставляется без промежуточных выкладок.
Найдем собственные числа и соответствующие им собственные векторы матрицы
Характерным уравнением для нахождения собственных чисел является уравнение
корнями которого будут числа 
Собственные числа и собственные векторы матриц имеют широкий спектр использования, в частности, в аналитической геометрии (Раздел 2), в задачах различных отраслей естественных наук и эконометрики.
Базис пространства из собственных векторов линейного оператора
По теореме 5.5 собственные векторы, принадлежащие разным собственным числам, являются линейно независимыми. Возникает вопрос, при каких условиях существует базис линейного пространства 
Лема. Если 





Доказательство. Согласно теореме 5.4 множество собственных векторов совпадает с множеством всех решений однородной системы линейных уравнений:
где 




Теорема 5.9 (о существовании базиса из собственных векторов матрицы). Пусть числа 





Доказательство. Согласно лемме каждое множество собственных векторов, соответствующих уравнению 


Поскольку собственные векторы матрицы 


Теорема 5.10 (о существовании базиса из собственных векторов симметричной матрицы). Если матрица 


Теорему принимаем без доказательств.
Построим ортонормированный базис пространства 
линейного преобразования 

Согласно теореме 5.9 такой базис существует, поскольку матрица 

и решим его: 

Для каждого из двух различных собственных чисел матрицы определим фундаментальную систему решений однородной системы уравнений: 

По последним шагом элементарных преобразований матрицы записываем общее решение системы:
Определяем фундаментальную систему решений однородной системы уравнений
Собственные векторы 

При 
По последнем шагом элементарных преобразований матрицы записываем общее решение системы:
Возлагаем 
Поскольку 



Это и есть ортогональный базис пространства 

По соотношению (5.13) определим матрицу 






По матричным уравнением (5.13) находим матрицу 

Следовательно, мы получили диагональную матрицу третьего порядка, элементами главной диагонали которой есть собственные числа матрицы 
Далее приведен пример применения собственных векторов и собственных чисел в одной из многих задач экономики.
Линейная модель обмена (модель международной торговли)
Практически все страны кроме внутреннего товарообмена осуществляют внешний товарообмен, то есть занимаются внешней торговлей. Торговля считается сбалансированной, или бездефицитной, если для каждой страны прибыль от торговли не меньше объем средств, которые она вкладывает в товарооборот (внутренний и внешний).
Постановка задачи. Несколько стран осуществляют взаимный товарообмен. Известную долю бюджетных средств, тратит каждая страна на закупку товаров у другой страны, учитывая и внутренний товарооборот. Определить, каким должно быть соотношение бюджетов партнеров для того, чтобы обеспечить бездефицитность торговли.
Построение математической модели. Введем обозначения количественных характеристик, описывающих торговлю между странами, и определим связь между этими характеристиками. Пусть 




Матрицу 

Эта матрица описывает взаимодействие стран в процессе международной торговли. Соотношение (5.34) означает, что сумма элементов каждого столбца матрицы равна
1. Если объем средств, которые тратит каждая страна на торговлю, обозначить через 


Чтобы торговля каждой страны была сбалансированной, по определению должно выполняться условие 



Группируя в левой части слагаемые, содержащие каждое из 
Учитывая соотношение (5.20), получим:
Отсюда следует, что сбалансированная торговля возможна только в случае знака равенства. Это, полагаем, понятно не только на основании аналитических выкладок, но и с экономической точки зрения (и даже просто с точки зрения здравого смысла): все страны в совокупности не могут получить прибыль. Более того, для одной из стран не может выполняться знак строгого неравенства 
Итак, условием сбалансированной торговли является равенства 

Введем в рассмотрение вектор (бюджетных) средств 
С (5.40) следует, что при условии сбалансированности торговли между странами вектор средств 



Рассмотрим товарообмен между тремя странами. Пусть структурная матрица торговли стран 
Найдем вектор средств, компонентами которого являются доли от общего объема торговли, должна вкладывать каждая из стран во внешней товарооборот для того, чтобы торговля была сбалансированной.
Искомый вектор средств является собственным вектором структурной матрицы, принадлежащий собственному значению 
Поскольку система является однородной, то расширенная матрица эквивалентна основной матрицы системы. Осуществим элементарные преобразования основной матрицы этой системы уравнений:
Находим общее решение системы, в котором 

Отсюда следует, что для сбалансированности торговли необходимо, чтобы средства, которые вкладывает в внешний товарооборот каждая страна, соотносились как
Лекции:
- Разложение в ряд Фурье четных и нечетных функций
- Функции многих переменных
- Наибольшее и наименьшее значение функции
- Уравнение плоскости
- Экстремум функции трёх переменных
- Как найти вероятность: пример решения
- Свойства определенного интеграла
- Комбинаторика
- Однородные дифференциальные уравнения
- Простейшие задачи аналитической геометрии
Набор обобщающих
примеров соответствует требованиям
«Семестрового плана» при изучении темы:
«Линейные
преобразования». Эти примеры
предназначены закрепить навыки применения
общих алгоритмов решений, установленных
в поясняющих примерах.
☺ ☻ ☺
Пример
1–1442:
Пусть задан вектор=(x1,x2,x3)
линейного пространства.
Записано преобразование пространства:=(x1,
x2+1,
x3+2).
Выяснить, является ли оно линейным. Если
преобразование линейное, найти его
матрицу в том же базисе, в котором заданы
векторыи
.
Решение:
1). Запишем базис
пространства:
=(1,0,0),
=(0,1,0),
=(0,0,1).
Это значит, что произвольный вектор
линейного пространства может быть
записан в виде:=x1
+x2
+x3
.
2). Пусть заданы
два произвольных вектора
и ,
принадлежащие .
В соответствии с определением операций
суммы векторов:=
+
=(x1+y1,x2+y2,x3+y3)
и=(
x1,
x2,
x3).
3). Запишем
векторы-образы для векторов, участвующих
в доказательстве линейности
:
=
(y1,
y2+1,
y3+2)
и =(
x1,
x2+1,
x3+2);
=
=
(+
,
+
y2+1,
x3+y3+2).
4). Из представленных
записей следует: требование
+
– выполняется, требование
– выполняется
→ преобразование
– не является линейным.
Ответ:
не является линейным преобразованием.
Пример
2–1445:
Пусть имеем совокупность векторов
:
=(2,3,5),
=(0,1,2),
=(1,0,0),
и совокупность векторов:
=(1,1,1),
=(1,1,-1),
=(2,1,2).
Доказать, что существует единственное
линейное преобразование, переводящее
совокупность векторовв совокупность
.
Найти матрицу этого преобразования в
той же базе, в которой заданы все векторы.
Решение:
Замечание:
обозначим базу, в которой записаны все
векторы, и в которой должно определиться
искомое линейное преобразование, как
совокупность векторов: i=(,
,
).
Общая
схема решения задачи:
R1
– имеем выражения:=
·
,
=
·
;
,
,
– матрицы-столбцы.
R2
–ищем
матрицу перехода от совокупности
векторов
к совокупности векторов
,
определяемую выражением:=
·
;
это выражение по форме соответствует
определению линейного преобразования,
задаваемого матрицейв базе
.
R3
– в задании указано, что
матрица преобразования,
должна быть определена в базе;
это значит, что нужно матрицуподвергнуть трансформированию матрицей
перехода от базы
к базе
,
то есть:=
·
.
R4
–определяем алгоритм
расчётов:=
·
→
=
,
где:=
и
=
.
1). Из координат
векторов составим матрицы:
=

=

Определители матриц: ||≠0
и||≠0
→ матрицыи
невырожденные →
матрица не вырожденной,
являясь произведением невырожденных
матриц.
2). Так как совокупности
векторов
и
могут использоваться в качестве баз
рассматриваемого векторного пространства,
то матрица перехода от базы к базе –
невырожденная.
Это обеспечивает единственность
представления матрицы линейного
преобразования.
3). В главе 9 показано,
что матрицу перехода от базы
к базе
для варианта-1, необходимо вычислять,
применяя выражение:=
·
.
4).
Используем выражение
=
.
Так как в нашем случае d
= 1, то
=
.
5)
Вычисляем матрицу
=

где
=
– алгебраическое дополнение к элементу
матрицы
.
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
1 |
2 |
0 |
|
2 |
0 |
1 |
|
|||||||||||||||||||||
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
|||||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
0;=
=
2;=
=
–1;
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
|
3 |
5 |
|
2 |
|
5 |
|
2 |
3 |
|
|
||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
|||||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
0;=
=
–5;=
=
3;
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
|
3 |
5 |
|
2 |
|
5 |
|
2 |
3 |
|
|
||||||||||||||||||
|
|
1 |
2 |
0 |
|
2 |
0 |
1 |
|
|||||||||||||||||||||
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
1;=
=
–4;=
=
2;
6). Учитывая
результаты вычислений, можем записать:
=
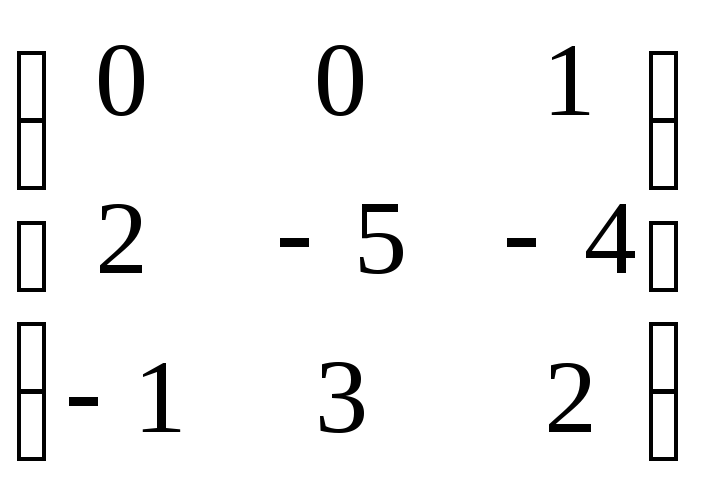
7). Вычисляем
произведение матриц:
=
·
=


применяя вычислительный шаблон для
произведения матриц 3-го порядка:
|
Столбец |
0 |
2 |
-1 |
Столбец |
Столбец |
0 |
-5 |
3 |
Столбец |
Столбец |
1 |
-4 |
2 |
Столбец |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-2 |
1 |
1 |
1 |
-1 |
|||
|
1 |
1 |
-1 |
3 |
1 |
1 |
-1 |
-8 |
1 |
1 |
-1 |
-5 |
|||
|
2 |
1 |
2 |
0 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
2 |
Из таблицы выписываем
матрицу:
=

это и есть матрица линейного преобразования
для рассматриваемого варианта для
рассматриваемого варианта:=
·
,
или в матричной форме:
=
·
,
или



8). Вычисляем
произведение матриц:
=
=
, применяя
вычислительный шаблон для произведения
матриц 3-го порядка: =


Применяем шаблон
для вычисления произведения матриц: GC
=T:
|
Столбец |
1 |
3 |
0 |
Столбец |
Столбец |
-2 |
-8 |
1 |
Столбец |
Столбец |
-1 |
-5 |
2 |
Столбец |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
2 |
|||
|
2 |
-5 |
-4 |
-13 |
2 |
-5 |
-4 |
32 |
2 |
-5 |
-4 |
15 |
|||
|
-1 |
3 |
2 |
8 |
-1 |
3 |
2 |
-20 |
-1 |
3 |
2 |
-10 |
Применяем шаблон
для вычисления произведения матриц:
D=TA:
|
Столбец |
2 |
0 |
1 |
Столбец |
Столбец |
3 |
1 |
0 |
Столбец |
Столбец |
5 |
2 |
0 |
Столбец |
|
0 |
1 |
2 |
2 |
0 |
1 |
2 |
1 |
0 |
1 |
2 |
2 |
|||
|
-13 |
32 |
15 |
-11 |
-13 |
32 |
15 |
-7 |
-13 |
32 |
15 |
-1 |
|||
|
8 |
-20 |
-10 |
6 |
8 |
-20 |
-10 |
4 |
8 |
-20 |
-10 |
0 |
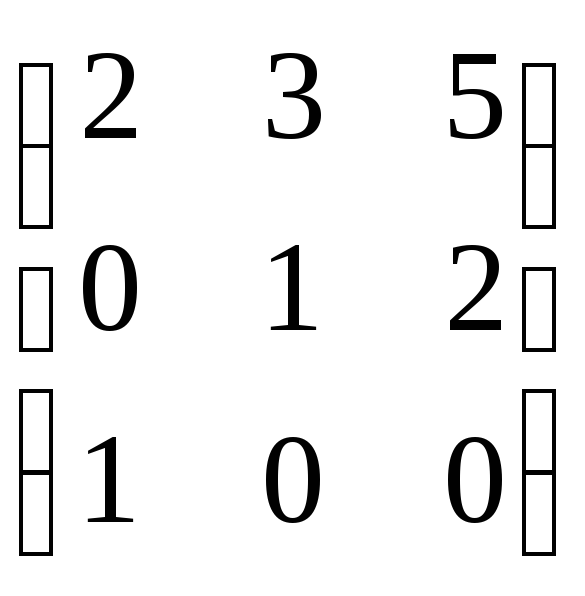
Из
таблицы видим матрицу D,
и записываем ответ =

Ответ:линейное
преобразование
матрица:
=

=
(,
,
).
Замечание:
использование в выражениях баз
матриц-строк приводит к матрице линейного
преобразования
,
то есть транспонированной.
Пример
3–1454:
В базе:a=(,
,
)
определено линейное преобразование
пространства ,
его матрица задана в базеa,
при условии, что база представлена в
виде матрицы-столбца. Задана новая база:b=(,
,
).Найти матрицу
преобразования
в базе:b.
Причём: =(8,-6,7),
=(-16,7,-13),
=(9,-3,7);
=(1,-2,1),
=(3,-1,2),
=(2,1,2).
Матрица в базеaимеет вид:

Решение:
1). Воспользуемся
формулой: b=·a,
где b==
·
.
Найдём матрицу,
используя записями:a=·
иb=
·
,
где,
a,
b-матрицы-столбцы.
Учитывая исходные данные примера,
запишем:
=

=

2). Убеждаемся, что
матрица
–
невырожденная: ||=5.
3). Для рассматриваемого
случая, когда
,
a,
b-матрицы-столбцы,
была получена формула для вычисления
матрицы перехода от базыaк базеb:
=
·
.
4). Вычислим
обратную матрицу
,
используя общую формулу для вычисления
обратной матрицы:
=
,
где
=
1. Так как
,
то матрица
существует.
Вычисляем
матрицу
=
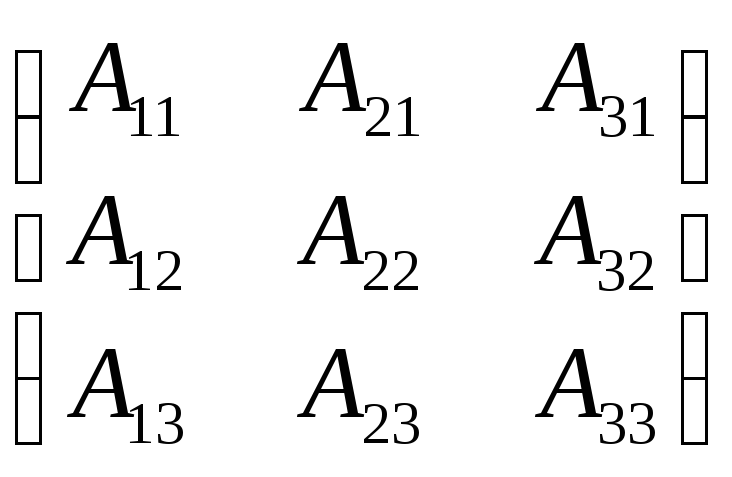
где
=
– алгебраическое дополнение к элементу
матрицы
.
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
7 |
-13 |
-16 |
|
-13 |
-16 |
7 |
|
|||||||||||||||||||||
|
|
-3 |
7 |
9 |
|
7 |
9 |
-3 |
|
|||||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
10;=
=
–5;=
=
–15;
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
|
-6 |
7 |
|
8 |
|
7 |
|
8 |
-6 |
|
|
||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
-3 |
7 |
9 |
|
7 |
9 |
-3 |
|
|||||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
21;=
=
–7;=
=
–30;
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
|
-6 |
7 |
|
8 |
|
7 |
|
8 |
-6 |
|
|
||||||||||||||||||
|
|
7 |
-13 |
-16 |
|
-13 |
-16 |
7 |
|
|||||||||||||||||||||
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
29;=
=
–8;=
=
–40;
Учитывая
результаты вычислений, можем записать:
=

5). Вычислим
произведение матриц:
=
·
=


DB,
применяя вычислительный шаблон:
|
Столбец |
10 |
-5 |
-15 |
Столбец |
Столбец |
21 |
-7 |
-30 |
Столбец |
Столбец |
29 |
-8 |
-40 |
Столбец |
|
1 |
-2 |
1 |
5 |
1 |
-2 |
1 |
5 |
1 |
-2 |
1 |
5 |
|||
|
3 |
-1 |
2 |
5 |
3 |
-1 |
2 |
10 |
3 |
-1 |
2 |
15 |
|||
|
2 |
1 |
2 |
-15 |
2 |
1 |
2 |
-25 |
2 |
1 |
2 |
-30 |
Из
таблицы видим ответ:
=

6). Для рассматриваемого
случая:
=
.
Найдём матрицу
=
,
при=1.
7)
Вычисляем матрицу
=

где
=
– алгебраическое дополнение к элементу
матрицы
.
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
2 |
3 |
1 |
|
3 |
1 |
2 |
|
|||||||||||||||||||||
|
|
-5 |
-6 |
-3 |
|
-6 |
-3 |
-5 |
|
|||||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
3;=
=
–3;=
=
1;
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
|
1 |
1 |
|
1 |
|
1 |
|
1 |
1 |
|
|
||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
-5 |
-6 |
-3 |
|
-6 |
-3 |
-5 |
|
|||||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
1;=
=
–3;=
=
2;
*Выделим миноры:к элементу
;
к элементу
;
к элементу
:
|
1 |
2 |
3 |
|||||||||||||||||||||||||||
|
|
1 |
1 |
|
1 |
|
1 |
|
1 |
1 |
|
|
||||||||||||||||||
|
|
2 |
3 |
1 |
|
3 |
1 |
2 |
|
|||||||||||||||||||||
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
||||||||||||||||||
и вычислим
алгебраические дополнения
,
,
выделенныхминоров:
=
=
1;=
=
–2;=
=
1;
8). Учитывая
результаты вычислений, можем записать:
=

9). Вычислим:
=
=



(CD)N.
Применяем шаблон
для вычисления произведения матриц:
CD=T:
|
Столбец |
1 |
-18 |
15 |
Столбец |
Столбец |
-1 |
-22 |
20 |
Столбец |
Столбец |
1 |
-25 |
22 |
Столбец |
|
1 |
1 |
1 |
-2 |
1 |
1 |
1 |
-3 |
1 |
1 |
1 |
-2 |
|||
|
1 |
2 |
3 |
10 |
1 |
2 |
3 |
15 |
1 |
2 |
3 |
17 |
|||
|
-3 |
-5 |
-6 |
-3 |
-3 |
-5 |
-6 |
-7 |
-3 |
-5 |
-6 |
-10 |
Применяем шаблон
для вычисления произведения матриц:
F=TN:
|
Столбец |
3 |
-3 |
1 |
Столбец |
Столбец |
1 |
-3 |
2 |
Столбец |
Столбец |
1 |
-2 |
1 |
Столбец |
|
-2 |
-3 |
-2 |
1 |
-2 |
-3 |
-2 |
3 |
-2 |
-3 |
-2 |
2 |
|||
|
10 |
15 |
17 |
2 |
10 |
15 |
17 |
-1 |
10 |
15 |
17 |
-3 |
|||
|
-3 |
-7 |
-10 |
2 |
-3 |
-7 |
-10 |
-2 |
-3 |
-7 |
-10 |
1 |
Из
таблицы видим матрицу F,
и записываем ответ
=

Ответ:матрицапреобразования
в базе
:
=

Пример
4–1457:
Пусть преобразование
в базе
:
(a1,a2)
задано матрицей
=
.
Преобразование
в базе
🙁b1,b2)
задано матрицей
=
.
Известно, что:
=(1,2),
=(2,3);
=(3,1),
=(4,2).
Найти матрицу преобразования:
+
в базе
.
Решение:
Замечание:
обозначим
базу, в которой записаны векторы
,
,
как совокупность векторов:
=
(i1,
).
Все базы:
,
,
записываем в виде матриц-столбцов.
1). Воспользуемся
формулой: b=·a,
где b==
·
.
Найдём матрицу,
используя записями:a=·
иb=
·
,
где,
a,
b-матрицы-столбцы.
Учитывая исходные данные примера,
запишем: =
,
=
.
Так как ||=–1,
то матрицаневырожденная и существует обратная
матрица.
2). Вычислим матрицу
=
,
при=–1.
Так как
=
,
то=
.
После этого можно вычислить матрицу=
·
.
Для обеспечения надёжности вычислений
воспользуемся шаблоном умножения матриц
2-го порядкаC
==BT:
|
Столбец |
–3 |
2 |
Столбец |
Столбец |
2 |
-1 |
Столбец |
|
3 |
1 |
-7 |
3 |
1 |
5 |
||
|
4 |
2 |
-8 |
4 |
2 |
6 |
из таблицы читаем
матрицу
=
.
3). Запишем матрицу
преобразования
в базе
:
=
.
Найдём матрицу
=
,
при=–2,
=
получаем:
=
.
4). Вычислим
матрицу: =
=
=
CDN=
TN,
используя вычислительный шаблон для
произведения матриц:
|
Столбец |
3 |
5 |
Столбец |
Столбец |
4 |
3 |
Столбец |
|
-7 |
5 |
4 |
-7 |
5 |
–13 |
||
|
-8 |
6 |
6 |
-8 |
6 |
–14 |
|
Столбец |
-6 |
-8 |
Столбец |
Столбец |
5 |
7 |
Столбец |
|
4 |
–13 |
80 |
4 |
–13 |
-71 |
||
|
6 |
–14 |
76 |
6 |
–14 |
-68 |
из таблицы читаем
матрицу
=
.
5). Матрица
преобразования:
+
в базе
:
=
+
=
+

.
Ответ: Матрица
преобразования:
+
в базе
:
=
.
Замечание:
полученный
числовой результат отличается от ответа,
представленного в задачнике: у нас
матрица
,
в задачнике – транспонированная матрица
.
Пример
5–1466:Найти собственные
векторы линейного преобразования
,
заданного в некотором базисе
матрицей:

Решение:
1).
Составляем характеристический многочлен
и находим его корни, используя свойства
определителя и правила нахождения
корней многочлена:
=
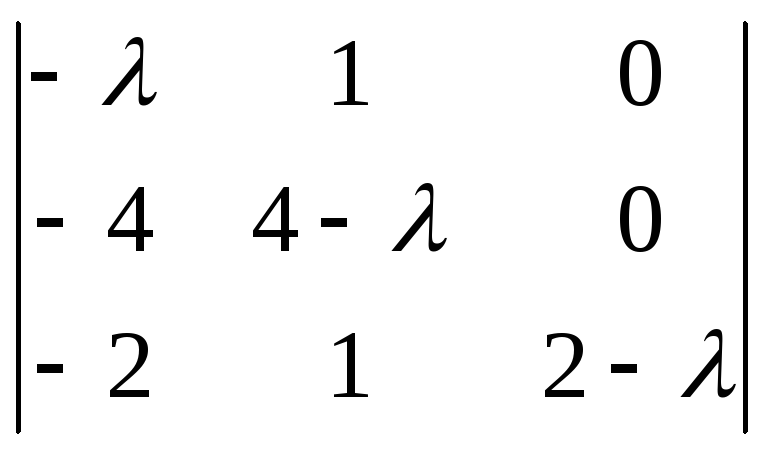
(2–)
=–
,
откуда корни: =
=
=2.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:

3).
Для собственного значения =
2 система (A)
принимает вид:
Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 1). Назначаем свободными
неизвестными: =2
,
=
,
тогда =
,
получаем собственный вектор: =
(,2
,
)=
(1,2,0)+
(0,0,1).
Ответ:
собственные значения: =
=
=
2; собственные векторы: =(
,2
,
),
где ,
0.
Пример
6–1473:Найти собственные
векторы линейного преобразования
,
заданного в некоторой базе матрицей:

Решение:
1).
Составляем характеристический многочлен
и находим его корни, используя свойства
определителя и правила нахождения
корней многочлена:
=

)
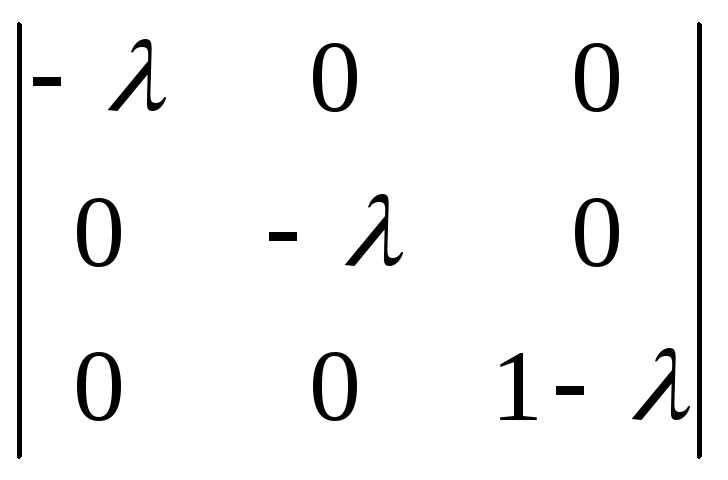
,
откуда
корни многочлена :
=
=0,
=
=1.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:

3).
Для собственного значения =
0 система (A)
принимает вид:
Так
как определитель системы равен нулю,
то независимых уравнений не более трёх
(в нашем случае 2). Назначаем свободными
неизвестными:
=
,
=
,
=
=0.
Найдём фундаментальную систему решений
для полученной системы:
-
x1
x4
x2
x3
α1
0
0
1
0
α2
0
0
0
1
Векторы-решения
и
есть ФСР для
=
0, тогда любойсобственный
вектор линейного преобразования можно
представить в виде: =
+=
(0,1,0,0)
+(0,0,1,0),
где ,
– произвольные постоянные.
4).
Для собственного значения =1
система (A)
принимает вид:
Так
как определитель системы равен нулю,
то независимых уравнений не более трёх
(в нашем случае 3). Назначаем свободными
неизвестными:
=
=
,
=
=0.
Найдём фундаментальную систему решений
для полученной системы:
-
x2
x3
x1
x4
α3
0
1
1
0
α4
0
0
0
1
Векторы-решения
и
есть ФСР для
=1,
тогда любой собственный вектор линейного
преобразования можно представить в
виде:=
+
=
(1,0,1,0)+
(0,0,0,1),
где,
– произвольные постоянные.
.
Ответ:
собственные значения:
=
=0,
=
=
1; собственные векторы:
=
(0,1,0,0)
+(0,0,1,0),
где
,
– не равны нулю одновременно,
=
(1,0,1,0)+
(0,0,0,1),
где
,
– не равны нулю одновременно.
Пример
7–1479:Линейное
преобразование
,
заданного матрицей:

.Можно ли привести матрицу преобразования
к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
Решение:
1).
Составляем характеристический многочлен
и находим его корни, используя свойства
определителя и правила нахождения
корней многочлена:
=

(1)
=
(–2)

(2)
=–
(–2)
(–1)
(+4),
откуда
корни многочлена :
=1,
=2,
=–4.
Выполнены
операции:
(1):
[R3]–[R2]
и выносим за скобку определителя
множитель: (–2);
меняем одновременно знаки в [C1]
и [C3].
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:

3).
Для собственного значения =
1 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 2). Назначаем свободной
неизвестной: =
,
из системы имеем: =
,
=
,
тогда получаем
собственный вектор, приняв =1:
=
(1,1,1).
4).
Для собственного значения =
2 система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 1). Назначаем свободной
неизвестной: =
,
=3
,
из системы имеем: =
–
,
тогда получаем
собственный вектор, приняв =1,
=0:
=
(1,1,0).
5).
Для собственного значения =–4
система (A)
принимает вид:

Так
как определитель системы равен нулю,
то независимых уравнений не более двух
(в нашем случае 2). Назначаем свободной
неизвестной: =
,
из системы имеем: =
,
3=2
,
тогда получаем
собственный вектор, приняв =3:
=
(–2,3,3).
Ответ:
собственные значения:
=1,
=2,
=–4;
собственные векторы:
=
(1,1,1),
=
(1,1,0),
=
(–2,3,3). Диагональная матрица:

Пример
8–1482:Линейное
преобразование
,
заданного матрицей:

.Можно ли привести матрицу преобразования
к диагональному виду. Если можно, найти
базис, в котором такая запись возможна.
Решение:
1).
Составляем характеристический многочлен
и находим его корни, используя свойства
определителя и правила нахождения
корней многочлена:
=

(1)
=
(2)
→
=(4–
)·


(3)
→
=(4–
)·


+
= (4) →
Выполнены
операции:
(1):
[R2]–[R4]·5;
[R3]–[R4]·6.
(2):
применяем разложение определителя по
первому столбцу. (3):
в первом слагаемом: [R2]+[R4]·2;
во втором слагаемом [R3]+[R1]·2;
(4):
далее вычислим отдельно
и .
=
(1)
=
(–4)·

(2)
=(–4)·

(3)
→
=
(–4)·
(–1)·

(4)
=(–4)·
(–1)·

(5)
→
=
(–4)·
(–1)·
=
(6)
=(–4)·(
–1)·
=
(7)
→
Выполнены
операции:
(1):
выносим (–1) из первого столбца. (2):
[R1]+[R3]·2–[R2].
(3):
выносим (–1)
из первой строки. (4):
[R3]–[R1]·3;
(5):
далее разложение определителя по первому
столбцу. (6):
вычисляем определитель. (7):
до вычисления
раскрывать скобки нецелесообразно.
=
(1)
=
=(–1)·
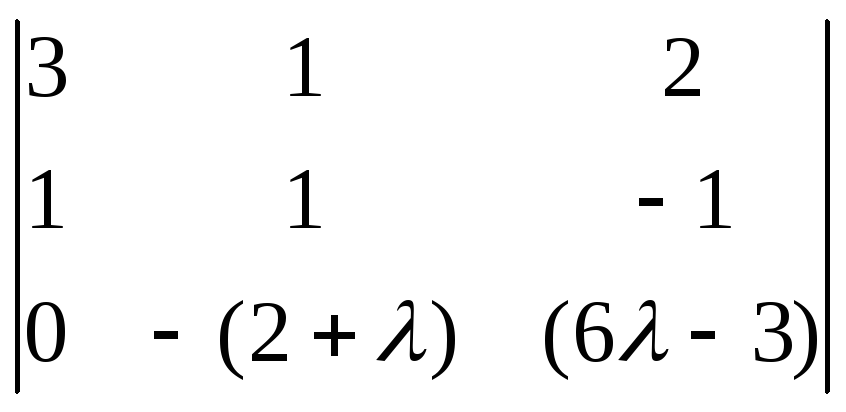
(3) →
=
(–1)·

=(–1)·
=
(–1)·
(–7+16)
.
Выполнены
операции:
(1):
выносим (–1) из первого столбца;
[R2]+[R1]·2–[R3].
(2):
выносим (–1)
из второй строки. (3):
[R1]–[R2]·3;
(4):
далее разложение определителя по первому
столбцу. (6):
вычисляем определитель.
Теперь
нетрудно получить: =(
–1)·
=
,
откуда следуют характеристические
корни: =
=1,
=
=2.
2).
Записываем систему уравнений для
нахождения собственных векторов
линейного преобразования, соответствующим
найденным собственным значениям:

3).
Для собственного значения =
1 система (A)
принимает вид:
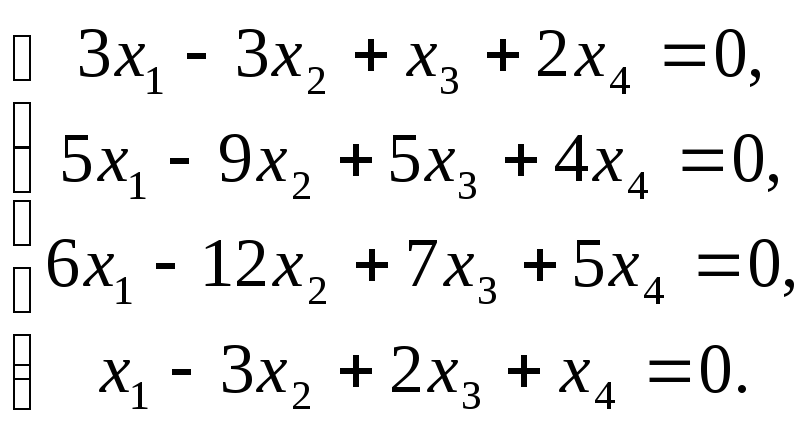
(B)
Так
как определитель системы равен нулю,
то независимых уравнений не более трёх.
Ранг системы уравнений (B)
равен двум. Это значит, что ФСР этой
системы уравнений содержит два независимых
решения, то есть система (B)
даст нам два независимых собственных
вектора линейного преобразования:
,
.
4).
Для собственного значения =
2 система (A)
принимает вид:
(C)
Ранг
системы уравнений (C)
равен трём. Это значит, что ФСР этой
системы уравнений содержит одно
независимое решения, то есть система
(С) даст нам один собственный вектор
линейного преобразования: .
5).
В соответствии с теоремой 10.4 совокупность
векторов ,
,
независима, но её недостаточно, чтобы
построить базу линейного пространства
.
Это значит: матрица заданного линейного
преобразования к диагональному виду
не приводится.
Ответ:
матрица
к диагональному виду не приводится.
☻
Вопросы
для самопроверки:
-
Что
такое линейное преобразование
пространства? -
Как
определяется матрица линейного
оператора? -
Как
изменяется матрица линейного
преобразования (оператора) при переходе
от одного базиса к другому? -
Что
такое произведение линейных преобразований? -
Что
такое характеристическая матрица
линейного преобразования? -
Что
такое характеристический многочлен
линейного преобразования? -
Что
называется собственным вектором
линейного преобразования, действующего
в линейном пространстве R
над числовым полем: K? -
Что
такое собственное значение линейного
преобразования, действующего в линейном
пространстве R над числовым
полем: K? -
Каким
может быть максимальное число собственных
значений у линейного оператора,
действующего в линейном пространстве
размерности n? -
Зависят
ли собственные значения линейного
преобразования от выбора базиса в
линейном пространстве, в котором
действует это преобразование? -
Всякий
ли линейный оператор, действующий в
линейном пространстве R
над числовым полем K,
имеет хотя бы одно собственное значение? -
Как
найти собственные значения линейного
оператора? -
Как
найти собственные векторы линейного
преобразования?
< * * *
* * >
Примеры решений. Линейные операторы
В этом разделе вы найдете бесплатные решения задач, касающиеся линейных операторов (преобразований, отображений): нахождение матрицы оператора в разных базисах, проверка его свойств, нахождение собственных (характеристических) значений и векторов.
Спасибо за ваши закладки и рекомендации
Решения задач: линейные операторы
Задача 1. Найти характеристические числа и собственные векторы линейного преобразования $A$, заданного уравнениями $x’=5x+4y, y’=8x+9y$.
Задача 2. Найти в ортонормированном базисе $(i,j,k)$ матрицу линейного оператора $f: E^3 rightarrow E^3$, переводящего любой вектор $x$ в вектор $y=f(x)$, $f(x)=(a,x)a$, если $a=i-j+2k$.
Задача 3. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее $x_1”, x_2”, x_3”$ через $x_1, x_2, x_3$.
Задача 4. Установить, являются ли заданные отображения $A: R^4 to R^4$ линейными. В случае линейности отображения записать матрицу оператора $A$ в каноническом базисе
$$ e_1=(1,0,0,0); e_2=(0,1,0,0); e_3=(0,0,1,0); e_4=(0,0,0,1). $$
$$ Ax=(x_1-2x_4; x_2+x_3; -x_1; x_1+3x_2);quad Ax=(x_1-2x_4; x_2cdot x_3; -x_1; x_1+3x_2). $$
Задача 5. Найти собственные значения и собственные вектора линейного оператора, заданного в некотором базисе матрицей $А$.
$$A=
begin{pmatrix}
-2 & -2 & -4\
-2 & 1 & -2\
5 & 2 & 7\
end{pmatrix}
$$
Задача 6. Линейный оператор $A: R^3 to R^3$ в базисе $e_1, e_2, e_3$ представлен данной матрицей. Найти матрицу этого линейного оператора в базисе $f_1, f_2, f_3$ .
$$A=
begin{pmatrix}
-2 & 1 & -1\
1 & 3 & -4\
-1 & 2 & 1\
end{pmatrix}, quad left{
begin{aligned}
f_1&=e_1-e_2+3e_3,\
f_2&=4e_1+e_2-e_3,\
f_3&=2e_1-3e_2.\
end{aligned}
right.
$$
Не получаются задачи? Решим быстро и подробно
Линейные операторы (преобразования)
Определение линейных операторов (преобразований)
Линейным преобразованием (линейным оператором) линейного пространства называется линейное отображение
пространства
в себя.
Поскольку линейное преобразование является частным случаем линейного отображения, к нему применимы все понятия и свойства, рассмотренные для отображений: инъективность, сюръективность, биективность, обратимость, ядро, образ, дефект, ранг и т.д.
Матрицей линейного оператора (преобразования) в базисе
пространства
называется квадратная матрица
, составленная из координатных столбцов образов базисных векторов
, найденных относительно базиса
.
Матрица биективного линейного оператора (преобразования) обратима, т.е. невырождена. Поэтому биективное (обратимое) преобразование называют также невырожденным.
Примеры линейных операторов (преобразований)
1. Обозначим — нулевое преобразование n-мерного пространства
, которое ставит в соответствие любому вектору
нулевой элемент
пространства
. Это преобразование не является инъективным, сюръективным, биективным, обратимым. Матрица нулевого преобразования (в любом базисе) нулевая, ядро преобразования
, образ преобразования
, дефект
, ранг
.
2. Обозначим — тождественное преобразование n-мерного пространства
, которое ставит в соответствие каждому вектору
этот же вектор
. Это преобразование является инъективным, сюръективным, биективным, обратимым. Матрица тождественного преобразования (в любом базисе) единичная n-го порядка, ядро преобразования
, образ преобразования
, дефект
, ранг
.
3. Обозначим — центральную симметрию n-мерного пространства
(относительно нулевого вектора
), т.е. преобразование, которое каждому вектору ставит в соответствие противоположный ему вектор:
. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Матрица преобразования противоположна единичной (в любом базисе):
; ядро преобразования
, образ преобразования
, дефект
, ранг
.
4. Обозначим — гомотетию n-мерного пространства
(с коэффициентом
), т.е. преобразование, которое каждому вектору ставит в соответствие коллинеарный ему вектор:
. Это преобразование линейное. При
оно инъективное, сюръективное, биективное, обратимое. Матрица преобразования пропорциональна единичной (в любом базисе):
, ядро преобразования
, образ преобразования
, дефект
, ранг
. При
(см. пункт 1); при
(см. пункт 2); при
(см. пункт 3).
5. Рассмотрим линейное пространство радиус-векторов (с общим началом в точке
), принадлежащих одной плоскости (рис. 9.1). Обозначим
— поворот вокруг точки
(на угол
в положительном направлении (против часовой стрелки)). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу поворота в стандартном ортонормированием базисе
. Раскладывая образы
базисных векторов по базису, получаем
Составляем матрицу (9.1) преобразования (оператора), записывая найденные координаты образов по столбцам:
Ядро оператора (преобразования) , образ преобразования
, дефект
, ранг
. При
(см. пункт 2); при
(см. пункт 3).
6. Обозначим — оператор дифференцирования, который каждому многочлену степени не выше и ставит в соответствие его производную, рассматриваемую как многочлен степени не выше
. Это преобразование линейное, неинъективное, несюръективное, небиективное, необратимое. Квадратная матрица ((n+l)-го порядка) преобразования в стандартном базисе имеет вид
Ядро преобразования — пространство многочленов нулевой степени, образ
— пространство многочленов степени не выше
, дефект
, ранг
.
Рассмотрим преобразование линейного пространства тригонометрических многочленов (частоты
) с действительными коэффициентами:
, т.е.
— множество функций вида
, где
. Заметим, что это множество является двумерным вещественным линейным пространством. Стандартный базис пространства
образуют функции
, поскольку они линейно независимы (тождественное равенство нулю
возможно только в тривиальном случае
). При дифференцировании функции
получаем функцию
того же вида. Следовательно, преобразование
определено. Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Найдем матрицу преобразования в стандартном базисе
. Раскладывая образы базисных векторов, получаем
Составляем матрицу (9.1) преобразования, записывая найденные координаты образов по столбцам: . Ядро преобразования
— нулевое подпространство, образ
, дефект
, ранг
,
.
Аналогичными свойствами обладает преобразование , где
— множество функций вида
с комплексными коэффициентами
и
. Множество
является двумерным комплексным линейным пространством.
7. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим
— оператор проектирования на подпространство
параллельно подпространству
, который каждому вектору
, где
, ставит в соответствие его составляющую (проекцию)
, т.е.
(рис.9.2). Это преобразование линейное. При
оно неинъективное, несюръективное, небиективное, необратимое. Ядро преобразования
, образ преобразования
, дефект
, Ранг
,. При
; при
.
8. Пусть линейное пространство разлагается в прямую сумму подпространств . Обозначим
— оператор отражения в подпространстве
параллельно подпространству
(или преобразование симметрии относительно подпространства
параллельно подпространству
), который каждому вектору
, где
, ставит в соответствие вектор
, т.е.
(рис. 9.3). Это преобразование линейное, инъективное, сюръективное, биективное, обратимое. Ядро преобразования
, образ преобразования
, дефект
, ранг
. При
.
Матрицы линейного оператора (преобразования) в разных базисах
Найдем связь матриц одного и того же линейного оператора (преобразования) в разных базисах.
Пусть в базисе преобразование
имеет матрицу
, а в базисе
— матрицу
. Если
— матрица перехода от базиса
к базису
, то
(9.4)
Докажем формулу (9.4). Пусть векторы и
в базисах
и
имеют координатные столбцы
и
соответственно. Если
, то по формуле (9.2) имеем
Подставляя в первое равенство связи координат векторов в разных базисах
получаем
или, учитывая обратимость матрицы
. Сравнивая последнее равенство с
, убеждаемся в справедливости (9.4).
Замечания 9.2
1. Матрицы линейного преобразования в разных базисах оказываются подобными. И наоборот, любые две подобные матрицы являются матрицами некоторого линейного преобразования, найденными относительно разных базисов.
2. Для матриц преобразований справедливы свойства, рассмотренные ранее. В частности, при фиксированном базисе матрица суммы преобразований равна сумме их матриц, матрица произведения преобразования на число равна произведению матрицы преобразования на это же число, матрица композиции преобразований равна произведению матриц преобразований, матрица обратного преобразования является обратной для матрицы обратимого преобразования.
Алгебра линейных операторов (преобразований)
Рассмотрим множество — линейных преобразований (операторов) n-мерного линейного пространства
. Напомним, что два преобразования
и
называются равными, если
.
На множестве определены две линейные операции: сложение преобразований и умножение преобразования на число, поскольку в результате этих операций получается линейное преобразование.
Нетрудно показать, что эти операции удовлетворяют условиям:
1. ;
2. ;
3. существует нулевое преобразование такое, что
;
4. для каждого преобразования существует противоположное преобразование
такое, что
;
5. и любого числа
;
6. и любых чисел
;
7. и любых чисел
;
8. .
В условиях 5-7 говорится о числах из того же числового поля, над которым определено линейное пространство .
Условия 1-8 повторяют аксиомы линейного пространства. Поэтому множество с линейными операциями является линейным пространством. Если пространство
вещественное (комплексное), то и пространство
вещественное (комплексное).
Найдем размерность пространства . При фиксированном базисе имеется взаимно однозначное соответствие между линейными преобразованиями и их матрицами, причем это соответствие сохраняет линейные операции. Следовательно, пространство
изоморфно пространству
— квадратных матриц n-го порядка. Размерность пространства
равна
. По теореме 8.3:
то есть
Кроме линейных операций в множестве определена операция умножения элементов. Произведением преобразований
и
назовем их композицию, т.е.
. В результате композиции линейных преобразований получается линейное преобразование. Операция умножения удовлетворяет следующим условиям:
1. ;
2. ;
3. ;
4. существует тождественное преобразование такое, что
.
Первое условие выражает ассоциативность операции умножения, условия 2 и 3 — законы дистрибутивности, условие 4 — существование нейтрального элемента. Множество с операциями сложения и умножения элементов является кольцом с единицей (вообще говоря, некоммутативное, так как в общем случае
).
Операции умножения операторов (преобразований) и произведения операторов на число (из заданного числового поля) удовлетворяют условию:
5.
Линейное пространство, которое является кольцом, удовлетворяющим условию 5, называется алгеброй. Поэтому множество называют алгеброй линейных операторов (преобразований).
Многочлены от линейного оператора (преобразования)
В алгебре можно определить целую неотрицательную степень оператора
, полагая по определению
Пусть — многочлен переменной
. Многочленом
от линейного преобразования
называется преобразование
.
Многочлен называется аннулирующим для линейного преобразования
, если
— нулевое преобразование. Заметим, что у каждого линейного преобразования
n-мерного линейного пространства
существует аннулирующий многочлен степени не выше
. Действительно, система из
элементов
линейного пространства
линейно зависима (так как
). Поэтому существуют такие числа
, не все равные нулю одновременно, что
. Следовательно, многочлен
— аннулирующий для преобразования
.
Замечания 9.3
1. При фиксированном базисе каждому преобразованию (оператору) можно сопоставить его матрицу. Свойства линейных операций 1-8, записанные для матриц преобразований, повторяют свойства линейных операций с матрицами, а свойствам 1-5 произведения операторов отвечают свойства операции умножения матриц.
2. При фиксированном базисе многочлен от линейного преобразования
имеет матрицу
, где
— матрица преобразования
в том же базисе. Поэтому свойства многочленов от матриц переносятся на многочлены от линейного преобразования. В частности, многочлены от одного преобразования перестановочны:
3. Функции от матриц определяются при помощи многочленов от матриц. Поэтому можно определить функции от линейных преобразований.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Ортогональные преобразования.
Начать изучение
-
Определение линейных преобразований.
Начать изучение
-
Произведение линейных преобразований.
Начать изучение
-
Образ вектора при линейном преобразовании.
Начать изучение
Ортогональные преобразования.
Определение.
Ортогональными называются такие преобразования плоскости, которые не меняют расстояния между любыми двумя точками, то есть преобразования (f) ортогональное, если для любых точек (A) и (B) выполнено (|AB|=|f(A)f(B)|).
Основными примерами ортогональных преобразований служат параллельный перенос, поворот и осевая симметрия.
Получим координатную запись ортогонального преобразования в декартовой прямоугольной системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Обозначим через (A) и (B) концы базисных векторов: (boldsymbol{e}_{1}=overrightarrow{OA}), (boldsymbol{e}_{2}=overrightarrow{OB}) (рис. 12.1). При ортогональном преобразовании равнобедренный прямоугольный треугольник (OAB) перейдет в равный ему треугольник (O^{*}A^{*}B^{*}). Рассмотрим произвольную точку (M(x, y)). Она перейдет в точку (M^{*}) с координатами ((x^{*}, y^{*})). Нам надо выразить ((x^{*}, y^{*})) через ((x, y)).
По определению координат (overrightarrow{OM}=xoverrightarrow{OA}+yoverrightarrow{OB}). Отсюда следует, что (overrightarrow{O^{*}M^{*}}=xoverrightarrow{O^{*}A^{*}}+yoverrightarrow{O^{*}B^{*}}). Действительно, векторы (overrightarrow{O^{*}A^{*}}) и (overrightarrow{O^{*}B^{*}}) взаимно перпендикулярны и по длине равны 1, а потому компоненты (overrightarrow{O^{*}M^{*}}) по этим векторам равны его скалярным проекциям на них. Эти проекции равны проекциям (overrightarrow{OM}) на (boldsymbol{e}_{1}, boldsymbol{e}_{2}), что видно из равенства соответствующих треугольников. Теперь мы можем написать
$$
overrightarrow{OM^{*}}=overrightarrow{OO^{*}}+overrightarrow{O^{*}M^{*}}=overrightarrow{OO^{*}}+xoverrightarrow{O^{*}A^{*}}+yoverrightarrow{O^{*}B^{*}}.label{ref1}
$$
Обозначим через (varphi) угол между (overrightarrow{O^{*}A^{*}}) и (boldsymbol{e}_{1}). Поскольку (|overrightarrow{O^{*}A^{*}}|=1), координаты этого вектора в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}) равны ((cos varphi, sin varphi)). Тогда перпендикулярный вектор единичной длины (overrightarrow{O^{*}B^{*}}) имеет координаты ((mp sin{y}, pm cos{y})), причем верхние знаки берутся в том случае, когда пара векторов (overrightarrow{O^{*}A^{*}}) и (overrightarrow{O^{*}B^{*}}) ориентирована так же, как (boldsymbol{e}_{1}, boldsymbol{e}_{2}). Координаты точки (O^{*}) обозначим через ((c_{1}, c_{2})).
Теперь мы можем разложить все члены равенства eqref{ref1} по базису:
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}label{ref2}
$$
Итак, мы доказали следующее утверждение.
Утверждение 1.
Произвольное ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами eqref{ref2}, где (varphi) — угол, на который поворачивается первый базисный вектор, a (c_{1}) и (c_{2}) — координаты образа начала координат. При этом выбираются верхние знаки, если образы базисных векторов ориентированы так же, как и сами эти векторы, и нижние знаки в противоположном случае.
Пример 1.
Параллельный перенос на вектор с сопоставляет точке (M) с координатами ((x, y)) в некоторой декартовой системе координат точку (M^{*}) с координатами
$$
x^{*}=x+c_{1}, y^{*}=y+c_{2},nonumber
$$
где (c_{1}) и (c_{2}) — координаты (c).
Пример 2.
Напишем уравнения поворота плоскости на угол (varphi) вокруг некоторой точки, приняв эту точку за начало декартовой прямоугольной системы координат. В этом случае (O=O^{*}) и, следовательно, (c_{1}=c_{2}=0). Должны быть выбраны верхние знаки. Итак
$$
x^{*}=x cos{varphi}-y sin{varphi}, y^{*}=x sin{varphi}+y cos{varphi},nonumber
$$
Пример 3.
Рассмотрим осевую симметрию относительно некоторой прямой. Примем ось симметрии за ось абсцисс декартовой прямоугольной системы координат. Тогда точка (M(x, y)) переходит в точку (M^{*}) с координатами
$$
x^{*}=x, y^{*}=-y.nonumber
$$
Здесь (c_{1}=c_{2}=0) и (varphi=0) при нижних знаках в формулах eqref{ref2}.
Определение линейных преобразований.
Основным объектом для нас будет более широкий класс преобразований, включающий в себя ортогональные преобразования.
Определение.
Преобразование (f) плоскости (P) называется линейным, если на (P) существует такая декартова система координат, в которой (f) может быть записано формулами
$$
begin{array}{cc}
& x^{*}=a_{1}x+b_{1}y+c_{1},\
& y^{*}=a_{2}x+b_{2}y+c_{2}.
end{array}label{ref3}
$$
Взаимно однозначное линейное преобразование называется аффинным преобразованием.
Подчеркнем, что в определении линейного преобразования, вовсе не требуется, чтобы коэффициенты в формулах eqref{ref3} не обращались в нуль одновременно. Они могут быть любыми. Докажем следующее утверждение.
Утверждение 2.
Для того чтобы преобразование, задаваемое формулами eqref{ref3}, было взаимно однозначным, необходимо и достаточно,
$$
begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix} neq 0.label{ref4}
$$
Таким образом, аффинное преобразование определяется формулами eqref{ref3} при условии eqref{ref4}.
Доказательство.
Наше утверждение вытекает по существу из утверждения о существовании решения системы линейных уравнений. Нам нужно узнать, при каком условии каждая точка плоскости имеет единственный прообраз. Формулы eqref{ref3} связывают координаты ((x^{*}, y^{*})) точки (M^{*}) и координаты ((x, y)) ее прообраза. Их можно рассматривать как систему линейных уравнений для нахождения (x) и (y), и эта система имеет единственное решение при любых свободных членах (x^{*}-c_{1}) и (y^{*}-c_{2}) (а значит, при любых (x^{*}) и (y^{*})) тогда и только тогда, когда выполнено условие eqref{ref4}.
Как видно из доказанного утверждения, ортогональные преобразования являются линейными. Проверка условия eqref{ref4} показывает, что они аффинные. Рассмотрим другие примеры.
Пример 4.
Рассмотрим сжатие к прямой и примем эту прямую за ось абсцисс декартовой прямоугольной системы координат. Легко видеть, что в такой системе координат сжатие с коэффициентом (lambda) записывается формулами
$$
x^{*}=x, y^{*}=lambda y.nonumber
$$
Сжатие к прямой — аффинное преобразование.
Пример 5.
Проектирование на прямую в такой декартовой прямоугольной системе координат, для которой эта прямая — ось абсцисс, записывается формулами
$$
x^{*}=x, y^{*}=0.nonumber
$$
Это — линейное, но не аффинное преобразование.
Пример 6.
Для записи уравнений гомотетии не существенно, чтобы система координат была прямоугольной, но уравнения проще, если начало координат поместить в центр гомотетии. По определению гомотетии с коэффициентом (lambda) вектор (overrightarrow{OM}) переходит в вектор (overrightarrow{OM^{*}}=lambdaoverrightarrow{OM}). Если (O) — начало координат, координаты точек (M) и (M^{*}) будут связаны равенствами
$$
x^{*}=lambda x, y^{*}=lambda y.nonumber
$$
Гомотетия — аффинное преобразование.
Пример 7.
Преобразование, сопоставляющее каждой точке плоскости одну и ту же точку (C), записывается формулами (x^{*}=c_{1}), (y^{*}=c_{2}), где (c_{1}) и (c_{2}) — координаты точки (C). Оно линейное, но не аффинное.
Определение аффинного преобразования содержит упоминание о некоторой определенной системе координат, и заранее не известно, будет ли преобразование записываться формулами вида eqref{ref3} в какой-либо другой системе координат. Давайте докажем следующее утверждение.
Утверждение 3.
В любой декартовой системе координат, линейное преобразование задается формулами вида eqref{ref3}, то есть:
$$
begin{array}{cc}
& x^{*}=a_{1}x+b_{1}y+c_{1},\
& y^{*}=a_{2}x+b_{2}y+c_{2}.
end{array}nonumber
$$
Доказательство.
Пусть преобразование задано равенствами eqref{ref3} в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Перейдем к системе координат (O’, boldsymbol{e}’_{1}, boldsymbol{e}’_{2}). Как мы знаем, старые координаты точки (M(x, y)) выражаются через новые координаты ((x’, y’)) по следующим формулам:
$$
x=alpha_{1}x’+beta_{1}y’+gamma_{1}, y=alpha_{2}x’+beta_{2}y’+gamma_{2}.label{ref5}
$$
Для образа (M^{*}) точки (M) нам нужно будет, наоборот, выразить новые координаты ((x’^{*}, y’^{*})) через его старые координаты ((x^{*}, y^{*})). Они выражаются такими же формулами, разумеется, с другими коэффициентами:
$$
x’^{*}=lambda_{1}(x^{*})+mu_{1}y^{*}+nu_{1}, y’^{*}=lambda_{2}x^{*}+mu_{2}y^{*}+nu_{2}.label{ref6}
$$
Нам требуется найти выражение новых координат ((x’^{*}, y’^{*})) точки (M^{*}) через новые координаты ((x’, y’)) точки (M). С этой целью подставим в равенства eqref{ref6} значения (x^{*}) и (y^{*}) из формул eqref{ref3}:
$$
begin{array}{cc}
& x’^{*}=lambda_{1}(a_{1}x+b_{1}y+c_{1})+mu_{1}(a_{2}x+b_{2}y+c_{2})+nu_{1},\
& y’^{*}=lambda_{2}(a_{1}x+b_{1}y+c_{1})+mu_{2}(a_{2}x+b_{2}y+c_{2})+nu_{2}.
end{array}nonumber
$$
Для нас важно, что правые части этих равенств — многочлены степени не выше 1 относительно (x) и (y):
$$
x’^{*}=A_{1}x+B_{1}y+C_{1}, y’^{*}=A_{2}x+B_{2}y+C_{2}.label{ref7}
$$
Подставив сюда выражения (x) и (y) по формулам eqref{ref5}, мы найдем искомую зависимость:
$$
begin{array}{cc}
& x’^{*}=A_{1}(alpha_{1}x’+beta_{1}y’+gamma_{1})+B_{1}(alpha_{2}x’+beta_{2}y’+gamma_{2})+C_{1},\
& y’^{*}=A_{2}(alpha_{1}x’+beta_{1}y’+gamma_{1})+B_{2}(alpha_{2}x’+beta_{2}y’+gamma_{2})+C_{2}.
end{array}nonumber
$$
Мы видим, что правые части этих равенств — многочлены степени не выше 1 относительно (x’) и (y’). Это нам и требовалось доказать.
Заметим, что аффинные преобразования выделяются из линейных требованием взаимной однозначности, которое не зависит от системы координат. Поэтому без дополнительных проверок мы можем быть уверены, что формулы, задающие аффинное преобразование в новой системе координат, удовлетворяют условию eqref{ref4}.
Произведение линейных преобразований.
Доказательство последнего утверждения было основано на том, что результат подстановки многочленов степени не выше 1 в многочлен степени не выше 1 оказывается таким же многочленом. Это же обстоятельство лежит в основе следующего утверждения.
Утверждение 4.
Произведение линейных преобразований является линейным преобразованием. Произведение аффинных преобразований — аффинное преобразование.
Доказательство.
Пусть заданы линейные преобразования (f) и (g) и выбрана система координат. Тогда координаты точки (f(M)) выражаются через координаты точки (M) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}.label{ref8}
$$
а координаты точки (g(f(M))) через координаты точки (f(M)) формулами
$$
x^{**}=d_{1}x^{*}+e_{1}y^{*}+f_{1}, y^{**}=d_{2}x^{*}+e_{2}y^{*}+f_{2}.label{ref9}
$$
Подстановка равенств eqref{ref9} в eqref{ref8} выражает координаты g(f(M)) через координаты (M). В результате подстановки мы получаем многочлены степени не выше 1, что и доказывает первую часть предложения.
Для доказательства второй части достаточно вспомнить, что по согласно ранее доказанного утверждения произведение двух взаимно однозначных преобразований взаимно однозначно.
Утверждение 5.
Преобразование, обратное аффинному преобразованию, также является аффинным.
Если преобразование (f) записано уравнениями eqref{ref3}, то координатная запись его обратного преобразования получается решением уравнений eqref{ref3} относительно (x) и (y). Для того чтобы решить эти уравнения, умножим первое из них на (b_{2}), второе — на (b_{1}) и вычтем одно уравнение из другого. Мы получим ((a_{1}b_{2}-a_{2}b_{1})x=b_{2}(x^{*}-c_{1})-b_{1}(y^{*}-c_{2})). Из условия eqref{ref4} следует, что (x) — линейный многочлен от (x^{*}) и (y^{*}). Выражение для (y) получается аналогично.
Образ вектора при линейном преобразовании.
Рассмотрим вектор (overrightarrow{M_{1}M_{2}}). Если координаты точек (M_{1}) и (M_{2}) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) обозначить соответственно (x_{1}, y_{1}) и (x_{2}, y_{2}), то компоненты вектора будут равны (x_{2}-x_{1}) и (y_{2}-y_{1}). Пусть формулы eqref{ref3} задают преобразование (f) в выбранной системе координат. Тогда образы (M_{2}^{*}) и (M_{1}^{*}) точек (M_{2}) и (M_{1}) имеют абсциссы
$$
x_{2}^{*}=a_{1}x_{2}+b_{1}y_{2}+c_{1}, x_{1}^{*}=a_{1}x_{1}+b_{1}y_{1}+c_{1}.nonumber
$$
Следовательно, первая компонента вектора (overrightarrow{M_{1}^{*}M_{2}^{*}}) равна
$$
x_{2}^{*}-x_{1}^{*}=a_{2}(x_{2}-x_{1})+b_{1}(y_{2}-y_{1}).nonumber
$$
Аналогично находим вторую компоненту этого вектора
$$
y_{2}^{*}-y_{1}^{*}=a_{2}(x_{2}-x_{1})+b_{2}(y_{2}-y_{1}).nonumber
$$
Обратим внимание на то, что компоненты (overrightarrow{M_{1}^{*}M_{2}^{*}}) выражаются только через компоненты (overrightarrow{M_{1}M_{2}}), а не через координаты точек (M_{1}) и (M_{2}) по отдельности. Два равных вектора имеют одинаковые компоненты и, следовательно, при линейном преобразовании перейдут в векторы, компоненты которых также одинаковы. Итак, мы получаем ещё одно утверждение.
Утверждение 6.
При линейном преобразовании равные векторы переходят в равные векторы. Компоненты (alpha_{1}^{*}), (alpha_{2}^{*}) образа вектора выражаются через его компоненты (alpha_{1}), (alpha_{2}) формулами
$$
begin{array}{cc}
& alpha_{1}^{*}=a_{1}alpha_{1}+b_{1}alpha_{2},\
& alpha_{2}^{*}=a_{2}alpha_{1}+b_{2}alpha_{2}.
end{array}label{ref10}
$$
Если быть точным, говорить об образе вектора при преобразовании (f) неправильно: преобразование отображает точки, а не векторы. Точнее было бы сказать, что (f) порождает преобразование (tilde{f}) множества векторов. Но ниже мы, тем не менее, будем придерживаться не совсем точной, но более удобной и общепринятой терминологии — говорить, что преобразование (f) переводит вектор (boldsymbol{a}) в вектор (boldsymbol{a}^{*}) и обозначать последний через (f(boldsymbol{a})).
Из формул eqref{ref10} вытекает, что для линейного преобразования (f) при любых векторах (boldsymbol{a}) и (boldsymbol{b}) и любом числе (lambda)
$$
begin{array}{cc}
& f(boldsymbol{a}+boldsymbol{b})=f(boldsymbol{a})+f(boldsymbol{b}),\
& f(lambdaboldsymbol{a})=lambda f(boldsymbol{a}).
end{array}label{ref11}
$$
Докажем, например, первое из этих равенств. Пусть (gamma_{1}^{*}) и (gamma_{2}^{*}) — компоненты вектора (f(boldsymbol{a}+boldsymbol{b})). Тогда
$$
gamma_{1}^{*}=a_{1}(alpha_{1}+beta_{1})+b_{1}(alpha_{2}+beta_{2}), gamma_{2}^{*}=a_{2}(alpha_{1}+beta_{1})+b_{2}(alpha_{2}+beta_{2}),nonumber
$$
где (alpha_{1}, alpha_{2}) и (beta_{1}, beta_{2}) — компоненты векторов (boldsymbol{a}) и (boldsymbol{b}). Отсюда
$$
begin{array}{cc}
& gamma_{1}^{*}=(a_{1}alpha_{1}+b_{1}alpha_{2})+(a_{1}beta_{1}+b_{1}beta_{2})=alpha_{1}^{*}+beta_{1}^{*},\
& gamma_{2}^{*}=(a_{2}alpha_{1}+b_{2}alpha_{2})+(a_{2}beta_{1}+b_{2}beta_{2})=alpha_{2}^{*}+beta_{2}^{*}.
end{array}nonumber
$$
Это — координатная запись доказываемого равенства. Второе из равенств eqref{ref11} доказывается аналогично.
Из равенств eqref{ref11} следует, что при линейном преобразовании (f) линейно зависимые векторы переходят в линейно зависимые. Действительно, как легко видеть, (f(boldsymbol{0})=boldsymbol{0}). Тогда любое соотношение вида (lambda boldsymbol{a}+mu boldsymbol{b}=boldsymbol{0}) влечет за собой (lambda f(boldsymbol{a})+mu f(boldsymbol{b})=boldsymbol{0}).
Если преобразование аффинное, то линейно независимые векторы переходят в линейно независимые. В самом деле, в противном случае из равенства (lambda f(boldsymbol{a})+mu f(boldsymbol{b})=boldsymbol{0}), (lambda^{2}+mu^{2} neq 0), при обратном преобразовании мы получили бы (lambda boldsymbol{a}+mu boldsymbol{b}=boldsymbol{0}).
Следующее утверждение устанавливает геометрический смысл коэффициентов в формулах, задающих линейное преобразование.
Утверждение 7.
Пусть преобразование (f) записано в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) формулами eqref{ref3}. Тогда (c_{1}) и (c_{2}) — координаты точки (f(O)), a (a_{1} a_{2}) и (b_{1}, b_{2}) — компоненты векторов (f(boldsymbol{e}_{1})) и (f(boldsymbol{e}_{2})) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}).
Доказательство.
Для доказательства подставим в формулы eqref{ref3} значения (x=0) и (y=0) координат точки (O) и увидим, что координаты (f(O)) равны (c_{1}) и (c_{2}).
Подставим в формулы eqref{ref10} координаты вектора (boldsymbol{e}_{1}) (alpha_{1}=1), (alpha_{2}=0) и найдем (a_{1}^{*}=a_{1}), (a_{2}^{*}=a_{2}). Следовательно, (f(boldsymbol{e}_{1})) имеет компоненты (a_{1}) и (a_{2}). Так же доказывается, что компоненты (f(boldsymbol{e}_{2})) равны (b_{1}) и (b_{2}).
Утверждение 8.
Каковы бы ни были три точки (L), (M), (N), не лежащие на одной прямой, и три точки (L^{*}), (M^{*}) и (N^{*}), существует единственное линейное преобразование (f) такое, что (L^{*}=f(L)), (M^{*}=f(M)) и (N^{*}=f(N)). Это преобразование аффинное тогда и только тогда, когда точки (L^{*}), (M^{*}) и (N^{*}) также не лежат на одной прямой.
Доказательство.
Векторы (overrightarrow{LM}) и (overrightarrow{LN}) не коллинеарны. Следовательно, (L), (overrightarrow{LM}), (overrightarrow{LN}) — декартова система координат. Пусть (c_{1}, c_{2}) — координаты (L^{*}), а (a_{1}, a_{2}) и (b_{1}, b_{2}) — компоненты векторов (overrightarrow{L^{*}M^{*}}) и (overrightarrow{L^{*}N^{*}}) в этой системе координат. Формулы
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}nonumber
$$
определяют линейное преобразование (f), которое, как легко видеть, обладает требуемым свойством. При этом согласно предложению 7, коэффициенты в формулах однозначно определены.
Условие eqref{ref4}, равносильное аффинности преобразования, необходимо и достаточно для того, чтобы векторы (overrightarrow{L^{*}M^{*}}) и (overrightarrow{L^{*}N^{*}}) были не коллинеарны, то есть (L^{*}), (M^{*}) и (N^{*}) не лежали на одной прямой. Предложение доказано.
Заметим, что в том случае, когда преобразование (f) аффинное, точка (f(O)) и векторы (f(boldsymbol{e}_{1})) и (f(boldsymbol{e}_{2})) могут быть использованы как система координат. Для этой системы координат имеет место ещё одно утверждение.
Утверждение 9.
При аффинном преобразовании (f) образ (M^{*}) точки (M) в системе координат (f(O)), (f(boldsymbol{e}_{1})), (f(boldsymbol{e}_{2})) имеет те же координаты, что и точка (M) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}).
Доказательство.
Равенство (overrightarrow{OM}=x boldsymbol{e}_{1}+y boldsymbol{e}_{2}) означает, что (x), (y) — координаты (M) в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Подействовав преобразованием (f) на обе части этого равенства, мы получаем (overrightarrow{f(O)f(M)}=x f(boldsymbol{e}_{1})+y f(boldsymbol{e}_{2})), которое означает, что (x) и (y) — координаты (M^{*}) в системе координат (f(O)), (f(boldsymbol{e}_{1})), (f(boldsymbol{e}_{2})).


































































































