Как найти две точки на сфере - Сайт, где вы сможете решить свои вопросы

Статистика

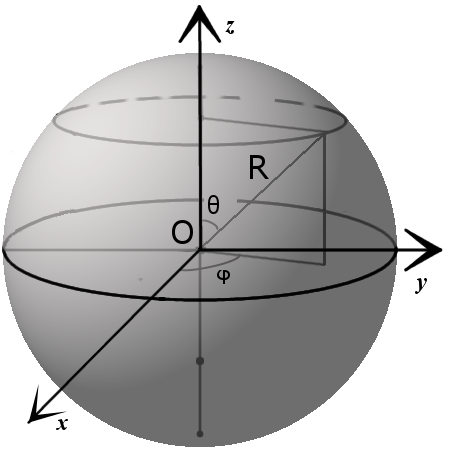
Координаты на сфере

Положение точки на сфере удобнее всего задавать так, как это делается в географии. На данной сфере радиуса R выберем какие-нибудь две диаметрально противоположные точки, одну из них N назовем условно северным полюсом, другую S — южным. Какой-нибудь из «меридианов» (кратчайший путь по сфере из S в N) назовем начальным меридианом; проходящую через центр О сферы и перпендикулярную оси SN плоскость назовем экваториальной, а пересечение ее со сферой — экватором, на экваторе изберем направление, скажем против часовой стрелки, если смотреть из N. Положение любой точки М на сфере определяется двумя координатами, одна из них, назовем ее долготой,—угол φ между плоскостью начального меридиана и плоскостью, проходящей через М и ось SN (угол должен отсчитываться в направлении, соответствующем выбранному на экваторе). Широтой точки М будем называть угол θ между радиусом ОМ и плоскостью экватора (θ считается положительным для точек северного полушария и отрицательным для южного). Будем писать: М < φ ; θ>, ставя на первое место долготу, на второе — широту.

Пример. Проверьте правильность координатного обозначения точек на рис. 21.

Все точки с одинаковой долготой φ₀ заполняют меридиан, уравнение которого поэтому φ=φ₀. Все точки с одинаковой широтой θ₀заполняют параллель θ=θ₀. Уравнение, связывающее текущие координаты φ и θ, определяет, как и в плоской геометрии, кривую; неравенство, соответствующее этому уравнению, определяет одну или несколько областей, на которые эта кривая разделяет сферу. Так, неравенство θ< 0 определяет южную полусферу,θ>0—северную;θ=0 есть уравнение экватора. Если сферу отнести к декартовым координатам в пространстве, приняв центр О сферы за начало, ось SN — за ось z, ось х направив через точку <0; 0>, ось у — через<90°; 0>, то декартовы координаты х, y, z любой точки М сферы легко выразить через долготу и широту этой точки. Для этого выразим сначала координаты ее проекции М₁ на плоскость Оху, где обычным образом расположим полярную систему координат. Из рис. 21 видно, что для М₁(х; у; 0) полярный радиус r=Rcosθ, а полярный угол φ совпадает с долготой точки М. Кроме того,

z=Rsinθ. Приняв во внимание формулы (11), получим:

По этим формулам вычисляют декартовы координаты точки М (х; у; z), если известны ее координаты φ и θ на сфере.

На эти же формулы можно взглянуть и с другой точки зрения. Будем считать со и 6 переменными, придавая им всевозможные значения в естественных пределах 0≤ φ<360°, -90°≤ θ≤+90°; тогда точка М<φ;θ> будет перемещаться по сфере, занимая всевозможные положения. Это напоминает параметрические уравнения линии, в которых декартовы координаты х, y, z выражены через один переменный параметр t. Разница лишь в том, что теперь х, у, z выражены через два параметра, поэтому получается не линия (одномерное образование), а поверхность (образование двумерное). Подобные уравнения называют параметрическими уравнениями поверхности; переменные параметры чаще всего здесь обозначают буквами и и v. Итак, уравнения сферы запишем в виде:

Если из этих уравнений исключить параметры и, v (для этого проще всего возвести (13) в квадрат и сложить; к сожалению, исключение переменных не всегда так просто), получим обычное ее уравнение x² + y²+z²=R².

УРАВНЕНИЯ И ФУНКЦИИ
Как люди учились решать уравнения
Метод двух ложных положений
Введение понятия неизвестного числа
Квадратные уравнения Совершенные числа
Уравнения степеней выше второй Сомножители, производящие кучу нулей
Что такое координаты и для чего они служат Пять зашифрованных действий
Декартовы координаты точки
Простейшие задачи
Задание фигуры, состоящей из бесчисленного множества точек
Прямая
Основные задачи на прямую
Окружность
Аналитическое решение геометрических задач
Неразрешимые задачи на построение
Полярные координаты
Координаты на сфере
Криволинейные координаты. Общая идея координат

Источник

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

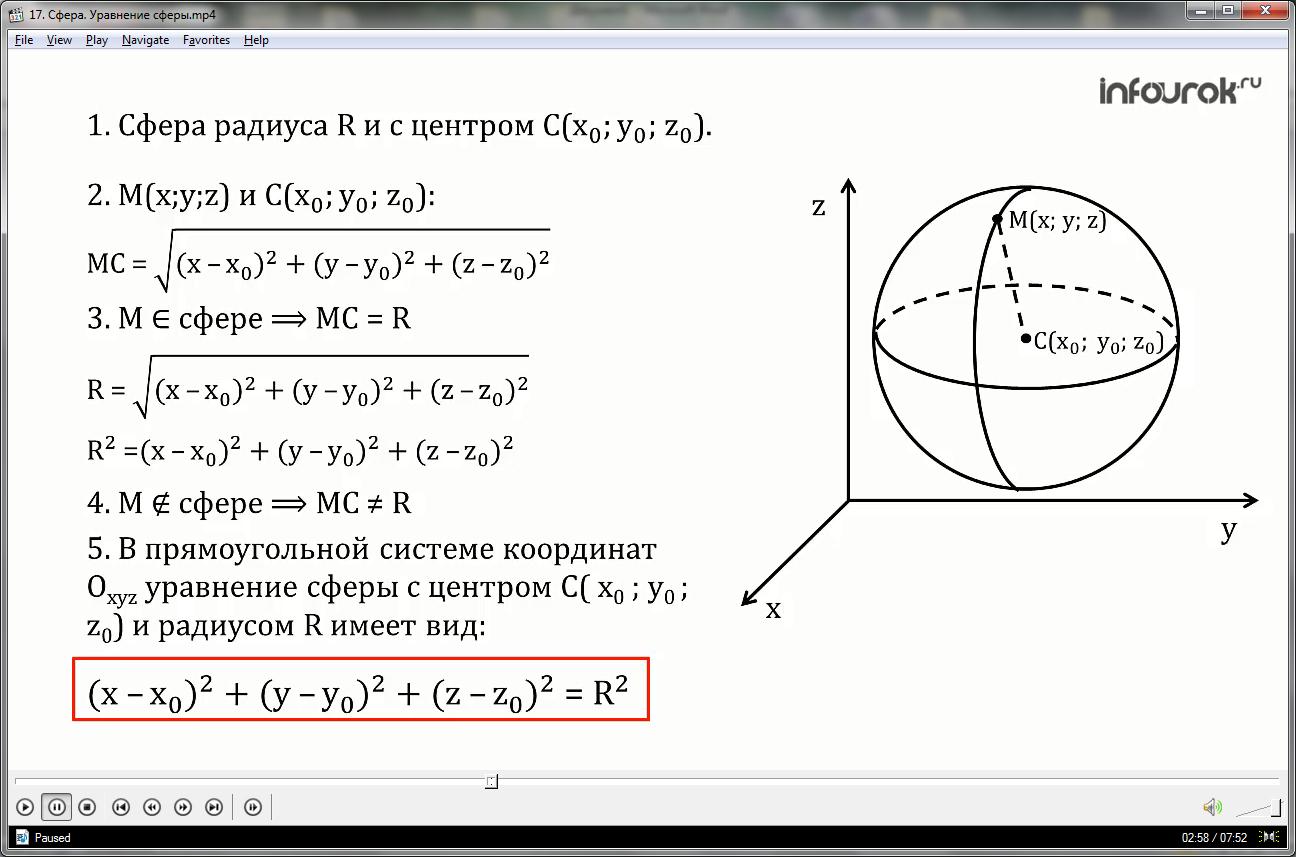
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

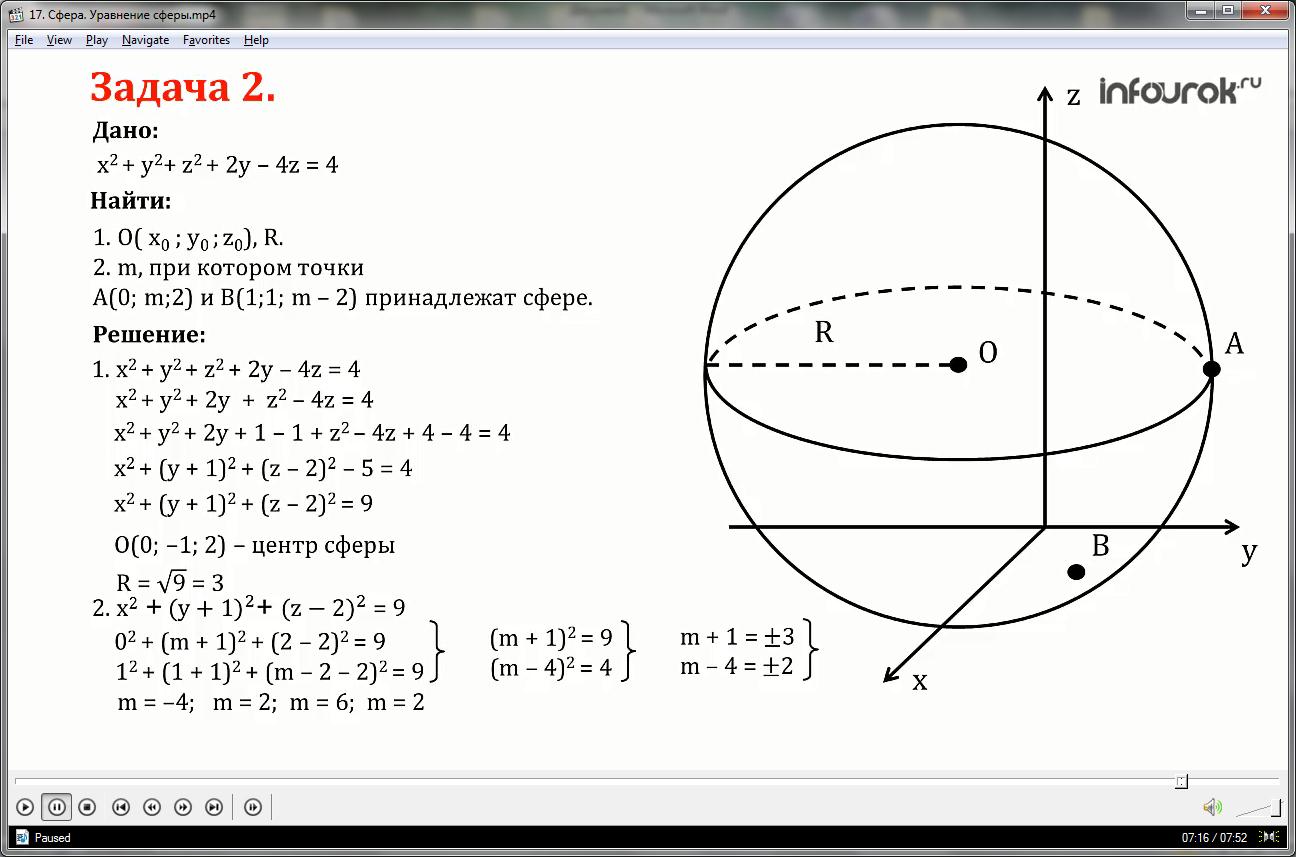
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

–> –>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

51763

1003

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

S = 4 π R 2 = π D 2

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x – x ₀) 2 + ( y – y ₀) 2 + ( z – z ₀) 2 = R 2

Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

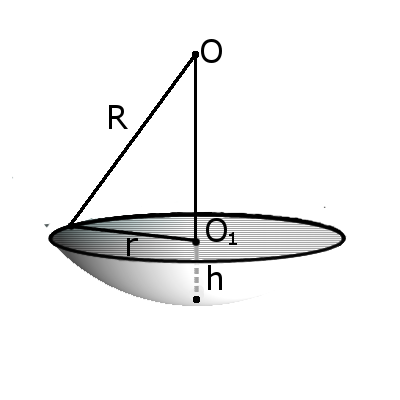
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

S = π R(2 h + √ 2 h R – h 2 )

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Координаты центра сферы через уравнение

19.1. Определения шара, сферы и их элементов

С шаром и сферой мы уже знакомы. Напомним их определения.

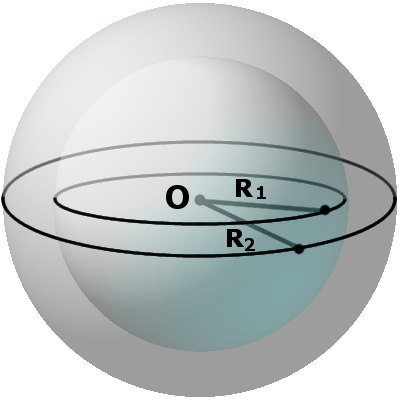
Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R ( R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара .

Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.

На рисунке 193 изображён шар с центром О и радиусом R = OА.

Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R ) .

Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара . Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара ( сферы ) . На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ , NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.

Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а ). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F 1 (рис. 194, б ). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F 1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F 1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.

Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара ( сферы ) . Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью ; большая окружность является пересечением сферы и её диаметральной плоскости.

19.2. Изображение сферы

Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а ). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором , а точки N и S — полюсами сферы . Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией .

Типичная ошибка (!) при изображении сферы (рис. 195, б ) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.

Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V ) , а другую — профильной (обозначают W ) плоскостями проекций.

Сферу расположим так, чтобы её ось N ′ S ′ была параллельна профильной ( W ), но не параллельна фронтальной ( V ) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W ; отрезки A 1 B 1 и N 1 S 1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C ′ D ′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a ; 196, a.

Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.

Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а ) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD ; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.

На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).

 ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.

Решени е. Если ∠ АМВ = 90 ° , то точка М принадлежит окружности с диаметром АВ (рис. 198, a ).

Проведём произвольную плоскость α , содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB , есть сфера с диаметром AB . Точки А и В этому множеству точек-вершин не принадлежат.

19.3. Уравнение сферы

Составим уравнение сферы с центром А ( a ; b ; с ) и радиусом R в декартовой прямоугольной системе координат Oxyz.

Пусть М ( x ; у ; z ) — любая точка этой сферы (рис. 199). Тогда MA = R или MA 2 = R 2 . Учитывая, что MA 2 = ( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 , получаем искомое уравнение cферы

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 .

Если начало системы координат совпадает с центром A сферы, то a = b = c = 0 , а сфера в такой системе координат имеет уравнение

x 2 + y 2 + z 2 = R 2 .

Из полученных уравнений следует, что сфера — поверхность второго порядка.

Так как для любой точки М ( х ; у ; z ) шара с центром А ( a ; b ; с ) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 ⩽ R 2 .

При этом для всех внутренних точек М шара выполняется условие МА 2 R 2 , т. е.

( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 R 2 ,

для точек М шаровой поверхности — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 ,

для точек М вне шара — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 > R 2 .

19.4. Пересечение шара и сферы с плоскостью

Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.

Теорема 30 (о пересечении шара и сферы с плоскостью ) . 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = , где R — радиус шара, a d — расстояние от центра шара до плоскости сечения. 2) Если расстояние от центра шара до данной плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку. 3) Если расстояние от центра шара до данной плоскости больше радиуса, то плоскость не имеет с шаром общих точек.

Доказательств о. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α . Обозначим ρ ( О ; α ) = | ОА | = d — расстояние от центра шара до плоскости α .

Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α .

1) ρ ( O ; α ) = d R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = . Для этого достаточно убедиться, что любая точка пересечения шара и плоскости α есть точка круга с центром А и радиусом r = и, обратно, любая точка этого круга есть точка указанного пересечения.

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM 2 = ОА 2 + АМ 2 , откуда AM = . Так как точка М принадлежит шару, то ОМ ⩽ R, тогда OM 2 – OA 2 ⩽ R 2 – d 2 , поэтому АМ ⩽ . Это означает, что точка М сечения шара плоскостью α находится от точки А на расстоянии, не большем , следовательно, она принадлежит кругу с центром А и радиусом .

Обратно, пусть М — произвольная точка плоскости α , принадлежащая кругу с центром А и радиусом r = . В прямоугольном треугольнике AOM по теореме Пифагора OM 2 = ОA 2 + AM 2 . Так как AM ⩽ r , то OM 2 ⩽ OA 2 + r 2 = d 2 + R 2 – d 2 = R 2 , откуда OM ⩽ R . Значит, точка М принадлежит данному шару. Учитывая, что точка М принадлежит и плоскости α , приходим к выводу: точка M принадлежит пересечению данного шара и плоскости α .

Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d R пересечением сферы и плоскости является окружность с центром А и радиусом r = . Проделайте это самостоятельно.

Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).

2) ρ ( O ; α ) = d = OA = R (рис. 201).

Так как ОА = ρ ( O ; α ) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α , принадлежит шаровой поверхности, ограничивающей данный шар.

Пусть M — произвольная точка плоскости α , отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α , удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.

3) ρ ( О ; α ) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼

 ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.

Решени е. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD ; α — секущая плоскость, проходящая через точку С перпендикулярно OD.

Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α .

Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R , откуда

АС = r = , где r — радиус сечения шара плоскостью α . Тогда площадь этого сечения равна π r 2 = .

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = .

Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна

π r • R = π • • R = ,

а площадь его полной поверхности — + = π R 2 • (2 + ).

в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = , боковое ребро OE пирамиды равно радиусу R данного шара (см. рис. 204).

Так как △ ЕFK — правильный, вписанный в окружность радиуса r = , то сторона этого треугольника равна r , т. е. EF = . Тогда S △ EFK = = .

Площадь боковой поверхности пирамиды равна 3 S △ EOF = EF • ОН, где OH — апофема пирамиды. В прямоугольном треугольнике OHF находим

ОН = = = .

Тогда EF • OH = — площадь боковой поверхности пирамиды.

Следовательно, площадь полной поверхности пирамиды равна

+ = R 2 ( + ).

Ответ: a) ; б) π R 2 (2 + ); в) ; R 2 ( + ).

19.5. Плоскость, касательная к сфере и шару

Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.

Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).

Также говорят, что плоскость касается сферы (шара) .

Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере ; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Заметим, что если прямая a касается сферы в точке М , то эта прямая касается в точке М той окружности большого круга, которая является сечением сферы и диаметральной плоскости, проходящей через прямую a.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М , то эта прямая касается в точке М самой сферы.

Более того, так как прямая a, касающаяся сферы в точке М , имеет со сферой лишь одну общую точку — точку М , то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R , точка А — центр окружности радиуса r , по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R • cos ϕ ( △ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).

Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.

Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.

Доказательств о. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α , касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α .

Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α . Значит, расстояние от центра сферы до плоскости α , равное длине перпендикуляра, проведённого из центра О на плоскость α , меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α . Теорема доказана. ▼

Справедлива обратная теорема.

Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.

Доказательств о. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M ). Теорема доказана. ▼

Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:

— диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;

— отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);

— произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R 2 – a 2 , где R — радиус шара, a — расстояние от центра шара до данной точки);

— если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a 2 – R 2 , где R — радиус шара, a — расстояние от центра шара до данной точки).

19.6. Вписанные и описанные шары и сферы

Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).

Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.

Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).

Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.

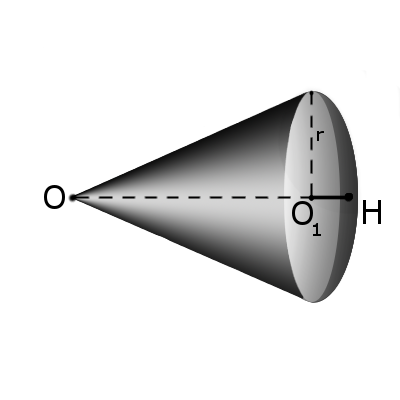
Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).

Конус при этом называют вписанным в шар.

Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.

Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.

Многогранник в таком случае называют описанным около шара (рис. 210).

Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.

При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением

V многогр = • r • S полн. поверх .

Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m • sin . Этой формулой часто пользуются при решении задач.

Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m • sin , где r — радиус шара, вписанного в многогранный угол, m — расстояние от центра шара до ребра многогранного угла, α — величина двугранного угла при этом ребре.

Если все плоские углы трёхгранного угла равны по 60 ° , то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3 r ; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r . Эти соотношения часто используют при решении задач, в которых рассматриваются те или иные комбинации шаров с правильными тетраэдрами или прямоугольными параллелепипедами.

Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211) . Многогранник при этом называют вписанным в шар.

Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.

Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.

Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.

Высота h пирамиды, радиус R к описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:

( R – h ) 2 + = R 2 .

Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.

В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен , где a — ребро куба.

19.7. Площади поверхностей шара и его частей

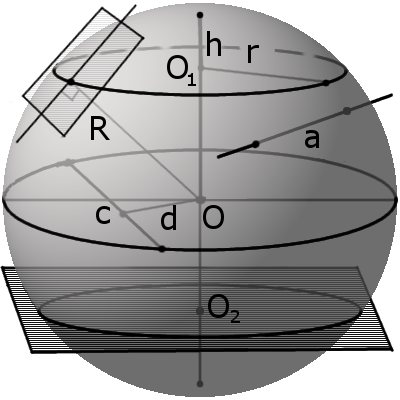
Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью : она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента ( сегментной поверхности ) .

Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя ( шарового пояса ).

Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA 1 D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA 1 — шаровой пояс.

Тело, образованное при вращении кругового сектора с углом ϕ ( ϕ ° ) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором .

Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а , б ) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г ).

На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).

Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.

а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф .

За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n- звенной ломаной линии, вписанной в полуокружность, при n → + ∞ ( число сторон неограниченно возрастает ).

Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).

При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь S i ( i = 1, 2, . n ) поверхности, образованной вращением любого звена, равна произведению 2 π , расстояния b i от середины звена до центра сферы и длины m i проекции этого звена на ось вращения, т. е. S i вращ = 2 π • b i • m i .

Так как ломаная — правильная, то все b i равны апофеме a n данной n- звенной ломаной, а m 1 + m 2 + m 3 + . + m n = 2 R и S 1 + S 2 + S 3 + . + S n = 4 π • a n • R . Причём a n = , где p n — периметр данной ломаной. Поскольку ограниченная переменная величина при n → + ∞ становится бесконечно малой, то при n → ∞ апофема a n стремится к радиусу R полуокружности.

Следовательно, предел площади поверхности Ф при n → ∞ равен 4 π R • R = 4 π R 2 . Этот предел и принимается за величину площади сферы радиуса R :

S сферы = 4 π R 2 .

б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:

S сегм. поверх = 2 π Rh ,

где h — высота сферического сегмента.

Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:

S шар. пояса = 2 π Rh ,

где h — высота шарового пояса.

Проделайте эти рассуждения самостоятельно.

в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б ) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г ).

Рассмотрим частный случай (см. рис. 213, а, б ). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R , и радиусом основания (докажите это) равна π R , а площадь сегментной поверхности равна 2 π Rh. Значит, для площади шарового сектора справедлива формула

S шар. сект = π R (2 h + ) .

 ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС , сторона которого равна 4. Известно также, что AS = BS = , a SC = 3. Найти площадь сферы, описанной около этой пирамиды.

Решени е. Решим эту задачу двумя методами.

Первый метод ( геометрич е ски й). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС ; точка Е — середина отрезка АВ (рис. 216).

Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.

Так как точка Е — середина отрезка АВ, то SE ⟂ АВ ( AS = BS ) и СЕ ⟂ АВ ( △ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ ( CSE ) , поэтому ( CSE ) ⟂ ( ABC ) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.

Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.

В правильном △ AВС имеем: CE = = 2 ; CD = СЕ = . Тогда CL = 2 CD = .

Далее △ BSE ( ∠ BES = 90 ° ): SE 2 = SB 2 – BE 2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):

cos C = = = ;

△ SLC (по теореме косинусов):

SL 2 = SC 2 + CL 2 – 2 SC • CL • cos C = ⇒ SL = .

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.

В треугольнике CSL имеем = 2 R. Так как в этом треугольнике cos C = , то sin C = = . Тогда R = = : = .

Находим площадь Q сферы:

Q = 4 π R 2 = 4 π • = π .

Второй метод ( коо р динатны й). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).

В этой системе координат вершины основания пирамиды имеют координаты: А (0; 0; 0), B (2; 2 ; 0), C (4; 0; 0).

Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = , CS = 3 .

AS 2 = x 2 + y 2 + z 2 = 19,
ВS 2 = ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19,
C S 2 = ( x – 4) 2 + y 2 + z 2 = 9.

Решая систему уравнений

x 2 + y 2 + z 2 = 19, ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19, ( x – 4) 2 + y 2 + z 2 = 9,

находим: х = , у = , z = .

Таким образом, вершина S имеет следующие координаты:

S .

Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA 2 = OB 2 = OC 2 = OS 2 = R 2 . Это соотношение в координатном виде равносильно системе уравнений

a 2 + b 2 + c 2 = R 2 , ( a – 2) 2 + ( b – 2 ) 2 + c 2 = R 2 , + + = R 2 , ( a – 4) 2 + b 2 + c 2 = R 2 .

Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = .

После вычитания третьего уравнения системы из первого её уравнения получаем:

= 0.

Подставив в это уравнение вместо a и b найденные их значения, получаем с = . Отсюда: R 2 = a 2 + b 2 + c 2 = 4 + + = . Тогда искомая площадь Q сферы равна:

Q = 4 π R 2 = π .

Ответ: π (кв. ед.).

19.8. Объёмы шара и его частей

Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2 R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а ). Объём этой фигуры равен разности объёма цилиндра с высотой 2 R , радиусом основания R и удвоенного объёма конуса высоты R , радиуса основания R :

V = π • R 2 • 2 R – 2 • π • R 2 • R = π • R 3 . (*)

Шар радиуса R (рис. 218, б ) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2 R . Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N , на рисунке не изображена.)

Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R ).

При х = 0 площади сечений обеих фигур равны π • R 2 ; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π • ( ) 2 = π • ( R 2 – x 2 ), а площадь сечения другой фигуры (ею является кольцо) равна π • R 2 – π • x 2 . Следовательно, площади равноудалённых от центра шара сечений рассматриваемых фигур равны (относятся, как 1 : 1). Поэтому на основании принципа Кавальери равны и объёмы этих тел. Тогда на основании (*):

V шара = • π • R 3 ,

гдe R — радиус шара.

Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h R ) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h , т. е.

V = π • h • R 2 – π • h • ( R 2 + R • ( R – h ) + ( R – h ) 2 ) =
= π • h 2 • (3 R – h ) .

При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2 R – h (рис. 220): V = π • R 3 – • π • (2 R – h ) 2 • (3 R – (2 R – h )) = π • h 2 (3 R – h ) , т. е. получаем ту же самую формулу. Подставляя в эту формулу h = R , получим V = π • R 2 (3 R – R ) = π • R 3 , что соответствует объёму полушара.

Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:

V шар. сегм = π • h 2 • (3 R – h ) ,

или в другом виде

V шар. сегм = π • h 2 • .

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/formula/sphere/

http://reader.lecta.rosuchebnik.ru/demo/8285/data/chapter20.xhtml

[/spoiler]

Источник

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

Инфоурок

07.11.2014

Геометрия

Видеоурок

51611

1003

АвторДата добавленияРазделПодразделПросмотровНомер материала

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

S = 4 π R 2 = π D 2

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x — x ₀) 2 + ( y — y ₀) 2 + ( z — z ₀) 2 = R 2

Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

Формула. Объём сегмента сферы с высотой h через радиус сферы R:

S = π R(2 h + √ 2 h R — h 2 )

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок №8. Сфера и шар

Перечень вопросов, рассматриваемых в теме:

что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
что такое шар и его элементы;
уравнение сферы;
формула для нахождения площади поверхности сферы;
взаимное расположение сферы и плоскости;
теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.

Глоссарий по теме:

Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.

Круг – это часть плоскости, ограниченная окружностью.

Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.

– уравнение сферы радиуса R и центром С(x₀; y₀; z₀).

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.

Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные теоретические факты

По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.

Рисунок 1 – Сфера с центром в точке О и радиусом R

Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.

Тело, ограниченное сферой, называется шаром.

Сферу можно получить ещё одним способом — вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.

2. Уравнение сферы

Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.

Пусть сфера имеет центром точку С (x₀; y₀; z₀) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:

МС=

Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС 2 =R 2 , то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x₀; y₀; z₀).

3. Взаимное расположение сферы и плоскости

Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.

1. Пусть dR. Если расстояние от центра сферы до плоскости меньше радиуса сферы, тогда сфера и плоскость пересекаются, и сечение сферы плоскостью есть окружность.

2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.

3. Пусть dR. Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

Рассмотрим случай касания более подробно.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.

Теорема (свойство касательной плоскости).

Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Теорема (признак касательной плоскости):

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.

4. Основные формулы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR 2 – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Примеры и разбор решения заданий тренировочного модуля

1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.

Площадь круга вычисляется по формуле: S_кр=πR 2 .

Площадь поверхности шара вычисляется по формуле: S_сф=4πR 2 . Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.

2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.

Площадь сферы равна S_сф=4πR 2 . То есть S_сф=100π.

По условию площадь круга некоторого радиуса r также равна 100π. Значит, r 2 =100, то есть r=10.

3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15

Окружность, вписанная в треугольник, является сечением сферы.

Найдем ее радиус.

Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

С другой стороны, S=p·r.

Теперь найдем расстояние от центра шара до секущей плоскости.

4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.

Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.

Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.

источники:

http://ru.onlinemschool.com/math/formula/sphere/

http://resh.edu.ru/subject/lesson/4034/conspect/

Источник

Время на прочтение
2 мин

Количество просмотров 17K

Мне очень понравился разбор задачи от 3Blue1Brown, выкладываю конспект для тех, кто любит изящные решения математических задач в читабельном виде.

Математическая олимпиада им. Уильяма Лоуэлла Патнема (William Lowell Putnam Mathematical Competition) — математическая олимпиада для студентов бакалавриата, обучающихся в университетах (колледжах) США и Канады. Вдохновителем олимпиады был Уильям Лоуэлл Патнем, американский юрист и банкир. Проводится Математической ассоциацией Америки ежегодно с 1938 года. Денежными призами награждаются пять лучших университетских команд (приз $25 000 за первое место) и двадцать пять студентов, лучших в личном зачете (приз $1000 за первое место).
— Википедия

Длится олимпиада два раза по 3 часа, всего 12 задач по 10 баллов за каждую. Средний балл, который набирают студенты — 1 или 2. Рассмотрим одну из самых сложных задач из этой олимпиады.

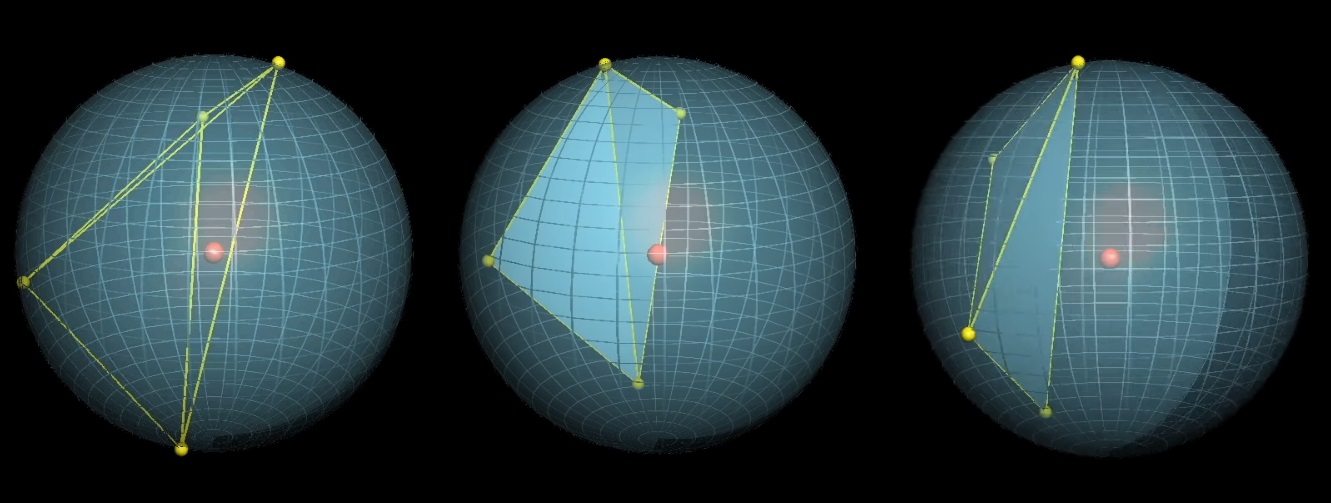
Выберем 4 случайные точки на сфере. Какова вероятность что центр сферы будет внутри тетраэдра, образованного этими точками?

Рассмотрим двумерный вариант этой задачи.

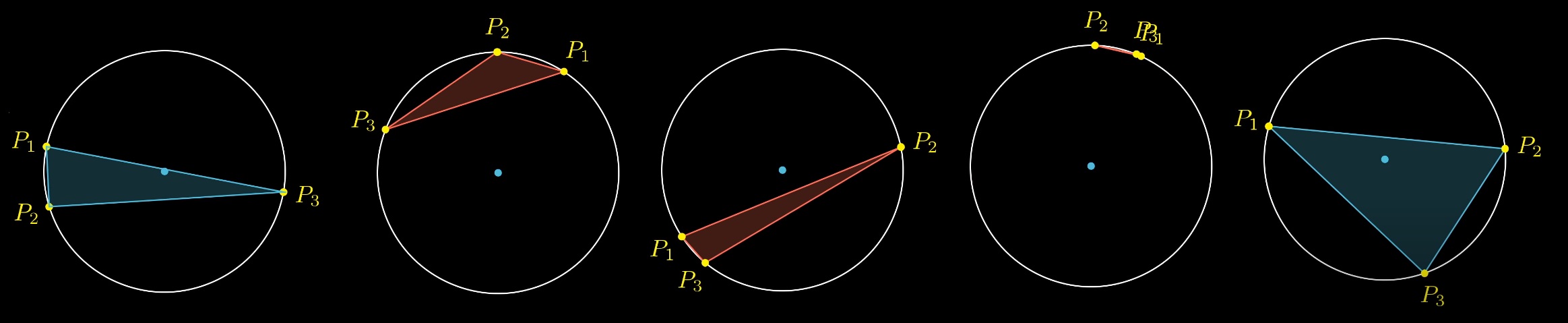
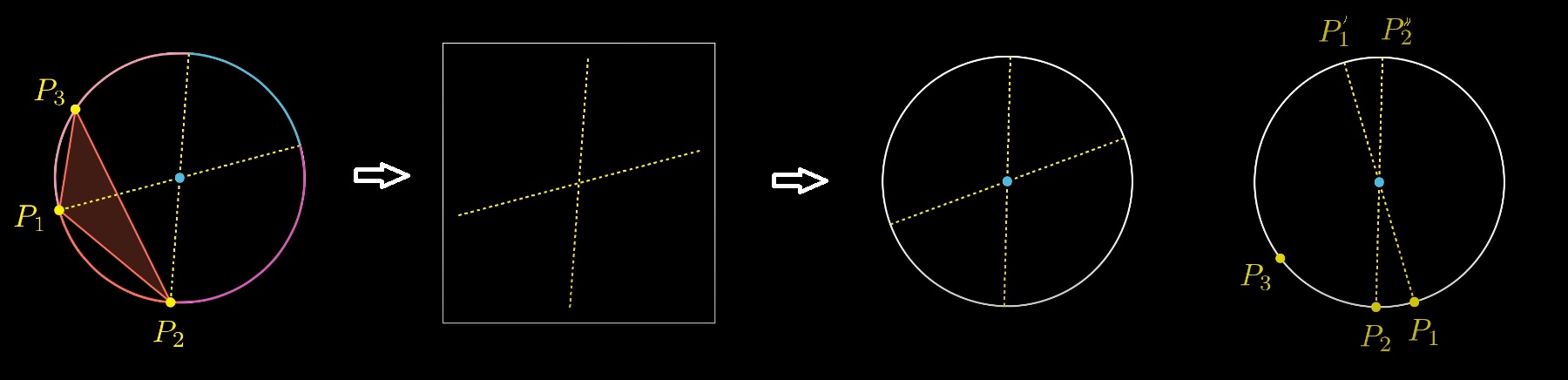
Рассмотрим 3 случайные точки на окружности. Какова вероятность, что центр окружности будет внутри треугольника?

Можно закрепить две точки и поиграться с третьей. Легко заметить, что есть определенная зона, проекции закрепленных точек относительно центра, внутрь которой должна попасть третья точка, чтобы выполнилось условие. Окружность тем самым разделяется на 4 части. Вероятность попадания третей точки в дугу, равна отношению длины дуги к длине окружности. Какова длина дуги?

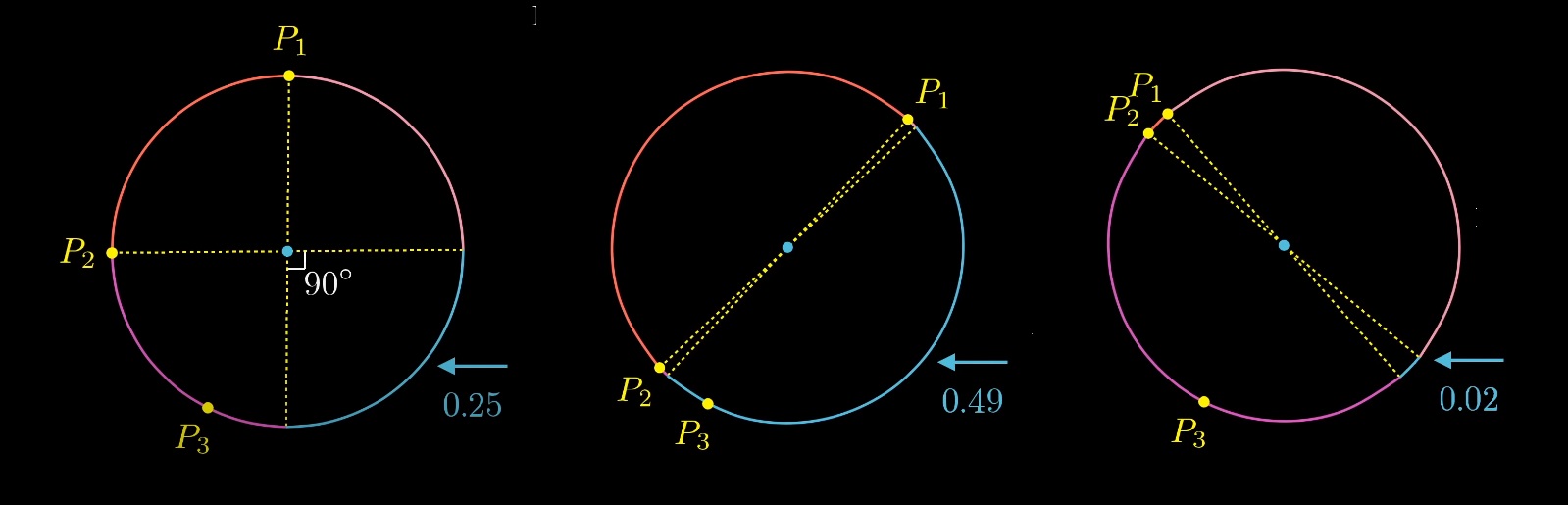
Вероятность колеблется от 0 до 0,5 в зависимости от расположения первых двух точек.

Какова средняя вероятность?

Зафиксируем первую точку и поиграемся со второй. Вероятность будет меняться от 0 до 0,5, то есть средняя вероятность будет 0,25.

Решение задачи для окружности и трёх точек — 25%.

Можно ли перенести такой подход на сферу и 4 точки?

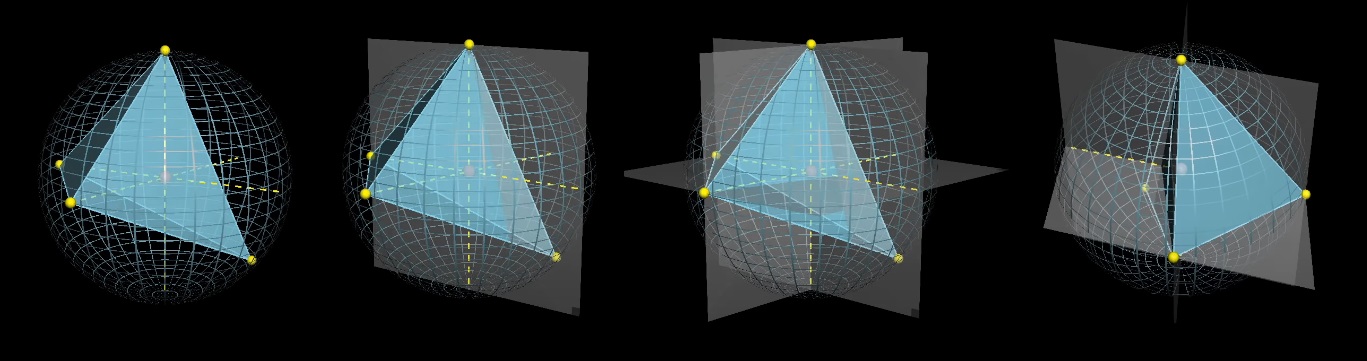
Фиксируем три точки и играем с четвертой. Нарисуем проекции фиксированных точек относительно центра и плоскостями разделим сферу на 8 частей.

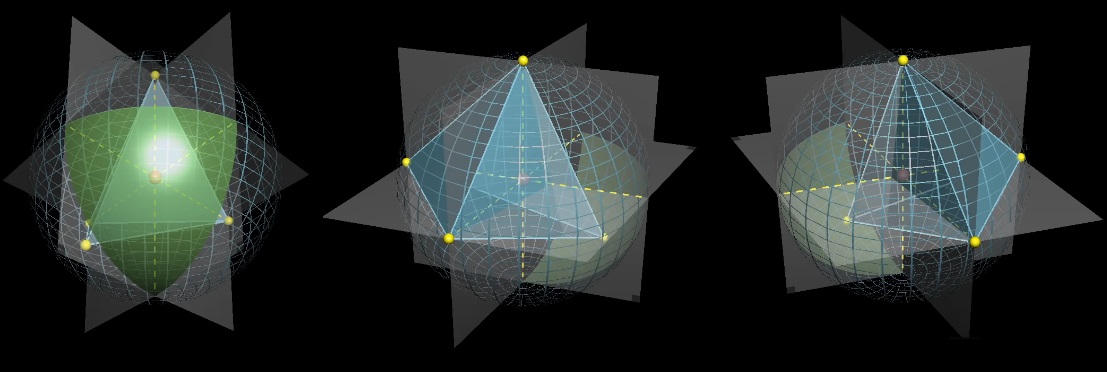
Центр сферы будет находиться внутри тетраэдра, если четвертая точка попадает на зеленый сферический треугольник, который находится «напротив» зафиксированных точек относительно центра. Каков средний размер зеленой секции?

//Дальше не придумали, импровизируй.

Можно вернуться к двумерному случаю и подумать откуда взялась 1/4. Откуда 4?

Можно перейти от 3 случайных точек на окружности к другой задаче. Выберем два случайных диаметра. Потом для каждого диаметра бросим монетку, выбирая тем самым, где будет точка Pi, с какого конца диаметра. Потом случайно выберем третью точку на окружности.

А потом еще хитрый ход.

Давайте сначала выберем случайным образом третью точку, а потом случайно выберем два диаметра. У нас будет 4 варианта размещения точек P2 P1:

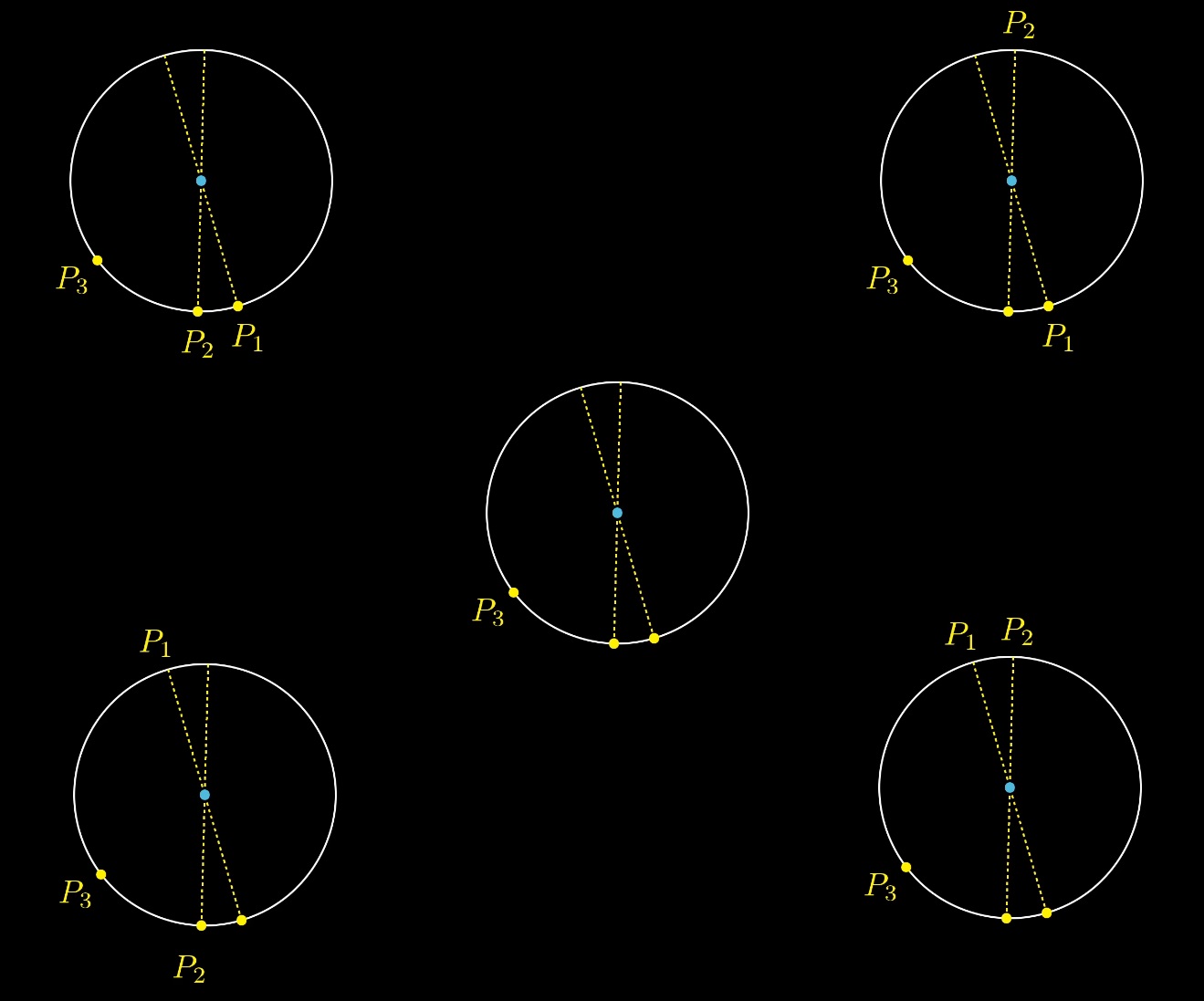
Но только один из этих 4 вариантов содержит решение, когда центр окружности внутри треугольника:

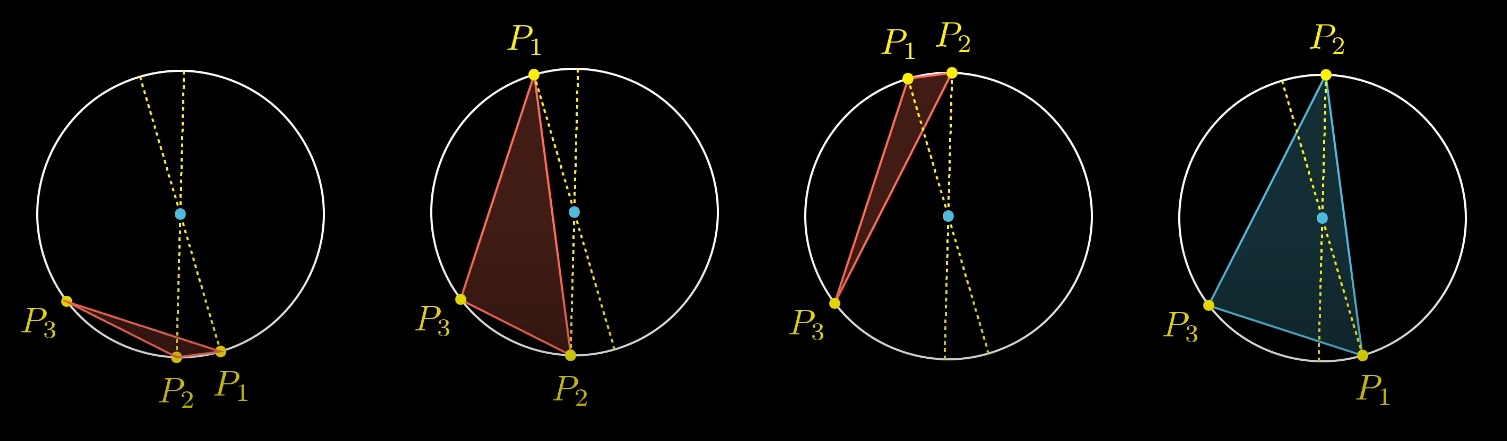
Какую бы мы ни выбирали рандомную начальную позицию третей точки и двух диаметров, только один из вариантов содержит центр окружности внутри треугольника:

То как мы переформулировали задачу:

Со сферой получается 8 вариантов выбора точек, после того, как зафиксирована первая точка и выбраны три диаметра:

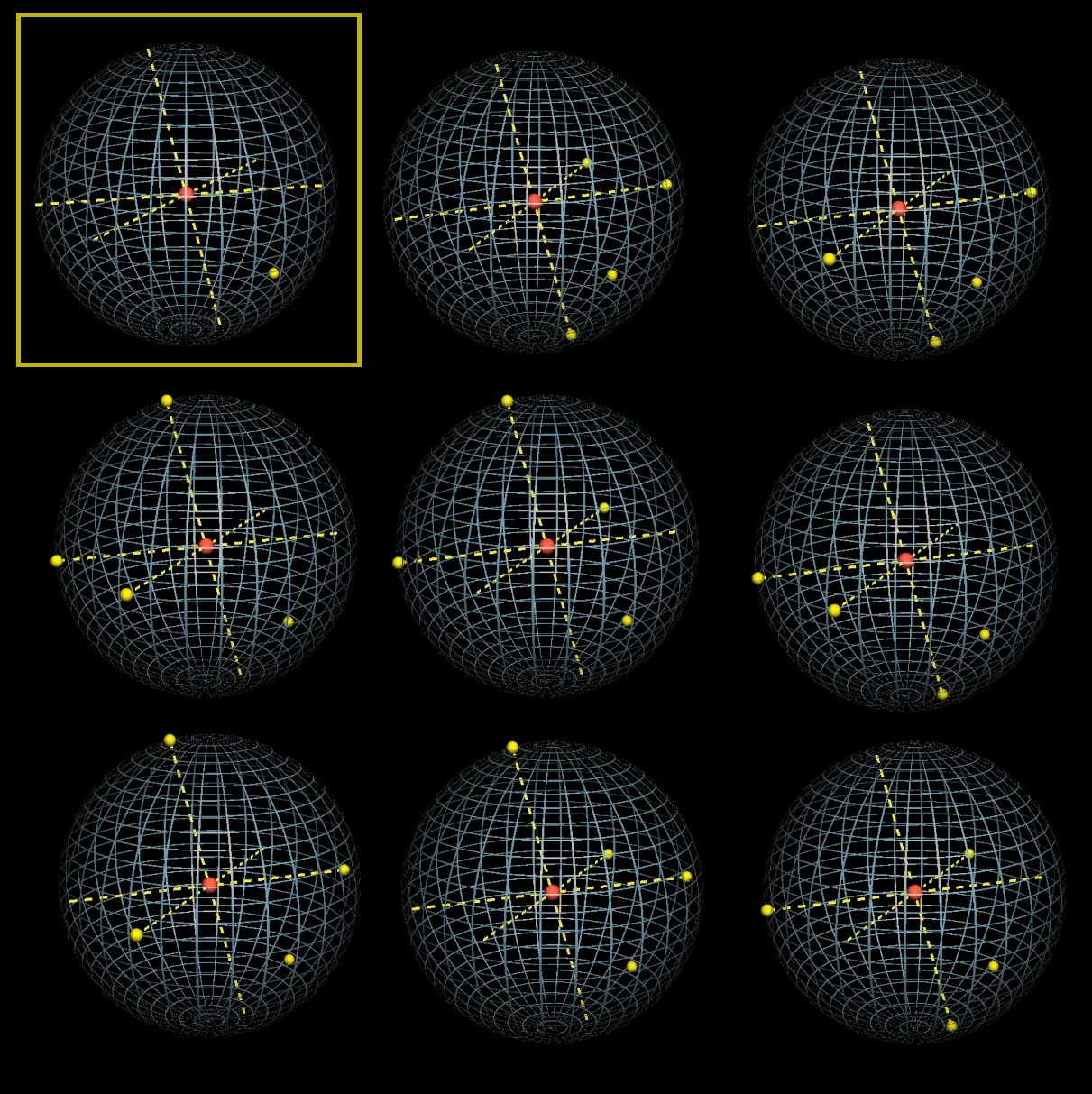
Только 1 из 8 удовлетворяет условию, что центр сферы внутри тетраэдра:

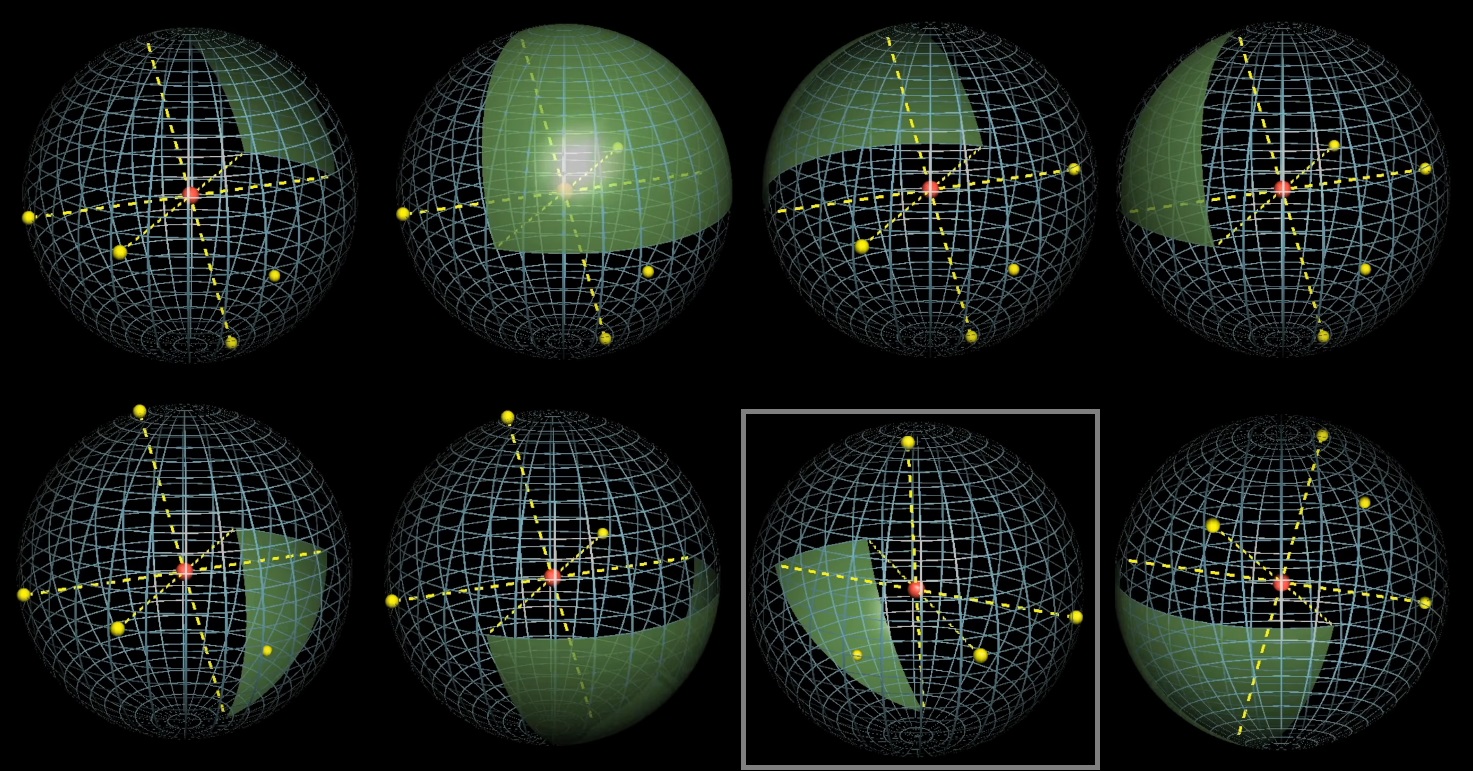
Ответ: 1/8

Хардкорная линейная алгебра здесь: Capturing the Origin with Random Points: Generalizations of a Putnam Problem
Все задачи олимпиады 1992 года: The 53rd William Lowell Putnam Mathematical Competition
Saturday, December 5, 1992

Источник

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

Государственное образовательное учреждение
высшего

Профессионального образования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ

ОБЛАСТНОЙ УНИВЕРСИТЕТ (МГОУ)

Кафедра высшей алгебры, элементарной
математики и методики преподавания математики

Основы структур алгебры

тема: Элементы сферической геометрии

Выполнила

Луценко Евгения Сергеевна

Научный руководитель:

Кандидат педагогических наук

Федяев Олег Ипполитович

Москва

2015

Содержание

Введение

1.Основные
понятия сферической геометрии…………………..4-9

2.Сферическии
треугольник……………………………………..9-13

3.Сферическая
теорема синусов…………………………………13-15

4.Сферическая
теорема косинусов………………………………16-19

5.Решение
сферических треугольников…………………………19-22

6.Примеры решения задач………………………………….22-25

Заключение……………………………………………………26

Список
литературы ………………………………………………..27

Введение

В настоящее время,
существуют различные науки, в основе которых лежит сферическая геометрия.
Например, значительный раздел математической картографии —
картометрия, которая позволяет по данным карты измерять расстояния, углы и
площади на реальной поверхности Земли.

В программе школьного курса геометрии изучению сферы отводится очень
мало времени, при этом рассматриваются только основные понятия, и совсем не
уделяется внимание фигурам на сфере.

Еще
древние греки считали окружность (круг) и сферу (шар) идеальными формами. Форму шара имеет наша планета и большинство космических тел. А так как
планеты, Солнце, Луна и звёзды движутся по воображаемой «небесной сфере», то
естественно, для изучения их движения потребовалось знание геометрии сферы.

Курсовая работа состоит из двух
частей: в первой приводится общая теория о сфере, понятие сферического
треугольника, сферические теоремы синусов и косинусов, двойственная теорема
косинусов.

Во второй части работы я рассмотрела решения задач на
применение рассмотренных теорем, а также задачи практического характера.

Теоретический материал представлен в форме
доступной для понимания учащимися старших классов, подобраны и решены задачи по
сферической геометрии.

Основные
понятия сферической геометрии

Сфера, большая и малая окружности.

Сферой
называется геометрическое место точек пространства, расположенных на данном
расстоянии от данной точки, называемой её центром.

Отрезок, соединяющий центр сферы с какой-либо его точкой,
называется радиусом сферы.

Отрезок, соединяющий две точки сферы и проходящий, кроме
того, через его центр, называется диаметром. Из определения следует, что
все радиусы равны и что диаметр равен удвоенному радиусу.

Плоскость, проходящая через центр сферы, называется диаметральной
плоскостью.

В этом случае окружность на сфере и называется большой
окружностью. В геометрии на сфере большие окружности играют роль прямых на
плоскости.

Так как через всякие три точки пространства, не лежащие на
одной прямой, проходит единственная плоскость, то через всякие две точки
сферы, не являющиеся диаметрально противоположными, проходит единственная
большая окружность (рис.1). Этот факт вполне аналогичен тому, что на
плоскости через всякие две точки проходит единственная прямая. Через две
диаметрально противоположные точки сферы, напротив, можно провести бесконечное
множество больших окружностей (рис.2).

Так как всякие две диаметральные плоскости сферы
пересекаются по её диаметру, то всякие две большие окружности пересекаются в
двух диаметрально противоположных точках сферы (рис.4). Здесь наблюдается
отличие сферической геометрии от плоской геометрии, в которой две прямые
пересекаются не более чем в одной точке.

Рис
1 Рис 2

-Так как плоскость делит пространство
на две области, то большая окружность делит сферу на две области; эти
области называются полусферами, а сама окружность – краем этих
полусфер.

– Так как две пересекающееся плоскости
делят пространство на четыре области, то две большие окружности делят сферу
на четыре области (рис.3).

-Так как три плоскости, пересекающиеся в одной точке, делят
пространство на восемь областей, то три большие окружности, не
пересекающиеся в одной точке,

делят сферу на восемь областей
(на рис.4)

Рис
3 Рис 4.

Если первые два из этих свойств
аналогичны свойствам прямых на плоскости, которая делится на две области прямой
и на четыре области двумя пересекающимися прямыми, то третье из указанных
свойств не вполне аналогично соответствующему свойству прямых на плоскости, так
как три попарно пересекающиеся прямые, не проходящие все три через одну точку,
делят плоскость не на восемь, а на семь частей (рис.5).

Рис 5.

Сферический отрезок, соединяющий две
точки на сфере– кратчайшая из двух дуг большой окружности (АВ), проходящей через
две не диаметрально противоположные точки A и В сферы.

Если две точки сферы А и В не являются диаметрально
противоположными, то существует единственная плоскость, проходящая через центр
сферы и эти две точки. Линия пересечения этой плоскости со сферой есть большая
окружность, а меньшую из двух дуг этой окружности, соединяющий точки А и В,
является единственным сферическим отрезком, соединяющим точки А и В.

Если точки А и В диаметрально противоположны на сфере,
существует бесконечное число больших окружностей, проходящих через эти две
точки, причем эти две точки делят каждую такую большую окружность на две
полуокружности, которые являются сферическими отрезками, соединяющими точки А и
В (рис.6).

Рис.6

Сферический
отрезок обладает замечательным минимальным свойством (как и отрезок на
плоскости).

Теорема (минимальное свойство сферического
отрезка).

Сферический
отрезок, соединяющий две точки на сфере, короче любой другой линии на сфере,
соединяющий эти две точки (рис.7).

Рис.7

Угол на сфере

Величина внутреннего угла при
вершине В сферического многоугольника, образованного дугами АВ и ВС на сфере,
определяется как угол между двумя лучами, которые выходят из точки В и касаются
дуг АВ и ВС в точке В. Поскольку эти лучи перпендикулярны радиусу ОВ, то угол
при вершине В равен двугранному углу между плоскостями ОАВ и ОВС. Понятно, что
два угла сферического двуугольника всегда равны (рис.8).

рис.8

Многоугольники на сфере

Сферическим многоугольником называется часть
сферы, ограниченная дугами больших окружностей, меньшими полуокружности,
концами которых служат точки пересечения этих больших окружностей, взятых в
последовательном порядке.

Сферический многоугольник называется выпуклым, если
он расположен по одну сторону от каждого из больших кругов, частью которых
служат его стороны; в противном случае он называется вогнутым.

В случае, когда многоугольник выпуклый каждый большой круг,
частью которого служит сторона многоугольника, делит сферу на две полусферы, из
которых одна содержит весь многоугольник; общая область R всех таких полусфер,
содержащих данный многоугольник, и будет внутренней областью многоугольника
(рис 9, 10).

Сферический
двуугольник-фигура,образованная двумя полуокружностями
больших кругов сферы, исходящими из диаметрально противоположных точек

В отличие от плоскости, где треугольник является
многоугольником с наименьшим числом сторон, на сфере имеются многоугольники с
числом сторон меньше трех- двуугольники. Двуугольником является часть сферы,
ограниченная двумя половинами больших окружностей с общими концами; эти общие
концы, называемые вершинами двуугольника, являются диаметрально
противоположными точками сферы.

Сферический треугольник

Сферическим треугольником называется фигура,
состоящая из трех точек сферы и трех отрезков, попарно соединяющей эти точки.
Здесь под отрезками понимаем меньшую из двух дуг большой окружности, проходящей
через эти точки.

Пусть ABC – сферический треугольник, – радиус векторы
вершин.(рис.12) Обозначим дуги , соответственно через с, b, а.

Углом между дугами понимают угол между их
касательными векторами. Обозначим – угол между дугами и , – угол между и , – между

Три больших
окружности, пересекаясь попарно в двух точках, образуют на сфере восемь
сферических треугольников. Зная элементы (стороны и углы) одного из них

можно
определить элементы всех остальных, поэтому рассматривают соотношение между
элементами одного из них, того, у которого все стороны меньше половины большой
окружности.(рис.13)

Многие свойства сферического треугольника (а оно
одновременно являются и свойствами трехгранных углов) почти полностью повторяют
свойства обычного треугольника, среди них- неравенство треугольника или,
например, три признака равенства треугольника. Все планиметрические следствия
упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере.

Сумма углов всякого сферического треугольника всегда больше
180 . Разность (измеряется в радианах) – величина положительная и называется сферическим
избытком данного сферического треугольника.

Равнобедренные сферические треугольники

Сферический треугольник называется равнобедренным, если две его стороны
равны.

Всякий сферический треугольник, наложимый на треугольник, ему
симметричный, – равнобедренный.

Действительно, в силу того, что оба треугольника имеют противоположное
расположение, невозможно наложить один треугольник на другой так, чтобы
совпадали соответственные вершины, т.е. вершины, находящиеся первоначально на
концах одного диаметра; если бы среди сторон треугольника не было равных между
собой, то такое наложение было бы невозможно и ни каким другим образом.

Обратно, всякий равнобедренный сферический треугольник
наложим на треугольник, ему симметричный.

Если треугольник А’В’С’ симметричен треугольнику АВС и если
АВ равно АС, то два треугольника АВС и А’С’В’, имеющие (при выбранном порядке
вершин каждого из них) одно и тоже расположение, равны по второму признаку
равенства.

Теорема. В равнобедренном
сферическом треугольнике углы, противолежащие равным сторонам, равны.

Действительно, при совмещении треугольника АВС (АВ=АС) с
симметричным ему треугольником А’С’В’ угол, совпадающий с углом В’, есть угол
С’; таким образом, оба эти угла равны, и тоже самое имеет место и для углов С и
В’.

Обратно, всякий сферический треугольник, два угла
которого равны, равнобедренный.

Действительно, если АВС сферический треугольник, в которомÐВ=ÐС и треугольник А’В’С’
– треугольник, ему симметричный, то треугольники АВС и А’С’В’, имеющие
одинаковое расположение равны по первому признаку равенства, и, следовательно,
АВ=А’С’=АС.

Площадь сферического треугольника

Будем называть площадью сферической
фигуры, по аналогии с площадью плоской фигуры, действительное число,
удовлетворяющее следующим четырём требованиям:

1)
площадь сферической фигуры является
положительным числом, (свойство позитивности),

2)
площадь сферической фигуры не изменяется при
движении (свойство инвариантности),

3)
если сферическая фигура разложена на две
сферические фигуры, то площадь данной фигуры равна сумме площадей двух фигур,
на которые она разложена (свойство аддитивности),

4)
Площадь всей сферы радиуса R равна 4pR² (свойство нормировки).

.Сферическая теорема синусов

Теорема.
Синусы сторон сферического треугольника относятся как синусы противолежащих
углов.

Пусть
длины сторон сферического треугольника (рис. 14) равны а, b, с, а
противолежащие им углы этого треугольника равны А, В, С соответственно, r-
радиус сферы, тогда

рис.15 рис.16

Доказательство:
В сферическом треугольнике ABC проведем высоту
СН — дугу большой окружности, перпендикулярную большой окружности АВ (рис.
15). Длине высоты |СН|_sотвечает величина угла СОH: если , то |CH|_s=Rφ. Это
наводит на следующее построение для соответствующего трехгранного угла ОАВС. Возьмем
на ребре ОС произвольную точку C₁ и
проведем из нее перпендикуляры С₁А₁ к (ОA), С₁В₁к
(ОB)
и С₁Н₁к плоскости ОАВ (рис. 16); мы опять рассматриваем
случай острых углов α, β, . По
теореме о трех перпендикулярах (H₁A₁)(OA), (H₁B₁)(OB), поэтому
углы C₁A₁H₁и C₁B₁H₁будут линейными углами соответствующих двугранных
углов:. Из
прямоугольных треугольников OA₁C₁и С₁Н₁А₁,
обозначив |OC₁|=z, находим:

(1.1)

Аналогично
из прямоугольных треугольников ОВ₁С₁и C₁H₁B₁

(1.2)

Приравнивая
правые части равенств (1.1) и (1.2), получим:

откуда

Точно так же
доказывается, что

Получающиеся в итоге
формулы

и
составляют содержание теоремы синусов для сферических треугольников или
трехгранных углов.

Сферическая теорема косинусов:

(1.4)

Доказательство
проведём с помощью проекций. На рисунке показан сферический треугольник ABC
на сфере радиуса R с центром в точке O. BP — перпендикуляр
к плоскости большого круга, проходящего через сторону b, BM —
перпендикуляр к OC, BN — перпендикуляр к OA. По
утверждению, обратному теореме о трёх перпендикулярах, PM
— перпендикуляр к OC, PN — перпендикуляр к OA. Заметим,
что угол PMB равен π – C,кроме того,ON = Rcosc и OM = R
cos a. Далее, проецируем ломаную OMPN на прямую, содержащую ON.

$mbox{pr } MP = PM cos (pi - (frac {pi}{2} - angle MPN)) = PM (- sin angle MPN),$

Подставляем три
последних выражения и указанное выше выражение ON = R cos c в первое выражение
и получаем:

Теоремы косинусов для
двух других сторон, то есть теорему для cos a и теорему для cos b, получаем
аналогично, их также можно получить сразу из формулы для стороны c при помощи
круговой перестановки букв:

Теоремы косинусов для сферического треугольника со сторонами a, b, c и
углами A, B, C имеют следующий вид:

Эти две теоремы двойственны
по отношению друг к другу, поскольку углы и стороны всякого сферического
треугольника дополняются до развёрнутого угла сторонами и углами
соответствующего полярного
треугольника.

Следствие.

Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:

Сформулируем и докажем двойственную
теорему косинусов:

(1.7)

Запишем
для полярного треугольника A’B’C’ теорему косинусов

С
учетом формул (1.6), получим (1.7).

Заметим, что внешне формулы косинусов на плоскости
и на сфере непохожи. С другой стороны, на маленьких участках сферу можно
считать «почти плоской», тогда (т. е. при малых по сравнению с радиусом R сферы длинах сторон сферического треугольника ABC) сферическая теорема косинусов должна «почти
перейти» в планиметрическую, и то же самое для теоремы синусов. Проверим, так
ли это.

Длины сторон а, b, сферического треугольника ABC связаны с соответствующими плоскими углами α, β, γ
трехгранного угла ОАВС формулами

поэтому
рассматриваемый случай (а, b, с много
меньше, чем R) отвечает тому,
что α0, β0, γ0. Вспомним, что при малых φ значение sinφ приближенно
равно φ:

Отсюда можно вывести
аналогичную приближенную формулу для соsφ при малых φ:

Подставляя
соответствующие приближения в формулы синусов и косинусов (формулы (6) и (3)),
получим приближенные формулы для малых сферических треугольников:

откуда

(отбросила в
предпоследнем соотношении слагаемое четвертой степени , поскольку оно мало по сравнению со слагаемыми
второй степени — ). Подставляя в полученные формулы , действительно получаются обычные теоремы синусов
и косинусов.

Решение сферических
треугольников

Выведенные
тригонометрические соотношения позволяют «решить сферический треугольник» по любым трем из его элементов (сторон и
углов).

1. Даны три
стороны сферического треугольника. Найти углы треугольника.

Решение: по формуле, выражающей теорему косинусов, находим

и аналогично находим соsВ и соs С.

2. Даны две стороны сферического треугольника и угол между ними, например стороны b,
с и угол А. Найти остальные элементы треугольника. Решение: сторону
а найдем из
теоремы косинусов. Зная все три стороны сферического треугольника, найдем его
остальные углы, как указано выше.

3. Даны две стороны сферического треугольника и угол, лежащий против одной из них,
например стороны а, b и угол A. . Найти остальные элементы треугольника.

Решение: по теореме синусов находим

Заметим, что эта формула даёт для В два значения,
дополняющих друг
друга доp; это
соответствует тому, что в общем случае два сферических треугольника с двумя соответственно
равными сторонами
и равными углами, лежащими против одной из этих сторон, не обязательно равны, а возможен
случай, когда углы этих треугольников, лежащих против другой стороны, дополняют друг друга
до p.

Для
определения стороны с и угла С проведём через вершину С дугу большой окружности
АВ. Если эти большие окружности
пересекаются в точке D, то рассмотрим прямоугольные сферические треугольники АСD
и ВСD (рис.
19). В этих треугольниках известны гипотенузы b и а и углы при вершинах Аи В. Второй
катет каждого из этих треугольников определяется по первым формулам тангенсов, а угол при вершине С определится
по формуле котангенсов.

Рис.19

Сторона
с и угол C
сферического
треугольника АВС являются суммами найденных сторон или углов прямоугольных треугольников, если точка D лежит на
стороне АВ, и разностям и этих сторон или углов, если точка D лежит на продолжении стороны АВ.
Именно, если
оба угла A,В в исходном треугольнике АВС являются острыми или оба тупыми, то
перпендикулярная к АВ окружность, проходящая через точку C, пересекает окружность АВ в
двух точках, одна из которых лежит на дуге АВ; эту точку и следует принять за D в рассматриваемом
случае. Таким образом, углы при вершинах Аи В в прямоугольных треугольниках АСD
и ВСD совпадают с углами А и В исходного треугольника
АВС, а сторона с и угол С треугольника АВС являются суммами
найденных нами сторон
или углов прямоугольных треугольников АСD и ВСD. Если же в треугольнике АВС один
из углов A, В острый, а второй—тупой, то перпендикулярная к АВ окружность,
проходящая через точку С, пересекает окружность АВ в двух точках, ни одна из которых не лежит на дуге АВ. В этом случае за D можно принять

Любую из этих точек, например ту, которая лежит на продолжении стороны АВ за точку В(рис. 20).

Рис. 20

Таким образом, угол при вершине А в ∆АСD равен углу А треугольника АВС,
а угол при вершине В в ∆ВСD
равен p — В. При этом сторона с и угол С треугольника АВС являются
разностями сторон АD, ВD или углов
при вершине С треугольников АСD и ВСD. Наконец, если один из углов A, В (например, А) прямой,
то треугольник АВС прямоугольный,
и для нахождения стороны с и угла С можно в атом случае воспользоваться формулами ,.

4. Даны три угла сферического треугольника. . Найти остальные элементы треугольника.

Решение: по формуле двойственной теоремы косинусов
находим

и аналогично находим и
.

5. Даны два угла сферического треугольника и сторона между ними, например сторона а
и углы B и C.
. Найти
остальные элементы треугольника.

Решение: угол А найдем по формуле двойственной теоремы
косинусов. Зная все три угла сферического треугольника, найдем его остальные стороны, как указано выше.

6. Даны два угла сферического треугольника и сторона, лежащая против
одного из них, например углы А и В и сторона а. . Найти остальные
элементы треугольника.

Решение: по теореме синусов находим

Заметим, что эта формула дает для b два значения, дополняющих друг друга до pr; это соответствует тому, что
в общем случае
два сферических треугольника с двумя соответственно равными углами и равными сторонами,
лежащими против одного из этих углов, не обязательно равны, а возможен случай, когда стороны
этих треугольников,
лежащие против другого угла, дополняют друг друга до pr. Сторону с и угол С по углам А,
В и сторонам а,
b найдем, как указано выше.

Примеры решения задач

Определение метра и морской мили

·
R=6367 км – радиус Земного шара.

·
Длина большой окружности Земли

·
L=2πR

·
L=2·3,1416·6367=40000 км.

·
Один метр – одна 40- миллионная часть длины
земного экватора.

·
Морская миля равна одной угловой минуте на
земном меридиане.

·
В 60·360=21600 раз короче длины большой
окружности земного шара.

·
1 морская миля равна 40000000м:21600=1852м

·
Длина
земного экватора равна ровно 21600 морских миль

Задача1.Мореплаватель Христофор Колумб проплыл 1800
миль в одном направлении из точки А к точке В, повернул на 60 градусов и
проплыл в новом направлении еще 2700
миль, оказался в точке С. Требуется найти расстояние между точками А и С (по
поверхности земного шара).

Решение:Обозначим
через a, b и с длины дуг ВС, АС и АВ соответственно, y — внутренний угол при вершине
В сферического треугольника АВС. Тогда,

где
R= — радиус земного шара, выраженный в морских милях.По теореме косинусов
для сферического треугольника

По
таблицам или с помощью калькулятора находим, что

радиан.

Следовательно,
длина дуги АС= b равна b = R*0.90662 = 3437.4*0.906623116.7 миль.

Ответ:
3117 морских миль 5772 км.

Задача 2. Вывести формулу длины ортодромии — кратчайшего расстояния между точками на земной
поверхности с известными координатами (в предположении сферичности Земли).

Решение:Обозначим географические широты двух данных точек и , разность долгот — $Deltalambda_{AB},$ , кратчайшее расстояние между ними обозначим d, длину дуги в 1
градус — a.(см.рис.) Тогда формула длины ортодромии:

$cosleft (frac{d}{a}right)=sinvarphi_Acdotsinvarphi_B+cosvarphi_Acdotcosvarphi_BcdotcosDeltalambda_{AB}$

Эта формула сразу получается применением теоремы косинусов
к стороне AB сферического треугольника P_nAB. Подобная формула справедлива для любой
сферической поверхности и поэтому её можно применять также для определения
углового расстояния между звёздами по известным их экваториальным координатам

Задача 3. Определить угловое расстояние между двумя светилами на небесной сфере
.

Решение: Определим
угловое расстояние (x) между звездой δ
Цефея (экваториальные координаты: α₁=22ч
29м, δ₁=+58° 25′) и галактикой Туманность Андромеды (α₂=0ч 43м, δ₂=+41°
16′) на небесной сфере. Выражаем α₁ в градусах и долях градуса:

$alpha_1 = left (22+frac{29}{60}right )cdotfrac{360}{24}=337^circ,25$

Аналогично получаем,
что α₂=10°,75. Выражаем δ₁ в градусах и долях градуса:

$delta_1 = 58+frac{25}{60}=58^circ,42$

Аналогично δ₂=41°,27.
Применяем теорему косинусов:

$begin{align} cos x & = cos(90^circ-delta_1)cdotcos(90^circ-delta_2)+sin(90^circ-delta_1)cdotsin(90^circ-delta_2)cdotcos(alpha_1-alpha_2)\ & =sin 58^circ,42cdotsin 41^circ,27+cos 58^circ,42cdotcos 41^circ,27cdotcos (337^circ,25-10^circ,75)\ &=0,89 end{align}$

Отсюда x=27°,11.

Заключение

В
данной курсовой работе я познакомилась со сферической геометрией, которая
изучает геометрические образы, находящиеся на сфере, подобно тому, как
планиметрия изучает геометрические образы, находящиеся на плоскости. Я
рассмотрела основные понятия, установила соответствие между сферической
геометрией и планиметрией. А также рассмотрела практические задачи, необходимые
мореплавателям, летчикам и космонавтам. В настоящее время сферическая геометрия
особенно широкое применение находит в астрономии и геодезии (науке о форме и
размерах Земли), навигации и картографии.

Одной из важнейших
астрономических задач, без которой невозможно решение всех остальных задач
астрономии, является определение положения небесного светила на небесной сфере.

Многие важные открытия, как в
прошлом, так и сегодня были бы невозможными без упорного, тяжелого и часто
незаметного труда ученых, посвятивших свою жизнь определению небесных координат
светил.

Без результатов
20-летнего труда Тихо Браге, этого искусного измерителя координат планет,
Иоганн Кеплер не смог бы открыть законы движения планет вокруг Солнца. Точные
определения положения светил на небесной сфере позволили установить, в
частности, место малых планет и комет в Солнечной системе, открыть Нептун и
Плутон. Методы определения координат небесных светил (их видимых положений на
небе) разрабатывались на протяжении свыше двух тысячелетий. Сегодня они
составляют один из важнейших разделов астрономии, который называется
астрометрией.

Список литературы

Избранные вопросы математики: 10 Кл. Факультативный курс/А.М.
Абрамов, Н.Я. Виленкин, Г.В. Дорофеев и др.; Сост.: С.И. Шварцбурд.- М.:
Просвещение, 1980. – 191 с.
Атаносян Л.С. Геометрия. Часть 2. – М.: Просвещение, 1974.
Энциклопедия элементарной математики, книга IV, V. Геометрия. – М.: Наука, 1966. – 624 с.
Адамар
Ж. Элементарная геометрия. Ч.2. М. Учпедгиз, 1958. Андреев
Базылев
В.Т. Геометрия. М: Просвещение, 1975.
Базылев
В.Т. Сборник задач по геометрии. М: Просвещение, 1980. -240с.
Егоров
И.П. Основания геометрии. – М: Просвещение, 1984. – 144с.
Розенфельд
Б.А. История неевклидовой геометрии. Развитие понятия о геометрическом
пространстве. М. Наука., 1976. – 408с.
Энциклопедия
элементарной математики. Кн.4 – Геометрия. М., 1963.
www.allbest.ru/referat
http://ru.wikipedia.org

Источник

Координаты на сфере

Координаты на сфере

Урок «Сфера. Уравнение сферы»

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Уравнение сферы

Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

Касательная, касательная плоскость к сфере и их свойства

Координаты центра сферы через уравнение

Урок «Сфера. Уравнение сферы»

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Уравнение сферы

Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

Касательная, касательная плоскость к сфере и их свойства

Геометрия. 11 класс

Конспект урока

Основные понятия сферической геометрии

Сфера, большая и малая окружности.

Сферой называется геометрическое место точек пространства, расположенных на данном расстоянии от данной точки, называемой её центром.

Угол на сфере

Многоугольники на сфере

Равнобедренные сферические треугольники

Площадь сферического треугольника

.Сферическая теорема синусов

Решение сферических треугольников

Вам также может понравиться

Msedge exe bad image как исправить

Как составить фин модель предприятия

Как составить схему по технике безопасности

Добавить комментарий Отменить ответ

Основные
понятия сферической геометрии

Сферой
называется геометрическое место точек пространства, расположенных на данном
расстоянии от данной точки, называемой её центром.

Решение сферических
треугольников