Содержание
- Как найти площадь прямоугольника – 9 способов с формулами и примерами
- По диагонали и стороне
- По стороне и диаметру описанной окружности
- По радиусу описанной окружности и стороне
- По стороне и периметру – 1 способ
- По стороне и периметру – 2 способ
- По диагонали и углу между диагоналями
- По радиусу описанной окружности и углу между диагоналями – первый способ
- По радиусу описанной окружности и углу между диагоналями – второй способ
- Математика. 3 класс
- Конспект урока математики в 3 классе по теме «Площадь прямоугольника»
Как найти площадь прямоугольника – 9 способов с формулами и примерами
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
По стороне и периметру – 2 способ
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
Источник
Математика. 3 класс
Конспект урока
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см 2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
Источник
Конспект урока математики в 3 классе по теме «Площадь прямоугольника»
Урок математики в 3 классе
Тема: «Площадь прямоугольника»
Обеспечить усвоение детьми способа нахождения площади прямоугольника.
Способствовать формированию ключевых компетентностей: познавательной, информационной, коммуникативной, развивающей.
Вывести правило вычисления площади прямоугольника.
Актуализировать знания о признаках и свойствах геометрических фигур.
Способствовать совершенствованию вычислительных навыков.
Способствовать развитию основных операций мышления (сравнение, обобщение, умение делать выводы на основе полученной информации).
Развитие умения анализировать и находить пути решения поднимаемой проблемы.
Формирование основных компонентов УУД (умение ставить учебную задачу, обобщать, делать выводы)
Формировать навыки самоанализа.
— Способность к самооценке на основе критерия успешности учебной деятельности.
— Уметь определять и формулировать цель на уроке с помощью учителя;
проговаривать последовательность действий на уроке;
уметь высказывать своё предположение на основе работы с материалом учебника;
уметь работать по коллективно составленному плану;
оценивать правильность выполнения действия на уровне адекватной оценки;
вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; планировать своё действие в соответствии с поставленной задачей.
— Уметь оформлять свои мысли в устной форме;
слушать и понимать речь других;
учиться работать в группе, формулировать собственное мнение и позицию.
— Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
— Уметь использовать в речи термины «длина», «ширина», «площадь».
— Уметь вычислять площадь прямоугольника.
— Знать основные понятия длина, ширина, площадь
Тип урока: урок открытия нового знания.
Технология деятельностного подхода.
1. Мотивация к учебной деятельности
-Придумано кем-то просто и мудро
При встрече здороваться: «Доброе утро!»
Доброе утро солнцу и птицам,
Доброе утро улыбчивым лицам.
-Мне очень хочется пожелать доброго утра всем-всем, каждому из вас.
-Доброе утро, ребята!
-Доброе утро всем, кто присутствует на нашем уроке!
-Хочу продолжить словами французского философа Ж.Руссо:
«Вы талантливы, дети! Когда-нибудь вы сами приятно поразитесь, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению».
-Ребята, на каждом уроке вы стремитесь сделать для себя открытие, получить новые знания. Вот и сегодня мы постараемся углубить математические знания, узнать новое. С маленькой удачи начинается большой успех. Улыбнитесь и пожелайте друг другу удачи. В добрый путь за знаниями!
2. Актуализация знаний
а) Индивидуальная работа – 3 детей на местах решают задачи.
—Внимание на доску.
Т Р Я И М Е Г О Е
48 54 100 56 36 24 12 27 42
-Какое число лишнее и почему?
-Произведением каких чисел является 48, 54, 56, 36, 24, 12, 27, 42?
— Что ещё интересного увидели?
—Над каждым числом написана какая-то буква.
— Какое задание можно здесь придумать?
-Расположите числа в порядке увеличения и узнаете название страны ,куда мы сегодня отправимся .
— Молодцы! Да, мы с вами отправимся в страну Геометрия.
— С какой величиной мы познакомились на предыдущих уроках?
-Что такое площадь?
3. Постановка учебной задачи
-А теперь послушайте математическую сказку. ( Рассказывает Ильмира)
Жила на свете важная фигура. Важность её признавалась всеми людьми, так как при изготовлении многих вещей форма её служила образцом. Кого бы ни встретила она на своём пути, всем хвалилась: «Посмотрите, какой у меня красивый вид: противоположные стороны равны, все углы прямые. Красивее меня нет фигуры на свете!»
— Как же тебя зовут? – спрашивали её.
— А зовут меня просто….(Прямоугольник)
— Признаки прямоугольника: противоположные стороны равны, все углы прямые.
— Найдите среди данных фигур прямоугольники. (слайд 1)
— Докажите, что они прямоугольники.
— О какой фигуре мы сегодня будем говорить?
-А над какой темой будем работать? (-Площадь прямоугольника ) (слайд)
— Посмотрите на два прямоугольника, которые я держу в руках. Как определить площадь которого прямоугольника больше? Какие способы сравнения площади фигур мы знаем?
-(На глаз, способом наложения фигур, разделив на одинаковые мерки и подсчитав их количество .)
( У доски все способы сравнения площади фигур демонстрируют дети. Вывод: площадь красного прямоугольника больше площади синего прямоугольника или площадь синего прямоугольника меньше площади красного прямоугольника)
— С какой единицей измерения площади мы познакомились на прошлом уроке?
-Что такое квадратный см?
— (Квадрат со стороной 1 см, единица измерения площади.)
( Ребёнок демонстрирует на одном из прямоугольников.)
-Открыли тетради, записываем число.
-Сколько сторон и углов у прямоугольника?
Прописываем цифру 4.
— Начертите в тетради прямоугольник со сторонами 4см и 6см. Разбейте его на см 2 .
— Сосчитайте сколько квадратиков получилось?
— Значит, какую площадь имеет наш прямоугольник?
— Ребята, где во взрослой жизни может пригодиться умение находить площадь прямоугольника? (поклеить обои, покрасить пол, поклеить потолок,стелить линолеум).
— Посмотрите на слайд, Том Сойер тоже задумался, какую площадь имеет забор, который ему нужно покрасить .
— В этих случаях удобно находить площади прямоугольников с подсчётом квадратов?
— Значит, какова цель нашего урока?
Цель урока : найти более удобный способ нахождения площади прямоугольника.
5. Открытие нового знания
— Итак, площадь ваших прямоугольников сколько кв.см?(24)
— Внимание на доску. Мой прямоугольник тоже разделён на квадраты ,Но как видите у меня мерка больше.( На доске разделённый на квадраты демонстрационный прямоугольник.)
-Сколько квадратов укладывается на этом прямоугольнике? Считаем хором
— Как же быстрее узнать , сколько всего квадратов помещается в прямоугольнике? Может кто-то догадался и сможет объяснить? (Показывает и объясняет у доски ребёнок )
— Сколько полос с квадратами по горизонтали? (4)
— Сколько квадратов в каждой полосе? (6)
— Значит, по 6 квадратов сколько раз взяли?
— Как же узнать, сколько всего квадратов помещается в прямоугольнике?
— Что обозначает число 6? (Длину — 6см)
— Что обозначает число 4? (Ширину — 4см)
— Сделайте вывод, как же найти площадь прямоугольника?
-(Площадь прямоугольника равна: длину умножить на ширину.)
— А я нашла площадь этого прямоугольника так: 4 * 6 = 24 см 2
Можно ли таким способом найти площадь прямоугольника?
-Какое правило мы здесь используем?
— Какой вывод можно сделать? (Чтобы найти площадь прямоугольника надо длину умножить на ширину или наоборот)
— В тетрадях запишите 6* 4 = 24 кв.см 4*6 = 24 кв.см)
— Сравните ваш вывод с правилом в учебнике, с.60. Мы сделали такой же вывод, как и авторы учебника?
— Это правило можно записать в виде формулы. Давайте подумаем как?
— Площадь в математике принято обозначать буквой – S . Длина прямоугольника – а, ширина – в. Как узнать площадь? Кто допишет формулу( S = а*в)
Один ученик у доски записывает формулу.
-Вот вы сами и вывели формулу нахождения площади прямоугольника, с помощью которой мы будем находить площадь любого прямоугольника. (слайд)
6 .Первичное закрепление
Начертите в тетрадях прямоугольник длина которого 9см, а ширина — 2см. Найдите его площадь. Выполняется задание с комментированием.
— Какими еще могут быть длины сторон прямоугольника с такой площадью?
7. Включение новых знаний в систему
— Умение находить площадь прямоугольника в жизни нам необходимо. Мы в этом убедились .Людям каких профессий чаще всего приходится находить площадь фигур? (архитектору, конструктору, инженеру, строителю)
-Предлагаю вам побыть в роли строителей. У вас на партах лежат геометрические фигуры, вы в паре должны построить из этих фигур свой дом.
-Поднимите и покажите у кого дом Жёлтого цвета, Синего цвета, Зелёного и Красного цвета.
-Молодцы! Дома построены, а теперь внимательно послушайте задания:
-У кого дом Синего цвета вы находите площадь двери, решение записываете в тетрадях, оформляете ,как сегодня учились.
— У кого дом Красного цвета вы находите периметр крыши дома.
— У кого дом Зелёного цвета вы находите площадь окна.( квадрат)
-У кого дом Жёлтого цвета для вас задание на экране( слайд)
— выразить в указанных единицах измерения
2 дм 4 см = …см 78 см = …дм …см
5 см 6мм = … мм 39 дм = …м …дм
-Чему равна длина двери? Ширина?
-Как нашли площадь?
-Покажите своё отношение.
— Что такое периметр? –
— Как нашли периметр треугольника?
-Покажите своё отношение.
– Чему равна длина окна? Ширина?
— Как нашли площадь квадрата?
-Кто запишет формулу нахождения площади квадрата.?
Ребята по очереди называют равенства, другие показывают своё отношение.
— В стране Геометрия мы построили свой коттеджный посёлок. У кого возникло желание быть строителем?
8. Рефлексия урока
-Какая величина была главной хозяйкой нашего урока?
-Площадь какой фигуры мы учились находить?
-Как найти площадь прямоугольника?
-Какими единицами измеряли площадь?
8. Домашнее задание
С. 61 № 4, №5 ( 3 , 4 столбик ), по желанию найти площадь своей комнаты.
А теперь послушайте притчу:
Шёл мудрец и встретил 3 работников.
« Что ты сегодня делал?» — спросил он каждого.
Первый ответил :- «Я целый день таскал ненавистные камни».
Второй ответил :- «Я немного устал, но добросовестно выполнял свою работу».
Третий ответил :- «Сегодняшняя работа принесла мне радость и большое удовлетворение».
— Кто из вас на уроке был первым работником, вторым работником, третьим работником? Очень хорошо, что работа на этом уроке принесла вам радость, вы открыли новые знания!
Источник
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
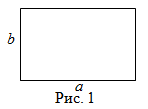
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
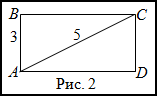
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.