Содержание:
Движение и силы:
Вы уже знаете, каким сложным является хаотическое движение молекул. В повседневной жизни мы встречаемся с более простыми видами движения. Движутся люди, автомобили (рис. 76), самолеты, Солнце, Луна и другие тела. Окружающий нас мир немыслим без движения. Характеристики многих движений можно легко определить и описать с помощью несложных математических формул.

Как установить, движется или нет данное физическое тело? Рассмотрим пример. Вы стоите на остановке и вдали видите автобус (рис. 77). Движется он или нет? Несмотря на то что вращения колес не видно, вы уверенно определяете, что автобус движется. Изменяется с течением времени его положение относительно киоска, деревьев, домов, неподвижных относительно поверхности Земли. Точно так же мы судим о движении облаков и птиц в небе, рыб в аквариуме, футболистов на поле, поездов и любых других тел.

Изменение положения тела в пространстве относительно других тел с течением времени называется механическим движением. Следовательно, движение происходит в пространстве и во времени.
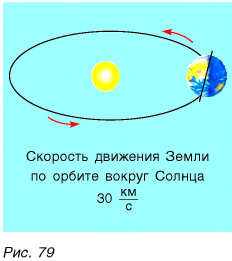
Рассмотрим еще один пример. Вы едете в электричке (рис. 78). Можно ли сказать, что, сидя в ней, вы находитесь в состоянии покоя? И да, и нет. Да — потому, что вы не движетесь по электричке, т. е. с течением времени ваше положение относительно электрички не меняется. Нет — потому, что вместе с электричкой вы движетесь относительно поверхности Земли. А если электричка остановилась? Теперь вы находитесь в состоянии покоя относительно электрички и поверхности Земли, но движетесь вместе с Землей вокруг Солнца (рис. 79), перемещаясь за каждую секунду примерно на 30 км относительно звезд.

Таким образом, покой и движение относительны. Относительны и характеристики движения. Это легко увидеть на опыте. Укрепите светоотражатель (фликер) на ободе колеса вашего велосипеда. Какова будет кривая, которую опишет фликер (ее называют траекторией) при движении колеса? Относительно вас или вашего друга, едущего рядом с вами, фликер будет двигаться по окружности. А стоящий человек, мимо которого вы проезжаете, увидит, что фликер описывает не окружность, а сложную кривую (рис. 80). Следовательно, траектория тоже относительна.

Главные выводы:
- Механическое движение — это изменение положения тела в пространстве относительно другого тела или тел с течением времени.
- Механическое движение и покой относительны.
Траектория, путь и время
Для решения научных и практических задач необходимо уметь описывать механическое движение тела или его частей, определять характеристики движения и устанавливать связи между ними.
Какими физическими величинами описывается механическое движение?
Проведите мелом по доске. Мел при движении описывает линию, которая хорошо видна на доске.
В голубом небе часто отчетливо видны белые следы позади летящих самолетов (рис. 81). Быстро мчащийся катер оставляет на поверхности воды пенистую дорожку (рис. 82).


Линия, которую описывает тело при своем движении, называется траекторией.
Мы привели примеры движений, когда траектория — видимая линия. Но чаще всего она невидима. Однако траекторию всегда можно изобразить, если отметить точками положения движущегося тела в различные моменты времени, а затем соединить эти точки. Несложно, например, представить траекторию летящего ядра (рис. 83).
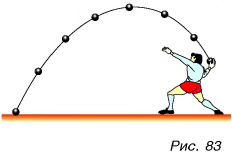
Если траектория движения — прямая линия, движение называется прямолинейным. Например, такова траектория падающего с дерева яблока (рис. 84). Если же траектория — кривая линия, то движение называется криволинейным (см. рис. 83).

Длина той части траектории, которую описывает тело за данный промежуток времени, называется путем, пройденным телом за этот промежуток времени.
Обозначается путь обычно буквой s. Путь это физическая величина. Его можно измерить или вычислить по формуле. Единицей пути в СИ является 1 метр (1 м). На практике путь часто измеряют в кратных единицах — километрах — или в дольных — сантиметрах, миллиметрах, микрометрах.
А что такое промежуток времени? Допустим, вы отправляетесь в путешествие на поезде «Минск — Москва». Поставим вопрос: за какой промежуток времени поезд пройдет путь s = 212 км от Минска до Орши? Ответить на этот вопрос очень легко. Во-первых, нужно знать момент времени, когда поезд отправляется из Минска. Обозначим его буквой t с индексом 1, т. е. 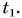 Во-вторых, нужно знать момент времени, когда поезд прибывает в Оршу. Обозначим его
Во-вторых, нужно знать момент времени, когда поезд прибывает в Оршу. Обозначим его 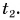 Промежуток времени, за который поезд проходит путь от Минска до Орши, равен:
Промежуток времени, за который поезд проходит путь от Минска до Орши, равен:
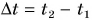
(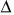 — греч. «дельта» — знак, обозначающий в математике и физике изменение величины, т. е. разность ее конечного и начального значений). Так, если в нашем примере
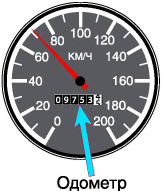
— греч. «дельта» — знак, обозначающий в математике и физике изменение величины, т. е. разность ее конечного и начального значений). Так, если в нашем примере 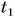 = 20 ч 10 мин,
= 20 ч 10 мин, 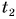 = 23 ч 15 мин, то
= 23 ч 15 мин, то 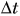 = 3 ч 5 мин.
= 3 ч 5 мин.
Для краткости вместо «промежуток времени» будем говорить «время».
Единицей времени в СИ является 1 секунда (1 с). Иногда удобнее использовать кратные единицы времени: минуту (мин) и час (ч). Существуют и такие единицы времени, как сутки (сут), год. Вы, конечно, знаете, что одни сутки равны 24 ч, 1 год равен 365 (366) сут.
Для измерения времени служат различные Рис. 87 приборы, например метроном (рис. 85), часы (рис. 86), секундомер (рис. 87).



Для практических целей полезно научиться отсчитывать про себя секунды, произнося числа через равные интервалы времени.
При прохождении лечебных процедур иногда необходимо фиксировать определенный промежуток времени, например 1 мин или 5 мин. В таких случаях удобно использовать песочные часы (рис. 88).

Для любознательных:
Для измерения пройденного пути в автомобилях имеется специальный прибор — одометр (от греч. «дорога» и «мера») (см. рис.). Одометр включает:
- датчик, фиксирующий обороты колеса;
- счетчик, подсчитывающий обороты;
- индикатор, фиксирующий путь, который проехал автомобиль.
Главные выводы:
- Траектория — линия, которую описывает тело при своем движении.
- Если траектория — прямая линия, то движение называется прямолинейным, если траектория — кривая линия, то движение криволинейное.
- Путь — длина той части траектории, которую описывает тело за данный промежуток времени.
Равномерное движение и скорость
Среди всего разнообразия движений тел наиболее просто описывается равномерное прямолинейное движение. Что представляет собой это движение? Как его охарактеризовать?
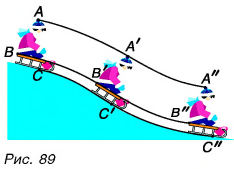
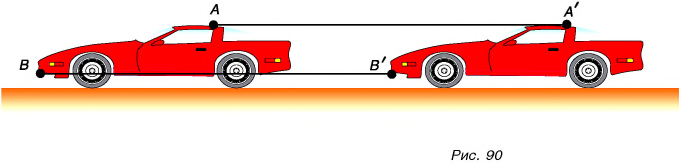
Рассмотрим пример. Девочка на санках спускается с горки. Понаблюдаем за движением нескольких точек, например А, B, С (рис. 89). Эти точки движутся совершенно одинаково, описывая равные траектории. Движение, при котором все точки тела описывают одинаковые по форме и равные по длине траектории, называется поступательным. А если тело движется поступательно, нужно ли изучать движение всего тела или достаточно изучить движение только одной его точки? Рис. 90 Ведь все точки (рис. 89, 90) движутся совершенно одинаково. В данном учебном пособии мы будем изучать движение тела, не рассматривая его форму, размеры, т. е. будем моделировать тело точкой.
Как определить, какой путь пройдет тело при движении за данный промежуток времени? Пусть тележка (рис. 91) движется прямолинейно. Будем отмечать ее положения, точнее положения точки A, через равные промежутки времени. Это можно сделать, установив на тележке капельницу с вытекающими через равные промежутки времени, например через 2 с, каплями. Определим пути, проходимые тележкой за 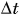 = 2 с на первом, втором, третьем и последующих участках движения.
= 2 с на первом, втором, третьем и последующих участках движения.
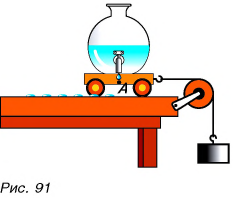
Подобрав груз, можно достичь того, что пути, пройденные тележкой за равные промежутки времени 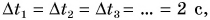 окажутся равными
окажутся равными 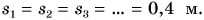 Если уменьшить промежутки времени, то во столько же раз уменьшатся и проходимые пути.
Если уменьшить промежутки времени, то во столько же раз уменьшатся и проходимые пути.
Движение, при котором тело за любые равные промежутки времени проходит равные пути, называется равномерным.
Найдем отношения путей к соответствующим промежуткам времени:
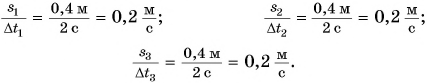
Величина 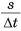 новая физическая величина, называемая скоростью. Обозначается скорость буквой
новая физическая величина, называемая скоростью. Обозначается скорость буквой 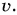
Тогда для равномерного прямолинейного движения можно записать формулу:

Из формулы (1) следует, что скорость равномерного прямолинейного движения есть физическая величина, равная отношению пути, пройденного телом, к промежутку времени.
Из формулы (1) легко найти путь, пройденный за любой промежуток времени, и промежуток времени:

На примере с капельницей вы убедились, что при равномерном прямолинейном движении скорость является постоянной величиной.
При равномерном прямолинейном движении с увеличением промежутка времени увеличивается путь (рис. 92), но скорость остается постоянной.
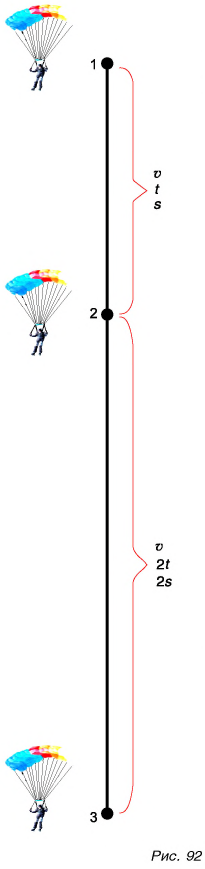
Значит, скорость является характеристикой движения. Теперь можно дать еще одно определение равномерного прямолинейного движения, используя его характеристику — скорость: равномерное прямолинейное движение — это движение но прямой с постоянной скоростью.
Единицей скорости в СИ является 1 метр в секунду 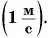 На практике часто используют другие единицы. Например, скорость обычных транспортных средств (автобуса, поезда, самолета и др.) удобно выражать в километрах в час
На практике часто используют другие единицы. Например, скорость обычных транспортных средств (автобуса, поезда, самолета и др.) удобно выражать в километрах в час 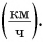 Скорость космических ракет, спутников (рис. 93) выражают в километрах в секунду
Скорость космических ракет, спутников (рис. 93) выражают в километрах в секунду 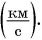 При решении задач, как правило, все физические величины выражают в основных единицах СИ.
При решении задач, как правило, все физические величины выражают в основных единицах СИ.
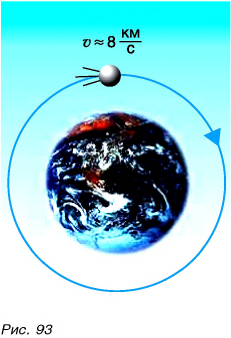
Пусть автомобиль движется но шоссе со скоростью 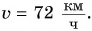 Выразим эту скорость в метрах в секунду
Выразим эту скорость в метрах в секунду 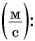
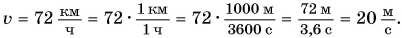
Скорость движения пешехода 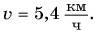 Выразите ее самостоятельно в метрах в секунду
Выразите ее самостоятельно в метрах в секунду 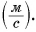
Максимальная скорость движения в природе — скорость распространения света в пустоте (рис. 94).

Она равна 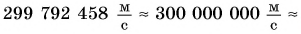
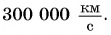 Вас не удивило огромное значение этой скорости? Сравните ее со скоростью звука в воздухе –
Вас не удивило огромное значение этой скорости? Сравните ее со скоростью звука в воздухе – 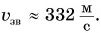 Теперь легко объяснить, почему гром вы слышите позже, чем видите молнию, хотя молния и гром возникают практически одновременно.
Теперь легко объяснить, почему гром вы слышите позже, чем видите молнию, хотя молния и гром возникают практически одновременно.
Из формулы 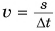 следует, что для нахождения скорости нужно знать путь и промежуток времени, за который этот путь пройден. Но люди изобрели и широко применяют приборы, которые непосредственно показывают скорость, например, стрелкой на циферблате. Такие приборы называются спидометрами (рис. 95). Если скорость движения автомобиля равна
следует, что для нахождения скорости нужно знать путь и промежуток времени, за который этот путь пройден. Но люди изобрели и широко применяют приборы, которые непосредственно показывают скорость, например, стрелкой на циферблате. Такие приборы называются спидометрами (рис. 95). Если скорость движения автомобиля равна 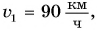 а самолета —
а самолета — 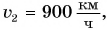 то за одно и то же время самолет преодолеет в 10 раз больший путь, а это значит, что самолет движется в 10 раз быстрее автомобиля.
то за одно и то же время самолет преодолеет в 10 раз больший путь, а это значит, что самолет движется в 10 раз быстрее автомобиля.
Таким образом, скорость характеризует быстроту движения, т. е. показывает, как быстро тело меняет свое положение в пространстве относительно других тел.
Главные выводы:
- Скорость — количественная характеристика быстроты движения.
- Определить скорость движения можно, разделив пройденный путь на затраченный промежуток времени.
- Если скорость постоянна, то движение равномерное.
Графики пути и скорости при равномерном прямолинейном движении
Можно ли выразить связь пути s и времени t не через формулы, а каким-либо другим способом? Для этого используются графики.
Поясним суть графического метода на конкретном примере. Пусть самолет движется равномерно и прямолинейно со скоростью 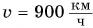 (рис. 96). Опишем движение самолета графически, т. е. построим графики зависимости пути и скорости движения самолета от времени движения.
(рис. 96). Опишем движение самолета графически, т. е. построим графики зависимости пути и скорости движения самолета от времени движения.

Путь s от начального момента времени 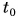 до момента времени t равен
до момента времени t равен 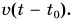 Начальный момент времени
Начальный момент времени 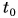 примем за нуль
примем за нуль 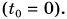 Тогда формула пути упростится:
Тогда формула пути упростится: 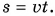
Найдем значения пути для различных значений промежутка времени и занесем их в таблицу 1.

Например, если t = 3ч, то
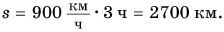
Теперь построим график зависимости пути от времени. По оси абсцисс в определенном масштабе (например, 1 см — 1 ч) будем откладывать промежутки времени движения, а по оси ординат (в масштабе 1 см — 900 км) — путь (рис. 97).
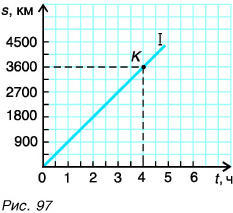
Прямая I выражает графическую зависимость пути от времени равномерного движения самолета. Эту прямую называют графиком пути. График пути напоминает известный вам из математики график функции 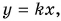 выражающей прямую пропорциональную зависимость у от х.
выражающей прямую пропорциональную зависимость у от х.
Ценность графика пути в том, что он, как и соотношение 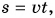 позволяет решить главную задачу — найти путь s, пройденный телом за произвольный промежуток времени
позволяет решить главную задачу — найти путь s, пройденный телом за произвольный промежуток времени
Например, нас интересует путь самолета за промежуток времени t = 4 ч. Для этого из точки на горизонтальной оси, соответствующей времени t = 4 ч (см. рис. 97), проводим перпендикуляр до пересечения с графиком (точка К). Из найденной точки К опускаем перпендикуляр на ось ординат и получаем ответ без вычислений. Путь s = 3600 км.
А что представляет собой график скорости? Он выражает зависимость скорости от времени. Так как скорость с течением времени не изменяется, то различным моментам времени соответствует одно и то же значение скорости. Составим таблицу 2 и построим прямую, выражающую зависимость скорости от времени, откладывая по оси абсцисс время, а по оси ординат — скорость (рис. 98).

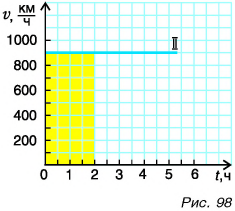
График скорости равномерного прямолинейного движения — прямая, параллельная оси времени.
Прямая II изображает график скорости движения самолета. Что дает график скорости? Он не только показывает значение скорости, но и позволяет найти пройденный путь. Рассчитаем путь самолета за промежуток времени t = 2 ч. Согласно формуле 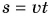 этот путь
этот путь 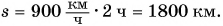 Посмотрим на это произведение с точки зрения геометрии. Первый множитель
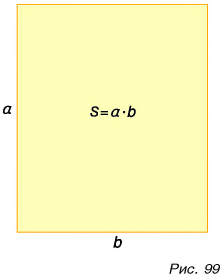
Посмотрим на это произведение с точки зрения геометрии. Первый множитель 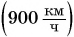 выражает одну сторону закрашенного прямоугольника (см. рис. 98), второй (2 ч) другую. Из математики вы уже знаете, что перемножением сторон a и b находят площадь S прямоугольника (рис. 99). Конечно, площадь не есть путь, речь идет только о численном равенстве. Пройденный путь численно равен площади фигуры под графиком скорости.
выражает одну сторону закрашенного прямоугольника (см. рис. 98), второй (2 ч) другую. Из математики вы уже знаете, что перемножением сторон a и b находят площадь S прямоугольника (рис. 99). Конечно, площадь не есть путь, речь идет только о численном равенстве. Пройденный путь численно равен площади фигуры под графиком скорости.
Для любознательных:
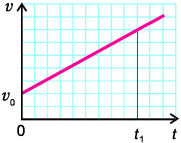
Площадью фигуры под графиком скорости определяется путь не только при равномерном прямолинейном, но и при любом другом движении. Например, путь за промежуток времени 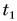 (см. рис.) численно равен площади закрашенной фигуры:
(см. рис.) численно равен площади закрашенной фигуры: 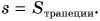
Главные выводы:
- График пути выражает зависимость пройденного пути от времени движения тела.
- Путь при равномерном прямолинейном движении можно определить по формуле
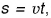 по графику пути или с помощью графика скорости.
по графику пути или с помощью графика скорости.
Пример №1
Легковой и грузовой автомобили равномерно движутся в одном направлении но параллельным полосам прямолинейного участка
шоссе. Скорость движения легкового автомобиля 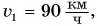 грузового —
грузового — 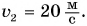 Каким будет расстояние между автомобилями через промежуток времени t = 3,0 мин, если в начальный момент автомобили находились рядом?
Каким будет расстояние между автомобилями через промежуток времени t = 3,0 мин, если в начальный момент автомобили находились рядом?
Запишем условие и выразим величины через основные единицы СИ.
Дано:
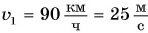
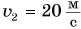
t = 3, 0 мин = 180 с
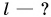
Решение:
Найдем путь, который проехал каждый из автомобилей за промежуток времени t:

Расстояние между автомобилями:
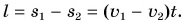
Подставим значения и вычислим:
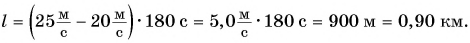
Ответ: 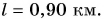
Пример №2
Графики зависимости пути от времени равномерных прямолинейных движений пешехода Димы (1) и велосипедиста Пети (2) представлены на рисунке 102. Во сколько раз отличаются скорости движения мальчиков?
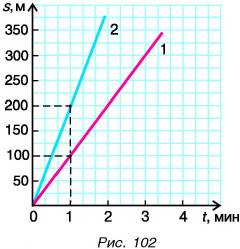
Решение
Из графиков следует, что за промежуток времени t = 1 мин Дима прошел путь 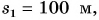 а Петя проехал
а Петя проехал 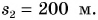
Скорость движения Димы:
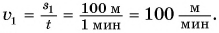
Скорость движения Пети:
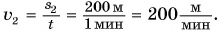
Отношение:
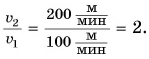
Ответ: скорость движения Пети на велосипеде в 2 раза больше скорости движения Димы пешком.
Этот же ответ можно было получить проще:
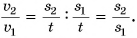
Из графика для одного и того же момента времени, например t = 1 мин (либо 2 мин и т. д.), определяем пути 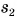 и
и 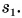 Тогда
Тогда
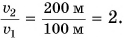
Неравномерное (переменное) движение. Средняя скорость
Проанализируйте движение автобуса. Он уменьшает скорость перед остановкой. Затем в течение какого-то промежутка времени стоит на остановке, т. е. его скорость равна нулю, после чего скорость увеличивается. Значит, скорость автобуса в процессе движения изменяется, т. е. является переменной величиной.
Движение, при котором скорость изменяется, называется неравномерным (переменным).
Практически все движения, наблюдаемые в природе и технике, — неравномерные. С изменяющейся скоростью движутся, например, люди, птицы (рис. 103), дельфины (рис. 104), поезда, падают предметы (рис. 105). Но как же тогда характеризовать это движение?



Неравномерное движение характеризуется средней скоростью. Как определить среднюю скорость? Рассмотрим пример. Вы едете на экскурсию в Брест поездом. Поезд проходит от Минска до Бреста путь s = 330 км. На прохождение этого пути затрачивается время t = 4,5 ч. В течение данного времени поезд стоит на станциях, движется то с увеличивающейся, то с уменьшающейся скоростью.
Среднюю скорость находят путем деления всего пути на весь промежуток времени, за который этот путь пройден. Обозначим среднюю скорость 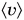 и запишем формулу:
и запишем формулу:
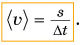
Тогда поезд «Минск — Брест» движется со средней скоростью

Вас не удивило, что мы использовали формулу равномерного движения? Да, действительно формально мы нашли среднюю скорость так, как будто поезд весь путь s = 330 км двигался равномерно с постоянной скоростью 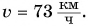 Это, конечно же, не означает, что он на самом деле двигался равномерно. На отдельных участках пути скорость движения поезда была как значительно большей
Это, конечно же, не означает, что он на самом деле двигался равномерно. На отдельных участках пути скорость движения поезда была как значительно большей 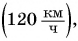 так и меньшей, чем
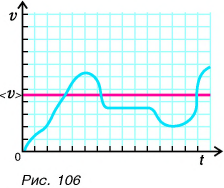
так и меньшей, чем 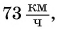 и даже равной нулю (рис. 106).
и даже равной нулю (рис. 106).
Для любознательных:
Средняя скорость дает лишь приблизительное представление о быстроте движения тела. Описание переменного движения более сложно по сравнению с описанием равномерного.
Например, если скорость поезда на участке разгона возрастает от О до 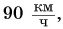 то в различных точках траектории она принимает различные значения из этого промежутка. Таким образом, можно говорить не только о средней скорости на данном участке траектории, но и о скорости в данной точке траектории. Такую скорость называют в физике мгновенной скоростью.
то в различных точках траектории она принимает различные значения из этого промежутка. Таким образом, можно говорить не только о средней скорости на данном участке траектории, но и о скорости в данной точке траектории. Такую скорость называют в физике мгновенной скоростью.
Главные выводы:
- Характеристикой неравномерного движения является средняя скорость.
- Для вычисления средней скорости нужно путь разделить на весь промежуток времени, затраченный на прохождение этого пути.
Пример №3
Катя прошла путь 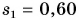 км за промежуток времени
км за промежуток времени 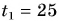 мин. Затем остановилась и в течение промежутка времени
мин. Затем остановилась и в течение промежутка времени 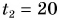 мин разговаривала с подругой, после чего прошла путь
мин разговаривала с подругой, после чего прошла путь 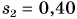 км за промежуток времени
км за промежуток времени 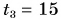 мин. Определите среднюю скорость движения Кати.
мин. Определите среднюю скорость движения Кати.
Дано:
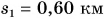
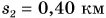
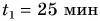
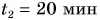
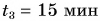
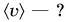
Решение
Весь путь, который прошла Катя:
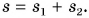
Весь затраченный промежуток времени:
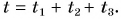
Средняя скорость движения Кати:
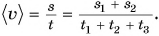
Вычислим 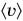 :
:
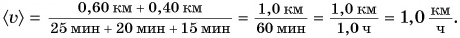
Ответ: 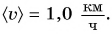
Пример №4
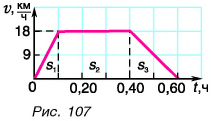
По графику скорости (рис. 107) определите путь и среднюю скорость движения велосипедиста за промежуток времени t = 0,60 ч.
Решение
Искомый путь численно равен площади фигуры под графиком скорости. Путь 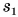 велосипедист проехал за промежуток времени
велосипедист проехал за промежуток времени 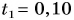 ч. Он численно равен площади прямоугольного треугольника, закрашенного в голубой цвет:
ч. Он численно равен площади прямоугольного треугольника, закрашенного в голубой цвет:
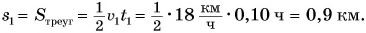
Аналогично можно найти пути 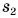 и
и 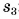 :
:
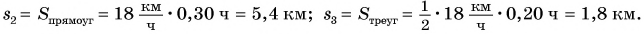
Весь путь: 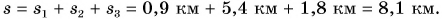
Средняя скорость движения велосипедиста:
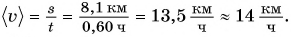
Ответ: 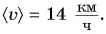
Почему изменяется скорость движения тела
Равномерное прямолинейное движение, т. е. движение с постоянной скоростью, — лишь модель реального движения. В жизни всякое движение (от движения огромных планет до движения невидимых частиц) чаще всего происходит с изменяющейся скоростью. Что является причиной изменения скорости?
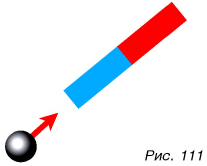
Рассмотрим опыты. На столе лежит стальной шарик Он находится в состоянии покоя относительно стола. Чтобы заставить шарик двигаться, можно толкнуть его рукой или приблизить к нему магнит (рис. 111). В обоих случаях на шарик действуют другие тела (рука, магнит), что и является причиной изменения скорости движения шарика. А как долго шарик будет двигаться после толчка? Опыт показывает, что скорость движения шарика уменьшается, а через некоторое время его движение прекращается. Почему?
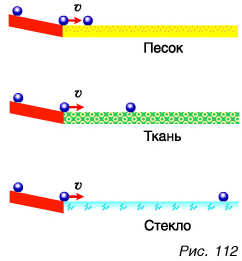
Проведем другой опыт. Три одинаковых шарика одновременно скатываются с одинаковой высоты (рис. 112). Дорожки, по которым затем о движутся шарики, отличаются: первая посыпана песком, вторая покрыта тканью, а третья — стеклом. Движение но третьей дорожке продолжается дольше, поскольку трение здесь наименьшее. Значит, причина прекращения движения шарика — трение между поверхностями шарика и стола и, конечно, сопротивление воздуха. А если бы мы смогли убрать эти причины, шарик двигался бы с постоянной скоростью сколько угодно долго.
Движение тела без действия на него других тел, как и покой, — его естественное состояние.
То, что тело остается в покое, если нет действия других тел, вполне понятно. Но как же тело может само но себе двигаться, если в повседневной жизни мы видим, что тело движется только тогда, когда Рис. 113 на него действует другое тело? Санки (рис. 113) надо тянуть за веревку, лодка плывет под действием весел (рис. 114). А были бы нужны веревка и весла, если бы не было сопротивления движению? Если бы вода не оказывала сопротивления движению, лодка после толчка двигалась бы бесконечно долго с постоянной скоростью.


Итак, если тело находится в состоянии покоя или в состоянии движения, то оно стремится сохранять это состояние (не изменять скорость), пока на него не подействуют другие тела.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения (сохранять свою скорость неизменной) при отсутствии действия на него других тел называется инерцией.
С инерцией нам приходится встречаться постоянно. При резком торможении автобуса пассажиры наклоняются вперед, так как продолжают двигаться по инерции. При резком разгоне автобуса они отклоняются назад. Почему? Л может ли автомобиль остановиться мгновенно? Нет. Как бы ни были сильны тормоза, инерция препятствует мгновенному торможению. Именно из-за инерции тормозной путь автомобиля тем больше, чем больше скорость его движения. Мы уверены, что, помня об инерции, вы не будете перебегать улицу перед движущимся транспортом и научите не делать этого своих младших братьев и сестер. А сколько неприятностей из-за инерции случается, пока мы учимся кататься на коньках!
Инерция может приносить человеку не только неприятности, но и огромную пользу. В водяных и паровых турбинах, а также в ветряных двигателях (рис. 115) используется инерция движения воды, пара, ветра. Инерция играет полезную роль при применении удара, от выколачивания пыли до насадки на рукоятку молотка. Космонавт благодаря инерции может выйти в открытый космос (рис. 116) и не отстать от корабля.


Для любознательных:
Древнегреческий философ Аристотель (IV в. до н. э.) считал, что только покой — естественное состояние тела, а движение — насильственное. Тело стремится к своему естественному состоянию, поэтому, если не поддерживать движение, оно прекращается.
Ошибка Аристотеля состояла в том, что он верил в инерцию покоя, но не понимал, что телам столь же свойственна инерция движения.
Спустя приблизительно 2000 лет после Аристотеля итальянский ученый Галилео Галилей смог вообразить идеализированный мир мир без трения. В результате он пришел к выводу о том, что движение тела без действия на него других тел, как и покой, является его естественным состоянием.
Главные выводы:
- Если на тело не действуют другие тела, то оно либо находится в состоянии покоя, либо движется равномерно и прямолинейно (по инерции).
- Изменить состояние покоя или движения тела можно только воздействием на него другого тела или тел.
Масса тела и плотность вещества
Одинаково ли легко изменить скорость различных тел? Мимо нас пролетает комар. Трудно ли изменить его скорость? Достаточно просто дунуть (рис. 117, а). А если проезжает груженый автомобиль МАЗ (рис. 117, б)? Инерция есть у всех тел, но это свойство проявляется у них в разной степени. Оно почти незаметно у комара, но очень заметно у автомобиля, для изменения скорости которого требуются большие и длительные воздействия.

Для характеристики инерции тела в физике используется физическая величина, называемая массой. Чем массивнее тело, тем труднее изменить его скорость, тем больше оно противится таким изменениям. Масса тела — мера его инерции. Иногда говорят: мера его инертности.
Обозначим массу тела буквой m. Основной единицей массы в СИ является 1 килограмм (1 кг). Полезно знать, что 1 л воды при комнатной температуре имеет массу, практически равную 1 кг. Соответственно, масса 1 мл равна 1 г. Обратите внимание! В килограммах измеряется единственная физическая величина — масса.
От чего зависит масса тела? Сравните разгон и торможение груженого и порожнего автомобилей. Понятно, что масса тела зависит от количества вещества в теле (от числа молекул). Дело в том, что массой (т. е. инерцией) обладает каждая молекула, поэтому массу всего тела можно рассматривать как сумму масс всех его молекул. Будут ли одинаковыми массы тел, если они содержат одинаковое число молекул? Да, если тела состоят из одного и того же вещества. Нет, если тела состоят из различных веществ (например, алюминиевая и золотая ложки). А теперь сравним массы разных веществ, имеющих одинаковый объем.
Задумайтесь над вопросом: какую тележку легче сдвинуть с места — нагруженную сухими дровами (рис. 118, а) или нагруженную камнями (рис. 118, б), имеющими равный с дровами объем? Конечно, тележку с дровами. Ее масса меньше. Значит, масса единицы объема дров и единицы объема камней разная.
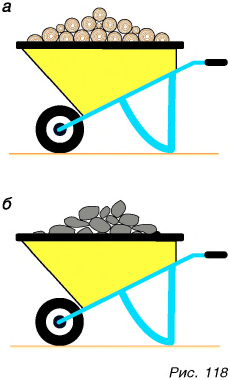
Масса вещества, содержащегося в единице объема, называется плотностью вещества.
Чтобы найти плотность, необходимо массу вещества разделить на его объем. Плотность обозначается греческой буквой 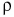 (ро). Тогда
(ро). Тогда
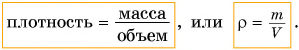
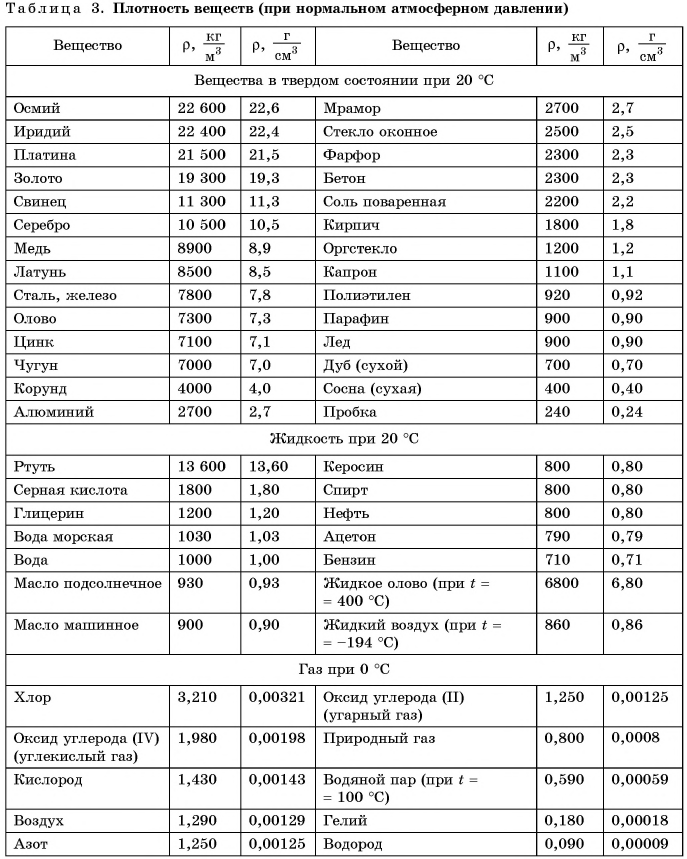
Единицей измерения плотности в СИ является 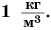 Плотности различных веществ определены на опыте и представлены в таблице 3.
Плотности различных веществ определены на опыте и представлены в таблице 3.
На рисунке 119 изображены массы известных вам веществ в объеме 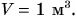
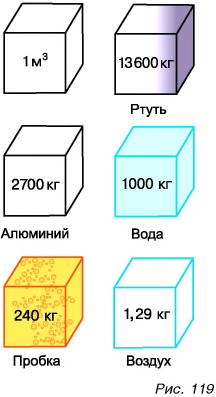
У большинства веществ плотность в твердом состоянии больше, чем в жидком. Например, плотность олова в твердом состоянии 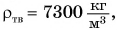 а в жидком (при температуре 400 °С)
а в жидком (при температуре 400 °С) 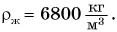
Плотность вещества в жидком состоянии больше, чем в газообразном. Чем это можно объяснить? Вспомните о различии в расстояниях между молекулами. Самые большие расстояния — между молекулами газа. Поэтому плотность сжиженного воздуха (при -194 °С) равна 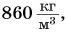 а в газообразном состоянии —
а в газообразном состоянии — 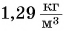 (при 0 °С).
(при 0 °С).
Зная плотность и объем тела, легко найти массу:
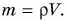
Формулу 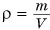 можно использовать не только для однородных тел, но и для тел, имеющих полости или состоящих из разных веществ. Только в этом случае формула выражает среднюю плотность тела (сравните со средней скоростью):
можно использовать не только для однородных тел, но и для тел, имеющих полости или состоящих из разных веществ. Только в этом случае формула выражает среднюю плотность тела (сравните со средней скоростью):
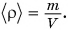
Для любознательных:
Твердое вещество, состоящее из молекул 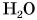 (лед), имеет плотность
(лед), имеет плотность 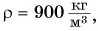 жидкое (вода) —
жидкое (вода) — 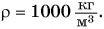
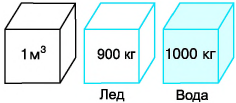
Вы заметили особенность? Плотность льда меньше плотности воды, что указывает на более плотную упаковку (т. е. меньшие промежутки) молекул в жидком состоянии вещества (вода), чем в твердом (лед).
Из всех видов деревьев наименьшей плотностью обладает древесина бальзового дерева 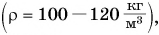 растущего в тропиках Центральной и Южной Америки.
растущего в тропиках Центральной и Южной Америки.
Средняя плотность Вселенной ничтожно мала 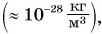 а вещество нейтронных звезд имеет очень большую плотность
а вещество нейтронных звезд имеет очень большую плотность 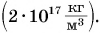
Главные выводы:
- Чем больше масса тела, тем труднее изменить скорость его движения.
- Плотность вещества показывает, какая масса вещества содержится в единице его объема.
- Плотность вещества в различных агрегатных состояниях разная.
- Тела, состоящие из разных веществ, характеризуются средней плотностью.
Пример №5
Средняя плотность тела человека примерно равна плотности воды. Зная свою массу, вычислите объем тела.
Дано:
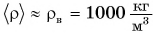

Решение
Определим с помощью весов свою массу m. Например, m = 50 кг. Тогда объем тела
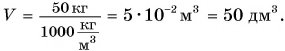
Ответ: 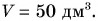
Сила
Изменить скорость движения тела можно воздействием на него другого тела. Чем больше это воздействие, тем сильнее изменяется скорость. Напрягая мышцы рук, вы увеличиваете скорость тележки. Ваш старший брат или отец может сильнее подействовать на тележку и увеличить скорость ее движения больше.
С помощью какой физической величины можно количественно определить, насколько сильно воздействует одно тело на другое, например человек на тележку? Такой величиной является сила.
Сила — количественная мера воздействия одного тела на другое.
В приведенном примере результатом воздействия является изменение скорости, значит, сила — причина изменения скорости движения тела.
Однако действие одного тела на другое приводит не только к изменению скорости. Подействуем на пружину гирей (подвесим ее к пружине) (рис. 120, а). Действие гири на пружину вызывает ее удлинение (рис. 120, б). Гиря, стоящая на тонкой доске (рис. 121), прогибает ее. Сжимая пальцами ластик, вы изменяете его форму. В этих случаях действие одного тела на другое, т. е. сила, вызывает изменение размеров или формы тела.
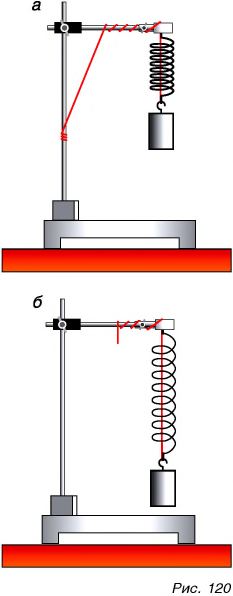
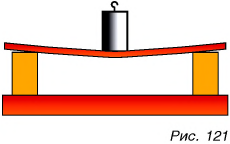
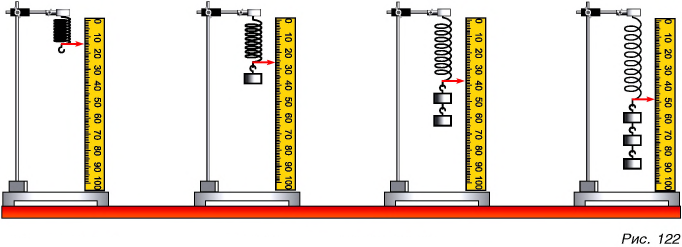
Изменение размеров или формы тела называется деформацией. Значит, сила является не только причиной изменения скорости, но и причиной деформации тела. Чем больше сила, тем больше деформация. Действительно, подействуйте на пружину более тяжелой гирей, т. е. большей силой, и растяжение пружины будет больше (рис. 122).
Сила не может существовать сама по себе. Если мы говорим, что на тело действует сила, это означает только то, что на тело действует другое тело.
Обычно силу обозначают буквой F и изображают в виде стрелки. Направление стрелки указывает направление действия силы. Начало стрелки совпадает с точкой приложения силы. Абсолютное число, выражающее длину стрелки, называют модулем силы.
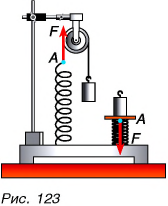
Итак, сила характеризуется модулем, направлением и точкой приложения. Пусть на одинаковые пружины действуют две одинаковые гири (рис. 123). Одна пружина растягивается под действием гири, другая — сжимается. Модули действующих на пружины сил одинаковы, но направления у сил разные.
На рисунке 124 изображены два тела (арбуз и яблоко), действующие на стол с одинаково направленными, но имеющими разные модули силами. Эти силы приложены к крышке стола в точках 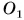 и
и 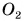 и направлены вертикально вниз. Модуль силы
и направлены вертикально вниз. Модуль силы 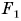 больше модуля силы
больше модуля силы 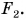
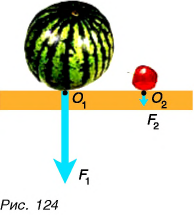
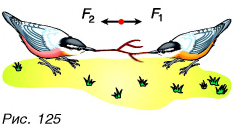
Чаще всего тело испытывает не одно, а сразу два или более действий, причем иногда противоположного направления. Как изменится скорость движения тела в этом случае? Если модули противоположно направленных сил равны, то, как и в математике при сложении равных но модулю, но противоположных но знаку чисел, мы получим в результате нуль. Такие силы мы будем называть компенсирующими друг друга. В этом случае, как и при отсутствии сил, скорость тела изменяться не будет. На рисунке 125 силы, приложенные к одному и тому же телу (ветке), компенсируют друг друга, и тело находится в состоянии покоя.
Для любознательных:
В повседневной жизни слово «сила» часто используется в сочетаниях «сила огня», «сила духа», «сила воли» и т. д. В физике слово «сила» употребляется только в смысле количественной меры такого воздействия, которое либо меняет скорость движения тела, либо деформирует его, либо вызывает то и другое одновременно. Действие даже самой малой силы обязательно приводит к тому или иному результату. От нажатия на стол пальцем крышка стола неизбежно прогнется, хотя это не всегда заметно.
Главные выводы:
- Сила является количественной мерой воздействия одного тела на другое.
- Сила является причиной изменения скорости движения тела и его деформации.
- Сила характеризуется модулем, направлением и точкой приложения.
Явление тяготения и сила тяжести
Посмотрите на глобус. Это модель Земли. Земля имеет форму, близкую к форме шара. Нам это кажется естественным. Но каково было недоумение людей, впервые услышавших об этом! Они никак не могли поверить, что люди, живущие на противоположной стороне Земли (рис. 126), не падают в бездну.

Почему люди одинаково устойчивы в любом месте Земли? Земля притягивает к себе все тела.
Если бы Земля не обладала притяжением, брошенные горизонтально или вверх тела, двигаясь но инерции, никогда не вернулись бы на Землю. Тем не менее мяч, брошенный вертикально вверх, возвращается обратно (рис. 127, а). Траектория мяча, брошенного горизонтально, но мере движения искривляется (рис. 127, б). Спутник движется вокруг Земли по круговой орбите (рис. 127, в). Искривление траектории мяча, спутника есть также результат притяжения этих тел к Земле.
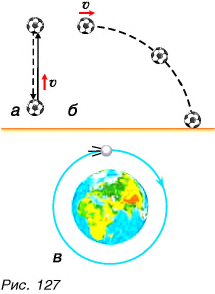
Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
Зависит ли сила тяжести от массы тела? Конечно, да. Из жизненного опыта мы хорошо знаем, что, чем больше масса налитой в ведро воды, тем труднее его удерживать. Слона Земля притягивает гораздо сильнее, чем зайца (рис. 128).
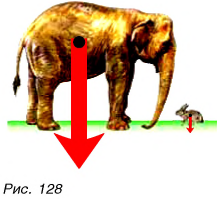
Во сколько раз увеличивается масса тела, во столько раз возрастает сила тяжести 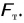 Иначе говоря, действующая на тело сила тяжести прямо пропорциональна массе тела:
Иначе говоря, действующая на тело сила тяжести прямо пропорциональна массе тела:
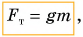
где 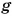 — коэффициент пропорциональности (о его числовом значении вы узнаете из § 25).
— коэффициент пропорциональности (о его числовом значении вы узнаете из § 25).
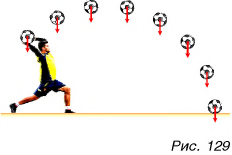
Сила тяжести направлена вертикально вниз (рис. 129) и приложена к центру однородного тела.
А обладают ли другие планеты притяжением, как Земля? Английский физик и математик Исаак Ньютон пришел к выводу, что притяжение свойственно всем планетам и вообще любому телу, обладающему массой, т. е. всем телам Вселенной. Поэтому явление взаимного притяжения тел названо всемирным тяготением.
Для любознательных:
Сила тяжести зависит не только от массы тела, которое притягивается, но и от массы того тела, которое притягивает (Земля, Луна и др.).
Все небесные тела притягивают к себе любые другие тела. Но так как массы и размеры небесных тел различны, то разной будет и действующая сила притяжения. Так, на Луне сила тяжести, действующая на тело, будет почти в 6 раз меньше, чем на Земле.
Масса Земли очень большая: 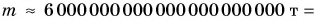
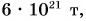 поэтому ее притяжение так велико. Земля притягивает не только тела, находящиеся на ее поверхности, но и удаленные от нее (искусственные спутники, Луну). Но мере удаления сила притяжения уменьшается (уменьшается
поэтому ее притяжение так велико. Земля притягивает не только тела, находящиеся на ее поверхности, но и удаленные от нее (искусственные спутники, Луну). Но мере удаления сила притяжения уменьшается (уменьшается 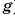 ), но сохраняется прямо пропорциональная зависимость силы тяжести от массы тела.
), но сохраняется прямо пропорциональная зависимость силы тяжести от массы тела.
Еще сильнее притяжение Солнца, так как его масса примерно в 300 000 раз больше массы Земли. Именно поэтому Земля и другие планеты движутся вокруг Солнца.
Главные выводы:
- Все тела во Вселенной обладают свойством притягивать к себе другие тела.
- Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
- Сила тяжести, действующая на тело, прямо пропорциональна его массе.
Пример №6
Плотность железного бруска в 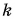 раз больше плотности деревянного. Объем железного бруска в
раз больше плотности деревянного. Объем железного бруска в 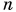 раз меньше объема деревянного. Во сколько раз отличаются силы тяжести, действующие на бруски?
раз меньше объема деревянного. Во сколько раз отличаются силы тяжести, действующие на бруски?
Дано:
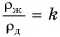
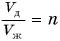
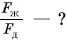
Решение
Силы тяжести, действующие на бруски, равны:
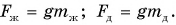
Массы брусков равны: 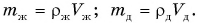
Отношение сил:
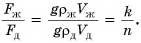
Ответ: 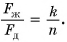
Сила упругости
На горизонтальном столе лежит шар. Как и на всякое тело, на него действует сила тяжести 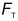 (рис. 132, а). Но почему он не падает вниз? Этому препятствует опора (крышка стола). В чем выражается действие опоры на лежащее на ней тело?
(рис. 132, а). Но почему он не падает вниз? Этому препятствует опора (крышка стола). В чем выражается действие опоры на лежащее на ней тело?
Из § 21 вы знаете, что приложенная к телу сила (даже очень большая) не вызывает изменения скорости движения тела, если она скомпенсирована (уравновешена) приложенной к нему противоположно направленной другой силой. Как возникает эта другая сила? В приведенном примере шар, притягиваясь Землей, давит на крышку стола. Сила давления 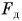 приложена к крышке стола и направлена вниз (рис. 132, б). Действуя на крышку, эта сила прогибает ее, т. е. деформирует крышку, хотя данная деформация и не заметна для глаз.
приложена к крышке стола и направлена вниз (рис. 132, б). Действуя на крышку, эта сила прогибает ее, т. е. деформирует крышку, хотя данная деформация и не заметна для глаз.
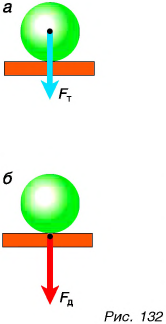
Вас. не должно удивлять утверждение, что любая, даже незначительная, сила давления (например, сила давления мухи, севшей на стол) вызывает деформацию. Деформации поверхности стола, на которую давит гиря, не видно. Но попробуйте положить под гирю поролон (рис. 133), и вы заметите его прогиб, т. е. деформация станет очевидной.
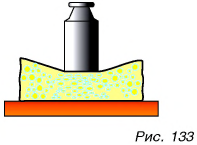
Вернемся к примеру с шаром. Деформированная опора, стремясь распрямиться, действует на шар с силой, направленной вверх (рис. 134), — силой упругости. Именно сила упругости 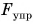 и компенсирует действие силы тяжести
и компенсирует действие силы тяжести 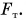
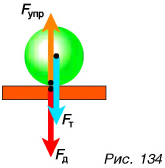
Проделаем еще один опыт. Подвесим шар к пружине, укрепленной на штативе. Шар, притягиваясь к Земле (рис. 135, а), движется и растягивает (деформирует) пружину. Деформирующая сила 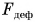 приложена к пружине и направлена вниз. Но движение шара не продолжается неограниченно. Что же препятствует движению?
приложена к пружине и направлена вниз. Но движение шара не продолжается неограниченно. Что же препятствует движению?
Как и в случае с лежащим шаром, сила упругости 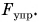 Она приложена к висящему шару, направлена противоположно деформирующей силе и равна ей по числовому значению. А теперь поместим шар на пружину сверху (рис. 135, б). Пружина сожмется под действием силы давления
Она приложена к висящему шару, направлена противоположно деформирующей силе и равна ей по числовому значению. А теперь поместим шар на пружину сверху (рис. 135, б). Пружина сожмется под действием силы давления 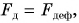 приложенной к ней. Препятствовать движению шара будет сила упругости
приложенной к ней. Препятствовать движению шара будет сила упругости 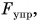 с которой пружина действует на шар.
с которой пружина действует на шар.
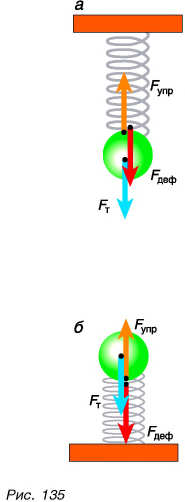
Итак, сила, действующая на тело со стороны деформированной опоры или подвеса, называется силой упругости.
Вы заметили закономерность? Сила упругости 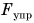 приложена к телу, вызвавшему деформацию опоры или подвеса. Она противоположна но направлению и численно равна деформирующей силе
приложена к телу, вызвавшему деформацию опоры или подвеса. Она противоположна но направлению и численно равна деформирующей силе 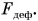 Но стоит убрать деформирующую силу — и растяжение, сжатие или прогиб исчезают, т. е. деформированное тело (пружина, стол) восстанавливает свои первоначальные размеры и форму.
Но стоит убрать деформирующую силу — и растяжение, сжатие или прогиб исчезают, т. е. деформированное тело (пружина, стол) восстанавливает свои первоначальные размеры и форму.
Для любознательных:
Иногда после действия большой деформирующей силы тело не возвращается к первоначальной форме. Например, покупая в магазине батон, вы определяете его свежесть, деформируя специальной ложкой. При действии на батон небольшой силы он после снятия воздействия восстанавливает форму, но если вы переусердствуете, нажимая ложкой, батон так и не сможет избавиться от своего непривлекательного деформированного вида.
Поскольку сила упругости возникает в ответ на воздействие (опора, подвес реагируют на воздействие), то силу упругости часто называют еще силой реакции.

Главные выводы:
- Сила упругости (сила реакции) возникает в ответ на действие деформирующей силы.
- Сила упругости приложена к телу, вызвавшему деформацию опоры или подвеса.
- Сила упругости противоположна деформирующей силе, но их модули равны.
Вес тела
При взаимодействии тел на каждое из них со стороны другого действует сила. Рассмотрим действие друг на друга тела и его горизонтальной опоры или тела и его вертикального подвеса.
На рисунке 140 представлены различные тела. Каждое из этих тел, притягиваясь к Земле, действует на опору или подвес с силой, которая вам хорошо знакома из предыдущего параграфа. Это сила давления на опору или сила натяжения подвеса. Иначе эту силу называют весом тела.

Почему тело действует на опору или подвес? Потому что его притягивает Земля. Неподвижные опора или подвес не позволяют телу падать и сами испытывают действие силы.
Вес — это сила, с которой тело вследствие притяжения Земли действует на опору или подвес.
Обозначим вес буквой Р и укажем вес каждого тела на рисунке 140. Вес мяча приложен к опоре (крышке стола), направлен вниз и является уже известной вам силой давления. Вес собаки приложен к земле в местах соприкосновения ее лап с землей и равен сумме четырех сил:
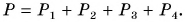
Определите сами и изобразите вес всех ос шальных тел, представленных на рисунке 140.
А теперь еще раз сравним силу тяжести и вес тела. У этих сил есть общее: они вызваны притяжением Земли. Эти силы очень часто (подчеркиваем — часто, но не всегда) численно равны друг другу. Но у силы тяжести и веса есть различия.
Во-первых, они приложены к разным телам: сила тяжести — к телу (шару), а вес. — к опоре или подвесу (крышке стола, нити) (рис. 141, а, б).
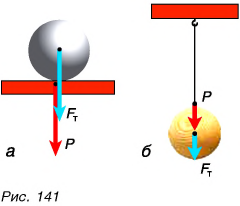
Во-вторых, сила тяжести в данном месте Земли имеет строго определенное значение 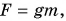 а вес тела может быть не только равен, но и больше или меньше этого значения.
а вес тела может быть не только равен, но и больше или меньше этого значения.
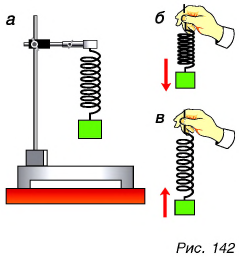
Докажем это с помощью опыта. Подвесим груз на пружине (рис. 142, а). Если мы будем равномерно поднимать и опускать этот груз, то удлинение пружины, а значит, и сила упругости и вес груза будут оставаться такими же, как в случае неподвижного груза. Но если мы неравномерно (с разгоном) опустим (рис. 142, б) или поднимем (рис. 142, в) груз в вертикальном направлении, то будут наблюдаться изменения в растяжении пружины, что указывает на изменения веса тела.
Для любознательных:
Вам известно, что действующая на тело сила тяжести на других планетах может быть как больше, так и меньше, чем на Земле. Значит, и вес тела на этих планетах будет другим.
А может ли тело вообще потерять вес? Космонавты и все тела в космическом корабле свободно парят, не оказывая действия на опору или подвес, т. е. их вес Р = 0. Это состояние тела называется невесомостью.
Невесомость можно создать и на Земле. Пустим свободно падать груз вместе с пружиной. Пружина не растягивается, а, значит, вес груза равен нулю. Это и есть невесомость.
Главные выводы:
- Вес тела — сила, приложенная к опоре или подвесу.
- Вес неподвижного или равномерно движущегося тела численно равен силе тяжести.
- Вес тела, движущегося неравномерно, может изменяться и быть больше силы тяжести, меньше и даже равным нулю.
Единица силы и измерение силы
Сила характеризуется числовым значением (модулем), направлением и точкой приложения. Чтобы определить числовое значение силы, нужно измерить силу, т. е. сравнить ее с другой силой, принятой в качестве единицы силы. Что принято за единицу силы?
Главный результат действия силы — изменение скорости движения тела, которая сама по себе никогда не изменяется. Исходя из этого, была выбрана в СИ единица силы — 1 ньютон (1 Н), названная в честь английского ученого Исаака Ньютона. Существуют кратные и дольные единицы силы: 1 кН = 1000 Н, 1 мН = 0,001 Н.
Сила, как вы знаете, может не только изменить скорость, но и вызвать деформацию тела. Пружина растягивается (рис. 143), потому что на нее действует вес груза, который притягивает Земля.
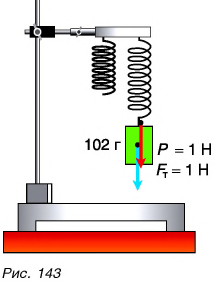
Какой массой должно обладать тело, чтобы действующая на него сила тяжести равнялась 1,0 И? Исследования показали, что с силой F = 1,0 Н Земля притягивает тело массой m = 0,102 кг.
Определим значение коэффициента 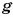 , входящего в формулу силы тяжести
, входящего в формулу силы тяжести 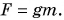 Из формулы видно, что
Из формулы видно, что 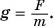 Так как на тело массой 0,102 кг Земля действует с силой
Так как на тело массой 0,102 кг Земля действует с силой 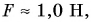 то:
то:
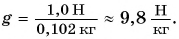
Значит, если масса тела равна 1,0 кг, то действующая на него сила тяжести 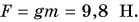 Следовательно, и вес этого тела (если оно находится в состоянии покоя или движется равномерно) Р = 9,8 Н. Ни в коем случае нельзя приравнивать вес и массу, что, к сожалению, часто встречается в быту. Это разные физические величины, и единицы у них разные. Масса измеряется в килограммах, вес — в ньютонах (рис. 144). Если ваша масса m = 50 кг, то ваш вес
Следовательно, и вес этого тела (если оно находится в состоянии покоя или движется равномерно) Р = 9,8 Н. Ни в коем случае нельзя приравнивать вес и массу, что, к сожалению, часто встречается в быту. Это разные физические величины, и единицы у них разные. Масса измеряется в килограммах, вес — в ньютонах (рис. 144). Если ваша масса m = 50 кг, то ваш вес 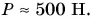

Как измерить силу? Для этого нужно создать измерительный прибор. Будем подвешивать к пружине сначала одну гирю массой m = 102 г = = 0,102 кг, затем две, три и т. д. Отметим метками положения указателя (рис. 145), напротив которых ставим значения 1 Н, 2 Н, 3 Н и т. д.
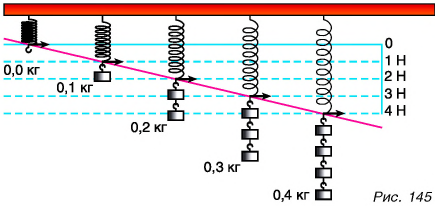
Пружина с указателем и шкалой представляет собой прибор для измерения сил — динамометр (от греч. dynamis — сила и metreo — измеряю) (рис. 146). Динамометром можно измерять не только вес тела, но и любые силы.

Динамометры бывают различных типов и размеров в зависимости от того, для измерения больших или малых сил они предназначены. Для измерения мускульной силы руки используют динамометр силомер (рис. 147, а). Определить силу тяги трактора позволяет тяговый динамо метр (рис. 147, б).

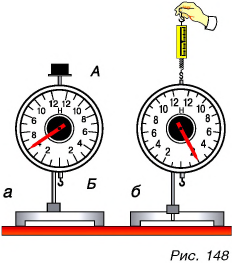
Для проведения различных исследований удобен динамометр с реечной передачей (рис. 148). Он позволяет измерять не только силу, направленную вниз, например создаваемую лежащим на опоре А телом (рис. 148, а), или вес подвешенного 1 к подвесу Б тела. Таким динамометром можно измерить и силу, направленную вверх (рис. 148, б).
Для любознательных:
Значение коэффициента 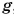 , равное
, равное 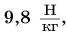 характерно только для Земли (оно несколько изменяется в зависимости от географической широты места и от высоты подъема тела над поверхностью Земли; с увеличением высоты значение
характерно только для Земли (оно несколько изменяется в зависимости от географической широты места и от высоты подъема тела над поверхностью Земли; с увеличением высоты значение 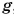 уменьшается).
уменьшается).
Для Луны этот коэффициент в б раз меньше, т. е. 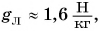 для Юпитера
для Юпитера 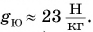 Для Солнца
Для Солнца 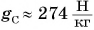 (почти в 30 раз больше, чем для Земли).
(почти в 30 раз больше, чем для Земли).
Главные выводы:
- В СИ единицей силы является 1 ньютон.
- Силу измеряют с помощью динамометра.
- С силой F = 1 Н Земля притягивает тело массой m = 0,102 кг.
- В формуле
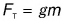 силы тяжести, с которой Земля действует на тело, постоянный коэффициент
силы тяжести, с которой Земля действует на тело, постоянный коэффициент 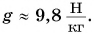
Пример №7
Зависимость силы тяжести, действующей на песок в песочных часах, от его объема представлена на рисунке 149. Определите плотность песка. Коэффициент 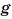 примите равным
примите равным 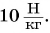
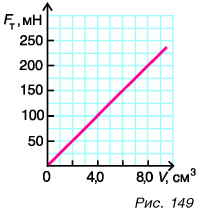
Решение
Плотность песка 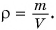 Масса песка
Масса песка 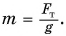 Силу тяжести для данного объема песка, например
Силу тяжести для данного объема песка, например 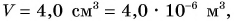 определим по данным графика
определим по данным графика 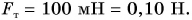 Тогда
Тогда 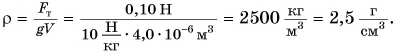
Ответ: 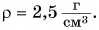
- Заказать решение задач по физике
Сложение сил и равнодействующая сила
На любое тело действует хотя бы одна сила — сила тяжести. Но чаще всего на тело действует несколько сил. Например, на шарик (рис. 151) действуют Земля и нить (две силы). Каков результат их действия?
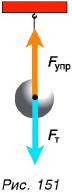
Решим такую задачу. Вы с другом перевозите на тележке груз, причем один из вас тянет тележку, прикладывая силу 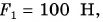 другой толкает ее, действуя с силой
другой толкает ее, действуя с силой 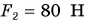 (рис. 152). Какова сила, которая двигает тележку?
(рис. 152). Какова сила, которая двигает тележку?
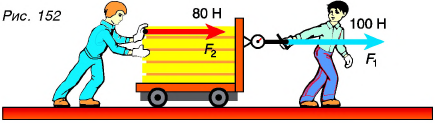
Эта сила 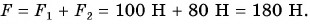 А изменилось бы движение тележки, если бы ее тянул один человек, прикладывая силу F = 180 Н? Нет, эффект был бы таким же. Значит, одна сила F оказывает на тележку такое же действие, как две одновременно действующие силы
А изменилось бы движение тележки, если бы ее тянул один человек, прикладывая силу F = 180 Н? Нет, эффект был бы таким же. Значит, одна сила F оказывает на тележку такое же действие, как две одновременно действующие силы 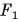 и
и 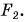
Сила, которая оказывает на тело такое же действие, как несколько одновременно действующих на него сил, называется равнодействующей этих сил.
Как направлена равнодействующая? Проведем опыт. К нижнему крючку динамометра подвесим груз весом 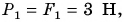 а на столик поместим груз весом
а на столик поместим груз весом 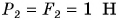 (рис. 153, а). Динамометр показывает действие на него силы F = 4 Н. Сила F — сумма весов нижнего и верхнего грузов. Эти силы направлены вертикально вниз. Заменим два груза одним весом 4 Н и подвесим его к динамометру (рис. 153, б). Динамометр показывает, что действие одного груза такое же, как и двух грузов весом
(рис. 153, а). Динамометр показывает действие на него силы F = 4 Н. Сила F — сумма весов нижнего и верхнего грузов. Эти силы направлены вертикально вниз. Заменим два груза одним весом 4 Н и подвесим его к динамометру (рис. 153, б). Динамометр показывает, что действие одного груза такое же, как и двух грузов весом 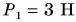 и
и 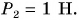 Значит, сила
Значит, сила 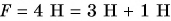 — равнодействующая двух сил, приложенных к динамометру. Изобразим эти силы схематически (см. рис. 153, в).
— равнодействующая двух сил, приложенных к динамометру. Изобразим эти силы схематически (см. рис. 153, в).
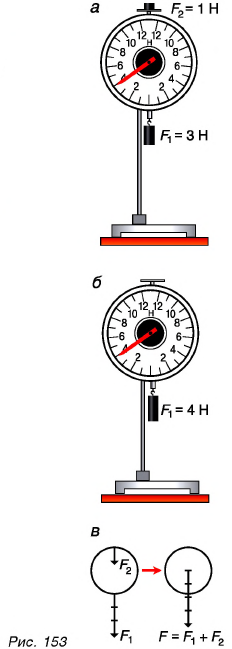
Модуль равнодействующей сил, действующих на тело в одном направлении но одной прямой, равен сумме модулей этих сил. Направление равнодействующей такое же, как и отдельных сил.
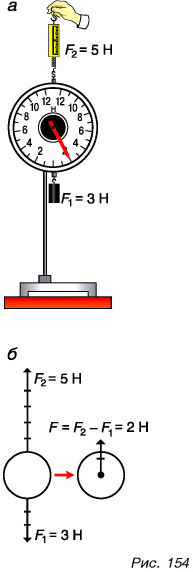
Изменим опыт: с помощью другого динамометра подействуем на данный динамометр вверх силой 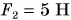 (рис. 154, а). Приложенные к динамометру силы направлены в противоположные стороны. Динамометр показывает силу
(рис. 154, а). Приложенные к динамометру силы направлены в противоположные стороны. Динамометр показывает силу 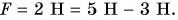 Это и есть равнодействующая двух противоположно направленных сил. Она направлена вверх, что подтверждается изменением направления поворота стрелки реечного динамометра.
Это и есть равнодействующая двух противоположно направленных сил. Она направлена вверх, что подтверждается изменением направления поворота стрелки реечного динамометра.
Значит, действие двух противоположно направленных сил можно заменить одной силой, модуль которой равен разности модулей двух приложенных сил и которая направлена в сторону большей силы (рис. 154, б).
А если силы 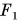 и
и 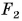 имеют равные модули? Тогда равнодействующая сила равна нулю. Происходит компенсация сил (см. § 21).
имеют равные модули? Тогда равнодействующая сила равна нулю. Происходит компенсация сил (см. § 21).
Ответим еще на один важный вопрос: как ведет себя тело при скомпенсированных силах, т. е. при нулевом значении равнодействующей?
Проведем опыт. Возьмем пенопластовую пластинку А очень малой массы. Подействуем на пластинку одинаковыми по модулю силами упругости нитей 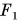 и
и 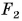 (рис. 155). Других сил нет. Силой тяжести, действующей на пластинку, можно пренебречь. Равнодействующая сил
(рис. 155). Других сил нет. Силой тяжести, действующей на пластинку, можно пренебречь. Равнодействующая сил 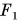 и
и 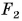 равна нулю. Пластинка находится в состоянии покоя. Толкнем пластинку. Она придет в движение и, если трение мало, будет двигаться равномерно, т. е. с постоянной скоростью. Но после прекращения толчка на пластинку по-прежнему действуют только силы
равна нулю. Пластинка находится в состоянии покоя. Толкнем пластинку. Она придет в движение и, если трение мало, будет двигаться равномерно, т. е. с постоянной скоростью. Но после прекращения толчка на пластинку по-прежнему действуют только силы 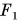 и
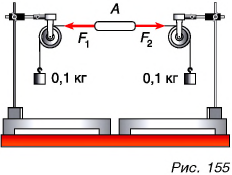
и 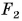 , их равнодействующая равна нулю. Опыт позволяет сделать очень важный вывод: если равнодействующая сил, приложенных к телу, равна нулю, тело находится в состоянии покоя или движется равномерно и прямолинейно. Приведите примеры, подтверждающие этот вывод.
, их равнодействующая равна нулю. Опыт позволяет сделать очень важный вывод: если равнодействующая сил, приложенных к телу, равна нулю, тело находится в состоянии покоя или движется равномерно и прямолинейно. Приведите примеры, подтверждающие этот вывод.
А если продолжить опыт и подвесить к одной нити два груза, а к другой — три? Пластинка придет в движение с увеличивающейся скоростью (рис. 156), ведь равнодействующая сил упругости нитей 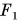 и
и 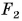 , приложенных к пластинке, уже не будет равна нулю.
, приложенных к пластинке, уже не будет равна нулю.
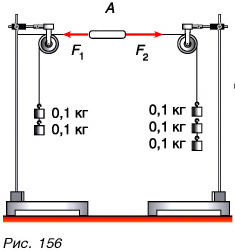
Внимание! Находить равнодействующую можно только для сил, приложенных к одному телу.
Для любознательных:
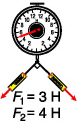
Если приложенные к телу силы действуют не вдоль одной прямой, то модуль равнодействующей силы не равен арифметической сумме этих сил. В показанном на рисунке опыте приложенные силы — 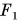 = 3 Н,
= 3 Н, 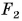 = 4 Н — перпендикулярны друг другу, а модуль равнодействующей F равен не 7 Н, а 5 Н, т. е. меньше суммы
= 4 Н — перпендикулярны друг другу, а модуль равнодействующей F равен не 7 Н, а 5 Н, т. е. меньше суммы 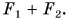
Главные выводы:
- Действие нескольких сил, приложенных к телу, можно заменить одной силой — их равнодействующей.
- Направление равнодействующей двух сил, действующих вдоль одной прямой, совпадает с направлением большей из них.
- Если равнодействующая сил, приложенных к телу, равна нулю, то оно либо покоится, либо движется равномерно и прямолинейно.
- Если равнодействующая всех сил, приложенных к телу, не равна нулю, скорость тела изменяется.
Пример №8
На автомобиль массой m = 2,0 т, движущийся равномерно по прямолинейному горизонтальному участку шоссе, действует сила сопротивления движению 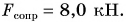 Определите силу тяги, развиваемую двигателем автомобиля. Изобразите все силы, действующие на автомобиль (масштаб: 0,5 см — 4000 Н). Найдите их равнодействующую.
Определите силу тяги, развиваемую двигателем автомобиля. Изобразите все силы, действующие на автомобиль (масштаб: 0,5 см — 4000 Н). Найдите их равнодействующую.
Дано:
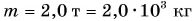
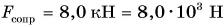
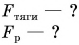
Решение
Если автомобиль движется равномерно, то равнодействующая всех сил, приложенных к нему, равна нулю. На автомобиль действуют: сила тяжести 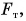 сила упругости
сила упругости 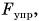 сила тяги
сила тяги 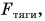 сила сопротивления
сила сопротивления 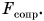
Изобразим 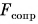 в рекомендуемом масштабе (рис. 157). Так как движение автомобиля равномерное, то равнодействующая сил:
в рекомендуемом масштабе (рис. 157). Так как движение автомобиля равномерное, то равнодействующая сил:
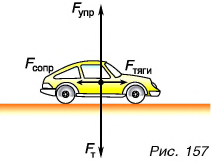
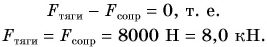
Аналогично 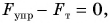 значит,
значит, 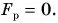
Ответ: 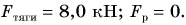
Трение и сила трения
Кто из вас не катался с горы на санках? Приобретя большую скорость, санки (рис. 158), выехав на горизонтальный участок, останавливаются. Почему? Вспомните, что действующая на тело сила может изменить скорость его движения. Этой силой является сила трения скольжения. А что нужно сделать, чтобы санки продолжали движение с той же скоростью? Необходимо скомпенсировать силу трения. Для этого следует тянуть санки горизонтально с силой, равной по модулю силе трения. От чего зависит сила трения?

Проведем опыт. Будем с помощью динамометра равномерно перемещать брусок по горизонтальной поверхности стола (рис. 159). Динамометр показывает, что на брусок действует сила тяги, но скорость движения бруска не изменяется. Значит, на брусок действует еще одна сила компенсирующая сила. Этой силой является сила трения 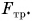 Равнодействующая сил
Равнодействующая сил 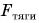 и
и 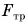 равна нулю. Обратите внимание, что модуль силы трения равен модулю силы тяги только в случае равномерного прямолинейного движения. Если же модуль силы тяги больше модуля силы трения, скорость движения тела будет возрастать. А если
равна нулю. Обратите внимание, что модуль силы трения равен модулю силы тяги только в случае равномерного прямолинейного движения. Если же модуль силы тяги больше модуля силы трения, скорость движения тела будет возрастать. А если 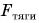 меньше
меньше 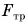 — убывать.
— убывать.
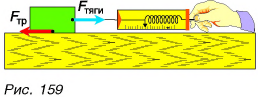
Итак, сила трения скольжения возникает при движении одного тела но поверхности другого и направлена в сторону, противоположную движению.
Почему возникает сила трения? Продолжим опыт. Будем равномерно перемещать брусок сначала по шероховатой, затем по обработанной поверхности доски. Сила тяги будет больше при движении по шероховатой поверхности (рис. 160, а). Значит, и модуль равной ей силы трения будет тем больше, чем более шероховатой, неровной окажется поверхность. При движении неровности цепляются друг за друга, деформируются, разрушаются. Это создает препятствия движению. А если бы поверхности были идеально гладкие, то возникла ли бы сила трения при движении одного тела по поверхности другого? Не спешите ответить «нет». При хорошо отполированных поверхностях расстояние между поверхностями тел или их участками при движении тел так мало, что станут существенными силы притяжения молекул поверхности одного тела к молекулам поверхности другого. Эти силы будут тормозить движение тел.
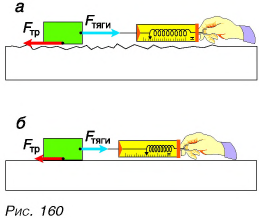
Значит, шероховатость поверхностей и силы притяжения между молекулами соприкасающихся поверхностей — причины возникновения сил трения.
Если при движении соприкасаются твердые поверхности тел, трение называют сухим.
От чего еще зависит сила сухого трения? Дадим ответ, исходя из опыта. Будем равномерно двигать брусок по различным поверхностям: по металлической, деревянной, резиновой — с примерно одинаковым качеством обработки (рис. 161). Динамометр показывает различную силу тяги. Следовательно, силы трения дерева но металлу, дерева по дереву, дерева по резине будут различны. Наибольшая сила трения возникнет при движении по поверхности резины. Не случайно подошвы в спортивной обуви (рис. 162) делают резиновыми и рельефными.
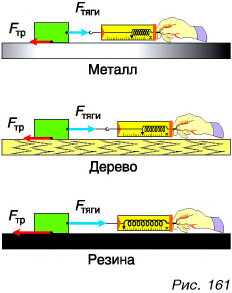

Поставим теперь на брусок гирю и сравним силы трения при равномерном движении ненагруженного бруска (рис. 163, а) и бруска с гирей (рис. 163, б). Видно, что во втором случае сила тяги, а значит, и сила трения увеличились. Но брусок с гирей с большей силой давит на поверхность, с которой соприкасается. Следовательно, сила трения тем больше, чем больше сила, прижимающая тело (брусок) к поверхности.
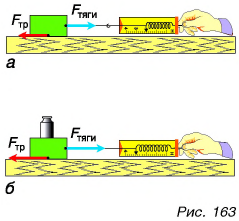
Как уменьшить трение? Здесь есть два пути. Первый — заменить трение скольжения трением качения. Проделаем такой опыт. Будем равномерно передвигать металлическую тележку по столу скольжением (рис. 164, а) и качением (рис. 164, б). Сила трения во втором случае значительно меньше, хотя материал поверхностей и прижимающая сила не изменяются. Значит, трение качения меньше трения скольжения. С тяжелым чемоданом справиться легко, если прикрепить к нему колеса.
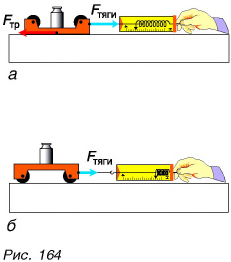
Второй путь уменьшения трения скольжения — это смазывание трущихся поверхностей. Смазка (например, масло) заполняет все неровности трущихся поверхностей и располагается тонким слоем между ними так, что поверхности перестают касаться друг друга. При этом сухое трение заменяется трением слоев жидкости (масла), а оно в 8—10 раз меньше.
Опытный водитель никогда не отправится в далекий путь, не проверив, достаточно ли масла в двигателе машины. Объясните, зачем он это делает.
Для любознательных:
А знаете ли вы, что с помощью катков перемещают дома? Например, в городе Москве во время реконструкции улицы Тверской некоторые дома были передвинуты на другое место именно таким способом.
В машинах для замены трения скольжения трением качения используют шариковые и роликовые подшипники (см. рис.). Подшипники диаметром 1,5—2 мм применяют в точных измерительных приборах. Вращающийся вал машины или другого механизма не скользит но неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах. Это снижает трение в 20—30 раз.

Главные выводы:
- Сила трения скольжения возникает при движении одного тела по поверхности другого.
- Сила трения скольжения направлена против движения.
- Сила трения зависит от свойств соприкасающихся поверхностей и силы, прижимающей тело к поверхности.
- Давление в физике
- Строение вещества в физике
- Физическое тело и вещество в физике
- Плотность и единицы плотности в физике
- Потенциальная энергия
- Кинетическая энергия
- Закон сохранения и превращения механической энергии
- Работа, мощность и энергия

В этой главе…
- Прилагаем силу
- Открываем три закона Ньютона
- Используем векторы силы для законов Ньютона
В этой главе описываются знаменитые три закона Ньютона. Вероятно, вам уже приходилось встречаться с разными формулировками этих законов, например “всякому действию всегда есть равное ему противодействие”. Эта формулировка не совсем верна, поскольку “всякой силе всегда есть равная ей противоположная сила”. В этой главе будут прояснены различия между этими формулировками. Законы Ньютона в данной главе используются для фокусировки вашего внимания на силах и их влиянии на окружающий нас мир.
Содержание
- Форсируем тему
- Первый закон Ньютона
- Поддерживаем движение: инерция и масса
- Измеряем массу
- Леди и джентльмены, встречайте второй закон Ньютона!
- Выбираем единицы измерения силы
- Вычисляем результирующую силу
- Вычисляем перемещение по известному времени, массе и действующим силам
- Вычисляем результирующую силу по известному времени и скорости
- Торжественный финал: третий закон Ньютона
- Учитываем трение
- Анализируем углы и величины в третьем законе Ньютона
- Ищем состояние равновесия
Форсируем тему
В окружающем нас мире нельзя избежать встречи с силами: силы используются для открытия двери, нажатия клавиш клавиатуры, управления автомобилем, подъема по ступенькам лестницы к Статуе Свободы, вытаскивания кошелька из кармана, разговора и даже для дыхания. Силы незримо присутствует всюду: во время пешеходной прогулки, катании на коньках, пережевывании хот-дога, открывании бутылки или моргании ресниц вашей ненаглядной спутницы. Сила неразрывно связана с движением объектов, а физика помогает понять, как эта связь работает.
Сила — это на самом деле довольно забавная тема. Как и другие физические темы, она кажется сложной только до настоящего знакомства с ней. Как наши старые “друзья”, перемещение, скорость и ускорение (см. главы 3 и 4), сила является вектором, т.е. имеет величину и направление.
Сэр Исаак Ньютон первым включил силу, массу и ускорение в одно уравнение в XVII веке. (Помните исторический анекдот с падением яблока на его голову, в результате чего он якобы придумал, как математически описать силу тяготения. Подробнее об этом рассказывается в главе 6, где Ньютон также является одним из основных действующих лиц.)
Законы Ньютона и скорость света
Законы Ньютона были пересмотрены Альбертом Эйнштейном в его теории относительности. В ней было показано, что законы Ньютона не выполняются для движения со скоростью, близкой к скорости света. Основная идея теории относительности заключается в том, что скорость света является наибольшей возможной скоростью. Это значит, что любое взаимодействие может происходить только с этой или меньшей скоростью. Следовательно, при приближении к этой скорости нужно учитывать изменяющийся характер взаимодействия; Например, измерение длины ракеты, движущейся со скоростью света, будет отличаться от измерения длины неподвижной ракеты. Как будет показано в главе 21, теория относительности Эйнштейна в значительной степени изменила представленный Ньютоном взгляд на мир и его законы.
Как часто происходит со многими физическими открытиями, Ньютон сначала внимательно наблюдал за поведением объектов, мысленно моделировал его, а затем выразил в математической форме. Зная основные сведения о векторах (которые изложены в главе 4), эта математика не вызовет у вас никаких трудностей.
Ньютон описал свою модель с помощью трех утверждений, которые теперь называются законами Ньютона. Однако нужно помнить, что на самом деле это не окончательные “законы природы”, ведь физики могут создавать лишь модели природы, которые часто впоследствии пересматриваются и уточняются.
Первый закон Ньютона
Барабанную дробь, пожалуйста! Законы Ньютона описывают силы и движение, а его первый закон гласит: “Объект находится в состоянии равновесия или прямолинейном движении с постоянной скоростью, если не подвергается внешнему воздействию”. Нужен перевод? Если вы не прилагаете силу к объекту в покое или “постоянном” движении, то он останется в покое или таком же движении по прямой. Причем вечно!
Например, при игре в хоккей шайба после удара движется к воротам по прямой, скользя по льду почти без трения. В случае удачи соперник не сможет зацепить шайбу своей клюшкой, т.е. не сможет изменить “постоянное” движение шайбы по прямой (и воспрепятствовать голу).
В повседневной жизни объекты не движутся так беспрепятственно, как в случае с шайбой на льду. Большинство окружающих нас объектов испытывает силу трения. Например, при скольжении кофейной чашки по гладкому столу она постепенно замедляет свое скольжение и останавливается (иногда с проливанием кофе не стоит чересчур упражняться, ибо вы рискуете испачкаться или ошпариться горячим кофе). Это совсем не значит, что первый закон Ньютона неверен. Наоборот, именно сила трения принуждает чашку изменить свое движение и остановиться.
Выражение “если не прилагать никакого действия к постоянно движущемуся объекту, он будет двигаться вечно” выглядит так же ужасно, как идея “вечного двигателя”. Однако полностью избавиться от внешнего воздействия сил невозможно, даже если объект находится в межзвездном пространстве. Даже на объекты в самых далеких уголках космоса оказывает воздействие (пусть даже очень слабое) масса других объектов Вселенной. А это значит, что на любое движение всегда оказывается внешнее воздействие, потому вечное постоянное движение в принципе невозможно.
Первый закон Ньютона утверждает лишь то, что единственным способом изменения движения является приложение внешней силы. Иначе говоря, сила является причиной движения. Кроме того, он гласит, что движущийся объект стремится оставаться в движении, что приводит к идее инерции.
Поддерживаем движение: инерция и масса
Инерция — это естественная тенденция объекта оставаться в покое или в движении с постоянной скоростью вдоль прямой линии. Инерция вызвана массой, а масса объекта является мерой инерции. Чтобы привести объект в движение, т.е. изменить его текущее состояние движения, необходимо приложить силу для преодоления инерции.
Представьте себе причал с маленькой шлюпкой и большим танкером с нефтью. Если попробовать толкнуть их ногой, то поведение этих судов будет разным. Шлюпка заскользит по водной глади, а танкер едва “вздрогнет” (да и для этого потребуется невероятно сильный толчок!). Дело в том, что они обладают совершенно разной массой и потому разной инерцией. В ответ на одинаковую силу объект с малой массой (и малой инерцией) ускорится в большей мере, чем объект с малой массой и большей инерцией.
Инерция, т.е. тенденция массы сохранять неизменность текущего состояния движения, иногда может представлять проблему. Например, в рефрижераторе тяжелые туши мороженного мяса подвешены к потолку кузова. Если рефрижератор войдет в крутой поворот на большой скорости, то туши по инерции начнут раскачиваться, как маятники, и их трудно будет остановить. Часто неопытные водители не учитывают инерцию туш мяса, и это приводит к печальным последствиям, например к опрокидыванию машины.
Поскольку масса обладает инерцией, то она сопротивляется изменению движения. Именно поэтому нам приходится прилагать силу для ускорения своего движения. Масса связывает силу и ускорение.
Измеряем массу
В разных системах измерения физических величин для указания массы (а значит, и инерции) используются разные единицы. В системе СГС используется грамм, а в системе СИ — килограмм, который содержит 1000 грамм.
А какая единица используется в Английской системе мер на основе фута-фунта- дюйма? Наберитесь мужества: в ней используется единица “слаг”, которая эквивалентна 14,5939 килограмма.
Учтите, что масса не равна весу. Масса — это мера инерции, а вес — это сила, которую оказывает сила притяжения Земли, измеренная на ее поверхности. Например, в Английской системе мер на основе фута-фунта-дюйма слаг имеет вес около 32 фунтов.
Леди и джентльмены, встречайте второй закон Ньютона!
Первый закон Ньютона очень и очень серьезен, но не выражается в математической формулировке, которая так необходима физикам. Потому Ньютон предложил свой второй закон: “если результирующая сила ( sum!F ) действует на объект массы ( m ), то ускорение ( a ) объекта можно вычислить по формуле ( sum!F=ma )”. В “переводе” это значит: сила равна массе, умноженной на ускорение. Символ ( sum ) означает суммирование, а значит, точнее говоря, закон гласит: суммарная, или результирующая, сила равна массе, умноженной на ускорение. (С точки зрения физики процесса, а не формальной математики, ускорение является следствием действия силы, а не наоборот. Потому логичнее было бы сформулировать второй закон Ньютона так: ( a=sum!F/m ), т.е. ускорение объекта прямо пропорционально результирующей силе на него и обратно пропорционально массе.)
Согласно первому закону Ньютона, движущееся тело остается в прямолинейном движении с постоянной скоростью, если на него не действует сила. Получается, что на самом деле он является частным случаем второго закона Ньютона, когда ( sum!F=0 ). Ведь в таком случае ускорение равняется нулю, о чем говорится в первом законе Ньютона. Взгляните на хоккейную шайбу на рис. 5.1: шайба ускоряется, пока на нее действует сила.
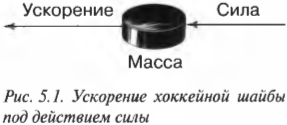
Попробуйте применить уже полученные знания физики в этом примере. Действительно, если даже на долю секунды с помощью клюшки применить силу к шайбе, то она ускорится и, несомненно, попадет в сетку! В данном примере сила применена к клюшке с определенной массой, которая ускорилась и придала это ускорение шайбе.
Чему равно это ускорение? Эта величина зависит не только от единиц измерения массы, но и от единиц измерения силы.
Выбираем единицы измерения силы
Итак, в каких единицах выражается сила? Поскольку ( sum!F=ma ), то, например, в системе СИ сила выражается следующим образом:
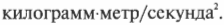
Поскольку большинство людей считают эту единицу чересчур сложной, то в системе СИ используется специальная единица — ньютон (угадайте, в честь кого?). Сокращенно “ньютон” записывается как Н. В системе СГС сила выражается следующим образом:
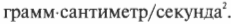
Это тоже довольно неуклюжая единица, и в системе СГС для силы предложено использовать особую единицу — дина, причем 1 ньютон равен 105 динам.
Еще проще выражается единица сила в Английской системе мер на основе фута-фунта-дюйма-секунды — фунт, который выражается следующим образом:
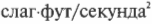
и равен 4,48 ньютонам.
Вычисляем результирующую силу
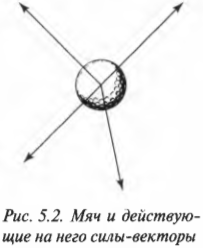
В большинстве учебников вместо полной записи ( sum!F=ma ) используется сокращенная — ( F=ma ), где под ( F ) подразумевается результирующая сила. Объект реагирует именно на результирующую силу, которая является суммой всех сил-векторов. Например, на рис. 5.2 показан мяч для игры в гольф и действующие на него силы. Как и в каком направлении будет двигаться мяч?
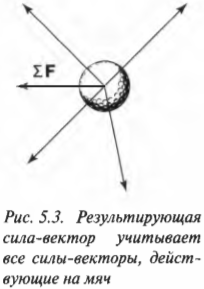
Поскольку во втором законе Ньютона говорится о результирующей силе, то задача упрощается. Все, что нужно сделать, так это сложить все силы-векторы для получения результирующей силы-вектора, как показано на рис. 5.3. Далее, для определения характера движения мяча нужно применить формулу ( sum!F=ma ).
Вычисляем перемещение по известному времени, массе и действующим силам
Допустим, что во время игры в мяч вы заинтересовались силами, действующими на мяч. Вот в одной из игровых ситуаций три игрока одновременно пытаются завладеть мячом и действуют на него тремя силами, как показано на рис. 5.4.
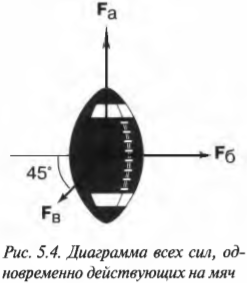
Схема на рис. 5.4 в физике называется диаграммой сил, действующих на тело. С ее помощью можно определить компоненты сил и результирующую силу.
Допустим, что с риском для жизни во имя науки вам удалось определить величины сил игроков:
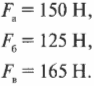
Допустим, что масса мяча точно равна 1,0 кг. Вопрос звучит так: где будет мяч через 1 секунду? Вот те этапы, которые нужно пройти, чтобы вычислить перемещение мяча по известному времени движения и ускорению (которое еще нужно определить по известной массе и действующим силам), т.е. дать окончательный ответ на этот вопрос.
- Найти результирующую силу ( sum!F) с помощью операции сложения векторов (подробное описание этой операции приводится в главе 4), складывая все силы, действующие на объект.
- Определить вектор ускорения по формуле ( sum!F=ma ).
- Вычислить пройденное расстояние за заданное время по формуле ( mathbf{s}=mathbf{v_0}(t_1-t_0)+{}^1!/!_2mathbf{a}(t_1-t_0)^2 ) (см. главу 3, где подробно описывается эта формула).
Пора подставлять числа и доставать калькулятор. Итак, для связи силы, массы и ускорения нужно, прежде всего, определить результирующую силу. Для этого нужно разложить на компоненты все векторы-силы на рис. 5.4, а потом сложить компоненты, чтобы получить компоненты вектора результирующей силы (более подробно операция разбиения вектора на компоненты приводится в главе 4).
Компоненты векторов ( mathbf{F_а} ) и ( mathbf{F_б} ) можно определить очень легко, поскольку вектор ( mathbf{F_а} ) ориентирован вдоль положительного направления оси Y, а вектор ( mathbf{F_б} ) — вдоль положительного направления оси X. Это значит, что компоненты этих векторов выражаются следующим образом:
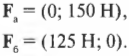
Компоненты вектора ( mathbf{F_в} ) определяются немного сложнее, поскольку нам все придется их вычислить:
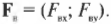
Вектор ( mathbf{F_в} ) направлен под углом 45° по отношению к отрицательному направлению оси Х, как показано на рис. 5.4, и под углом ( theta ) = 180°+45°=225° к положительному направлению оси X. Тогда компоненты вектора ( mathbf{F_в} ) определяются следующим образом:
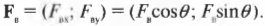
После подстановки чисел получим:
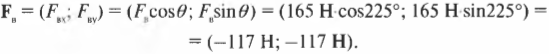
Обратите внимание на знак “минус” — оба компонента вектора ( mathbf{F_в} ) отрицательные. Полученный результат всегда можно быстро проверить на непротиворечивость. Вектор ( mathbf{F_в} ) направлен вниз и вправо, т.е. вдоль отрицательных направлений оси X и Y. Это значит, что оба компонента ( F_{вx} ) и ( F_{вy} ) должны быть отрицательными. Мне доводилось видеть людей, которые не могли правильно определить знак компонентов вектора, поскольку они не умели выполнять такую простую проверку непротиворечивости.
Всегда сравнивайте знаки компонентов векторов с фактическим направлением вдоль осей. Такая простая и быстрая проверка позволяет избежать многих потенциальных проблем.
Теперь нам известно, что:

И можно приступать к сложению векторов:
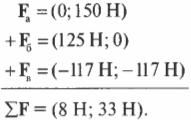
Итак, мы вычислили результирующую силу ( sum!mathbf{F} ), которая равна (8 Н; 33 Н). Мы тем самым также определили направление движения мяча. На следующем этапе нужно определить ускорение на основании второго закона Ньютона:
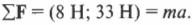
Это означает, что:
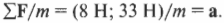
Поскольку масса мяча равна 1 кг, то, подставляя это значение в предыдущую формулу, получим:
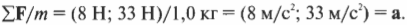
Неплохой прогресс: теперь вы знаете ускорение мяча. Теперь, чтобы узнать расстояние ( mathbf{s} ), которое преодолеет мяч за 1 секунду, нужно использовать приведенную ниже формулу (из главы 3):
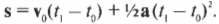
После подстановки чисел получим:
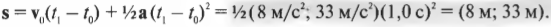
Ну что ж, совсем неплохо. После 1 секунды движения мяч продвинется на 8 метров вдоль положительного направления оси X и на 33 метра вдоль положительного направления оси Y. Достаньте секундомер, засеките промежуток времени длительностью 1 с и убедитесь, что мяч продвинулся на 8 метров вдоль горизонтальной линии и на 33 метра вдоль вертикальной линии. Вот вам еще один успешный физический эксперимент.
Вычисляем результирующую силу по известному времени и скорости
В предыдущем разделе перемещение объекта было вычислено по известному времени движения с постоянным ускорением. А как поступить, если нужно решить обратную задачу: как определить результирующую силу по известному времени и достигнутой скорости? Допустим, что нужно ускорить автомобиль от 0 до 60 миль в час за 10 секунд. Какую силу нужно приложить для этого? Сначала нужно преобразовать единицы измерения для более удобной работы со значениями скоростей, т.е. мили в час преобразовать в футы в секунды.

Обратите внимание на то, что часы и минуты в итоге сократились, а остались только мили и секунды. Теперь нужно выразить результат в футах в секунду:
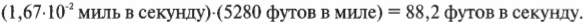
Итак, за 10 секунд автомобиль разгонится до скорости около 88 футов в секунду. Если автомобиль весит около 2000 фунтов, то какая сила потребуется для такого ускорения? Сначала найдем величину самого ускорения на основе приведенной ниже формулы (более подробно она описывается в главе 3):
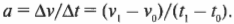
Подставляя числа, получим:
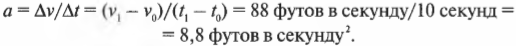
Итак, искомое ускорение равно 8,8 футов в секунду2. Согласно второму закону Ньютона:
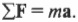
Нам известно, что вес автомобиля равен 2000 фунтам. Чему равна масса автомобиля в другой системе единиц измерения, а именно в системе на основе фута-фунта-дюйма- секунды или в слагах? В этой системе единиц измерения нужно поделить вес на ускорение свободного падения под действием гравитации, т.е. 32,17 фута в секунду2 (эта величина получена после преобразования уже известной нам величины 9,8 метра в секунду2):
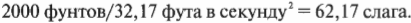
Теперь у нас есть все, что нужно для вычисления силы. Какая сила потребуется, чтобы автомобиль весом 62,17 слага двигался с ускорением 8,8 фута в секунду2. Нам нужно просто перемножить эти численные значения:
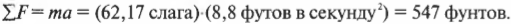
Итак, после округления до 2 значащих цифр получим, что для ускорения автомобиля до скорости 60 миль в час за 10 секунд потребуется сила 550 фунтов.
Учтите, что в данной задаче игнорируются такие особенности, как трение и наклон дороги. Более подробно эти вопросы рассматриваются в главе 6. Даже при движении по плоской поверхности без наклона трение может играть очень большую роль, и для ускорения автомобиля с учетом трения часто требуется приложить силу на 30% больше, чем 550 фунтов.
Торжественный финал: третий закон Ньютона
Этот закон движения особенно популярен среди борцов и инструкторов вождения автомобилей. Он гласит: сила действия одного объекта на другой равна по величине силе противодействия другого объекта, направленной в противоположную сторону.
Наиболее популярной формулировкой этого закона является следующая: “для любого действия всегда найдется равное ему и противоположное действие”. Однако физики предпочитают вместо неконкретного термина “действие” использовать более точный термин “сила”. Дело в том, что под действием часто подразумеваются совершенно разные явления, например характер голосования на избирательном участке или изменение температуры.
Допустим, что вы едете в автомобиле и для движения шина автомобиля должна прилагать силу к дороге (т.е. отталкиваться от нее), ибо иначе автомобиль не сможет двигаться. В таком случае дорога оказывает такую же силу на шину автомобиля, как показано на рис. 5.5.
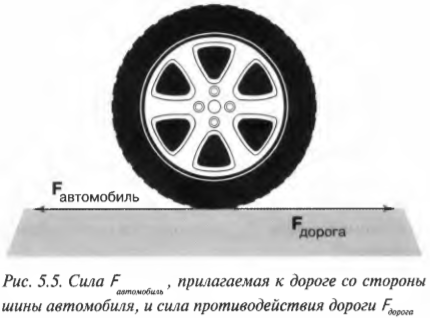
Если бы силы действия автомобиля была больше силы противодействия, то шина проскальзывала бы по дороге, как при движении по льду.
У внимательного читателя может возникнуть вопрос: а почему дорога не движется в обратную сторону? На самом деле, верьте или нет, но третий закон Ньютона действует и дорога движется в обратную сторону. Действительно, шина автомобиля прилагает силу к поверхности дороги и приводит в движение Землю. Однако, учитывая, что масса Земли в 6⋅1021 раз больше массы автомобиля, это действие практически незаметно.
Учитываем трение
Когда хоккеист бьет клюшкой по шайбе, она ускоряется с места удара и ускоряется сам хоккеист. Если бы шайба имела массу 1000 кг (а не 105-185 г), то хоккеист, несомненно, ощутил бы это ускорение в гораздо большей мере. При таком нереальном соотношении масс хоккеиста и шайбы могло случиться так, что после удара шайба едва сдвинулась бы, а хоккеист заскользил бы в обратном направлении. (Более подробно такая ситуация описывается в части III.)
Допустим, что в данном фантасмагорическом примере по окончании игры нужно оттащить такую чудовищно тяжелую шайбу в сторону с помощью каната, как показано на рис. 5.6.
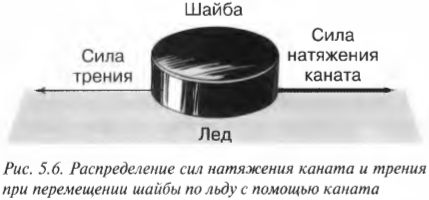
В физических задачах часто используются канаты, а также блоки, причем сила, с которой канат тянут с одного конца, равна силе сопротивления на другом конце каната.
В данном случае 1000-килограммовая шайба будет испытывать силу трения, пусть небольшую, но ощутимую. Итак, результирующая сила равна:

Поскольку сила натяжения каната ( F_{канат} ) больше силы трения ( F_{трение} ), то шайба начнет движение, причем ускоренное. Величину ускорения можно определить по известной формуле из второго закона Ньютона:
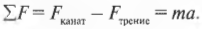
Одна часть силы натяжения каната ( F_{канат} ) расходуется на ускорение шайбы, а другая — на преодоление силы трения ( F_{трение} ):
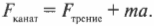
Однако сила натяжения каната с одной стороны равна силе натяжения каната с другой, согласно третьему закону Ньютона.
Рассмотрим теперь немного другую ситуацию, показанную на рис. 5.7. Допустим, что канат перекинут через блок и таким образом вам нужно поднять груз массы ( M ). Чтобы поднять груз, нужно преодолеть силу тяжести, которая действует на груз весом ( Mg ). Здесь ( g ) — это ускорение свободного падения под действием гравитации, равное 9,8 см/с2 (более подробно сила гравитации описывается в главе 6). На рис. 5.7 показана общая схема приложения силы к канату, необходимая для удержания груза.
Канат и блок используются не только для удержания груза, но и для изменения направления приложения силы. Сила прилагается вниз, а груз под ее действием движется вверх, поскольку канат перекинут через блок, где и происходит изменение направления действия силы. В данном случае, если сила натяжения каната ( F ) на свободном конце больше веса груза ( Mg ), то груз будет двигаться вверх с ускорением ( a ), согласно формуле:
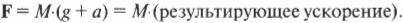
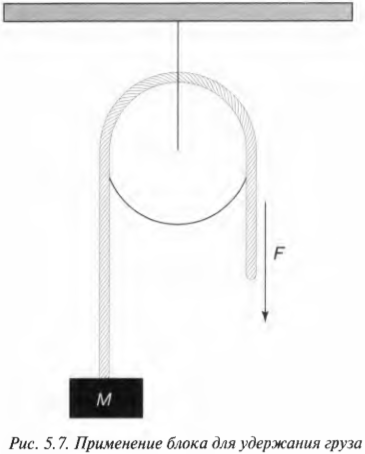
Подсчитаем теперь силу, действующую на потолок, к которому прикреплен блок. Если блок находится в покое, то действующая на него результирующая сила ( sum!F=0 ). Это значит, что все силы, которые действуют на блок, в сумме дают 0.
На блок действуют две силы, направленные вниз: сила натяжения каната ( F ) на свободном конце и сила со стороны груза с весом ( Mg ), движущегося с ускорением ( a ). Согласно третьему закону Ньютона, они равны, и сумма двух сил, направленных вниз, равна ( 2F ). Поскольку действующая на блок результирующая сила ( sum!F=0 ), то действующая на блок и направленная вверх сила со стороны потолка тоже равна ( 2F ).
Ни одна сила не может прилагаться к объекту без возникновения равной по величине и противоположной по направлению силы (даже если какая-то ее часть порождается ускоренным движением объекта). В предыдущем примере канат и блок позволяют изменять направление действия силы. Однако такое изменение направления силы от ( -F ) до ( +F ) возможно за счет приложение силы ( 2F ) к блоку со стороны потолка.
Анализируем углы и величины в третьем законе Ньютона
Чтобы учесть углы приложения силы, нужно вспомнить правила сложения векторов. Взгляните на рис. 5.8, где с помощью каната и блока сила ( F ) прилагается для удержания в состоянии покоя груза с массой ( M ). Вопрос: с какой величиной и в каком направлении действует сила ( F_{опора} ) на опору блока?
Поскольку блок не движется, то действующая на него результирующая сила ( sum!F=0 ). Теперь нужно найти все силы, которые действуют на блок. Во-первых, нужно учесть силу тяжести ( mathbf{F_{груз}}=Mmathbf{g} ), которая действует на груз. После разложения вектора этой силы на компоненты (подробнее об этом рассказывается в главе 4) получим (Y-компонента силы имеет отрицательный знак, поскольку она направлена вниз, т.е. вдоль отрицательного направления оси Y):
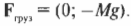
Теперь вычислим силу натяжения каната с другого конца ( F_{канат} ). Поскольку груз не движется, то сила натяжения каната на одном конце равна силе натяжения каната на другом конце. После разложения вектора силы натяжения каната на компоненты получим (Х-компонента силы имеет положительный знак, поскольку она направлена вправо, т.е. вдоль положительного направления оси X):
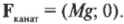
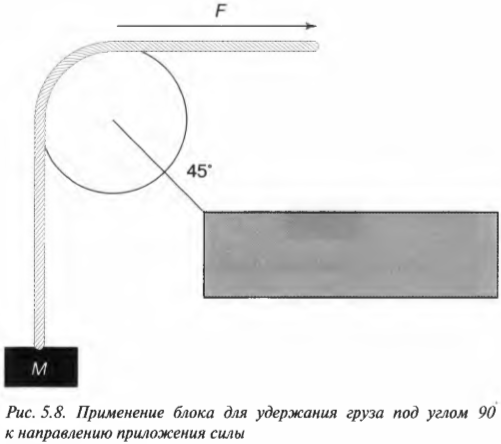
Теперь, чтобы найти результирующую силу, действующую на блок со стороны каната, нужно сложить компоненты сил ( F_{груз} ) и ( F_{канат} ):
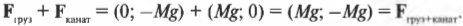
Нам известно, что:

где ( F_{опора} ) — это сила, которая действует на опору блока.
Это значит, что:
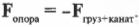
Следовательно:
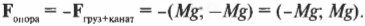
Глядя на рис. 5.8, можно легко проверить направление этого вектора. Действительно, блок должен противостоять силе тяжести груза (т.е. возникает сила противодействия, направленная вверх) и натяжению каната (т.е. возникает сила противодействия, направленная вправо).
Попробуем теперь определить величину и направление вектора силы ( F_{опора} ) (подробнее об этом рассказывается в главе 4). Величина этого вектора определяется по теореме Пифагора:
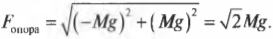
Обратите внимание на то, что здесь (как и в предыдущем примере) величина силы на опору блока больше величины каждой из сил по отдельности. Такова плата за изменение направления силы.
А в каком направлении действует сила ( F_{опора} )? Из рис. 5.8 ясно, что сила ( F_{опора} ) должна быть направлена влево и вверх, а теперь попробуем проверить это предположение с помощью тригонометрии. Если ( theta ) — это угол, под которым сила ( F_{опора} ) направлена по отношению к положительному направлению оси X, то Х-компонента силы ( F_{опора} ) имеет вид:
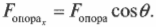
Следовательно:
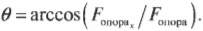
Нам уже известно, что:
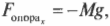
а также:
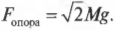
В итоге получим:
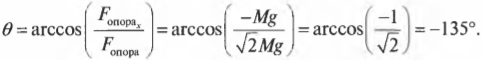
Нетрудно проверить, глядя на рис. 5.8, что найденное значение для направления силы на опору (-135) соответствует нашим предварительным оценкам и ожиданиям.
Если вы не уверены в правильности определения знаков сил, то всегда пробуйте проверить полученные значения с помощью визуального анализа нарисованной схемы распределения сил. Один рисунок порой стоит больше тысячи слов, особенно в физике!
Ищем состояние равновесия
В физике считается, что объект находится в состоянии равновесия, если его ускорение равно нулю, т.е. действующая на него результирующая сила равна 0. При этом объект необязательно должен находиться в покое — он может двигаться даже со скоростью 1000 километров в час, но без ускорения. Конечно, на объект в состоянии равновесия могут действовать самые разные силы, но их векторная сумма должна быть равна нулю.
На рис. 5.9 показана схема распределения сил, действующих на рекламную вывеску перед магазином, которую вы собираетесь подвесить на проволоке, выдерживающей силу 15 Н.
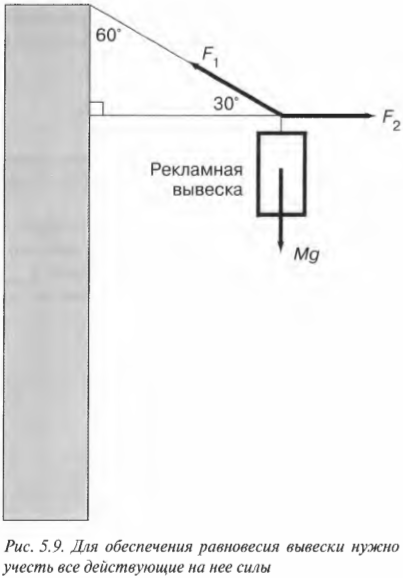
Допустим, что вес вывески равен 8 Н. Хватит ли прочности проволоки для ее подвешивания? Иначе говоря, чему равна сила натяжения проволоки ( F_1 ) на этой схеме? Вывеска должна быть в состоянии равновесия, значит, результирующая сила на нее ( sum!F=0 ). Следовательно, весь вес вывески ( Mg ) должен быть уравновешен силой натяжения проволоки ( F_1 ).
В данном примере единственная направленная вверх сила — это Y-компонента силы ( F_1 ), как показано на рис. 5.9. Сила сопротивления ( F_2 ) горизонтальной балки направлена только по горизонтали, а потому не оказывает никакого влияния на вертикальную компоненту результирующей силы. С помощью навыков тригонометрии (более подробно базовые сведения по тригонометрии приводились в главе 4) можно определить Y-компоненту силы ( F_1 ):
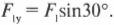
Величина этой компоненты силы равна весу вывески:
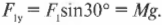
Отсюда получаем натяжение проволоки:
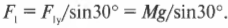
Поскольку вес ( Mg ) вывески равен 8 Н, то получим
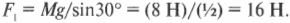
Ну и дела! Похоже, что проволока должна выдерживать силу 16 Н, а мы уже купили проволоку, выдерживающую всего 15 Н. Мораль сей задачи такова: нужно купить проволоку попрочнее!
Допустим, что мы купили более прочную проволоку и теперь интересуемся, достаточно ли прочна горизонтальная балка, чтобы выдержать силу сопротивления ( F_2 ), как показано на рис. 5.9. Какую прочность должна иметь балка, чтобы выдержать вес вывески? Иначе говоря, какую силу должна выдержать балка? На рис. 5.9 показаны только две горизонтальные силы: сила сопротивления балки ( F_2=F_{балка} ) и Х-компонента силы ( F_1 ). Нам уже известно, что ( F_1 ) = 16 Н. Теперь нам осталось только вычислить ( F_2 ). Для начала нужно определить Х-компоненту силы ( F_1 ) Глядя на рис. 5.9 и используя тригонометрию, получим:
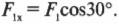
Именно эта компонента силы натяжения проволоки равна силе сопротивления балки:
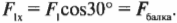
Это значит, что:
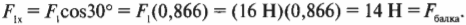
Итак, балка должна выдерживать силу около 14 Н.
Для подвешивания вывески весом около 8 Н потребуется проволока, выдерживающая силу около 16 Н, и балка, выдерживающая силу около 14 Н. Посмотрите снова на рис. 5.9: Y-компонента силы натяжения проволоки должна выдерживать вес груза. Такая прочность проволоки и балки нужна для того, чтобы изменить направление силы тяжести груза.
Глава 5. Толкаем, чтобы привести в действие: сила
2.9 (58.71%) 31 votes
Содержание:
- Определение и формула силы
- Второй закон Ньютона
- Единицы измерения силы
- Примеры решения задач
Определение и формула силы
Определение
Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень»
(интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.
Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.
Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.
Второй закон Ньютона
Равнодействующая всех сил приложенных к телу (векторная сумма всех сил)
($bar{F}$) равна производной от импульса тела по времени:
$$bar{F}=sum_{i=1}^{n} bar{F}_{i}=frac{d bar{p}}{d t}(1)$$
где $bar{p}=m bar{v}$ – импульс тела, m–масса рассматриваемого тела,
$bar{v}$ – скорость. Надо отметить, что уравнение (1) строго применимо только относительно
материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней
(второй закон Ньютона) можно представить в виде:
$$bar{F}=m frac{d bar{v}}{d t}=m bar{a}(2)$$
где $bar{a}$ – ускорение, которое материальная точка приобретает в результате
воздействия на нее силы. Выражение (2) показывает то, что если
$bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=frac{Delta p}{Delta t}=frac{mleft(v_{2}-v_{1}right)}{t_{2}-t_{1}}$$
Единицы измерения силы
Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с2
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. Уравнения $x=alpha t^{3}, y=beta t$ ($alpha$ и
$beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const.
Как изменяется по модулю сила, которая действует на точку?
Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:
$bar{F} = mbar{a} (1.1)$
Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения.
Для этого найдем производные по времени от соответствующих координат:
$$
begin{array}{c}
a_{x}=frac{d^{2} x}{d t^{2}}=6 alpha t(1.2) \
a_{y}=frac{d^{2} y}{d t^{2}}=0(1.3)
end{array}
$$
Так как модуль ускорения равен:
$$a=sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$
то, учитывая выражения (1.2) и (1.3), получаем:
$a = 6 alpha t (1.5)$
Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили:
$$bar{a}=6 alpha t cdot bar{i}(1.6)$$
где $bar{i}$ – единичный вектор, направленный по оси X.
Исходя из второго закона Ньютона, имеем:
$$F=m cdot 6 alpha t, bar{F}=m 6 alpha t cdot bar{i}$$
Ответ. Так как $F=m cdot 6 alpha t$, то с течением времени сила увеличивается по модулю.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m1, второго – m2. Первое тело толкнули с силой F0.
Какова сила давления тел друг на друга (F)?
Решение. Сделаем рисунок.
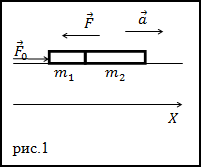
Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:
$$bar{F}_{0}+bar{F}+m_{1} bar{g}+bar{N}=m_{1} bar{a}(2.1)$$
где $m_{1} bar{g}$ – сила тяжести,
$bar{N}$ – реакция опоры,
$bar{a}$ – ускорение тела.
В проекции на ось Xуравнение (2.1) примет вид:
$$F_{0}-F=m_{1} a rightarrow F=F_{0}-m_{1} a(2.2)$$
Рассмотрим силы, приложенные к двум параллелепипедам как системе:
$$bar{F}_{0}+left(m_{1}+m_{2}right) bar{g}+overline{N^{prime}}=left(m_{1}+m_{2}right) bar{a}(2.3)$$
В проекции на ось X уравнение (2.3) примет вид:
$$F_{0}=left(m_{1}+m_{2}right) a(2.4)$$
Из уравнения (2.4) выразим ускорение:
$$a=frac{F_{0}}{m_{1}+m_{2}}$$
Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$$
Ответ. $F=F_{0}-m_{1} cdot frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение. Сформулированы второй и третий Законы Ньютона. Дано понятие равнодействующей силы.
 Сила в механике
Сила в механике
Определение силы
Твердые тела могут вступать во взаимодействие, в результате которого изменяется характер их движения. Мерой этого взаимодействия является физическая величина, которую называют силой.
Сила – векторная величина, количественная мера механического взаимодействия физических тел, приводящего к изменению их скорости или к их деформациям.
Действие силы на тело определяется тремя факторами:
- направлением;
- точкой приложения;
- численным значением.
Это означает, что сила является векторной величиной (вектором).
Обозначение силы
На схемах вектор силы обозначается отрезком, на конце которого ставится стрелка. Начало отрезка указывает точку приложения силы, а стрелка указывает направление действия силы. Длина отрезка в выбранном масштабе соответствует численному значению силы (рис.1).

В тексте чаще всего сила обозначается латинской буквой F со стрелкой или чертой над ней. Чтобы различать силы, их обозначают посредством нижнего индекса, который ставится после буквы F. Например: Fтяж — сила тяжести; Fупр — сила упругости; Fтр — сила трения; Fм — сила тяги мышц. Иногда за конкретным видом силы стандартно закрепляется определенная буква латинского алфавита, например буква Р (со стрелкой сверху) обозначает вес тела.
Точка приложения силы
При расчетах очень важно знать точку приложения силы. В прикладной механике такие силы называют сосредоточенными. Например, точкой приложения силы тяжести является центр масс (центр тяжести) тела. Также, зная направление и точку приложения силы, можно определить линию действия силы.
Прямая, вдоль которой направлена сила, проходящая через точку ее приложения называется линией действия силы.
Численное значение силы
Численное значение силы (модуль) измеряется в Ньютонах (Н).
С точки зрения механики, все силы возникают при взаимодействии двух или более тел, и у каждой силы есть противодействующая ей сила. Об этом говорит третий закон Ньютона.
Третий закон Ньютона
«Силы, с которыми действуют два тела друг на друга, равны по численному значению и противоположны по направлению. При этом одна сила приложена к одному телу, другая – к другому».
Третий закон Ньютона записывается в следующем виде: F1= — F2.
Второй закон Ньютона (основной закон динамики)
«Ускорения, которые силы сообщают телам, прямо пропорциональны величинам этих сил и обратно пропорциональны массам тел и направлены в сторону действия сил».
Это позволяет определить численное значение силы, если известна масса тела и его ускорение по формуле: F=m*a.
Равнодействующая сила
Если на тело действует несколько сил, приложенных к одной точке, можно найти равнодействующую (результирующую) силу, действие которой на тело эквивалентно воздействию на тела нескольких сил.
Равнодействующая сила – это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Так как сила – это векторная величина, к ней можно применять правила операции над векторами, например, сложение. Чтобы найти равнодействующую силу, необходимо сложить два или несколько векторов (рис.2).

Для анализа силовых упражнений, необходимо познакомится с некоторыми видами сил:
- силой тяжести,
- весом тела,
- силой реакции опоры,
- силой упругости,
- силой тяги мышц.
С уважением, А.В. Самсонова
Похожие записи:
Мышечно-сухожильный комплекс
Приведена рецензия на книгу В.Т.Тураева и В.В. Тюпа «Мышечно-сухожильный комплекс: анатомия, биомеханика, спортивная практика» зав. кафедрой биомеханики НГУ…
Сила тяжести
Дано определение силы тяжести. Показано, что сила тяжести является частным случаем силы гравитации. Описаны факторы, определяющие силу тяжести:…
Звенья тела человека как рычаги
Дано описание опорно-двигательного аппарата (ОДА) человека как системы рычагов. Приведен пример расчета силы двуглавой мышцы плеча…
Типы телосложения (соматотип) по Башкирову
Описана краткая биография П.Н. Башкирова и его научные труды. Дается классификация типов телосложения человека: долихоморфного (астенического), мезоморфного…
Типы телосложения (конституции) по Э. Кречмеру
Описана биография Эрнста Кречмера – немецкого психиатра и психолога, разработавшего типологию тела человека. Дано описание типов телосложения…
Типы конституции женщин по И.Б. Галанту
Описана биография известного советского психиатра И.Б.Галанта, предложившего естественную систему конституциональных типов женщин. Дана характеристика предложенных И.Б.Галантом конституциональных…
Это мера внешнего воздействия на тело, которое возникает в процессе его взаимодействия с другим телом.
По характеру взаимодействия в механике различают три типа сил: упругие силы, силы трения и силы тяжести. Силы первых двух типов возникают в результате взаимодействия тел через прикосновение. Силы притяжения проявляются в результате взаимодействия тел на расстоянии через особое гравитационное поле, которое существует как отдельный вид материи вокруг каждого тела.
Сила – это векторная величина. Когда к данной точке приложено несколько сил, то их можно добавить по правилу параллелограмма и найти равнодействующую силу.
Если под действием нескольких сил тело сохраняет свое состояние покоя или равномерного прямолинейного движения, то такую систему действующих сил называют уравновешенной, или эквивалентной нулю.
Статическая и динамическая составляющие силы
Заслуживают внимания случаи, когда сила одновременно оказывается частично как статическая и частично как динамическая. Например, в движении тела по гладкой наклонной плоскости составляющая его силы тяжести, перпендикулярная плоскости, оказывается статической, а составляющая силы тяжести, параллельная плоскости, проявляется динамической:
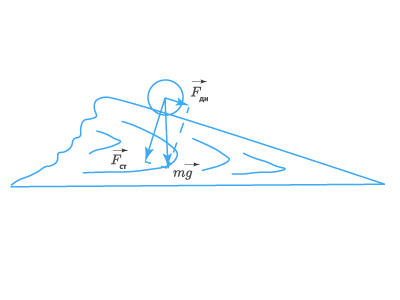
Когда автомашина проезжает выпуклый мост, ее сила тяжести оказывается частично динамической, как центростремительная сила и частично статической, как сила давления на мост:
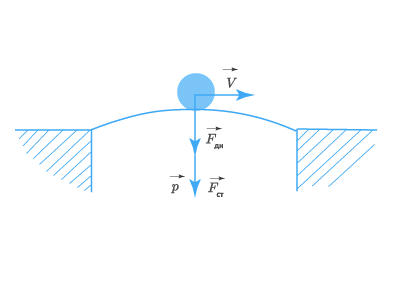
Поэтому сила давления автомашины на выпуклый мост меньше ее силы притяжения к Земле.
Вес тела и сила тяжести
Соотношение между статическим и динамическим проявлениями силы тяжести можно проиллюстрировать следующим примером. Пусть в кабине лифта пассажир стоит на площадке пружинных весов:
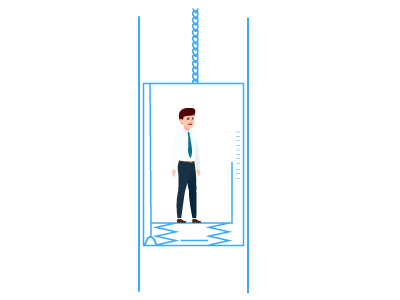
В неподвижном положении вес пассажира 588 Н. Что покажут весы, когда кабина опускаться?
Ставя такой вопрос, мы требуем указать на величину статического проявления силы тяжести. Это можно сделать, если вычислить сначала величину динамического проявления силы.
Рассмотрим некоторые возможные случаи:
- когда кабина равномерно опускается (v=Constv = Const), величина динамического проявления силы тяжести равна нулю, поэтому весы показывают 588 Н;
- если кабина опускается с ускорением, скажем, 4,9 м / с2, то динамическое проявление силы тяжести равно 294 Н, а статическое 588 Н – 294 Н = 294 Н. Такую силу будут показывать весы;
- если кабина будет опускаться с ускорением 9,8 м/с2, то вся сила притяжения будет проявляться динамически, поэтому весы будут показывать ноль.
Случаи, в которых сила тяжести тела полностью реализуется динамически, называют состоянием невесомости тела.
Это бывает, когда тело свободно падает, движется по вертикальной петле (в верхней точке), а также во время движения искусственных спутников Земли. Состояние невесомости для человека необычно. Стоя на полу, он не чувствует обычного напряжения ног, поднимая руку или предмет, не испытывает обычных усилий. Для неподготовленного человека это может вызвать психические и физиологические расстройства, однако полеты космонавтов показали, что в состоянии невесомости подготовленный человек может хорошо себя чувствовать и выполнять различные виды работы.
Из изложенного следует, что нельзя путать вес тела с силой тяжести.
Вес тела – это только составляющая силы тяжести, проявляющаяся статически.
Весом тела называют силу, с которой тело действует на неподвижную в отношении его горизонтальную подставку или неподвижный относительно него подвес. Вес тела приложен к опорам и может существенно меняться в зависимости от их движения.
