Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
- Последовательно выполнять деление десятичного числа и получаемых целых частных на 2, до тех пор, пока частное не станет равным 0.
- Для получения ответа в двоичном коде, необходимо записать, полученные, в результате деления остатки, в обратном порядке.
Пример 1: перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
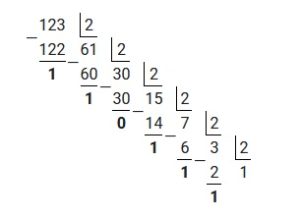
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Ответ: 12310=11110112
Алгоритм перевода десятичной дроби в двоичную систему
- Последовательно выполнять умножение исходной дроби на 2, до тех пор, пока, дробная часть не станет равна 0 или пока не будет достигнута необходимая точность вычисления.
- Полученная дробь в двоичной системе будет равна прямой последовательности целых частей произведений.
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Ответ: 0.12310=0.000111110112
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
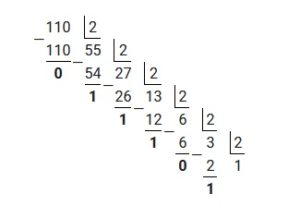
11010=11011102
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
0.62510=0.1012
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Таблица соответствия десятичных и двоичных чисел
| Десятичная система | Двоичная система |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
Оцените материал:
![]() Загрузка…
Загрузка…
Сохраненные расчеты (0)
Сохраненные расчеты
Исходное число
Направление перевода
Сообщить об ошибке
В избранное
Виджет
Как перевести
Для того, чтобы преобразовать число из десятичной системы счисления в двоичную, необходимо выполнить следующие действия.
- Делим десятичное число на 2 и записываем остаток от деления.
- Результат деления вновь делим на 2 и опять записываем остаток.
- Повторяем операцию до тех пор пока результат деления не будет равен нулю.
- Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в двоичную систему:
375 / 2 = 187 (остаток 1)
187 / 2 = 93 (остаток 1)
93 / 2 = 46 (остаток 1)
46 / 2 = 23 (остаток 0)
23 / 2 = 11 (остаток 1)
11 / 2 = 5 (остаток 1)
5 / 2 = 2 (остаток 1)
2 / 2 = 1 (остаток 0)
1 / 2 = 0 (остаток 1)
Записываем остатки в обратном порядке, получаем результат: 1011101112
Смотрите также
- Перевод из десятичной в восьмеричную
- Перевод из двоичной в десятичную
- Перевод из двоичной в восьмеричную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в двоичную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в двоичную
- Перевод из шестнадцатеричной в десятичную
|
Чтобы перевести любое число из десятеричной системы в двоичную, его нужно делить на 2, пока делить уже будет нечего. Причем четное число делится на 2 ровно, а из нечетного сначала надо вычесть единицу, а затем делить на 2. Полученное четное число считается нулем, нечетное считается единицей. Например, число 55 55 – нечетное 1 (55-1)/2=27 – нечетное 1 (27-1)/2=13 – нечетное 1 (13-1)/2=6 – четное 0 6/2=3 – нечетное 1 (3-1)/2=1 – нечетное 1 Полученные результаты от деления записываем в обратном порядке их нахождения, т.е. НЕ 111011, а 110111. система выбрала этот ответ лучшим Альтернативный способ перевода числа из десятичной системы счисления в двоичную систему счисления:Так как способ делением уже описали, напишу ещё один способ, которым можно перевести десятичное число в двоичное. В этом способе делить ничего не надо, а только отнимать. У двоичных чисел есть ступени, каждая последующая ступень больше предыдущей вдвое. Вот эти ступени: Эту цепочку можно продолжать до бесконечности, просто домножая числа на 2. Смотрите на своё число и находите между какими ступенями оно находится. Возьмём для примера число 356. Оно меньше 10-й ступени, но больше 9-й. Значит наше двоичное число будет 9-тизначным. Составляем таблицу из 9-ти граф по горизонтали и из двух по вертикали:
Теперь будем эту таблицу заполнять. Так как максимальная ступень, помещающаяся в нашем числе 356 это 9-я ступень, то в таблицу с ячейкой, над которой написано 9 вписываем 1. Теперь отнимаем от нашего числа 356 эту 9-ю ступень: 356-256=100. Теперь смотрим, раз 8-я ступень не помещается в нашем числе 100, то под 8-кой ставим 0 (ноль). Седьмая ступень 64 – помещается в нашем числе 100. Значит вписываем под 7-кой число 1 и отнимаем от 100 седьмую ступень: 100-64=36. Шестая ступень также помещается в 36-ти, поэтому под 6-кой пишем 1 и отнимаем шестую ступень от 36: 36-32=4. Пятая ступень не помещается в 4-х, поэтому под 5-кой пишем 0. Четвёртая ступень также не помещается в 4-х, поэтому под 4-кой также пишем 0. Третья ступень помещается в 4-ке, поэтому под 3-кой пишем 1 и отнимаем третью ступень от 4-ки: 4-4=0. Полученный ноль не помещается во 2-й и 1-й ступенях, поэтому там пишем нули. В итоге наша таблица заполнилась вот так:
То есть наше полученное число: 101100100 Десятичное число 356 в двоичном виде будет 101100100. А если вам срочно нужно перевести числа из десятичной системы счисления в двоичную, то можете воспользоваться калькулятором Windows, только переключите его с обычного на продвинутый, для чего в меню нажмите Вид – Инженерный. Там впишите своё число и переключите точку с надписи Dec на надпись Bin.
Рыжий Нос 3 года назад В настоящий момент времени наибольшее распространение получила десятичная система счисления, однако есть и системы с другим основанием, которые либо использовались ранее, либо которые используются в специальных отраслях знаний таких, как информатика (к этому сегменту относятся, в основном, шестнадцатеричная и двоичная системы, иногда и восьмеричная). Как здесь уже описали, чтобы получить из десятичного числа двоичное, необходимо последовательно сначала разделить первоначальное число на 2 и в зависимости от наличия или отсутствия остатка от деления записывать 1 или 0, далее необходимо делить на двойку уже результат предыдущего деления и продолжать в том же духе, пока будет что делить. Чтобы не утруждаться подобными вычислениями, можно воспользоваться калькулятором, в которых предусмотрена функция перевода числа из одного основания в другое. В довершение к написанному, привожу первые несколько десятков десятичных чисел и их соответствие числам в иных системах счисления.
SeaMan75 7 лет назад Очень много рекомендаций, но зачем так усложнять все? Любое число можно составить из степеней двойки обычным суммированием этих самых степеней! Например, число 255: 255 = 128+64+32+16+8+4+2+1 = 11111111 240 = 128+64+32+16 = 11110000 число 5 = 4+1 = 101 И почему никто не сказал, как перевести в двоичную систему счисления отрицательные числа? Отрицательное число – это тоже число, поэтому, надо взять за основу максимальную степень двойки, в пределах которой нам надо перевести число. Например – все посчитаем в пределах 2 в 8 степени, то есть – 256. Возьмем число -5, то есть 256-5=251 = 11111011. По такой схеме получается, что все, что до 127 включительно – будут положительными числами, то есть 01111111 = +127, а все, что больше – уже отрицательными. 10000000 = 256-128 = -128! А как же быть, если число, например = -30000. Тогда надо просто увеличить разрядность двоичной сетки, например – до двух байт: 2 в степени 16=65536. -30000 = 65536-30000 = 35536 35536/256=138 – старший байт. 35536-(138*256)= 208 – младший байт. Итого: 138=128+10=10001010, 208=13*16 = 11010000. И -30000 = 1000101011010000! Ну а как быть с дробями? Тоже проще простого! Берем дробь, умножаем ее на степень двойки, например 16: 65536*0,6464618=42.366. Полученное число – целую часть и приводим в двоичном виде: 1010010101111110. Чем выше степень двойки, тем точнее число. Тут надо еще помнить про мантиссу и экспоненту и форматы представления чисел в ПЭВМ…
Simple Ein 3 года назад В повседневной жизни мы пользуемся десятеричной системой счисления. Существуют и другие системы. Например, двоичная, восьмеричная, шестнадцатиричная. Для перевода из одной системы в другую необходимо соблюдать определенные правила. В двоичной системе счисления используется всего 2 знака записи числа: 0 и 1. Такая система используется в электронике. Для перевода числа из десятеричной системы счисления в двоичную необходимо разделить десятеричное число на 2 пока не получим неделимый остаток.
Полученное число записывается “задом наперед”. Для перевода числа из шестнацатиричной системы в двоичную проще всего воспользоваться таблицей перевода.
Пример. Необходимо представить число А2D8 в двоичную систему. Для этого заменим каждый символ на соответствующий ему из таблицы. Получается А2D8(16) = 1010001011011000(2).
Galina7v7 6 лет назад Как видите вариантов перевода из десятичной системы счисления в двоичную несколько.И многие из них схематизированы, то есть приведены к некоторому удобному для вычисления виду.На мой взгляд самый логичный, и который не забудется,это способ сложения”весов” двойки.Выписать все необходимые значения степени двойки, а многие их помнят наизусть. 2^(0)=1, 2^(1)=2, 2^(2)=4, 2^(3)=8, 2^(4)=16, 2^(5)=32, 2^(6)=64, 2^(7)=128, 2^(8)=256, 2^(9)=512, 2^(10)=1024. Это просто магические числа для математика, инженера, программиста.Теперь, пусть нужно перевести в двоичную систему число десятичной системы 1727(специально взяла число менее чем в два раза больше, чем 1024, чтобы хватило “весов”. 1727=1024+703=1024+512+191=1024+512+128+63=1024+128+32+31=1024+128+32+16+15=1024*1+512*1+256*0+128*1+64*0+32*1+16*1+8*1+4*1+2*1+1*1.В малых “весах я написала не расписывая подробно.Те “веса “двойки,которые вошли в число будут учитываться как “1”,а которые не вошли будут считаться как “0”. Итак:1727=11010111111Самый простой способ перевести в двоичную систему это конечно взять калькулятор и перевести (благо современные калькуляторы это умеют 😉 Как уже было сказано выше для перевода в двоичную систему нужно десятичное число делить на 2 (на цело), затем полученный результат, целую его часть, опять делить на 2 и так продолжать до того пока полученное число (результат от деления) не будет меньше системы исчисления, тоесть меньше 2. Как только в результате деления получили число меньше 2 – деление прекращаем. Более наглядно и эффективно это делать в столбик, при этом полученный результат записывается с права налево. Пример для десятичных цифр 7 (111) и 10 (1010):
Skiyers 3 года назад К счастью, сейчас такие рассчеты могут выполнять калькуляторы и вовсе не обязательно тратить на переведение чисел из одной системы счисления в другую много времени, но всё равно тем, кто занимается программированием, желательно знать принципы такого перевода. Способов перевести число в двоичную систему есть несколько. Самый популярный и простой – деление на 2 до упора (то есть до остатка, меньшего или равного единице). Остаток от каждого деления – нули и единицы – записываются в обратном порядке.
Sedaia 12 лет назад Простое объяснение о том, как перевести числа в двоичную систему. Его хорошо понимают дети. Представьте себе, что у вас есть по одной монете достоинством 256,128,64,32,16,8,4,2,1,запишите их в указанном порядке, и набирайте из них нужную вам сумму. Если используете монету, то пишите под ней 1, если какая то монета не потребовалась, то ставите под ней 0. В результате на нижней строке получится число в двоичной системе.
Andrei 9 лет назад Для перевода десятичного числа в двоичную систему счисления необходимо произвести следующие математические действия:
Например:
Знаете ответ? |
Перевод из десятичной системы счисления в двоичную
Правила перевода
чисел из десятичной системы в двоичную
вытекают из формулы представления
числа. Рассмотрим сначала целое десятичное
число N,
представленное
в виде пока неизвестных нам двоичных
цифр:
![]() .
.
Как найти неизвестные
цифры
![]() ?
?
Попробуем разделить десятичное числоN
на 2. Очевидно, что получится какое-то
частное, равное целой части от деления
N
пополам, и остаток. Последний будет
равным 0, если исходное число N
было четным, и 1 – если нечетным. А теперь
посмотрим, что произойдет при делении
на 2 эквивалентного выражения:
![]() .
.
Очевидно, что
![]() первых слагаемых делятся на 2 без остатка,
первых слагаемых делятся на 2 без остатка,
т.к. в их состав входят сомножители из
степеней двойки. Единственное слагаемое,
которое может дать ненулевой остаток,
это – цифра![]() ,
,
не превосходящая единицы. Но ведь мы
делили на 2 одно и то же, поэтому остаток
от деленияN
пополам должен совпасть с цифрой
![]() .
.
Итак, младшую цифру в двоичном разложении
числаN
мы установили.
Теперь внимательно
приглядимся к частному от нашего первого
деления. Обозначим его через
![]() :
:
![]() .
.
Что произойдет
при следующем делении
![]() на 2? Очевидно, получится новое частое
на 2? Очевидно, получится новое частое![]() ,
,
а очередной остаток должен совпасть со
следующей двоичной цифрой![]() .
.
И так продолжают до тех пор, пока частное
после очередного деления на 2 не
превратится в нуль. Процесс этот
обязательно завершится через конечное
число шагов. К этому моменту мы будем
знать уже все цифры двоичного разложения
исходного числаN.
Пример: N
= 96
|
|
о |
|
|
остаток |
|
|
остаток |
|
|
остаток |
|
|
остаток |
|
|
остаток |
|
|
остаток |
Пишем двоичные
цифры, начиная с последней:
9610=11000002
Что изменится,
если потребуется преобразовать число
дробное десятичное число m
![]() в двоичную систему? Вспомним формулу
в двоичную систему? Вспомним формулу
разложения:
![]()
Попытка разделить
левую и правую части на 2 ни к чему
хорошему не приводит. А вот если
попробовать умножать на 2, получится
то, что надо:
![]()
Оказалось, что в
целую часть произведения «перебралась»
старшая цифра
![]() .
.
Отбросим найденную цифру в левой и
правой частях равенства:
![]()
После очередного
умножения
![]() на 2 в разряд целых перекочует двоичная
на 2 в разряд целых перекочует двоичная
цифра![]() и т. д.
и т. д.
Пример:
![]() .
.
Выполним действия:




И поскольку
очередная дробная часть оказалась
равной нулю, то последующие умножения
ничего нового не принесут. В данном
случае пишем двоичные цифры, начиная с
первой. В результате:
![]()
На
практике удобнее запись процесса
перевода дробных чисел вести следующим
образом:
|
875 |
|
|
|
|
Возникает
вопрос: а всегда ли такой процесс
завершится через конечное число шагов?
С целыми числами такой проблемы не
существовало. Любое целое число после
многократного деления пополам, в конце
концов, превратится в нуль. С дробями
дело обстоит несколько иначе:
Пример:
![]()
|
|
6 |
|
1 0 0 1 1 |
2 4 8 6 2 |
Обратите
внимание, что этот процесс будет
продолжаться бесконечно долго, но
периодичность повторяющихся цифр уже
установлена:
![]()
Этот
пример показывает, что не любая конечная
десятичная дробь преобразуется в
конечную же двоичную. Поэтому некоторые
числа в машине могут быть представлены
неточно за счет потери «хвоста». Если
ЭВМ будет прибавлять 1/10, то может
получиться не ожидаемая единица, а
число, которое чуть-чуть меньше. В этом
таятся подводные камни приближенных
вычислений, с которыми иногда приходиться
считаться. Но с целыми числами ошибок
такого рода не бывает, и результат
умножения 2 на 2 в ЭВМ всегда будет равен
4.
Теперь
представим себе, что необходимо перевести
в двоичную систему смешанное число
96,875. В таких случаях отдельно переводят
целую часть числа путем последовательных
делений на 2, а затем переводят дробную
часть и объединяют полученные результаты:
96,87510=1100000,1112
Десятичная
система счисления, с которой начинается
наша школьная, а порой и дошкольная
математика, относится к позиционным
системам счисления. Для нее характерно
наличие – числа 10 и цифр
![]() ,
,
не превосходящих основание![]() .
.
В зависимости от номера позиции,
занимаемой в числе, каждая цифра множится
на соответствующую степень основания:
![]()
![]()
1996 = 6•1 + 9•10 +
9•100 + 1•1000
По-другому это
можно записать так:
1996 = 1•103
+ 9•102
+ 9•101
+ 6•100.
Отсюда также ясно,
как записать любое четырехзначное число
:
N
= a3•103
+ a2•102
+ a1•101
+ a0•100,
где a0,
a1,
a2,
a3
десятичные
цифры числа, причем цифра a3
не должна быть нулем, иначе число не
будет четырехзначным.
Пример
1.
Число 534110
запишем в форме многочлена:
534110
= 5 • 103
+ 3 • 102
+ 4 • 101
+ 1 • 100
Пример
2.
Число
32110
запишем в двоичной системе счисления.
Для этого необходимо разложить число
в виде суммы
по степеням 2:
32110
= 1• 28+
1• 26
+ 1• 20.
Записываем
коэффициенты при степенях двойки (от
минимальной
нулевой степени к максимальной) справа
налево.
Поэтому данное число в двоичной системе
счисления
будет иметь вид: 1010000012.
Пример
3.
Для
того чтобы решить обратную задачу:
перевести число из двоичной системы
счисления в десятичную, необходимо
воспользоваться формулой и произвести
вычисления
в десятичной
системе
счисления.
Число
101001012
перевести в 10-ную систему
счисления:
101001012
= 1 • 20
+ 1 • 22
+ 1 • 23
+ 1 • 27
= 16510.
Пример
4.
Для перевода
целого числа из десятичной в двоичную
систему
счисления необходимо
это число делить на двойку.
Если поделилось без остатка, то пишем
0; если с остатком 1, то пишем 1. Это
будет последняя цифра в записи
числа. Например:
25 — 24 = 1 (остаток
1)
25/2 = 12
12 – 12 = 0 (остаток 0)
12/2 = 6
6 — 6 = 0 (остаток 0)
6/2 = 3
3 — 2 = 1 (остаток 1)
3/2 = 1
(остаток от деления числа 25 на 2) — это
и будет первая цифра в записи числа 25 в
двоичной системе. То есть 2510
= 110012.
Пример
5.
Для
перевода
целого числа из двоичной системы в
десятичную
необходимо
цифры умножать на двойку в степени
номера позиции (номер позиции начинается
с нуля и нумеруется справа налево, а для
дробей – слева направо). Например:
110012
= 1 • 20
+ 0 • 21
+ 0 • 22
+ 1 • 23
+ 1 • 24
= = 1 + 0 + 0 + 8 +16 = 25.
0,1022=1•
2-1+0•
2-2+1•
2-3
= 0,62510
4,3,2,1,0
—
номера позиций цифр в числе — они
являются
степенями двойки.
Таблица систем
счисления
-
№
Двоичная
Восьмеричная
Десятичная
Шестнадцатеричная
0
000
0
0
0
1
001
1
1
1
2
010
2
2
2
3
011
3
3
3
4
100
4
4
4
5
101
5
5
5
6
110
6
6
6
7
111
7
7
7
8
1000
10
8
8
9
1001
11
9
9
10
1010
12
10
A
11
1011
13
11
B
12
1100
14
12
C
13
1101
15
13
D
14
1110
16
14
E
15
1111
17
15
F
16
10000
20
16
10
17
10001
21
17
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как перевести число из десятичной системы в двоичную? желательно с примером, заранее спасибо)))
Ученик
(112),
закрыт
7 лет назад
открытки@mail.ru
Просветленный
(41202)
9 лет назад
В обыденной жизни мы используем привычную всем десятичную систему счисления. В данной системе все числа записываются в виде комбинации из 10 цифр (знаков) : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Десятичная система наиболее удобна для использования в повседневной жизни, поскольку очень просто воспринимается человеком. Однако помимо нее существуют другие системы счисления, также обладающие некоторыми преимуществами в определенных сферах. Например, двоичная.
В двоичной системе для представления чисел используются только 2 цифры: 0 и 1. Данная система нашла свое применение в компьютерной технике, поскольку ее легко реализовать, легко определить два состояния: есть заряд или нет, намагничено или нет; и поставить в соответствие каждому состоянию 0 или 1.
Запись чисел в двоичной системе основана на том, что любое натуральное число X можно представить как сумму степеней двойки:
X = an2n + an-12n-1 + .+a222 + a121 + a020, где ai принимает значение либо 0, либо 1.
Поставленные в ряд числа anan-1…a2a1a0 и будут представлять собой число X в двоичной системе счисления.
Почему ai не может быть больше 1? Пусть ai = 3, но тогда 3*2m = (2 + 1) * 2m = 2*2m + 1*2m = 2m+1 + 2m, то есть в этом случае сумму можно разложить по степеням двойки дальше.
Чтобы перевести число из десятичной системы в двоичную, нужно последовательно делить его на 2 записывать справа налево остаток от каждого деления. Возьмем к примеру число 179:
179 : 2 = 89 и остаток 1;
89 : 2 = 44 и остаток 1;
44 : 2 = 22 и остаток 0;
22 : 2 = 11 и остаток 0;
11 : 2 = 5 и остаток 1;
5 : 2 = 2 и остаток 1;
2 : 2 = 1 и остаток 0;
1 : 2 = 0 и остаток 1.
Если мы запишем остатки справа налево, начиная с верхнего, мы получим 10110011 – это и будет 179 в двоичной системе. Чтобы не перепутать в какой системе записано число (основание) , принято снизу дописывать в какой системе оно представлено. То есть 17910 = 101100112.
Чтобы сделать обратное преобразование, то есть перевести число из двоичной системы в десятичную, необходимо представить его в виде суммы степеней двойки с соответствующими коэффициентами:
101100112 = 1*27 + 0*26 + 1*25 + 1*24 + 0*23 + 0*22 + 1*21 + 1*20 = 128 + 32 + 16 + 2 + 1 = 17910
Все предельно просто.
Как перевести число в двоичную систему Очень легко переводить числа из одной системы счисления в другую с помощью программы «Калькулятор» , идущей в комплекте с операционной системой Windows. Вызвать данную программу можно через «Пуск -> Все программы -> Стандартные -> Калькулятор» . После запуска калькулятора вам необходимо переключиться в режим Инженерный («Вид -> Инженерный») . Как перевести число в двоичную систему Выберите ту систему, из которой переводите, («Dec» – десятичная, «Bin» – двоичная) , введите число и переключитесь в нужную систему. Калькулятор автоматически переведет число в новую систему и выведет на экран.
Люда
Мастер
(1584)
9 лет назад
Чтобы перевести десятичное число в двоичную систему счисления, необходимо последовательно делить его на 2, записывая каждый новый результат деления в виде целого числа и остатка (0 или 1). Деление нужно производить до тех пор, пока результат деления не станет равным 1. Двоичное число получается путём записи последнего результата деления и остатков от предыдущих делений в обратном порядке.
Примеры на почту отправлю.
Никифор Николаевич
Знаток
(259)
9 лет назад
Это просто – открыть стандартный виндовский калькулятор и перевести его в инженерный вид, менять переключатель Дек/Бин
А если серьёзно, то надо делить число на 2 пока не останется в остатке 0 или 1, затем записать все полученные при делении остатки в обратном порядке.
Пример:
35 делим на 2 = 17, остаток 1
17 на 2 = 8 остаток 1
8 на 2 = 4 остаток 0
4 на 2 = 2 остаток 0
2 на 2 = 1 остаток 0
записываем в обратном порядке и в начале ставим оставшуюся от деления единицу – 100011
Kornet_33
Ученик
(210)
5 лет назад
Восьмибитное число в двоичной системе выглядит так:
10110001 (эквивалентно 177 в десятичной системе).
Таблица ниже демонстрирует, как это работает.










 статок
статок

