Двоичное число: прямой, обратный и дополнительный коды
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Прямой, обратный и дополнительный коды двоичного числа – способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел
Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Прямой код – способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) – для записи только неотрицательных чисел:
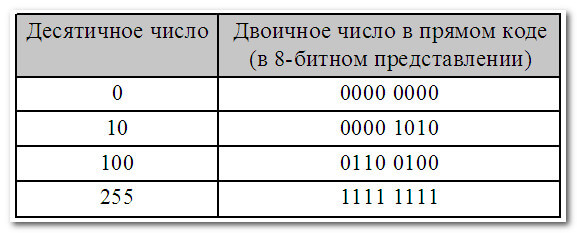
Второй вариант – для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае – восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
– знаковый разряд равен 0, то число положительное
– знаковый разряд равен 1, то число отрицательное
В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от – 127 до +127:
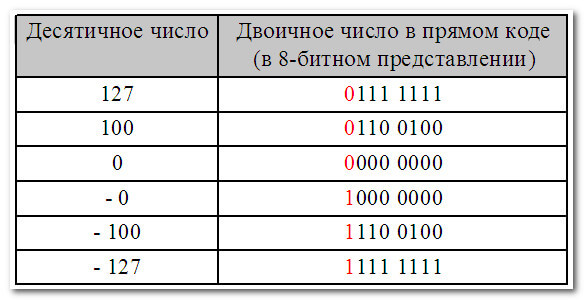
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным – очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля – положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код – метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) – двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе – знаковый бит (как и в прямом коде) старший (8-й)
Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
(Арифметические операции с двоичными числами)
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = – 0001 1001
Необходимо их сложить:
100 + (-25) = 100 – 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд – переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = – 0000 1010
Необходимо их сложить:
5 + (-10) = 5 – 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 —-> 1000 0101
Проверяем:
1000 0101 = – 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
– арифметические операции проводятся в два этапа
– как и в прямом коде два представления нуля – положительный и отрицательный
Дополнительный код
Дополнительный код – наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.
Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
– инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
– к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 —-> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 —-> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 – десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 – 0000 1010 = 1111 0110 – десятичное число -10 в дополнительном коде
Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере – дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
Предыдущие статьи:
1. Микроконтроллеры – первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

Загрузка…
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 января 2021 года; проверки требуют 29 правок.
Дополнительный код (англ. “two’s complement”, иногда “twos-complement”) — наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ. В англоязычной литературе «обратный код» называют «дополнением единиц» (англ. “ones’ complement”), а «дополнительный код» называют «дополнением двойки» (англ. “two’s complement”).
Дополнительный код для отрицательного числа можно получить инвертированием его двоичного модуля и прибавлением к инверсии единицы, либо вычитанием числа из нуля.
Дополнительный код двоичного числа определяется как величина, полученная вычитанием числа из наибольшей степени двух (из 2N для N-битного второго дополнения).
Представление отрицательного числа в дополнительном коде[править | править код]
При записи числа в дополнительном коде старший разряд является знаковым. Если значение старшего разряда равно 0, то это значит, что в остальных разрядах записано положительное двоичное число, совпадающее с прямым кодом.
Двоичное 8-разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если старший разряд равен нулю, то наибольшее целое число, которое может быть записано в оставшихся 7 разрядах, равно 
Примеры:
| Десятичное представление |
Двоичное представление (8 бит), код: | ||
|---|---|---|---|
| прямой | обратный | дополнительный | |
| 127 | 0111 1111
|
0111 1111
|
0111 1111
|
| 1 | 0000 0001
|
0000 0001
|
0000 0001
|
| 0 | 0000 0000
|
0000 0000
|
0000 0000
|
| −0 | 1000 0000
|
1111 1111
|
— |
| −1 | 1000 0001
|
1111 1110
|
1111 1111
|
| −2 | 1000 0010
|
1111 1101
|
1111 1110
|
| −3 | 1000 0011
|
1111 1100
|
1111 1101
|
| −4 | 1000 0100
|
1111 1011
|
1111 1100
|
| −5 | 1000 0101
|
1111 1010
|
1111 1011
|
| −6 | 1000 0110
|
1111 1001
|
1111 1010
|
| −7 | 1000 0111
|
1111 1000
|
1111 1001
|
| −8 | 1000 1000
|
1111 0111
|
1111 1000
|
| −9 | 1000 1001
|
1111 0110
|
1111 0111
|
| −10 | 1000 1010
|
1111 0101
|
1111 0110
|
| −11 | 1000 1011
|
1111 0100
|
1111 0101
|
| −127 | 1111 1111
|
1000 0000
|
1000 0001
|
| −128 | — | — | 1000 0000
|
Дополнительный код в иной системе счисления[править | править код]
Тот же принцип можно использовать и в компьютерном представлении любой системы счисления, например, для десятичных чисел.
Преобразования на примере десятичной системы счисления[1][править | править код]
Положительное число[править | править код]
Изменение значений текущих разрядов числа не производится, но дописывается знаковый старший разряд, значение которого равно 0. Например число [+12’345] будет иметь следующее представление – [012’345]
Отрицательное число[править | править код]
Дописываем знаковый старший разряд, равный большей цифре данной системы счисления, в нашем случае – это 9, а также изменяем остальные разряды по определённому правилу; пусть значение цифры каждого разряда будет представлено переменной x , кроме знакового, тогда представим следующий алгоритм действий:
- Присвоим переменной x новое значение, равное выражению 9 – x (процесс получения обратного кода) – например отрицательное число [-12345] в прямом коде от старшего к младшему разряду будет иметь вид [9′12345], где 9 – знаковая цифра, а в обратном представлении кода будет иметь следующий вид – [9’87654].
- К результирующему числу прибавим 1, так число [9’87654] (первое дополнение) будет иметь вид [987’655] (доп. код).
- Если возникла ситуация переноса разряда, в результате которого образовался новый разряд, то его (старший разряд) опускаем, а результирующее число считаем положительным. Результирующее положительное число будет одинаково представлено, как в прямом, так и в дополнительном коде. Например, имея возможность представить в таком виде отрицательный и положительный нуль, разберём их перевод в дополнительный код (1 знаковый и 4 дополнительных разряда):
- [+0] в прямом коде [0’0000]. Первое и второе дополнения равны [0’0000].
- [-0] в прямом коде [9’0000]. Первое дополнение – [9’9999]. При получении второго дополнения старший разряд числа [(1)0’0000] опускаем и получаем результирующее значение [0’0000], как у числа [+0].
Идея представления десятичного (как и любого другого) числа в дополнительном коде, идентична правилам для двоичной системы счисления и может использоваться в гипотетическом процессоре:
| Привычное
представление |
Прямой
код |
Первое
дополнение |
Второе
дополнение |
|---|---|---|---|
| … | … | … | … |
| +13 | 0’0013 | 0’0013 | 0’0013 |
| +12 | 0’0012 | 0’0012 | 0’0012 |
| +11 | 0’0011 | 0’0011 | 0’0011 |
| +10 | 0’0010 | 0’0010 | 0’0010 |
| +9 | 0’0009 | 0’0009 | 0’0009 |
| +8 | 0’0008 | 0’0008 | 0’0008 |
| … | … | … | … |
| +2 | 0’0002 | 0’0002 | 0’0002 |
| +1 | 0’0001 | 0’0001 | 0’0001 |
| +0 | 0’0000 | 0’0000 | 0’0000 |
| -0 | 9’0000 | 9’9999 | 0’0000 |
| -1 | 9’0001 | 9’9998 | 9’9999 |
| -2 | 9’0002 | 9’9997 | 9’9998 |
| -3 | 9’0003 | 9’9996 | 9’9997 |
| -4 | 9’0004 | 9’9995 | 9’9996 |
| … | … | … | … |
| -9 | 9’0009 | 9’9990 | 9’9991 |
| -10 | 9’0010 | 9’9989 | 9’9990 |
| -11 | 9’0011 | 9’9988 | 9’9989 |
| -12 | 9’0012 | 9’9987 | 9’9988 |
| -13 | 9’0013 | 9’9986 | 9’9987 |
Арифметика в дополнительном коде[править | править код]
Сложение и вычитание[править | править код]
Оба числа представляются в дополнительном коде. Дополнительный код обоих чисел имеет одинаковое количество разрядов. В данном представлении числа складываются.
Знаки разные: Если в процессе сложения образуется выходящий за пределы первоначальных чисел разряд, то он опускается. Результирующее значение считается положительным, где прямой и дополнительный коды являются идентичными. Иначе — отрицательным в виде дополнительного кода.
Например:
- [1234] + [-78] → [0’1234] + [9’9922] = [(1)0’1156] = [1156].
- [-1234] + [78] → [9’8766] + [0’0078] = [9’8844] = [-1156].
Знаки одинаковые:
- Положительные числа. Разряд не опускается, результат положительный.
- Отрицательные числа. Разряд опускается, результат отрицательный в дополнительном коде.
Например:
- [1234] + [78] → [0’1234] + [0’0078] = [0’1312] = [1312].
- [-1234] + [-78] → [9’8766] + [9’9922] = [(1)9’8688] → (первое дополнение) [0’1311] → (второе дополнение или обычное представление) [0’1312]. При переводе из дополнительного кода в обычное представление результирующее значение является абсолютным.
Преобразование в дополнительный код[править | править код]
Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму.
- Если старший (знаковый) разряд числа, записанного в прямом коде, равен 0, то число положительное и никаких преобразований не делается;
- Если старший (знаковый) разряд числа, записанного в прямом коде, равен 1, то число отрицательное, все разряды числа, кроме знакового, инвертируются, а к результату прибавляется 1.
Пример.
Преобразуем отрицательное число −5, записанное в прямом коде, в дополнительный код.
Прямой код отрицательного числа -5:
1000 0101
Инвертируем все разряды числа, кроме знакового, получая таким образом обратный код (первое дополнение) отрицательного числа -5:
1111 1010
Добавим к результату 1, получая таким образом дополнительный код (второе дополнение) отрицательного числа -5:
1111 1011
Для преобразования отрицательного числа -5, записанного в дополнительном коде, в положительное число 5, записанное в прямом коде, используется похожий алгоритм. А именно:
1111 1011
Инвертируем все разряды отрицательного числа -5, получая таким образом положительное число 4 в прямом коде:
0000 0100
Добавив к результату 1 получим положительное число 5 в прямом коде:
0101
И проверим, сложив с дополнительным кодом
0000 0101 + 1111 1011 = 0000 0000, пятый и старше разряды выбрасываются.
p-адические числа[править | править код]
В системе p-адических чисел изменение знака числа осуществляется преобразованием числа в его дополнительный код. Например, если используется 5-ичная система счисления, то число, противоположное 00015 (110), равно 44445 (−110).
Реализация алгоритма преобразования в дополнительный код (для 8-битных чисел)[править | править код]
Pascal[править | править код]
if (a < 0) then a := ((not a) or 128) + 1;
C/C++[править | править код]
int convert(int a) { if (a<0) a = ~(-a) + 1; return a; }
Преимущества и недостатки[править | править код]
Преимущества[править | править код]
- Общие инструкции (процессора) для сложения, вычитания и левого сдвига для знаковых и беззнаковых чисел (различия только в арифметических флагах, которые нужно проверять для контроля переполнения в результате).
- Отсутствие числа «минус ноль».
Недостатки[править | править код]
- Представление отрицательного числа визуально не читается по обычным правилам, для его восприятия нужен особый навык или дополнительные вычисления для приведения в обычный вид.
- В некоторых представлениях (например, двоично-десятичный код) или их составных частях (например, мантисса числа с плавающей запятой) дополнительное кодирование неудобно.
- Модуль наибольшего числа не равен модулю наименьшего числа. Например, для восьмибитного целого со знаком, максимальное число: 12710 = 011111112, минимальное число: -12810 = 100000002. Соответственно, не для любого числа существует противоположное. Операция изменения знака может потребовать дополнительной проверки.
Пример программного преобразования[править | править код]
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными.
C# .NET / C style[править | править код]
byte b1 = 254; //11111110 (бинарное) byte b2 = 121; //01111001 (бинарное) byte c = 1<<(sizeof(byte)*8-1); //2 возводится в степень 7. Результат: 10000000 (бинарное) byte b1Conversion=(c ^ b1) - c; //Результат: -2. А фактически, двоичный дополнительный код. byte b2Conversion=(c ^ b2) - c; //Результат остаётся 121, потому что знаковый разряд - ноль.
Расширение знака[править | править код]
Расширение знака (англ. Sign extension) — операция над двоичным числом, которая позволяет увеличить разрядность числа с сохранением знака и значения. Выполняется добавлением цифр со стороны старшего значащего разряда. Если число положительное (старший разряд равен 0), то добавляются нули, если отрицательное (старший разряд равен 1) — единицы.
Пример[править | править код]
| Десятичное число | Двоичное число
(8 разрядов) |
Двоичное число
(16 разрядов) |
|---|---|---|
| 10 | 0000 1010
|
0000 0000 0000 1010
|
| −15 | 1111 0001
|
1111 1111 1111 0001
|
См. также[править | править код]
- Обратный код
- Прямой код
- Целый тип
- Алгоритм Бута — специализированный алгоритм умножения для чисел в дополнительном коде
Литература[править | править код]
- Behrooz Parhami. 2.3. Complement Representation, 2.4. Two’s- and 1’s-complement numbers // Computer Arithmetic: Algorithms and Hardware Designs. — New York: Oxford University Press, 2000. — P. 22-27. — 510 p. — ISBN 0-19-512583-5.
- Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. — К.: Вища школа, 1987. — 375 с.
Ссылки[править | править код]
- ↑ Florida Tech. Дата обращения: 28 ноября 2020. Архивировано 8 октября 2016 года.
Как расписать целое отрицательное число в двоичном коде?
Ответ вот на такой загадочный вопрос:
Представление отрицательных целых чисел – дополнительный код.
я понял что если в первом разряде стоит 0 то число положительное
а если 1 то отрицательное… а как посчитать?
Не понял, что конкретно ты хотел сделать?
Узнать, как двоичное представление отрицательного числа расписать, что ли?
Например, так.
Имеем десятичное число -2013, надо его записать в двоичном коде.
Переводим положительное число 2013 в двоичную систему, получаем
11111011101.
Дописываем слева нули, чтоб вышло 16 разрядов (если число двухбайтовое), имеем
0000011111011101 (прямой код).
Инвертируем все биты (то есть, 0 заменяем на 1, а 1 на 0), имеем
1111100000100010 (обратный код).
Прибавляем в двоичной системе 1 к обратному коду, имеем
1111100000100011. Это значение равно -2013.
Проверить можно стандартным калькулятором Windows:
Запускаешь Калькулятор (Программы – Стандартные – Калькулятор), в XP выбираешь в меню программы Вид – Инженерный, в “семерке”, по-моему, Вид – Программист, набираешь выражение, ответом для которого будет нужное отрицательное число, например,
0-2013 = -2013,
переключаешь систему счисления на двоичную (Bin), а ёмкость числа – на 2 байта,
видишь 1111100000100011.
Или у нас сразу есть отрицательное двоичное
число, скажем, 1111111111101111 (самый левый бит – единица, значит, отрицательное)… левая “1” обозначает знак “-“, отбрасываем её, а от оставшегося двоичного числа отнимаем 1, получаем
111111111101110, заменяем все нули на 1, а единицы на нули, получаем
000000000010001, а это есть десятичное 17. Значит, код обозначал -17.
19.01.2013, 10:53 [63999 просмотров]
К этой статье пока нет комментариев, Ваш будет первым
Представление положительных и отрицательных чисел в памяти компьютера. Прямой и дополнительный код числа
Прямой код
Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
Операция сложения положительного числа и отрицательного числа, представленного в прямом коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа.
- Если числа имеют разные знаки, то вместо операции сложения используется операция вычитания из большего по модулю значения меньшего. При этом первый (знаковый) разряд в операции не участвует.
_ 000 0111 000 0101 ------------- 000 0010 - После выполнения операции учитывается первый разряд. Результат операции 1 000 0010, или -210.
Операция сложения положительного числа и отрицательного числа, представленного в дополнительном коде
- Прямой код числа 5: 0 000 0101
Прямой код числа -7: 1 000 0111 - Формирование дополнительного кода числа -7.
Прямой код : 1 000 0111
Инверсия : 1 111 1000
Добавление единицы: 1 111 1001 - Операция сложения.
0 000 0101 + 1 111 1001 -------------- 1 111 1110 - Проверка результата путем преобразования к прямому коду.
Дополнительный код: 1 111 1110
Вычитание единицы : 1 111 1101
Инверсия : 1 000 0010 (или -210)






