Как найти двойной дифференциал - Сайт, где вы сможете решить свои вопросы

Дифференциалом
второго порядка функции
называется дифференциал от дифференциала
первого порядка:

Пример 4.
Для функции
найти дифференциал второго порядка.

Найдем частные
производные первого и второго порядка:

;
;

;
;;

Дифференциал
второго порядка равен

7. Градиент функции двух переменных

Свойства градиента

Градиент показывает
направление
наибольшего
возрастания значений функции.
Длина вектора
градиента равен максимальной
скорости
изменения функции в направлении
градиента.
Для функции
градиент
перпендикулярен
линии уровня,
проходящей через точку
.

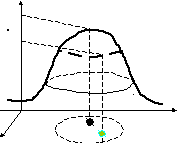
Пример 5.
Дана функция
.
Найти градиентв точкеи построить его.

Найдем координаты
градиента – частные производные.

В точке
градиент
равен
.
Начало векторав точке,
а конец – в точке.

0
2 4

Аналогично
определяется градиент функции трех
переменных
:

Контрольные вопросы

Дайте определение
функции двух переменных
.
Что является
областью определения функции
?
Что является
графиком функции двух переменных
?
Графиком какой
функции двух переменных является
плоскость?
Что называется
линией уровня функции
?
Как расположены
линии уровня линейной функции
?
Как расположены
линии уровня функции
?
Запишите
частное приращение функции двух
переменных по переменной
.
Как
определяется частная производная
функции
по переменной?
По переменной?
Как вычисляются
частные производные?
Дайте
определение частных производных второго
порядка, третьего,
-го
порядка функции.
Что
означает символическая запись
?
Сформулируйте
свойство смешанных частных производных
функций двух переменных.
Запишите полное
приращение для функций двух переменных.
Что называется
полным дифференциалом функции
?
Как найти полный
дифференциал функции
?
Запишите формулу
для нахождения дифференциала второго
порядка функции
.
Какова связь между
полным дифференциалом функции нескольких
переменных и ее полным приращением?
Сформулируйте
свойства градиента.
Как
расположен градиент функции
относительно линий уровня?

Тема 2. Экстремум функции двух переменных

Содержание

Локальный
экстремум
Условный
экстремум функции двух переменных

1. Локальный экстремум

Максимумы и
минимумы функции называются экстремумами
функции.

На рисунке точка
является точкой максимума функции.

Точка
называетсястационарной
точкой функции
,
если она является внутренней
точкой
области определения функции и все
частные производные первого
порядка в
ней равны
нулю.
Точка
,
в которой частные производные равны
нулю или не существуют, называетсякритической
точкой функции

.

Таким образом,
точки экстремума следует искать среди
ее критических точек.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Дифференциалы различных порядков

Щебетун Виктор

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Что такое дифференциал функции

Определение

Дифференциалом функции называется произведение производной этой функции на приращение независимой переменной.

Дифференциал функции обозначается dy и имеет запись вида:

$dy = f ‘(x) Delta $х

Пусть дана функция y = f(x), где х – независимая переменная. Дифференциал этой функции есть некоторая функция от х но от х зависит только первый сомножитель f ‘(x) второй же сомножитель dx является приращением независимой переменной x и от значения этой переменной не зависит.

dy = f ‘(x)dx

Функция dy есть функция от x и называется дифференциалом.

Что такое второй, третий дифференциал

Определение

Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y.

$d^2y = d(dy)$

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Определение

Третьим дифференциалом или дифференциалом третьего порядка функции называется дифференциал от ее второго дифференциала:

$d^3y = d(d2y) = f ”'(x)dx^3$

Что такое дифференциал n-го порядка

Определение

Дифференциалом n-го порядка является дифференциал от дифференциала (n-1)-го порядка:

$d^ny = d(d^{n-1}y)$

Пользуясь дифференциалами различных порядков, производную любого порядка можно представить как отношение дифференциалов соответствующего порядка:

[f'(x)=frac{dx}{dy} ]

[f^{n} (x)=frac{d^{n} y}{dx^{n} } ]

Пример 1

Найти дифференциал функции.

[d(2x^{3} +1)]

Решение.

По правилу дифференцирования, дифференциал суммы равен сумме дифференциалов функций.

[d(2x^{3} +1)=d(2x^{3} )+d(1)]

Найдем производные данных функций и добавим к ним знак дифференциала. Производная второй функции так же как и дифференциал равна 0.

[d(2x^{3} +1)=6x^{2} dx]

«Дифференциалы различных порядков» 👇

Пример 2

Найти дифференциал второго порядка функции.

[y(x)=x^{3} -arccos x]

Решение.

По определению дифференциала, дифференциал второго порядка равен:

[d^{2} y=y”(x)dx^{2} ]

Продифференцируем данную функцию по х:

[y'(x)=(x^{3} -arccos x)’=(x^{3} )’-(arccos x)’=3x^{2} +frac{1}{sqrt{1-x^{2} } } ]

Вычислим вторую производную

[y”(x)=left(3x^{2} +frac{1}{sqrt{1-x^{2} } } right)^{{‘} } =6x+left((1-x^{2} )^{-frac{1}{2} } right)^{{‘} } =6x-frac{1}{2} (1-x^{2} )^{-frac{3}{2} } (1-x^{2} )’]

[y”(x)=6x+x(1-x^{2} )^{-frac{3}{2} } ]

Подставим полученную производную в формулу дифференциала второго порядка:

[d^{2} y=y”(x)dx^{2} =left(6x+x(1-x^{2} )^{-frac{3}{2} } right)dx^{2} =left(6x+frac{x}{sqrt[{}]{(1-x^{2} )^{3} } } right)dx^{2} ]

Пример 3

Найти дифференциал второго порядка функции заданной неявно.

[xy-y^{2} =3]

Решение.

Перенесем все члены функции в одну сторону

[xy-y^{2} -3=0]

Найдем первый дифференциал dy

[dleft(xy-y^{2} right)-dleft(3right)=0]

Дифференциал разности равен разности дифференциалов

[dleft(xyright)-dleft(y^{2} right)-dleft(3right)=0]

Распишем дифференциал произведения и вычислим

[dleft(xright)cdot y+xdy-dleft(y^{2} right)-dleft(3right)=0]

[ydx+xdy-2ydy-0=0]

Выразим dy

[dyleft(x-2yright)=-ydx]

[dy=-frac{ydx}{x-2y} ]

Вычислим дифференциал второго порядка по свойству частного:

[d^{2} y=d(dy)=dleft(-frac{ydx}{x-2y} right)]

[d^{2} y=dleft(-frac{y}{x-2y} right)dx=frac{d(-y)(x-2y)-(-y)cdot d(x-2y)}{left(x-2yright)^{2} } dx]

[d^{2} y=frac{-dy(x-2y)+ycdot d(x)-2dy}{left(x-2yright)^{2} } dx]

Выполним замену dy

[d^{2} y=frac{-frac{-ydxleft(x-2yright)}{x-2y} +ydx-2ydy}{left(x-2yright)^{2} } dx]

[d^{2} y=frac{ydx+ydx-2ydy}{left(x-2yright)^{2} } dx=frac{2ydx-2yleft(-frac{ydx}{x-2y} right)}{left(x-2yright)^{2} } dx]

[d^{2} y=frac{2ydx+frac{2y^{2} }{x-2y} }{left(x-2yright)^{2} } dx=frac{2ydx+2y^{2} }{left(x-2yright)^{3} } dx]

[d^{2} y=frac{2y(x+2y)+2y^{2} }{left(x-2yright)^{3} } dx^{2} =frac{2xy+4y^{2} +2y^{2} }{left(x-2yright)^{3} } dx^{2} =frac{2xy+6y^{2} }{left(x-2yright)^{3} } dx^{2} ]

[d^{2} y=frac{2yleft(x+3yright)dx^{2} }{left(x-2yright)^{3} } ]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 15.12.2022

Источник

Содержание:

Случай независимой переменной
Случай зависимой переменной

Пусть функция $y=f(x)$ зависит от переменной
$x$ и дифференцируема в точке
$x$. Может оказаться, что в точке
$x$ дифференциал
$d y=f^{prime}(x) d x$, рассматриваемый как функция от
$x$, есть также дифференцируемая функция. Тогда существует
дифференциал от дифференциала $d(dy)$ данной функции,
который называется дифференциалом второго порядка функции $y=f(x)$.
Дифференциал второго порядка обозначается следующим образом:

$d^2y=d(dy)$

Аналогично определяются дифференциалы более высоких порядков.

Определение

Дифференциалом
$n$-го порядка
$d_ny$ функции
$y=f(x)$ называется дифференциал от дифференциала
$(n-1)$-го порядка этой функции, то есть

$$d^{n} y=dleft(d^{n-1} yright)$$

Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.

Случай независимой переменной

Пусть $y=f(x)$ – функция независимой переменной
$x$, имеющая дифференциалы любого порядка.
Первый дифференциал функции

$$d y=f^{prime}(x) d x$$

где $dx=Delta x$ – некоторое приращение независимой
переменной $x$, которое мы задаем сами и которое не
зависит от $x$. По определению

$$d^{2} y=d(d y)=dleft(f^{prime}(x) d xright)$$

Переменной является аргумент $x$. Значит, для
дифференциала величина $dx$ является постоянной и
поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка

$$d^{2} y=dleft(f^{prime}(x) d xright)=d x cdot dleft(f^{prime}(x)right)$$

Для вычисления дифференциала $dleft(f^{prime}(x)right)$ применим формулу
дифференциала первого порядка к функции $f^{prime}(x)$. Тогда получим:

$$dleft(f^{prime}(x)right)=left(f^{prime}(x)right)^{prime} cdot d x=d x cdot f^{prime prime}(x) d x=f^{prime prime}(x)(d x)^{2}=f^{prime prime}(x) d x^{2}$$

Итак,

$$d^{2} y=f^{prime prime}(x) d x^{2}$$

Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
$n$-го порядка:

$$d^{n} y=f^{n}(x) d x^{n}$$

Пример

Задание. Найти дифференциал третьего порядка функции $y(x)=4x^3-12x+5$

Решение. По формуле

$$d^{3} y=y^{prime prime prime}(x) d x^{3}$$

Найдем третью производную заданной функции:

$$begin{array}{c}
y^{prime}(x)=left(4 x^{3}-12 x+5right)^{prime}=left(4 x^{3}right)^{prime}-(12 x)^{prime}+(5)^{prime}= \
4left(x^{3}right)^{prime}-12(x)^{prime}+0=4 cdot 3 x^{2}-12 cdot 1=12 x^{2}-12 \
y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(12 x^{2}-12right)^{prime}=left(12 x^{2}right)^{prime}-(12)^{prime}= \
=12left(x^{2}right)^{prime}-0=12 cdot 2 x=24 x \
y^{prime prime prime}(x)=left(y^{prime prime}(x)right)^{prime}=(24 x)^{prime}=24(x)^{prime}=24
end{array}$$

Тогда

$$d^{3}y=24dx^3$$

Ответ. $d^{3}y=24dx^3$

Случай зависимой переменной

Пусть задана дифференцируемая функция $y=f(u(x))$. Тогда

$$d y=f^{prime}(u) d u$$

где $d u=u^{prime}(x) d x$ в общем случае не является постоянной величиной.
Поэтому дифференциал от функции $f^{prime}(u) d u$ берем как дифференциал от произведения

$$d^{2} y=dleft(f^{prime}(u) d uright)=dleft(f^{prime}(u)right) cdot d u+f^{prime}(u) cdot d(d u)=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти дифференциал второго порядка
$d^{2}u$ функции $f(u)=sqrt{u}$, где
$u(x)=3x+7$ и $x$ – независимая переменная.

Решение. Решим пример разными способами и сравним ответы.

1-ый способ. Согласно формуле, имеем, что искомый дифференциал

$$d^{2} y=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$

Найдем все необходимые компоненты формулы. Из условия имеем:

$$begin{array}{c}
f^{prime}(u)=(sqrt{u})^{prime}=frac{1}{2 sqrt{u}} \
f^{prime prime}(u)=left(f^{prime}(u)right)^{prime}=left(frac{1}{2 sqrt{u}}right)^{prime}=frac{1}{2} cdotleft(u^{-frac{1}{2}}right)^{prime}= \
=frac{1}{2} cdotleft(-frac{1}{2}right) cdot u^{-frac{3}{2}}=-frac{1}{4 sqrt{u^{3}}} \
d u=d(3 x+7)=(3 x+7)^{prime} d x=left[(3 x)^{prime}+(7)^{prime}right] d x= \
=left[3(x)^{prime}+0right] d x=3 cdot 1 cdot d x=3 d x \
d^{2} u=d(3 d x)=d x cdot d(3)=d x cdot 0=0
end{array}$$

А тогда:

$$begin{aligned}
d^{2} y=&-frac{1}{4 sqrt{u^{3}}} d u^{2}+frac{1}{2 sqrt{u}} cdot 0=-frac{1}{4 sqrt{u^{3}}} cdot(3 d x)^{2}=\
&=-frac{9}{4 sqrt{u^{3}}} d x^{2}=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}
end{aligned}$$

2-ой способ. Из того, что $f(u)=sqrt{u}$ и
$u(x)=3 x+7$, получаем:

$$f(x)=sqrt{3 x+7}$$

А тогда

$$d^{2} y=f^{prime prime}(x) d x^{2}$$

Найдем вторую производную функции $f(x)=sqrt{3 x+7}$:

$$f^{prime}(x)=(sqrt{3 x+7})^{prime}=frac{1}{2 sqrt{3 x+7}} cdot(3 x+7)^{prime}=$$
$$=frac{1}{2 sqrt{3 x+7}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=frac{1}{2 sqrt{3 x+7}} cdotleft[3(x)^{prime}+0right]=$$
$$=frac{3 cdot 1}{2 sqrt{3 x+7}}=frac{3}{2 sqrt{3 x+7}}$$
$$f^{prime prime}(x)=left(f^{prime}(x)right)^{prime}=left(frac{3}{2 sqrt{3 x+7}}right)^{prime}=frac{3}{2}left((3 x+7)^{-frac{1}{2}}right)^{prime}=$$
$$=frac{3}{2} cdotleft(-frac{1}{2}right) cdot(3 x+7)^{-frac{3}{2}} cdot(3 x+7)^{prime}=$$
$$=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdot 3(x)^{prime}=$$
$$=-frac{3 cdot 3 cdot 1}{4 sqrt{(3 x+7)^{3}}}=-frac{9}{4 sqrt{(3 x+7)^{3}}}$$

Окончательно имеем:

$$d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$$

Ответ. $d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$

Читать дальше: производная функции, заданной неявно.

Источник

ПОИСК

Страницы

«Назад | Вперед »

Партнеры сайта

_________________________________

Примеры Дифференциал функции двух переменных

Примеры нахождения производных

Исследование функции и построение графика с помощью производной

Производная от функции онлайн

Примеры Дифференциал функции двух переменных

Примеры Частные производные функции нескольких переменных

Примеры Экстремумы функции нескольких переменных

Частные производные функции нескольких переменных онлайн

Найти дифференциалы первого и второго порядка
функции нескольких переменных

Решение

Найдем частные производные
первого порядка:

Тогда дифференциал первого
порядка равен:

Найдем частные производные
второго порядка:

Тогда дифференциал второго
порядка равен:

Ответ: , .

меню пользователя

Не зарегистрирован

Вход

Забыли пароль?

Регистрация

Новости

30.11.16

Свойства треугольников

17.03.15

Новые материалы на сайте

25.03.14

Новые разделы на сайте

29.08.13

С новым учебным годом!

05.05.13

Новые разделы на сайте

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 сентября 2019 года; проверки требуют 7 правок.

Дифференциалом порядка n, где n > 1, от функции в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть

${displaystyle d^{n}z=d(d^{n-1}z)}$

Дифференциал высшего порядка функции одной переменной[править | править код]

Для функции, зависящей от одной независимой переменной второй и третий дифференциалы выглядят так:

${displaystyle d^{2}z=d(dz)=d(z'dx)=dz'dx=(z''dx)dx=z''dx^{2}}$

${displaystyle d^{3}z=d(d^{2}z)=d(z''dx^{2})=dz''dx^{2}=(z'''dx)dx^{2}=z'''dx^{3}}$

Отсюда можно вывести общий вид дифференциала n-го порядка от функции , при условии, что — независимая переменная:

${displaystyle d^{n}z=z^{(n)}dx^{n}}$

При вычислении дифференциалов высших порядков очень важно, что есть произвольное и не зависящее от , которое при дифференцировании по следует рассматривать как постоянный множитель. Если не является независимой переменной, то дифференциал будет другим (см. ниже)^[1].

Дифференциал высшего порядка функции нескольких переменных[править | править код]

Если функция имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так: ${displaystyle d^{2}z=d(dz)}$ .

${displaystyle d^{2}z=dleft({frac {partial z}{partial x}}dx+{frac {partial z}{partial y}}dyright)=left({frac {partial z}{partial x}}dx+{frac {partial z}{partial y}}dyright)'_{x}dx+left({frac {partial z}{partial x}}dx+{frac {partial z}{partial y}}dyright)'_{y}dy=}$

${displaystyle =left({frac {partial ^{2}z}{partial x^{2}}}dx+{frac {partial ^{2}z}{partial ypartial x}}dyright)dx+left({frac {partial ^{2}z}{partial xpartial y}}dx+{frac {partial ^{2}z}{partial y^{2}}}dyright)dy}$

$d^{2}z={frac {partial ^{2}z}{partial x^{2}}}dx^{2}+2{frac {partial ^{2}z}{partial xpartial y}}dxdy+{frac {partial ^{2}z}{partial y^{2}}}dy^{2}$

${displaystyle d^{2}z=left({frac {partial }{partial x}}dx+{frac {partial }{partial y}}dyright)^{2}z}$

Символически общий вид дифференциала n-го порядка от функции
${displaystyle z=f(x_{1},...,x_{r})}$ выглядит следующим образом:

${displaystyle d^{n}z=left({frac {partial }{partial x_{1}}}dx_{1}+{frac {partial }{partial x_{2}}}dx_{2}+...+{frac {partial }{partial x_{r}}}dx_{r}right)^{n}z}$

где ${displaystyle z=f(x_{1},x_{2},...x_{r})}$ , а ${displaystyle dx_{1},...,dx_{r}}$ произвольные приращения независимых переменных ${displaystyle x_{1},...,x_{r}}$ .
Приращения ${displaystyle dx_{1},...,dx_{r}}$ рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.
Сложность выражения дифференциала возрастает с увеличением числа переменных.

Неинвариантность дифференциалов высшего порядка[править | править код]

При -й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение ${displaystyle d^{n}f}$ зависит, вообще говоря, от того, рассматривается ли переменная как независимая, либо как некоторая промежуточная функция другого переменного, например, .

Так, для независимой переменной второй дифференциал, как было сказано выше, имеет вид:

${displaystyle d^{2}z=z''(dx)^{2}}$

Если же переменная сама может зависеть от других переменных, то ${displaystyle d(dx)=d^{2}xneq 0}$ . В этом случае формула для второго дифференциала будет иметь вид^[1]:

${displaystyle d^{2}z=d(dz)=d(z'dx)=z'',(dx)^{2}+z'd^{2}x}$

Аналогично, третий дифференциал примет вид:

${displaystyle d^{3}z=z''',(dx)^{3}+3z''dx,d^{2}x+z'd^{3}x}$

Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
При n = 2 и ${displaystyle y=f(x)=x^{3}}$ :

С учётом зависимости ${displaystyle x=t^{2}}$ , уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.

Дополнения[править | править код]

для функции с одной переменной:

${displaystyle {mathcal {4}}F(x_{0})=dF(x_{0})+{frac {d^{2}F(x_{0})}{2!}}+...+{frac {d^{n}F(x_{0})}{n!}}+{frac {d^{n+1}F(x_{0}+theta {mathcal {4}}x)}{(n+1)!}}}$

;

для функции с несколькими переменными:

${displaystyle {mathcal {4}}F(x_{0},y_{0})=dF(x_{0},y_{0})+{frac {d^{2}F(x_{0},y_{0})}{2!}}+...+{frac {d^{n}F(x_{0},y_{0})}{n!}}+{frac {d^{n+1}F(x_{0}+theta {mathcal {4}}x,y_{0}+theta {mathcal {4}}y)}{(n+1)!}}}$

Примечания[править | править код]

↑ ¹ ² Баранова Елена Семеновна, Васильева Наталья Викторовна, Федотов Валерий Павлович. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие. 2-е изд.. — “Издательский дом “”Питер”””, 2012. — С. 196-197. — 400 с. — ISBN 9785496000123.

Литература[править | править код]

Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1

Источник

7. Градиент функции двух переменных

Контрольные вопросы

Тема 2. Экстремум функции двух переменных

1. Локальный экстремум

Дифференциалы различных порядков

Что такое дифференциал функции

Что такое второй, третий дифференциал

Что такое дифференциал n-го порядка

Случай независимой переменной

Случай зависимой переменной

ПОИСК

Страницы

Партнеры сайта

Примеры Дифференциал функции двух переменных

Найти дифференциалы первого и второго порядка функции нескольких переменных

меню пользователя

Новости

Дифференциал высшего порядка функции одной переменной[править | править код]

Дифференциал высшего порядка функции нескольких переменных[править | править код]

Неинвариантность дифференциалов высшего порядка[править | править код]

Дополнения[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти драйвер клавиатуры на компьютере

Как найти все камни жнеца

Как составить родословное дерево презентация

Добавить комментарий Отменить ответ

Найти дифференциалы первого и второго порядка
функции нескольких переменных