Как найти двойной фокус линзы

Как найти двойной фокус линзы

Для введённых нами линз существует два условно разных типа задач:

  • задачи на построение в собирающей и рассеивающей линзах
  • задачи на формулу для тонкой линзы

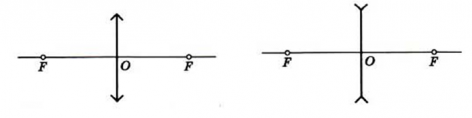
Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения преломлённых в линзах лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от линз. Для собирающей и рассеивающей линзу существуют рассмотренные (не нами) траектории распространения луча (рис. 1) от источника displaystyle S.

Собирающая и рассеивающая линзы (ход лучей)

Рис.1. Собирающая и рассеивающая линзы (ход лучей)

Для собирающей линзы (рис. 1.1) лучи:

  1. синий. Луч, идущий вдоль главной оптической оси, после преломления проходит через передний фокус.
  2. зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
  3. красный. Луч, идущий через передний фокус, после преломления распространяется параллельно главной оптической оси.

Пересечение любых из этих двух лучей (чаще всего выбирают лучи 1 и 2) дают изображение (displaystyle S').

Для рассеивающей линзы (рис. 1.2) лучи:

  1. синий. Луч, идущий параллельно главной оптической оси, преломляется так, что продолжения луча проходит через задний фокус.
  2. зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).

Пересечение продолжений рассмотренных лучей даёт изображение (displaystyle S').

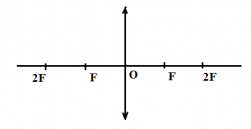
Аналогично сферическому зеркалу, получим набор изображений от предмета, расположенного на различных расстояниях от зеркала. Введём те же обозначения: пусть displaystyle f — расстояние от предмета до линзы, displaystyle F — расстояние от изображения до линзы, displaystyle F — фокусное расстояние (расстояние от фокуса до линзы).

Для собирающей линзы:

  • displaystyle dto infty (источник находится очень далеко от линзы). В этом случае мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси линзы.

Собирающая линза (источник в бесконечности)

Рис. 2. Собирающая линза (источник в бесконечности)

Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе проходят через фокус, то точка фокуса и является точкой пересечения преломлённых лучей, тогда она же и есть изображение источника (точечное, действительное).

  • displaystyle d>2F (источник находится за двойным фокусным расстоянием) (рис. 3).

Собирающая линза (источник за двойным фокусом)

Рис. 3. Собирающая линза (источник за двойным фокусом)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения преломившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.

  • displaystyle d=2F (источник находится ровно в двойном фокусе) (рис. 4).

Собирающая линза (источник в двойном фокусе)

Рис. 4. Собирающая линза (источник в двойном фокусе)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.

  • displaystyle 2F>d>F (источник между фокусом и двойным фокусом) (рис. 5)

Собирающая линза (источник между двойным фокусом и фокусом)

Рис. 5. Собирающая линза (источник между двойным фокусом и фокусом)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется).  Точка пересечения преломившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.

  • displaystyle d=F (источник находится ровно в фокусе собирающей линзы) (рис. 6)

Собирающая линза (источник в фокусе)

Рис. 6. Собирающая линза (источник в фокусе)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). В этом случае, оба преломлённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.

  • displaystyle d<F (источник находится между фокусом и главным оптическим центром) (рис. 7)

Собирающая линза (источник перед фокусом)

Рис. 7. Собирающая линза (источник перед фокусом)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Однако преломлённые лучи расходятся, т.е. сами преломлённые лучи не пересекутся, зато могут пересечься продолжения этих лучей. Точка пересечения продолжений преломлённых лучей — изображение (увеличенное, мнимое, прямое). Положение — по ту же сторону, что и предмет.

Для рассеивающей линзы построение изображений предметов практически не зависит от положения предмета, так что ограничимся произвольным положением самого предмета и характеристикой изображения.

  • displaystyle dto infty (источник находится очень далеко от линзы). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 8). Пустим два луча параллельно главной оптической оси линзы.

Рассеивающая линза (источник в бесконечности)

Рис. 8. Рассеивающая линза (источник в бесконечности)

Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе должны проходить через фокус (свойство фокуса), однако после преломления в рассеивающей линзе лучи должны расходится. Тогда в фокусе сходятся продолжения преломившихся лучей. Тогда точка фокуса и является точкой пересечения продолжений преломлённых лучей, т.е. она же и есть изображение источника (точечное, мнимое).

  • любое другое положение источника (рис. 9).

Рассеивающая линза (произвольное положение источника)

Рис. 9. Рассеивающая линза (произвольное положение источника)

Воспользуемся ходом луча, идущего параллельно главной оптической оси (продолжение отражённого луча проходит через передний фокус) и идущего через главный оптический центр линзы (не преломляется). Тогда изображением будет пересечение продолжений преломлённых лучей.

Второй тип задач связан с формулой тонкой линзы. Такие задачи основываются на числовых данных параметров, характеризующих положение источника, изображения или фокуса линзы. Рассмотрим произвольную систему (рис. 10). Пусть положение источника (displaystyle f), изображения (displaystyle F) и фокуса системы (displaystyle F) задано.

Формула тонкой линзы

Рис. 10. Формула тонкой линзы

Тогда взаимосвязь между параметрами положения элементов можно описать формулой:

displaystyle pm frac{1}{F}=pm frac{1}{d}pm frac{1}{f} (1)

Важно: для использования формулы (1) необходимо помнить правило расстановки знаков. Если линза собирающая, то displaystyle F<0, если рассеивающая, то displaystyle d>0. В случае действительных предметов и изображений: displaystyle f>0, displaystyle d<0, а в случае мнимых предметов и изображений: displaystyle f<0 и displaystyle f<0.

И последним параметром, характеризующим линзы или систему линз, является оптическая сила линзы (displaystyle D). Её нахождение довольно простое:

displaystyle D=frac{1}{F} (2)

Размерность оптической силы линзы: displaystyle ^{-1}мdisplaystyle ^{-1}=дптр (диоптрии). Оптическая сила собирающей линзы положительна, рассеивающей — отрицательна.

Вывод: задачи с линзами, в целом, разделены на два класса. Задачи на построение основываются на рисунках 2-9. Достаточно проанализировать ход лучей и найти изображение (рис.1). Численные значения в дано указывают на задачи на формулу тонкой линзы (1).

Источник

Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.

Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.

Внимание!

Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.

Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.

Определение

Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.

Построение изображения в собирающей линзе

Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:

Два вида лучей при построении изображений в линзе

Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).

Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.

На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.

В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.

Схема построения изображения Расположение предмета относительно линзы + характеристика изображение
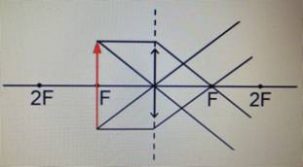
Если предмет располагается за двойным фокусом Предмет располагается за двойным фокусом.

Изображение:

  • уменьшенное;
  • перевернутое;
  • действительное.
Если предмет располагается в точке двойного фокуса Предмет располагается в фокальной плоскости второго фокуса.

Изображение:

  • перевернутое;
  • действительное.
Если предмет располагается в пространстве между фокусом и двойным фокусом Предмет располагается в пространстве между фокусом и двойным фокусом.

Изображение:

  • увеличенное;
  • перевернутое;
  • действительное.
Если предмет находится в фокальной плоскости Предмет находится в фокальной плоскости.

Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются.
https://static-interneturok.cdnvideo.ru/content/konspekt_image/72857/a744ac20_1bd0_0131_9837_12313b01b931.jpg Предмет располагается между линзой и фокусом.

Изображение:

  • увеличенное;
  • прямое;
  • мнимое.

Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.

Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.

Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.

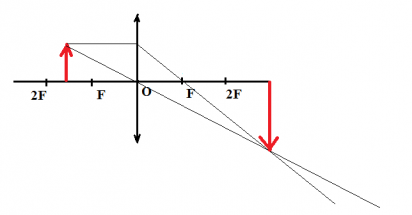
Частный случай — построение изображения точки

Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.

Тонкие линзы. Построение изображений - материалы для подготовки к ЕГЭ по Физике | ЕГЭ

Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.

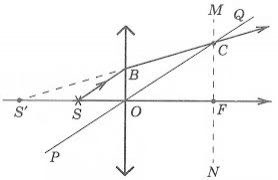
Министерство образования и науки РФ Федеральное государственное авт

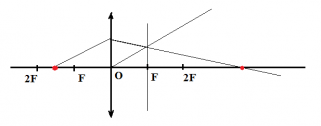
Пример №2. Построить изображение точки, расположенной на главной оптической оси.

Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.

Построение изображения в рассеивающей линзе

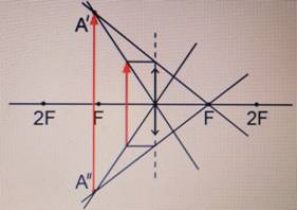
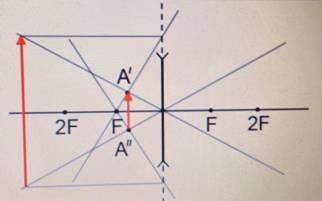
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:

  1. Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
  2. Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
  3. Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).

График рассеивающей линзы

Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.

Пример №3. Построить изображение предмета в рассеивающей линзе.

Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.

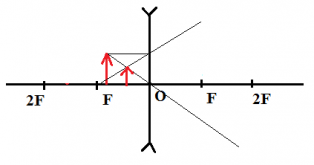
Построение изображений в плоском зеркале

Определение

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.

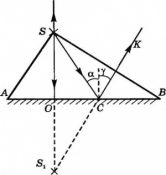
http://www.physbook.ru/images/thumb/8/8c/Aksen-16.10.jpg/300px-Aksen-16.10.jpg

Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC.  Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.

Таким образом, чтобы получить изображение в плоском зеркале, нужно:

  • Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
  • Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
  • Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
  • Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).

Внимание!

Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.

Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.

При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.

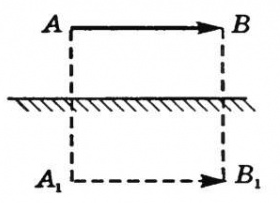
Изображение и сам предмет всегда симметричны относительно зеркала.

Пример №4. Построить изображение треугольника ABC в плоском зеркале.

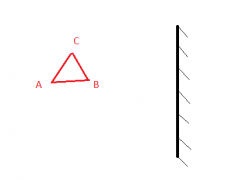
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.

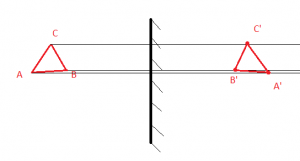
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.

Задание EF17760

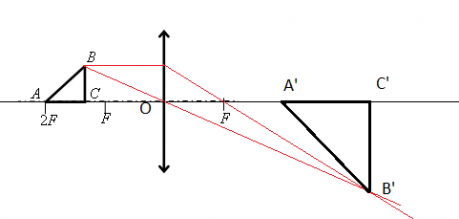
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения в СИ.

2.Сделать рисунок — построить изображение в линзе.

3.Записать формулу для нахождения площади полученной фигуры.

4.Выполнить решение в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Оптическая сила линзы: D = 2,5 дптр.

• Сторона треугольника AC = 4 см.

4 см = 0,04 м

Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.

Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.

Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:

1d+1f=1F

Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:

12F+1f=1F

1f=1F−12F=2−12F=12F

f=2F

Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:

S=A´C´·B´C´2

Из формулы оптической силы линзы найдем фокусное расстояние:

F=1D=12,5=0,4 (м)

Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:

dC=2F−AC=2·0,4−0,04=0,76 (м)

Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:

10,76+1f=1F

1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4

fC=0,76·0,40,76−0,4=0,844 (м)

Тогда длина катета A´ C´ будет равна:

A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)

Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:

BCB´C´=ACA´C´

Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:

ACB´C´=ACA´C´

Следовательно:

B´C´=A´C´

Отсюда площадь треугольника равна:

S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)

pазбирался: Алиса Никитина | обсудить разбор

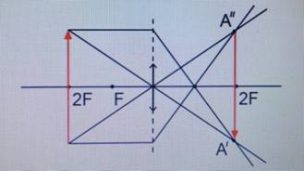
Задание EF18181

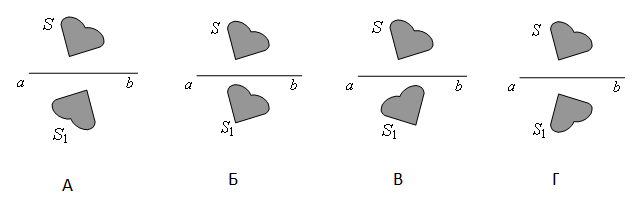
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?

Ответ:

Алгоритм решения

  1. Записать, какое изображение дает плоское зеркало.
  2. Выбрать изображение, которое соответствует типу описанного изображения.

Решение

Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.

Ответ: Г

pазбирался: Алиса Никитина | обсудить разбор

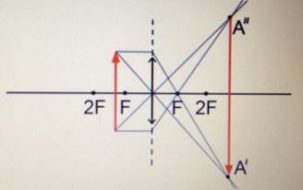
Задание EF18876

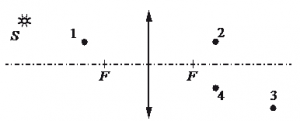Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?

Алгоритм решения

1.Построить изображение точки.

Решение

Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.

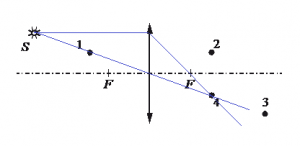
Ответ: 4

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 31.8k

Источник

В
данной теме будет рассмотрено решение задач на построение изображений в линзе.

Задача
1.
На рисунке изображен предмет АВ и собирающая линза. Постройте
изображение предмета если он находится а) за двойным фокусом  б) между фокусом
и двойным фокусом.

РЕШЕНИЕ

Изобразим
на чертеже собирающую линзу, её главную оптическую ось, фокусы и двойные
фокусы.

Двойной
фокус – это точка, находящаяся на оптической оси на расстоянии от оптического
центра, вдвое большем, чем фокусное расстояние. Изобразим предмет АВ,
находящийся за двойным фокусом.

Точка
А находится на оптической оси линзы, поэтому её изображение тоже будет находится
на оптической оси. Чтобы получить изображение точки В, понадобится два
луча. Один направим параллельно оптической оси, а второй – через оптический
центр. Лучи, проходящие через оптический центр, не преломляются, поэтому легко
можем продолжить последний луч. Луч, параллельный оптической оси преломляется,
и после преломления проходит через фокус линзы. На пересечении этих лучей и
формируется изображение точки В, которое обозначим как B’.
Точка A’
будет
находится на главной оптической оси.

Во
втором случаи поступаем таким же образом используя два луча.

Таким
образом, получено действительное и перевёрнутое изображение. Только в этот раз
оно является увеличенным и находится за двойным фокусом.

Задача
2.
На рисунке указан источник света и его изображение в линзе. Также на рисунке
указана главная оптическая ось линзы. На основании этих данных, найдите
положение оптического центра линзы, её фокусов, а также определите тип линзы.

РЕШЕНИЕ

В
первую очередь, проведём прямую через источник света и его изображение (она называется
побочной оптической осью). Точка пересечения этой прямой с главной оптической
осью является оптическим центром линзы.

Обозначим
на нашем чертеже линзу. От источника света направим луч на линзу параллельно
главной оптической оси. Известно, что луч преломляясь идёт через фокус и через
изображение (или же, через изображение идёт продолжение луча). Проведём
пунктирную прямую через точку, в которой луч падает на линзу и через изображение
источника света. Точка, в которой данная прямая пересекает главную оптическую
ось и будет являться фокусом линзы.

Теперь,
с уверенностью можно сказать, что прямая, которую построили является
продолжением преломлённого луча. По характеру преломления луча или, исходя из
того, что изображение мнимое и находится ближе фокуса, можно заключить, что
линза является рассеивающей.

Задача
3.
На рисунке изображен луч АВ, прошедший через рассевающую линзу. Также,
на рисунке указаны положения фокусов линзы. Постройте ход падающего луча.

РЕШЕНИЕ

Отметим
на чертеже оптический центр линзы. Поскольку имеются положения фокусов линзы, можно
провести фокальную плоскость. Теперь проведём продолжение преломлённого луча до
пересечения с фокальной плоскостью. Точку пересечения обозначим за F’.

Через
эту точку и оптический центр линзы пройдёт побочная оптическая ось. Луч, идущий
вдоль этой оси пройдёт, не меняя своего направления (поскольку он пройдёт через
оптический центр). Луч, параллельный побочной оси, преломляется таким образом,
что продолжение преломлённого луча пройдёт через точку F’.
Таким образом, построен падающий луч.

Задача
4.
Постройте изображение предмета АВ в соответствии с указанным рисунком.

РЕШЕНИЕ

Здесь
сложность заключается в том, что предмет проходит через фокус, причём, таким
образом, что часть предмета находится на расстоянии, ближе фокусного, а часть –
между фокусом и двойным фокусом.

Можно
попытаться разбить предмет на два отрезка: AF
и FB. Очевидно, что
изображения и того, и другого отрезка будут уходить в бесконечность, поскольку,
точка F, естественно,
находится на фокусном расстоянии от линзы. А, как изветно, изображения
предметов, находящихся на фокусном расстоянии от линзы, не формируются (или
формируются в бесконечности).

Однако,
следует заметить, что луч, идущий в направлении от точки А к  точке В
преломляется таким образом, что преломлённый луч параллелен главной оптической
оси. Можно построить продолжение этого луча.

Таким
образом, все точки изображения предмета АВ будут лежать на прямой,
проходящей через указанный луч и его продолжение. Проведём прямую через точку А
и оптический центр до пересечения с указанной ранее прямой. В точке пересечения
получится изображение точки А, которое обозначим как A’.

Аналогично,
проведём прямую через оптический центр и точку D
– таким образом, получим точку B’.
Если попытаться получить изображения других точек аналогичным способом, то можно
убедиться, что изображение данного предмета получается разрозненным (то есть,
делится на две части). Действительно, ведь изображение той части предмета,
которая находится перед фокусом, является мнимым, а изображение части,
находящейся между фокусом и двойным фокусом является действительным.

Задача
5.
На рисунке указан предмет, который находится на таком расстоянии от линзы, что
его изображение является действительным и увеличенным ровно в 2 раза. Постройте
это изображение и найдите длину отрезка A’C’,
если длина отрезка AB
равна 15 см, а длина
отрезка A’B’
равна 35 см. Угол BAC
прямой.

РЕШЕНИЕ

Отметим
на чертеже фокусы и двойные фокусы линзы. Отметим эти точки таким образом,
чтобы наш предмет находился между фокусом и двойным фокусом, поскольку именно в
этом случае получается действительное и увеличенное изображение (которое будет
находится за двойным фокусом). Итак, чтобы построить изображение, необходимо
получить изображения точек А, В и С. Построим эти точки
используя два луча.

Т.к.
изображение больше предмета в два раза, то

По
теореме Пифагора

Ответ: 18 см.

Источник

Используя лупу, мы видим увеличенное изображение предмета. Другие линзы уменьшают действительные размеры предмета. От чего же это зависит? Как правильно построить изображение, даваемое линзой?

На прошлом уроке мы с вами научились строить изображения светящейся точки, даваемое собирающей или рассеивающей линзой. Теперь перед нами стоит задача выяснить закономерности получения различных изображений предмета и научиться самостоятельно их получать с помощью чертежей.

Изображение предмета и фокус линзы

Рассмотрим простой опыт, схожий с тем, что был в прошлом уроке. У нас так же имеется большая собирающая линза, но вместо маленькой лампочки — свеча (рисунок 1). Свечу мы уже можем рассматривать как протяженный предмет. Поместим ее между линзой и ее фокусом $F$.

Рисунок 1. Прямое изображение предмета, даваемое собирающей линзой

Теперь посмотрим на свечу через линзу. Мы увидим ее изображение с той же стороны, где она действительно находится.

Но нам будет казаться, что свеча находится немного дальше своего истинного положения. Кроме того, изображение будет увеличенным. 

Изображение не будет наклоненным или перевернутым. Такое изображение называется прямым.

Если мы начнем перемещать свечу относительно ее фокуса (ближе и дальше от линзы), то увидим, что ее изображение будет существенно изменяться. Например, если мы переместим свечу за фокус линзы, то изображение пропадет. Но при этом оно появится с другой стороны линзы, далеко от нее. Чтобы его увидеть, нужно расположить экран с той стороны, где на рисунке 1 находится Образавр.

Это изображение будет не только увеличенным, но и перевернутым по отношению к свече.

Значит, передвигая свечу на различные расстояния от линзы и ее фокуса, мы можем получить различные изображения.

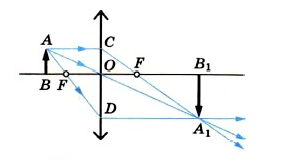
Построение изображения предмета, находящегося за двойным фокусом линзы

Теперь мы можем рассмотреть, как строятся изображения протяженных предметов, находящихся на разных расстояниях от собирающей линзы.

Разберем рисунок 2. Мы провели оптическую ось и отметили на рисунке собирающую линзу. По обе стороны от нее отметили две равноудаленные точки — фокусы линзы $F$. Так же мы отметили двойные фокусные расстояния — $2F$.

Предмет на чертежах мы будем изображать с помощью стрелки. Ее концы отмечаем точками $A$ и $B$. Такое обозначение поможет нам легко оценивать полученное изображение: будет оно прямым или перевернутым.

Начнем с того, что поместим наш предмет за двойной фокус линзы.

Рисунок 2. Изображение предмета, находящегося за двойным фокусом собирающей линзы

Чтобы получить изображение предмета, даваемое линзой, нам необходимо получить изображения двух точек $A$ и $B$ и соединить их между собой.

Получим изображение точки $A$. Для этого начертим ход двух световых лучей, выходящих из этой точки:

  • Луч $AC$ параллелен оптической оси. После преломления в линзе он проходит через ее фокус $F$
  • Луч $AO$ проходит через оптический центр $O$. После прохождения свозь линзу направление его распространения не изменяется

Эти два луча пересекутся в точке $A_1$. Эта точка является изображением точки $A$.

Точка $B$ лежит на оптической оси линзы. Мы можем построить ее изображение способом из прошлого урока, использую фокальную плоскость, побочную ось и побочный фокус. Но при построении изображения предмета, который располагается перпендикулярно оптической оси, мы можем сделать это проще. Для этого нам просто необходимо опустить перпендикуляр из полученной точки $A_1$ на оптическую ось. Так мы получаем изображение точки $B$ — $B_1$.

Если предмет будет располагаться под каким-то углом к оптической оси или обе его точки будут находиться не на оптической оси, необходимо выполнять построение изображения каждой точки предмета способами, описанными в прошлом уроке.

Теперь нам осталось соединить точки $A_1$ и $B_1$ между собой. Не перепутайте направление стрелки: если у предмета ее острие было в точке $A$, то у изображения предмета острие стрелки должно быть в точке $A_1$.

Характеристики изображения предмета

Итак, мы получили изображение предмета $A_1B_1$. Для того чтобы описать его, введем новые обозначения. Обозначим расстояние от предмета до линзы как $d$, а от линзы до изображения предмета как $f$.

Если $d > 2F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
4. $F < f < 2F$

Изображение действительное, потому оно образовано на пересечении преломленных линзой лучей.

Уменьшенное — мы можем судить об этом, посмотрев на полученный чертеж.

Перевернутое — если вернуться к опыту со свечей и поместить ее за двойной фокус линзы, то мы увидим изображение свечи огоньком вниз.

Последняя строчка нашей характеристики полученного изображения ($F < f < 2F$) говорит нам о том, что изображение предмета находится ближе к линзе, чем в действительности. Чтобы увидеть это изображение, нужно расположить экран (как экран проектора) именно на этом расстоянии.

Получим ли мы на практике точно такое же изображение? Возьмем большую собирающую линзу и свечу. Расположим свечу с помощью подставки таким образом, чтобы ее крайняя нижняя точка находилась на оптической оси (рисунок 3). Поместим ее за двойным фокусом линзы.

Рисунок 3. Изображение предмета, даваемое собирающей линзой, в действительности

Передвигая экран ближе и дальше от линзы, найдем такое его положение, когда на нем появится изображение свечи. Мы увидим, что оно совпадаем с тем, которое мы получили на чертеже: уменьшенное, перевернутое и находится между фокусом и двойным фокусом линзы.

Настраивая фотоаппарат вручную, можно получить такое изображение.

Изображение предмета, находящегося между фокусом и двойным фокусом собирающей линзы

Будем постепенно приближать предмет к линзе. Теперь разместим его между фокусом и двойным фокусом линзы: $F < d < 2F$ (рисунок 4).

Рисунок 4. Изображение предмета, находящегося между фокусом и двойным фокусом собирающей линзы

Построение изображения выполняется точно таким же образом, как и в прошлом случае. Отмечаем на чертеже ход двух лучей, выходящих из точки $A$. На их пересечении получаем точку $A_1$. Опускаем перпендикуляр на оптическую ось и отмечаем точку $B_1$. Соединяем две полученные точки между собой и получаем изображение предмета — $A_1B_1$. Охарактеризуем его.

Если $F < d < 2F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 2F$

Получается, что по мере приближения предмета к линзе (но не доходя до фокуса линзы), перевернутое изображение предмета будет удаляться от линзы, а его размеры будут увеличиваться.

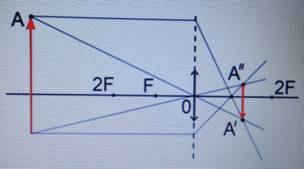
Изображение предмета, находящегося перед фокусом собирающей линзы

Пододвинем предмет еще ближе к линзе. Теперь он находится между линзой и ее фокусом: $d < F$ (рисунок 5).

Рисунок 5. Изображение предмета, находящегося между собирающей линзой и ее фокусом

Луч $AC$ преломляется после прохождения сквозь линзу и проходит через фокус. Мы получили преломленный луч $CC_1$.

Луч $AO$ проходит через оптический центр и не меняет своего направления. Из линзы выходит преломленный луч $OD$, совпадающий по направлению с падающим лучом.

Мы видим, что преломленные лучи $CC_1$ и $OD$ не пересекутся. Но если мы их продолжим в левую сторону чертежа, то получим точку пересечения — изображение точки $A$. Мы можем сразу сказать, что такое изображение будет мнимым, потому что пересекаются не сами преломленные лучи, а их продолжения.

Опустив перпендикуляр на оптическую ось, мы получим точку $B_1$. Соединим друг с другом точки $A_1$ и $B_1$, и изображение предмета $A_1B_1$ готово. Охарактеризуем его.

Если $d < F$, то изображение предмета, даваемое собирающей линзой:
1. Мнимое
2. Увеличенное
3. Прямое
4. $F < f < 2F$ (со стороны предмета)

Изображение предмета, даваемого рассеивающей линзой

Рассмотрим построение изображений, которые можно получить с помощью рассеивающей линзы (рисунок 6).

Такая линза никогда не даст действительного изображения, оно всегда будет мнимым. Ведь лучи, проходящие через рассеивающую линзу, расходятся. Это значит, что они никогда не пересекутся в противоположной от расположения предмета стороне. Будут пересекаться продолжения световых лучей на той же стороне от линзы, где находится предмет.

Рисунок 6. Изображение предмета, даваемое рассеивающей линзой

Рассмотрим чертеж. Из точки $A$ выходят два луча $AC$ и $AO$. Луч $AC$ достигает линзы и преломляется. Луч $AO$ после прохождения сквозь линзу не изменяет своего направления.

Из чертежа сразу ясно, что преломленные лучи не пересекутся. Значит, должны пересечься их продолжения. Продолжение первого преломленного луча пройдет через мнимый фокус по определению рассеивающей линзы. Продолжение луча второго преломленного луча совпадает с лучом $AO$.

Эти продолжения пересекаются в точке $A_1$ — мнимом изображении точки $A$. Опустим перпендикуляр на оптическую ось и получим точку $B_1$. Соединим точки и получим изображение предмета $A_1B_1$.

Изображение, даваемое рассеивающей линзой:
1. Мнимое
2. Уменьшенное
3. Прямое

Подтвердим вышесказанное опытом. Возьмем большую рассеивающую линзу и свечу. Свечу установим на подставке так, чтобы ее крайняя нижняя точка находилась на оптической оси линзы (рисунок 7).

Рисунок 7. Изображение предмета, даваемое рассеивающей линзой, в действительности

Смотря через линзу мы не увидим реальную свечу. Мы увидим ее мнимое, прямое и уменьшенное изображение $A_1B_1$. Все совпало с нашим чертежом.

Если мы начнем передвигать свечу относительно линзы, то увидим, что характеристики ее изображения будут сохраняться. Вне зависимости от положения свечи, ее изображение всегда будет мнимым, прямым и уменьшенным.

Выводы

Размеры и расположение изображения предмета в собирающей линзе зависят от положения предмета относительно линзы.

Рассеивающая линза дает уменьшенное, мнимое и прямое изображение, которое находится по ту же сторону от линзы, что и предмет. Оно не зависит от положения предмета относительно линзы.

Памятка построения изображений предмета

  1. Нарисуйте обозначение линзы и проведите ее оптическую ось. Отметьте оптический центр линзы
  2. Отметьте два фокуса линзы по обе стороны от нее. При этом фокусная длина выбирается произвольной, но одинаковой для обеих от линзы сторон
  3. Обозначьте на чертеже предмет там, где указано в задании
  4. Начертите ход двух лучей, исходящих от крайней точке предмета, если предмет перпендикулярен оптической оси и одна из точек расположена на ней.
  5. Если предмет находится под углом к оптической оси, или ни одна из точек не лежит на оптической оси, начертите ход двух лучей от каждой крайней точки предмета
  6. Используя точки пересечения лучей (или их продолжений), нарисуйте изображение предмета
  7. Охарактеризуйте его: действительное изображение или мнимое, прямое или перевернутое, его размеры и расположение относительно линзы

Пример построения изображения

Постройте изображение, которое даст собирающая линза, если предмет находится в двойном фокусе, как показано на рисунке 8.

Рисунок 8. Условия для построения изображения предмета

Показать готовой чертеж и пояснения

Скрыть

При таком положении предмета нам нужно выполнить построение для каждой точки (рисунок 9).

Выберем два луча для точки $A$: $AC$ и $AO$. Луч $AC$ преломляется в линзе и после этого проходит через фокус линзы $F$. Луч $AO$ после преломления в линзе не меняет своего направления распространения. Эти преломленные лучи пересекутся в точке $A_1$.

Рисунок 9. Изображение предмета, находящегося в двойном фокусе собирающей линзы

То же самое проделаем с точкой $B$. Преломленные лучи пересекутся в точке $B_1$. Соединим полученные точки $A_1$ и $B_1$ — получим изображение предмета $A_1B_1$. Охарактеризуем его. (Напоминание: $d$ — это расстояние от предмета до линзы, $f$ — расстояние от изображения предмета до линзы).

Если $d = 2F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Равного размера с предметом
3. Перевернутое
4. $f = 2F$

Источник

Тонкие линзы. Ход лучей.

  • Понятие тонкой линзы.

  • Оптический центр и фокальная плоскость.

  • Ход луча через оптический центр.

  • Ход лучей в собирающей линзе.

  • Ход лучей в рассеивающей линзе.

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: линзы, оптическая сила линзы

Взгляните ещё раз на рисунки линз из предыдущего листка: эти линзы обладают заметной толщиной и существенной кривизной своих сферических границ. Мы намеренно рисовали такие линзы – чтобы основные закономерности хода световых лучей проявились как можно более чётко.

к оглавлению ▴

Понятие тонкой линзы.

Теперь, когда эти закономерности достаточно ясны, мы рассмотрим очень полезную идеализацию, которая называется тонкой линзой.
В качестве примера на рис. 1 приведена двояковыпуклая линза; точки O_{1} и O_{2} являются центрами её сферических поверхностей, R_{1} и R_{2}– радиусы кривизны этих поверхностей. O_{1}O_{2} – главная оптическая ось линзы.

Рис. 1. К определению тонкой линзы

Так вот, линза считается тонкой, если её толщина MN очень мала. Нужно, правда, уточнить: мала по сравнению с чем?

Во-первых, предполагается, что MN ll R_{1} и MN ll R_{2}. Тогда поверхности линзы хоть и будут выпуклыми, но могут восприниматься как “почти плоские”. Этот факт нам очень скоро пригодится.
Во-вторых, MN ll a, где a – характерное расстояние от линзы до интересующего нас предмета. Собственно, лишь в таком случае мы и
сможем корректно говорить о “расстоянии от предмета до линзы”, не уточняя, до какой именно точки линзы берётся это самое расстояние.

Мы дали определение тонкой линзы, имея в виду двояковыпуклую линзу на рис. 1. Это определение без каких-либо изменений переносится на все остальные виды линз. Итак: линза является тонкой, если толщина линзы много меньше радиусов кривизны её сферических границ и расстояния от линзы до предмета.

Условное обозначение тонкой собирающей линзы показано на рис. 2.

Рис. 2. Обозначение тонкой собирающей линзы

Условное обозначение тонкой рассеивающей линзы показано на рис. 3.

Рис. 3. Обозначение тонкой рассеивающей линзы

В каждом случае прямая FF – это главная оптическая ось линзы, а сами точки F – её
фокусы. Оба фокуса тонкой линзы расположены симметрично относительно линзы.

к оглавлению ▴

Оптический центр и фокальная плоскость.

Точки M и N, обозначенные на рис. 1, у тонкой линзы фактически сливаются в одну точку. Это точка O на рис. 2 и 3, называемая оптическим центром линзы. Оптический центр находится на Пересечении линзы с её главной оптической осью.

Расстояние OF от оптического центра до фокуса называется фокусным расстоянием линзы. Мы будем обозначать фокусное расстояние буквой f. Величина D, обратная фокусному расстоянию, есть оптическая сила – линзы:

D=frac{displaystyle 1}{displaystyle f}.

Оптическая сила измеряется в диоптриях (дптр). Так, если фокусное расстояние линзы равно 25 см, то её оптическая сила:

D=frac{displaystyle 1}{displaystyle 0,25}=4 дптр

Продолжаем вводить новые понятия. Всякая прямая, проходящая через оптический центр линзы и отличная от главной оптической оси, называется побочной оптической осью . На рис. 4 изображена побочная оптическая ось – прямая OP.

Рис. 4. Побочная оптическая ось, фокальная плоскость и побочный фокус

Плоскость pi , проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью. Фокальная плоскость, таким образом, параллельна плоскости линзы. Имея два фокуса, линза соответственно имеет и две фокальных плоскости, расположенных симметрично относительно линзы.

Точка P, в которой побочная оптическая ось пересекает фокальную плоскость, называется побочным фокусом. Собственно, каждая точка фокальной плоскости (кроме F) есть побочный фокус – мы ведь всегда сможем провести побочную оптическую ось, соединив данную точку с оптическим центром линзы. А сама точка F – фокус линзы – в связи с этим называется ещё главным фокусом.

То, что на рис. 4 изображена собирающая линза, никакой роли не играет. Понятия побочной оптической оси, фокальной плоскости и побочного фокуса совершенно аналогично определяются и для рассеивающей линзы – с заменой на рис. 4 собирающей линзы на рассеивающую.

Теперь мы переходим к рассмотрению хода лучей в тонких линзах. Мы будем предполагать, что лучи являются параксиальными, то есть образуют достаточно малые углы с главной оптической осью. Если параксиальные лучи исходят из одной точки, то после прохождения линзы преломлённые лучи или их продолжения также пересекаются в одной точке. Поэтому изображения предметов, даваемые линзой, в параксиальных лучах получаются весьма чёткими.

к оглавлению ▴

Ход луча через оптический центр.

Как мы знаем из предыдущего раздела, луч, идущий вдоль главной оптической оси, не преломляется. В случае тонкой линзы оказывается, что луч, идущий вдоль побочной оптической оси, также не преломляется!

Объяснить это можно следующим образом. Вблизи оптического центра O обе поверхности линзы неотличимы от параллельных плоскостей, и луч в данном случае идёт как будто через плоскопараллельную стеклянную пластинку (рис. 5).

Рис. 5. Ход луча через оптический центр линзы

Угол преломления луча AB равен углу падения преломлённого луча BC на вторую поверхность. Поэтому второй преломлённый луч CD выходит из плоскопараллельной пластинки параллельно падающему лучу AB. Плоскопараллельная пластинка лишь смещает луч, не изменяя его направления, и это смещение тем меньше, чем меньше толщина пластинки.

Но для тонкой линзы мы можем считать, что эта толщина равна нулю. Тогда точки B, O, C фактически сольются в одну точку, и луч CD окажется просто продолжением луча AB. Вот поэтому и получается, что луч, идущий вдоль побочной оптической оси, не преломляется тонкой линзой (рис. 6).

Рис. 6. Луч, идущий через оптический центр тонкой линзы, не преломляется

Это единственное общее свойство собирающих и рассеивающих линз. В остальном ход лучей в них оказывается различным, и дальше нам придётся рассматривать собирающую и рассеивающую линзу по отдельности.

к оглавлению ▴

Ход лучей в собирающей линзе.

Как мы помним, собирающая линза называется так потому, что световой пучок, параллельный главной оптической оси, после прохождения линзы собирается в её главном фокусе (рис. 7).

Рис. 7. Параллельный пучок собирается в главном фокусе

Пользуясь обратимостью световых лучей, приходим к следующему выводу: если в главном фокусе собирающей линзы находится точечный источник света, то на выходе из линзы получится световой пучок, параллельный главной оптической оси (рис. 8).

Рис. 8. Преломление пучка, идущего из главного фокуса

Оказывается, что пучок параллельных лучей, падающих на собирающую линзу наклонно, тоже соберётся в фокусе – но в побочном. Этот побочный фокус P отвечает тому лучу, который проходит через оптический центр линзы и не преломляется (рис. 9).

Рис. 9. Параллельный пучок собирается в побочном фокусе

Теперь мы можем сформулировать правила хода лучей в собирающей линзе. Эти правила вытекают из рисунков 6-9,

1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления пойдёт через главный фокус (рис. 10).

Рис. 10. К правилу 2

3. Если луч падает на линзу наклонно, то для построения его дальнейшего хода мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Вот через этот побочный фокус и пойдёт преломлённый луч (рис. 11).

Рис. 11. К правилу 3

В частности, если падающий луч проходит через фокус линзы, то после преломления он пойдёт параллельно главной оптической оси.

к оглавлению ▴

Ход лучей в рассеивающей линзе.

Переходим к рассеивающей линзе. Она преобразует пучок света, параллельный главной оптической оси, в расходящийся пучок, как бы выходящий из главного фокуса (рис. 12)

Рис. 12. Рассеяние параллельного пучка

Наблюдая этот расходящийся пучок, мы увидим светящуюся точку, расположенную в фокусе F позади линзы.

Если параллельный пучок падает на линзу наклонно, то после преломления он также станет расходящимся. Продолжения лучей расходящегося пучка соберутся в побочном фокусе P, отвечающем тому лучу, который проходит через через оптический центр линзы и не преломляется (рис. 13).

Рис. 13. Рассеяние наклонного параллельного пучка

Этот расходящийся пучок создаст у нас иллюзию светящейся точки, расположенной в побочном фокусе P за линзой.

Теперь мы готовы сформулировать правила хода лучей в рассеивающей линзе. Эти правила следуют из рисунков 6, 12 и 13.

1. Луч, идущий через оптический центр линзы, не преломляется.
2. Луч, идущий параллельно главной оптической оси линзы, после преломления начнёт удаляться от главной оптической оси; при этом продолжение преломлённого луча пройдёт через главный фокус (рис. 14).

Рис. 14. К правилу 2

3. Если луч падает на линзу наклонно, то мы проводим побочную оптическую ось, параллельную этому лучу, и находим соответствующий побочный фокус. Преломлённый луч пойдёт так, словно он исходит из этого побочного фокуса (рис. 15).

Рис. 15. К правилу 3

Пользуясь правилами хода лучей 1–3 для собирающей и рассеивающей линзы, мы теперь научимся самому главному – строить изображения предметов, даваемые линзами.

Разберем задачи ЕГЭ по теме: Тонкие линзы.

1. На экране с помощью тонкой линзы получено изображение предмета с пятикратным увеличением. Экран передвинули на 30 см вдоль главной оптической оси линзы. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. В этом случае получилось изображение с трехкратным увеличением. На сколько пришлось передвинуть предмет относительно первоначального положения?
Дано:
Г₁=5
Г₂=3
а = 30 см = 0,3 м.
Найти:
Δd – ?

Решение.

При решении этой задачи главным является создание модели, которая поясняет изменения в увеличении линзы и позволяет правильно определить перемещение экрана и предмета. На представленных ниже рис.1 и рис.2 выполнены все необходимые построения для двух случаев задачи. Так как увеличение линзы уменьшается, то предмет смещается в сторону двойного фокуса. Именно в этом случае возможно уменьшение изображения, по сравнению с первым случаем.

Особое внимание надо обратить на фразу, что изображение снова стало резким. Это возможно только при выполнении всех соотношений в формуле тонкой линзы frac{1}{d}+frac{1}{f}=frac{1}{F}.

Для каждого случая запишем формулу тонкой линзы и учтем соотношения между d и f через значение увеличения (Г), даваемое линзой.

frac{1}{d_1}+frac{1}{f_1}=frac{1}{F} ~~(1)

frac{1}{d_2}+frac{1}{f_2}=frac{1}{F} ~~(2)

frac{f_1}{d_1}= Г₁ =5 ~~(3), отсюда d_1=frac{f_1}{5}.

frac{f_2}{d_2}= Г₂ =3 ~~(4), отсюда d_2=frac{f_2}{3}.

Тогда формулы (1) и (2) примут вид:

frac{5}{f_1}+frac{1}{f_1}=frac{1}{F}

frac{3}{f_2}+frac{1}{f_2}=frac{1}{F}

frac{6}{f_1}=frac{1}{F}~~(5)

frac{4}{f_2}=frac{1}{F}~~(6)

Остается решить следующую систему из двух уравнений:

begin{cases}frac{6}{f_1}=frac{4}{f_2} \f_1-f_2=aend{cases}

Решение этой системы можно провести с подстановкой численных значений.

frac{6}{f_1}=frac{4}{f_1=0,3}
6f_1-1,8=4f_1
2f_1=1,8
f_1=0,9 (м). Тогда f_2=0,9-0,3=0,6 (м)

d_1=frac{0,9}{5}=0,18 (м)

d_2=frac{0,6}{3}=0,2 (м)

Delta d=0,2-0,18=0,02 (м).

Ответ: 0,02 м

2. На оси ОХ в точке x_1=0 находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием F_1=-20 см, а в точке x_2=20 см – тонкой собирающей линзы. Главные оптические ос обеих линз лежат на оси ОХ. На рассеивающую линзу вдоль оси ОХ падает параллельный пучок света из области х<0. Пройдя данную оптическую систему, лучи собираются в точке с координатой x_3=30 см. Найдите фокусное расстояние собирающей линзы F_2.

Дано:
x_1=0
F_1=-20 см = -0,2 м
x_2=20 см = 0,2 м
x_3=30 см = 0,6 м
Найти:
F_2 – ?

Решение
На рисунке представлен ход лучей через систему рассеивающей и собирающей линз. При решении подобных задач необходимо рассматривать отдельно ход лучей сквозь каждую линзу.

Рассмотрим сначала ход лучей через рассеивающую линзу. Для этого воспользуемся формулой тонкой линзы и учтем, что d_1 rightarrow infty, так как на рассеивающую линзу падает параллельный пучок света из области x<0. Тогда дробь frac{1}{d_1}rightarrow 0 и формула примет вид:

-frac{1}{f_1}=-frac{1}{F_1}

Перед f_1 стоит знак (-), так как линза рассеивающая и она дает всегда мнимое изображение.

Поэтому f_1=F_1=0,2 (м).

В точке S сформировалось мнимое изображение светового пучка, который падает на собирающую линзу из области x<0.

Теперь отдельно рассмотрим собирающую линзу. Для нее расстояние d_2 будет равно 0,4 м (согласно рисунку). Применим для собирающей линзы формулу тонкой линзы с учетом d_2 и f_2. Расстояние f_2=f=x_3-x_2; f=0,6-0,2=0,4 (м).

frac{1}{d_2}+frac{1}{f_2}=frac{1}{F}

frac{d_2+f_2}{d_2cdot f_2}=frac{1}{F}

F=frac{d_2cdot f_2}{d_2+f_2}

F=frac{0,4 cdot 0,4}{0,4+0,4}=0,2 (м) = 20 (см).

Ответ: 20 см.

3. Точечный источник света движется со скоростью v вокруг главной оптической оси собирающей линзы в плоскости, параллельной плоскости линзы на расстоянии d=15 см от линзы. Фокусное расстояние линзы F= 10 cм. Скорость движения изображения точечного источника света V=10 м/с. Найдите скорость движения источника света.

Дано:
d=15 см = 0,15 м
F= 10 см = 0,1 м
V=10 м/с
Найти: v-?

Решение.

Для решения этой задачи воспользуемся формулой тонкой линзы.

frac{1}{d}+frac{1}{f}=frac{1}{F}

frac{1}{f}=frac{1}{F}-frac{1}{d}

frac{1}{f}=frac{d-F}{Fd}

f=frac{Fd}{d-F}

Проведем расчет для определения расстояния от линзы до изображения.

f=frac{0,1 cdot 0,15}{0,15-0,1}=0,3 (м).

Полученный результат говорит о том, что увеличение линзы Г>1.

Г = frac{0,3}{0,15}=2.

Точечный источник и его изображение будут двигаться с разными линейными скоростями, но в тоже самое время период их обращения, частота обращения и угловые скорости у них будут равными. Радиусы окружностей, которые будут описывать источник света и его изображения, будут отличаться в 2 раза. Радиус окружности изображения R будет превышать радиус окружности источника r в 2 раза (frac{R}{r}=2 или frac{r}{R}=frac{1}{2}).

Воспользуемся формулой равенства периодов обращения.

T_1=frac{2pi r}{v}

T_2=frac{2pi R}{V}

T_1=T_2

frac{2pi r}{v}=frac{2pi R}{V}

v=frac{rcdot V}{R}

v=frac{1cdot 10}{2}=5 (м/с)

4. Точечный источник света S расположен на расстоянии 40 cм от оптического центра тонкой собирающей линзы с фокусным расстоянием 0,2 м на её главной оптической оси АВ. На сколько сместиться вдоль прямой АВ изображение источника, если линзу повернуть на угол alpha=30° относительно оси, перпендикулярной плоскости рисунка и проходящей через оптический центр линзы? Сделайте пояснительный чертеж, указав ход лучей в линзе для обоих случаев её расположения.

Дано:
d_1= 40 cм = 0,4 м
F = 0,2 м
alpha = 30°
Найти:
Delta f – ?

Решение.

Применим формулу тонкой линзы для первого случая.

frac{1}{d_1}+frac{1}{f_1}=frac{1}{F}

frac{1}{f_1}=frac{1}{F}-frac{1}{d_1}

frac{1}{f_1}=frac{d_1-F}{Fd_1}

f_1=frac{Fd_1}{d_1-F}

f_1=frac{0,2cdot 0,4}{0,4-0,2}=0,4 (м).

Применим формулу тонкой линзы для второго случая.

frac{1}{d_2}+frac{1}{f_2}=frac{1}{F}

frac{1}{f_2}=frac{1}{F}-frac{1}{d_2}

frac{1}{f_2}=frac{d_2-F}{Fd_2}

f_2=frac{Fd_2}{d_2-F}

Здесь необходимо учесть, что d_2=d_1cosalpha=0,4cos30textdegree approx 0,35 (м).

f_2=frac{0,2 cdot 0,35}{0,35-0,2}approx 0,47 (м).

Изображение источника во втором случае также формируется на прямой АВ. Для нахождения расстояния OS_2 необходимо

OS_2cosalpha = f_2

OS_2=frac{f_2}{cosalpha}

OS_2=frac{0,47}{cos 30textdegree } = 0,54 (м).

Таким образом, изображения источников в обоих случаях получились на прямой АВ на расстоянии Delta f = 0,54-0,4=0,14 (м).
Ответ: 0,14 м.

Если вам нравятся наши материалы – записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Тонкие линзы. Ход лучей.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Добавить комментарий