Определение.
Функция
называется двойственной к функции
,
если
=
.
Таблица двойственной
функции получается из таблицы функции
инвертированием столбца значений
функции и последующим переворачиванием
полученного столбца.
Пример.
Для функции f
(,
,
)
построим двойственную функцию:
|
Таблица |
|||||
|
|
|
|
f |
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Пары двойственных
элементарных функций представлены в
табл. 1.11.
|
Таблица |
|
|
0 |
1 |
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим функцию
.
Функция f
зависит от m
аргументов, которые, в свою очередь,
тоже являются функциями.

Как получить
функцию
?
Ответ на этот вопрос дается следующей
теоремой.
Теорема 1.3.
=
.
Доказательство.
Построим двойственную функцию
,
используя определение
=
=
=
=
=
=
=
=
.
Ч.Т.Д.
Теорема 1.4 (принцип
двойственности).
Если формула B
= C[]
реализует функцию
,
то формула
=
C[],
то есть формула, полученная из B
заменой функций
на двойственные им функции
,
соответственно реализует функцию
.
Пусть существует
некоторая формула A
= C[0,
1, x,
,
,
],
тогда
=
= C[1,
0, x,
,
,
].
Пример.
Задана формула
.
Используя принцип двойственности,
построим двойственную формулу ()(
)(
).
КАДР
1.8. Полнота систем булевых функций
Пусть задана
некоторая система булевых функций, не
обязательно конечная,
M
= {}.
Определение.
Система M
называется полной, если каждую функцию
f
можно представить формулой над M.
Теорема 1.5 (теорема
I
о полноте систем булевых функций).
Пусть система M
= {}
полна и любая ее функция может быть
представлена формулой над множеством
N
= {},
тогда система N
тоже является полной.
Доказательство.
Так как система M
полна, то любую булеву функцию
можно представить формулой над M:
h
= C[].
Представим функции
формулами над N:
=
[
],
=
[
],
…
=
[
].
Тогда h
= C[[
],
[
],…,
[
]]
=
=[
].
Итак, имеем: любая функция из
может быть представлена формулой над
N,
следовательно, система N
полна.
Ч.Т.Д.
Пример.
Система M
= {,
,
}
является полной, покажем, что система
N
= {,
}
также полна. Функции {,
}
системы N
входят в систему M,
осталось выразить функцию
через ,
.
Используя эквивалентные соотношения,
можно записать: ()
= x
y.
Итак, все функции системы M
выражены через функции системы N,
то есть система N
является полной.
Определение.
Задана система M
= {}.
Замыканием над M
(обозначается [M])
называется множество всех булевых
функций, представимых формулами над M.
[M]
обязательно содержит M.
Отметим некоторые
свойства замыкания:
1. [[M]]
= [M].
2. []
=
.
3. Если M
N,
то [M]
[N].
4. [M]
[N]
[MN].
Определение.
Класс M
называется замкнутым если [M]
= M.
Пример.
– замкнутый класс, так как []
=
.
[[M]]
= [M]
также является замкнутым классом.
Определение.
Система M
полна, если ее замыкание совпадает с
множеством всех булевых функций, [M]
=.
КАДР
Рассмотрим основные
замкнутые классы.
1 класс.
–
класс булевых функций, которые на наборе
из всех нулей принимают значение 0. Если
f
(0, 0,…, 0) = 0, то f
.
Например, функции
,
,
,
0 принадлежат классу
,
а функции /, ~, ,
1 этому классу не принадлежат.
Число функций от
n
переменных, попадающих в класс
,
равняется
.
Покажем, что
– замкнутый класс. Доказательство
замкнутости здесь и далее сведем к
рассмотрению одного шага подстановки,
при котором новая функция оказывается
принадлежащей тому же классу.
Покажем, что функция
=
=
,
если
.
Подставим в правую и левую части равенства
вместо переменных нули:
=
=
f(0,…,0)
.
Итак, любая формула,
являющаяся суперпозицией функций из
,
представляет функцию из
.
Это значит, что класс
замкнут.
2 класс.
– класс всех булевых функций, которые
на наборе из всех единиц принимают
значение 1. Если f
(1, 1,…, 1) = 1, то f
.
Например, функции
,
,
~, ,
1 принадлежат классу
,
а функции ,
0, /,
этому классу не принадлежат.
Замкнутость класса
доказывается аналогично классу
.
3 класс.
S
– класс самодвойственных функций. Если
= =
(двойственная
функция для
f),
то f
S.
Функция
называется двойственной к функции
,
если
=
.
Например, функции
x,
принадлежат классу S,
а функции ,
этому классу не принадлежат.
Определение.
Наборы
и
называются противоположными.
Свойство
самодвойственной функции. Самодвойственная
функция на противоположных наборах
принимает противоположные значения.
Поэтому число самодвойственных функций
от n
переменных равно
.
Пример.
Рассмотрим мажоритарную функцию f
=
.
Ее значение на любом наборе равно
значению большинства аргументов набора.
Покажем, что функция f
самодвойственна:
=
()(
)(
)
= ()(
)
=
.
|
|
|
|
f |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Докажем, что класс
S
замкнут, рассматривая, как и ранее, один
шаг подстановки:
=
принадлежит S,
если
S.
Построим
=
==
==
=
,
то есть
S.
Итак, S
– замкнутый класс.
Лемма о
несамодвойственной функции.
Если функция
S,
то из нее путем замены переменных на x
или
можно получить несамодвойственную
функцию одной переменной, то есть
константу.
Доказательство.
Так как f
S,
то существует такой набор значений
переменных
,
что
=
.
Строим функцию
,
где
,
i
= ().
Будем иметь в виду, что
и
.
Заметим, что
получена из
заменой ее аргументов на x или
.
Если
в наборе
равно 0, то аргумент
заменяется на
,
иначе – на
.
Это значит, что
получена из несамодвойственной функции
в соответствии с условием леммы. Выясним
свойства
.
Имеем
=
=
=
=
=
==
=
функция
константа.
Ч.Т.Д.
Пример.
Получим константу из несамодвойственной
функции по лемме. Пусть f
=
.
f
(0, 1) = f
(1, 0) = 1,
= (0, 1),
=
,
=
,
=
=
x
= 1.
КАДР
4 класс.
M
– класс монотонных функций.
Определение.
Рассмотрим два набора значений переменных
,
и
,
будем говорить, что
предшествует
(),
если
,
(0 предшествует 1).
Например, набор
= (0, 1, 0, 1, 0, 0) предшествует
= (0, 1, 1, 1, 1, 0), то есть
.
Определение.
Пара наборов (,
)
сравнимы, если один из них предшествует
другому. Иначе – несравнимы.
Например,
= (0, 1, 0, 1) и
= (1, 0, 0, 1) – несравнимы.
Определение.
Функция
называется монотонной, если для любых
двух наборов
и
таких, что
,
имеет место неравенство
f
()
f
().
Например, функции
0, 1, x,
принадлежат классу M,
а функции ,
~ этому классу не принадлежат.
Покажем, что класс
монотонных функций замкнут. Для этого
выясним, является ли функция
=
монотонной, если
M.
Пусть заданны два
набора значений переменных
,
и
таких, что
.
Подставим наборы в обе части равенства:
=
и
=
.
Имеем
,
…
.
Так как
M,
то
,
…
.
Так как f
M,
то справедливо неравенство
,
из которого следует
,
то есть
M.
Следовательно,
класс монотонных функций замкнут.
Лемма о немонотонной
функции.
Если
M,
то из нее путем замены переменных на
константы 0, 1 и x
можно получить немонотонную функцию
одной переменной, а именно
.
Доказательство.
Сначала докажем, что если функция
немонотонна, то для нее найдется пара
соседних
наборов
и
таких, что
и f
()
> > f
().
Наборы
,
называются соседними по i-й
переменной, если они отличаются значениями
только этой переменной. Соседние наборы
сравнимы.
Если функция
немонотонна, то для нее найдется пара
наборов
,
для которых f
()
> f
()
(из определения монотонности). Если
и
соседние, то цель достигнута. Рассмотрим
ситуацию, когда
и
не соседние. Пусть наборы отличаются
значениями в t
компонентах (t
> 1), причем эти t
компонент в наборе
имеют значение 0, а в наборе
– 1. Поэтому между
и
можно вставить t
– 1 промежуточных наборов таких, что
…
.
Очевидно, что
наборы, стоящие в этой цепочке рядом,
будут соседние. Пусть
и
– соседние элементы этого ряда (
),
на которых происходит смена значения
функции. Пусть они отличаются в i-й
компоненте, тогда
>
,
причем
и
.
Рассмотрим функцию
.
(x)
получена из f(,…,
)
заменой i-й
переменной на x,
а всех остальных переменных – на
константы из наборов
,
(эти наборы отличаются только по i-й
переменной). Это значит, что (x)
получена из немонотонной функции
f(,…,
)
в соответствие с леммой. Выясним свойства
(x).
Имеем
>
.
Последнее означает,
что
и
,
то есть
.
Ч.Т.Д.
Пример.
Получим функцию
из немонотонной функции f
=
.
=
(1, 0),
=
(1, 1), наборы
,
являются соседними по переменной
,
f
(1, 0) > f
(1, 1), (x)
= 1
x
=
.
КАДР
5 класс.
L
– класс линейных функций.
Определение.
Формула
называется полиномом
Жегалкина булевой функции, коэффициенты
{0, 1} определяют какие конъюнкции входят
в полином.
Например,
– полином Жегалкина.
В дальнейшем будем
иметь ввиду следующие тождества:
1.
=
,
2.
(
)
=
,
3.
1 =
,
-
4.
если
число слагаемых четно,если
число слагаемых нечетно.
Эти тождества
позволяют любую ДНФ преобразовать в
полином Жегалкина.
Пример.
Приведем к полиному Жегалкина рассмотренную
ранее мажоритарную функцию f
=
= (
)
= =(
)
(
)
= =
=
.
Теорема 1.6.
Любую булеву функцию можно представить
полиномом Жегалкина единственным
образом.
Доказательство.
Рассмотрим всевозможные произведения
булевых переменных без инверсий. Их
столько, сколько всевозможных подмножеств
из n
переменных, то есть
(пустое подмножество соответствует
константе 1). Каждое из
произведений может либо входить в
полином, либо нет. Это значит, что одному
полиному сопоставляется некоторое
подмножество из рассматриваемых
произведений. Всевозможных полиномов
столько, сколько подмножеств из
элементов, то есть
.
Известно, что
есть число булевых функций от n
переменных. Следовательно, каждая булева
функция представима полиномом Жегалкина
единственным образом.
Ч.Т.Д.
КАДР
Определение.
Линейным полиномом называется формула
,
где
{0, 1}.
Пример.
– линейный полином.
Определение.
Функция, представимая линейным полиномом,
называется линейной булевой функцией.
Множество всех
линейных функций образует класс линейных
функций (L).
Например, функции
1, 0, x,
,
являются линейными, а функции ,
– нет.
Покажем замкнутость
класса линейных функций.
Докажем, что функция
=
принадлежит L,
если
L.
=
=
=.
После раскрытия
скобок получим линейный полином, то
есть
L.
Следовательно, класс линейных функций
замкнут. Всего линейных функций от n
переменных
.
Лемма о нелинейной
функции.
Если функция
нелинейная, то из нее путем замены
переменных на константы 0, 1, x,
,
и, быть может, путем инвертирования
самой функции можно получить нелинейную
функцию, а именно конъюнкцию.
Доказательство.
Представим функцию
в виде полинома
Жегалкина,
поскольку f
L,
то в полиноме найдется слагаемое,
содержащее 2 и более переменные (конъюнкция
ранга 2).
Без ограничений общности предположим,
что это слагаемое содержит произведение
переменных
.
Тогда полином функции f(,…,
)
можно представить следующим образом:
Формула
называется полиномом Жегалкина булевой
функции, коэффициенты
{0, 1} определяют, какие конъюнкции входят
в полином.
.
Собрав вместе
слагаемые, содержащие
,
и вынеся
за скобки, получим в скобках функцию
;
собрав далее вместе слагаемые, содержащие
,
и вынеся
за скобки, получим в скобках функцию
;
собрав вместе слагаемые, содержащие
,
и вынеся
за скобки, получим в скобках функцию
,
оставшиеся слагаемые образуют функцию
.
Пусть
– набор, на котором функция
= 1. Этот набор обязательно существует,
так как полином функции
содержит конъюнкции ранга 2.
Тогда
=
=
=
,
где ,
,
{0, 1}.
получена из
нелинейной
заменой переменных
на константы из набора
,
что согласно лемме допустимо. В результате
функции
,
,
превратились в константы ,
,
.
Рассмотрим функцию
,
получаемую из
,
следующим образом:
=
.
Это значит, что
получается из
заменой переменной
()
либо на себя, если
= 0 (
= 0), либо на инверсную переменную, если
= 1 (
= 1). Кроме того, если выражение
есть константа 1, функция
заменяется на инверсную. Все эти изменения
допускаются леммой. Следовательно,
получена из
в соответствии с условием леммы. Исследуем
.
Надо раскрыть скобки и привести к подобию
=
==
.
Ч.Т.Д.
Пример.
Получим функцию
из нелинейной функции f,
заданной в виде f
=
=
1
1
1
,
здесь
=
=
=1,
а
=
.
Пусть
=
(1, 1), тогда
=
1,
=
=
= 1.
=
1 = (
1)(
1)
(
1)
(
1)
1
1 =
1
1
1
1
1
1 =
.
Все замкнутые
классы попарно различны:
|
Таблица |
|||||
|
|
|
S |
M |
L |
|
|
0 |
+ |
– |
– |
+ |
+ |
|
1 |
+ |
+ |
– |
+ |
+ |
|
|
– |
– |
+ |
– |
+ |
КАДР
Теорема 1.7 (теорема
II
о необходимом и достаточном условии
полноты систем булевых функций).
Система M
= {}
полна, если и только если она не содержится
целиком ни в одном из пяти замкнутых
классов
,
,
S,
M,
L.
Доказательство.
Необходимость.
Пусть система M
полна, то есть [M]
=.
Допустим, что система содержится в
некотором замкнутом классе из этих
пяти, например в N,
то есть M
N.
Из полноты M
следует, что [M]
=.
N
– замкнута, значит, [N]
= N.
Так как M
N,
то по свойству замыкания [M]
[N],
из чего следует
N,
то есть множество всех булевых функций
содержится в одном из замкнутых классов,
что не так. Действительно, при рассмотрении
замкнутых классов для каждого из них
оказывалась хотя бы одна элементарная
функция, не содержащаяся в нем.
Необходимость доказана.
Достаточность.
Пусть система не содержится ни в одном
из пяти замкнутых классов. Покажем, что
она полна. Выделим из системы M
подсистему функций {},
которые не принадлежат соответственно
классам
,
,
S,
M,
L.
Докажем, что выделенная подсистема
полна.
1. С помощью
,
,
выразим константы 0 и 1. По определению
(0,…,
0) = 1, при этом возможны следующие ситуации:
а)
(1,…,
1) = 1, построим функцию
=
,
в данном случае
= 1 и
= 1, то есть
представляет константу 1. Имея
и константу 1, можем получить константу
0, так как
(1,
…, 1) = 0;
б)
(1,…,
1) = 0, построим функцию
=
,
в данном случае
= 0 и
= 1, то есть
представляет
.
Из несамодвойственной
функции
по лемме о несамодвойственной функции
можно получить некоторую константу
(либо 0, либо 1). Имея
,
можем получить другую константу.
2. По лемме о
немонотонной функции следует, что, имея
и константы 0, 1, можно получить немонотонную
функцию
.
Эту функцию необходимо получить,
поскольку в ситуации “а” на шаге 1 она
не построена.
3. По лемме о
нелинейной функции из функции
можно получить конъюнкцию, так как
константы 0, 1 и
уже получены на предыдущих этапах
доказательства.
Итак, с помощью
мы выразили функции полной системы {,
}.
По теореме 1.5 (I)
система {}
также полна, следствием чего является
полнота системы M.
Ч.Т.Д.
Пример.
Рассмотрим систему булевых функций {0,
1,
,
}.
Докажем полноту системы, используя
теорему 1.6 (II).
Определим принадлежность функций
системы пяти замкнутым классам, результат
оформим в виде табл. 1.13.
|
Таблица |
|||||
|
|
|
S |
M |
L |
|
|
0 |
+ |
– |
– |
+ |
+ |
|
1 |
– |
+ |
– |
+ |
+ |
|
|
+ |
+ |
– |
+ |
– |
|
|
+ |
+ |
+ |
– |
+ |
Так как система
не принадлежит ни одному из пяти замкнутых
классов, то по теореме 1.7 (II)
она является полной. Более того, любая
ее подсистема не является полной.
КАДР
Теорема 1.8.
Из полной системы булевых функций M
можно выделить полную подсистему,
содержащую не более четырех функций.
Доказательство.
Построим подсистему из пяти функций
{},
которые не принадлежат соответственно
классам
,
,
S,
M,
L.
Рассмотрим функцию
,
для которой
(0,…,
0) = 1. Возможны две ситуации:
а)
(1,…,
1) = 1, то есть функция
не является самодвойственной, тогда
число функций системы можно сократить
до четырех (=
);
б)
(1,…,
1) = 0, тогда
=
и
=
,
то есть число функций можно сократить
до трех.
Ч.Т.Д.
КАДР
Описание презентации по отдельным слайдам:
-
1 слайд
Двойственные функции
Булевы функции -
2 слайд
Двойственные функции
Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из
f(x1, …, xn) инверсией всех аргументов и самой функции, то есть -
3 слайд
Пример
Построим функцию, двойственную стрелке Пирса.
Значения двойственной функции можно получить переворотом и инверсией столбца значений исходной функции -
4 слайд
Пары двойственных элементарных функций:
0 – 1
Дизъюнкция – конъюнкция
Штрих Шеффера – стрелка Пирса
Эквивалентность – антиэквивалентность -
5 слайд
Пример.
Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания): -
6 слайд
Двойственная формула
Определение
Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.
Пример -
7 слайд
Пример
Рассмотрим формулу
задающую булеву функцию НЕ-ИЛИ, то есть стрелку Пирса.
Двойственная ей формула должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом делеэто функция НЕ-И, то есть штрих Шеффера.
-
8 слайд
Самодвойственная функция
Функция, совпадающая со своей двойственной, называется самодвойственной.
F*=FСледствие из принципа двойственности.
Если формулы F1 и F2 равносильны, то двойственные им формулы F*1 и F*2, также равносильны. -
9 слайд
Способы получения двойственной функции
– по определению двойственной функции – инверсией в формуле Ff всех аргументов и самой функции;
– по определению двойственной формулы и принципу двойственности – заменой в формуле Ff символов функций на символы двойственных им функций;
– построением таблицы истинности исходной функции по заданной формуле Ff, а затем переходом к таблице истинности двойственной функции (переворотом и инверсией столбца значений исходной функции). -
10 слайд
Упражнение 1
Построить формулы для функций, двойственных данным, пользуясь двумя разными способами: определением двойственной функции и принципом двойственности. Сравнить таблицы истинности, построенные по полученным формулам. -
11 слайд
Упражнение 2
Двойственны ли формулы Ff и Gg?
Функции f и g?
Повторение
Законы и тождества алгебры логики
1) Коммутативность конъюнкции и дизъюнкции
x y = y x x y = y x
2) Ассоциативность конъюнкции и дизъюнкции
x ( y z )= ( x y ) z x ( y z )=( x y ) z
3) Дистрибутивность конъюнкции и дизъюнкции относительно друг друга
x (y z) = (x y) (x z)
x (y z) = (x y) (x z)
Законы и тождества алгебры логики
4) Идемпотентность конъюнкции и дизъюнкции
x x = х x x = х
5) Закон исключенного третьего
6) Закон противоречия
8) Закон элиминации
x ( x y ) = х
x ( x y ) = х
1
0
Законы и тождества алгебры логики
7) Тождества с константами .
x 0 = х x 1 = х
x 1 = 1 x 0 = 0
9) Закон двойного отрицания .
10) Законы де Моргана .
x
Двойственность булевых функций. Теорема Поста.
План
- Двойственные булевы функции
- Самодвойственные булевы функции
Двойственные булевы функции
Функция f*(x 1 ,…,x n ) называется двойственной к функции f(x 1 ,…,x n ) , если
Пример построения двойственной функции
Пример
Най ти двойственные функции
Самодвойственные булевы функции
Функция, равная своей двойственной, называется самодвойственной .
f = f*
x
0
x
y
0
f(x,y)=f*(x,y)
0
y
0
1
f(0,0)= (1,1)
0
f(x,y)
1
0
1
1
f*(x,y)
1
f(0,1)= (1,0)
f(0,0)
0
1
(1,1)
0
f(1,0)= (0,1)
1
f(0,1)
1
f(1,0)
(1,0)
f(1,1)= (0,0)
f(1,1)
(0,1)
(0,0)
Пример
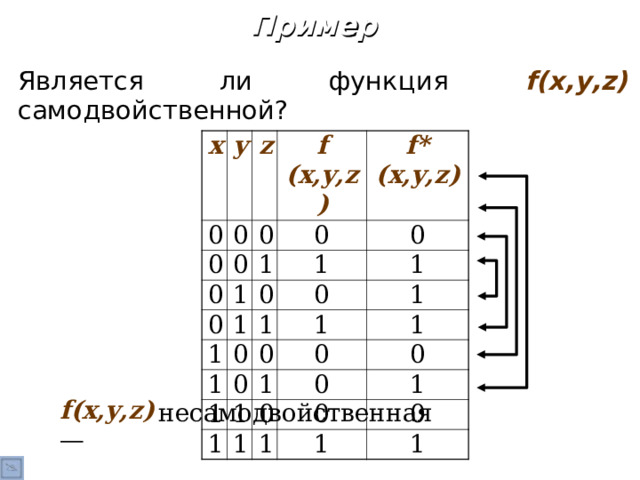
Является ли функция f(x,y,z) самодвойственной ?
x
y
0
z
0
0
0
f (x,y,z)
0
0
1
1
0
0
f* (x,y,z)
1
1
0
1
0
0
1
1
1
0
1
0
1
0
1
1
1
1
1
0
1
0
0
0
1
0
1
1
0
1
f(x,y,z) —
несамодвойственная
Принцип двойственности
Пусть функция F заданна суперпозицией функций f 0 ,…,f n , где n N . Функцию F* , двойственную F , можно получить, заменив в формуле F функции f 0 ,…,f n на двойственные им f 0 * ,…,f n * .
Правило получения двойственных формул
Для того чтобы получить двойственную формулу булевой алгебры необходимо заменить в ней все конъюнкции на дизъюнкции, дизъюнкции на конъюнкции, 0 на 1, 1 на 0, и использовать скобки, где необходимо, чтобы порядок выполнения операций остался прежним .
Правило получения двойственных формул
Пример
Найти функцию, двойственную функции
Решение
Правило получения двойственных формул
Если функции равны, то и двойственные им функции также равны .
Пусть f 1 и f 2 – некоторые функции, заданные формулами. Тогда если
f 1 = f 2 ,
то
f 1 * = f 2 *
Замкнутые классы функций
свойства замыкания:
Теорема Поста
Пример
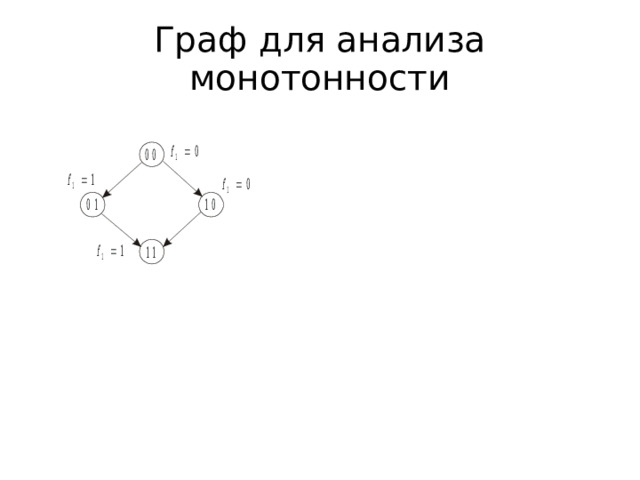
Граф для анализа монотонности
Вопросы.
- Какие функции называются двойственными?
- Какие функции называются самодвойственными?
- Как определить полному системы функций?
3. Является ли полной система