Как найти двойственные формулы

§ 2.2. Совершенные дизъюнктивные и конъюнктивные нормальные формы

Двойственная функция. Принцип двойственности. Разложение булевой функции по переменным. Совершенная дизъюнктивная нормальная форма (СДНФ). Совершенная конъюнктивная нормальная форма (СКНФ). Представление булевой функции в виде СДНФ и СКНФ.

Базовые понятия и утверждения

1. Принцип двойственности. Функция,
заданная формулой
,
называется двойственной к функции
.

Функцию, двойственную к
,
обозначают
,
таким образом,
.

Пример 1. Используя
определение, найти функции, двойственные
к дизъюнкции, конъюнкции и функциям
одной переменной.

◄ Пусть
.
Тогда

.

Пусть
.
Тогда

.

Пусть
.
Тогда
.

Пусть
.
Тогда
.

Пусть
.
Тогда
.

Пусть
.
Тогда
.
►

Сравним таблицы истинности произвольной
функции

и двойственной к ней функции

(табл. 2.17).

Таблица 2.17
0	0
0	1
1	0
1	1

Нетрудно заметить, что столбец значений
функции

можно получить из столбца значений
функции

действуя по следующему алгоритму:

1) столбец значений функции

переписать в обратном порядке (т.е.
число, стоящее в первой строке, записать
в последнюю строку; число, стоящее во
второй строке, – в предпоследнюю строку
и т.д.);

2) в получившемся в результате выполнения
п. 1 столбце значений каждое число
заменить его отрицанием (0
заменить 1 и 1
заменить 0).

Очевидно, что этот алгоритм можно
использовать для построения двойственной
функции в случае любого числа аргументов.

Если функция задана вектором значений,
то роль столбца значений в алгоритме
выполняет вектор значений.

Пример 2.
Задать вектором значений функцию,
двойственную к данной:

а); б).

◄ а)
;

б)
.
►

На примерах мы имели возможность
убедиться, что отношение двойственности
между функциями симметрично, т.е. если
функция
,
то функция
.
Это утверждение несложно обосновать
теоретически.

Действительно, пусть
.
Тогда

.

Пусть функция

задана формулой, и мы хотим построить
формулу для двойственной к ней функции
.
Согласно определению, это можно сделать,
заменив в формуле, которой задана
,
каждую переменную ее отрицанием и взяв
отрицание от самой формулы (именно так
мы поступили в примере 1).

Рассмотрим другой способ построения
формулы для

по формуле, представляющей
.
Этот способ основан на принципе
двойственности: если формула

задает функцию
,
то формула, полученная из нее заменой
символов функций

на символы двойственных к ним функций
,
задает функцию,
двойственную к функции
.
Полученную таким образом формулу
будем называть двойственной к

и обозначать
.

Доказательство принципа двойственности
приведено во второй части параграфа.

Если функция задана формулой над
множеством
,
то, используя пример 1, принципу
двойственности можно придать более
конкретный вид: если в формуле
,
представляющей функцию
,
все конъюнкции заменить на дизъюнкции,
дизъюнкции – на конъюнкции, 1
на 0, 0
на 1, то получим
формулу
,
представляющую функцию
,
двойственную к
.

Пример 3. Задать
формулой функцию, двойственную к данной:

а)
; б)
.

◄ а)
.

Обратим внимание на следующее
обстоятельство. В записи формулы,
представляющей
,
конъюнкция вследствие соглашения о
краткой записи формул в скобки не взята.
Строя двойственную формулу, мы меняем
конъюнкцию на дизъюнкцию. При этом
следует учитывать, что связка «»
имеет меньший приоритет выполнения,
чем «»,
значит, чтобы двойственная формула
сохранила структуру исходной формулы,
при переходе от конъюнкции к дизъюнкции
нужно взять дизъюнкцию в скобки. В то
же время при переходе от дизъюнкции к
конъюнкции скобки можно опустить.

б)
.
►

Если функции равны, то и двойственные
к ним функции равны. В сочетании с
принципом двойственности это очевидное
обстоятельство позволяет получать
новые равносильности, переходя от
равенства

к равенству
.
Например, из равносильности 1 (см. теорему
2.1) можно получить равносильность 2, а
из равносильности 2 – равносильность 1.

Действительно, от равенства

перейдем к равенству

и, заменив дизъюнкцию на конъюнкцию, а
конъюнкцию на дизъюнкцию, получим
равенство
.

Примерами других пар, связанных законом
двойственности, являются равносильности
3 и 4, 5 и 6, 7 и 8, 9 и 10, 11 и 12, 13 и 14, 15 и 16, 17 и
18.

Пример 4. Задать
функцию, двойственную к функции
:

а) вектором значений; б) формулой.

◄ а) Начнем с того, что зададим таблично
(табл. 2.18) саму функцию
.

Таблица 2.18
0	0	0	1	0	1	1
0	0	1	0	0	1	1
0	1	0	1	0	0	0
0	1	1	0	0	0	0
1	0	0	1	1	0	1
1	0	1	0	0	0	0
1	1	0	1	1	0	1
1	1	1	0	0	0	0

Далее:
.

б) Используя принцип двойственности и
результат выполнения упр. 2.12, из формулы

получим формулу
.
►

2. Задание функции совершенной
дизъюнктивной нормальной формой. Мы
умеем переходить от реализации функции
формулой к заданию ее таблицей истинности.
Не меньший интерес представляет обратный
переход – от таблицы истинности к формуле.
Этот переход неоднозначен – формул,
которыми можно задать любую булеву
функцию, бесконечно много. Особый интерес
имеет задание функций через дизъюнкцию,
конъюнкцию и отрицание.

Введем обозначения:
,
.

Каждую булеву функцию

от

переменных, за исключением тождественно
равной нулю, можно задать формулой

(здесь
дизъюнкция берется по всевозможным
наборам значений переменных
,
на которых функция

равна 1).

Эту формулу называют совершенной
дизъюнктивной нормальной формой
(сокращенно СДНФ).

Доказательство этого утверждения
приведено во второй части параграфа.

Чтобы построить СДНФ функции, нужно
действовать следующим образом:

1) выбрать в таблице истинности функции
все наборы значений переменных, на
которых функция равна 1;

2) для каждого такого набора записать
конъюнкцию, в которую войдут все
переменные, причем, если значение
переменной на данном наборе равно 0, то
она войдет в конъюнкцию со знаком
отрицания, а если 1, то без знака отрицания;

3) записать дизъюнкцию всех выписанных
в п. 2 конъюнкций.

Пример 5. Задать
функцию в виде СДНФ:

а)
; б)
;

в)
; г)
.

◄ а) – в) Зададим функции таблично (табл.
2.19) и выпишем для них СДНФ.

Таблица 2.19
0	0	1	1	1
0	1	1	1	0
1	0	0	1	0
1	1	1	0	0

;

;

.

г) Запишем СДНФ, воспользовавшись
таблицей истинности функции
(см.
табл. 2.18):

.
►

3. Задание функции совершенной
конъюнктивной нормальной формой.
Рассмотрим еще один способ задания
функции формулой над множеством,
состоящим из дизъюнкции, конъюнкции и
отрицания.

Каждую булеву функцию
,
не равную тождественно единице, можно
задать формулой

(здесь
конъюнкция берется по всевозможным
наборам значений переменных
,
на которых функция

равна 0).

Эту формулу называют совершенной
конъюнктивной нормальной формой
(сокращенно СКНФ).

Доказательство этого утверждения
приведено во второй части параграфа.

Чтобы записать СКНФ функции, нужно
действовать следующим образом:

1) выбрать в таблице истинности функции
все наборы значений переменных, на
которых функция равна 0;

2) для каждого такого набора записать
дизъюнкцию, в которую войдут все
переменные, причем, если значение
переменной на данном наборе равно 1,
то она войдет в дизъюнкцию со знаком
отрицания, а если 0, то без знака отрицания;

3) записать конъюнкцию всех выписанных
в п. 2 дизъюнкций.

Пример 6. Задать
функцию в виде СКНФ:

а)
; б)
;

в)
; г)
.

◄ а) – г) Опираясь на таблицы истинности
функций (см. табл. 2.19 и 2.18), запишем:

а)
;

б)
;

в)
;

г)
.
►

Каждая булева функция может быть
задана формулой над множеством
.

Действительно, если
,
то

можно задать в виде СКНФ. Если
,
то

можно задать в виде СДНФ.

Соседние файлы в папке discretka_1

• #
• #
• #
• #
• #
• #
• #
• #
• #

Определение 1. Функции F*(X1, …, Xn) называется двойственной к функции F(X1, …, Xn), если F*(X1, …, Xn) = ( 1, …, N).

Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:

Функции F(X) = X и G(X) = двойственны сами себе:

X	F	F*	G	G*
0 1	0 1	0 1	1 0	1 0

Так как F*(0)= (1).

Определение 2. Если F*(X1, …, Xn) = F(X1, …, Xn), то F(X1, …, Xn) называется самодвойственной.

Пример 2. Покажем, что F(X1,X2,X3)=X1ÅX2ÅX3 – самодвойственна:

X1	X2	X3	F	F*
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 0 1 0 0 1	0 1 1 0 1 0 0 1

Если F*– самодвойственна, то ( 1, …, n) = F(X1, …, Xn), т. е. на противоположных наборах функция принимает противоположные значения.

Пример 3. Покажем, что функция Х1ÚХ2 двойственна к X1&X2, функция Х1 Х2 двойственна к функции X1|X2.

X1 X2	F=Х1ÚХ2	F*	G=X1|X2	G*=X1 X2
0 0 0 1 1 0 1 1	0 1 1 1	0 0 0 1	1 1 1 0	1 0 0 0

Теорема о двойственных функциях

Если F* двойственна к F, то F двойственна к F*.

Доказательство. F*(X1, …, Xn) = ( 1, …, N). Найдем двойственную функцию к F*, т. е. (F*( X1, …, Xn))* = ( ( 1, …, N))* = ( 1, …, N) = F(X1, .., Xn).

Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.

Принцип двойственности

Теорема: Пусть функция H(X1, …, Xn) реализована формулой H(X1, …, Xn) = =G(G1, …, Gm) = G(F1(X1, …, Xn), …, Fm(X1, …, Xn)), где какие-то переменные могут быть фиктивными. Тогда H*( x1, …, Xn) = G*(F1*( X1, …, Xn), …, Fm*(X1, …, Xn)), это означает, что если функция задана некоторой формулой, то чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные, 0 на 1, 1 на 0.

Доказательство. H*(X1, …, Xn) = ( 1, …, n) = (F1( 1, …, n), …, Fm( 1, …, n)) = ( 1( 1, …, n), …, ( 1, …, n)) = G(( ), …, (( ) = G*(F1*( X1, …, Xn), …, Fm*( X1, …, Xn)), что и требовалось доказать.

Если функция H(X1, …, Xn) реализуется формулой N[F1, …, Fn], то формулу, полученную из N заменой Fi, входящих в нее, на Fi* и реализующую функцию H*(X1, …, Xn), будем называть двойственной и обозначать N*(X1, …, Xn).

Пример 4. Построить формулу, реализующую F*, если F = ((X Y) Ú Z) (Y (XÅYz)). Покажем, что она эквивалентна формуле N = Z(XÅY).

Найдем (XÅY)* и (X Y)*.

X y	XÅY	(XÅY)*	X Y	(X Y)*
0 0 0 1 1 0 1 1	0 1 1 0	1 0 0 1	1 1 0 1	0 1 0 0

Из таблиц видно, что

(X Y)* = X ~ Y = = X Y 1, X Y = Y X ,

(X Y)* = Y X Y = Y.

По принципу двойственности:

F* = Yz ( (X (Y Z) 1)) = Yz Z(X (Y Z) 1) = Z( YÚ( XÅ ZÅ )) = Z( YÚ (XÅZÅ1)) = Z( YÚ (XÅ )) = Z YÚ(Z XÅZ ) = Z( YÚX ) = Z(XÅY).

Тогда F = (F*)* = [Z(XÅY)]* = ZÚ(X~Y).

Пример 5. Найти формулу для f* и показать, что она эквивалентна формуле N = (XÚ(ZÅT)) , если F = (Xyz~(TÚX ))Ú T.

F* = ((XÚYÚZ)ÅT( ÚY))( ÚT) = ( T( ÚY)Ú(XÚYÚZ) )( ÚT) =

= ( TÚ(XÚYÚZ)( ÚX ))( ÚT) = TÚ(XÚYÚZ)( ÚX ÚTx ) =

= TÚ(XÚYÚZ)( ÚX ) = ( XÚ TÚ ZÚXÚXz) = ( TÚXÚ ZÚXz)

= (XÚ(ZÅT)).

Лемма о несамодвойственной функции

Подстановкой функций и в несамодвойственную функцию можно получить одну из констант.

Доказательство. Пусть – несамодвойственная функция. Тогда существует набор , для которого . Построим функцию , заменив единицы в на , а нули – на . Так как , то . Заметим, что .

Тогда , т. е. . Следовательно, функция есть одна из констант.

< Предыдущая		Следующая >

Булевы функции

Содержание

1 Понятие булевой функции

В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п. Так или иначе область определения – непрерывное множество. В курсе дискретной математики изучаться должны функции, область определения которых – дискретное множество * . Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов. * Так мы и приходим к понятию булевой функции.

Определение 1 (Булева функция). Булевой функцией от n аргументов называется функция f из n -ой степени множества < 0, 1 >в множество < 0, 1 >.

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству < 0, 1 >. Множество < 0, 1 >мы будем в дальнейшем обозначать через B .

Булеву функцию от n аргументов можно рассматривать как n -местную алгебраическую операцию на множестве B . При этом алгебра W >, где W – множество всевозможных булевых функций, называется алгеброй логики .

Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 n наборов. Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:

x 1	x 2	.	x n- 1	x n	f
0	0	.	0	0	f(0,0. 0,0)
0	0	.	0	1	f(0,0. 0,1)
0	0	.	1	0	f(0,0. 1,0)
0	0	.	1	1	f(0,0. 1,1)
.	.	.	.	.	.
1	1	.	0	0	f(1,1. 0,0)
1	1	.	0	1	f(1,1. 0,1)
1	1	.	1	0	f(1,1. 1,0)
1	1	.	1	1	f(1,1. 1,1)

Раз у нас есть стандартный порядок записывания наборов, то для того, чтобы задать функцию, нам достаточно выписать значения f (0,0. 0,0) , f (0,0. 0,1) , f (0,0. 1,0) , f (0,0. 1,1). f (1,1. 0,0) , f (1,1. 0,1) , f (1,1. 1,0) , f (1,1. 1,1). Этот набор называют вектором значений функции .

Таким образом, различных функций n переменных столько, сколько различных двоичных наборов длины 2 n * . А их 2 в степени 2 n .

Множество B содержит два элемента – их можно рассматривать как булевы функции от нуля (пустого множества) переменных – константу 0 и константу 1 .

Функций от одной переменной четыре: это константа 0, константа 1, тождественная функция , т.е. функция, значение которой совпадает с аргументом и так называемая функция “ отрицание ”. Отрицание будем обозначать символом ¬ как унарную операцию. Приведём таблицы этих четырёх функций:

x	0	x	¬ x	1
0	0	0	1	1
1	0	1	0	1

Как видим, функции от некоторого числа переменных можно рассматривать как функции от большего числа переменных. При этом значения функции не меняется при изменении этих “добавочных” переменных. Такие переменные называются фиктивными , в отличие от остальных – существенных .

Определение 2 (Фиктивные и существенные переменные). Переменная x i называется фиктивной (несущественной) переменной функции f ( x 1 ,···,x n ), если f ( x 1 ,···,x i- 1 ,0 ,x i+ 1 ,···,x n ) = f ( x 1 ,···,x i- 1 ,1 ,x i+ 1 ,···,x n ) для любых значений x 1 ,···,x i- 1 ,x i+ 1 ,···,x n . Иначе переменная x i называется существенной .

Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций (только те, которые существенно зависят от обеих переменных) мы приводим в следующей таблице:

x 1	x 2	x 1 & x 2	x 1 Ъ x 2	x 1 Й x 2	x 1 Е x 2	x 1 є x 2	x 1 | x 2
0	0	0	0	1	0	1	0
0	1	0	1	1	1	0	1
1	0	0	1	0	1	0	1
1	1	1	1	1	0	1	1

Эти функции записываются как бинарные операции в инфиксной нотации. x 1 & x 2 называется конъюнкцией , x 1 Ъ x 2 – дизъюнкцией , x 1 Й x 2 – импликацией , x 1 є x 2 – эквивалентностью , x 1 Е x 2 – суммой по модулю 2 , x 1 | x 2 – штрихом Шеффера .

Значения 0 и 1 часто интерпретируют как “ложь” и “истину”. Тогда понятным становится название функции “отрицание” – она меняет “ложь” на “истину”, а “истину” на “ложь”. Отрицание читается как “не”. Конъюнкция читается обычно как “и” – действительно, конъюнкция равна 1 тогда и только тогда, когда равны 1 и первая и вторая переменная. * Кроме x 1 & x 2 часто используют обозначение x 1 Щ x 2 или x 1 · x 2 или x 1 x 2 или min( x 1 ,x 2 ). Дизъюнкция читается “или” – дизъюнкция равна 1 тогда и только тогда, когда равны 1 первая или вторая переменная. * Импликация выражает факт, что из x 1 следует x 2 . * Импликацию часто также обозначают x 1 ® x 2 .

2 Суперпозиция функций

Определение 3 (Суперпозиция функций). Суперпозицией булевых функций f 0 и f 1 . f n называется функция f ( x 1 . x m ) = f 0 ( g 1 ( x 1 . x m ) . g k ( x 1 . x m )), где каждая из функций g i ( x 1 , . x m ) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f 1 . f n .

Пример 1 (суперпозиция функций).

Функция f ( x,y ) = ¬ ( x & y ) является суперпозицией функций ¬ и &. Функция g ( x,y ) = x Е ( x Ъ y ) является суперпозицией функций Е и Ъ . Функция h ( x,y,z ) = ( x & y ) Е z является суперпозицией функций Е и &. Построим таблицы этих функций.

Суперпозицию ( x & y ) Е ( ¬x Ъ ¬y ) можно прочитать как “ x и y плюс не x или не y ”.

Следующие соотношения могут быть проверены прямым сравнением значений функций в левой и правой части соотношения на всевозможных наборах аргументов.

1. x & y = y & x
2. x Ъ y = y Ъ x
3. x Е y = y Е x
4. x & ( y & z ) = ( x & y ) & z
5. x Ъ ( y Ъ z ) = ( x Ъ y ) Ъ z
6. x Е ( y Е z ) = ( x Е y ) Е z
7. x Ъ ( y & z ) = ( x Ъ y ) & ( x Ъ z )
8. x & ( y Ъ z ) = ( x & y ) Ъ ( x & z )
9. ¬¬x = x
10. ¬ ( x & y ) = ¬x Ъ ¬y
11. ¬ ( x Ъ y ) = ¬x & ¬y
12. x & x = x
13. x & ¬x = 0
14. x & 0 = 0
15. x & 1 = x
16. x Ъ x = x
17. x Ъ ¬x = 1
18. x Ъ 0 = x
19. x Ъ 1 = 1
20. x Е y = ( x & ¬y ) Ъ ( ¬x & y )
21. x Й y = ¬x Ъ y
22. x є y = ( x & y ) Ъ ( ¬x & ¬y )

3 Двойственные функции

Определение 4 (Двойственная функция). Функция g ( x 1 . x n ) = ¬f ( ¬x 1 . ¬x n ) называется двойственной функцией к функции f и обозначается f * .

Пример 2 (двойственные функции).

( x & y ) * = ¬ ( ¬x & ¬y ) = x Ъ y .

Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f * ( x 1 . x n ) * = ( ¬f ( ¬x 1 . ¬x n )) * = *
= ¬¬f ( ¬¬x 1 . ¬¬x n ) = *
= f ( x 1 . x n ) *

Рассмотрим, что происходит с таблицей двойственной функции. Замена набора ( x 1 . x n ) на ( ¬x 1 . ¬x n ) соответствует “переворачиванию” таблицы. Действительно, наборы ( x 1 . x n ) и ( ¬x 1 . ¬x n ) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию ¬ к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Пример 3 (вектор двойственной функции).

Функции x & y и x Ъ y , задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являются x Е y и x є y , задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функций x и ¬x (векторы (0,1) и (1,0) соответственно) двойственна сама себе.

Теорема 1 (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее: f 0 ( f 1 . f m ) * = f 0 * ( f 1 * . f m * )

Доказательство. f 0 ( f 1 ( x 1 . x n ) . f m ( x 1 . x n )) * =

= ¬f 0 ( f 1 ( ¬x 1 . ¬x n ) . f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬¬f 1 ( ¬x 1 . ¬x n ) . ¬¬f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬f 1 * ( x 1 . x n ) . ¬f m * ( x 1 . x n )) =	*
= f 0 * ( f 1 * ( x 1 . x n ) . f m * ( x 1 . x n ))	*

4 Разложение функции по переменным

x s =

м ¬x, если s =0 н о x, если s =1

.

Теорема 2 (Разложение в дизъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m )

Доказательство. Покажем, что для любого набора значений переменных ( x 1 . x n ,x n+ 1 . x m ) значения левой и правой частей совпадают. Возьмём фиксированный набор ( x 1 . x n ,x n+ 1 . x m ). Рассмотрим выражение x 1 s 1 & . & x n s n . Если одно из значений x i s i равно 0, то и всё выражение равно 0. Тогда и выражение x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m ) равно 0. Единице же выражение x 1 s 1 & . & x n s n равно только в том случае, если s 1 = x 1 , . s n = x n . При этом f ( s 1 . s n ,x n+ 1 . x m ) = f ( x 1 . x n ,x n+ 1 . x m ) Таким образом, значение правой части всегда равно равно f ( x 1 . x m ), то есть значению левой части.

Теорема 3 (Разложение в конъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x n ¬ s n Ъ f ( s 1 . s n ,x n+ 1 . x m )

Разложения по всем переменным дают суперпозицию конъюнкции, дизъюнкции и отрицания.

Следствие 1 (Совершенная дизъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: *

f ( x 1 . x m ) = x 1 s 1 & . & x m s m & f ( s 1 . s m ) = *

= x 1 s 1 & . & x m s m

Следствие 2 (Совершенная конъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: * f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x m ¬ s m

Таким образом, любая булева функция может быть представлена суперпозицией конъюнкции, дизъюнкции и отрицания. Разложение по всем переменным в дизъюнкцию называется совершенной дизъюнктивной нормальной формой функции, а в конъюнкцию – совершенной конъюнктивной нормальной формой . *

Совершенная дизъюнктивная и конъюнктивная нормальная формы дают способ представления булевой функции через суперпозицию конъюнкции, дизъюнкции и отрицания если у нас есть таблица значений функции.

Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.

Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.

Пример 4 (совершенная дизъюнктивная нормальная форма).

Построим совершенную дизъюнктивную нормальную форму функции, заданной следующей таблицей.

x	y	z	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Наборы, на которых функция равна 1 – это (0,1,1), (1,0,1), (1,1,0), (1,1,1). Первый набор даёт конъюнкцию ¬x & y & z , второй – x & ¬y & z , третий – x & y & ¬z , четвёртый – x & y & z . В результате получаем ( ¬x & y & z ) Ъ ( x & ¬y & z ) Ъ ( x & y & ¬z ) Ъ ( x & y & z ).

Вектор значений двойственной функции

Определение. Булева функция f * (x₁, …, x_n) называется двойственной булевой функции f(x₁, …, x_n), если она получена из f(x₁, …, x_n) инверсией всех аргументов и самой функции, то есть

Пример. Построим функцию, двойственную стрелке Пирса.

Пусть булева функция f(x₁, …, x_n) задана формулой F_f. Чтобы получить формулу F’_{f *} для функции f * (x₁, …, x_n), двойственной функции f(x₁, …, x_n), необходимо, согласно определению, проинвертировать все переменные, пользуясь при этом законом двойного отрицания, и саму функцию. При этом формулу F’_{f *} можно упростить (убрать длинную инверсию над формулой), заменив символ функции, которая вычисляется последней, на символ инверсной ей функции.

Пример. Пусть F_f = x ↓ (y ( x y z) ) ( y x ). Последней должна вычислятьси импликация, инверсная ей функция это обратная импликация, поэтому формула для двойственной функции примет вид:

Алгоритм построения таблицы истинности двойственной функции (основан на определении двойственной функции).

Инверсия всех переменных превращает наборы в их антиподы. Поскольку в таблице истинности антипод первого набора расположен последним, антипод второго набора – предпоследним и так далее, то для построения функции f( x ₁, …, x _n) нужно перевернуть вектор-столбец значений исходной функции f(x₁, …, x_n), а для получения функции f ( x ₁, …, x _n) еще и инвертировать компоненты столбца.

Пример. Построим функцию, двойственную стрелке Пирса.

Пары двойственных элементарных функций:

0 1 , , ↓ / , , , .

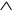
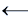
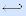
Тождественная функция и инверсия двойственны каждая самой себе.

Для доказательства можно воспользоваться алгоритмом построения таблицы истинности двойственной функции (именно так предыдущий пример демонстрирует, что штрих Шеффера двойственен стрелке Пирса), или применить равносильные преобразования.

Пример. Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания):

Презентация по математической логике на тему “Двойственные функции”

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Двойственные функции Булевы функции

Двойственные функции Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть

Пример Построим функцию, двойственную стрелке Пирса. Значения двойственной функции можно получить переворотом и инверсией столбца значений исходной функции

Пары двойственных элементарных функций: 0 – 1 Дизъюнкция – конъюнкция Штрих Шеффера – стрелка Пирса Эквивалентность – антиэквивалентность

Пример. Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания):

Двойственная формула Определение Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций. Пример

Пример Рассмотрим формулу задающую булеву функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом деле это функция НЕ-И, то есть штрих Шеффера.

Самодвойственная функция Функция, совпадающая со своей двойственной, называется самодвойственной. F*=F Следствие из принципа двойственности. Если формулы F1 и F2 равносильны, то двойственные им формулы F*1 и F*2, также равносильны.

Способы получения двойственной функции – по определению двойственной функции – инверсией в формуле Ff всех аргументов и самой функции; – по определению двойственной формулы и принципу двойственности – заменой в формуле Ff символов функций на символы двойственных им функций; – построением таблицы истинности исходной функции по заданной формуле Ff, а затем переходом к таблице истинности двойственной функции (переворотом и инверсией столбца значений исходной функции).

Упражнение 1 Построить формулы для функций, двойственных данным, пользуясь двумя разными способами: определением двойственной функции и принципом двойственности. Сравнить таблицы истинности, построенные по полученным формулам.

Упражнение 2 Двойственны ли формулы Ff и Gg? Функции f и g?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 940 человек из 80 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 318 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 695 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 479 299 материалов в базе

Дистанционные курсы для педагогов

Другие материалы

• 11.12.2016
• 2643

• 11.12.2016
• 907

• 11.12.2016
• 461

• 11.12.2016
• 433

• 11.12.2016
• 547

• 11.12.2016
• 737

• 11.12.2016
• 755

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 11.12.2016 3203 –> –> –> –>
• PPTX 136 кбайт –> –>
• Оцените материал:

Настоящий материал опубликован пользователем Ялина Янина Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На проекте: 5 лет и 10 месяцев
• Подписчики: 0
• Всего просмотров: 18291
• Всего материалов: 11

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

Ретроспектива культовой сказки «Вечера на Хуторе близ Диканьки»

Время чтения: 5 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В России могут создать комиссию по поддержке одаренных детей

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

[spoiler title=”источники:”]

http://ido.tsu.ru/iop_res/bulevfunc/text/g5_1.html

http://infourok.ru/prezentaciya-po-matematicheskoy-logike-na-temu-dvoystvennie-funkcii-1433222.html

[/spoiler]