Задача по стереометрии, многогранники
Татьяна Перетятько
Профи
(559),
закрыт
2 года назад
Найти двугранные углы правильного тетраэдра. Как решить, даже углов не надо?
Владимир Лёшин
Просветленный
(43237)
2 года назад
правильный тетраэдр – фигура из 4 равносторонних треугольников
нужно найти углы между гранями
пусть а – ребро тетраэдра
h- высота любой из граней
h=a√3 /2
по т косинусов
a^2=2h^2-2h^2cos(x)
cos(x)=(2h^2-a^2)/2h^2=(2(a√3 /2)^2 -a^2) /(2(a√3 /2)^2)=(2a^2*3/4 -a^2) /(2a^2*3/4)=0.5a^2 /1.5a^2=1/3
cos(x)=1/3 -> x≈70грд
План урока:
Понятие правильного многогранника
Пять правильных многогранников
Задачи на правильные многогранники
Понятие правильного многогранника
Ранее мы уже рассматривали такой выпуклый многогранник, как куб. Легко заметить, что каждая грань куба – это квадрат, то есть правильный многоугольник. Более того, все грани куба одинаковы, а из каждой вершины исходит одинаковое количество ребер (по три ребра).
Однако куб – не единственная фигура, обладающая такими свойствами. Так же нам знаком правильный тетраэдр. У него каждая грань – это равносторонний треугольник (а это правильный многоуг-к), а из каждой вершины также выходит по 3 ребра тетраэдра.
И куб, и правильный тетраэдр являются примерами так называемых правильных многогранников. Дадим определение понятию правильного многогранника:

Иногда правильные многогранники именуют иначе – платоновыми телами. Дело в том, что древнегреческий философ Платон использовал их в своей философии, однако огромный вклад в их исследование внес другой ученый – Теэтет Афинский.
Ясно, что все ребра правильных многогранников имеют одинаковую длину. Можно доказать, что и двугранные углы, образованные смежными гранями таких многогранников, также одинаковы.
Пять правильных многогранников
Вероятно, куб и правильный тетраэдр являются первыми правильными многогранниками, открытыми человечеством. Уже во времена Пифагора люди знали и о третьем правильном многограннике – октаэдре. Каждая его грань – это равносторонний треуг-к, но, в отличие от тетраэдра, из каждой его вершины исходит уже не три, а четыре ребра. Выглядит правильный октаэдр так:

Можно доказать, что октаэдр состоит из двух правильных пирамид, у которых общее основание, но вершины располагаются по разные стороны от плоскости основания. Название октаэдра происходит от греческого слова «окта», означающее число 8. Легко увидеть, что у октаэдра как раз 8 граней. Также видно, что он имеет 6 вершин и 12 ребер.
Следующие два правильных многогранника как раз и были открыты Теэтетем Афинским. Это икосаэдр и додекаэдр. Икосаэдр также состоит из равносторонних треуг-ков, но каждая его вершина принадлежит сразу 5 ребрам.Правильный икосаэдр довольно сложно нарисовать на плоскости, поэтому его внешний вид мы покажем с помощью анимации:

Гранями додекаэдра являются правильные пятиугольники, причем в каждой его вершине соприкасаются ровно 3 грани, и, соответственно, сходятся 3 ребра. Нарисовать правильный додекаэдр ещё тяжелее, поэтому снова посмотрим на него с помощью gif-анимации:

Для подсчета количества ребер, граней и вершин у додекаэдра и икосаэдра можно применить теорему Эйлера. Начнем с икосаэдра. Обозначим количество его граней буквой Г. Теперь подсчитаем ребра (Р), принадлежащие каждой грани. Так как эти грани являются треуг-ками, то получится 3Г ребер. Но при этом каждое ребро мы посчитали дважды, ведь ребра принадлежат строго двум граням. То есть у икосаэдра количество ребер равно 3Г/2 = 1,5Г.
Также подсчитаем и вершины (В), находящиеся вокруг граней. На каждую грань приходится 3 вершины, но при этом каждая вершины принадлежит уже 5 граням. Тогда общее количество вершин составит 3Г/5 = 0,6Г.
Записываем теорему Эйлера и подставляем в ней полученные значения:

Теперь проведем аналогичные расчеты для додекаэдра. Его грани – пятиугольники, поэтому количество его ребер составляет 5Г/2. В каждой вершине додекаэдра сходятся три грани, а потому количество вершин составит 5Г/3. Используем теорему Эйлера:

Теперь составим таблицу, в которой отразим основные сведения о пяти известным нам правильных многогранниках:

Возникает вопрос – существуют ли ещё какие-нибудь правильные многогранники? Оказывается, что нет. Действительно, каждая вершина правильного многогранника является одновременно и вершиной многогранного угла. Напомним, что сумма плоских углов в многогранном угле всегда меньше 360°. Легко подсчитать, что в правильном шестиугольнике каждый угол составляет 120°, а в многоуг-ках с большим количеством сторон (семиугольник, восьмиугольник…) этот угол ещё больше. Это значит, что если трехгранный угол образован тремя шестигранниками, то сумма его плоских углов составит ровно 120°•3 = 360°, что невозможно. Также невозможно, чтобы трехгранный угол и любой другой многогранный угол был образован правильными семиугольниками, восьмиугольниками и т. д. То есть грани правильного многогранника могут быть исключительно треуг-ками, четырехуг-ками или пятиугольниками.
Рассмотрим случай, когда грани – это треуг-ки. У равностороннего треуг-ка угол составляет 60°. У тетраэдра в вершине смыкаются 3 грани, у октаэдра – 4 грани, а у икосаэдра – 5 граней. А 6 треуг-ков уже не могут образовать многогранный угол, ведь сумма углов составит 6•60° = 360°.
Теперь рассмотрим случай с четырехуг-ком. Правильный четырехуг-к – это квадрат с углом 90°. Варианту с 3 смыкающимися квадратами соответствует куб, а 4 квадрата уже не образуют многогранный угол, ведь сумма углов снова составит 4•90° = 360°.
Остался случай с пятиугольником. У правильного пятиугольника угол равен 108°. Значит, 4 таких фигуры не смогут сомкнуться и образовать многогранный угол, а варианту с тремя пятиугольниками соответствует додекаэдр.
Итак, мы рассмотрели все возможные варианты, и оказалось, что никаких других правильных многогранников, кроме пяти описанных, существовать не может, ч. т. д. Отметим также, что этот факт можно доказать и без применения свойства многогранного угла, используя только теорему Эйлера.
Задачи на правильные многогранники
Задание. Центры смежных граней куба со стороной, равной единице, соединили отрезками. Докажите, что получившийся в результате этого многогранник – это октаэдр, и найдите длину его стороны.

Решение. Грани куба – это квадраты. Напомним, что у любого правильного многоуг-ка, в том числе и квадрата, можно опустить из центра перпендикуляры на стороны, которые будут радиусами вписанной окружности. Все эти радиусы будут иметь одну и ту же длину, при этом они будут падать на середины сторон многоуг-ка. При этом у квадрата радиус вписанной окружности будет вдвое меньше стороны квадрата. В частности, у рассматриваемого куба перпендикуляры, опущенные на середины ребер, будут иметь длину 1:2 = 0,5:

Теперь возьмем любые два центра смежных граней А и В и опустим из них перпендикуляры на ребро, по которому эти грани пересекаются. Перпендикуляры упадут в одну точку – середину ребра Н:

В результате мы получили прямоугольный ∆АВН. Найдем длину его гипотенузы АВ:

Так как мы выбрали центры смежных граней произвольно, то ясно, что расстояние между любыми двумя другими вершинами многогранника, вписанного в куб, будет иметь такую же длину. Тогда каждая его грань оказывается равносторонним треуг-ком. В каждой вершине смыкается 4 ребра, поэтому многогранник оказывается октаэдром.

Задание. Вычислите площадь поверхности икосаэдра, если его ребро имеет длину 1.
Решение. Найдем площадь одной грани икосаэдра. Она представляет собой равносторонний треуг-к со стороной 1. Удобно вычислить его площадь по формуле Герона. Сначала найдем полупериметр треуг-ка:

Задание. Найдите двугранный угол, который образуют грани правильного тетраэдра
Решение. Обозначим вершины тетраэдра буквами А, В, С и D. Далее соединим середину ребра АС, обозначенную как М, с вершинами B и D:
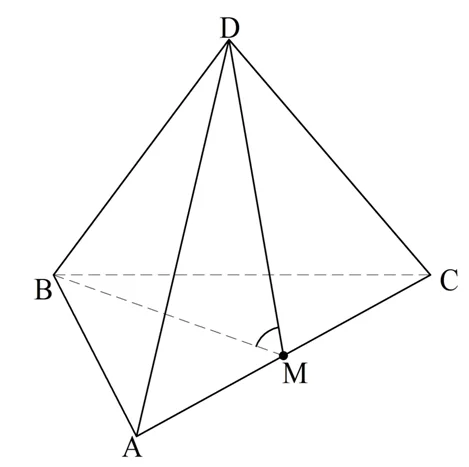
Так как М – середина АС, то ВМ и DM будут медианами ∆АВС и ∆ADC. Но эти треуг-ки равносторонние, поэтому ВМ и DM ещё и высоты. То есть ВМ⊥АС и DM⊥АС. Тогда по определению ∠DMB и будет плоским углом двугранного угла, то есть его как раз и надо вычислить. Предварительно обозначим длину грани тетраэдра буквой а.
∠ВАС составляет 60° как угол равностороннего ∆АВС. Тогда ВМ можно найти из прямоугольного ∆АВМ:

Аналогично из ∆DMC получаем, что и DM имеет такую же длину.
Теперь используем теорему косинусов для ∆BDM:

Задание. Вычислите двугранный угол, который образуют смежные грани октаэдра
Решение. Мы уже говорили, что октаэдр состоит из двух правильных четырехугольных пирамид с общим основанием. Поэтому нам надо просто найти двугранный угол между двумя боковыми гранями такой пирамиды:
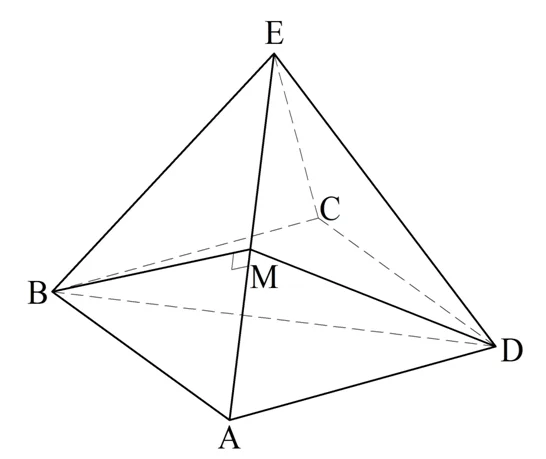
Для этого на ребре АЕ отметим середину М и соединим ее с вершинами B и D. Как и в предыдущей задаче с тетраэдром, ВМ и МD окажутся медианами и высотами в равносторонних ∆АЕВ и ∆АЕD, а потому ∠ВМD является искомым.
Обозначим сторону октаэдра буквой а. Тогда длина ВМ и МD, медиан в равносторонних треуг-ках будет такой же, как и в предыдущей задаче:

Задание. Вычислите двугранный угол, образованный смежными гранями додекаэдра
Решение. Нет необходимости строить весь додекаэдр для решения задачи. Построим только трехгранный угол, образованный ребрами, выходящими из одной вершины. То есть нам достаточно рассмотреть только область, выделенную на додекаэдре красным цветом:

Каждый плоский угол такого трехгранного угла будет равен углу правильного пятиугольника, который в свою очередь рассчитывается так:

Итак, надо найти двугранный угол между гранями ADC и ADB. Они пересекаются по прямой AD. Опустим из В и С перпендикуляры на AD. ∆ABD и ∆ADC равны, ведь у них есть одинаковый угол 108°, сторона AD– общая, а BD и DC одинаковы как ребра правильного многогранника. Это значит, что перпендикуляры на AD упадут в одну точку, которую мы обозначим как H. Нам надо вычислить ∠BНС.Обратите внимание, что так как ∆ABD и ∆ADC тупоугольные, то точка Н будет находиться не на отрезке AD, а на его продолжении.
Обозначим длину ребра додекаэдра буквой а. Мы можем найти ∠HDC:

Примечание. Здесь мы использовали одну из тригонометрических формул приведения.
Аналогично из ∆BHD получаем, что BH имеет такую же длину. Теперь из ∆BDC вычисляем величину ВС2:

Задание. Вычислите площадь поверхность додекаэдра, если его ребро имеет длину 1
Решение. Каждая грань додекаэдра – правильный пятиугольник. Для нахождения его площади используем уже известные нам формулы для правильных многоугольников:

Здесь n – число сторон у многоуг-ка, Р – его периметр, S – площадь, an – длина стороны, R и r – радиусы соответственно описанной и вписанной окружности. По условию

Теперь вспомним, что у додекаэдра 12 граней. Значит, площадь всей его поверхности будет в 12 раз больше:

Ответ: ≈ 20,646.
Сегодня мы познакомились с особыми телами – правильными многогранниками. Важно запомнить, что существует всего 5 типов правильных многогранников. Эти фигуры встречаются не только в геометрии, но и в других науках. Например, атомы в никеле и меди могут выстраиваться в форме октаэдра, а оболочки некоторых вирусов похожи на икосаэдр. Правильные многогранники могут использоваться в настольных играх в качестве игральных костей. Чаще всего применяются кости в виде куба, но встречаются кости в виде додекаэдра и икосаэдра.
ГДЗ и решебники
вип уровня
Условие
Найдите двугранные углы правильного тетраэдра.
Решение 1
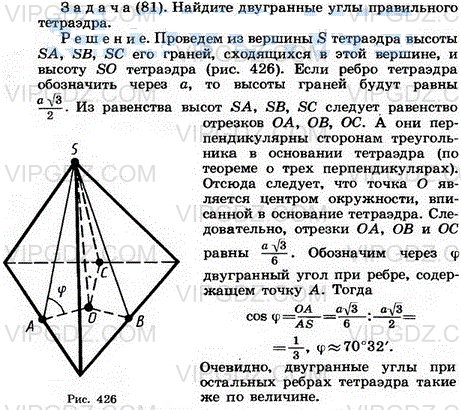
Популярные решебники
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 декабря 2019 года; проверки требуют 8 правок.
| Правильный тетраэдр | |||
|---|---|---|---|
 |
|||
 |
|||
| Тип | правильный многогранник | ||
| Комбинаторика | |||
| Элементы |
|
||
| Грани | правильные треугольники | ||
| Конфигурация вершины | 3.3.3 | ||
| Двойственный многогранник | тоже правильный тетраэдр | ||
| Классификация | |||
| Символ Шлефли | {3,3} | ||
| Группа симметрии |
 |
||
| Количественные данные | |||
| Длина ребра |
 |
||
| Площадь поверхности |
 |
||
| Объём |
 |
||
| Телесный угол при вершине |
 ср ср |
Тетраэдр называется правильным, если все его грани — равносторонние треугольники.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.
Свойства правильного тетраэдра[править | править код]
- Каждая его вершина является вершиной трех равносторонних треугольников. А значит, сумма плоских углов при каждой вершине будет равна
.
- В правильный тетраэдр можно вписать октаэдр, притом четыре из восьми граней октаэдра будут совмещены с серединными треугольниками четырёх граней тетраэдра, а все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
- Правильный тетраэдр можно вписать в куб, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба, а все шесть рёбер тетраэдра будут совмещены с диагоналями граней куба.
Интересные факты[править | править код]
Середины граней правильного тетраэдра также образуют правильный тетраэдр.
Соотношения:
- рёбер и высот правильных тетрадров, радиусов переписанных, описанных и писанных сфер соответственно равны
;
- площадей поверхности равно
;
- объёмов равно
.

Autodualité du tétraèdre régulier.
Примечания[править | править код]
- ↑ 1 2 3 4 5 Coxeter, 1948.
Литература[править | править код]
- Harold Scott MacDonald Coxeter. Table I(i) // Regular Polytopes. — Methuen and Co., 1948.

