Как найти двугранный угол при боковом ребре

Как найти угол между плоскостями?

Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.

Геометрический способ

При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.

Алгебраический способ

Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.

Вот такая:

( displaystyle cos gamma =frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}})

Здесь ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}) — коэффициенты уравнений плоскостей ( displaystyle alpha ) и ( displaystyle beta ) соответственно.

Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!

( displaystyle alpha ): ( displaystyle {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+D=0)

( displaystyle beta ): ( displaystyle {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+D=0).

Какой же способ лучше? Зависит от задачи.

Если нужно найти, скажем, двугранный угол при основании правильной , то проще использовать геометрический способ.

А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.

Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}), а потом ещё и ( displaystyle cos gamma ).

Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.

стереометрия – Найти двугранный угол

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, – это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово “пирамида”. Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

Двугранные углы фигуры

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

• При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n – число сторон многоугольника.
• Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип – на боковых ребрах.

Как рассчитать углы пирамиды?

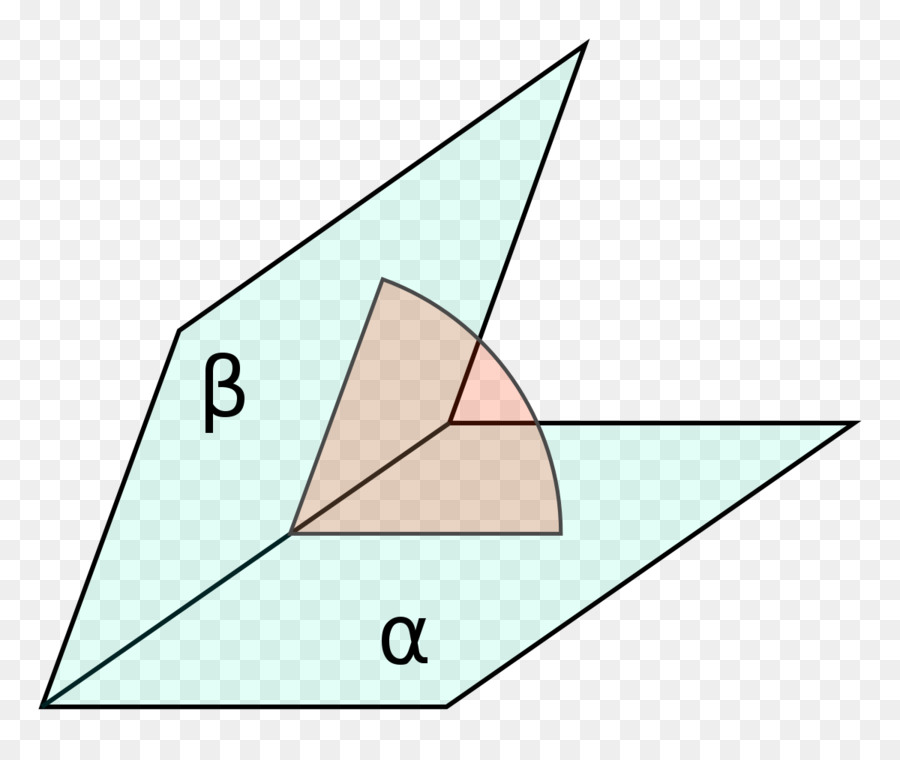
Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D – это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

n¯ = [A; B; C]

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

n₁¯ = [A₁; B₁; C₁];

n₂¯ = [A₂; B₂; C₂]

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

φ = arccos(|(n₁¯*n₂¯)|/(|n₁¯|*|n₂¯|))

Или в координатной форме:

φ = arccos(|A₁*A₂ + B₁*B₂ + C₁*C₂|/(√(A₁² + B₁²+C₁²)*√(A₂² + B₂² + C₂²)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

Углы правильной пирамиды четырехугольной

Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

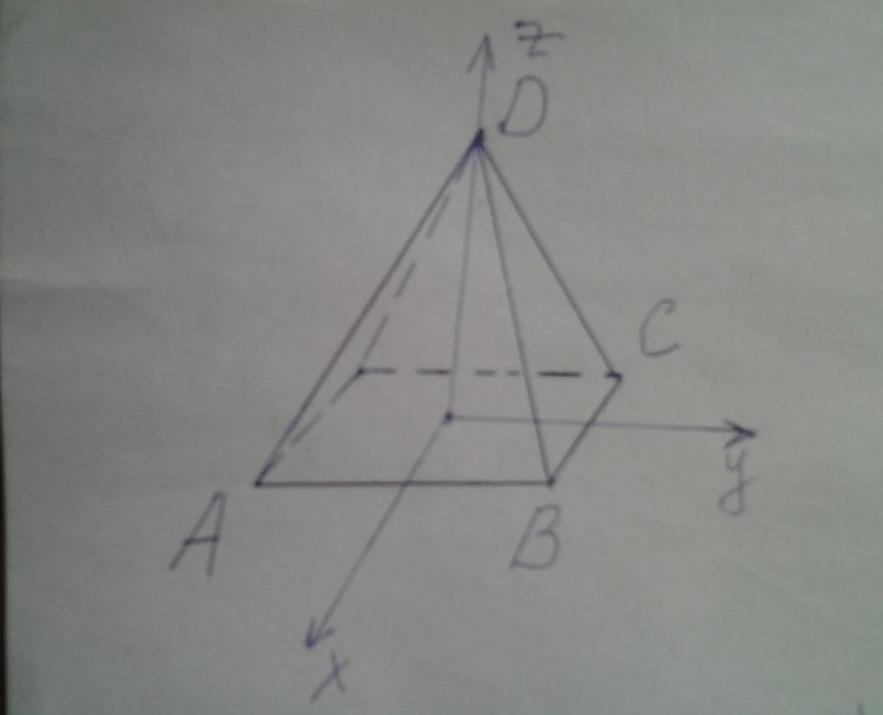
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

A(a/2; -a/2; 0);

B(a/2; a/2; 0);

C(-a/2; a/2; 0);

D(0; 0; h)

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

Для ABC:

AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n₁¯ = [AB¯*AC¯] = (0; 0; a²)

Для ABD:

AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n₂¯ = [AB¯*AD¯] = (a*h; 0; a²/2)

Для BCD:

BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n₃¯ = [BC¯*BD¯] = (0; a*h; a²/2)

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

(n₁¯*n₂¯) = a⁴/2; |n₁¯| = a²; |n₂¯| = a*√(h² + a²/4);

φ = arccos(a⁴/2/(a²*a*√(h² + a²/4))) = arccos(a/(2*√(h² + a²/4))) = 67,38^o

Угол между ABD и BDC:

(n₂¯*n₃¯) = a⁴/4; |n₂¯| = a*√(h² + a²/4) ; |n₃¯| = a*√(h² + a²/4);

φ = arccos(a⁴/(4*a²*(h²+a²/4)) = arccos(a²/(4*(h²+a²/4))) = 81,49^o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

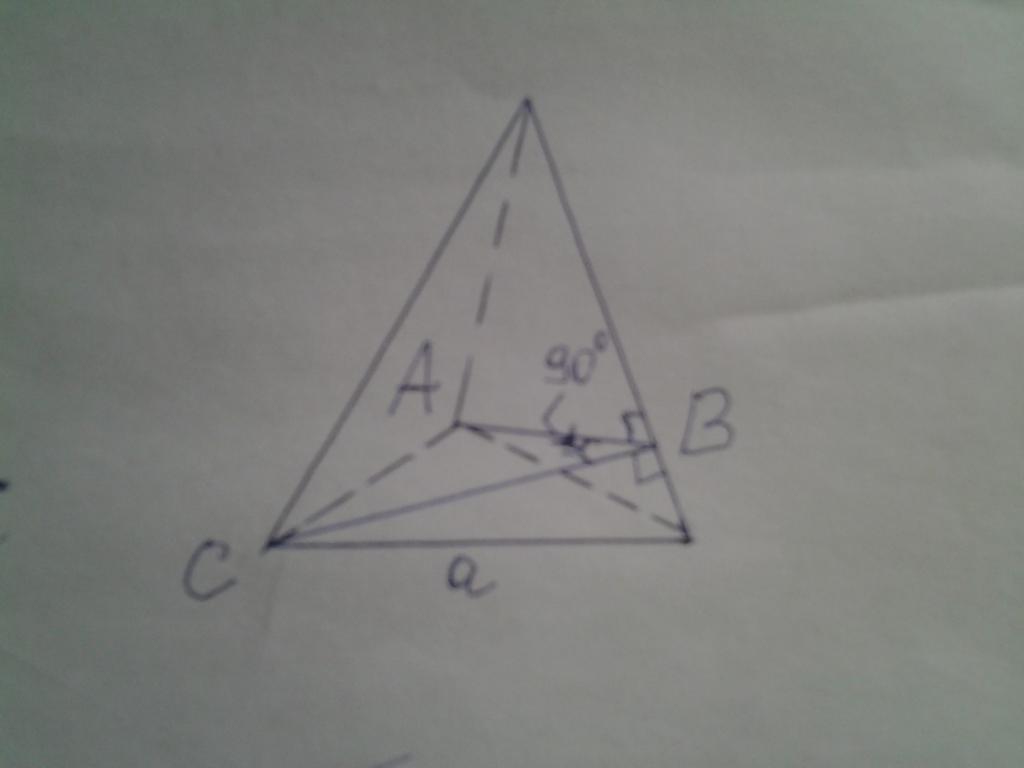
Двугранный угол, равный 90^o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры – h, апофему – h_b и боковое ребро – b. Теперь можно записать следующие формулы:

S = 1/2*a*h_b;

b² = h_b² + a²/4;

b² = h² + a²/3

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

x = a/√2;

S = 1/2*b*a/√2

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

1/2*a*h_b = 1/2*b*a/√2 =>

h_b = b/√2;

b² = b ²/2 + a²/4 =>

b = a/√2;

a²/2 = h² + a²/3 =>

a = h*√6

Площадь равностороннего треугольника рассчитывается так:

S = √3/4*a² = 3*√3/2*h²

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см².

Двугранный
угол образуется в результате пересечения
двух плоскостей. Ребром двугранного
угла называется линия пересечения этих
двух плоскостей. Мерой
двугранного
угла является плоский угол, получающийся
при пересечении двугранного угла
плоскостью, перпендикулярной ребру
двугранного угла.

Для
того, чтобы определить величину
двугранного угла, необходимо провести
построения методом замены плоскостей
проекций, в результате которых в новой
системе плоскостей проекций ребро
двугранного угла примет положение
проецирующей прямой, а плоскости,
образующие двугранный угол, сделаются
проецирующими плоскостями.

Найдем
двугранный угол при ребре SB,
образованный плоскостями ABS
и BCS.
Путем замены плоскостей проекций
необходимо сделать ребро SB
проецирующей
прямой. Поскольку ребро SB
является прямой общего положения, его
необходимо при первой замене плоскостей
проекций сделать прямой уровня, а при
второй замене плоскостей проекций
сделать проецирующей прямой (рис. 8).

Рис.8.
Нахождение двухгранного угла

при
ребре пирамиды BS

Порядок построений.

1. Проведем
   новую ось системы плоскостей П₁/П₄
   || S₁B₁,
   найдем проекции точек A₄,
   B₄,
   C₄,
   S₄.
   Ребро SB
   в системе плоскостей проекций П₁/П₄
   стало прямой уровня.

2. Проведем
   новую ось системы плоскостей П₄/П_{5
   ┴}
   B₄S₄.
   Найдем проекции точек A₅,
   B₅,
   C₅,
   S₅.
   Ребро SB
   в системе плоскостей проекций П₄/П₅
   стало проецирующей прямой. Его проекция
   на плоскости П₅
   выродилась в точку S₅≡В₅.
   Боковые грани двугранного угла ABS
   и CBS
   стали проецирующими плоскостями. Их
   проекции на плоскость П₅
   выродились
   в прямые линии A₅B₅
   и C₅B₅,
   которые необходимо выделить красным
   цветом. Угол φ
   между этими прямыми есть натуральная
   величина плоского угла, являющегося
   мерой двугранного угла при ребре SB.

Список литературы

1. Гордон В.О.
   Курс начертательной геометрии. Учеб.
   пособие для вузов. / В.О. Гордон, М.А.
   Семенцов-Огиевский.; Под ред. В.О.
   Гордона, Ю.Б. Иванова. -24-е изд., стереотип.
   – М.: Высш. шк., 2002.-272с.:ил.; Рекомендовано
   М-вом образования РФ.-ISBN 5060035182:75.00,90.00

2. Гордон
   В.О. Сборник задач по курсу начертательной
   геометрии. Учеб. пособие. / В. О. Гордон,
   Ю. Б. Иванов, Т.Е. Солнцева; Под ред. Ю.Б.
   Иванова. – 8-е изд., стер .-М.: Высшая школа,
   2002.-320с.:ил.;.- Допущено М-вом образования
   РФ.-ISBN 5060035190:87.00

3. Начертательная
   геометрия: Учебник для вузов /
   Н.Н.Крылов, Г.С. Иконникова, В.Л. Николаев
   и др.; Под ред. Н.Н.Крылова.-8-е изд., испр.-
   М.: Высш. шк., 2002. -224с.: ил.; .- Рекомендовано
   М-вом образования РФ.-ISBN 5060043193:68.64

4. ГОСТ 2.302-68. Форматы.-
   Взамен ГОСТ 3450-60; введен с 01.01.1971. // Общие
   правила выполнения чертежей: ЕСКД.–
   М.: Издательство стандартов, 1988. С. 3-4.

5. ГОСТ 2.302-68 Масштабы.
   Взамен ГОСТ 3451-59; введен с 01.01.1971. // Общие
   правила выполнения чертежей: ЕСКД.–
   М.: Издательство стандартов, 1988. С. 5.

6. ГОСТ 2.303-68 Линии.
   Взамен ГОСТ 3456-59; введен с 01.01.1971. // Общие
   правила выполнения чертежей: ЕСКД.–
   М.: Издательство стандартов, 1988. С. 6-8.

7. ГОСТ
   2.304-81 Шрифты чертежные. Взамен ГОСТ
   3004-68; введен с 01.01.1982. // Общие правила
   выполнения чертежей: ЕСКД.– М.:
   Издательство стандартов, 1988. С. 12-39.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #