Определение: “Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при
пересечении двугранного угла плоскостью, перпендикулярной его
ребру (то есть перпендикулярной к обеим плоскостям)”.
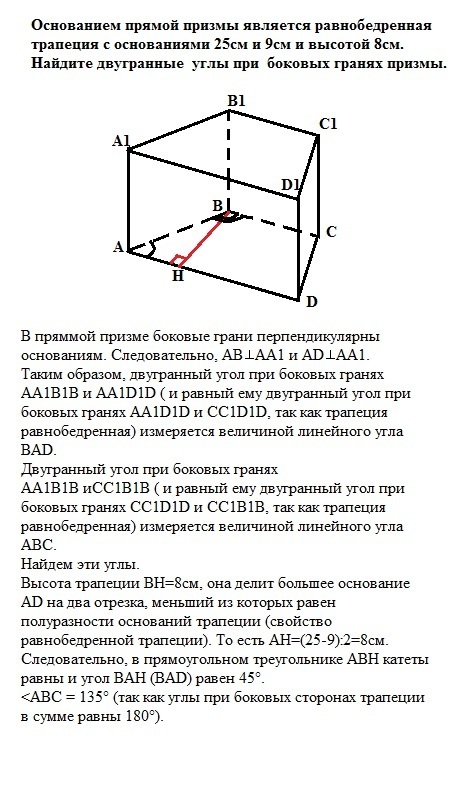
В прямой призме боковые грани перпендикулярны основаниям.
Следовательно, AB⊥AA1 и AD⊥AA1.
Таким образом, двугранный угол при боковых гранях
АА1В1B и AA1D1D ( и равный ему двугранный угол при боковых
гранях АА1D1D и CC1D1D, так как трапеция равнобедренная)
измеряется величиной линейного угла ВАD. Двугранный угол при
боковых гранях АА1В1B иСС1В1В ( и равный ему двугранный угол
при боковых гранях СС1D1D и CC1В1В, так как трапеция равнобедренная) измеряется величиной линейного угла AВС.
Найдем эти углы.
Высота трапеции ВН=8см, она делит большее основание AD на два
отрезка, меньший из которых равен полуразности оснований
трапеции (свойство равнобедренной трапеции).
То есть АН=(25-9):2=8см.
Следовательно, в прямоугольном треугольнике АВН катеты равны и
угол ВАН (ВАD) равен 45°.
<АВС = 135° (так как углы при боковых сторонах трапеции в сумме
равны 180°).
Ответ: искомые углы равны 45° и 135°.
Решение:
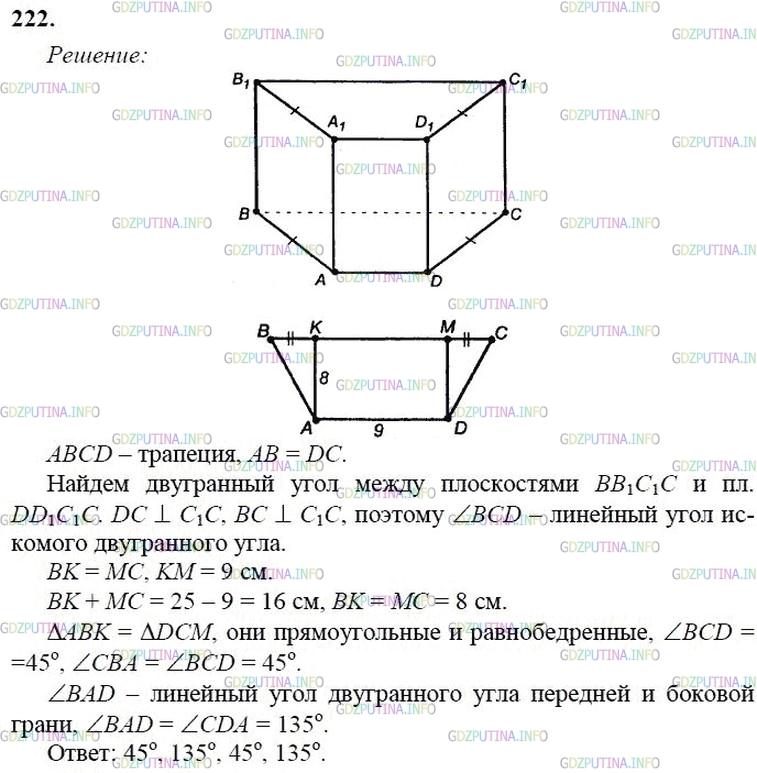
Рассмотрим прямую призму ABCDA1B1C1D1.ABCDA_1B_1C_1D_1. Где ABCDABCD — равнобедренная трапеция. Проведём высоты D1МD_1М и С1NС_1N верхнего основания призмы. Поскольку призма прямая, то её боковые грани перпендикулярны плоскостям основания, следовательно ∠MAD1=αangle MAD_1=alpha и ∠A1D1C1=βangle A_1D_1C_1=beta — двугранные углы при боковых ребрах призмы.
A1M=A1B1−D1C12=50−182=16 см.A_1M=dfrac{A_1B_1-D_1C_1}{2}=dfrac{50-18}{2}=16,см.
Учитывая условие задач, имеем:
A1M=D1M=16 см.A_1M=D_1M=16,см.
Поскольку ΔA1MD1Delta A_1MD_1 — прямоугольный и равнобедренный, то ∠MA1D1=α=45°.angle MA_1D_1=alpha=45°.
Тогда ∠A1D1C1=β=180°−α=180°−45°=135°angle A_1D_1C_1=beta =180°-alpha=180°-45°=135° как внутренние односторонние углы.
Ответ: 45°45° и 135°.135°.
Условие
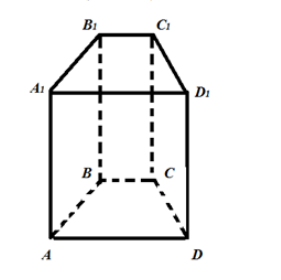
Равнобедренная трапеция ABCD является основанием прямой призмы. Основания трапеции AD=37; DC=25.
Высота трапеции равна 6. Найдите двугранные углы при боковых ребрах призмы.
математика 10-11 класс
4062
Решение
★
Так как призма прямая, то двугранные углы между боковыми рёбрами равны углам между сторонами основания.
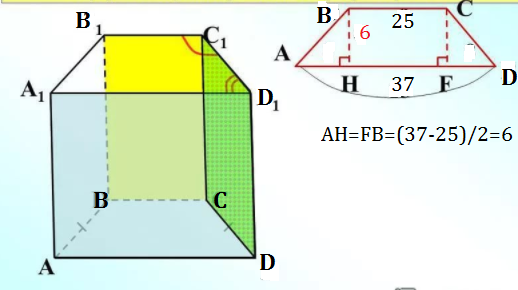
Опустим высоту ВМ на сторону АD.
АМ=(АD-ВС)/2=(37-25)/2=6.
В тр-ке АВМ АМ=ВМ=6, ВМ⊥АD, значит ∠ВАМ=45°.
∠АВС=180-∠ВАD=180-45-135°.
Трапеция равнобедренная,
углы при основаниях равны.
Ответ: двугранные углы между боковыми сторонами призмы равны 45°, 45°, 135° и 135°.
Написать комментарий
ГДЗ (готовое домашние задание из решебника) на Номер №222 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 22-е изд. – Просвещение, 2013-2019г
Условие
Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.
Решение 1
Решение 2
Решение 3
Решение 4
Решение 5
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Как найти угол между плоскостями?
Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.
Геометрический способ
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
Алгебраический способ
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Вот такая:
( displaystyle cos gamma =frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}})
Здесь ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}) — коэффициенты уравнений плоскостей ( displaystyle alpha ) и ( displaystyle beta ) соответственно.
Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!
( displaystyle alpha ): ( displaystyle {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+D=0)
( displaystyle beta ): ( displaystyle {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+D=0).
Какой же способ лучше? Зависит от задачи.
Если нужно найти, скажем, двугранный угол при основании правильной , то проще использовать геометрический способ.
А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.
Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}), а потом ещё и ( displaystyle cos gamma ).
Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.