1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы ![]() и
и ![]() ,
, ![]() и противоположно направленные им векторы, например:
и противоположно направленные им векторы, например:
![]()
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам ![]() .
.
А теперь рассмотрим произвольный вектор ![]() либо
либо
![]() и поставим задачу найти
и поставим задачу найти
единичный вектор ![]() , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора
, коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора ![]() разделить на его длину:
разделить на его длину:
![]() либо
либо ![]() ,
,
или, что то же самое – умножить каждую координату вектора ![]() на
на ![]() . То
. То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
![]() либо
либо ![]()
Задача 10
Найти единичные векторы, коллинеарные векторам а) ![]() , б)
, б) ![]() . Выполнить проверку.
. Выполнить проверку.
Решение: а) вычислим длину вектора ![]() и найдём
и найдём
сонаправленный единичный вектор:
![]() , от иррациональности в знаменателе (корня) тут
, от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
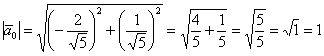 , что и требовалось проверить.
, что и требовалось проверить.
Второй вектор очевиден: ![]() , как очевидна и его
, как очевидна и его
длина ![]() .
.
Ответ: ![]()
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.
 1.5.6. Деление отрезка в данном отношении
1.5.6. Деление отрезка в данном отношении
 1.5.4. Действия с векторами в координатах
1.5.4. Действия с векторами в координатах
| Оглавление |
Автор: Aлeксaндр Eмeлин
Единичный вектор
Единичный вектор (орты координатных осей) — это вектор, длина которого равна единице.
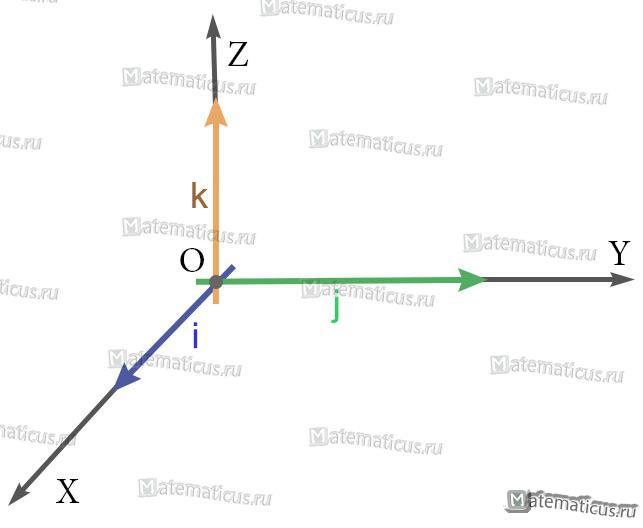
i — единичный вектор оси абсцисс;
j — единичный вектор оси ординат;
k — единичный вектор оси аппликат.
i⊥j⊥k, i=j=k=1
В прямоугольной системе координат в пространстве координаты векторов равны:
i(1;0;0), j(0;1;0), k(0;0;1)
Единичные векторы являются некомпланарными.
Любой вектор можно разложить в виде вектора по ортам координатных осей, формула ниже.
a=xi+уj+zk
где x, y, z — координаты вектора проекции на соответствующие координатные оси.
Эта формула называется разложением вектора по ортам координатных осей.
Единичный вектор определяется по формуле:
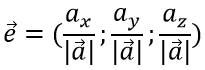
Дан вектор а = (1; 2; -2)
Требуется найти длину (модуль) и единичный вектор e направления вектора а
Находим длину вектора a
затем вычисляем единичный вектор e
Векторное произведения единичных векторов
Если направление кратчайшего пути от первого вектора ко второму вектору совпадает с направлением стрелки, то произведение равно третьему вектору, а если не совпадает, то третий вектор берется со знаком «минус» . Смотрите схему 1.
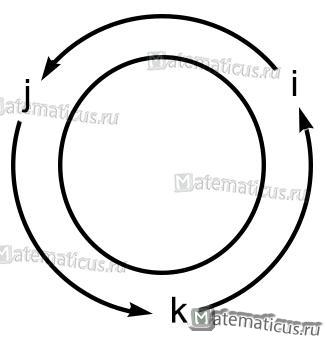
На основании схемы получаем таблицу векторного произведения единичных векторов
Пример 1
Найти векторное произведение iхj, где i, j — единичные векторы (орты) правой системы координат.
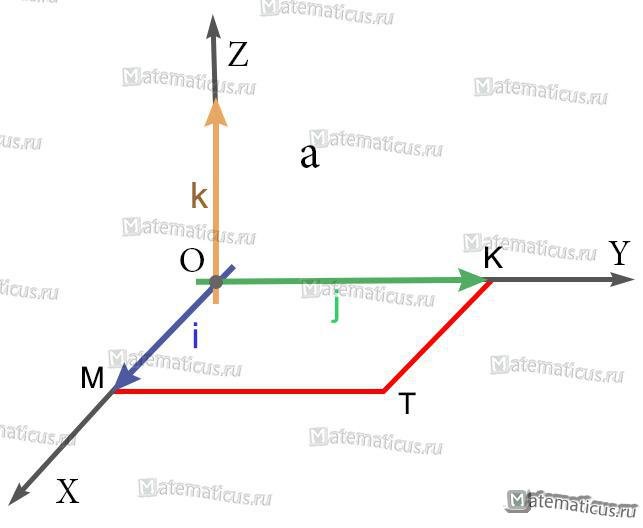
Решение
1) Так как длины основных векторов равны единице масштаба, то площадь параллелограмма MOKT численно равна единице. Значит, модуль векторного произведения равен единице.
2) Так как перпендикуляр к плоскости MOKT есть ось OZ, то искомое векторное произведение есть вектор, коллинеарный с вектором k; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3) Из этих двух возможных векторов надо выбрать первый, так как векторы i, j, k образуют правую систему (а векторы i, j, -k — левую).
iхj=k
Пример 2
Найти векторное произведение jхi.
Решение
Как в примере 1, заключаем, что вектор jхi равен либо k, либо —k. Но теперь надо выбрать -k, ибо векторы j, i, —k образуют правую систему (а векторы i, j, —k -левую).
jхi = −k
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.5 / 5. Количество оценок: 4
Вектор: определение и основные понятия
Определение вектора
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом – точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Нулевой вектор
Нулевой вектор обычно обозначается как 0 .
Длина нулевого вектора равна нулю.
Коллинеарные вектора
 |
| рис. 2 |
Сонаправленные вектора
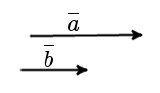 |
| рис. 3 |
Противоположно направленные вектора
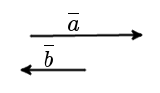 |
| рис. 4 |
Компланарные вектора
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
Единичный вектор
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Геометрия для новичков. Часть 1: координаты и векторы – теория
Внимание! Этот документ ещё не опубликован.
О чем данная статья
В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.
На кого рассчитана статья
Прежде чем читать эту статью, нужно знать:
- что такое прямоугольная система координат и координаты точки на плоскости
- что такое теорема Пифагора
Введение
Зачем нужны координаты точек в играх
В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:

На этом рисунке крупные черные точки – это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:
- координаты Марио равны (-0.5, -2)
- координаты улитки равны (3, -2)
- координаты кубика равны (4, 1)
Пример координат вектора

Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.
Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:
Ax + x = Bx
Ay + y = By
Решая эти 2 уравнения, получаем:
x = Bx – Ax
y = By – Ay
Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это – лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.
Векторы
Что такое направленный отрезок

Стрелка показывает, что А – начало отрезка, а B – конец.
Что такое вектор

Что у этих отрезков общего? Хм, пожалуй 2 вещи:
- Направление
- Длина
Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это – не вектор.
В нашем примере направленный отрезок  представляет вектор
представляет вектор  . Разницу в черточках наверху заметили? Еще часто вектор обозначают 1 буквой, например:
. Разницу в черточках наверху заметили? Еще часто вектор обозначают 1 буквой, например: 
Примечание: о тонкостях приведенного мной определения – в конце статьи.
Равенство векторов
Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:
Два вектора  и
и  , представленные направленными отрезками
, представленные направленными отрезками  и
и  называются равными, если:
называются равными, если:
Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.
Длина вектора
Коллинеарные векторы

На рисунке любая пара из векторов  ,
,  ,
,  является коллинеарными векторами
является коллинеарными векторами
Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:

Пишут: 


Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:

Пишут: 


Нулевой вектор
Единичные векторы
 =1
=1
Обратный вектор

Арифметические операции над векторами
- Вектор можно умножать на число. Вектор
 , умноженный на число, записывается как k*
, умноженный на число, записывается как k* . Вектор будет сонаправлен (противоположно направлен) с вектором
. Вектор будет сонаправлен (противоположно направлен) с вектором  , если k – положительное (отрицательное) число. Вектор k*
, если k – положительное (отрицательное) число. Вектор k*  будет иметь длину |k|*|
будет иметь длину |k|*| |:
|:
|k* | = |k|*|
| = |k|*| |
|
k* 

 , если k>0
, если k>0
k* 

 , если k 0, такое, что:
, если k 0, такое, что:
|k *  |=1
|=1
Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором 
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:
|k* | = |k|*|
| = |k|*| | = k * 0 = 0
| = k * 0 = 0
Итак, как же найти это число k?
Распишем |k *  | по определению:
| по определению:
|k *  | = |k| * |
| = |k| * | | = k * |
| = k * | | = 1
| = 1
Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:
k * | | = 1
| = 1
Из этого следует, что:
k = 1 / | |
|
Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.
Координаты вектора
Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора – разность координат конца и начала направленного отрезка, представляющего вектор.
Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.
Разложение вектора по 2 неколлинеарным векторам
В геометрии доказывается следующий факт.
Ecли мы возьмем 2 неколлинеарных вектора  и
и  ,
,
то для каждого вектора  можно подобрать 2 числа k и s, для которых выполняется равенство:
можно подобрать 2 числа k и s, для которых выполняется равенство:
 = k*
= k*  + s*
+ s*
Теперь возьмем в качестве таких неколлинеарных векторов  и
и  следующие векторы:
следующие векторы:
- вектор
 – направление – вдоль оси Ox, длина равна 1
– направление – вдоль оси Ox, длина равна 1 - вектор
 – направление – вдоль оси Oy, длина равна 1
– направление – вдоль оси Oy, длина равна 1

Векторы  и
и  называют координатными векторами.
называют координатными векторами.
Определение координат вектора
 = x*
= x*  + y*
+ y*
то пара чисел (x, y) будет называться координатами вектора  .
.
Часто пишут:
 = (x, y)
= (x, y)
Эта запись означает, что вектор  имеет координаты x и y.
имеет координаты x и y.
Арифметические операции над координатами векторов
–  = (-ax, -ay)
= (-ax, -ay)
Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:
k*  = (k*ax, k*ay)
= (k*ax, k*ay)
Пусть у нас есть 2 произвольных вектора  =(ax, ay) и
=(ax, ay) и  =(bx, by). Тогда:
=(bx, by). Тогда:
- кoординаты суммы 2 векторов равны сумме x- и y-координат векторов:
 +
+  = (ax + bx, ay + by)
= (ax + bx, ay + by) - как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов:
 –
–  = (ax – bx, ay – by)
= (ax – bx, ay – by)
Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.
Радиус-вектор

Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт:  =(Ax, Ay)
=(Ax, Ay)
где (Ax, Ay) – координаты точки A
Связь между координатами вектора и координатами концов отрезка
если  – направленный отрезок, представляющий вектор
– направленный отрезок, представляющий вектор  , то значения координат вектора
, то значения координат вектора  (x, y) вычисляются по формуле:
(x, y) вычисляются по формуле:
(x, y) = (Bx – Ax, By – Ay)
где (Ax, Ay), (Bx, By) – координаты точек А и B соответственно.
Докажем это.
Мы можем записать простое равенство для произвольного вектора  :
:
 =
=  –
– 

Заметим, что  и
и  – радиус векторы.
– радиус векторы.
Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:
(x, y) = (Bx – Ax, By – Ay)
Нахождение длины вектора по его координатам
Пусть у нас есть вектор  , представленный отрезком
, представленный отрезком  . Координаты вектора
. Координаты вектора  равны (x, y).
равны (x, y).
Чтобы найти длину вектора  через его координаты, воспользуемся теоремой Пифагора и равенством:
через его координаты, воспользуемся теоремой Пифагора и равенством:
 =
=  +
+ 

По теореме Пифагора:

AC = | | = |x|,
| = |x|,
СB = | | = |y|
| = |y|
то в итоге получаем равенство:

Заключение
Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.
Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.
Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.
Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».
PS: корректность определения вектора в статье
Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.
Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.
Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.
Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.
Надеюсь, вышесказанное объясняет, почему я привел в данной статье “свое” определение вектора.
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/library/vector/vector-definition/
http://gamedev.ru/code/articles/geometry_for_beginners_1
[/spoiler]
Download Article
Learn how to calculate a unit vector and pass your math test with flying colors
Download Article
- Unit Vector Formula
- How to Calculate a Unit Vector
- Vectors
- Unit Vectors
- Magnitude
- Example Problems
- Solutions
|
|
|
|
|
|
At some point in your algebra course, you might have to learn about vectors, including unit vectors and magnitude. While your teacher or tutor may have taught a whole class on calculating a unit vector, you might still have some questions about the process. That’s why we’ve broken it down for you, below! Check out our guide to finding a unit vector, including a refresher on what vectors are and the formula for calculating magnitude, so you can ace your next pop quiz.
Things You Should Know
-

The formula to find unit vector is
. You can calculate the unit vector
of any vector by dividing the vector by its magnitude
. For instance, to calculate the unit vector of vector
, you would follow this equation:
.[1]
Advertisement
-

1
-
2
Divide the vector by its magnitude. Once you’ve determined the magnitude of the vector, take the vector and divide it by its magnitude. So if vector
is
, then
=
= (
,
). The unit vector, then, is (
).[3]
Advertisement
-
A vector is an object that contains both direction and magnitude. A vector is represented as a line on the Cartesian coordinate system, and it is denoted as a set of numbers representing its relationship to the x-axis (the vertical line on the graph) and the y-axis (the horizontal line). A vector’s magnitude refers to the size of the vector and is represented by a line with an arrow on the end. The length of the line denotes the length of the vector, while the direction of the arrow denotes the direction of the vector. Vectors possess both a starting point (the tail) and an ending point (the head, where the arrow is).[4]
-
A unit vector is a vector with a magnitude of 1. Unit vectors, also called direction vectors, are used to describe the direction of a given vector—or, the angle the vector makes on an x-axis. Unit vectors are marked with a cap symbol, which looks like a little arrow pointing upward: ^.[5]
Advertisement
-
The magnitude is the length or size of the vector. A vector’s magnitude, also called its norm, denotes its length on an x-axis (or the vertical line on the graph on which the vector appears), giving it numeric value. The magnitude on summarizes the length of the vector on the x-axis, y-axis (the horizontal line), and z-axis. Magnitude is denoted as 2 vertical lines, one on each side of the vector:
. To calculate the magnitude of a given vector with the direction of the x-axis, y-axis, or z-axis, follow the Pythagorean Theorem: add the squares of the vector’s direction ratios. Then, calculate the square root of that sum.[6]
- The magnitude of
would be
, the magnitude of
would be
, and the magnitude of
would be
.
- To find the magnitude of vector
, where
=
(and where
,
, and
represent the x-axis, y-axis, and z-axis, respectively), use the following equation:
= √
.
- For example, if
and
and
, then
, and
= √
= √
=
. Thus, the magnitude of vector
would be 3 units.
- The magnitude of
-
1
Given vector
=
+
+
, find
.
-
2
Given vector
=
+
, find
.
Advertisement
-

1
Answer #1:
=
. In this problem, we’re asked to find the unit vector of a 3-dimensional vector; hence, the inclusion of the z-axis in the equation. To find the unit vector, we identified the magnitude of the vector and then divided the vector by its magnitude:[7]
-

2
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Thanks to all authors for creating a page that has been read 1,380 times.
Did this article help you?
Единичный вектор
находится:
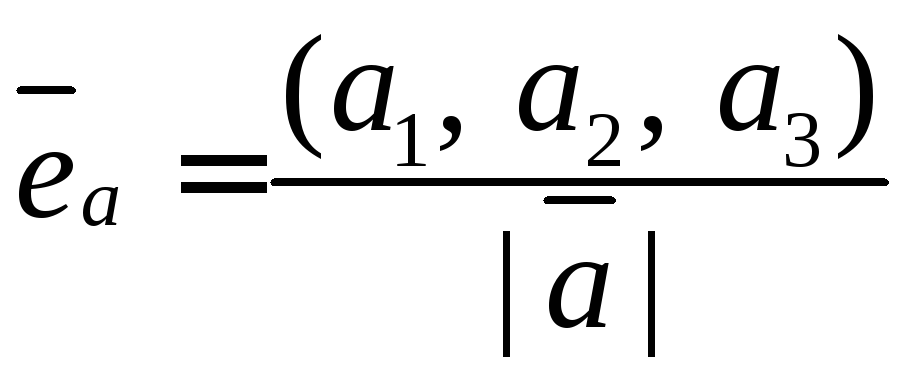 ,
,
где![]() – модуль вектора.
– модуль вектора.
Находим
![]()
тогда
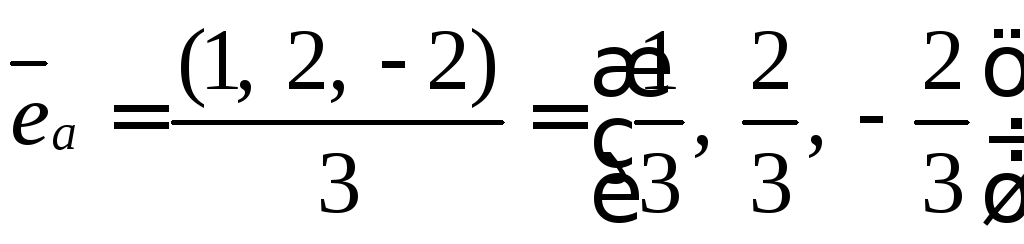
Ответ:
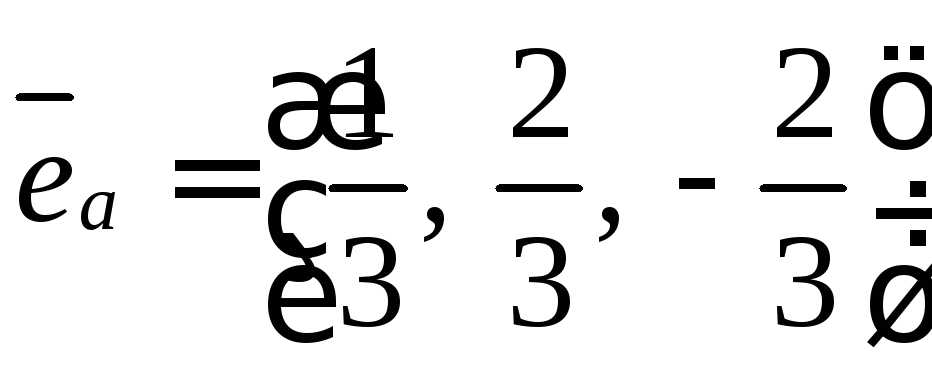 .
.
Примечание.
Координаты единичного вектора должны
быть не больше единицы.
6.3. Найти длину
и направляющие косинусы вектора
![]() .
.
Сравните с ответом в предыдущем пункте.
Сделайте выводы.
Длина вектора –
это есть его модуль:
![]() ,
,
а направляющие косинусы мы можем найти
по формуле одного из способов задания
векторов:

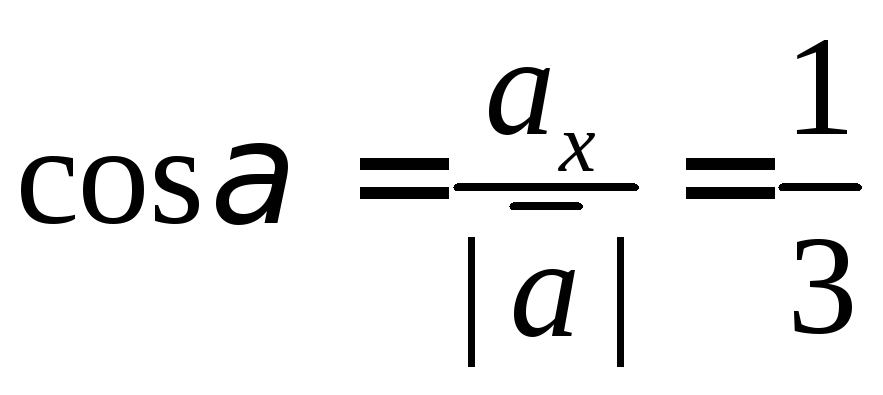
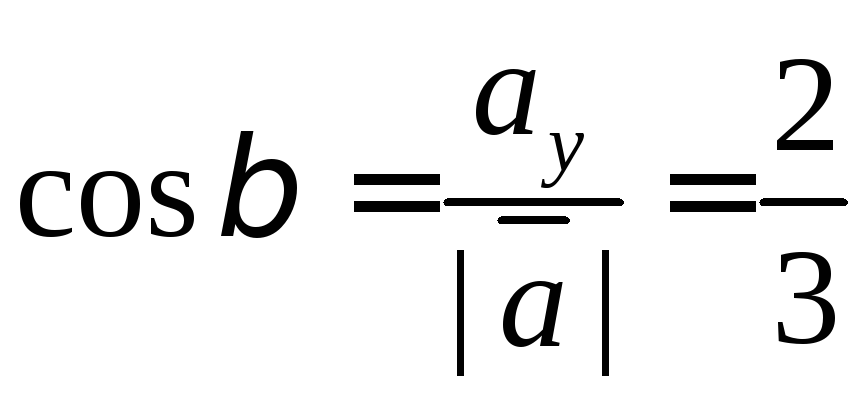
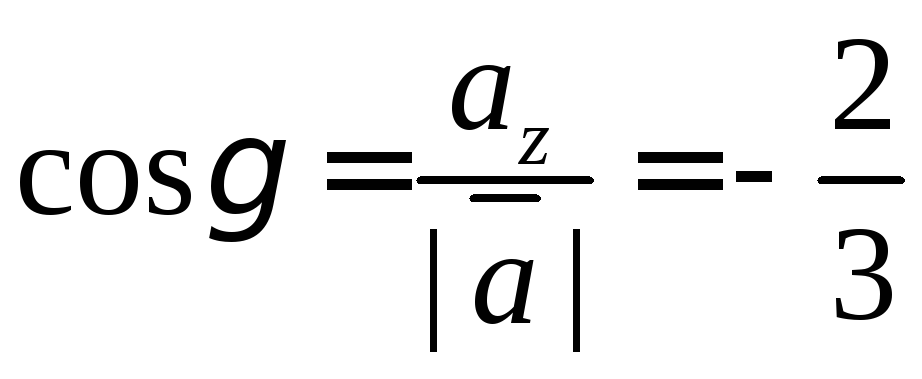
Из полученного мы
видим, что направляющие косинусы это и
есть координаты единичного вектора.
Ответ:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
6.4. Найти
![]() .
.
Необходимо выполнить
действия умножения вектора на число,
сложения и модуль.
![]()
Почленно перемножаем
координаты векторов на число.
![]()
Почленно складываем
координаты векторов.
![]()
Находим модуль
вектора.
![]()
Ответ:
![]()
6.5. Определить
координаты вектора
![]() ,
,
коллинеарного вектору![]() ,
,
зная, что![]() и он направлен в сторону, противоположную
и он направлен в сторону, противоположную
вектору![]() .
.
Вектор
![]() коллинеарен вектору
коллинеарен вектору![]() ,
,
значит, его единичный вектор равен
единичному вектору![]() только со знаком минус, т.к. направлен
только со знаком минус, т.к. направлен
в противоположную сторону.
Единичный вектор
имеет длину равную 1, значит, если его
умножить на 5, то его длинна будет равна
пяти.
Находим
![]()
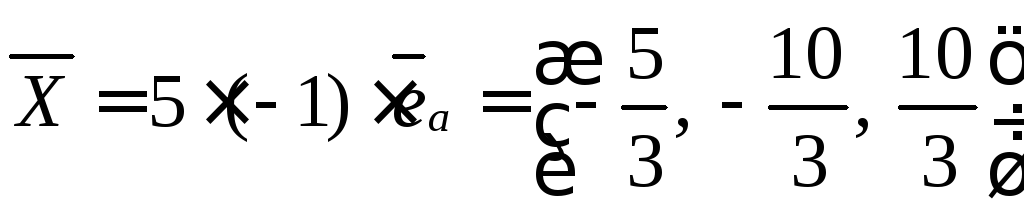
Ответ:
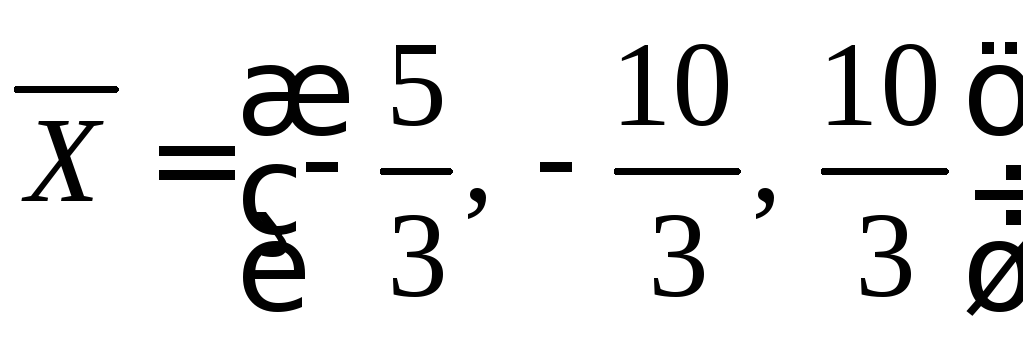
6.6. Вычислить
скалярные произведения
![]() и
и![]() .
.
Перпендикулярны ли векторы![]() и
и![]() ,
,![]() и
и![]() между собой?
между собой?
Выполним скалярное
произведение векторов.
![]()
![]()
Если вектора
перпендикулярны, их скалярное произведение
равно нулю.
М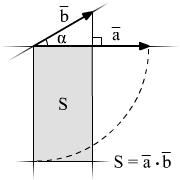 ы
ы
видим, что в нашем случае вектора![]() и
и![]() перпендикулярны.
перпендикулярны.
Ответ:
![]() ,
,![]() ,
,
векторы не перпендикулярны.
Примечание.
Геометрический смысл скалярного
произведения малоприменим на практике,
но все-таки существует. Результат такого
действия можно изобразить и вычислить
геометрически.
6.7. Найти работу,
совершённую материальной точкой к
которой приложена сила
![]() ,
,
при перемещении её из точки B в точку С.
Физический смысл
скалярного произведения – это работа.
Вектор силы здесь
![]() ,
,
вектор перемещения – это![]() .
.
А произведение этих векторов и будет
искомой работой.
![]()
Находим работу
![]()
Ответ: -3.
6.8. Найти
внутренний угол при вершине A
и внешний угол при вершине C
треугольника ABC.
Из определения,
скалярного произведения векторов
получим формулу нахождения угла:
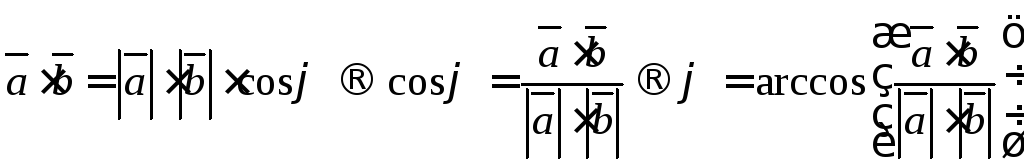 .
.
Далее, нам нужно
определить вектора, между которыми
будем искать угол.
В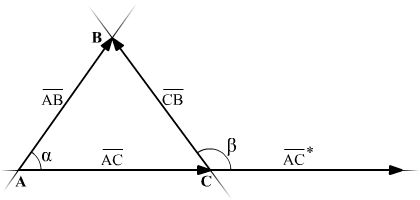 нутренний
нутренний
угол будем искать как угол между
векторами, выходящими из одной точки.
Для нахождения
внешнего угла нужно совмещать вектора,
таким образом, чтоб они выходили из
одной точки. Рисунок это поясняет.
Стоит заметить,
что
![]() ,
,
только имеют разные начальные координаты.
Находим необходимые
вектора и углы
![]()
![]()
![]()
![]()
![]()
![]()
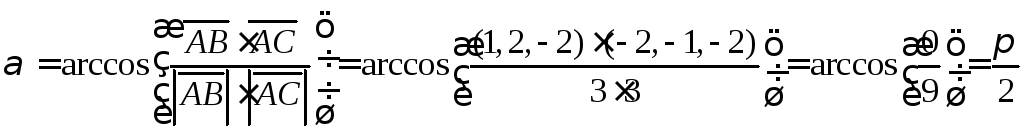
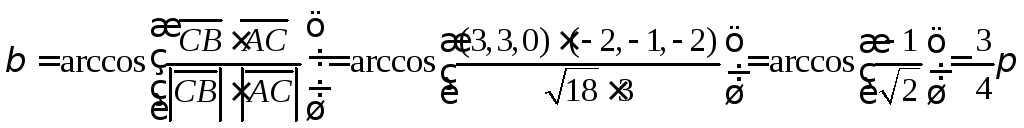
Ответ: внутренний
угол при вершине А =
![]() ,
,
внешний угол при вершине В =![]() .
.
6.9. Найти проекции векторов: и
Вспомним вектора-орты:
![]() ,
,![]() ,
,![]() .
.
Проекция находится
также из скалярного произведения
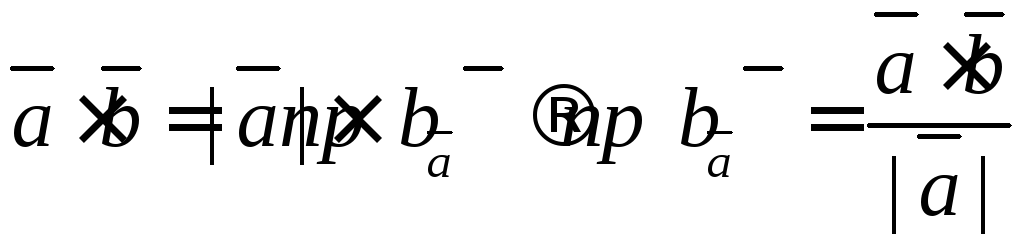 –проекция b
–проекция b
на a.
Ранее полученные
нами вектора
![]() ,
,
![]() ,
,![]()
Находим проекцию
![]()
![]()
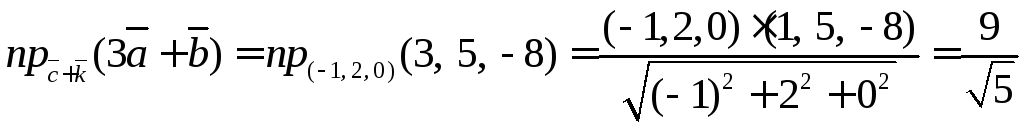
Находим вторую
проекцию
![]()
![]()
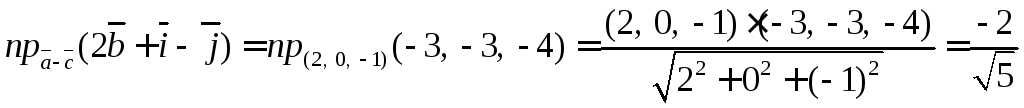
Ответ:
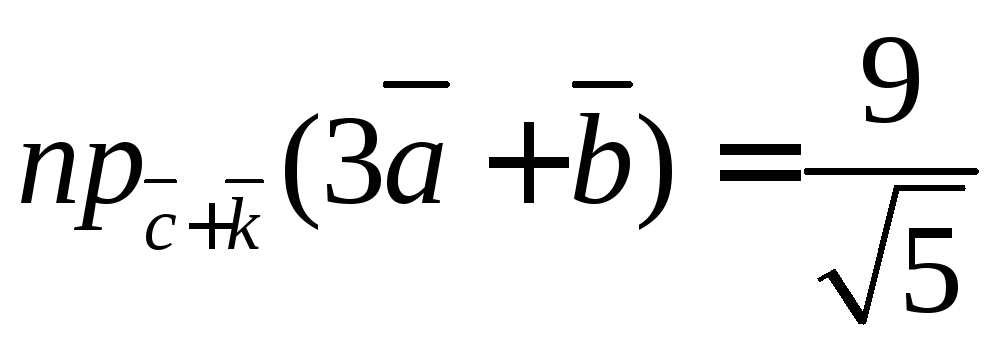 ,
,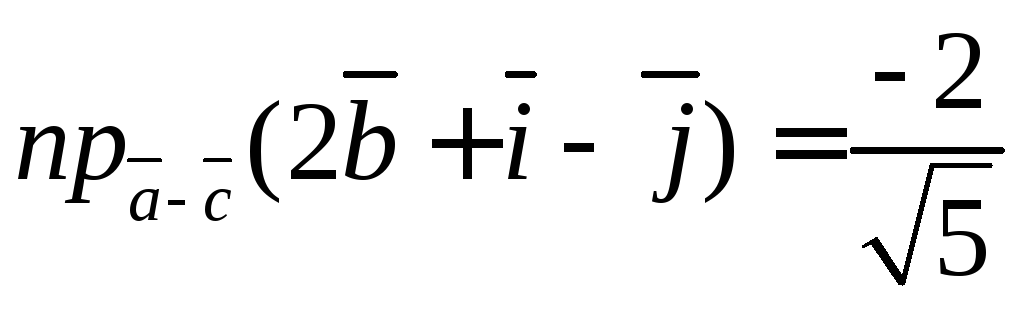
Примечание.
Знак минуса при нахождении проекции
означает то, что проекция опускается
не на сам вектор, а в противоположную
сторону, на линию на которой лежит этот
вектор.
6.10. Вычислить
![]() .
.
Выполним векторное
произведение векторов

![]()
Найдем модуль
![]()
Синус угла между
векторами найдём из определения
векторного произведения векторов
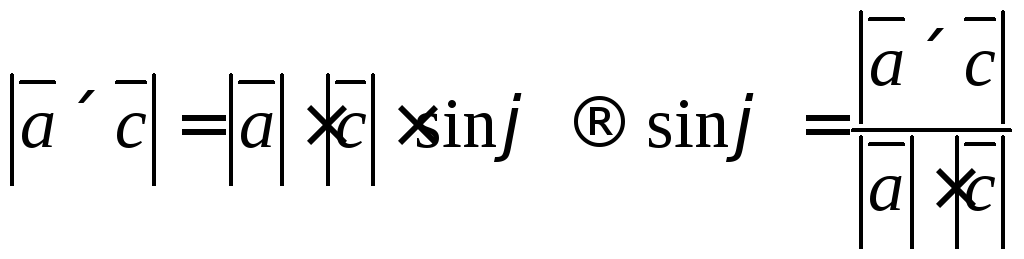
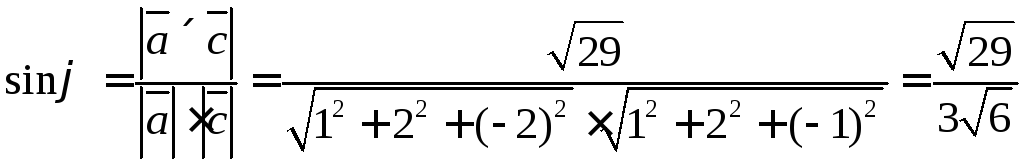
Ответ:
![]() ,
,![]() ,
,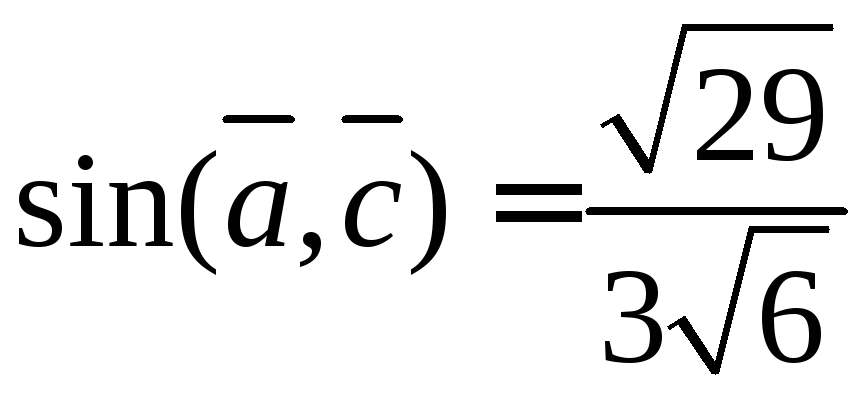 .
.
6.11. Найти площадь
треугольника ABC
и длину высоты, опушенной из точки С.
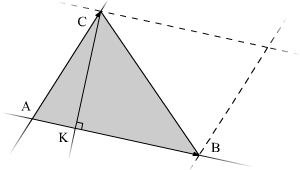
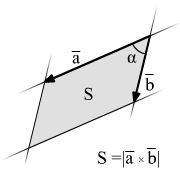
Геометрический
смысл модуля векторного произведения
состоит в том, что это площадь
параллелограмма, образованного этими
векторами. А площадь треугольника равна
половине площади параллелограмма.
![]()
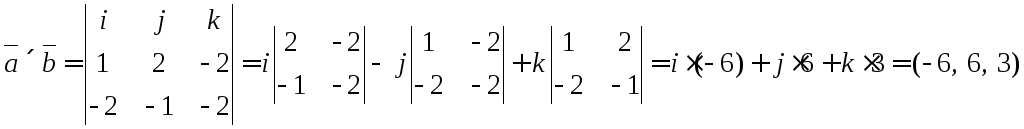
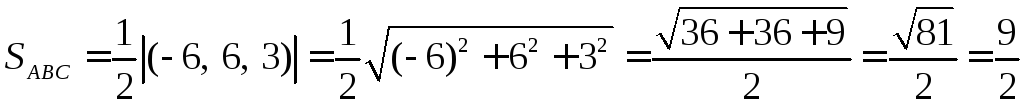
Площадь треугольника
также можно найти как произведение
высоты, на основание, делённое на два,
из этого можно вывести формулу нахождения
высоты.
![]()
Таким образом,
найдём высоту
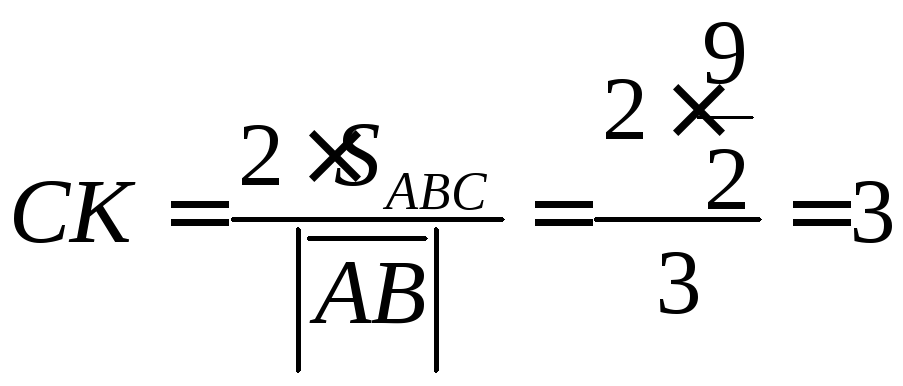
Ответ:
![]() ,
,![]() .
.
6.12. Найти
единичный вектор, перпендикулярный
векторам
![]() и
и![]() .
.
Результатом
скалярного произведения есть вектор,
который перпендикулярный двум исходным.
А единичный вектор – это вектор, делённый
на его длину.
Ранее, нами было
найдено:
![]() ,
,
![]()
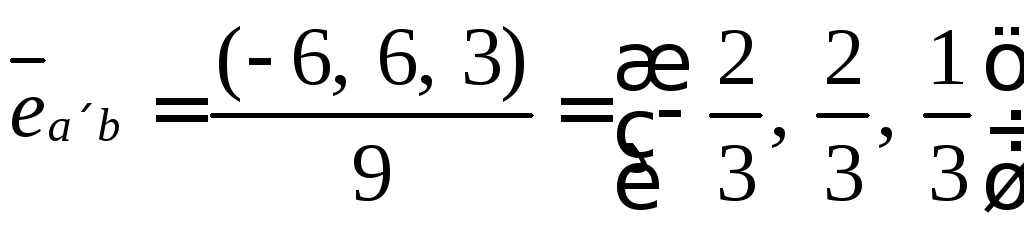
Ответ:
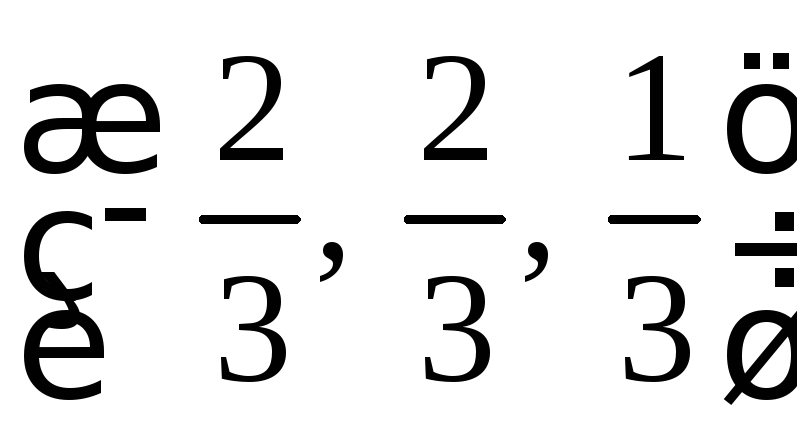 .
.
6.13. Определить
величину и направляющие косинусы момента
силы
![]() ,
,
приложенной к А относительно точки С.
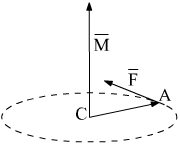
Физический смысл
векторного произведения – это момент
силы. Приведём иллюстрацию к данному
заданию.
Находим момент
силы
![]()
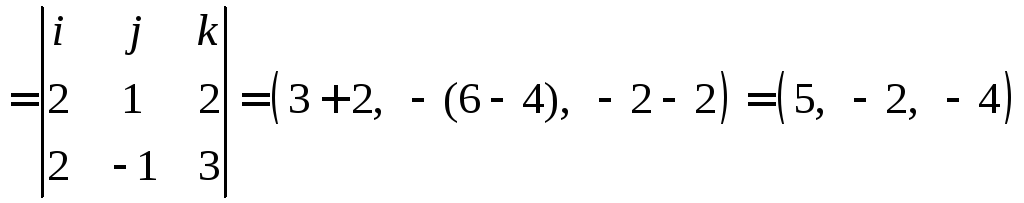
Ответ:
![]() .
.
6.14. Лежат ли
векторы
![]() ,
,![]() и
и![]() в одной плоскости? Могут ли эти векторы
в одной плоскости? Могут ли эти векторы
образовывать базис пространства? Почему?
Если могут, разложите по этому базису
вектор![]() .
.
Чтобы проверить
лежат ли вектора в одной плоскости
необходимо выполнить смешанное
произведение этих векторов.
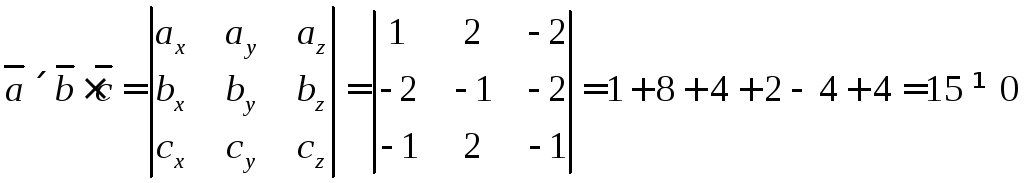
Смешанное
произведение не равно нулю, следовательно,
вектора не лежат в одной плоскости (не
компланарные) и могут образовывать
базис. Разложим
![]() по этому базису.
по этому базису.
Разложим по базису,
решив уравнение
![]()
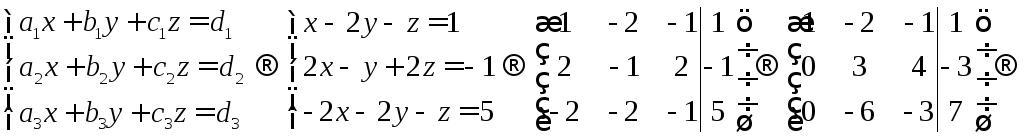
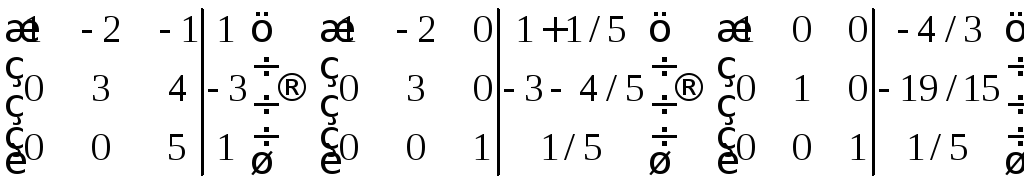
Ответ: Векторы
![]() ,
,![]() и
и![]() не лежат в одной плоскости.
не лежат в одной плоскости.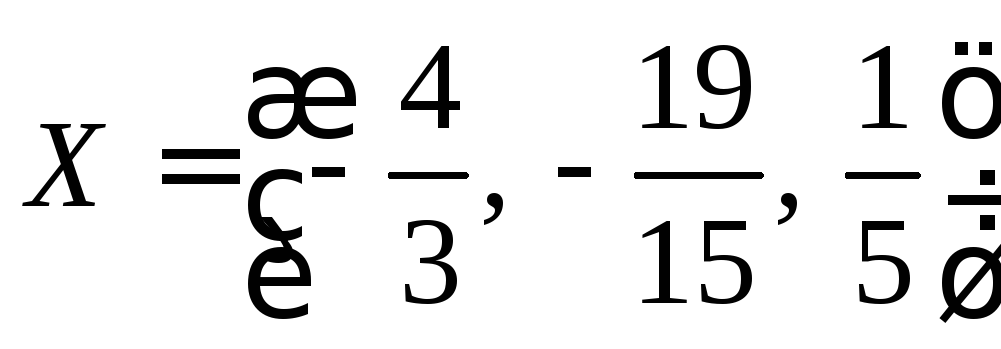 .
.
6.15. Найти
![]() .
.
Чему равен объём пирамиды с вершинами
A, B, C, D и её высота, опущенная из точки A
на основание BCD.
Г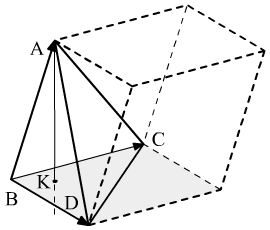 еометрический
еометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.
Объём же пирамиды
в шесть раз меньше объёма параллелепипеда.
![]()
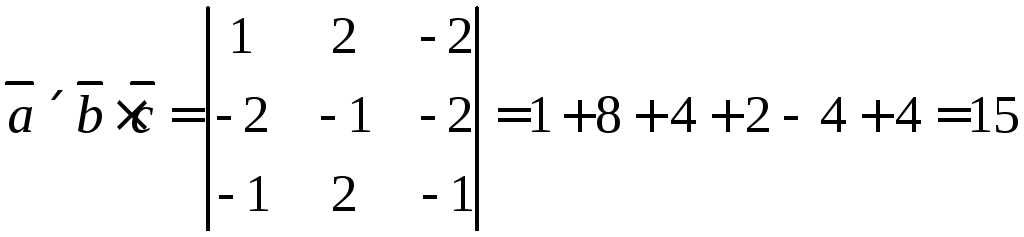
![]()
Объём пирамиды,
ещё можно найти так:
![]()
Получим формулу
нахождения высоты
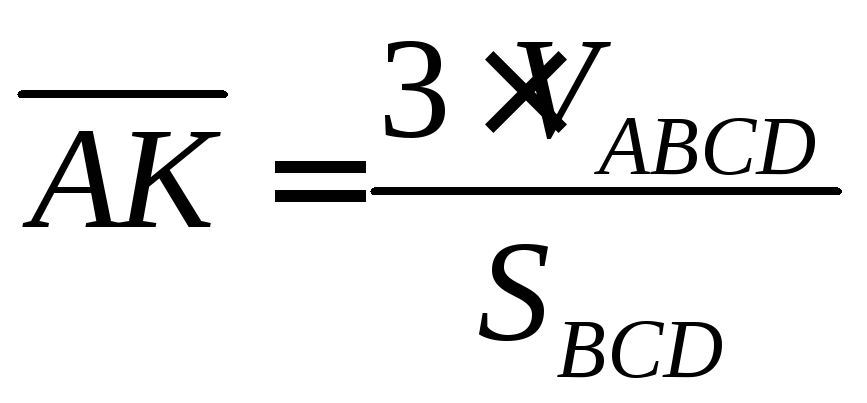
Находим
![]()
![]()
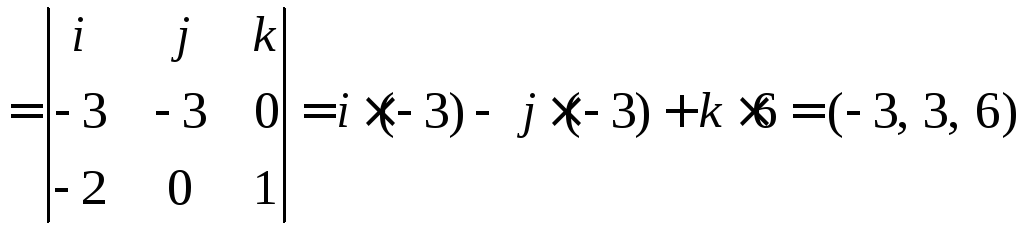
![]()
![]()
Находим высоту
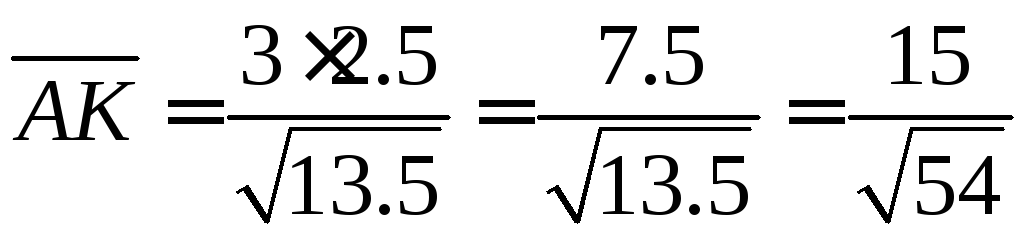
Ответ: объём = 2.5,
высота =![]() .
.
6.16. Вычислить
![]() и
и![]() .
.
![]() –над этим заданием
–над этим заданием
предлагаем вам подумать самим.
![]() –выполним
–выполним
произведение.
Ранее было получено
![]()
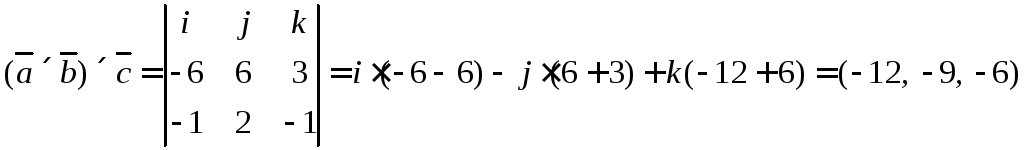
Ответ:
![]() .
.
6.17. Вычислить
![]()
Выполним действия
по частям

1)
![]()
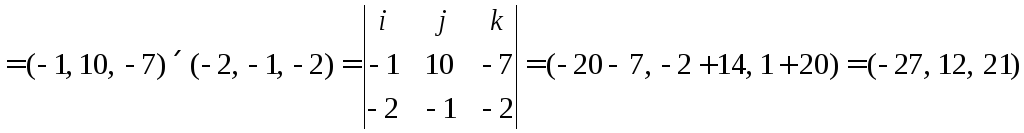 2)
2)
![]()
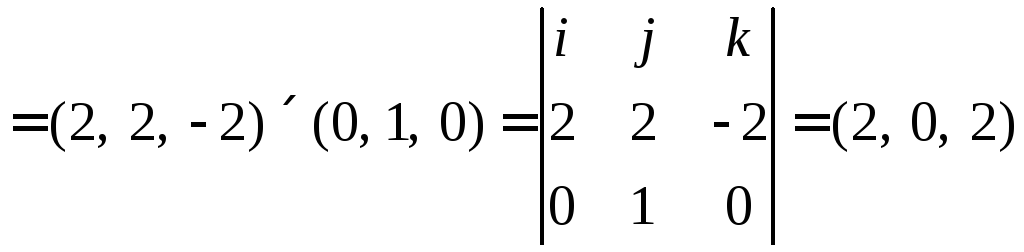
3)
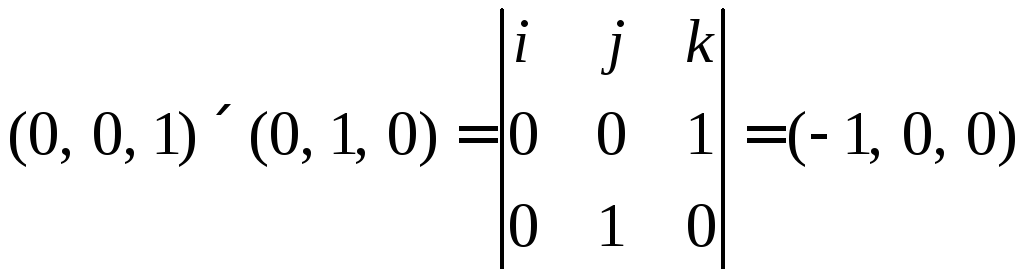
4)
![]()
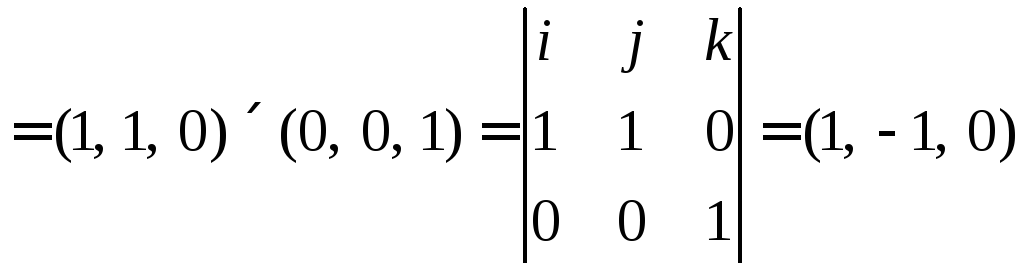
5)
![]()
Суммируем полученные
значения
![]()
Ответ:
![]() .
.
6.18. Найти вектор
![]() ,
,
зная, что он перпендикулярен векторам![]() и
и![]() ,
,
а его проекция на вектор![]() равна 5.
равна 5.
Разобьем данную
задачу на две подзадачи
1) Найдём вектор,
перпендикулярный векторам
![]() и
и![]() произвольной длинны.
произвольной длинны.
Перпендикулярный
вектор мы получим в результате векторного
произведения
Ранее, нами было
найдено:
![]()
Искомый вектор
отличается лишь длинной, от полученного
![]()
2) Найдем
![]() через уравнение
через уравнение
![]()
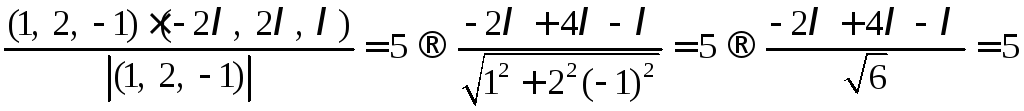
![]()
Ответ:
![]()
6.19. Найти вектор
![]() ,
,
удовлетворяющий условиям![]() ,
,![]() ,
,![]() .
.
Рассмотрим более
детально данные условия.
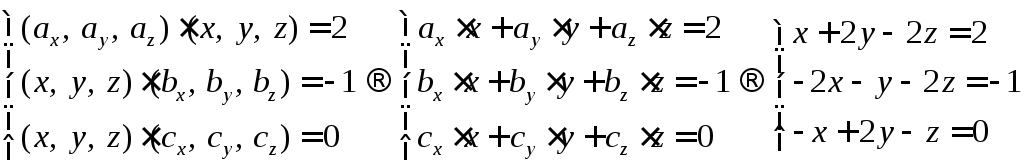
Это система линейных
уравнений. Составим и решим данную
систему.
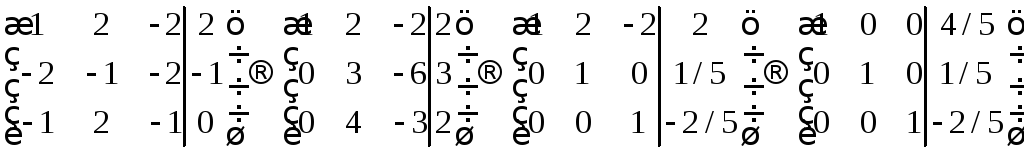
Ответ:

6.20. Определить
координаты какого-либо вектора
![]() ,
,
компланарного с векторами![]() и
и![]() ,
,
и перпендикулярного вектору![]() .
.
В данном задании
два условия: компланарность векторов
и перпендикулярность, выполним сначала
первое условие, а потом второе.
1) Если вектора
компланарны, значит их смешанное
произведение равно нулю.
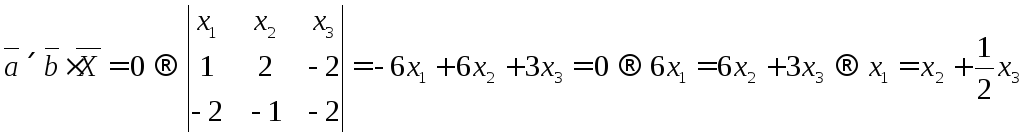 Отсюда
Отсюда
получим некоторую зависимость координат
вектора
![]()
Найдем вектор
![]() .
.
![]()
2) Если вектора
перпендикулярны, значит их скалярное
произведение равно нулю
![]()
![]()
Мы получили вторую
зависимость координат искомого вектора
![]()
Для любого значения
![]() вектор будет удовлетворять условиям.
вектор будет удовлетворять условиям.
Подставим![]() .
.
Ответ:
![]() .
.
Аналитическая
геометрия
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2016959.94 Кб5PT.pdf
- #
Загрузить PDF
Загрузить PDF
Вектор является геометрическим объектом, он характеризуется направлением и величиной. Его можно представить в виде отрезка с начальной точкой на одном конце и стрелкой на втором, при этом длина отрезка соответствует величине вектора, а стрелка указывает на его направление. Нормирование вектора является стандартной операцией в математике, на практике она используется в компьютерной графике.
-

1
Определим единичный вектор. Единичным вектором вектора A называется такой вектор, направление которого совпадает с направлением вектора A, а длина равна 1. Можно строго доказать, что каждый вектор имеет один и только один соответствующий ему единичный вектор.
-

2
Узнайте, что такое нормирование вектора. Это процедура нахождения единичного вектора для заданного вектора A.
-

3
Определим связанный вектор. В декартовой системе координат связанный вектор выходит из начала координат, то есть для 2-мерного случая из точки (0,0). Это позволяет задавать вектор лишь координатами его конечной точки.
-

4
Освойте запись векторов. Если ограничиться связанными векторами, то в записи A = (x, y) пара координат (x,y) указывает на конечную точку вектора A.
Реклама
-

1
Установите, что известно. Из определения единичного вектора мы знаем, что начальная точка и направление этого вектора совпадают с аналогичными характеристиками вектора A. Кроме того, длина единичного вектора равна 1.
-

2
Определите, что необходимо найти. Требуется найти координаты конечной точки единичного вектора.
Реклама
- Найдите конечную точку единичного вектора для вектора A = (x, y). Единичный вектор и вектор А образуют подобные прямоугольные треугольники, поэтому конечная точка единичного вектора будет иметь координаты (x/c, y/c), где необходимо найти c. Кроме того, длина единичного вектора равна 1. Таким образом, согласно теореме Пифагора имеем: [x^2/c^2 + y^2/c^2]^(1/2) = 1 -> [(x^2 + y^2)/c^2]^(1/2) -> (x^2 + y^2)^(1/2)/c = 1 -> c = (x^2 + y^2)^(1/2). То есть единичный вектор вектора A = (x, y) задается выражением u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)).

- Предположим, что вектор A начинается в начале координат, а его конечная точка расположена в (2,3), то есть A = (2,3). Найдем единичный вектор: u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)) = (2/(2^2 + 3^2)^(1/2), 3/(2^2 + 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Таким образом, нормирование вектора A = (2,3) приводит к вектору u = (2/(13^(1/2)), 3/(13^(1/2))).

- Обобщим формулу для нормирования вектора на случай пространства с произвольным числом измерений. Чтобы нормировать вектор A (a, b, c, …), необходимо найти вектор u = (a/z, b/z, c/z, …), где z = (a^2 + b^2 + c^2 …)^(1/2).
Об этой статье
Эту страницу просматривали 29 237 раз.
