1.5.5. Как найти единичный вектор?
Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами
координатные векторы 
и 
, 
и противоположно направленные им векторы, например:
То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам 
.
А теперь рассмотрим произвольный вектор 
либо
и поставим задачу найти
единичный вектор 
, коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора 
разделить на его длину:
либо 
,
или, что то же самое – умножить каждую координату вектора 
на 
. То
есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный
вектор очевиден:
либо 
Задача 10
Найти единичные векторы, коллинеарные векторам а) 
, б) 
. Выполнить проверку.
Решение: а) вычислим длину вектора 
и найдём
сонаправленный единичный вектор:
, от иррациональности в знаменателе (корня) тут
обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
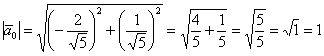, что и требовалось проверить.
Второй вектор очевиден: 
, как очевидна и его
длина 
.
Ответ: 
Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)
самостоятельно.
1.5.6. Деление отрезка в данном отношении
1.5.4. Действия с векторами в координатах
| Оглавление |
Автор: Aлeксaндр Eмeлин
Как найти вектор коллинеарный вектору
Формула
Примеры нахождения коллинеарного вектора
Подставим координаты заданных векторов в это равенство и найдем значение $m$:
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac<3><2>=1,5$$
А тогда значения неизвестных параметров $m$ и $n$ находим из равенств
$$frac<3>=2 Rightarrow m=6$$ $$frac<1>=2 Rightarrow n=frac<1><2>=0,5$$
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Как найти вектор, коллинеарный вектору
Вы будете перенаправлены на Автор24
Понятие коллинеарности векторов
Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Обозначение: $overline$ – вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $overline$ (рис. 1).
Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Далее рассмотрим, какие векторы называются коллинеарными.
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).
Готовые работы на аналогичную тему
Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ
Также введем определение векторного произведения, которое будет нам необходимо далее.
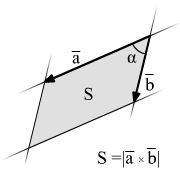
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Чтобы найти векторное произведение, будем пользоваться формулой
Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам
Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.
Доказательство.
Необходимость: Пусть нам даны векторы $overline<α>$ и $overline<β>$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Так как векторы $overline<α>$ и $overline<β>$ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $overline<α>↑↑overline<β>$. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $roverline<α>$ и $overline<β>$ были равны между собой. По определению умножения векторов на число, получим, что $roverline<α>↑↑overline<β>$. Но тогда, по определению равенства векторов, получим, что $roverline<α>=overline<β>$. Из этого равенства получим, что
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $overline<α>$ и $overline<β>$ будут коллинеарными.
Из данных равенств следует, что $roverline<α>=overline<β>$.
Имеются два случая:
В этом случае, по определению умножения вектора на число, получим, что $roverline<α>↑↓overline<β>$.
В этом случае получим, что $roverline<α>↑↑overline<β>$.
Тогда, в обоих случаях получаем доказательство коллинеарности векторов $overline<α>$ и $overline<β>$.
Ответ: теорема доказана.
Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.
Доказательство.
Разложим второй вектор:
Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.
Признаки и свойства коллинеарности векторов через их произведение
Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.
Доказательство.
Необходимость: Пусть нам даны векторы $overline<α>$ и $overline<β>$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать, что $overline<α>хoverline<β>=overline<0>$.
Так как векторы коллинеарны, то, по теореме 1, верны равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Найдем $overline<α>хoverline<β>$ по формуле
Достаточность: Пусть верно равенство $overline<α>хoverline<β>=overline<0>$, докажем, что векторы $overline<α>$ и $overline<β>$ коллинеарны. Так как векторное произведение равняется $overline<0>$, то его длина также равняется нулю. Следовательно, угол между $overline<α>$ и $overline<β>$ равняется $180^circ$ или $0^circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 07 2022
Как найти коллинеарный единичный вектор
Как найти вектор, коллинеарный вектору
Вы будете перенаправлены на Автор24
Понятие коллинеарности векторов
Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Иначе одной маленькой буквой: $overline$ (рис. 1).
Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Далее рассмотрим, какие векторы называются коллинеарными.
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).
Готовые работы на аналогичную тему
Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ
Также введем определение векторного произведения, которое будет нам необходимо далее.
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Чтобы найти векторное произведение, будем пользоваться формулой
Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам
Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.
Доказательство.
Необходимость: Пусть нам даны векторы $overline $ и $overline $, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Так как векторы $overline $ и $overline $ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $overline ↑↑overline $. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $roverline $ и $overline $ были равны между собой. По определению умножения векторов на число, получим, что $roverline ↑↑overline $. Но тогда, по определению равенства векторов, получим, что $roverline =overline $. Из этого равенства получим, что
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $overline $ и $overline $ будут коллинеарными.
Из данных равенств следует, что $roverline =overline $.
Имеются два случая:
В этом случае, по определению умножения вектора на число, получим, что $roverline ↑↓overline $.
В этом случае получим, что $roverline ↑↑overline $.
Тогда, в обоих случаях получаем доказательство коллинеарности векторов $overline $ и $overline $.
Ответ: теорема доказана.
Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.
Доказательство.
Разложим второй вектор:
Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.
Признаки и свойства коллинеарности векторов через их произведение
Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.
Доказательство.
Необходимость: Пусть нам даны векторы $overline $ и $overline $, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать, что $overline хoverline =overline $.
Так как векторы коллинеарны, то, по теореме 1, верны равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Найдем $overline хoverline $ по формуле
Достаточность: Пусть верно равенство $overline хoverline =overline $, докажем, что векторы $overline $ и $overline $ коллинеарны. Так как векторное произведение равняется $overline $, то его длина также равняется нулю. Следовательно, угол между $overline $ и $overline $ равняется $180^circ$ или $0^circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 19 07 2022
Как найти вектор коллинеарный вектору
Формула
Примеры нахождения коллинеарного вектора
Подставим координаты заданных векторов в это равенство и найдем значение $m$:
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac =1,5$$
А тогда значения неизвестных параметров $m$ и $n$ находим из равенств
$$frac =2 Rightarrow m=6$$ $$frac =2 Rightarrow n=frac =0,5$$
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Все еще сложно?
Наши эксперты помогут разобраться
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = и b = . Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
Для этого найдем ненулевой компонент вектора a в данном случае это ay . Если вектора колинеарны то
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Так как b = n a , то вектора a и b коллинеарны.
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
| 3 | = | 2 | = | m |
| 9 | n | 12 |
Из этого соотношения получим два уравнения:
Решим эти уравнения:
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
[spoiler title=”источники:”]
http://spravochnick.ru/geometriya/vektory/kak_nayti_vektor_kollinearnyy_vektoru/
http://b4.cooksy.ru/articles/kak-nayti-kollinearnyy-edinichnyy-vektor
[/spoiler]
Единичный вектор
находится:
,
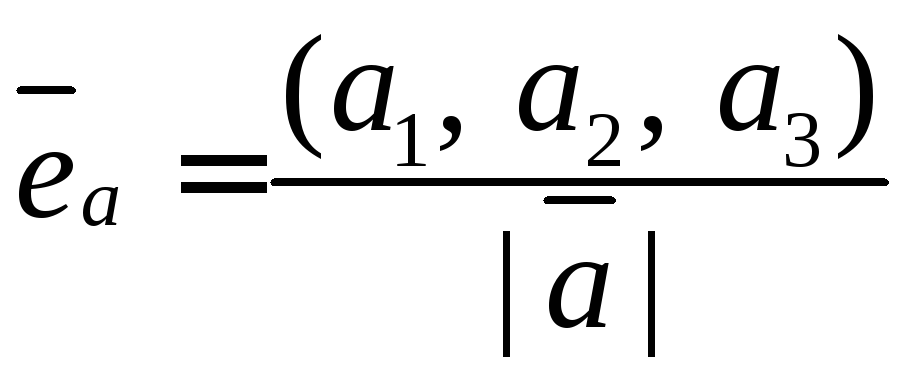где
– модуль вектора.
Находим
тогда
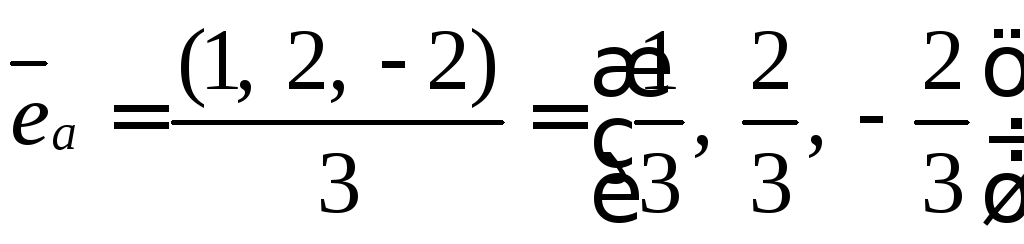
Ответ:
.
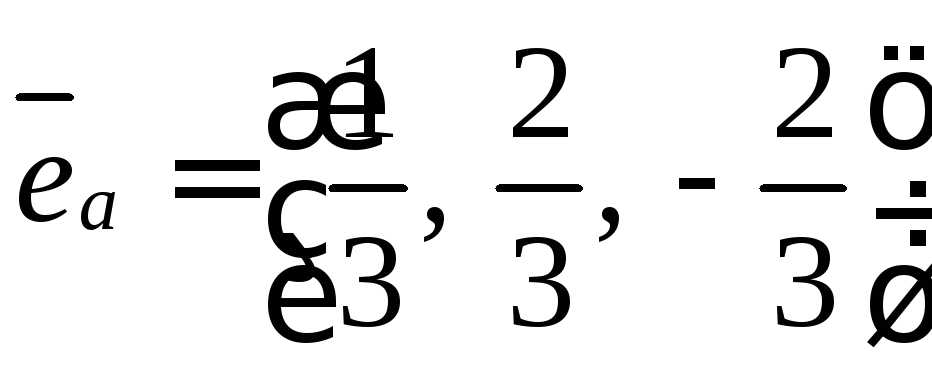Примечание.
Координаты единичного вектора должны
быть не больше единицы.
6.3. Найти длину
и направляющие косинусы вектора
.
Сравните с ответом в предыдущем пункте.
Сделайте выводы.
Длина вектора –
это есть его модуль:
,
а направляющие косинусы мы можем найти
по формуле одного из способов задания
векторов:
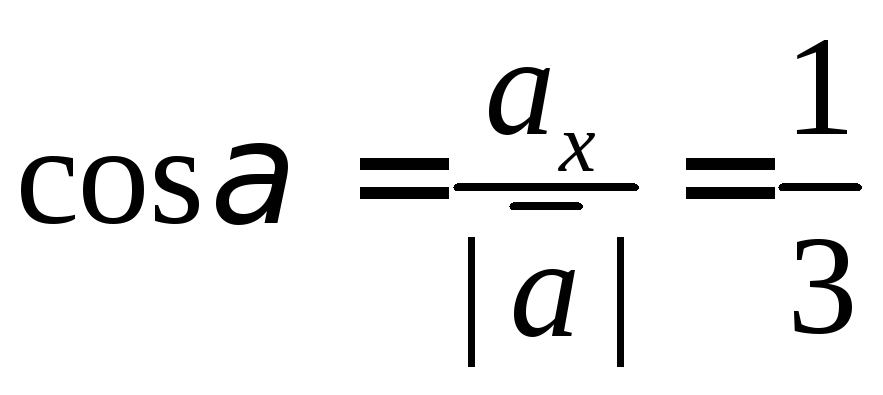
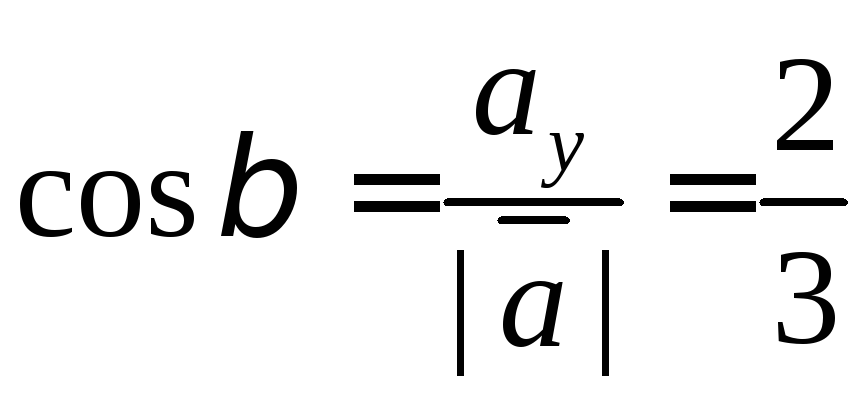
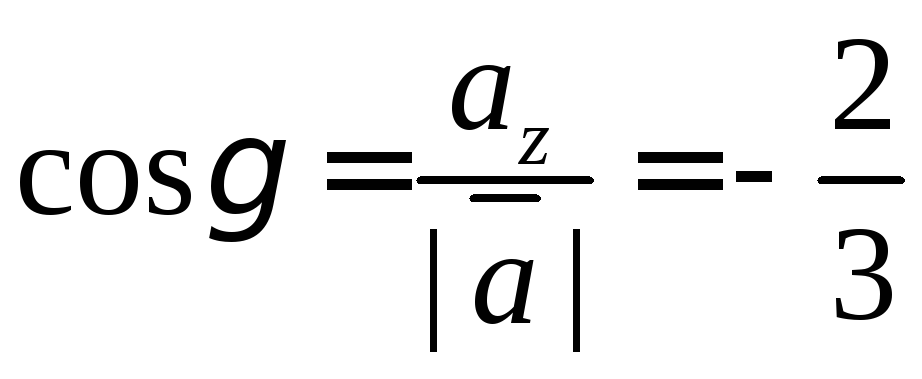
Из полученного мы
видим, что направляющие косинусы это и
есть координаты единичного вектора.
Ответ:
,
,
,
.
6.4. Найти
.
Необходимо выполнить
действия умножения вектора на число,
сложения и модуль.
Почленно перемножаем
координаты векторов на число.
Почленно складываем
координаты векторов.
Находим модуль
вектора.
Ответ:
6.5. Определить
координаты вектора
,
коллинеарного вектору
,
зная, что
и он направлен в сторону, противоположную
вектору
.
Вектор
коллинеарен вектору
,
значит, его единичный вектор равен
единичному вектору
только со знаком минус, т.к. направлен
в противоположную сторону.
Единичный вектор
имеет длину равную 1, значит, если его
умножить на 5, то его длинна будет равна
пяти.
Находим
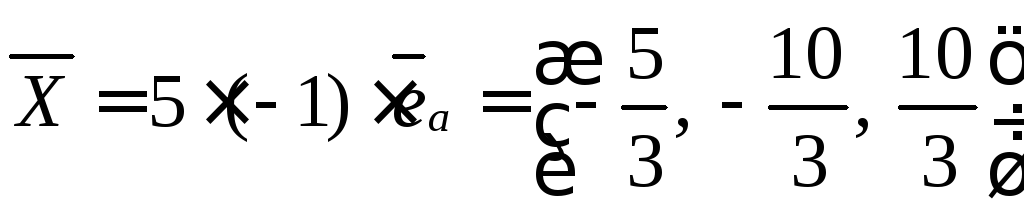
Ответ:
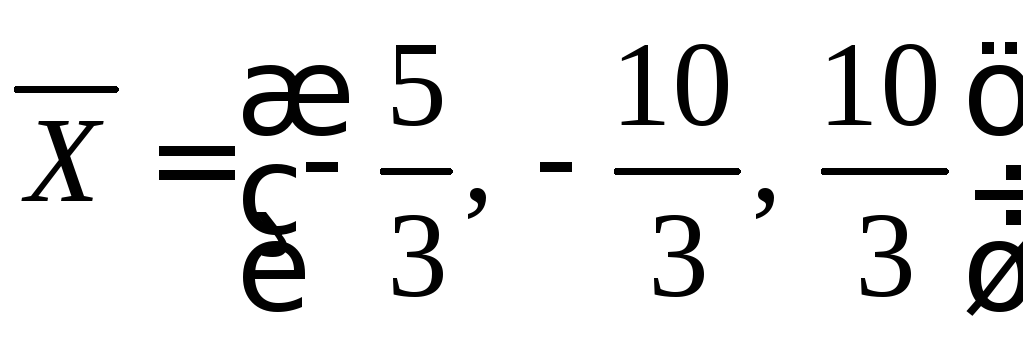
6.6. Вычислить
скалярные произведения
и
.
Перпендикулярны ли векторы
и
,
и
между собой?
Выполним скалярное
произведение векторов.
Если вектора
перпендикулярны, их скалярное произведение
равно нулю.
М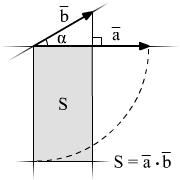
ы
видим, что в нашем случае вектора
и
перпендикулярны.
Ответ:
,
,
векторы не перпендикулярны.
Примечание.
Геометрический смысл скалярного
произведения малоприменим на практике,
но все-таки существует. Результат такого
действия можно изобразить и вычислить
геометрически.
6.7. Найти работу,
совершённую материальной точкой к
которой приложена сила
,
при перемещении её из точки B в точку С.
Физический смысл
скалярного произведения – это работа.
Вектор силы здесь
,
вектор перемещения – это
.
А произведение этих векторов и будет
искомой работой.
Находим работу
Ответ: -3.
6.8. Найти
внутренний угол при вершине A
и внешний угол при вершине C
треугольника ABC.
Из определения,
скалярного произведения векторов
получим формулу нахождения угла:
.
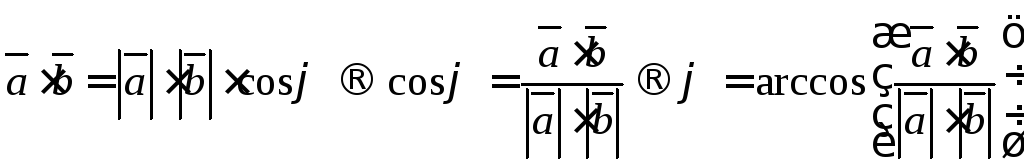Далее, нам нужно
определить вектора, между которыми
будем искать угол.
В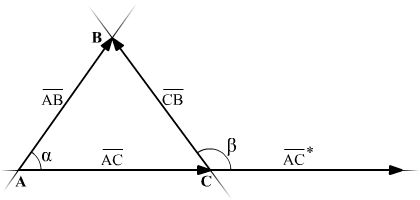
нутренний
угол будем искать как угол между
векторами, выходящими из одной точки.
Для нахождения
внешнего угла нужно совмещать вектора,
таким образом, чтоб они выходили из
одной точки. Рисунок это поясняет.
Стоит заметить,
что
,
только имеют разные начальные координаты.
Находим необходимые
вектора и углы
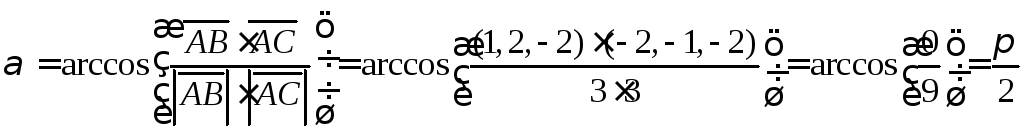
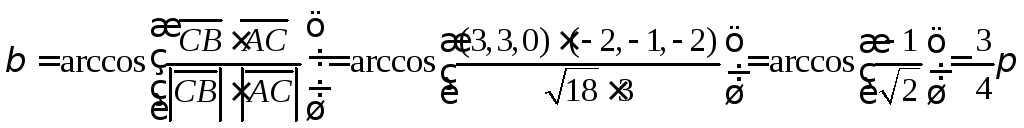
Ответ: внутренний
угол при вершине А =
,
внешний угол при вершине В =
.
6.9. Найти проекции векторов: и
Вспомним вектора-орты:
,
,
.
Проекция находится
также из скалярного произведения
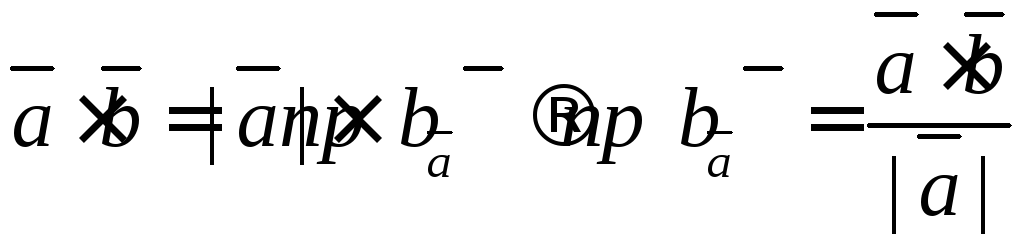–проекция b
на a.
Ранее полученные
нами вектора
,
,
Находим проекцию
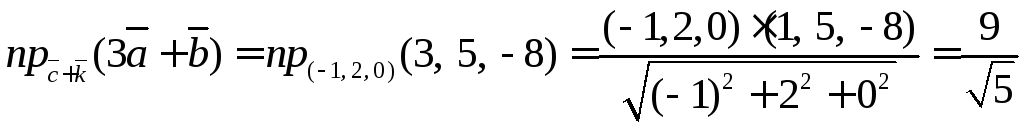
Находим вторую
проекцию
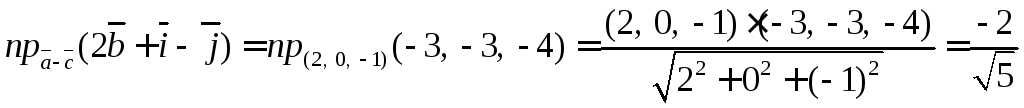
Ответ:
,
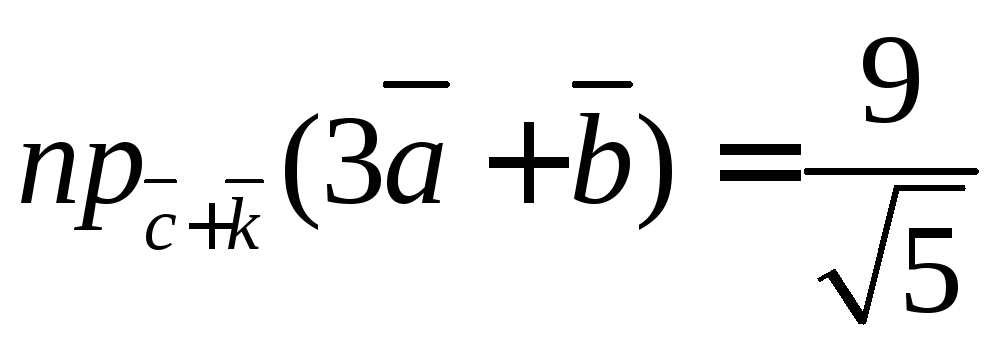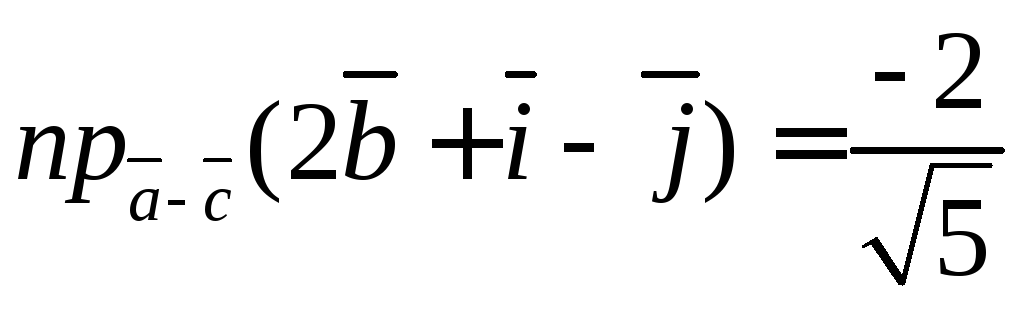
Примечание.
Знак минуса при нахождении проекции
означает то, что проекция опускается
не на сам вектор, а в противоположную
сторону, на линию на которой лежит этот
вектор.
6.10. Вычислить
.
Выполним векторное
произведение векторов
Найдем модуль
Синус угла между
векторами найдём из определения
векторного произведения векторов
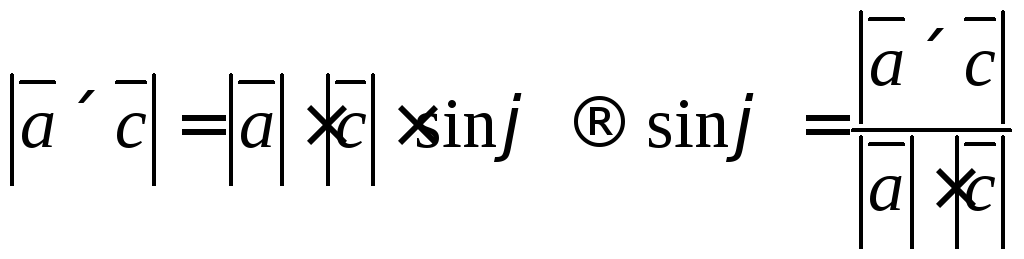
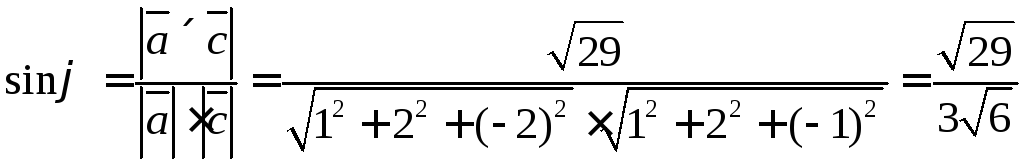
Ответ:
,
,
.
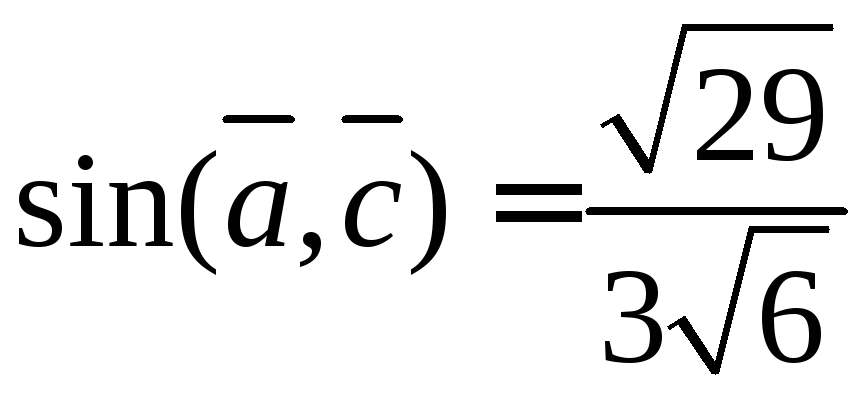6.11. Найти площадь
треугольника ABC
и длину высоты, опушенной из точки С.
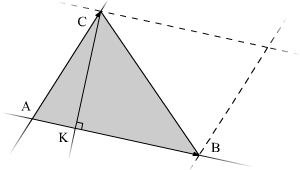
Геометрический
смысл модуля векторного произведения
состоит в том, что это площадь
параллелограмма, образованного этими
векторами. А площадь треугольника равна
половине площади параллелограмма.
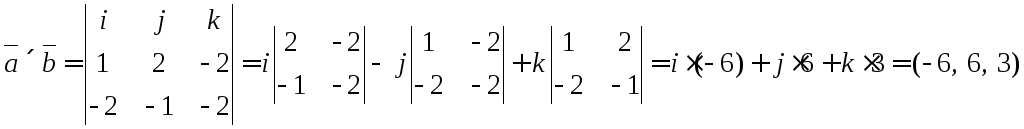
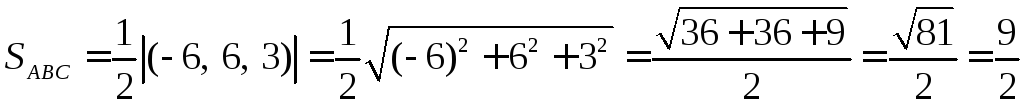
Площадь треугольника
также можно найти как произведение
высоты, на основание, делённое на два,
из этого можно вывести формулу нахождения
высоты.
Таким образом,
найдём высоту
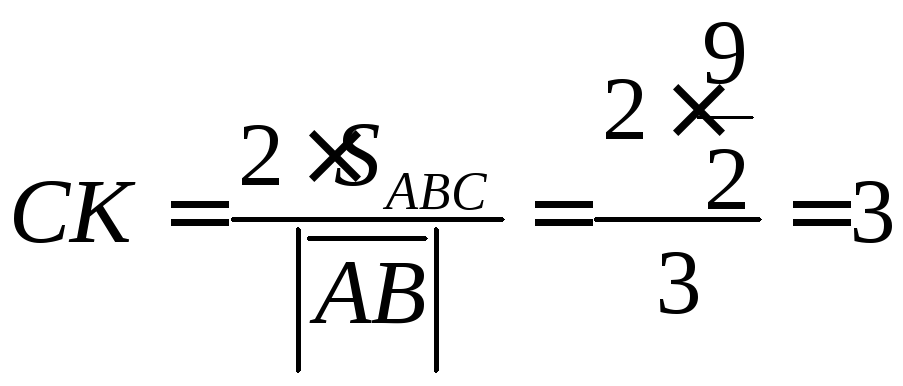
Ответ:
,
.
6.12. Найти
единичный вектор, перпендикулярный
векторам
и
.
Результатом
скалярного произведения есть вектор,
который перпендикулярный двум исходным.
А единичный вектор – это вектор, делённый
на его длину.
Ранее, нами было
найдено:
,
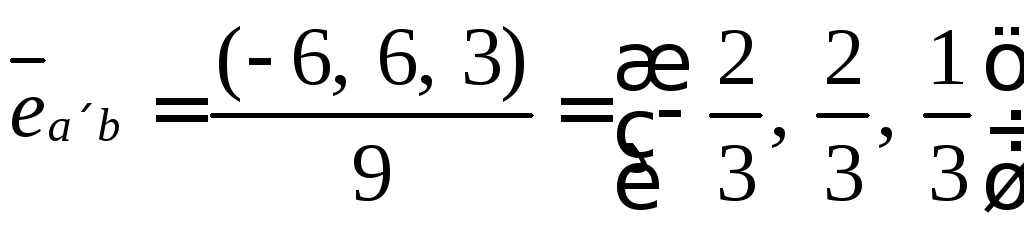
Ответ:
.
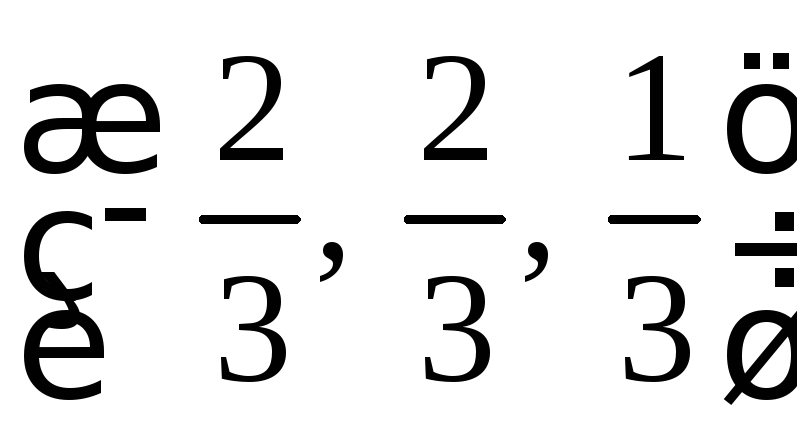6.13. Определить
величину и направляющие косинусы момента
силы
,
приложенной к А относительно точки С.
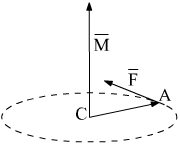
Физический смысл
векторного произведения – это момент
силы. Приведём иллюстрацию к данному
заданию.
Находим момент
силы
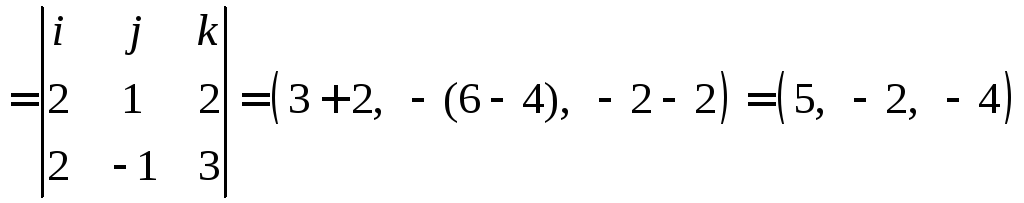
Ответ:
.
6.14. Лежат ли
векторы
,
и
в одной плоскости? Могут ли эти векторы
образовывать базис пространства? Почему?
Если могут, разложите по этому базису
вектор
.
Чтобы проверить
лежат ли вектора в одной плоскости
необходимо выполнить смешанное
произведение этих векторов.
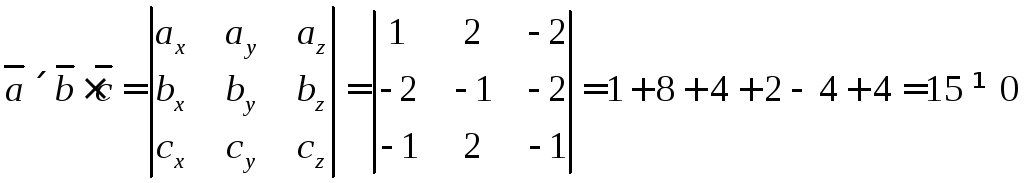
Смешанное
произведение не равно нулю, следовательно,
вектора не лежат в одной плоскости (не
компланарные) и могут образовывать
базис. Разложим
по этому базису.
Разложим по базису,
решив уравнение
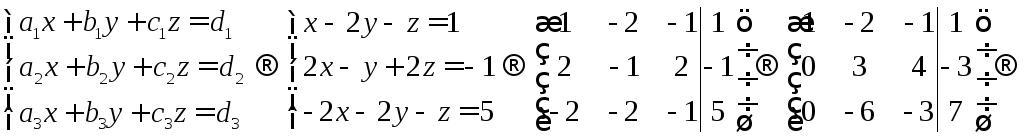
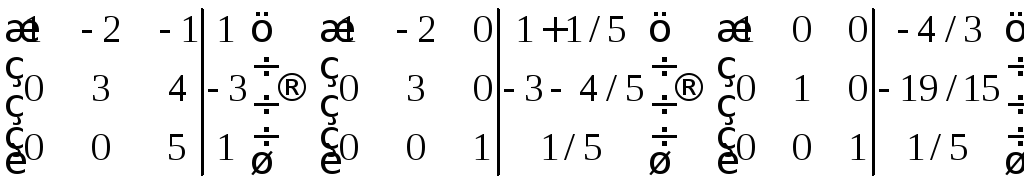
Ответ: Векторы
,
и
не лежат в одной плоскости.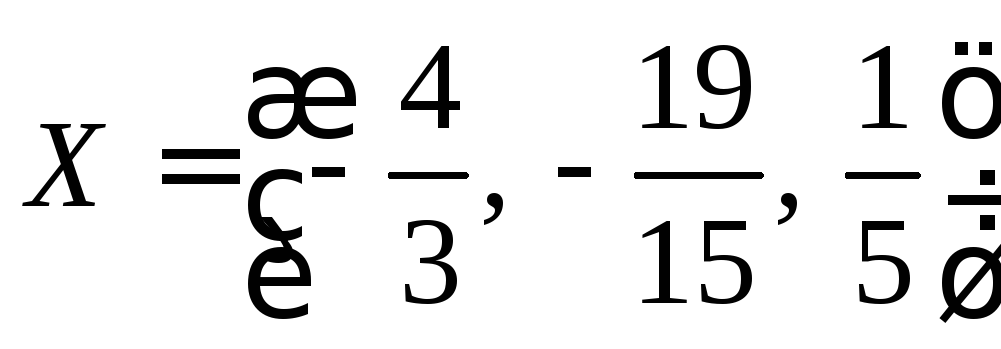
.
6.15. Найти
.
Чему равен объём пирамиды с вершинами
A, B, C, D и её высота, опущенная из точки A
на основание BCD.
Г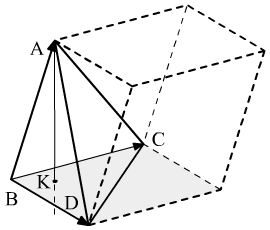
еометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.
Объём же пирамиды
в шесть раз меньше объёма параллелепипеда.
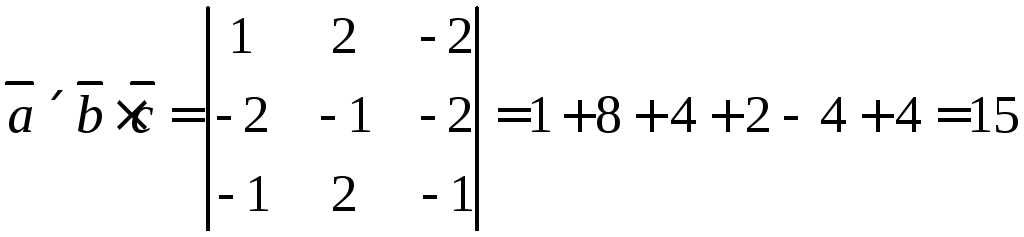
Объём пирамиды,
ещё можно найти так:
Получим формулу
нахождения высоты
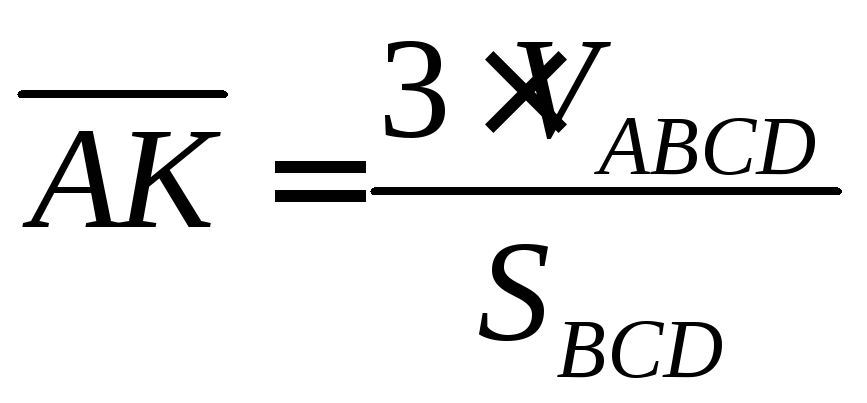
Находим
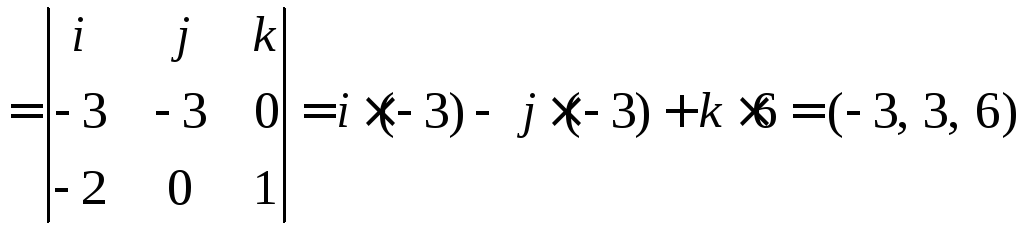
Находим высоту
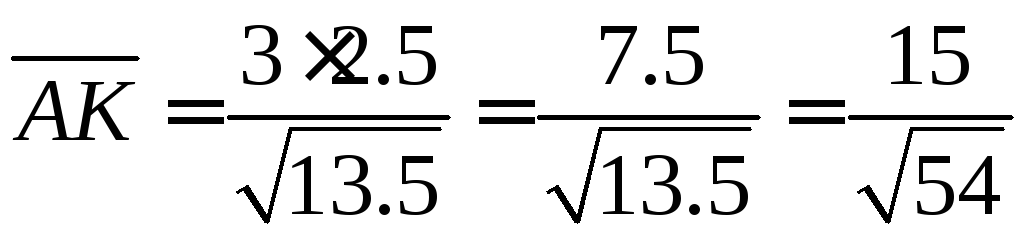
Ответ: объём = 2.5,
высота =
.
6.16. Вычислить
и
.
–над этим заданием
предлагаем вам подумать самим.
–выполним
произведение.
Ранее было получено
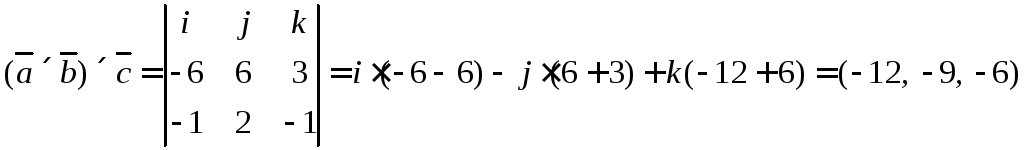
Ответ:
.
6.17. Вычислить
Выполним действия
по частям
1)
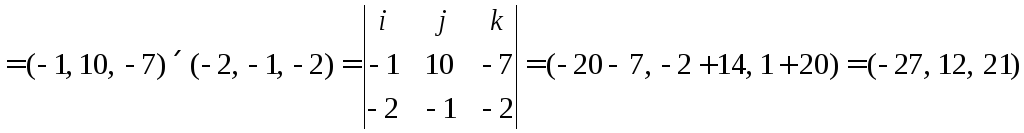2)
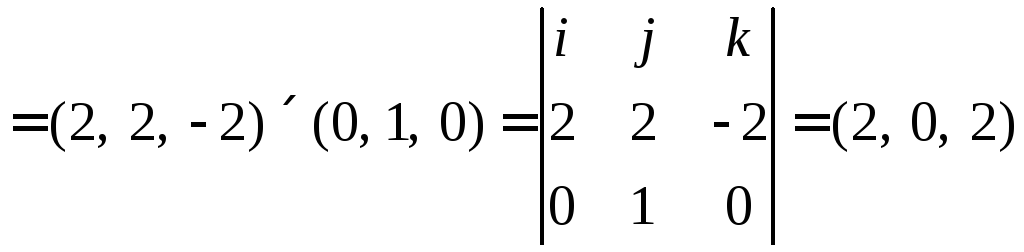
3)
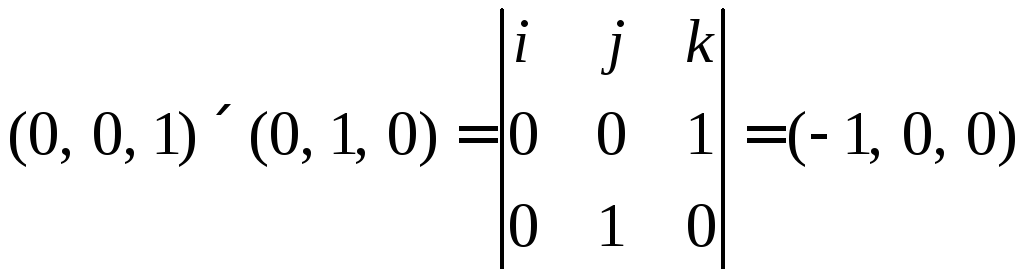
4)
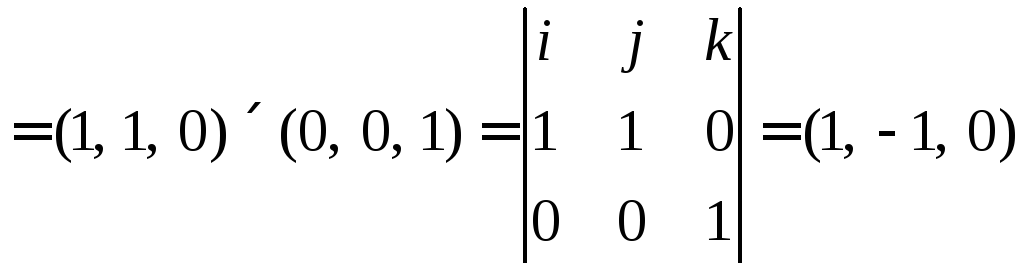
5)
Суммируем полученные
значения
Ответ:
.
6.18. Найти вектор
,
зная, что он перпендикулярен векторам
и
,
а его проекция на вектор
равна 5.
Разобьем данную
задачу на две подзадачи
1) Найдём вектор,
перпендикулярный векторам
и
произвольной длинны.
Перпендикулярный
вектор мы получим в результате векторного
произведения
Ранее, нами было
найдено:
Искомый вектор
отличается лишь длинной, от полученного
2) Найдем
через уравнение
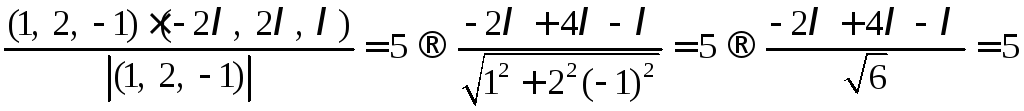
Ответ:
6.19. Найти вектор
,
удовлетворяющий условиям
,
,
.
Рассмотрим более
детально данные условия.
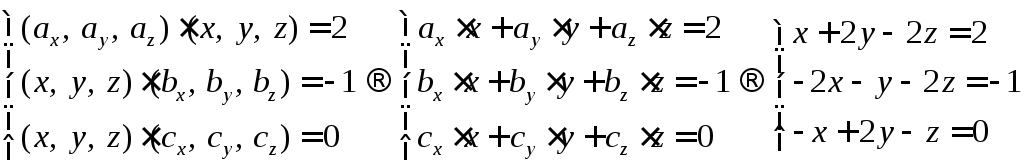
Это система линейных
уравнений. Составим и решим данную
систему.
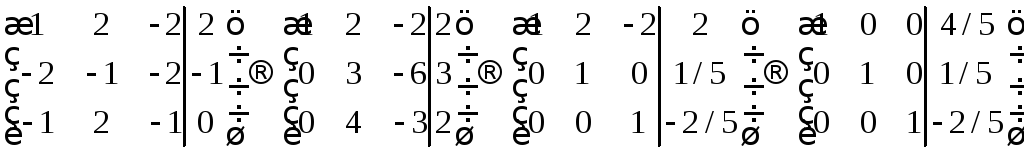
Ответ:
6.20. Определить
координаты какого-либо вектора
,
компланарного с векторами
и
,
и перпендикулярного вектору
.
В данном задании
два условия: компланарность векторов
и перпендикулярность, выполним сначала
первое условие, а потом второе.
1) Если вектора
компланарны, значит их смешанное
произведение равно нулю.
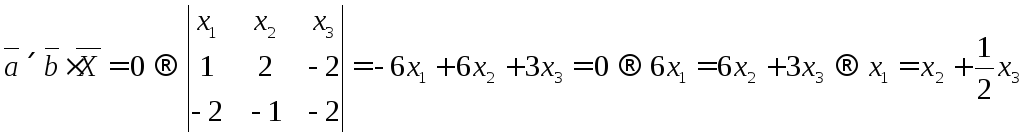Отсюда
получим некоторую зависимость координат
вектора
Найдем вектор
.
2) Если вектора
перпендикулярны, значит их скалярное
произведение равно нулю
Мы получили вторую
зависимость координат искомого вектора
Для любого значения
вектор будет удовлетворять условиям.
Подставим
.
Ответ:
.
Аналитическая
геометрия
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2016959.94 Кб5PT.pdf
- #
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b→=λ·a→ коллинеарен вектору a→ , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b→ коллинеарен вектору a→, его можно представить в виде λ·a→. Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.
Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b→=λ·a→ или a→=μ·b→, μ∈R
Координатная форма условия коллинеарности векторов
Исходные данные: вектор a→ задан в некоторой прямоугольной системе координат на плоскости и имеет координаты (ax, ay), тогда, согласно полученному выше условию, вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay).
По аналогии: если вектор a→ задан в трехмерном пространстве, то он будет представлен в виде координат a=(ax, ay, az) , а вектор b→=λ·a→ имеет координаты (λ·ax, λ·ay, λ·az). Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.
- Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay или ax=μ·bxay=μ·by
- Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: bx=λ·axby=λ·ay bz=λ·azили ax=μ·bxay=μ·by az=μ·bz
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Если ненулевые векторы a→=(ax, ay, az) и b→=(bx, by, bz) коллинеарны, то согласно векторному определению произведения a→×b→=0→. И это также соответствует равенству: i→j→k→axayazbxbybz=0→, что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b→=λ·a→ и a→=μ·b→ , где μ – произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Исходные данные: векторы a→=(3-22, 1) и b→=(12+1, 2+1) . Необходимо определить, коллинеарны ли они.
Решение
Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: bx=λ·axby=λ·ay Подставив заданные значения координат, получим: bx=λ·ax⇔12+1=λ·(3-22)⇒λ=1(2+1)·(3-22)=132-4+3-22=12-1by=λ·ay⇔2+1=12-1·1⇔(2+1)·(2-1)=1 ⇔1≡1
Т.е. b→=12-1·a→, следовательно, заданные векторы коллинеарны.
Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a→=(1, 0, -2) и b→=(-3, 0, 6) . Необходимо убедиться в их коллинеарности.
Решение
Т.к. bx=λ·axby=λ·ay bz=λ·az⇔-3=-3·10=-3·06=-3·(-2) , то верным будет равенство: b→=-3·a→ , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.
Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a→×b→=i→j→k→axayazbxbybz=i→j→k→10-2-306=i→·0·6+j→·(-2)·(-3)+k→·1·0-k→·0·(-3)-j→·1·6-i→·(-2)·0=0→Ответ: заданные векторы коллинеарны.
Исходные данные: векторы a→=(2, 7) и b→=(p, 3) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b→=λ·a→⇔bx=λ·axby=λ·ay⇔p=λ·23=λ·7
тогда λ=37, а p=λ·2⇔p=67 .
Ответ: при p=67 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Исходные данные: вектор a→=(2, -6) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.
Решение
Ответом может послужить, например, 12·a→=(1, -3) или вектор 3·a→=(6, -18) .
Ответ: вектор, коллинеарный заданному имеет координаты (1, -3).
Исходные данные: вектор a→=(3, 4, -5) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.
Решение
Вычислим длину заданного вектора по его координатам: a→=ax2+bx2+cx2=32+42+(-5)2=52 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1a→·a→=(352, 452,- 12)
Ответ: (352, 452,- 12)
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
- Формула
- Примеры нахождения коллинеарного вектора
Формула
Для того чтобы вектор
$bar{a}=left(a_{x} ; a_{y}right)$ был коллинеарным вектору $bar{b}=left(b_{x} ; b_{y}right)$ необходимо, чтобы их соответствующие
координаты были пропорциональны, то есть их координаты удовлетворяли условию
$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}$$
Если векторы заданны в пространстве своими координатами:
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right), bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, тогда условие коллинеарности имеет вид:
$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}=frac{a_{z}}{b_{z}}$$
Примеры нахождения коллинеарного вектора
Пример
Задание. Даны два вектора
$bar{a}=(2 ;-3)$ и $bar{b}=(-1 ; m)$. При каком значении
$m$ эти векторы будут коллинеарными?
Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были коллинеарными необходимо,
чтобы их координаты были пропорциональными, то есть удовлетворяли условию:
$$frac{a_{x}}{b_{x}}=frac{a_{y}}{b_{y}}$$
Подставим координаты заданных векторов в это равенство и найдем значение
$m$:
$$frac{2}{-1}=frac{-3}{m}$$
По пропорции имеем:
$$2 cdot m=(-1) cdot(-3) Rightarrow 2 cdot m=3 Rightarrow m=frac{3}{2}=1,5$$
Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными при
$m=1,5$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы два вектора
$bar{a}=(4 ;-m ; 1)$ и $bar{b}=(2 ;-3 ; n)$. При каких значениях
$m$ и
$n$ векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными?
Решение. Для того чтобы векторы
$bar{a}$ и
$bar{b}$ были коллинеарными необходимо, чтобы их координаты
были пропорциональными, то есть чтобы выполнялись следующие равенства:
$$frac{4}{2}=frac{-m}{-3}=frac{1}{n}$$
А тогда значения неизвестных параметров
$m$ и
$n$ находим из равенств
$$frac{m}{3}=2 Rightarrow m=6$$
$$frac{1}{n}=2 Rightarrow n=frac{1}{2}=0,5$$
Ответ. Векторы
$bar{a}$ и
$bar{b}$ будут коллинеарными при
$m=6$ и $n=0,5$
Читать дальше: как найти вектор перпендикулярный вектору.
