Как найти единичный вектор ортогональный векторам

Ортогональность векторов. Перпендикулярность векторов.

Вектора a и b называются ортогональными, если угол между ними равен 90°. (рис. 1).

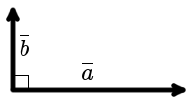рис. 1

Примеры задач на ортогональность векторов

Примеры плоских задач на ортогональность векторов

Так в случае плоской задачи для векторов a = < a_x ; a_y > и b = < b_x ; b_y > , условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) = 2 – 2 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 3 · 7 + (-1) · 5 = 21 – 5 = 16

Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 = 2 n + 4
2 n + 4 = 0
2 n = -4
n = -2

Ответ: вектора a и b будут ортогональны при n = -2.

Примеры пространственных задач на ортогональность векторов

Так в случае пространственной задачи для векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z >, условие ортогональности запишется следующим образом:

Найдем скалярное произведение этих векторов:

a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 – 2 + 0 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0

Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.

Найдем скалярное произведение этих векторов:

a · b = 2 · n + 4 · 1 + 1 · (-8)= 2 n + 4 – 8 = 2 n – 4
2 n – 4 = 0
2 n = 4
n = 2

Ответ: вектора a и b будут ортогональны при n = 2.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Ортогональные векторы и условие ортогональности

В данной статье мы расскажем, что такое ортогональные векторы, какие существуют условия ортогональности, а также приведем подробные примеры для решения задач с ортогональными векторами.

Ортогональные векторы: определение и условие

Ортогональные векторы — это векторы a ¯ и b ¯ , угол между которыми равен 90 0 .

Необходимое условие для ортогональности векторов — два вектора a ¯ и b ¯ являются ортогональными (перпендикулярными), если их скалярное произведение равно нулю.

Примеры решения задач на ортогональность векторов

Плоские задачи на ортогональность векторов

Если дана плоская задача, то ортогональность для векторов a ¯ = < a x × a y >и b ¯ = < b x × b y >записывают следующим образом:

a ¯ × b ¯ = a x × b x + a y × b y = 0

Задача 1. Докажем, что векторы a ¯ = < 1 ; 2 >и b ¯ = < 2 ; – 1 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) = 2 – 2 = 0

Ответ: поскольку произведение равняется нулю, то векторы являются ортогональными.

Задача 2. Докажем, что векторы a ¯ = < 3 ; – 1 >и b ¯ = < 7 ; 5 >ортогональны.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 3 × 7 + ( – 1 ) × 5 = 21 – 5 = 16

Ответ: поскольку скалярное произведение не равняется нулю, то и векторы не являются ортогональными.

Задача 3. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 >и b ¯ = < n ; 1 >будут ортогональными.

Как решить?

Найдем скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 = 2 n + 4 2 n + 4 = 0 2 n = – 4 n = – 2

Ответ: векторы являются ортогональными при значении n = 2 .

Примеры пространственных задач на ортогональность векторов

При решении пространственной задачи на ортогональность векторов a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >условие записывается следующим образом: a ¯ × b ¯ = a x × b x + a y × b y + a z × b z = 0 .

Задача 4. Докажем, что векторы a ¯ = < 1 ; 2 ; 0 >и b ¯ = < 2 ; – 1 ; 10 >являются ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 1 × 2 + 2 × ( – 1 ) + 0 × 10 = 2 – 2 = 0

Ответ: поскольку произведение векторов равняется нулю, то они являются ортогональными.

Задача 5. Найдем значение числа n , при котором векторы a ¯ = < 2 ; 4 ; 1 >и b ¯ = < n ; 1 ; – 8 >будут являться ортогональными.

Как решить?

Находим скалярное произведение данных векторов:

a ¯ × b ¯ = 2 × n + 4 × 1 + 1 × ( – 8 ) = 2 n + 4 – 8 = 2 n – 4 2 n – 4 = 0 2 n = 4 n = 2

Ответ: векторы a ¯ и b ¯ будут ортогональными при значении n = 2 .

Найти единичный вектор, ортогональный векторам a = i + j + 2k и b = 2i + j + k Помогите решить пожалуйста срочно надо?

Алгебра | 10 – 11 классы

Найти единичный вектор, ортогональный векторам a = i + j + 2k и b = 2i + j + k Помогите решить пожалуйста срочно надо.

Надо вычислить векторное произведение

Значит вектор с = – i + 3j – k.

Чтобы он был единичным мы должны его нормировать.

Теперь надо поделить каждую координату на длину вектора.

В итоге получим единичный вектор.

Какой угол образует единичные векторы a и b, если известно, что векторы a + 2b и 5a – 4b взаимно перпендикулярны?

Какой угол образует единичные векторы a и b, если известно, что векторы a + 2b и 5a – 4b взаимно перпендикулярны?

Определите координаты единичного вектора, сонаправленного с вектором p( – √7 ; 3)?

Определите координаты единичного вектора, сонаправленного с вектором p( – √7 ; 3).

Найти координаты вектора единичной длины , который направлен противоположно вектору ВА, если даны координаты точек А(7, 4, – 2) и В(1, 2, 1)?

Найти координаты вектора единичной длины , который направлен противоположно вектору ВА, если даны координаты точек А(7, 4, – 2) и В(1, 2, 1).

Найти (вектор m + вектор n ) ^ 2 , если векторы m и n – единичные векторы с углом 120градусов меж ними?

Найти (вектор m + вектор n ) ^ 2 , если векторы m и n – единичные векторы с углом 120градусов меж ними.

Найдите координаты единичного вектора, сонаправленного с вектором a( – 2 ; 6 ; 3)?

Найдите координаты единичного вектора, сонаправленного с вектором a( – 2 ; 6 ; 3).

Найти единичный вектор перпендикулярный плоскости 2x – y + 3z – 5 = 0?

Найти единичный вектор перпендикулярный плоскости 2x – y + 3z – 5 = 0.

Вычислить угол между векторами a = 3p + 2q и b = p + 5q, где p и q, где p и q – единичные взаимно перпендикулярные векторы Помогите кто сможет?

Вычислить угол между векторами a = 3p + 2q и b = p + 5q, где p и q, где p и q – единичные взаимно перпендикулярные векторы Помогите кто сможет.

Пожалуйста ооочень надо?

Пожалуйста ооочень надо!

Даны векторы а и б.

Б! = кореньиз2, угол между векторами а и б = 135 найти : а) координаты вектора а, если он противоположно направлен с вектором с <4 ; – 12 ; 6>б) длинну вектора а – 3б.

Дан вектор а( 2 ; 4 )найти вектор 3а?

Дан вектор а( 2 ; 4 )найти вектор 3а.

Найдите единичный вектор , коллинеарный вектору а (0 ; 4 ; 3)?

Найдите единичный вектор , коллинеарный вектору а (0 ; 4 ; 3).

На этой странице вы найдете ответ на вопрос Найти единичный вектор, ортогональный векторам a = i + j + 2k и b = 2i + j + k Помогите решить пожалуйста срочно надо?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 10 – 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Х = 57 + 22 х = 79 Вот решение.

Х = 57 + 22 = 79 вот собственно и все цифры переноси в одну сторону а х в другую с противоположными знаками.

ОДЗ : x≠15 2x – 1 = 10(x + 15) 2x – 1 = 10x + 150 2x – 10x = 150 + 1 – 8x = 151 / : ( – 8) x = – 151 / 8.

1)функция под буквой г является гиперболой ; 2)y = – 4x + 1 – 4x + 1.

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vektory/ortogonalnye-vektory-i-uslovie-ortogonalnosti/

http://algebra.my-dict.ru/q/298834_najti-edinicnyj-vektor-ortogonalnyj-vektoram-a/

[/spoiler]

$vec{a}=(2, -4, 3), vec{b}=(-4, 8, -6)$ are elements of $Bbb R^3$. Notice that $vec b = -2vec a$, thus the two vectors are collinear. So the space of vectors that are orthogonal the both of these vectors will just be the space of vectors orthogonal to the line that passes through both of them. Can you see that this space will be a plane?

So you just need to specify a plane with a vector equation. The vector equation of a plane is $vec r(s,t) = vec us + vec vt + vec c$.

We just need to find any two non-collinear vectors orthogonal to $vec a$ or $vec b$ (any we find orthogonal to one will automatically be orthogonal to the other).

So we need $(x,y,z) cdot (2,-4,3) = 2x-4y+3z=0$. Being a linear equation in three variables, we should just be able to choose two of the variables and solve for the last (though don’t choose them both zero or you’ll just end up with the zero vector which is collinear with every other vector). Let’s choose $x=3$ and $y=0$. Plugging in, we see that $z=-2$. So one vector orthogonal to $(2,-4,3)$ is $(3,0,-2)$. Now let’s choose $x=0$ and $y=3$ (You could choose the the two numbers to be whatever you like, but notice I chose them so that I’d get integer solutions because no one likes unnecessary fractions). Then $z=4$. So another vector orthogonal to $(2,-4,3)$ is $(0,3,4)$. Notice that $(3,0,-2)$ and $(0,3,4)$ are not collinear (they are not scalar multiples of each other).

So let $vec u=(3,0,-2)$ and $vec v=(0,3,4)$. Then to find $vec c$ we need any point on the line $operatorname{span}(2,-4,3)$. $(0,0,0)$ is in that span. So let $vec c = vec 0$.

Then the equation representing our plane — and thus every vector orthogonal to $vec a$ and $vec b$ — is just $$vec r(s,t) = (3,0,-2)s + (0,3,4)t$$

Надо вычислить векторное произведение

 Значит вектор с=-i+3j-k.

Чтобы он был единичным мы должны его нормировать.

 – это длина вектора с. Теперь надо поделить каждую координату на длину вектора. В итоге получим единичный вектор.

Ответ: 



1.5.5. Как найти единичный вектор?

Единичный вектор – это вектор, длина которого в ортонормированном базисе равна единице. Таковыми являются сами

координатные векторы  и ,  и противоположно направленные им векторы, например:

То, что их длина равна единице, элементарно видно не только по чертежам, но и по формулам .

А теперь рассмотрим произвольный вектор  либо

 и поставим задачу найти

единичный вектор , коллинеарный исходному. Таких векторов будет два. Чтобы найти сонаправленный единичный вектор нужно каждую координату вектора  разделить на его длину:
 либо ,
или, что то же самое – умножить каждую координату вектора   на . То

есть, деление – это частный случай умножения (осознаём и привыкаем). Противоположно направленный единичный

вектор очевиден:
 либо

Задача 10

Найти единичные векторы, коллинеарные векторам а) , б) . Выполнить проверку.

Решение: а) вычислим длину вектора  и найдём

сонаправленный единичный вектор:
, от иррациональности в знаменателе (корня) тут

обычно не избавляются. Проверка состоит в нахождении длины полученного вектора:
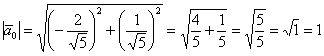, что и требовалось проверить.
Второй вектор очевиден: , как очевидна и его

длина .

Ответ:

Потребность найти единичный вектор возникает не только в геометрических задачах, и поэтому обязательно прорешайте пункт б)

самостоятельно.

1.5.6. Деление отрезка в данном отношении

1.5.4. Действия с векторами в координатах

| Оглавление |



Автор: Aлeксaндр Eмeлин